Fatigue Life Assessment of API Steel Grade X65 Pipeline Using a Modified Basquin Parameter of the Magnetic Flux Leakage Signal
Abstract
:1. Introduction
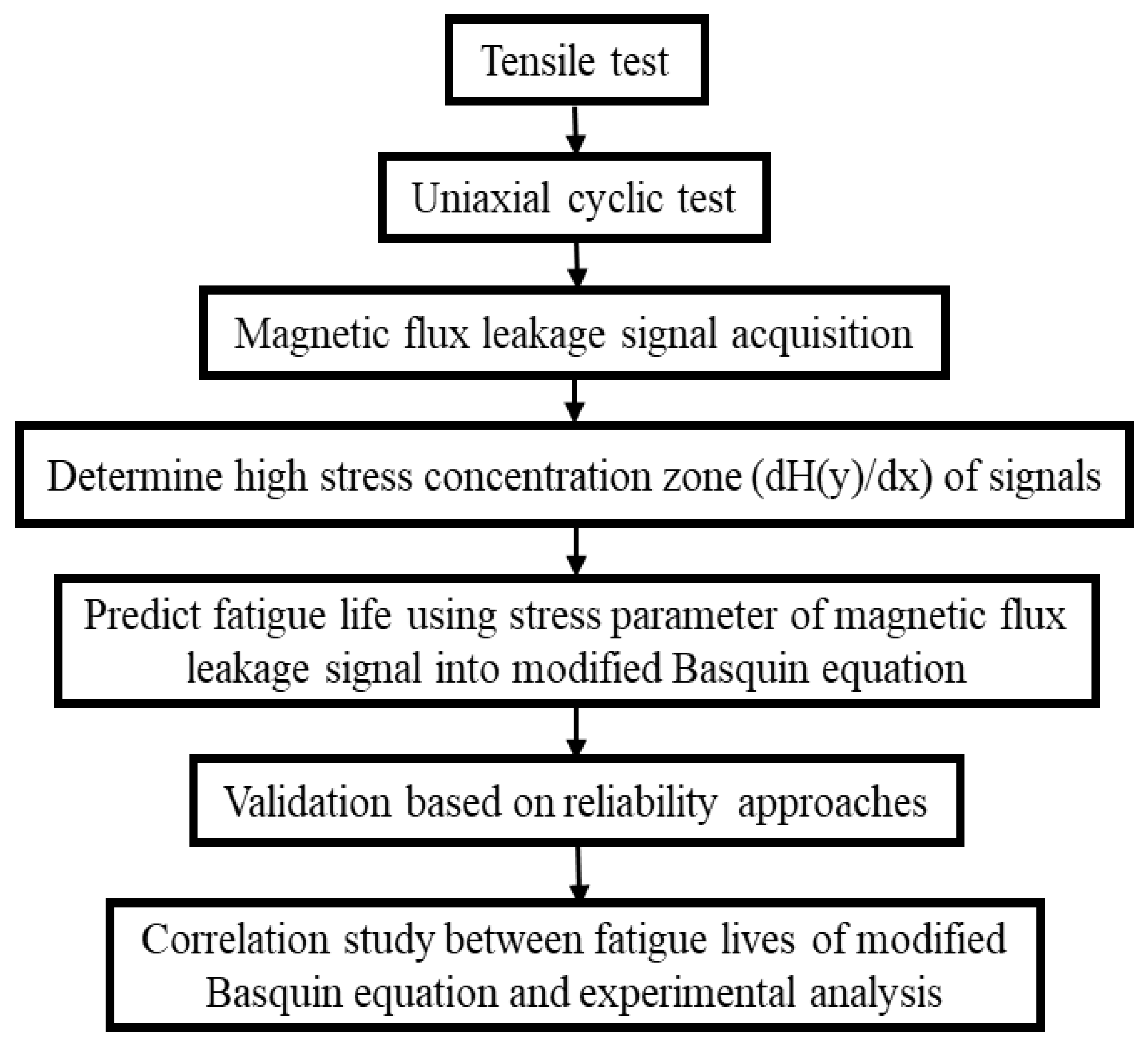
2. Materials and Methods
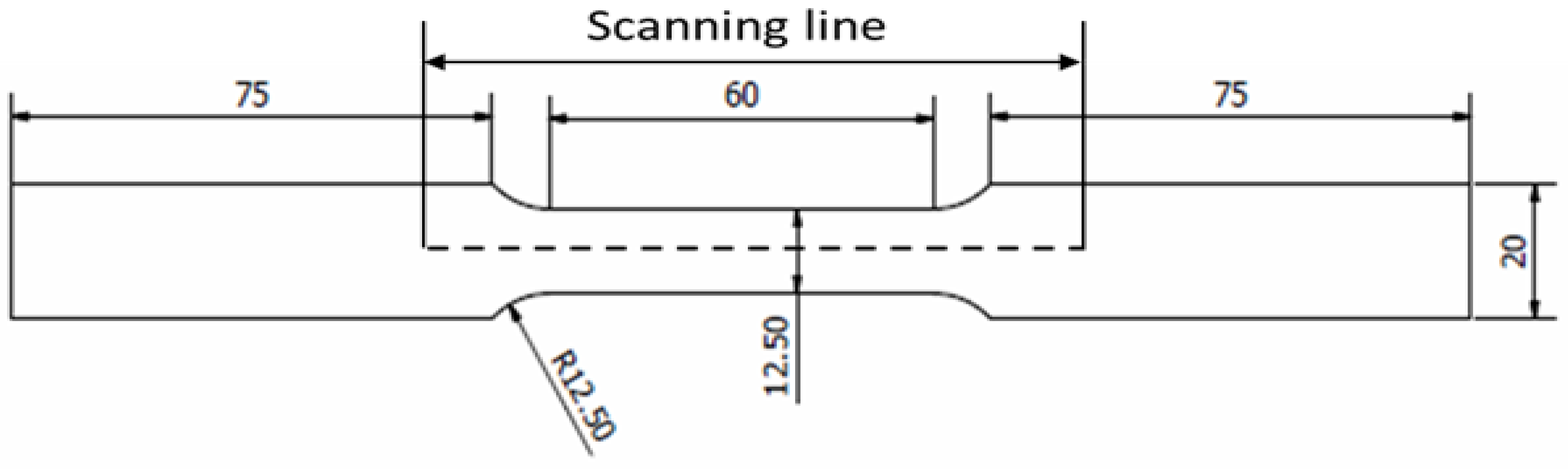
2.1. Tensile and Cyclic Test
2.2. The Acquisition of Magnetic Flux Leakage Data
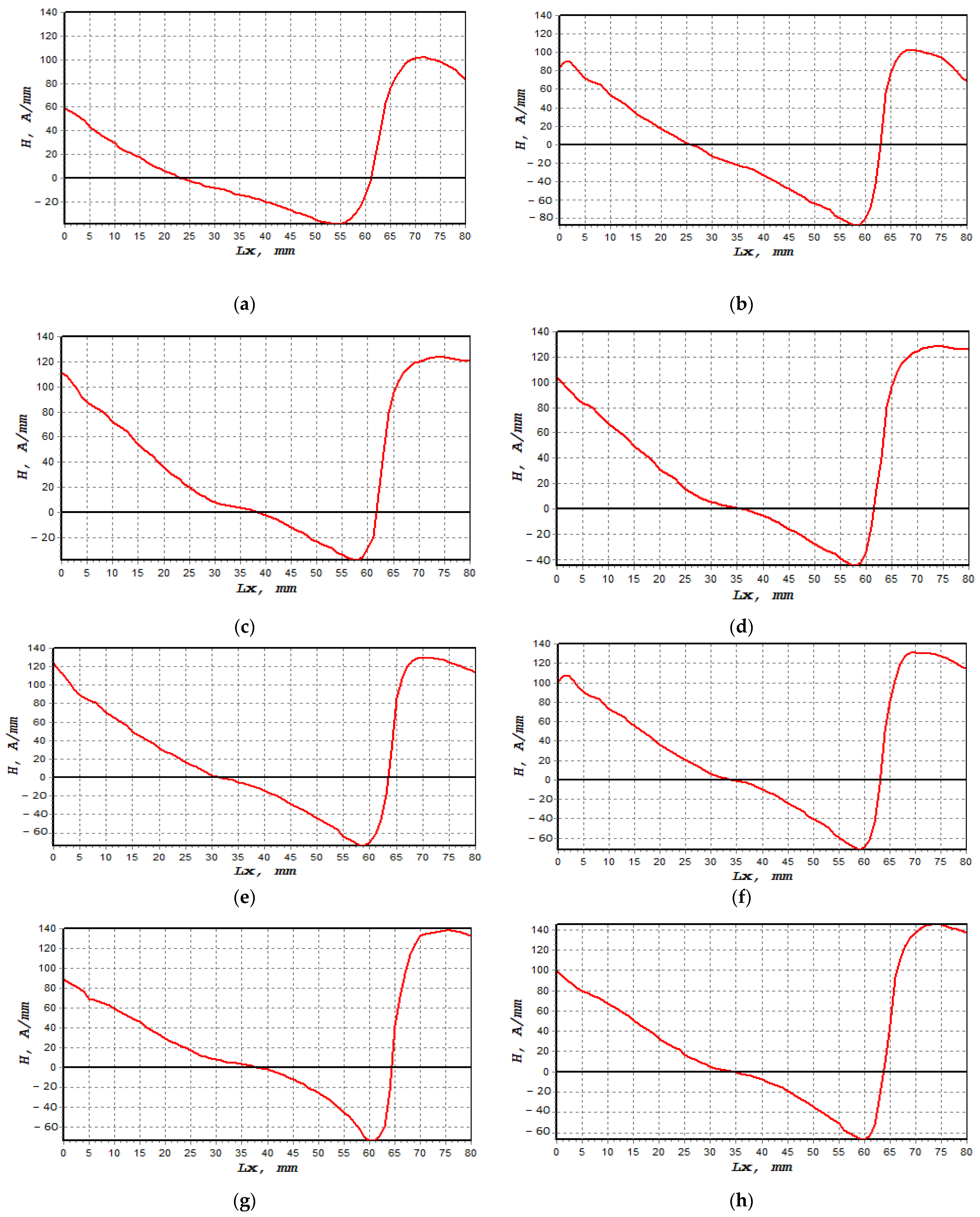
2.3. Determination of Signals from High Stress Concentration Zones
2.4. Stress Parameter Adaptation in the Basquin Equation for Fatigue Life Prediction
2.5. Fatigue Reliability Assessment
3. Results and Discussion
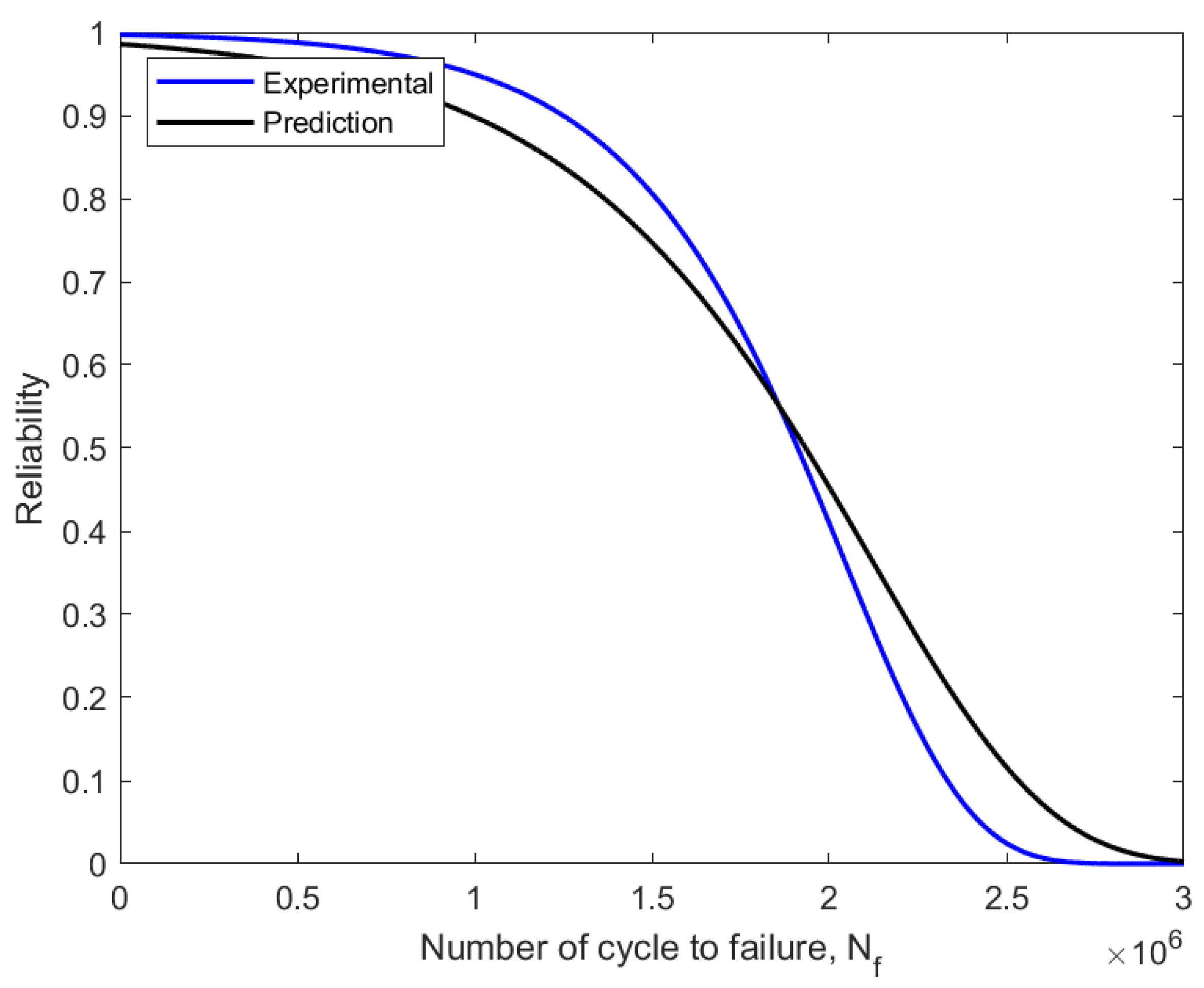
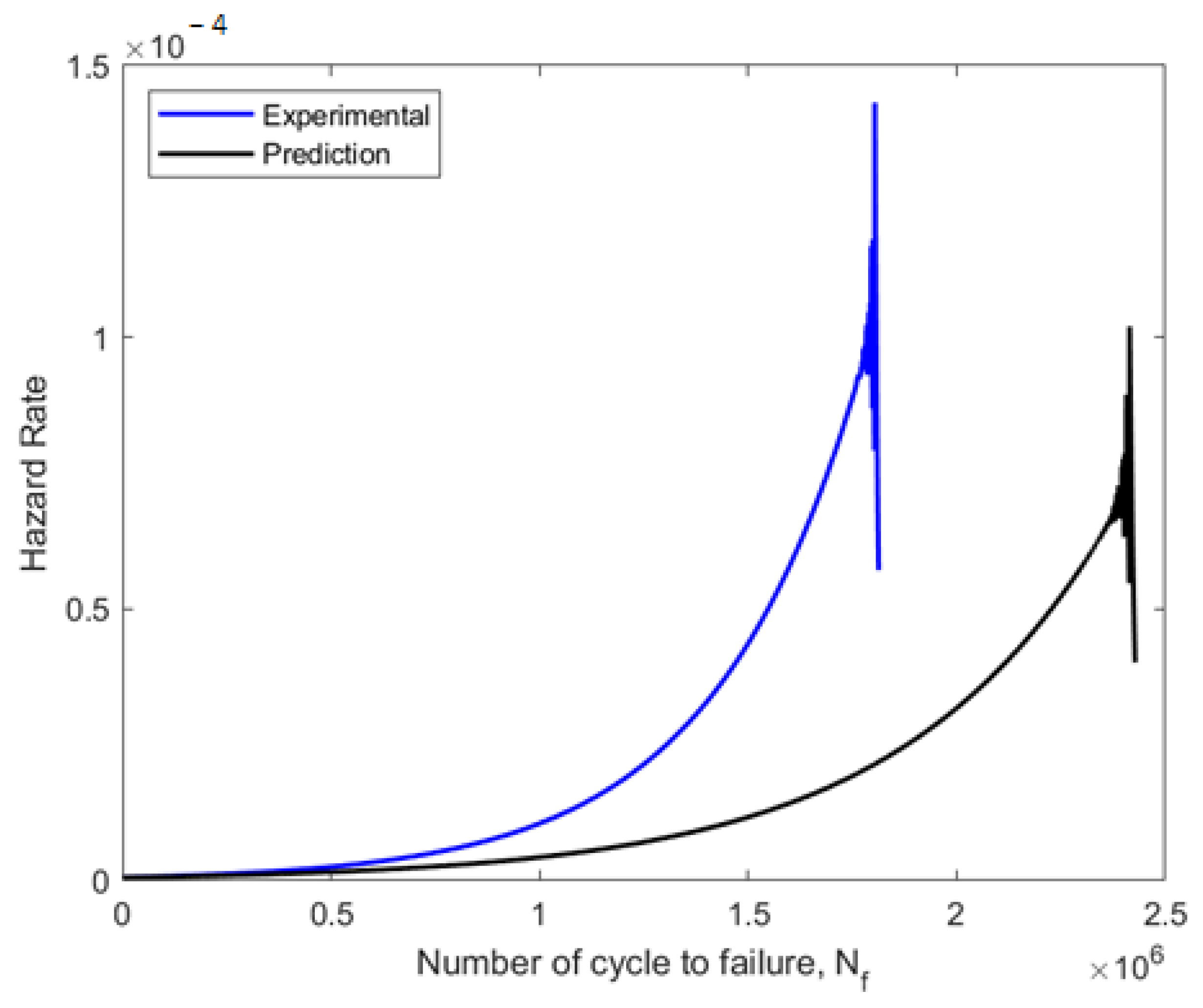
3.1. Fatigue Reliability Assessment
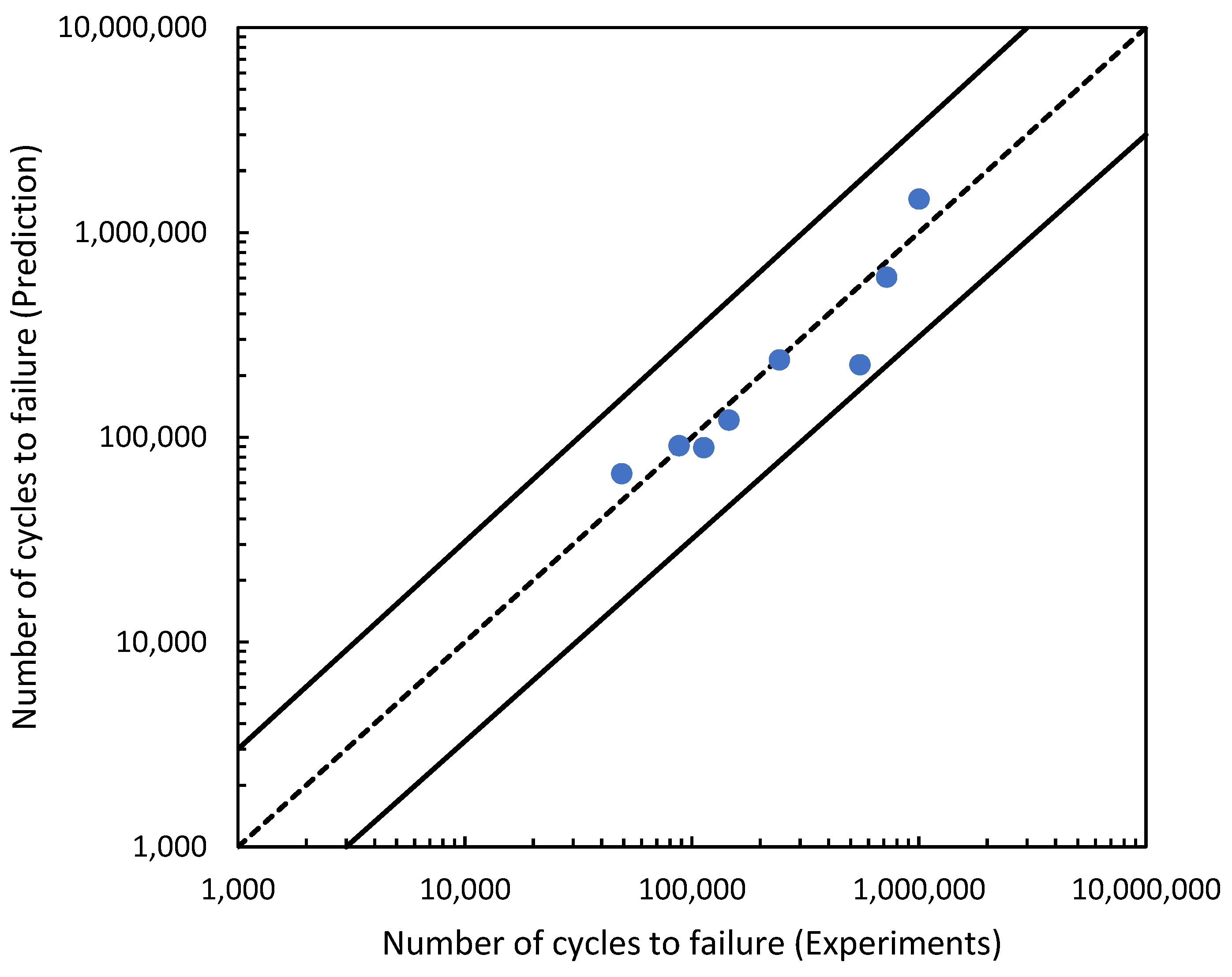
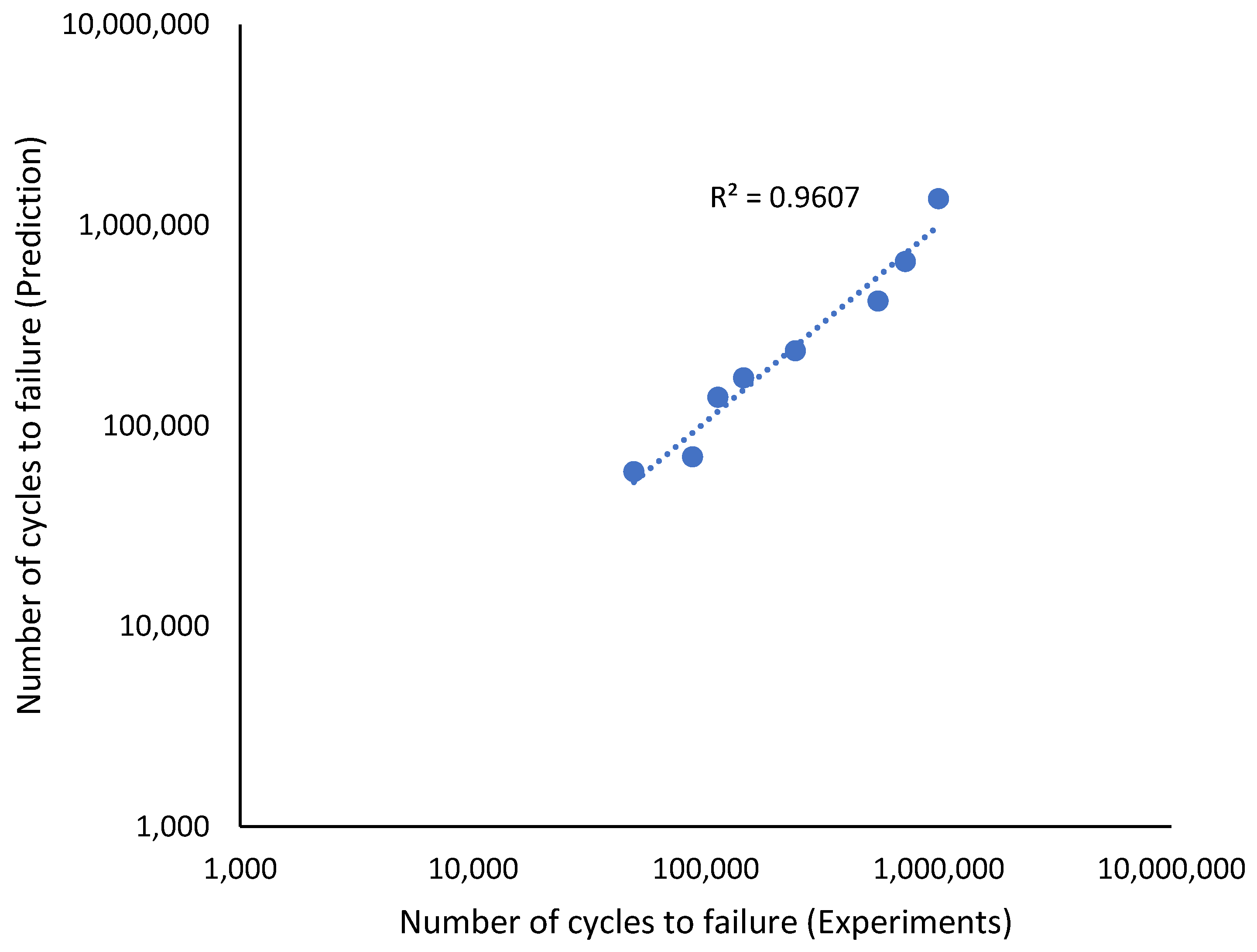
3.2. Application of Magnetic Flux Leakage Stress Parameter into the Basquin Equation for Fatigue Life Prediction
3.3. Validation Based on Fatigue Reliability Analysis
4. Conclusions
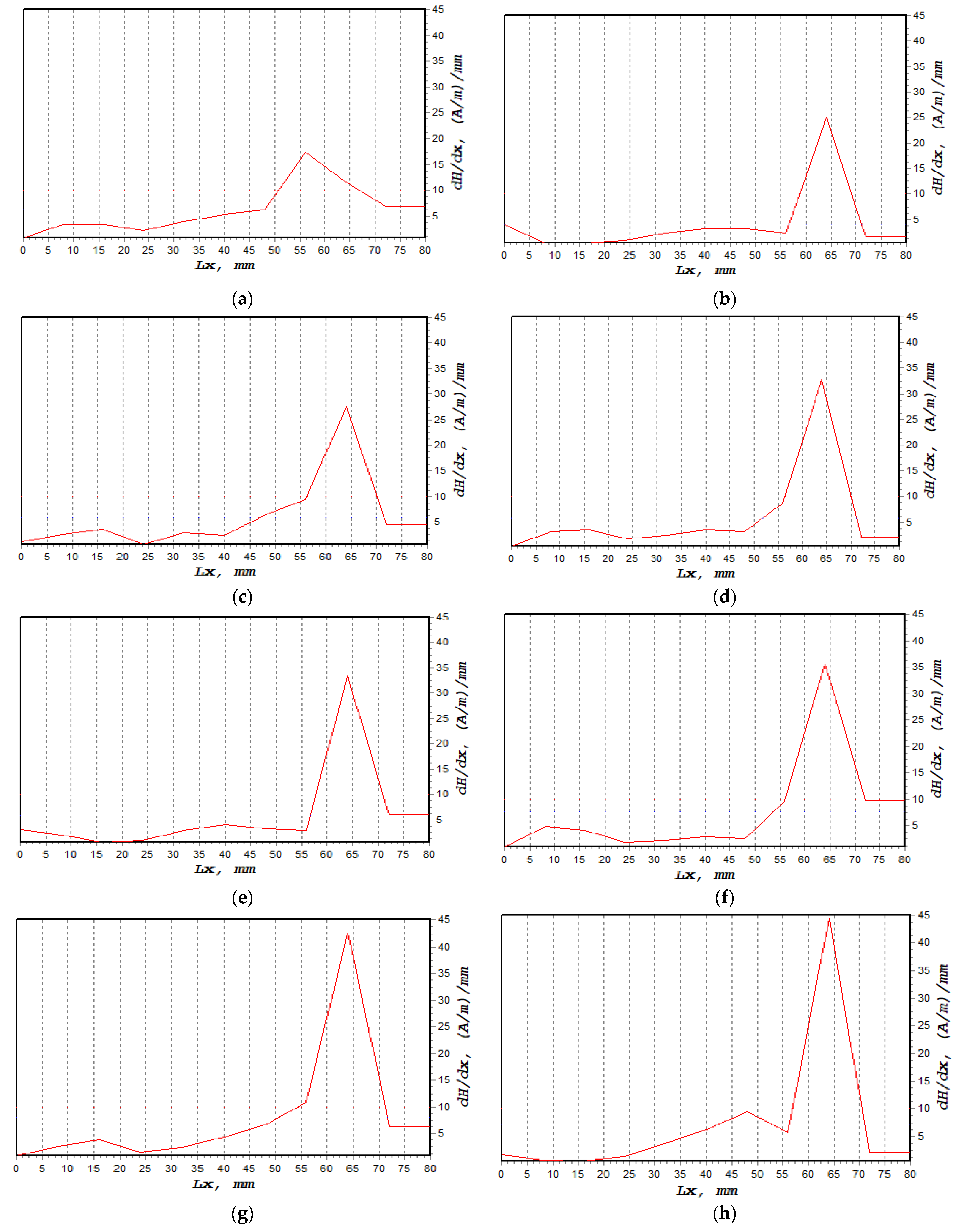
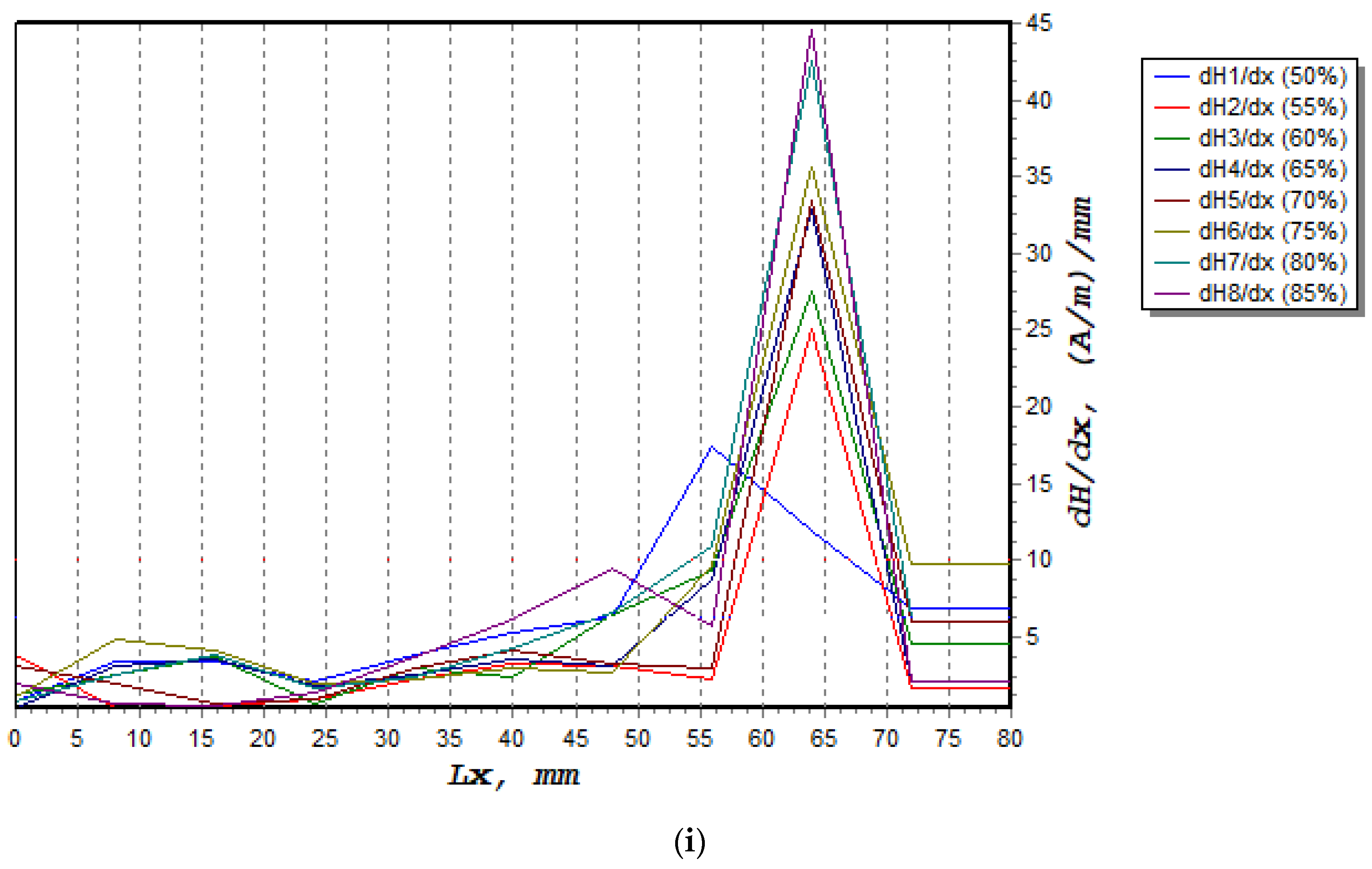
- The MMM approach was employed in this investigation to characterise the uniaxial fatigue loading, which ranged from 50% to 85% UTS loading, based on the magnetic flux leakage measurements. The results showed that 85% UTS load gave higher H(y) and dH(y)/dx values as a higher load affected the magnetic flux leakage reading. All the magnetic flux leakage signals indicated that regions of abnormalities were detected from 50 mm to 75 mm.
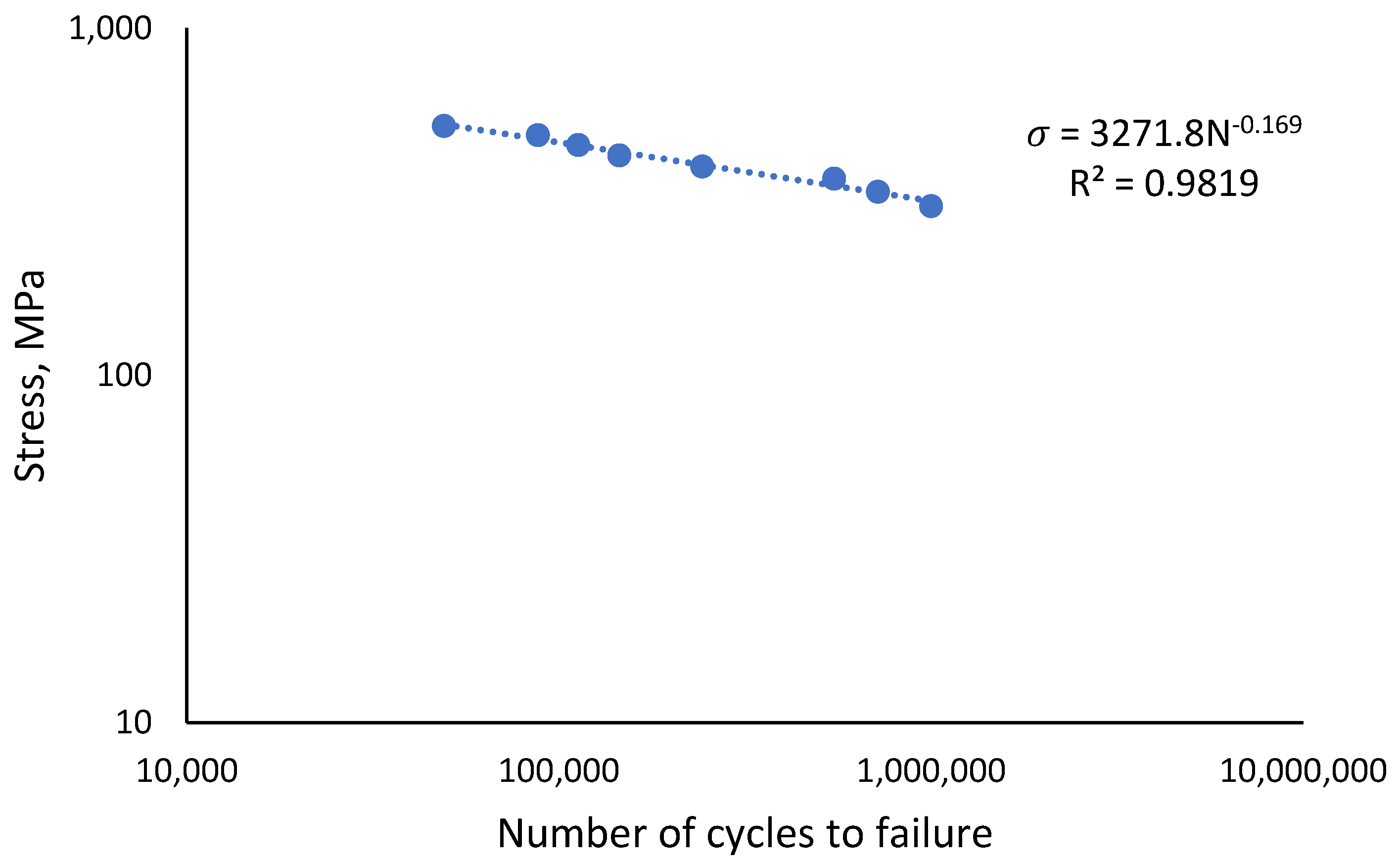
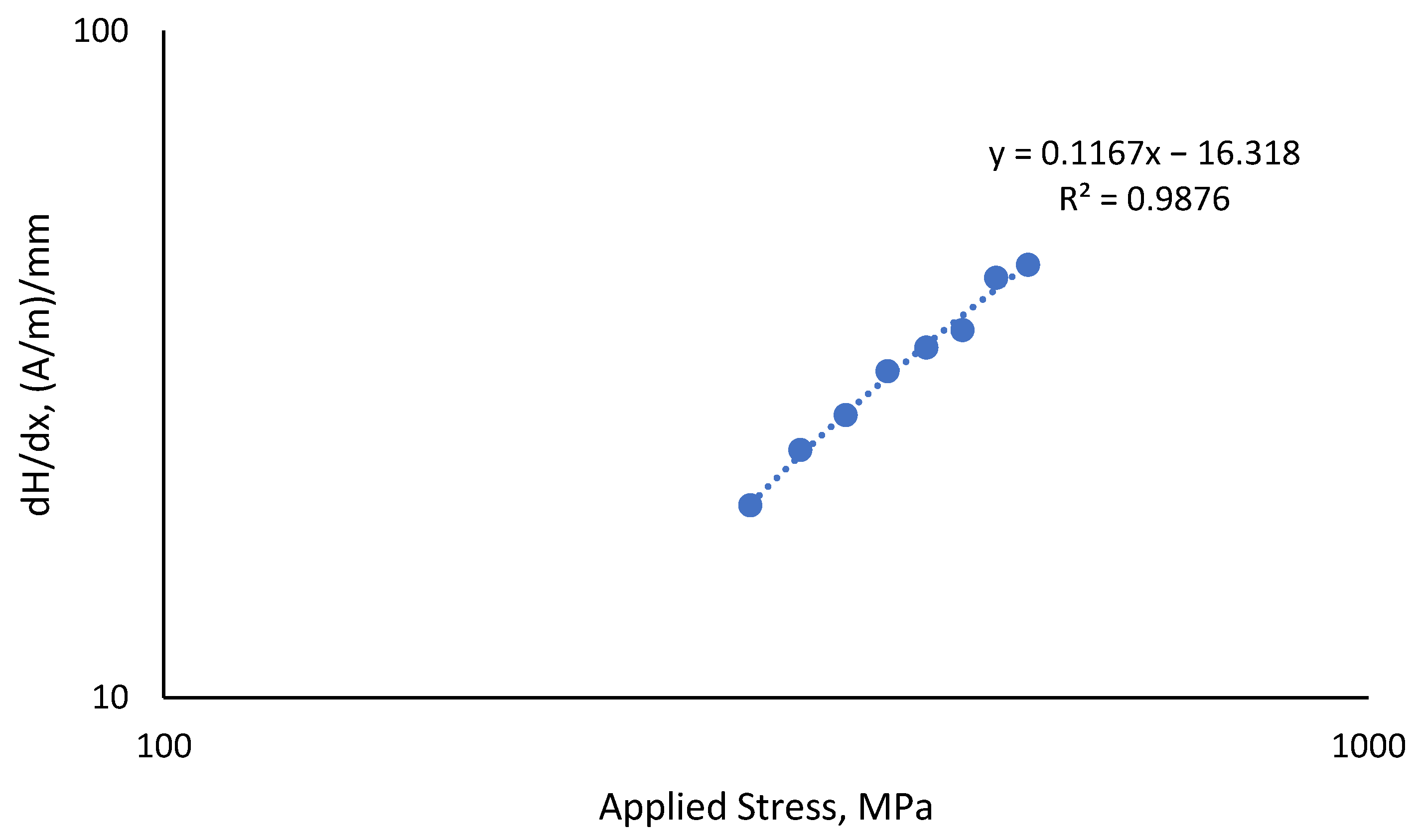
- The stress-life curve showed the fatigue behaviour of the API steel grad X65, which achieved an endurance limit of 307 MPa, approximated at 50% of the UTS cyclic load. The curve shows a good R2 correlation value of 0.9819 between the stress applied and the number of cycles to failure.
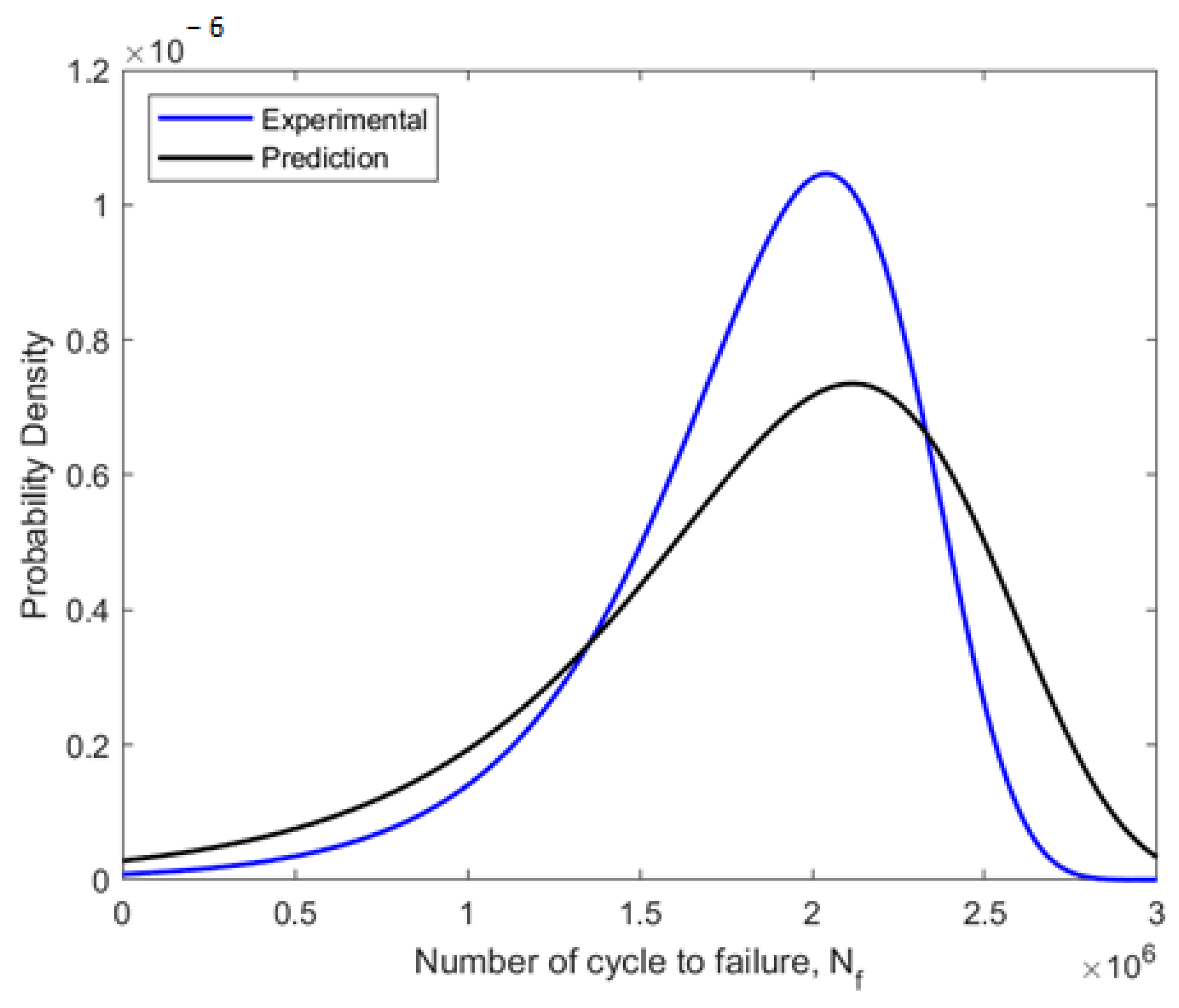
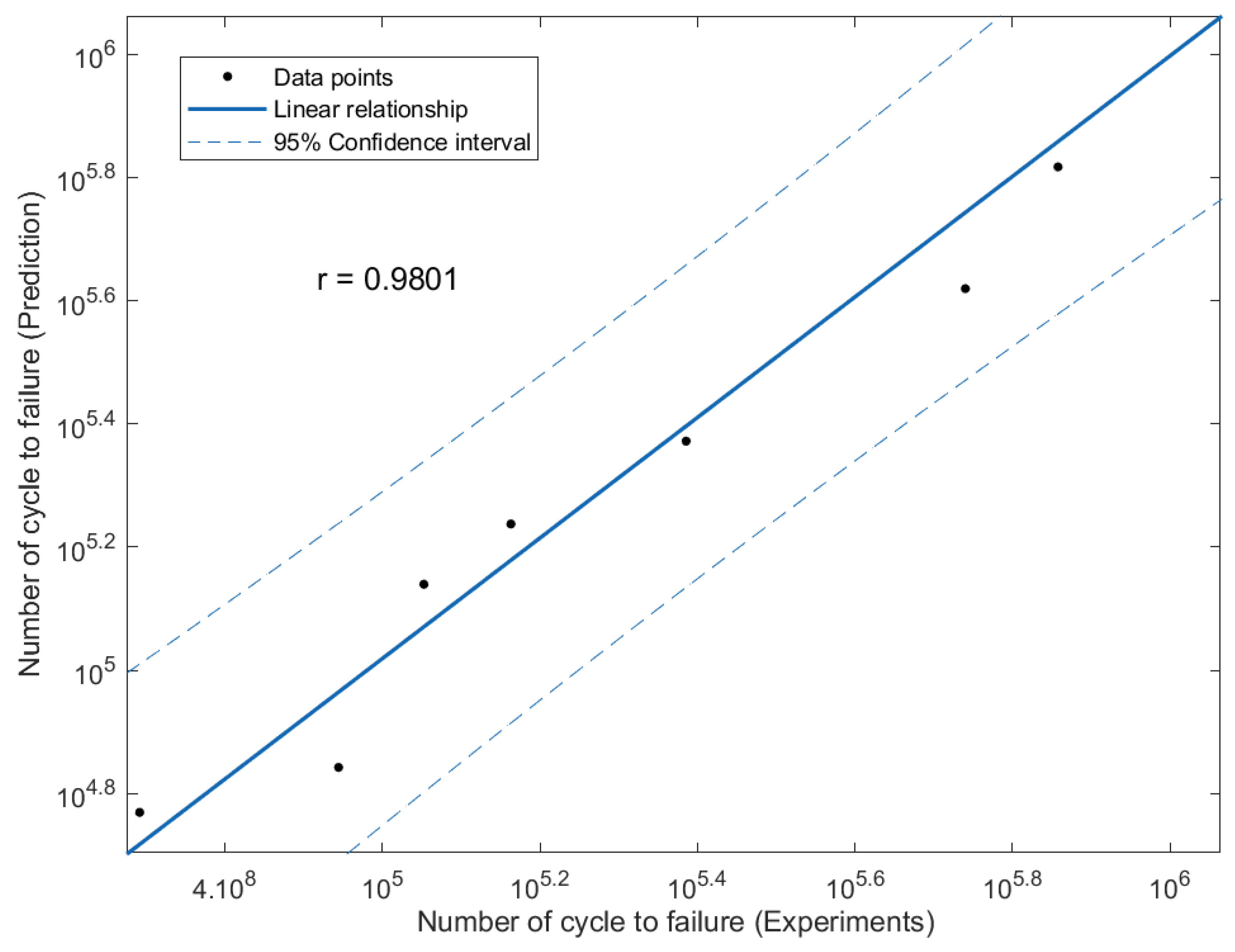
- In comparison to the magnetic flux leakage value, the dH(y)/dx obtained for the experimental fatigue life showed a good correlation analysis, with an R2 value of 0.9156 and a Pearson correlation value of 0.9801.
- The localised stress of the magnetic flux leakage and the fatigue life from the experimental model indicated that the parameter could substitute for the stress parameter of the Basquin equation. The MCTF value of the reliability assessment and the linear regression between these fatigue lives also indicated a good correlation, with slightly different values.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mansor, N.I.I.; Abdullah, S.; Ariffin, A.K. Effect of loading sequences on fatigue crack growth and crack closure in API X65 steel. Mar. Struct. 2019, 65, 181–196. [Google Scholar] [CrossRef]
- Slifka, A.J.; Drexler, E.S.; Nanninga, N.E.; Levy, Y.S.; McColskey, J.D.; Amaro, R.L.; Stevenson, A.E. Fatigue crack growth of two pipeline steels in a pressurized hydrogen environment. Corros. Sci. 2014, 78, 313–321. [Google Scholar] [CrossRef]
- Fassina, P.; Brunella, M.F.; Lazzari, L.; Re, G.; Vergani, L.; Sciuccati, A. Effect of hydrogen and low temperature on fatigue crack growth of pipeline steels. Eng. Fract. Mech. 2013, 103, 10–25. [Google Scholar] [CrossRef]
- Hredil, M.; Krechkovska, H.; Tsyrulnyk, O.; Student, O. Fatigue crack growth in operated gas pipeline steels. Procedia Struct. Integr. 2020, 26, 409–416. [Google Scholar] [CrossRef]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, 159–164. [Google Scholar] [CrossRef]
- Starke, P.; Eifler, D.; Boller, C. Fatigue assessment of metallic materials beyond strain measurement. Int. J. Fatigue 2016, 82, 274–279. [Google Scholar] [CrossRef]
- Meneghetti, G. Analysis of the fatigue strength of a stainless steel based on the energy dissipation. Int. J. Fatigue 2007, 29, 81–94. [Google Scholar] [CrossRef]
- Falamarzi, A.; Moridpour, S.; Nazem, M. A review on existing sensors and devices for inspecting railway infrastructure. J. Kejuruter. 2019, 31, 1–10. [Google Scholar]
- Blitz, J. Electrical and Magnetic Methods of Nondestructive Testing; Adam Hilger IOP Publishing, Ltd.: Bristol, UK, 1991. [Google Scholar]
- Jiles, D.C. Review of magnetic methods for nondestructive evaluation. NDT Int. 1990, 23, 83–92. [Google Scholar] [CrossRef]
- Wang, Z.D.; Gu, Y.; Wang, Y.S. A review of three magnetic NDT technologies. J. Magn. Dan Magn. Mater. 2012, 324, 382–388. [Google Scholar] [CrossRef]
- Arifin, A.; Sahadan, S.N.; Abdullah, S. Evaluating the contraction value of ferromagnetic material at early fatigue loading stage using magnetic flux leakage signature. IOP Conf. Ser. Mater. Sci. Eng. 2019, 606, 01204. [Google Scholar] [CrossRef]
- Dubov, A.A. Energy diagnostics-is a physical basis of the metal magnetic memory method. In Proceedings of the 11th European Conference on Non-Destructive Testing (ECNDT 2014), Prague, Czech Republic, 6–10 October 2014. [Google Scholar]
- Doubov, A. Screening of weld quality using the magnetic metal memory effect. Weld World 1998, 41, 196–199. [Google Scholar]
- Shi, P.; Jin, K.; Zheng, X. A magnetomechanical model for the magnetic memory method. Int. J. Mech. Sci. 2017, 124–125, 229–241. [Google Scholar] [CrossRef]
- Shi, P.; Zheng, X. Magnetic charge model for 3D MMM signals. Nondestruct. Test. Eval. 2015, 31, 45–60. [Google Scholar]
- Dobmann, G.; Seibold, A. First attempts towards the early detection of fatigued substructures using cyclic-loaded 20MnMoNi 5 5 steel. Nucl. Eng. Des. 1992, 137, 363–369. [Google Scholar] [CrossRef]
- Xie, Z.; Zhang, D.; Ueda, T.; Jin, W. Fatigue damage analysis of prefabricated concrete composite beams based on metal magnetic memory technique. J. Magn. Magn. Mater. 2022, 544, 168722. [Google Scholar] [CrossRef]
- Xu, W.; Cui, C.; Luo, C.; Zhang, Q. Fatigue crack monitoring of steel bridge with coating sensor based on potential difference method. Constr. Build. Mater. 2022, 350, 128868. [Google Scholar] [CrossRef]
- Meng, X.; Qin, Q.; Qu, C.; Kang, K.; Wang, Z.; Qiu, W.; Qu, C.; Fu, D. The characterization of bovine compact bone fatigue damage using terahertz spectroscopy. Z. Med. Phys. 2022. [Google Scholar] [CrossRef]
- Taheri, H.; Jones, C.; Taheri, M. Assessment and detection of stress corrosion cracking by advanced eddy current array nondestructive testing and material characterization. J. Nat. Gas Sci. Eng. 2022, 102, 104568. [Google Scholar] [CrossRef]
- Sahraei, H.N.; Modiri, F.A.; Kahrobaee, S.; Akhlaghi, I.A. Application of Nondestructive Magnetic Flux Leakage Method in Characterization of Mechanical Properties of API X65 Steel. Nondestruct. Test. Technol. 2021, 2, 114–120. [Google Scholar]
- Shen, Z.; Chen, H.; Huang, H.; Chai, J.; Niu, Y.; Wang, D.; Zhang, Z. A method for quickly evaluating heat treatment quality of 35CrMo steel cylinder using magnetic properties. J. Magn. Magn. Mater. 2022, 543, 168622. [Google Scholar] [CrossRef]
- Huang, H.; Yao, J.; Li, Z.; Liu, Z. Residual magnetic field variation induced by applied magnetic field and cyclic tensile stress. NDT E Int. 2014, 63, 38–42. [Google Scholar] [CrossRef]
- Ni, C.; Hua, L.; Wang, X. Crack propagation analysis and fatigue life prediction for structural alloy steel based on metal magnetic memory testing. J. Magn. Magn. Mater. 2018, 462, 144–152. [Google Scholar] [CrossRef]
- Mousavi, S.H.; Arab, G.; Sabzi, M.; Sadeghi, M.; Eivani, A.R.; Jafarian, H.R. Sensitivity to hydrogen induced cracking, and corrosion performance of an API X65 pipeline steel in H2S containing environment: Influence of heat treatment and its subsequent microstructural changes. J. Mater. Res. Technol. 2021, 15, 1–16. [Google Scholar] [CrossRef]
- Sun, B.; Yang, L.; Guo, Y. A high-cycle fatigue accumulation model based on electrical resistance for structural steels. Fatigue Fract. Eng. Mater. Struct. 2007, 30, 1052–1062. [Google Scholar] [CrossRef]
- Firdaus, S.M.; Arifin, A.; Abdullah, S.; Singh, S.S.K.; Nor, N.M. Detection of Uniaxial Fatigue Stress under Magnetic Flux Leakage Signals using Morlet Wavelet. Frat. Integrità Strutt. 2022, 61, 254–265. [Google Scholar] [CrossRef]
- Wan, H.; Du, C.; Liu, Z.; Song, D.; Li, X. The effect of hydrogen on stress corrosion behavior of X65 steel welded joint in simulated deep sea environment. Ocean. Eng. 2016, 114, 216–223. [Google Scholar] [CrossRef]
- Čapek, J.; Trojan, K.; Kec, J.; Černý, I.; Ganev, N.; Němeček, S. On the Weldability of Thick P355NL1 Pressure Vessel Steel Plates Using Laser Welding. Materials 2020, 14, 131. [Google Scholar] [CrossRef]
- Ariduru, S. Fatigue Life Calculation By Rainflow Cycle Counting Method. Ph.D. Thesis, Middle East Technical University, Ankara, Turkey, 2004. [Google Scholar]
- Chongchong, L.; Lihong, D.; Haidou, W.; Guolu, L.; Binshi, X. Metal magnetic memory technique used to predict the fatigue crack propagation behavior of 0.45%C steel. J. Magn. Magn. Mater. 2016, 405, 150–157. [Google Scholar] [CrossRef]
- Han, G.; Huang, H. A dual-dipole model for stress concentration evaluation based on magnetic scalar potential analysis. NDT Int. 2022, 118, 102394. [Google Scholar] [CrossRef]
- Arifin, A.; Abdullah, S.; Ariffin, A.K.; Jamaludin, N.; Singh, S.S.K. Characterising the stress ratio effect for fatigue crack propagation parameters of SAE 1045 steel based on magnetic flux leakage. Theor. Appl. Fract. Mech. 2022, 121, 103514. [Google Scholar] [CrossRef]
- Venkatachalapathi, N.; Basha, S.M.D.J.; Raju, G.J.; Raghavulu, P. Characterization of fatigued steel states with metal magnetic memory method. Mater. Today Proc. 2018, 5, 8645–8654. [Google Scholar] [CrossRef]
- Shi, C.L.; Dong, S.Y.; Xu, B.S.; He, P. Metal magnetic memory effect caused by static tension load in a case-hardened steel. J. Magn. Magn. Mater. 2010, 322, 413–416. [Google Scholar] [CrossRef]
- Sahadan, S.N.; Abdullah, S.; Arifin, A.; Singh, S.S.K. Assessing the magnetic flux leakage contraction parameters for the fatigue life prediction of SAE1045 steel specimens. Structures 2021, 34, 4077–4085. [Google Scholar] [CrossRef]
- Bader, Q.; Kadum, E. Mean Stress Correction Effects on the Fatigue Life Behavior of Steel Alloys by Using Stress Life Approach Theories. Int. J. Eng. Technol. 2014, 14, 50–58. [Google Scholar]
- Xu, J.; Kong, F. Adaptive scaled unscented transformation for highly efficient structural reliability analysis by maximum entropy method. Struct. Saf. 2019, 76, 123–134. [Google Scholar] [CrossRef]
- Altamura, A.; Beretta, S. Reliability assessment of hydraulic cylinders considering service loads and flaw distribution. Int. J. Press. Vessel. Pip. 2012, 98, 76–88. [Google Scholar] [CrossRef]
- Jin, C.; Ran, Y.; Wang, Z.; Huang, G.; Xiao, L.; Zhang, G. Reliability analysis of gear rotation meta-action unit based on Weibull and inverse Gaussian competing failure process. Eng. Fail. Anal. 2020, 117, 104953. [Google Scholar] [CrossRef]
- Chin, C.H.; Rahim, A.A.A.; Abdullah, S.; Singh, S.S.K.; Nor, N.M. Acceptability of the effective strain damage model for fatigue life assessment considering the load sequence effect for automotive coil spring. Eng. Fail. Anal. 2021, 126, 105462. [Google Scholar] [CrossRef]
- Guilani, P.P.; Azimi, P.; Niaki, S.T.A.; Niaki, S.A.A. Redundancy allocation problem of a system with increasing failure rates of components based on Weibull distribution: A simulation-based optimization approach. Reliab. Eng. Syst. Saf. 2016, 152, 187–196. [Google Scholar] [CrossRef]
- Safari, M.A.M.; Masseran, N.; Abdul Majid, M.H. Robust reliability estimation for Lindley distribution—A probability integral transform statistical approach. Mathematics 2020, 8, 1634. [Google Scholar] [CrossRef]
- Karolczuk, A. Analysis of revised fatigue life calculation algorithm under proportional and non-proportional loading with constant amplitude. Int. J. Fatigue 2016, 88, 111–120. [Google Scholar] [CrossRef]
- Sivák, P.; Ostertagová, E. Evaluation of Fatigue Tests by Means of Mathematical Statistics. Procedia Eng. 2012, 48, 639–642. [Google Scholar] [CrossRef] [Green Version]







| Elements | C | Mn | Ni | Mo | Ti | Si | Cr | S | Fe |
|---|---|---|---|---|---|---|---|---|---|
| Weight | 0.06 | 1.60 | 1.29 | 0.60 | 0.30 | 0.23 | 0.16 | 0.11 | Balance |
| Load (%) | Pmin (kN) | Pmax (kN) | Stress Ratio, R |
|---|---|---|---|
| 50 | 1.9 | 19.5 | 0.1 |
| 55 | 1.8 | 18.4 | 0.1 |
| 60 | 1.7 | 17.2 | 0.1 |
| 65 | 1.6 | 16.1 | 0.1 |
| 70 | 1.5 | 14.9 | 0.1 |
| 75 | 1.3 | 13.8 | 0.1 |
| 80 | 1.2 | 12.6 | 0.1 |
| 85 | 1.1 | 11.5 | 0.1 |
| Properties | Yield Strength, MPa | Ultimate Tensile Strength, MPa | Young’s Modulus, GPa |
|---|---|---|---|
| Values | 572 | 614 | 220 |
| UTS Load, % | Applied Stress, MPa | Experimental Number of Cycles to Failure, Nf | dH(y)/dx, (A/m)/mm |
|---|---|---|---|
| 50 | 307.0 | 1,002,150 | 19.4 |
| 55 | 337.7 | 721,273 | 23.5 |
| 60 | 368.4 | 550,000 | 26.5 |
| 65 | 399.1 | 243,067 | 30.8 |
| 70 | 429.8 | 145,608 | 33.4 |
| 75 | 460.5 | 112,868 | 35.5 |
| 80 | 491.2 | 87,952 | 42.5 |
| 85 | 521.9 | 49,158 | 44.5 |
| UTS Load, % | dH(y)/dx, (A/m)/mm | Experimental Number of Cycles to Failure, Nf | Prediction (Basquin) Number of Cycles to Failure, Nf | Difference, % | Prediction (Modified Basquin) Number of Cycles to Failure, Nf | Difference, % |
|---|---|---|---|---|---|---|
| 50 | 19.4 | 1,002,150 | 1,204,369 | 10. 7 | 1,349,201 | 25.7 |
| 55 | 23.5 | 721,273 | 685,223 | 4.4 | 656,072 | 9.9 |
| 60 | 26.5 | 550,000 | 409,478 | 1.6 | 416,306 | 32.4 |
| 65 | 30.8 | 243,067 | 254,999 | 8.2 | 235,505 | 3.2 |
| 70 | 33.4 | 145,608 | 164,473 | 4.8 | 172,774 | 15.7 |
| 75 | 35.5 | 112,868 | 129,345 | 6.2 | 137,943 | 18.1 |
| 80 | 42.5 | 87,952 | 74,636 | 7.2 | 69,595 | 26.3 |
| 85 | 44.5 | 49,158 | 52,138 | 11.3 | 58,833 | 16.4 |
| Model | Weibull Parameter | |
|---|---|---|
| Scale Parameter | Shape Parameter | |
| Experimental | 3.76 × 105 | 1.0833 |
| Prediction | 3.89 × 105 | 1.0153 |
| Obtained Fatigue Life | Mean-Cycle-to-Failure, Cycles |
|---|---|
| Experimental | 3.37 × 105 |
| Prediction | 3.28 × 105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Firdaus, S.M.; Arifin, A.; Abdullah, S.; Singh, S.S.K.; Nor, N.M. Fatigue Life Assessment of API Steel Grade X65 Pipeline Using a Modified Basquin Parameter of the Magnetic Flux Leakage Signal. Materials 2023, 16, 464. https://doi.org/10.3390/ma16020464
Firdaus SM, Arifin A, Abdullah S, Singh SSK, Nor NM. Fatigue Life Assessment of API Steel Grade X65 Pipeline Using a Modified Basquin Parameter of the Magnetic Flux Leakage Signal. Materials. 2023; 16(2):464. https://doi.org/10.3390/ma16020464
Chicago/Turabian StyleFirdaus, Syed Muhamad, Azli Arifin, Shahrum Abdullah, Salvinder Singh Karam Singh, and Noorsuhada Md Nor. 2023. "Fatigue Life Assessment of API Steel Grade X65 Pipeline Using a Modified Basquin Parameter of the Magnetic Flux Leakage Signal" Materials 16, no. 2: 464. https://doi.org/10.3390/ma16020464
APA StyleFirdaus, S. M., Arifin, A., Abdullah, S., Singh, S. S. K., & Nor, N. M. (2023). Fatigue Life Assessment of API Steel Grade X65 Pipeline Using a Modified Basquin Parameter of the Magnetic Flux Leakage Signal. Materials, 16(2), 464. https://doi.org/10.3390/ma16020464







