Mechanical Behavior of Al-Si10-Mg P-TPMS Structure Fabricated by Selective Laser Melting and a Unified Mathematical Model with Geometrical Parameter
Abstract
:1. Introduction
2. Experimental Details
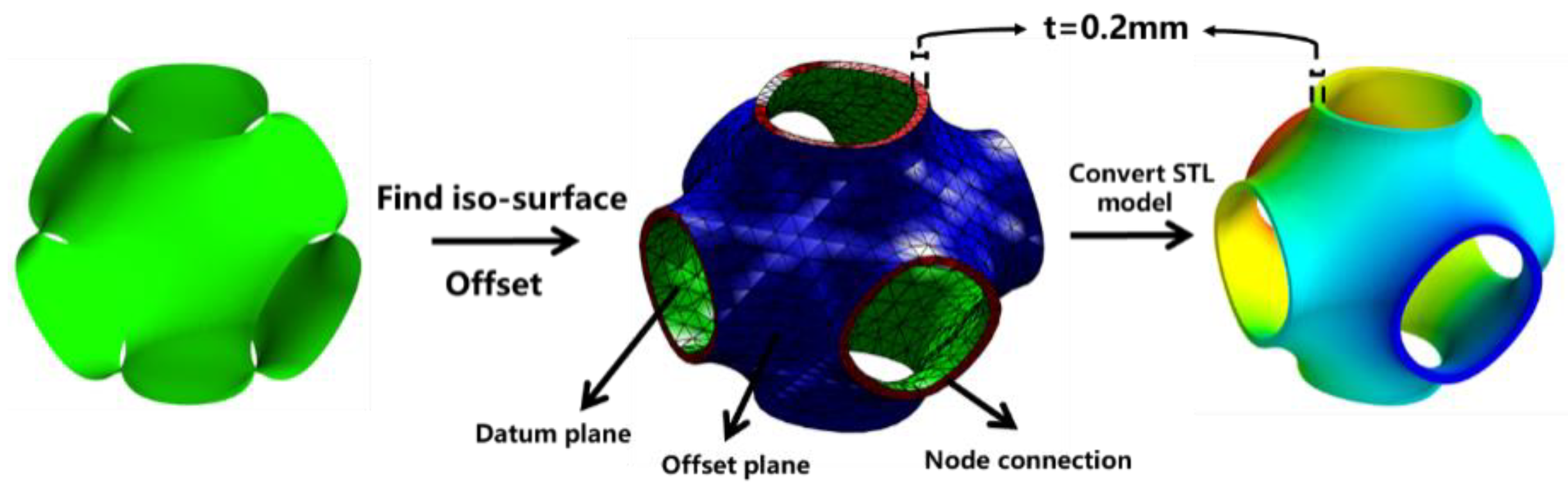
2.1. Primitive Structure Design
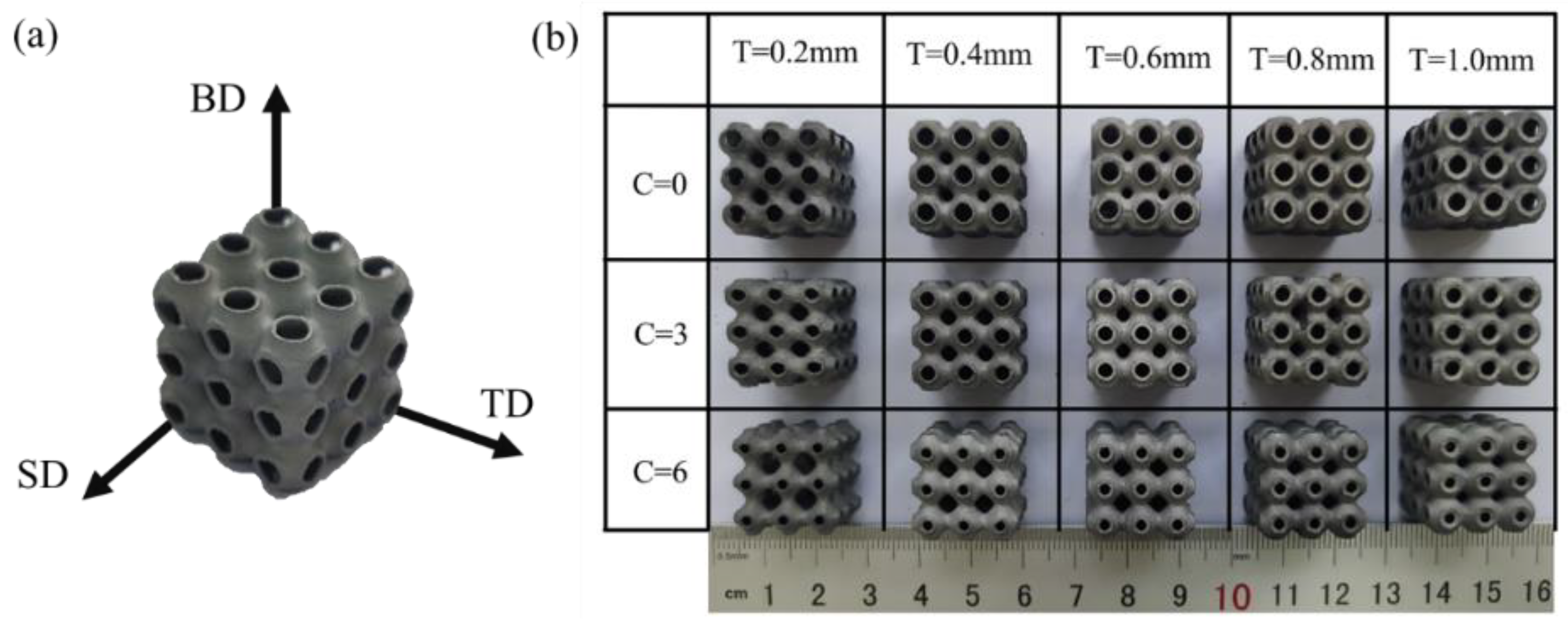
2.2. Manufacturing
2.3. Sample Parameters
2.4. Compression Performance Test
2.5. Finite Element Modelling
3. Results and Discussion
3.1. Structural Defects Induced by SLM
3.2. Deformation Mode
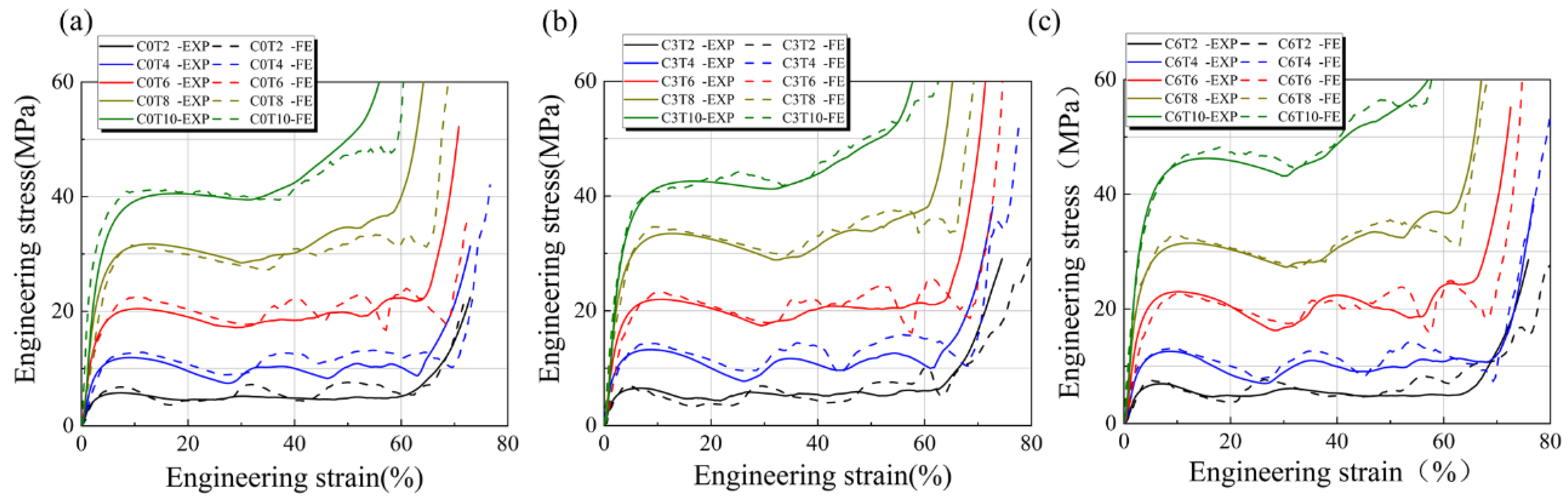
3.3. Stress–Strain Curve
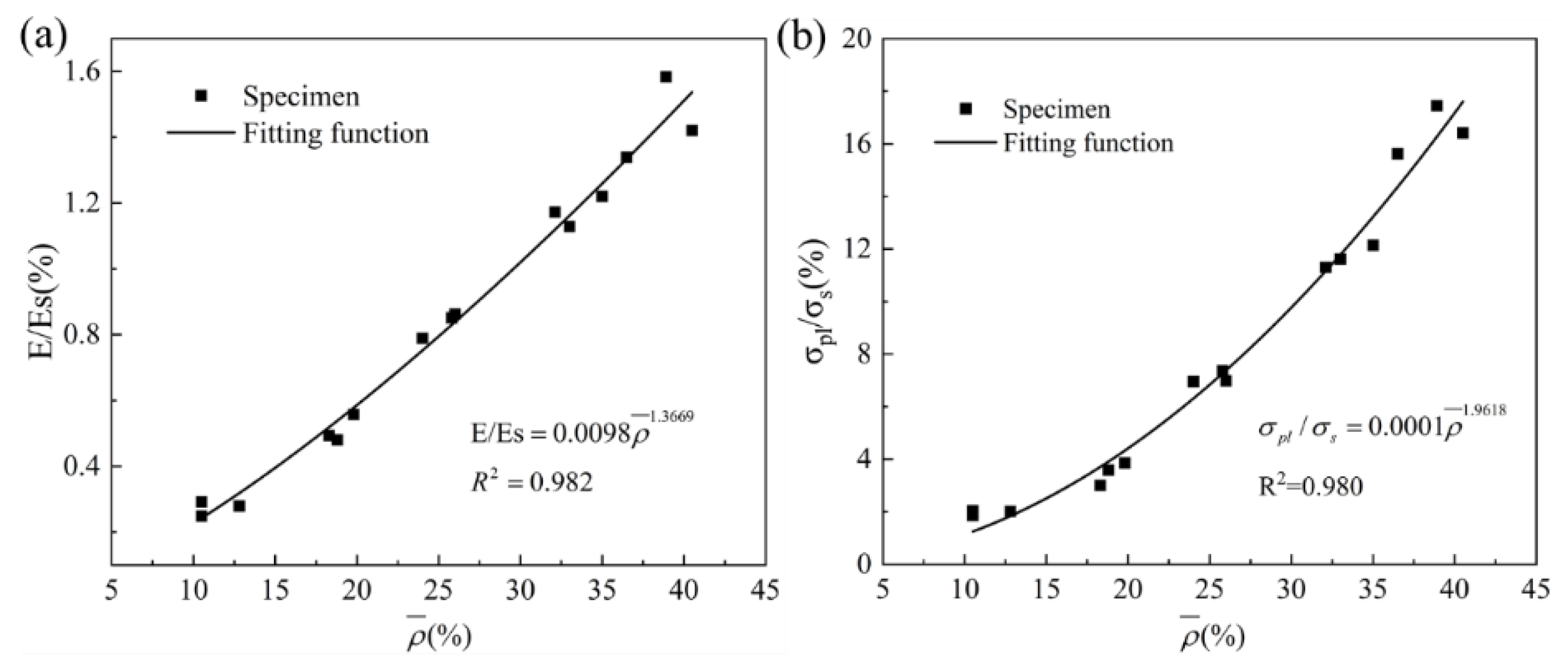
3.4. Relationship between Structural Parameters and Mechanical Properties
3.5. Energy Absorption
4. Conclusions
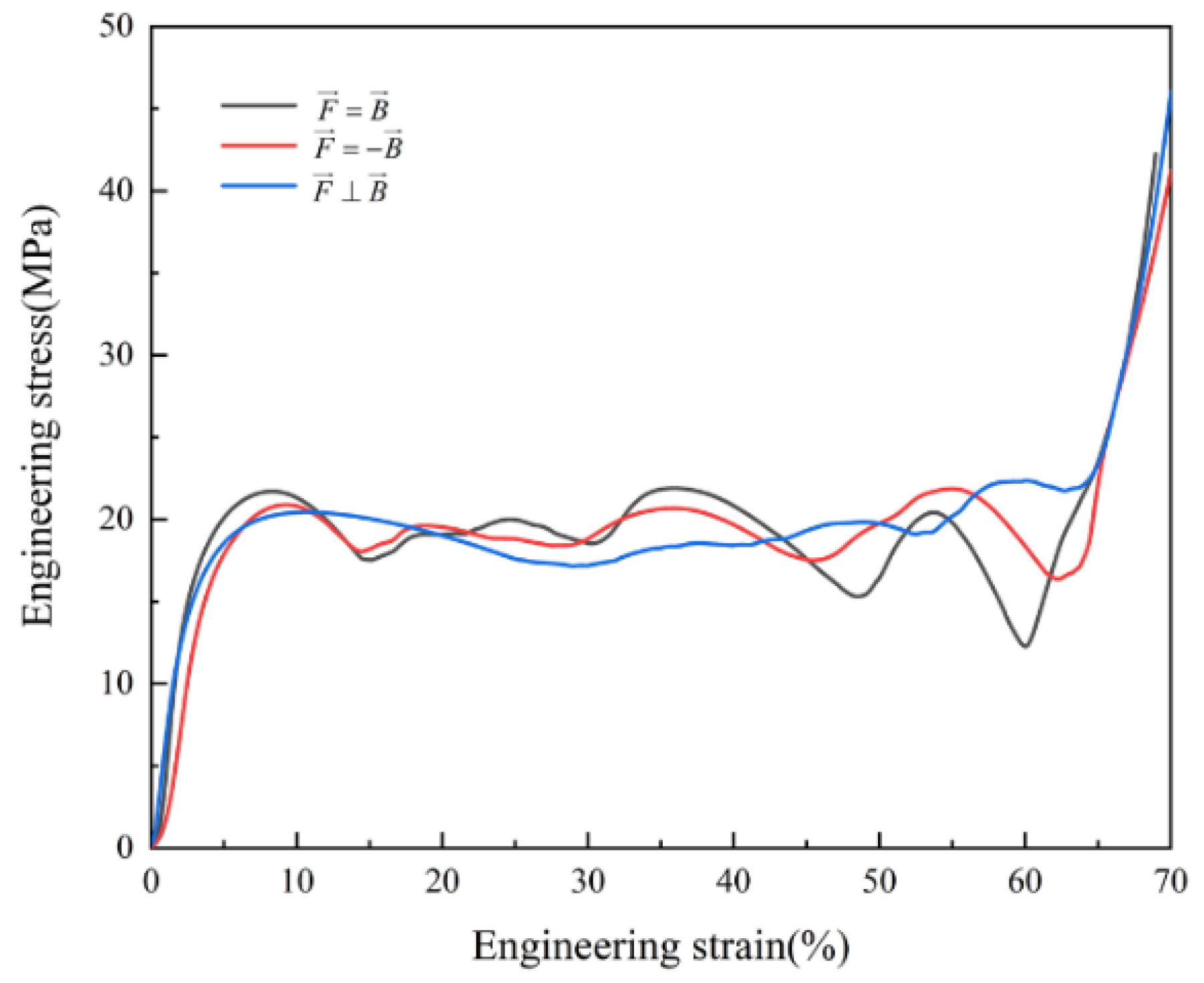
- In the SLM process of the primitive structure, the print quality of the bottom surface is inferior to the top, which results in the inhomogeneity of the mechanical properties along the building direction. It is easily ignored when testing the mechanical properties of 3D-printed specimens. The loading direction is parallel to the building direction, the deformation mode will become crushed layer by layer along the building direction.
- However, when the loading direction is perpendicular to the building direction, the as-built primitive structure presents symmetrical buckling and has more stable plateau stress.
- The compression deformation mode of primitive structure can be divided into three stages: linear elastic stage, plateau stage, and densification stage. The thicker the structure thickness in the range of 0.2–1.0 mm, the longer the elastic deformation stage and the shorter the stress platform. The greater the value of C in the range of 0–0.6, the greater the fluctuation of the stress platform of the structure.
- A unified mathematical model between minimal surface design parameters and Young’s modulus, plateau stress is established, which can directly predict the real mechanical properties of Al-Si10-Mg primitive TPMS structure fabricated by SLM through structural parameters (C, T).
- When the C value is 0–0.6 and the thickness T is 0.2–1.0mm, the specific energy absorption of the primitive structure is 14.37–25.65 J/g. Under the same thickness, properly increasing the C value can improve the energy absorption performance of the structure. Meanwhile, a mathematical model is established to predict the energy absorption performance of structures of different parameters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Z. Recent advances in novel metallic honeycomb structure. Compos. Part B Eng. 2019, 166, 731–741. [Google Scholar] [CrossRef]
- Dong, Z.; Li, Y. Experimental and numerical studies on the compressive mechanical properties of the metallic auxetic reentrant honeycomb. Mater. Des. 2019, 182, 108036. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z. Experimental investigation on bending behavior of honeycomb sandwich panel with ceramic tile face-sheet. Compos. B Eng. 2019, 164, 280–286. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z. Blast resistance and parametric study of sandwich structure consisting of honeycomb core filled with circular metallic tubes. Compos. B Eng. 2018, 145, 261–269. [Google Scholar] [CrossRef]
- Cao, X.; Jiang, Y. Compression experiment and numerical evaluation on mechanical responses of the lattice structures with stochastic geometric defects originated from additive-manufacturing. Compos. B Eng. 2020, 194, 108030. [Google Scholar] [CrossRef]
- Liu, L.; Kamm, P.; García-Moreno, F. Elastic and failure response of imperfect three-dimensional metallic lattices: The role of geometric defects induced by Selective Laser Melting. J. Mech. Phys. Solids. 2017, 107, 160–184. [Google Scholar]
- Dong, L.; Deshpande, V. Mechanical response of Ti–6Al–4V octet-truss lattice structures. Int. J. Solids Struct. 2015, 60, 107–124. [Google Scholar] [CrossRef]
- Wang, T.; An, J. A novel 3D impact energy absor-ption structure with negative Poisson’s ratio and its application in aircraft crashworthiness. Compos. Struct. 2021, 262, 113663. [Google Scholar] [CrossRef]
- Zhou, G.; Yan, P. Design optimization for protective shell of hydrogen cylinder for vehicle based on NPR structure. Struct. Multidiscipl. Optim. 2021, 64, 369–388. [Google Scholar] [CrossRef]
- Song, K.; Wang, Z. Porous structure design and mechanical behavior analysis based on TPMS for customized root analogue implant. J. Mech. Behav. Mater. 2021, 115, 104222. [Google Scholar] [CrossRef]
- Yan, C.; Hao, L. Ti–6Al–4V triply periodic minimal surface structures for bone implants fabricated via selective laser melting. J. Mech. Behav. Mater. 2015, 51, 61–73. [Google Scholar] [CrossRef]
- Fan, X.; Tang, Q.; Feng, Q. Design, mechanical properties and energy absorption capability of graded-thickness triply periodic minimal surface structures fabricated by selective laser melting. Int. J. Mech. Sci. 2021, 204, 106586. [Google Scholar] [CrossRef]
- Bauer, J.; Kraus, J.A. Tensegrity metamaterials: Toward failure-resistant engineering systems through delocalized deformation. Adv. Mater. 2021, 33, 2005647. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zheng, H.; Yang, L. Mechanical responses of sheet-based gyroid-type triply periodic minimal surface lattice structures fabricated using selective laser melting. Mater. Des. 2022, 214, 110407. [Google Scholar] [CrossRef]
- Qureshi, Z.A. On the effect of porosity and functional grading of 3D printable triply periodic minimal surface (TPMS) based architected lattices embedded with a phase change material. Int. J. Mass Tran. 2022, 183, 122111. [Google Scholar] [CrossRef]
- Corkery, R.W.; Tyrode, E.C. On the colour of wing scales in butterflies: Iridescence and preferred orientation of single gyroid photonic crystals. Interface Focus. 2017, 7, 20160154. [Google Scholar] [CrossRef] [Green Version]
- Galusha, J.W.; Richey, L.R.; Gardner, J.S. Discovery of a diamond-based photonic crystal structure in beetle scales. Phys. Rev. E. 2008, 77, 050904. [Google Scholar] [CrossRef]
- Schwarz, H.A. Monatsberichte der koniglichen Akademie der Wissenscaften zu Berlin. Jahrgang 1865, 149–153. [Google Scholar]
- Han, L.; Che, S. An overview of materials with triply periodic minimal surfaces and related geometry: From biological structures to self-assembled systems. Adv. Mater. 2018, 30, 171705708. [Google Scholar] [CrossRef]
- Schoen, H.A. Infinite Periodic Minimal Surfaces without Self-Intersections; National Aeronautics and Space Administration: Washington, DC, USA, 1970.
- Do Carmo, M.P. Differential Geometry of Curves and Surfaces: Revised and Updated Second Edition; Courier Dover Publications: Mineola, NY, USA, 2016. [Google Scholar]
- Zhao, M.; Liu, F.; Fu, G. Improved Mechanical Properties and Energy Absorption of BCC Lattice Structures with Triply Periodic Minimal Surfaces Fabricated by SLM. Materials 2018, 11, 2411. [Google Scholar] [CrossRef] [Green Version]
- Park, K.M.; Kim, G.O. Mechanical properties of additive manufactured variable-density Kelvin lattice structures: A novel design method for Kelvin unit cells. J. Struct. Integr. Main. 2022, 7, 34–45. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rowshan, R. Topology-mechanical property relationship of 3D printed strut, skeletal, and sheet based periodic metallic cellular materials. Addit. Manuf. 2018, 19, 167–183. [Google Scholar] [CrossRef]
- Zhang, L.; Feih, S. Energy absorption characteristics of metallic triply periodic minimal surface sheet structures under compressive loading. Addit. Manuf. 2018, 23, 505–515. [Google Scholar] [CrossRef]
- Maskery, I. Insights into the mechanical properties of several triply periodic minimal surface lattice structures made by polymer additive manufacturing. Polymer 2018, 152, 62–71. [Google Scholar] [CrossRef]
- Lu, C.; Zhang, C. Mechanical behavior of Al–Si10–Mg gyroid surface with variable topological parameters fabricated via laser powder bed fusion. J. Mater. Res. Technol. 2021, 15, 5650–5661. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.O. A mechanical property evaluation of graded density Al-Si10-Mg lattice structures manufactured by selective laser melting. Mater. Sci. Eng. A 2016, 670, 264–274. [Google Scholar] [CrossRef] [Green Version]
- Schwarz, H.A. Gesammelte Mathematische Abhandlun-Gen; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Yu, K.B. Study on Microstructures and Mechanical Properties of AlSi10Mg Alloy Produced by Selective Laser Melting; South China University of Technology: Guangzhou, China, 2018. [Google Scholar]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.O. Compressive failure modes and energy absorption in additively manufactured double gyroid lattices. Addit Manuf. 2017, 16, 24–29. [Google Scholar] [CrossRef]
- ISO 13314; Mechanical Testing of Metals- Ductility Testing- Compression Test for Porous and Cellular Metals. International Standard: Geneva, Switzerland, 2011; pp. 1–7.
- Zhou, H.; He, N.; Zhang, D.Z. Mechanical properties of functionally graded rotating lattice structures fabricated with SLM process. Mater. Today Commun. 2022, 33, 104740. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, NY, USA, 1997. [Google Scholar]
- Li, Q.M.; Magkiriadis, I. Compressive Strain at the Onset of Densification of Cellular Solids. J. Cell. Plast. 2006, 42, 371–392. [Google Scholar] [CrossRef]
- Avalle, M.; Belingardi, G. Characterization of polymeric structural foams under compressive impact loading by means of energy-absorption diagram. Int. J. Impact Eng. 2001, 25, 455–472. [Google Scholar] [CrossRef]

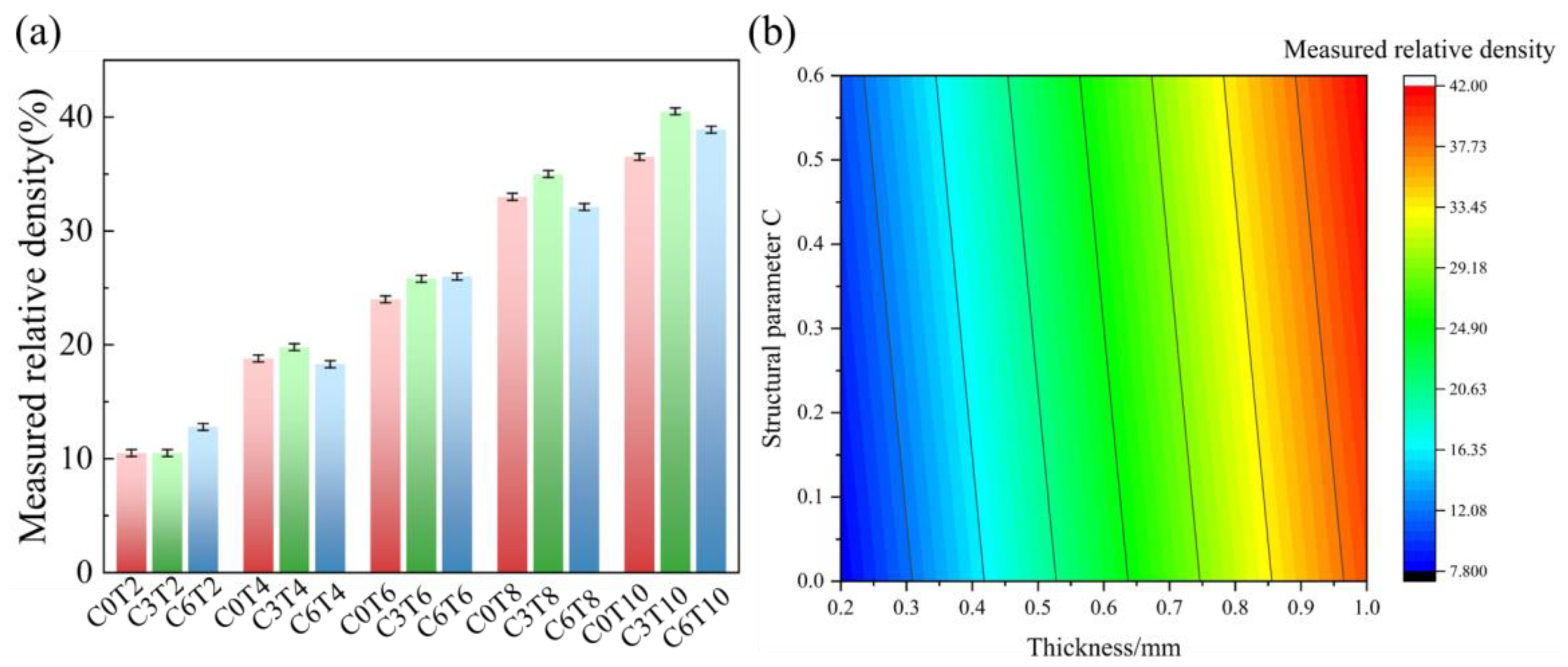





| Sample | Level-Set Value | Nominal Shell Thickness (mm) | Measured Shell Thickness (mm) | Nominal Relative Density (%) | Measured Relative Density (%) |
|---|---|---|---|---|---|
| C0T2 | 0 | 0.2 | 0.21 ± 0.01 | 7.4 | 10.5 ± 0.3 |
| C0T4 | 0 | 0.4 | 0.42 ± 0.02 | 14.7 | 18.8 ± 0.3 |
| C0T6 | 0 | 0.6 | 0.62 ± 0.01 | 21.7 | 24.0 ± 0.3 |
| C0T8 | 0 | 0.8 | 0.83 ± 0.02 | 28.4 | 33.0 ± 0.3 |
| C0T10 | 0 | 1.0 | 1.03 ± 0.02 | 34.5 | 36.5 ± 0.3 |
| C3T2 | 0.3 | 0.2 | 0.22 ± 0.01 | 7.4 | 10.5 ± 0.3 |
| C3T4 | 0.3 | 0.4 | 0.42 ± 0.02 | 14.9 | 19.8 ± 0.3 |
| C3T6 | 0.3 | 0.6 | 0.63 ± 0.02 | 22.3 | 25.8 ± 0.3 |
| C3T8 | 0.3 | 0.8 | 0.82 ± 0.02 | 29.5 | 35.0 ± 0.3 |
| C3T10 | 0.3 | 1.0 | 1.04 ± 0.03 | 36.4 | 40.5 ± 0.3 |
| C6T2 | 0.6 | 0.2 | 0.23 ± 0.02 | 7.1 | 12.8 ± 0.3 |
| C6T4 | 0.6 | 0.4 | 0.42 ± 0.01 | 14.6 | 18.3 ± 0.3 |
| C6T6 | 0.6 | 0.6 | 0.63 ± 0.02 | 22.3 | 26.0 ± 0.3 |
| C6T8 | 0.6 | 0.8 | 0.84 ± 0.02 | 30.0 | 32.1 ± 0.3 |
| C6T10 | 0.6 | 1.0 | 1.04 ± 0.02 | 37.6 | 38.9 ± 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Xie, X.; Li, Y.; Li, B.; Yan, S.; Wen, P. Mechanical Behavior of Al-Si10-Mg P-TPMS Structure Fabricated by Selective Laser Melting and a Unified Mathematical Model with Geometrical Parameter. Materials 2023, 16, 468. https://doi.org/10.3390/ma16020468
Zhang X, Xie X, Li Y, Li B, Yan S, Wen P. Mechanical Behavior of Al-Si10-Mg P-TPMS Structure Fabricated by Selective Laser Melting and a Unified Mathematical Model with Geometrical Parameter. Materials. 2023; 16(2):468. https://doi.org/10.3390/ma16020468
Chicago/Turabian StyleZhang, Xiaonan, Xiangyu Xie, Yongjing Li, Bin Li, Shilin Yan, and Pin Wen. 2023. "Mechanical Behavior of Al-Si10-Mg P-TPMS Structure Fabricated by Selective Laser Melting and a Unified Mathematical Model with Geometrical Parameter" Materials 16, no. 2: 468. https://doi.org/10.3390/ma16020468
APA StyleZhang, X., Xie, X., Li, Y., Li, B., Yan, S., & Wen, P. (2023). Mechanical Behavior of Al-Si10-Mg P-TPMS Structure Fabricated by Selective Laser Melting and a Unified Mathematical Model with Geometrical Parameter. Materials, 16(2), 468. https://doi.org/10.3390/ma16020468







