Prediction of Temperature Development of Concrete with Set-Controlling Admixture Based on a New Hydration Kinetics Model
Abstract
:1. Introduction
2. Relevant Kinetics Mechanisms and Models
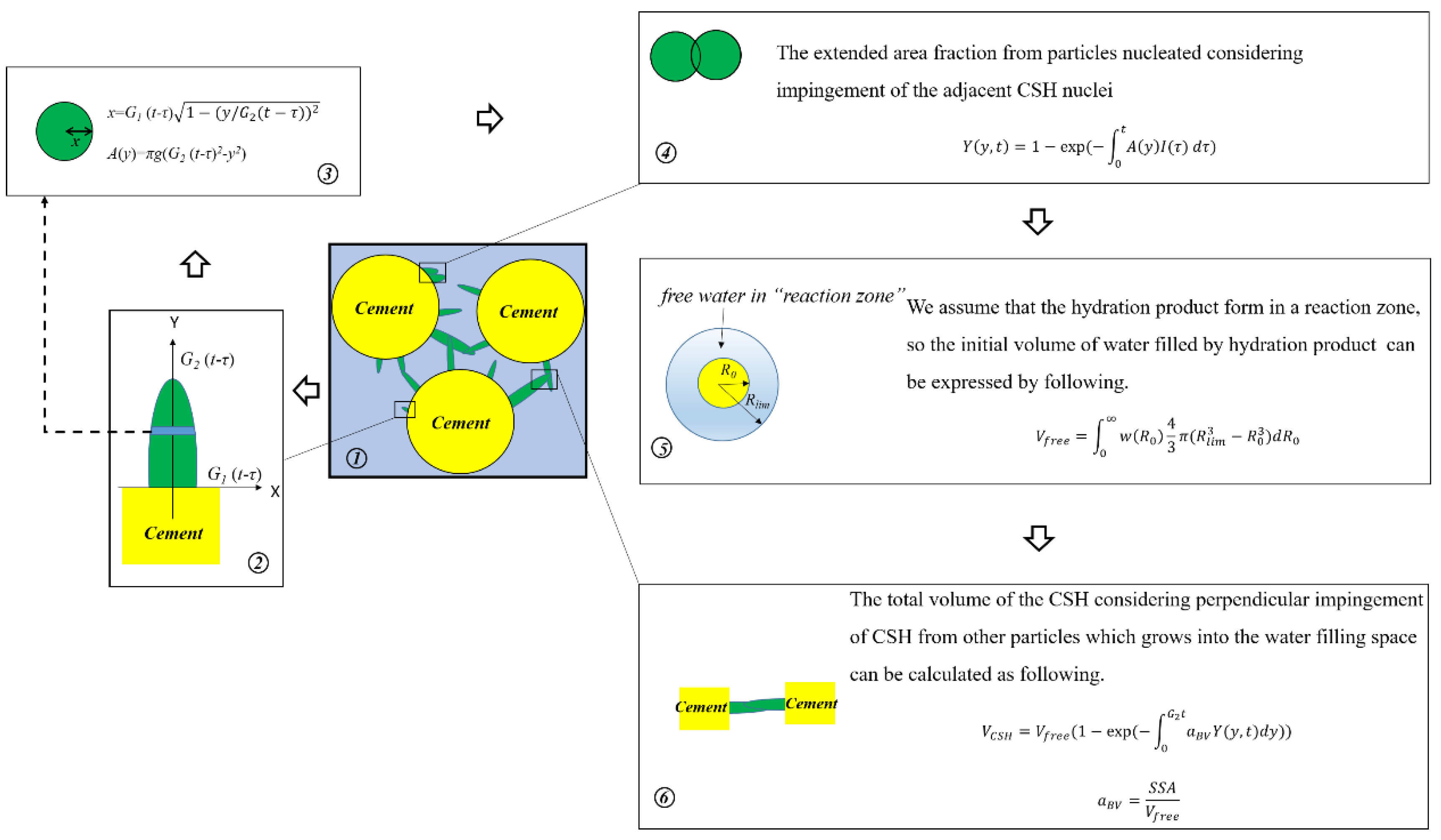
2.1. Boundary Nucleation and Growth
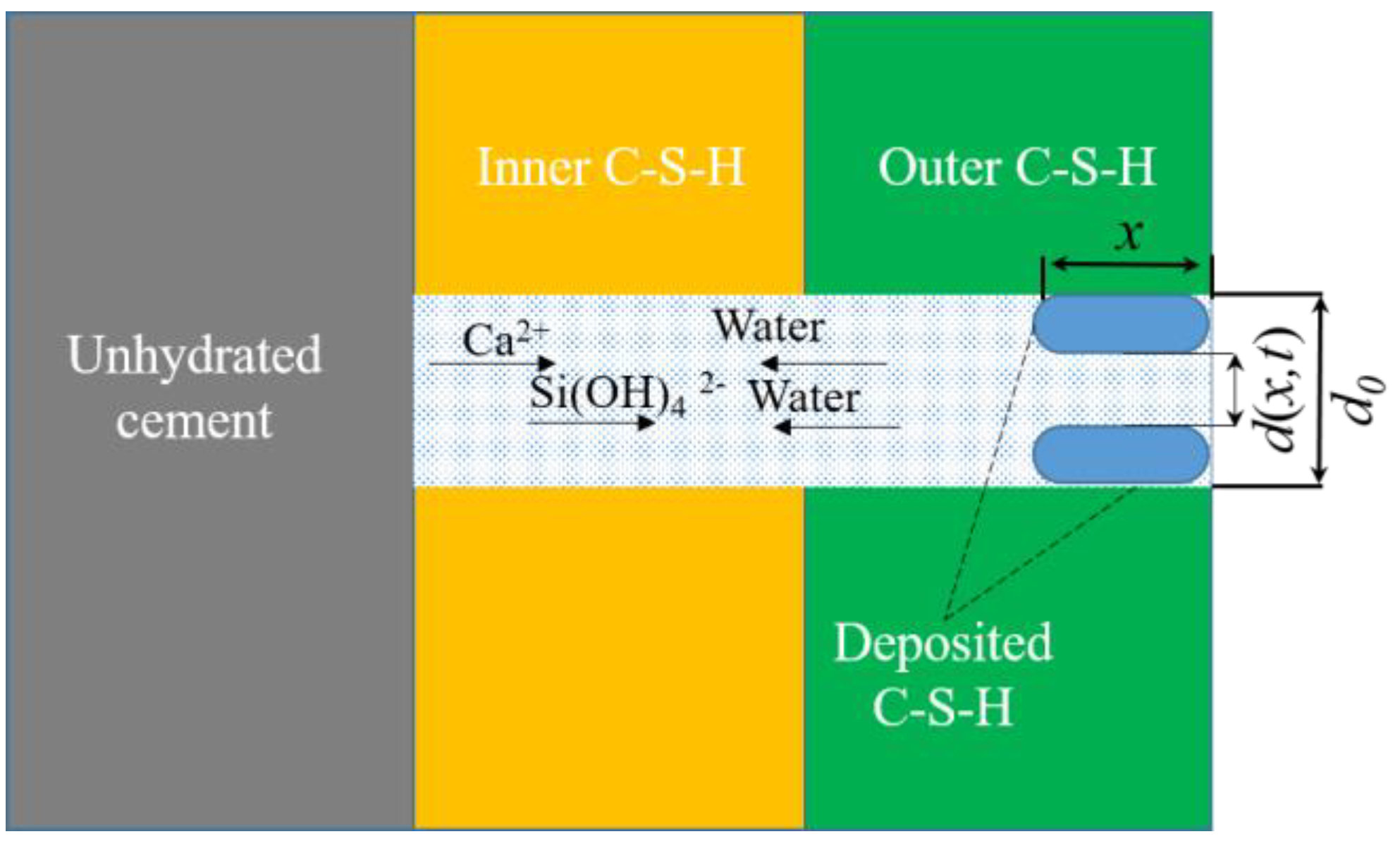
2.2. Diffusion
3. Construction of the New Hydration Kinetics Model
3.1. Nucleation and Growth Model
3.2. Modified Diffusion Model
3.2.1. Effects of the PSD on Hydration Kinetics
3.2.2. Effects of the Effective Diffusion Coefficient on Hydration Kinetics
3.2.3. Effects of Temperature on Hydration Kinetics
3.2.4. Effects of Cement Composition on Hydration Kinetics
3.2.5. Determination of the Transition Time
3.3. Hydration Kinetics Model for Cement with Set-Controlling Admixture
3.3.1. Influence of Retarder on Cement Hydration
3.3.2. Influence of Accelerator on Cement Hydration
3.3.3. Modified Hydration Kinetics Model
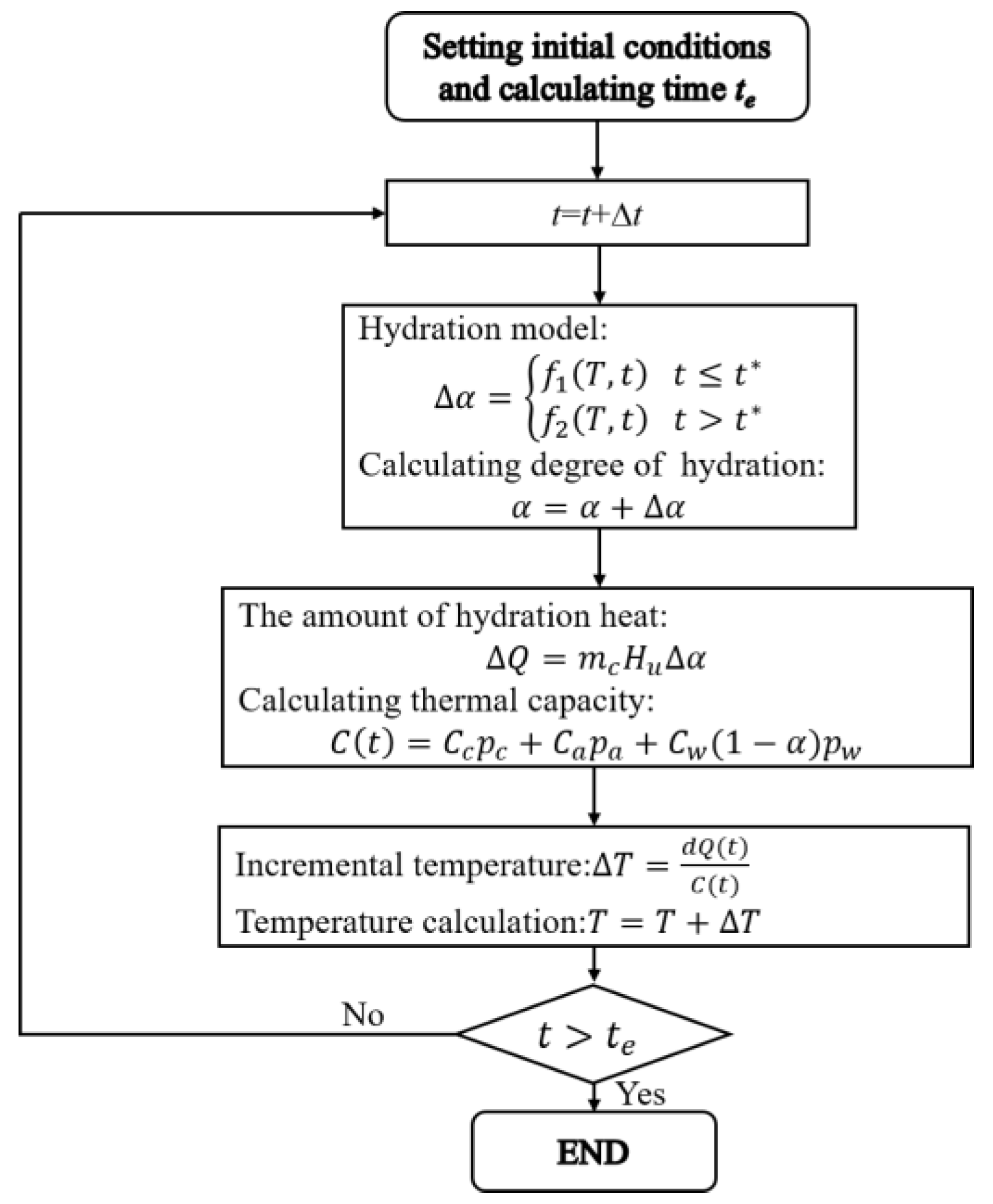
4. Predicting Temperature Development of Concrete with Set-Controlling Admixture
4.1. Materials and Methods
4.1.1. Materials
4.1.2. Methods
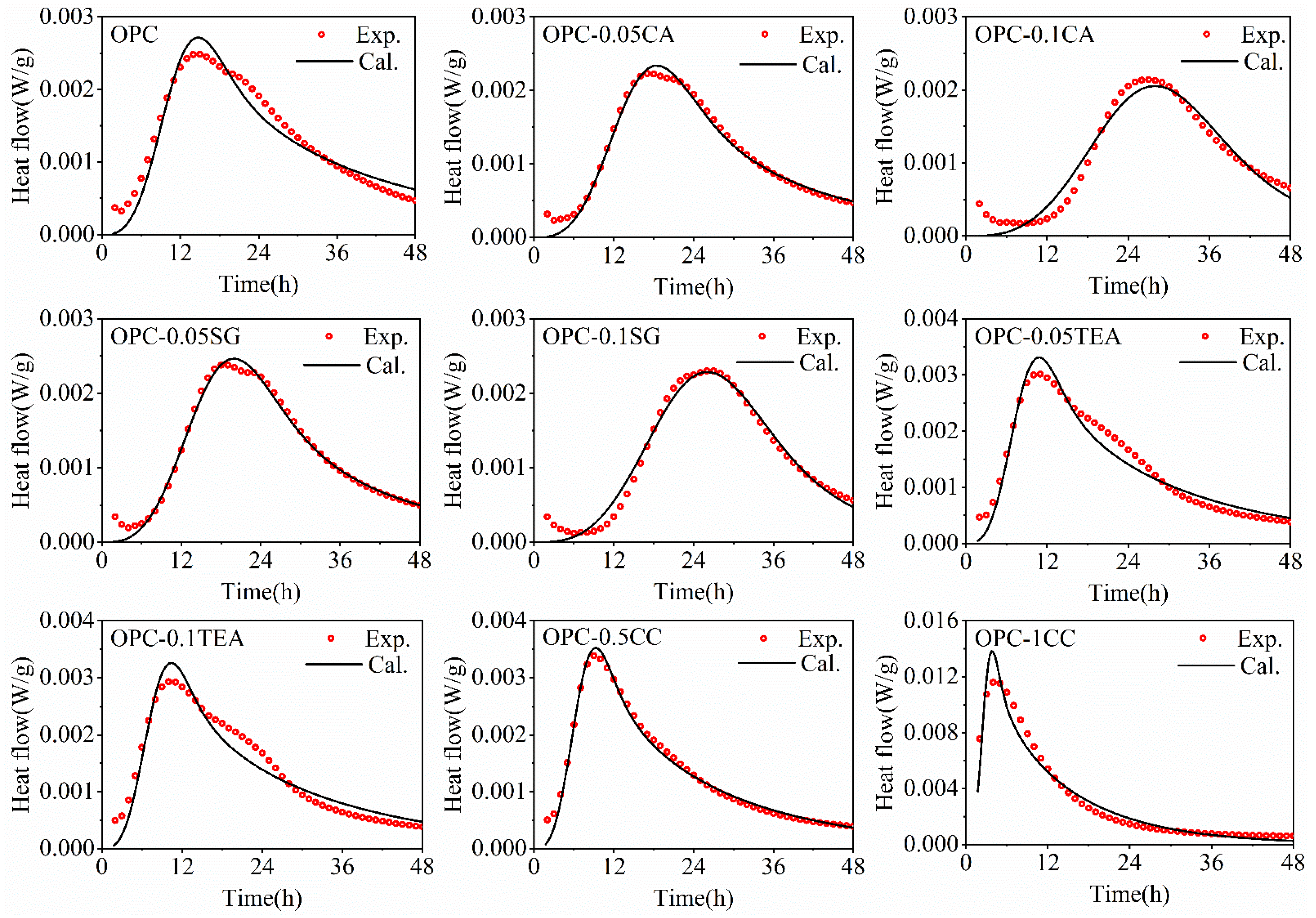
4.2. Analysis of Hydration Kinetic
4.3. Predicting the Adiabatic Temperature Rise History of Concrete
5. Conclusions
- The influence of retarders on the nucleation and growth of hydration products shows in two ways: (1) the retarder occupies the nucleus of hydration products, thereby reducing the rate of nucleation and rate of growth and (2) the retarder blocks the surface of cement, reducing the area of boundary of nucleation and growth.
- The influence of accelerators on the nucleation and growth of hydration products shows in two ways: (1) the accelerators increase the rate of nucleation and rate of growth and (2) organic accelerators can block the surface of cement, reducing the area of boundary of nucleation and growth.
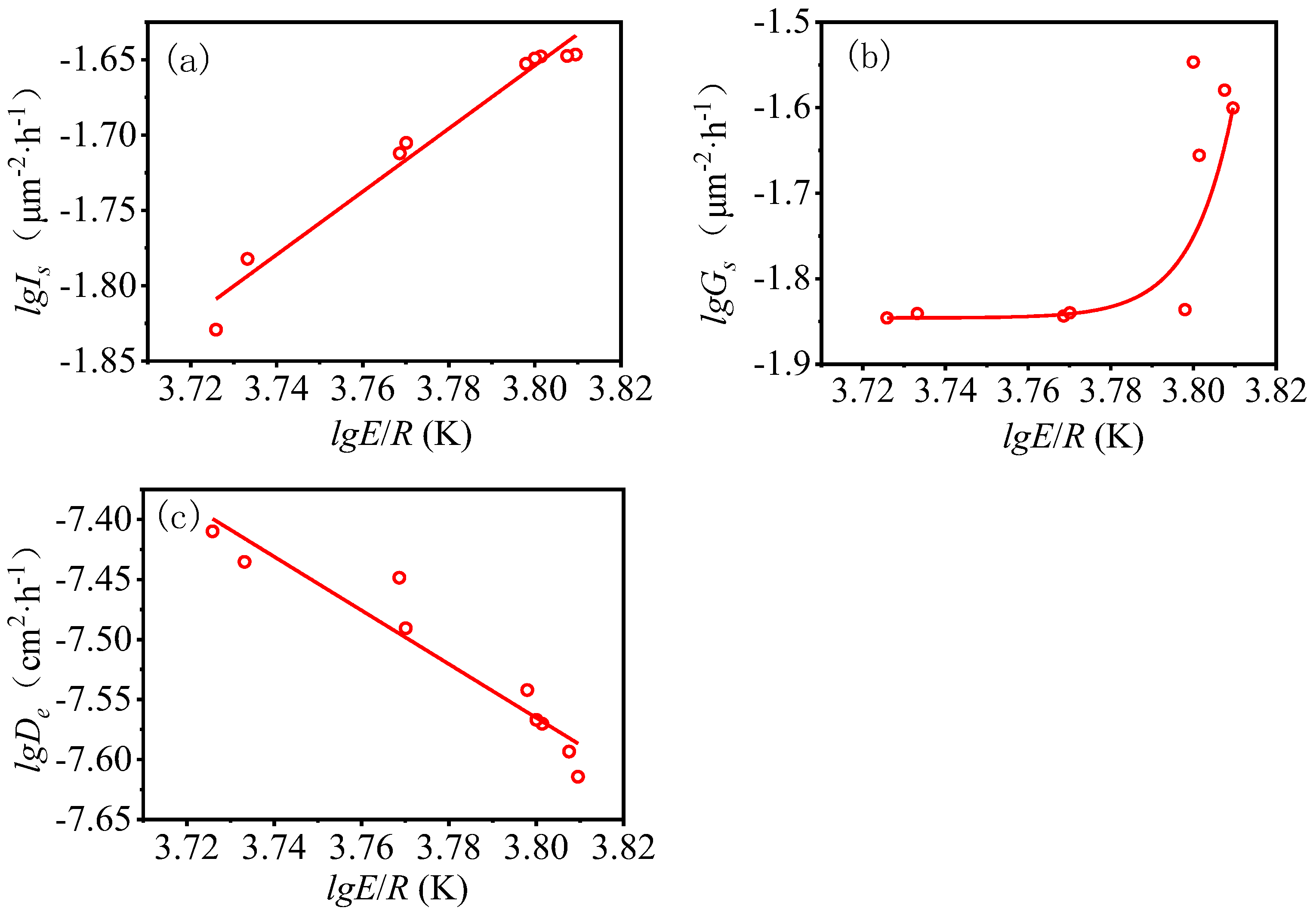
- The nucleation rate increases with the increase of apparent activation energy, and this is a linear relationship. The growth rate increases with the increasing of apparent activation energy, and this is an exponential relationship. The effective diffusion coefficient decreases with the increasing of apparent activation energy, and this is a linear relationship.
- The hydration rate of cement determines the heat release rate of concrete. Furthermore, the temperature development of concrete can be calculated by the hydration degree of cement and the modeled results agree with the experimental results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Evsukoff, A.G.; Fairbairn, E.M.; Faria, F.; Silvoso, M.M.; Filho, R.D.T. Modeling adiabatic temperature rise during concrete hydration: A data mining approach. Comput. Struct. 2006, 84, 2351–2362. [Google Scholar] [CrossRef]
- An, G.-H.; Park, J.-M.; Cha, S.-L.; Kim, J.-K. Development of a portable device and compensation method for the prediction of the adiabatic temperature rise of concrete. Constr. Build. Mater. 2016, 102, 640–647. [Google Scholar] [CrossRef]
- Zheng, J.J.; Zhang, J.; Scherer, G.W. Prediction of the degree of hydration at initial setting time of cement paste with particle agglomeration. Cem. Concr. Res. 2012, 42, 1280–1285. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, W.; Han, F.; Yan, P. A new hydration kinetics model of composite cementitious materials, Part 2: Physical effect of SCMs. J. Am. Ceram. Soc. 2020, 103, 3880–3895. [Google Scholar] [CrossRef]
- Wang, X.; Lee, H. Modeling the hydration of concrete incorporating fly ash or slag. Cem. Concr. Res. 2010, 40, 984–996. [Google Scholar] [CrossRef]
- Liu, K.; Yu, J.; Xia, Y.; Wang, H.; Wang, D.; Du, J.; Tian, Y.; Zhang, X. Quantitative determination of the hydrostatic pressure of oil-well cement slurry using its hydration kinetics. Constr. Build. Mater. 2022, 340, 127704. [Google Scholar] [CrossRef]
- Zhou, L.; Gou, M.; Guan, X. Hydration kinetics of cement-calcined activated bauxite tailings composite binder. Constr. Build. Mater. 2021, 301, 124296. [Google Scholar] [CrossRef]
- Pang, X.; Sun, L.; Sun, F.; Zhang, G.; Guo, S.; Bu, Y. Cement hydration kinetics study in the temperature range from 15 °C to 95 °C. Cem. Concr. Res. 2021, 148, 106552. [Google Scholar] [CrossRef]
- Taplin, J. On the Hydration Kinetics of Hydraulic Cements. In Proceedings of the 5th International Symposium on Chemistry of Cement, Tokyo, Japan, 7–11 October 1968; pp. 337–348. [Google Scholar]
- Brown, P. Effects of particle size distribution on the kinetics of hydration of tricalcium silicate. J. Am. Ceram. Soc. 1989, 72, 1829–1832. [Google Scholar] [CrossRef]
- Xie, T.; Biernacki, J. The origins and evolution of cement hydration models. Comput. Concr. 2011, 8, 647–675. [Google Scholar] [CrossRef]
- Thomas, J.; Biernacki, J.; Bullard, J. Modeling and simulation of cement hydration kinetics and microstructure development. Cem. Conc. Res. 2011, 41, 1257–1278. [Google Scholar] [CrossRef]
- Liu, J.; Yu, C.; Shu, X.; Ran, Q.; Yang, Y. Recent advance of chemical admixtures in concrete. Cem. Concr. Res. 2019, 124, 105834. [Google Scholar] [CrossRef]
- Teng, Y.; Liu, S.; Zhang, Z. Effect of triethanolamine on the chloride binding capacity of cement paste with a high volume of fly ash. Constr. Build. Mater. 2021, 315, 125612. [Google Scholar] [CrossRef]
- Gao, Y.; Guo, T.; Li, Z. Mechanism of retarder on hydration process and mechanical properties of red mud-based geopolymer cementitious materials. Constr. Build. Mater. 2022, 350, 129306. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. II transformation-time relations for random distribution of nuclei. J. Chem. Phys. 1940, 2, 212–224. [Google Scholar] [CrossRef]
- Masoero, E.; Thomas, J.; Jennings, H. A Reaction Zone Hypothesis for the Effects of Particle Size and Water-to-Cement Ratio on the Early Hydration Kinetics of C3S. J. Am. Ceram. Soc. 2013, 97, 967–975. [Google Scholar] [CrossRef] [Green Version]
- Ouzia, A.; Scrivener, K. The needle model: A new model for the main hydration peak of alite. Cem. Concr. Res. 2018, 115, 339–360. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Huang, L.; Yan, P. A new hydration kinetics model of composite cementitious materials, part 1: Hydration kinetic model of Portland cement. J. Am. Ceram. Soc. 2019, 103, 1970–1991. [Google Scholar] [CrossRef]
- Fujii, K.; Kondo, W. Kinetics of the hydration of tricalcium silicate. J. Am. Ceram. Soc. 1974, 11, 492–497. [Google Scholar] [CrossRef]
- Honorio, T.; Bary, B.; Benboudjema, F.; Poyet, S. Modeling hydration kinetics based on boundary nucleation and space-filling growth in a fixed confined zone. Cem. Concr. Res. 2016, 83, 31–44. [Google Scholar] [CrossRef]
- Park, K.; Noguchi, T.; Plawsky, J. Modeling of hydration reactions using neural networks to predict the average properties of cement paste. Cem. Concr. Res. 2005, 35, 1676–1684. [Google Scholar] [CrossRef]
- Park, K.; Jee, N.; Yoon, I.; Lee, H. Prediction of Temperature Distribution in High-Strength Concrete Using Hydration Model. Aci. Mater. J. 2008, 105, 180. [Google Scholar]
- Cheung, J.; Jeknavorian, A.; Roberts, L.; Silva, D. Impact of admixtures on the hydration kinetics of Portland cement. Cem. Concr. Res. 2011, 41, 1289–1309. [Google Scholar] [CrossRef]
- Previte, R.; W.R. Grace & Co. Some insights on the mechanism of saccharide set retardation of portland cement. Cem. Concr. Res. 1971, 1, 301–316. [Google Scholar] [CrossRef]
- Young, J. A review of the mechanisms of set-retardation in portland cement pastes containing organic admixtures. Cem. Concr. Res. 1972, 2, 415–433. [Google Scholar] [CrossRef]
- Thomas, N.; Birchall, J. The Retarding Action of Sugars on Cement Hydration. Cem. Concr. Res. 1983, 13, 830–842. [Google Scholar] [CrossRef]
- Juilland, P.; Gallucci, E.; Flatt, R.; Scrivener, K. Dissolution Theory Applied to the Induction Period in Alite Hydration. Cem. Concr. Res. 2010, 40, 831–844. [Google Scholar] [CrossRef]
- Yan, Y.; Ouzia, A.; Yu, C.; Liu, J.; Scrivener, K. Effect of a novel starch-based temperature rise inhibitor on cement hydration and microstructure development. Cem. Concr. Res. 2020, 129, 105961. [Google Scholar] [CrossRef]
- Perez, J.-P. The mechanism of action of sodium gluconate on the fluidity and set of Portland cement. In Proceedings of the 12th International Congress on the Chemistry of Cement, Montreal, QC, Canada, 8–13 July 2007. [Google Scholar]
- Zajac, M.; Skocek, J.; Bullerjahn, F.; Haha, M. Effect of retarders on the early hydration of calcium-sulpho-aluminate (CSA) type cements. Cem. Concr. Res. 2016, 84, 62–75. [Google Scholar] [CrossRef]
- Yaphary, Y.; Yu, Z.; Lam, R.; Lau, D. Effect of triethanolamine on cement hydration toward initial setting time. Constr. Build. Mater. 2017, 141, 94–103. [Google Scholar] [CrossRef]
- Jachiet, M.; Azéma, N.; Le Saoût, G.; Garcia-Diaz, E.; Kocaba, V. Influence of triethanolamine on cement pastes at early age of hydration. Adv. Cem. Res. 2018, 30, 159–171. [Google Scholar] [CrossRef]
- Lu, Z.; Kong, X.; Jansen, D.; Zhang, C.; Yin, J. Towards a further understanding of cement hydration in the presence of triethanolamine. Cem. Concr. Res. 2020, 132, 106041. [Google Scholar] [CrossRef]
- Riding, K.; Poole, J.; Folliard, K.; Juenger, M.; Schindler, A. Modeling hydration of cementitious systems. Aci. Mater. J. 2012, 109, 225–234. [Google Scholar]



| SiO2 | Al2O3 | Fe2O3 | CaO | MgO | K2O | Na2O | SO3 | Ignition Loss |
|---|---|---|---|---|---|---|---|---|
| 20.71 | 5.29 | 3.55 | 62.81 | 1.43 | 1.1 | 0.167 | 1.54 | 1.36 |
| Sample Code | OPC | CA | SG | TEA | CC |
|---|---|---|---|---|---|
| OPC | 100 | - | - | - | - |
| OPC-0.05CA | 100 | 0.05 | - | - | - |
| OPC-0.1CA | 100 | 0.1 | - | - | - |
| OPC-0.05SG | 100 | - | 0.05 | - | - |
| OPC-0.1SG | 100 | - | 0.1 | - | - |
| OPC-0.05TEA | 100 | - | - | 0.05 | - |
| OPC-0.1TEA | 100 | - | - | 0.1 | - |
| OPC-0.5CC | 100 | - | - | - | 0.5 |
| OPC-1CC | 100 | - | - | - | 1 |
| Sample Code | Water | OPC | Fine Aggregate | Coarse Aggregate | CA | SG | TEA | CC |
|---|---|---|---|---|---|---|---|---|
| PC | 214.5 | 390 | 825 | 1238 | - | - | - | - |
| PC-0.05CA | 214.5 | 390 | 825 | 1238 | 0.195 | - | - | - |
| PC-0.05SG | 214.5 | 390 | 825 | 1238 | - | 0.195 | - | - |
| PC-0.05TEA | 214.5 | 390 | 825 | 1238 | - | - | 0.195 | - |
| PC-1CC | 214.5 | 390 | 825 | 1238 | - | - | - | 0.390 |
| Sample Code | Is (μm−2·h−1) | Ieff | Gs (μm−2·h−1) | Geff | SSAs (m2·kg−1) | SSAr | De (cm2·h−1) | E/R (K) |
|---|---|---|---|---|---|---|---|---|
| OPC | 0.022250 | 1.000 | 0.014580 | 1.000 | 369.5 | 1.000 | 2.87 × 10−8 | 6280 |
| OPC-0.05CA | 0.019402 | 0.872 | 0.014332 | 0.983 | 341.0 | 0.923 | 3.56 × 10−8 | 5870 |
| OPC-0.1CA | 0.014819 | 0.666 | 0.014259 | 0.978 | 334.0 | 0.904 | 3.89 × 10−8 | 5320 |
| OPC-0.05SG | 0.019714 | 0.886 | 0.014449 | 0.991 | 345.1 | 0.934 | 3.23 × 10−8 | 5890 |
| OPC-0.1SG | 0.016510 | 0.742 | 0.014420 | 0.989 | 335.9 | 0.909 | 3.67 × 10−8 | 5410 |
| OPC-0.05TEA | 0.022495 | 1.011 | 0.022089 | 1.515 | 359.9 | 0.974 | 2.69 × 10−8 | 6330 |
| OPC-0.1TEA | 0.022562 | 1.014 | 0.025092 | 1.721 | 354.4 | 0.959 | 2.43 × 10−8 | 6450 |
| OPC-0.5CC | 0.022428 | 1.008 | 0.032384 | 2.907 | 369.5 | 1.000 | 2.71 × 10−8 | 6310 |
| OPC-1CC | 0.022517 | 1.012 | 0.030316 | 3.451 | 369.5 | 1.000 | 2.55 × 10−8 | 6420 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Zhu, P.; Shi, Y.; Xu, F.; Jiang, L.; Chu, H.; Xu, N.; Liu, M.; Jia, Y.; Peng, T. Prediction of Temperature Development of Concrete with Set-Controlling Admixture Based on a New Hydration Kinetics Model. Materials 2023, 16, 497. https://doi.org/10.3390/ma16020497
Yu Y, Zhu P, Shi Y, Xu F, Jiang L, Chu H, Xu N, Liu M, Jia Y, Peng T. Prediction of Temperature Development of Concrete with Set-Controlling Admixture Based on a New Hydration Kinetics Model. Materials. 2023; 16(2):497. https://doi.org/10.3390/ma16020497
Chicago/Turabian StyleYu, Yi, Pengfei Zhu, Yanran Shi, Fei Xu, Linhua Jiang, Hongqiang Chu, Ning Xu, Mingwei Liu, Yu Jia, and Tao Peng. 2023. "Prediction of Temperature Development of Concrete with Set-Controlling Admixture Based on a New Hydration Kinetics Model" Materials 16, no. 2: 497. https://doi.org/10.3390/ma16020497
APA StyleYu, Y., Zhu, P., Shi, Y., Xu, F., Jiang, L., Chu, H., Xu, N., Liu, M., Jia, Y., & Peng, T. (2023). Prediction of Temperature Development of Concrete with Set-Controlling Admixture Based on a New Hydration Kinetics Model. Materials, 16(2), 497. https://doi.org/10.3390/ma16020497






