Nondestructive Examination of Carbon Fiber-Reinforced Composites Using the Eddy Current Method
Abstract
1. Introduction
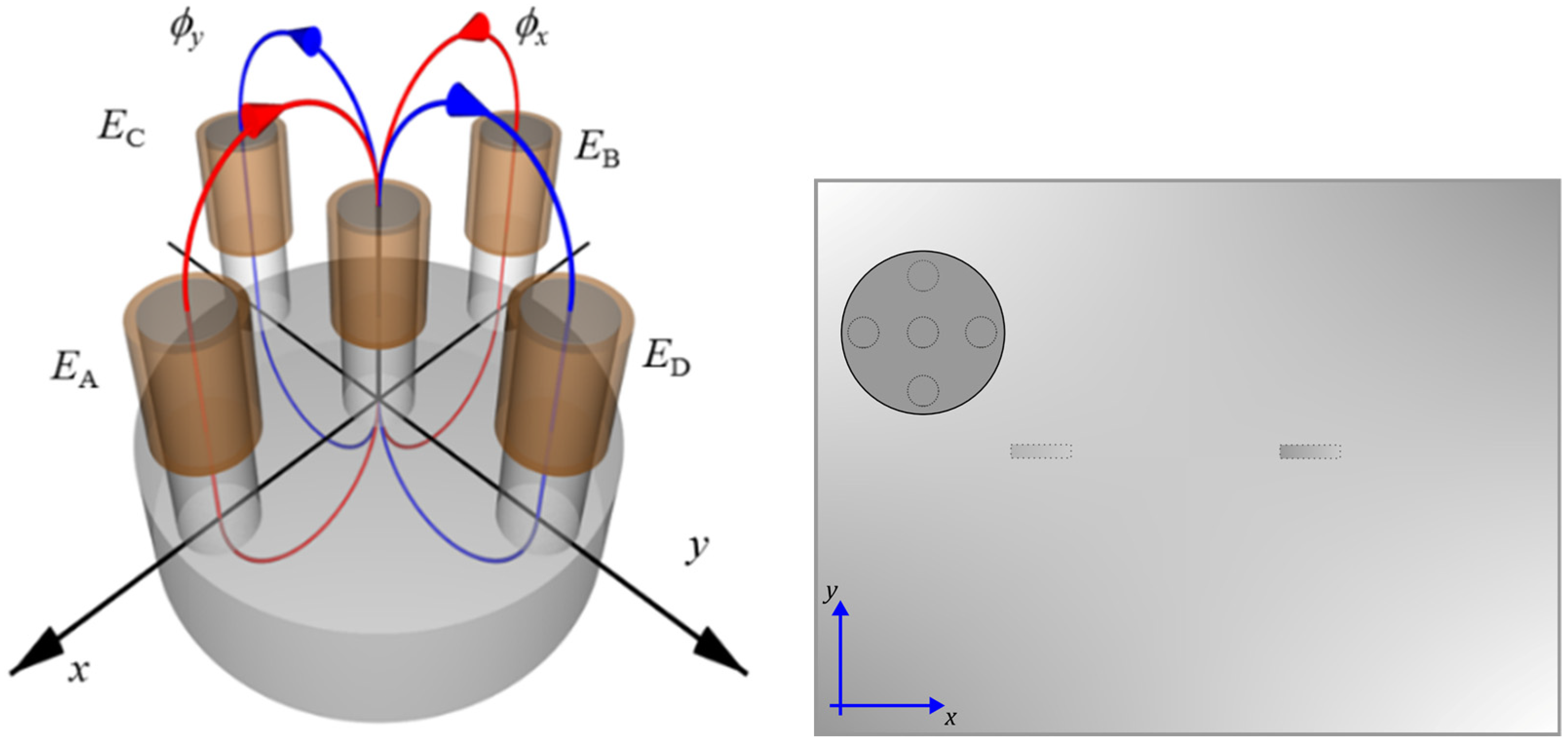
2. Materials and Methods
3. Results of Experiments and Discussion
3.1. Preliminary Investigation of the Transducer
- (a)
- the transducer was placed over the central unflawed part of the sample, and the voltage U1 was measured
- (b)
- the transducer was placed at the edge of the sample (one of the excitation coils was outside the sample), and the voltage U2 was measured.
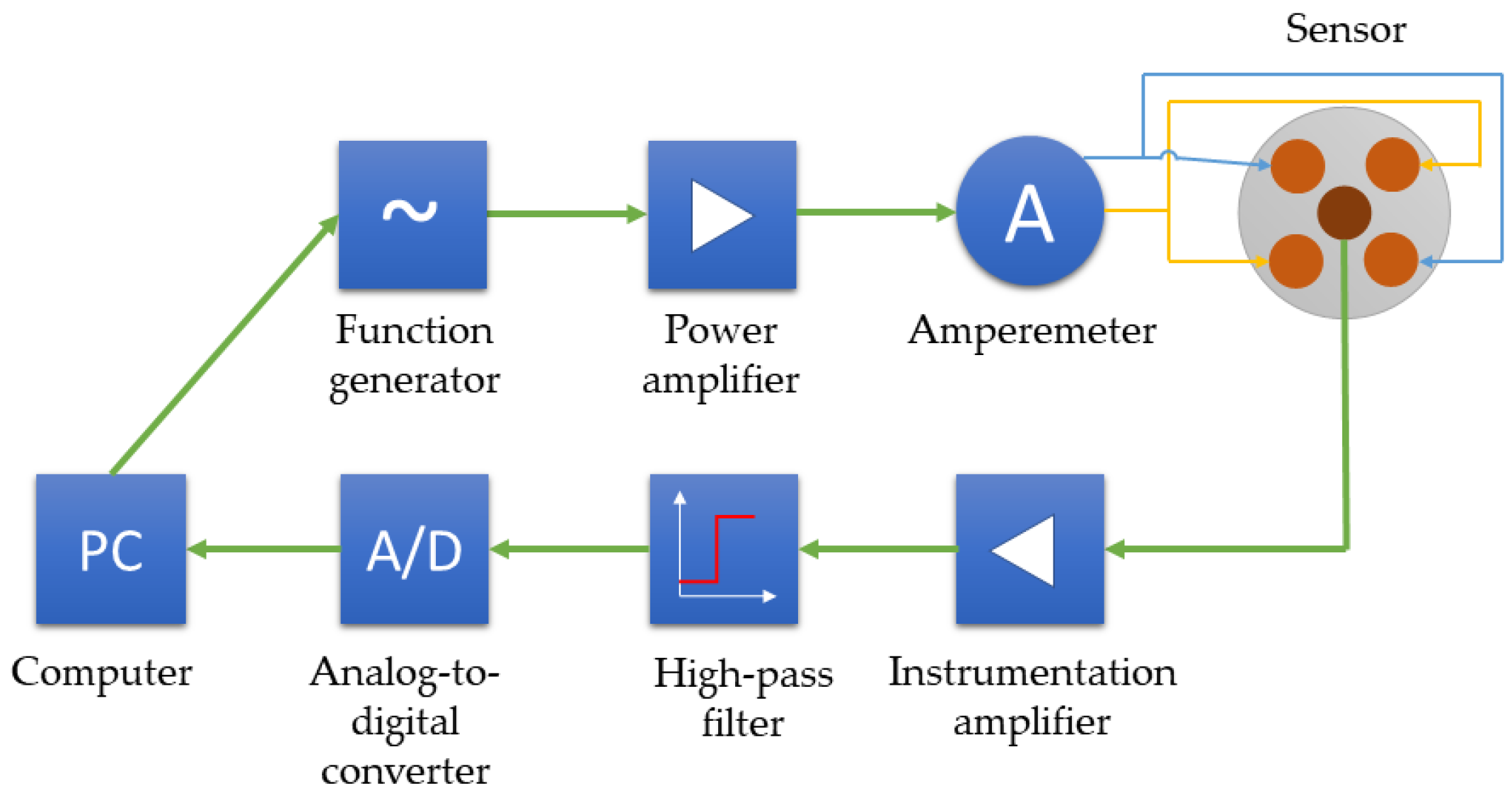
3.2. Measurement and Data Processing
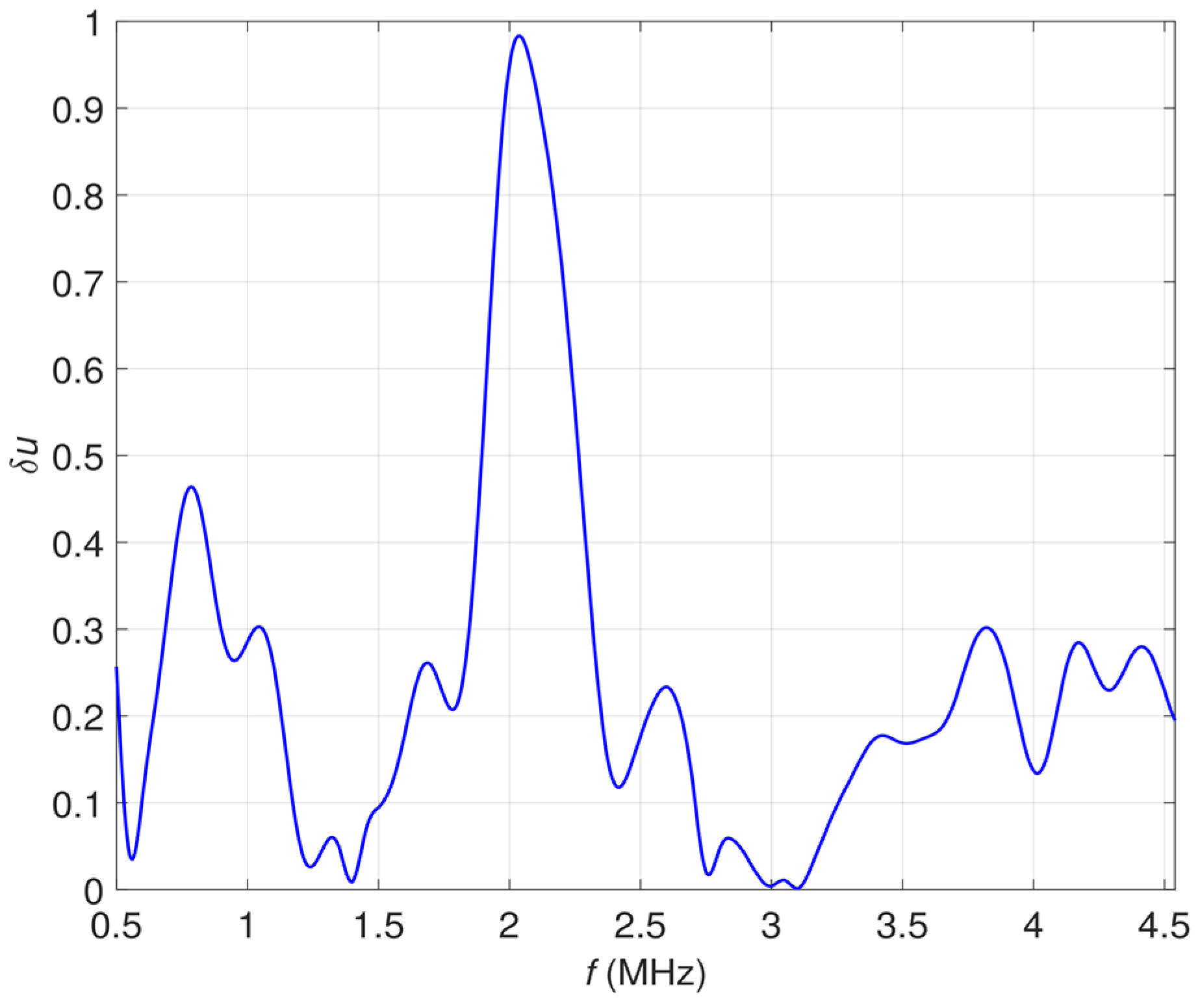
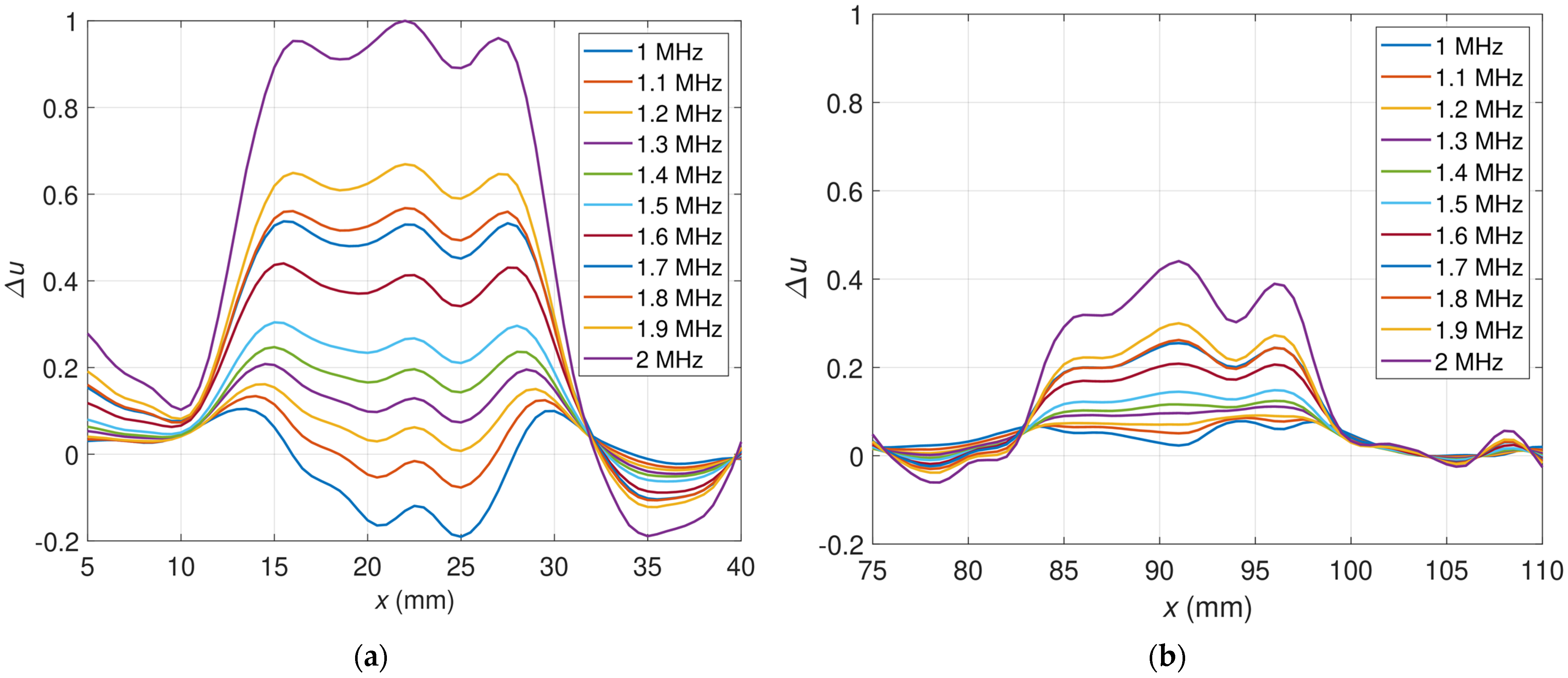
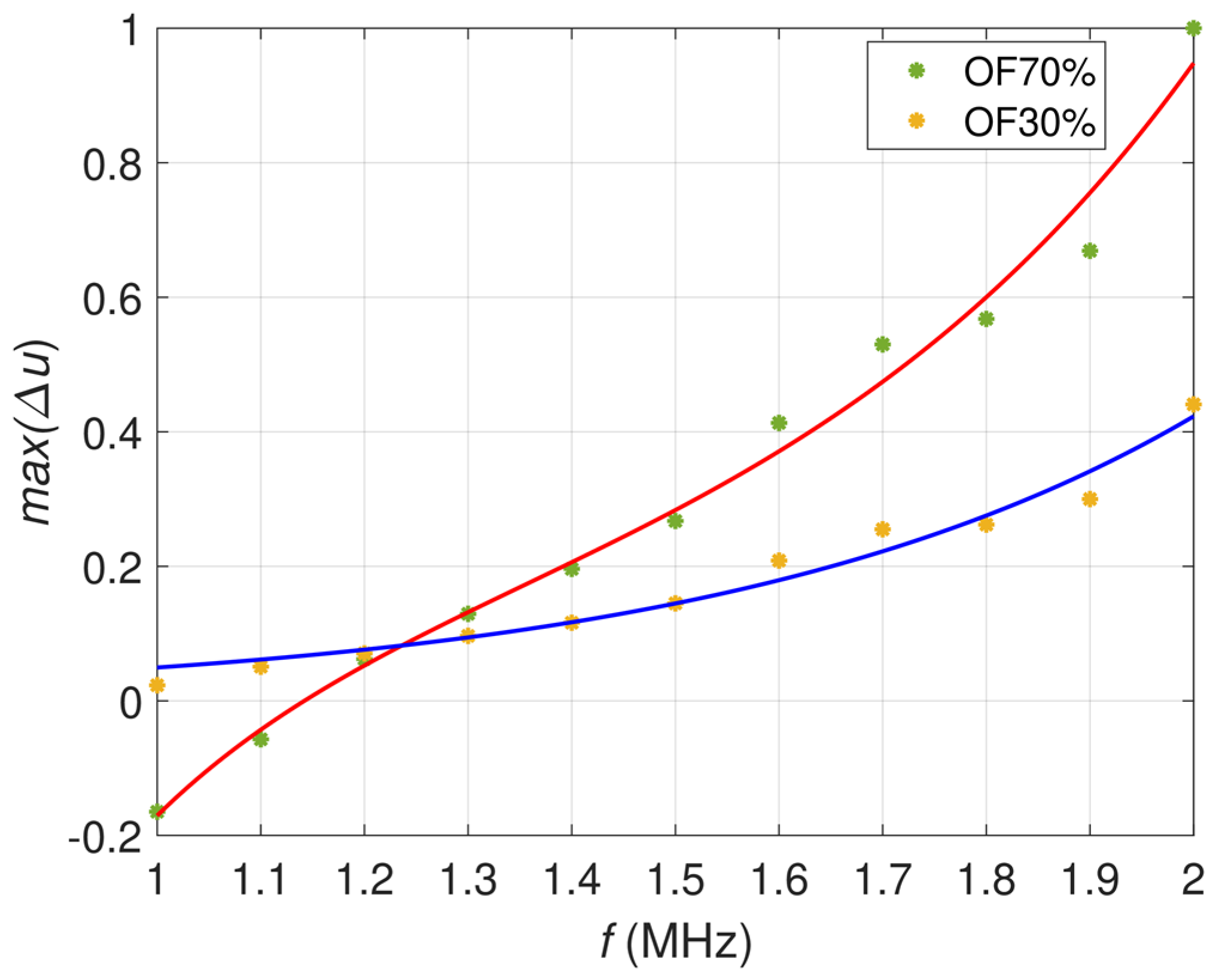
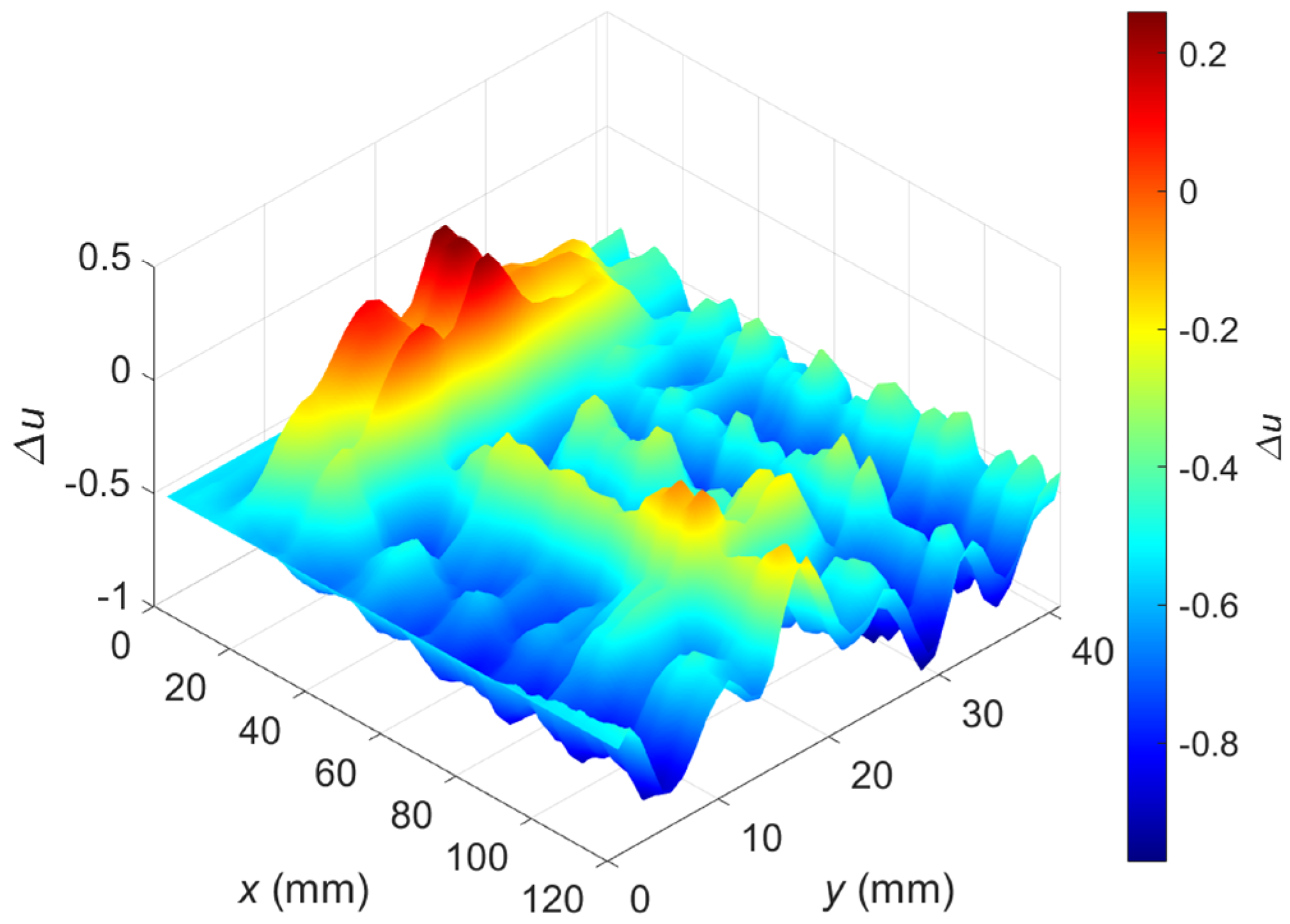
3.3. Results of Multifrequency 1D Examination
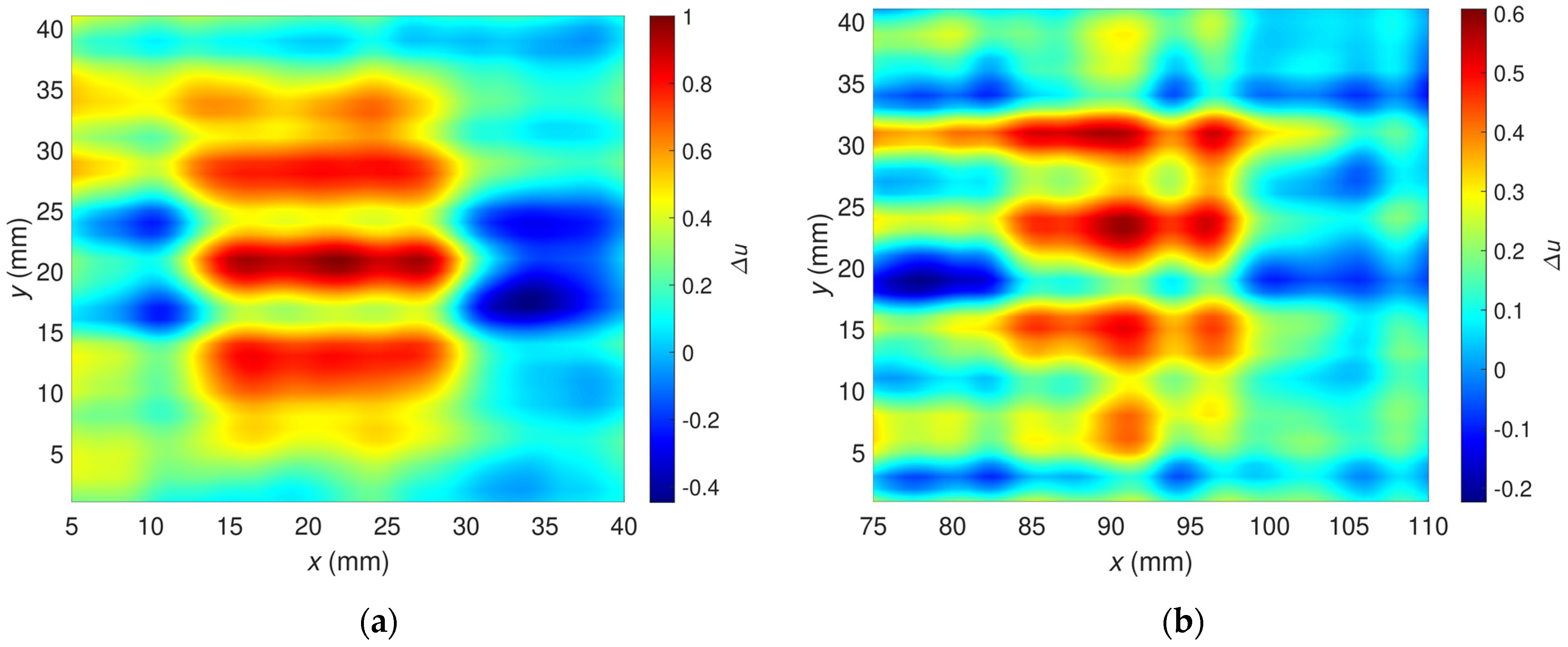
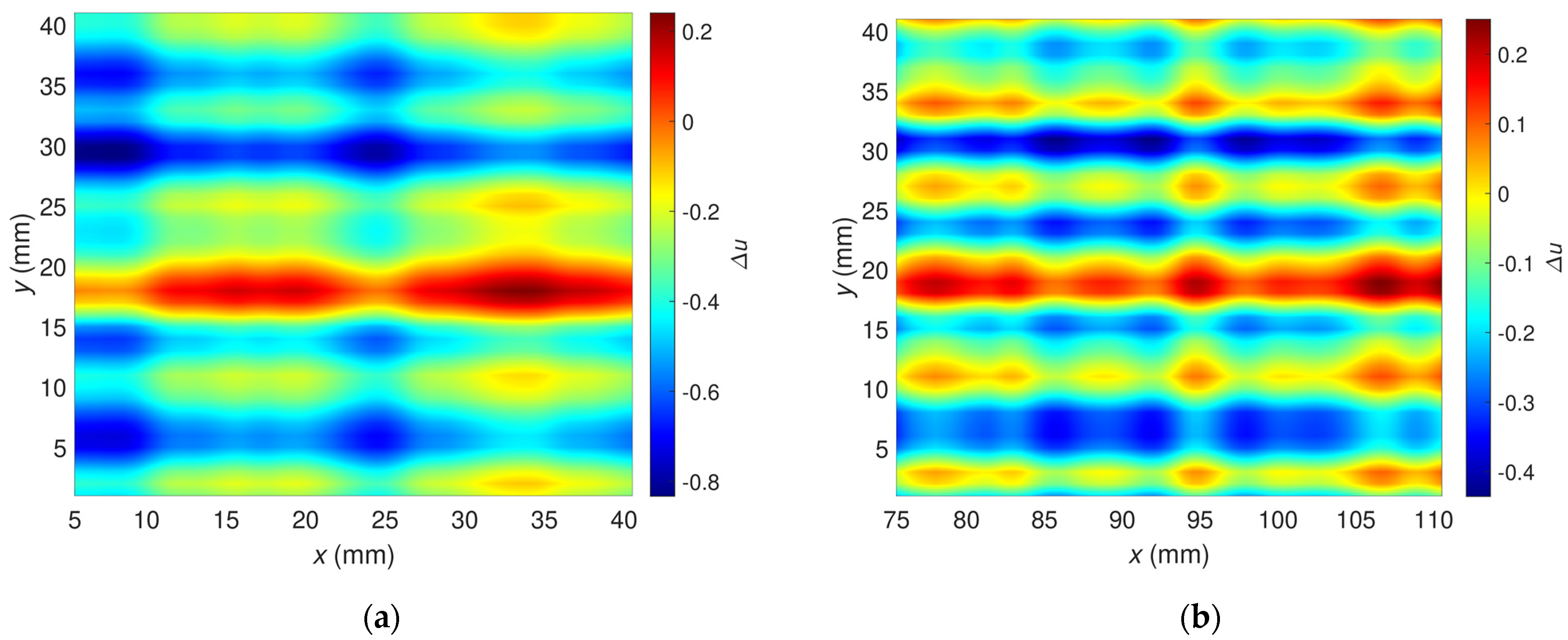
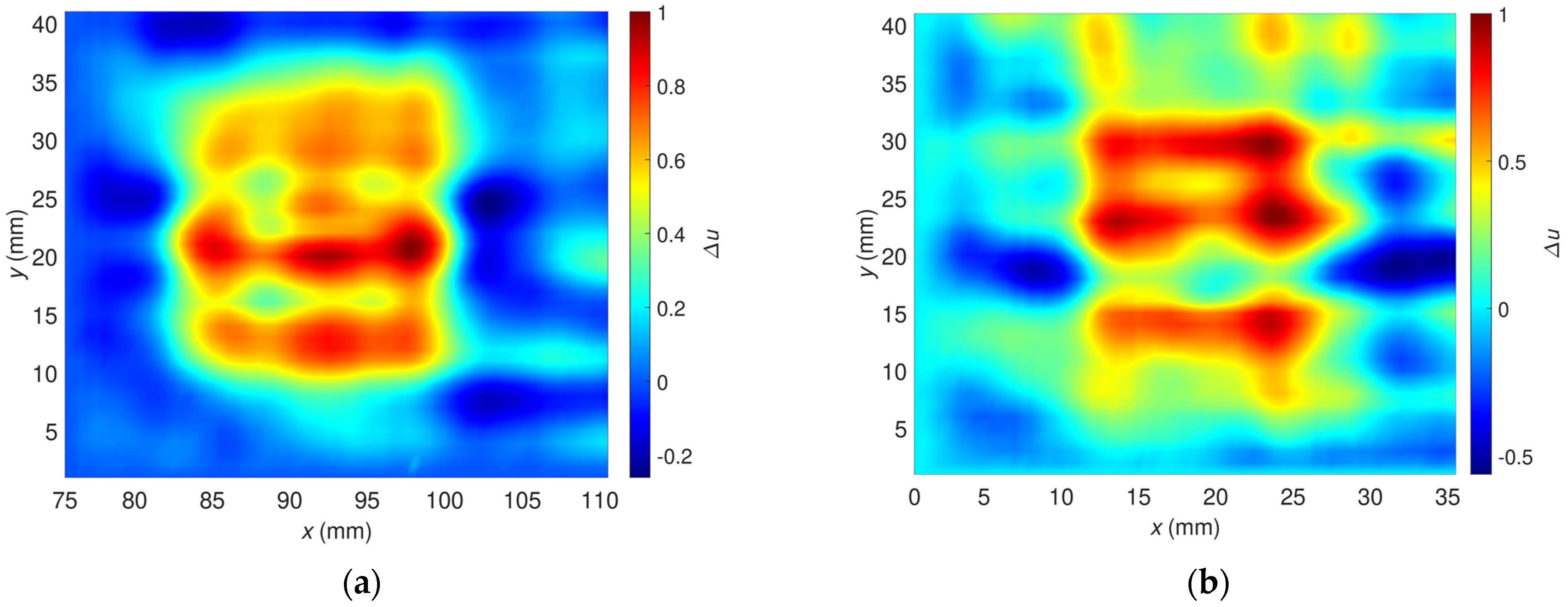
3.4. Results of Two-Dimensional Examination with a Single-Frequency Excitation
4. Conclusions
- A differential transducer allows for a significant increase in sensitivity, but placing the reference sensor close to the measured material is not an effective solution due to the anisotropy of the tested material; a more effective solution seems to be the use of a reference sensor with the reference material;
- The ability to detect defects can be improved by using signal processing, such as the proposed background signal removal;
- The use of resonant frequencies allows for multiple increases in the sensitivity of the transducer; at the same time, it is more complicated to use the frequency response to identify the type and depth of the defect;
- The use of even a relatively low excitation frequency that guarantees the appropriate depth of penetration does not prevent the effective detection of surface defects;
- The use of the frequency response to defects identification in the case of the composite materials requires the use of a much wider range of excitation frequencies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Backens, S.; Unseld, J.; Glück, N.; Wolter, A. Incombustible, Inorganic Fiber-reinforced Composites for Shipbuilding. Light. Des. Worldw. 2019, 12, 38–43. [Google Scholar] [CrossRef]
- Wang, X.; Qi, X.; Lin, Z.; Battocchi, D. Graphene Reinforced Composites as Protective Coatings for Oil and Gas Pipelines. Nanomaterials 2018, 8, 1005. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, F.; Sena-Cruz, J.; Branco, F.G.; Júlio, E.; Castro, F. Analytical hybrid effect prediction and evolution of the tensile response of unidirectional hybrid fibre-reinforced polymers composites for civil engineering applications. J. Compos. Mater. 2020, 54, 3205–3228. [Google Scholar] [CrossRef]
- Murray, R.E.; Beach, R.; Barnes, D.; Snowberg, D.; Berry, D.; Rooney, S.; Jenks, M.; Gage, B.; Boro, T.; Wallen, S.; et al. Structural validation of a thermoplastic composite wind turbine blade with comparison to a thermoset composite blade. Renew. Energy 2020, 164, 1100–1107. [Google Scholar] [CrossRef]
- Fereiduni, E.; Ghasemi, A.; Elbestawi, M. Selective Laser Melting of Aluminum and Titanium Matrix Composites: Recent Progress and Potential Applications in the Aerospace Industry. Aerospace 2020, 7, 77. [Google Scholar] [CrossRef]
- Mishnaevsky, L.; Thomsen, K. Costs of repair of wind turbine blades: Influence of technology aspects. Wind. Energy 2020, 23, 2247–2255. [Google Scholar] [CrossRef]
- Márquez, F.P.G.; Chacón, A.M.P. A review of non-destructive testing on wind turbines blades. Renew. Energy 2020, 161, 998–1010. [Google Scholar] [CrossRef]
- Carroll, J.; McDonald, A.; McMillan, D. Failure rate, repair time and unscheduled O&M cost analysis of offshore wind turbines. Wind Energy 2016, 19, 1107–1119. [Google Scholar] [CrossRef]
- Gao, Z.; Liu, X. An Overview on Fault Diagnosis, Prognosis and Resilient Control for Wind Turbine Systems. Processes 2021, 9, 300. [Google Scholar] [CrossRef]
- Wang, D.; Liao, B.; Zheng, J.; Huang, G.; Hua, Z.; Gu, C.; Xu, P. Development of regulations, codes and standards on composite tanks for on-board gaseous hydrogen storage. Int. J. Hydrog. Energy 2019, 44, 22643–22653. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, J.; Pan, Z.-B.; Liu, J.; Ma, L.-H.; Zhou, J.-Y.; Su, Y.-F. Review on optimization design, failure analysis and non-destructive testing of composite hydrogen storage vessel. Int. J. Hydrog. Energy 2022, 47, 38862–38883. [Google Scholar] [CrossRef]
- Abdalla, A.N.; Ali, K.; Paw, J.K.S.; Rifai, D.; Faraj, M.A. A Novel Eddy Current Testing Error Compensation Technique Based on Mamdani-Type Fuzzy Coupled Differential and Absolute Probes. Sensors 2018, 18, 2108. [Google Scholar] [CrossRef]
- Rifai, D.; Abdalla, A.N.; Khamsah, N.; Aizat, M.; Fadzli, M. Subsurface Defects Evaluation using Eddy Current Testing. Indian J. Sci. Technol. 2016, 9, 1–7. [Google Scholar] [CrossRef]
- Mizukami, K.; bin Ibrahim, A.S.; Ogi, K.; Matvieieva, N.; Kharabet, I.; Schulze, M.; Heuer, H. Enhancement of sensitivity to delamination in eddy current testing of carbon fiber composites by varying probe geometry. Compos. Struct. 2019, 226, 111227. [Google Scholar] [CrossRef]
- Wu, D.; Yang, F.; Wang, T.; Chen, W. A novel electromagnetic nondestructive testing method for carbon fiber reinforced polymer laminates based on power loss. Compos. Struct. 2021, 276, 114421. [Google Scholar] [CrossRef]
- Pasadas, D.J.; Barzegar, M.; Ribeiro, A.L.; Ramos, H.G. Locating and Imaging Fiber Breaks in CFRP Using Guided Wave Tomography and Eddy Current Testing. Sensors 2022, 22, 7377. [Google Scholar] [CrossRef]
- Wu, D.; Chen, W.; Yang, J.; Yang, F. Self-resonance eddy-current testing method in noncontact detection of carbon fiber reinforced plastics. Compos. Struct. 2020, 259, 113247. [Google Scholar] [CrossRef]
- Zeng, Z.; Wang, J.; Liu, X.; Lin, J.; Dai, Y. Detection of fiber waviness in CFRP using eddy current method. Compos. Struct. 2019, 229, 111411. [Google Scholar] [CrossRef]
- Fan, W.; Zhang, H. Damage Detection of Cross-Plied CFRP Laminates Based on Rectangular Differential Pulse Eddy Current Sensors. Res. Nondestruct. Eval. 2021, 32, 223–237. [Google Scholar] [CrossRef]
- Cheng, J.; Xu, S.; Wang, B.; Xu, D.; Jang, J.; Qu, J. Application of Self-nulling Pancake-tangent Eddy Current Probe for Mesoscopic Imaging of CFRP Composites. Chin. J. Mech. Eng. 2021, 57, 27–35. [Google Scholar] [CrossRef]
- Underhill, P.R.; Rellinger, T.; Krause, T.W.; Wowk, D. Eddy Current Array Inspection of Damaged CFRP Sandwich Panels. J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2020, 3, 031104. [Google Scholar] [CrossRef]
- Krishnan, R.; Pandiaraj, S.; Muthusamy, S.; Panchal, H.; Alsoufi, M.S.; Ibrahim, A.M.M.; Elsheikh, A. Biodegradable magnesium metal matrix composites for biomedical implants: Synthesis, mechanical performance, and corrosion behavior—A review. J. Mater. Res. Technol. 2022, 20, 650–670. [Google Scholar] [CrossRef]
- Chady, T.; Enokizono, M.; Todaka, T.; Tsuchida, Y.; Sikora, R. Evaluation of the JSAEM round robin test samples using mul-tifrequency excitation and spectrogram method. In Electromagnetic Nondestructive Evaluation (V); Pávó, J., Vértesy, G., Takagi, T., Udpa, S.S., Eds.; Studies in Applied Electromagnetics and Mechanics; IOS Press: Amsterdam, The Netherlands; Washington, DC, USA, 2001; Volume 21, pp. 171–178. ISBN 978-1-58603-155-8. [Google Scholar]





| Sample S03 | |
|---|---|
| Dimensions | 210 mm 148 mm |
| Thickness | 2 mm |
| Mass | ca. 90 g |
| Face reinforcement weight | |
| Internal reinforcement weight | and/or |
| Surface coating | matt coating |
| Heat treatment | annealing at a temperature of 60 °C |
| Parameter | Value |
|---|---|
| Excitation coil EA turns | 25 |
| Excitation coil EB turns | 25 |
| Excitation coil EC turns | 25 |
| Excitation coil ED turns | 25 |
| Pick-up coil S turns | 100 |
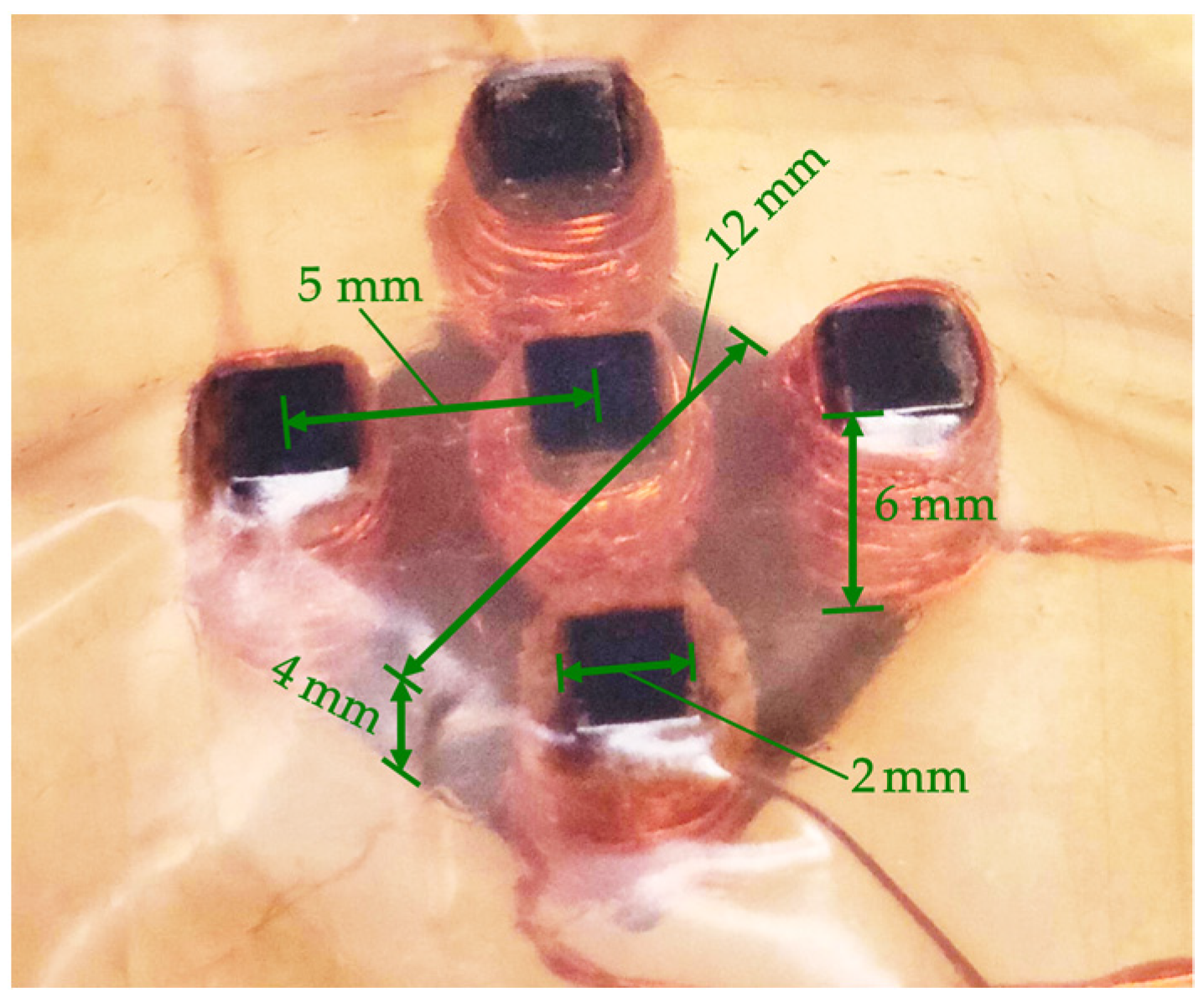
| Ferrite core diameter | 12 mm |
| Excitation coils—pick-up coil distance | 5 mm |
| Core column diameter | 2 mm |
| Core column height | 6 mm |
| Core height | 10 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łukaszuk, R.; Chady, T. Nondestructive Examination of Carbon Fiber-Reinforced Composites Using the Eddy Current Method. Materials 2023, 16, 506. https://doi.org/10.3390/ma16020506
Łukaszuk R, Chady T. Nondestructive Examination of Carbon Fiber-Reinforced Composites Using the Eddy Current Method. Materials. 2023; 16(2):506. https://doi.org/10.3390/ma16020506
Chicago/Turabian StyleŁukaszuk, Ryszard, and Tomasz Chady. 2023. "Nondestructive Examination of Carbon Fiber-Reinforced Composites Using the Eddy Current Method" Materials 16, no. 2: 506. https://doi.org/10.3390/ma16020506
APA StyleŁukaszuk, R., & Chady, T. (2023). Nondestructive Examination of Carbon Fiber-Reinforced Composites Using the Eddy Current Method. Materials, 16(2), 506. https://doi.org/10.3390/ma16020506






