Insight into the Physical Properties of Fluoro-Perovskites Compounds of Tl-Based TlMF3 (M = Au, Ga) Compounds Studied for Energy Generation Utilizing the TB-MBJ Potential Approximation Approach
Abstract
:1. Introduction
2. Methodology
3. Results and Discussions
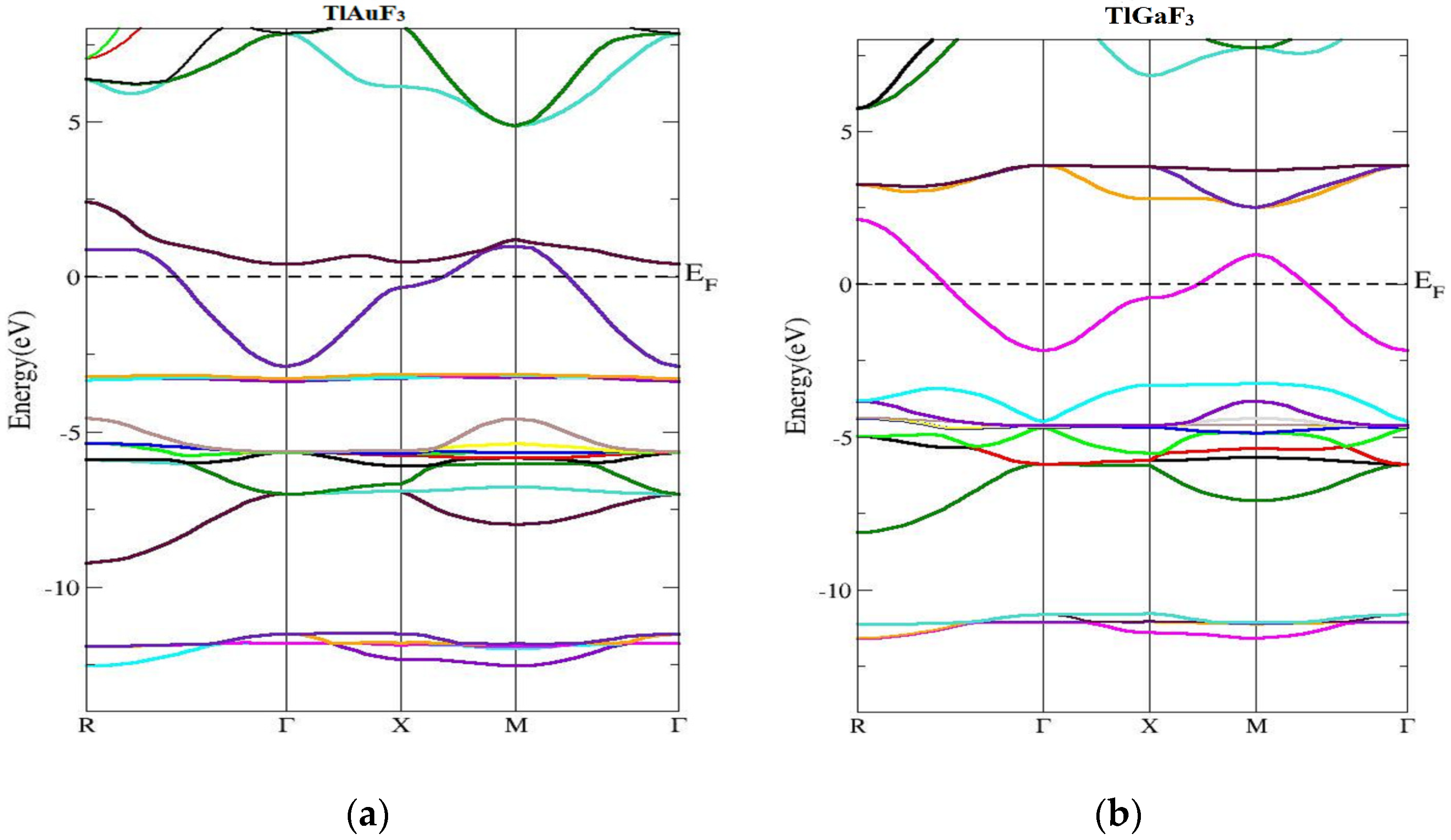
3.1. Electronic Properties
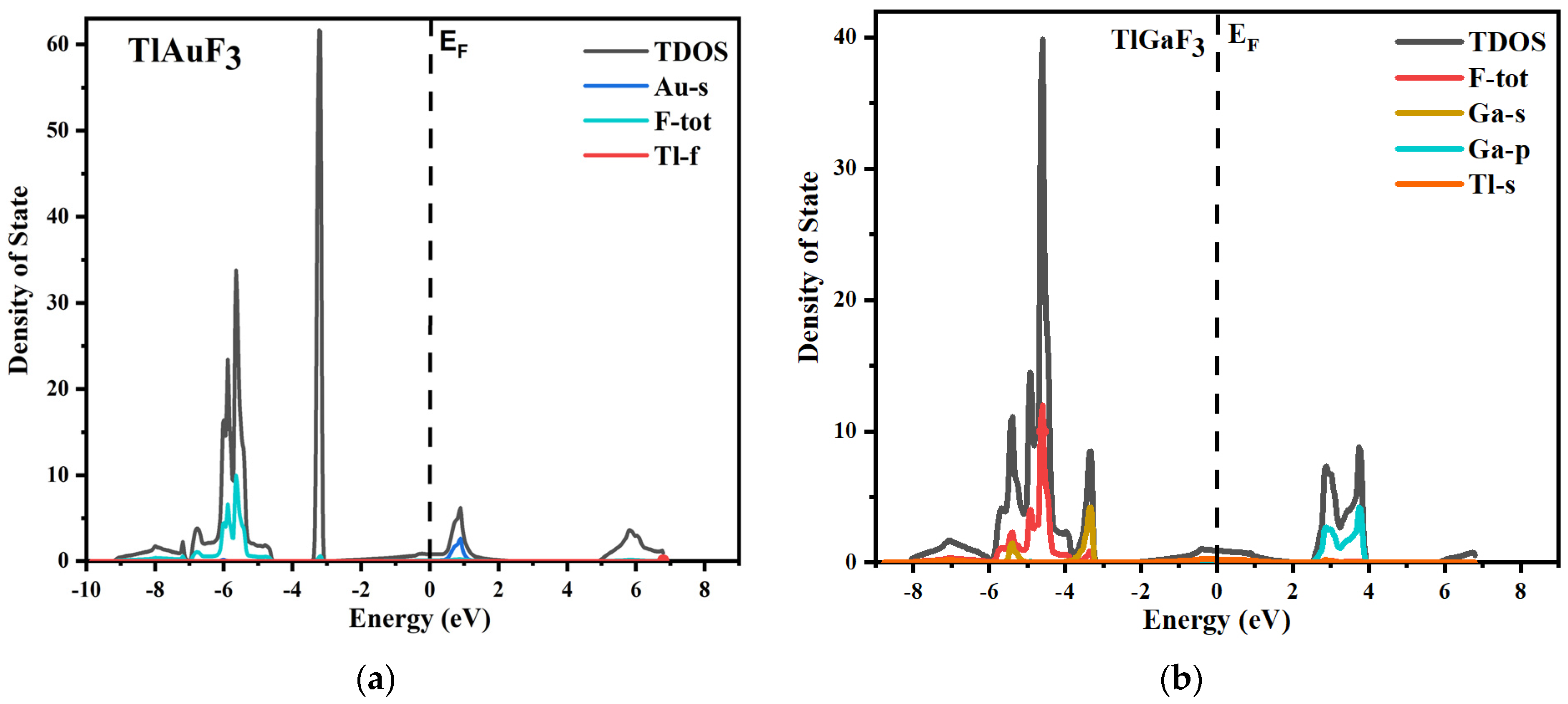
3.2. Density of States
3.3. Elastic Properties
| Compounds | C11 | C12 | C44 | B | G | E | A | v | B/G |
|---|---|---|---|---|---|---|---|---|---|
| TlAuF3 | 86.88 | 30.29 | 1.70 | 172.03 | 3.68 | 30.30 | −0.06 | 0.47 | 46.78 |
| TlGaF3 | 85.28 | 24.27 | 0.29 | 172.03 | 6.43 | 36.30 | 0.01 | 0.47 | 26.74 |
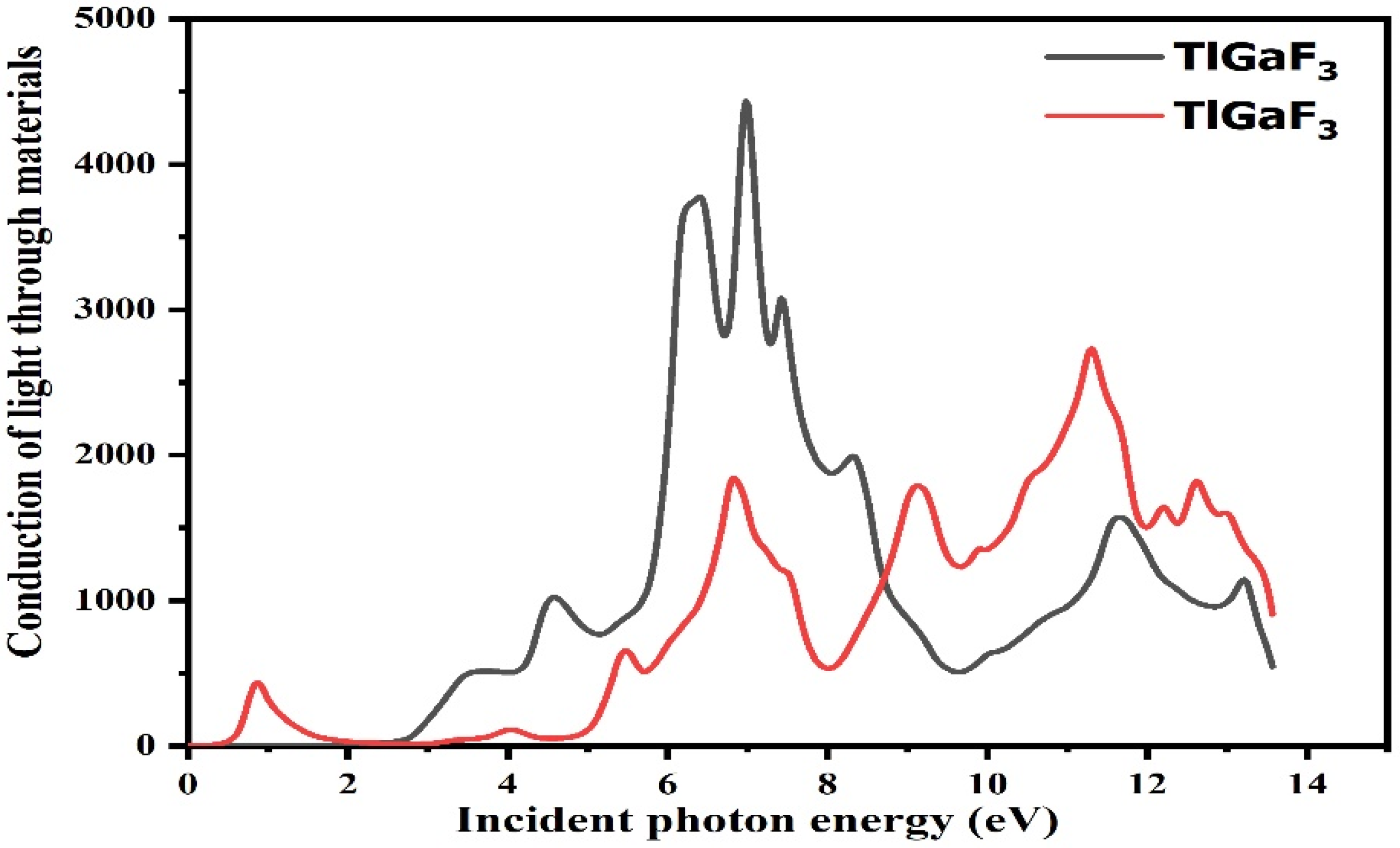
3.4. Optical Properties
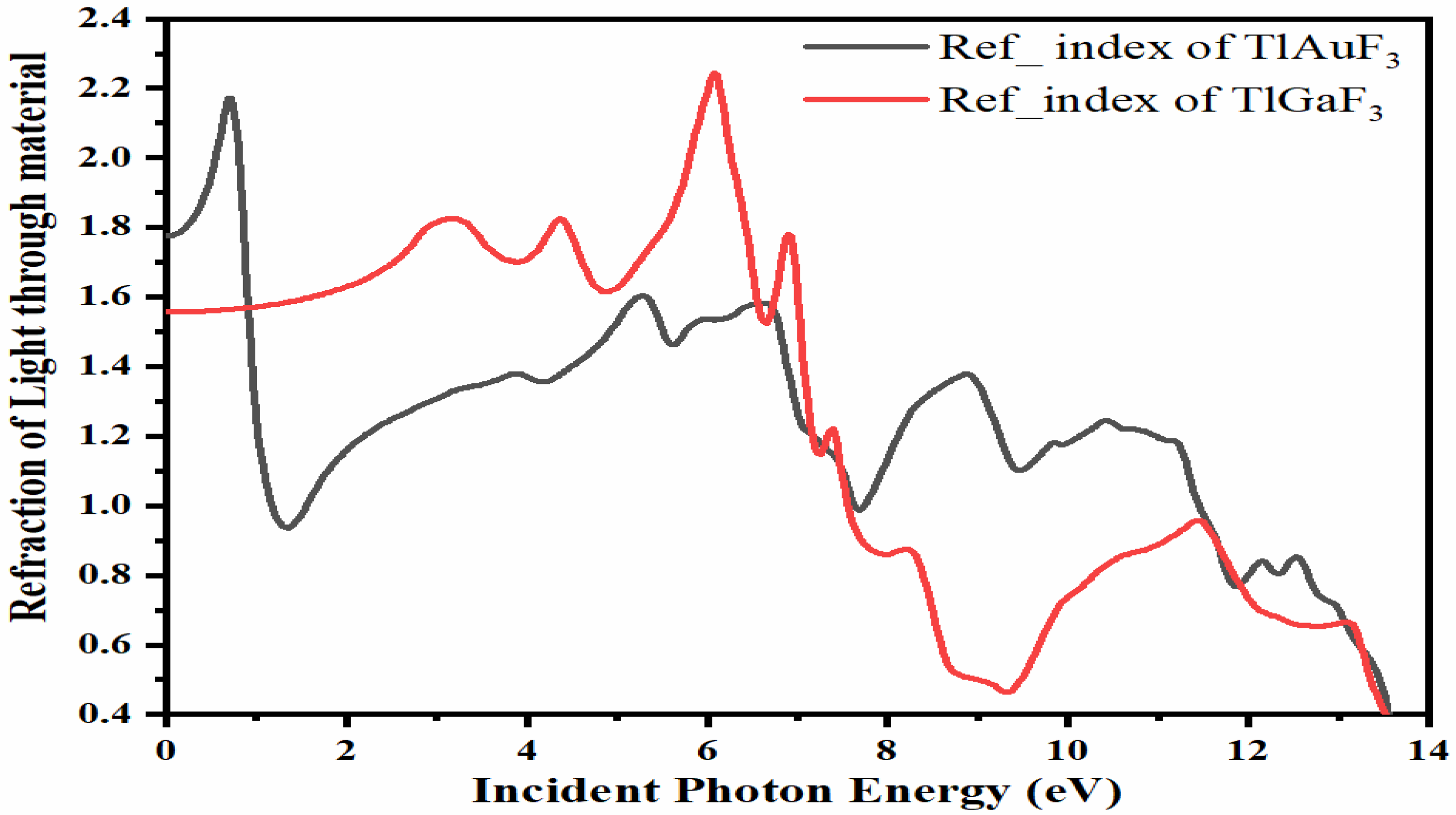
3.5. Refractive Index
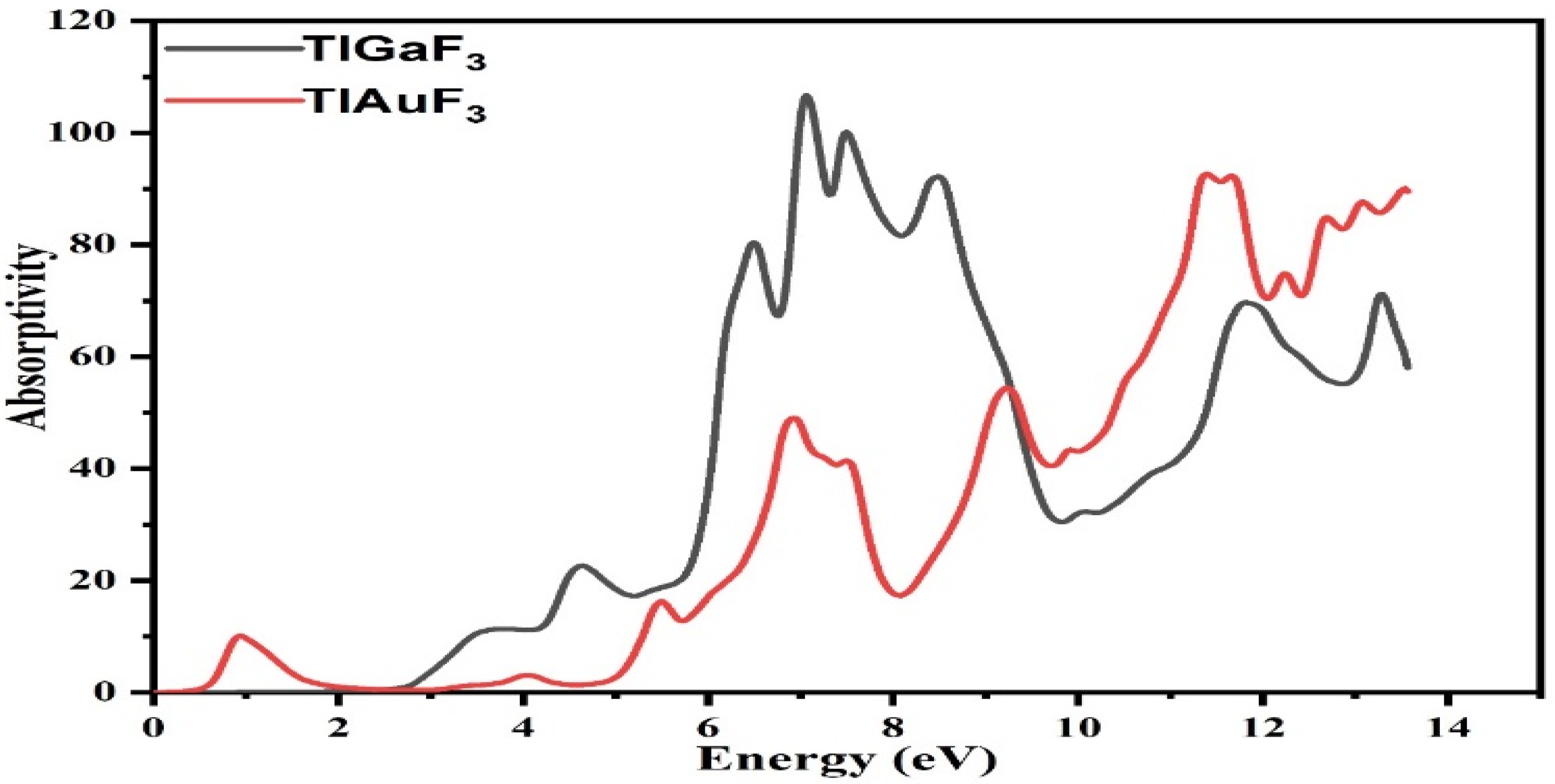
3.6. Absorption Coefficient
3.7. Reflectivity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nishimatsu, T.; Terakubo, N.; Mizuseki, H.; Kawazoe, Y.; Pawlak, D.A.; Shimamura, K.; Fukuda, T. Band structures of perovskite-like fluorides for vacuum-ultraviolet-transparent lens materials. Jpn. J. Appl. Phys. 2002, 41, L365–L367. [Google Scholar] [CrossRef]
- Husain, M.; Rahman, N.; Reshak, A.H.; Zulfiqar; Habib, A.; Ali, S.; Laref, A.; Al Bakri, A.M.M.; Bila, J. Insight into the physical properties of the inter-metallic titanium-based binary compounds. Eur. Phys. J. Plus 2021, 136, 624. [Google Scholar] [CrossRef]
- Rahman, N.; Husain, M.; Yang, J.; Sajjad, M.; Murtaza, G.; Ul Haq, M.; Habib, A.; Zulfiqar; Rauf, A.; Karim, A.; et al. First principle study of structural, electronic, optical and mechanical properties of cubic fluoro-perovskites:(CdXF 3, X= Y, Bi). Eur. Phys. J. Plus 2021, 136, 347. [Google Scholar] [CrossRef]
- Körbel, S.; Marques, M.A.L.; Botti, S. Stability and electronic properties of new inorganic perovskites from high-throughput ab initio calculations. J. Mater. Chem. C 2016, 4, 3157–3167. [Google Scholar] [CrossRef]
- Chouit, N.; Korba, S.A.; Slimani, M.; Meradji, H.; Ghemid, S.; Khenata, R. First-principles study of the structural, electronic and thermal properties of CaLiF3. Phys. Scr. 2013, 88, 035702. [Google Scholar] [CrossRef]
- Seddik, T.; Khenata, R.; Merabiha, O.; Bouhemadou, A.; Bin-Omran, S.; Rached, D. Elastic, electronic and thermodynamic properties of fluoro-perovskite KZnF 3 via first-principles calculations. Appl. Phys. A 2011, 106, 645–653. [Google Scholar] [CrossRef]
- Harmel, M.; Khachai, H.; Haddou, A.; Khenata, R.; Murtaza, G.; Abbar, B.; Bin Omran, S.; Khalfa, M. Ab initio study of the mechanical, thermal and optoelectronic properties of the cubic CsBaF3. Acta Phys. Pol. A 2015, 128, 34–42. [Google Scholar] [CrossRef]
- Vaitheeswaran, G.; Kanchana, V.; Kumar, R.S.; Cornelius, A.L.; Nicol, M.F.; Svane, A.; Delin, A.; Johansson, B. High-pressure structural, elastic, and electronic properties of the scintillator host material K Mg F3. Phys. Rev. B 2007, 76, 014107. [Google Scholar] [CrossRef] [Green Version]
- Korba, S.A.; Meradji, H.; Ghemid, S.; Bouhafs, B. First principles calculations of structural, electronic and optical properties of BaLiF3. Comput. Mater. Sci. 2009, 44, 1265–1271. [Google Scholar] [CrossRef]
- Furetta, C.; Santopietro, F.; Sanipoli, C.; Kitis, G. Thermoluminescent (TL) properties of the perovskite KMgF3 activated by Ce and Er impurities. Appl. Radiat. Isot. 2001, 55, 533–542. [Google Scholar] [CrossRef]
- Murtaza, G.; Sadique, G.; Aliabad, H.R.; Khalid, M.; Naeem, S.; Afaq, A.; Amin, B.; Ahmad, I. First principle study of cubic perovskites: AgTF3 (T= Mg, Zn). Phys. B Condens. Matter 2011, 406, 4584–4589. [Google Scholar] [CrossRef]
- Khan, I.; Shehzad, N.; Ahmad, I.; Ali, Z.; Jalali-Asadabadi, S. First-principle studies of the optoelectronic properties of ASnF3 (A= Na, K, Rb and Cs). Int. J. Mod. Phys. B 2017, 31, 1750148. [Google Scholar] [CrossRef]
- Hamioud, F.; AlGhamdi, G.S.; Al-Omari, S.; Mubarak, A.A. Ab initio investigation of the structural, electronic, magnetic and optical properties of the perovskite TlMnX3 (X= F, Cl) compounds. Int. J. Mod. Phys. B 2016, 30, 1650031. [Google Scholar] [CrossRef]
- Cheriet, A.; Lagoun, B.; Halit, M.; Zaabat, M.; Abdelhakim, C.; Hamza, L. First-principles study of structural, electronic, optical and elastic properties of cadmium based Fluoro-Perovskite MCdF3 (M= Rb, Tl). Solid State Phenom. 2019, 297, 173–186. [Google Scholar]
- Kim, H.; Rooh, G.; Park, H.; Kim, S. Luminescence and scintillation properties of the new Ce-doped Tl2LiGdCl6 single crystals. J. Lumin. 2015, 164, 86–89. [Google Scholar] [CrossRef]
- Khan, A.; Rooh, G.; Kim, H.; Kim, S. Ce3+-activated Tl2GdCl5: Novel halide scintillator for X-ray and γ-ray detection. J. Alloy. Compd. 2018, 741, 878–882. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Madsen, G.K.; Kvasnicka, D.; Luitz, J. wien2k. In An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties; Vienna University Technology press: Vienna, Austria, 2001; Volume 60. [Google Scholar]
- Ambrosch-Draxl, C.; Sofo, J.O. Linear optical properties of solids within the full-potential linearized augmented planewave method. Comput. Phys. Commun. 2006, 175, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Reshak, A.H.; Jamal, M. DFT calculation for elastic constants of orthorhombic structure within WIEN2K code: A new package (ortho-elastic). J. Alloy. Compd. 2012, 543, 147–151. [Google Scholar] [CrossRef]
- Jamal, M.; Bilal, M.; Ahmad, I.; Jalali-Asadabadi, S. IRelast package. J. Alloys Compd. 2018, 735, 569–579. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef] [Green Version]
- Berger, J.; Hauret, G.; Rousseau, M. Brillouin scattering investigation of the structural phase transition of TlCdF3 and RbCaF3. Solid State Commun. 1978, 25, 569–571. [Google Scholar] [CrossRef]
- Grimvall, G. Thermophysical Properties of Materials; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Shah, S.A.; Husain, M.; Rahman, N.; Sohail, M.; Khan, R.; Alataway, A.; Dewidar, A.Z.; Elansary, H.O.; Abu El Maati, L.; Yessoufou, K.; et al. Insight into the Structural, Electronic, Elastic, Optical, and Magnetic Properties of Cubic Fluoroperovskites ABF3 (A = Tl, B = Nb, V) Compounds: Probed by DFT. Materials 2022, 15, 5684. [Google Scholar] [CrossRef] [PubMed]
- Duan, C.G.; Mei, W.N.; Liu, J.; Yin, W.G.; Hardy, J.R.; Smith, R.W.; Mehl, M.J.; Boyer, L.L. Electronic properties of NaCdF3: A first-principles prediction. Phys. Rev. B 2004, 69, 033102. [Google Scholar] [CrossRef]
- Bakri, B.; Driss, Z.; Berri, S.; Khenata, R. First-principles investigation for some physical properties of some fluoroperovskites compounds ABF3 (A= K, Na; B= Mg, Zn). Indian J. Phys. 2017, 91, 1513–1523. [Google Scholar] [CrossRef]
- Azam, S.; Khan, S.A. A first principles study of electronic and optical properties of the polar quaternary chalcogenides β-A2Hg3Ge2S8 (A= K and Rb). Mater. Sci. Semicond. Process. 2015, 34, 250–259. [Google Scholar] [CrossRef]
- Makhdoom, M.; Jamil, M.I.; Azam, S.; Irfan, M.; Abbas, Z.; Gul, B.; Khan, S.A.; Wang, X. First-Principles Description of the Different Phases in the Li2 NH Compound: Electronic Structure and Optical Properties. J. Korean Phys. Soc. 2019, 74, 1140–1145. [Google Scholar] [CrossRef]
- Azam, S.; Irfan, M.; Abbas, Z.; Rani, M.; Saleem, T.; Younus, A.; Akhtar, N.; Liaqat, B.; Shabbir, M.; Al-Sehemi, A.G. DFT study of the electronic and optical properties of ternary chalcogenides AlX2Te4. Mater. Res. Express 2019, 6, 116314. [Google Scholar] [CrossRef]
- Dressel, M.; Grüner, G. Electrodynamics of solids: Optical properties of electrons in matter. Am. J. Phys. 2002, 70, 1269. [Google Scholar] [CrossRef] [Green Version]
- Rousseau, M.; Gesland, J.Y.; Julliard, J.; Nouet, J.; Zarembowitch, J.; Zarembowitch, A. Crystallographic, elastic, and Raman scattering investigations of structural phase transitions in RbCd F3 and TlCd F3. Phys. Rev. B 1975, 12, 1579. [Google Scholar] [CrossRef]

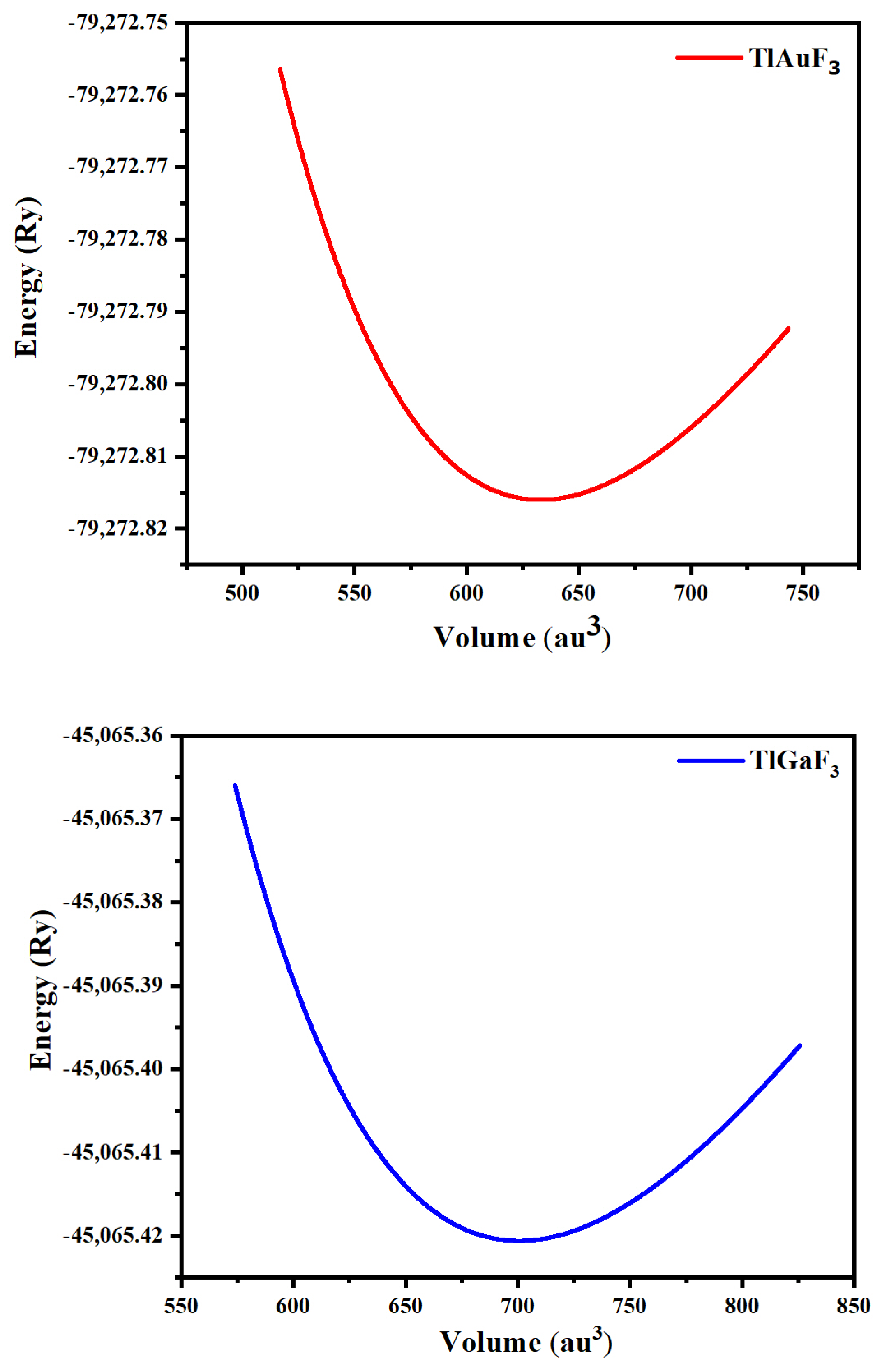

| Compounds | ao (Lattice Constant in Å) | B (Bulk Modulus in GPa) | B/(Derivative of Bulk Modulus in GPa) | V0 (Ground State Volume in a.u3) | E0 (Ground State Energy in Ry) |
|---|---|---|---|---|---|
| TlAuF3 | 4.6999 | 44.8590 | 5.8250 | 700.5558 | −4505.421 |
| TlGaF3 | 4.5433 | 52.0630 | 5.8722 | 632.8047 | −79,272.815 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, H.; Sohail, M.; Arif, M.S.; Abodayeh, K. Insight into the Physical Properties of Fluoro-Perovskites Compounds of Tl-Based TlMF3 (M = Au, Ga) Compounds Studied for Energy Generation Utilizing the TB-MBJ Potential Approximation Approach. Materials 2023, 16, 686. https://doi.org/10.3390/ma16020686
Khan H, Sohail M, Arif MS, Abodayeh K. Insight into the Physical Properties of Fluoro-Perovskites Compounds of Tl-Based TlMF3 (M = Au, Ga) Compounds Studied for Energy Generation Utilizing the TB-MBJ Potential Approximation Approach. Materials. 2023; 16(2):686. https://doi.org/10.3390/ma16020686
Chicago/Turabian StyleKhan, Hukam, Mohammad Sohail, Muhammad Shoaib Arif, and Kamaleldin Abodayeh. 2023. "Insight into the Physical Properties of Fluoro-Perovskites Compounds of Tl-Based TlMF3 (M = Au, Ga) Compounds Studied for Energy Generation Utilizing the TB-MBJ Potential Approximation Approach" Materials 16, no. 2: 686. https://doi.org/10.3390/ma16020686
APA StyleKhan, H., Sohail, M., Arif, M. S., & Abodayeh, K. (2023). Insight into the Physical Properties of Fluoro-Perovskites Compounds of Tl-Based TlMF3 (M = Au, Ga) Compounds Studied for Energy Generation Utilizing the TB-MBJ Potential Approximation Approach. Materials, 16(2), 686. https://doi.org/10.3390/ma16020686









