Phase-Field Simulation of Temperature-Dependent Thermal Shock Fracture of Al2O3/ZrO2 Multilayer Ceramics with Phase Transition Residual Stress
Abstract
:1. Introduction
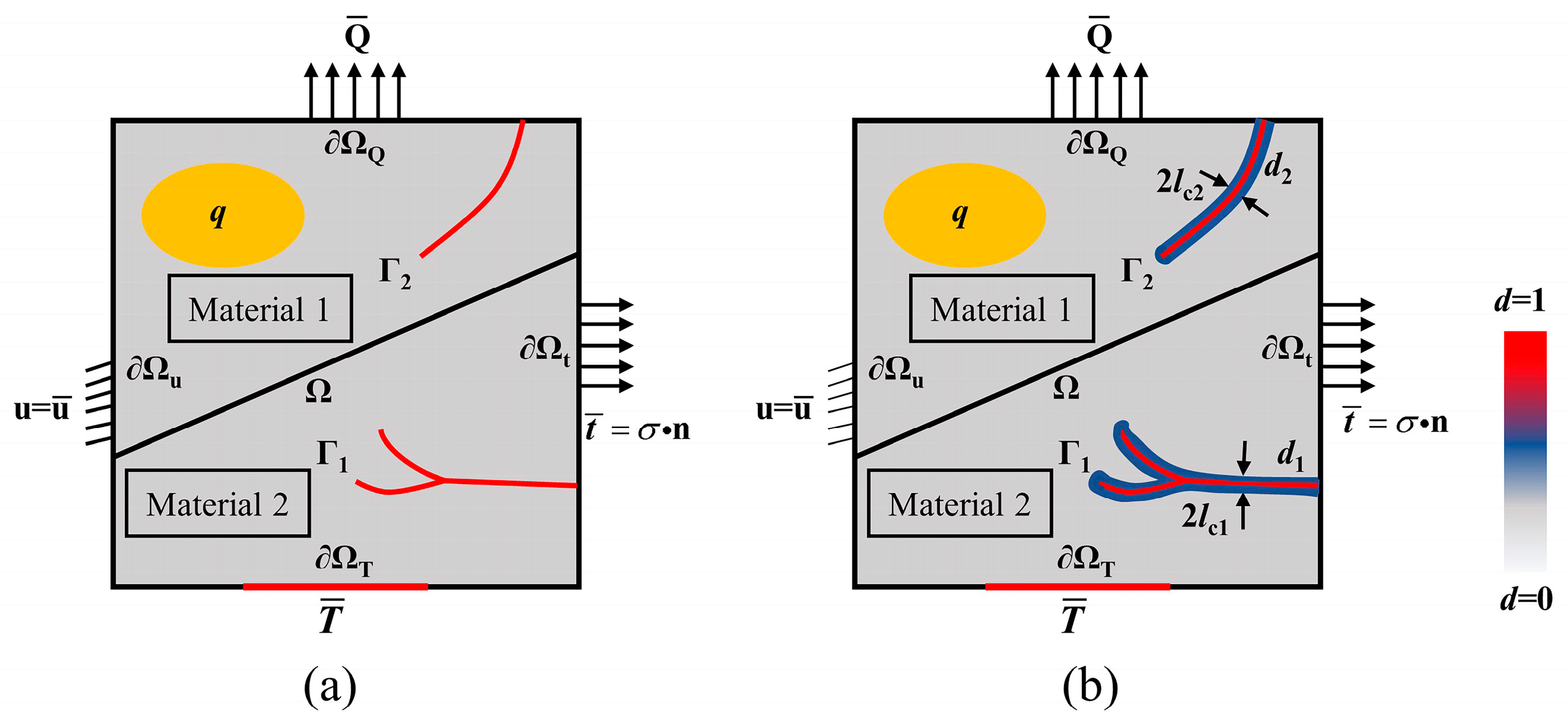
2. Thermodynamic Coupling Damage Fracture Phase-Field Model
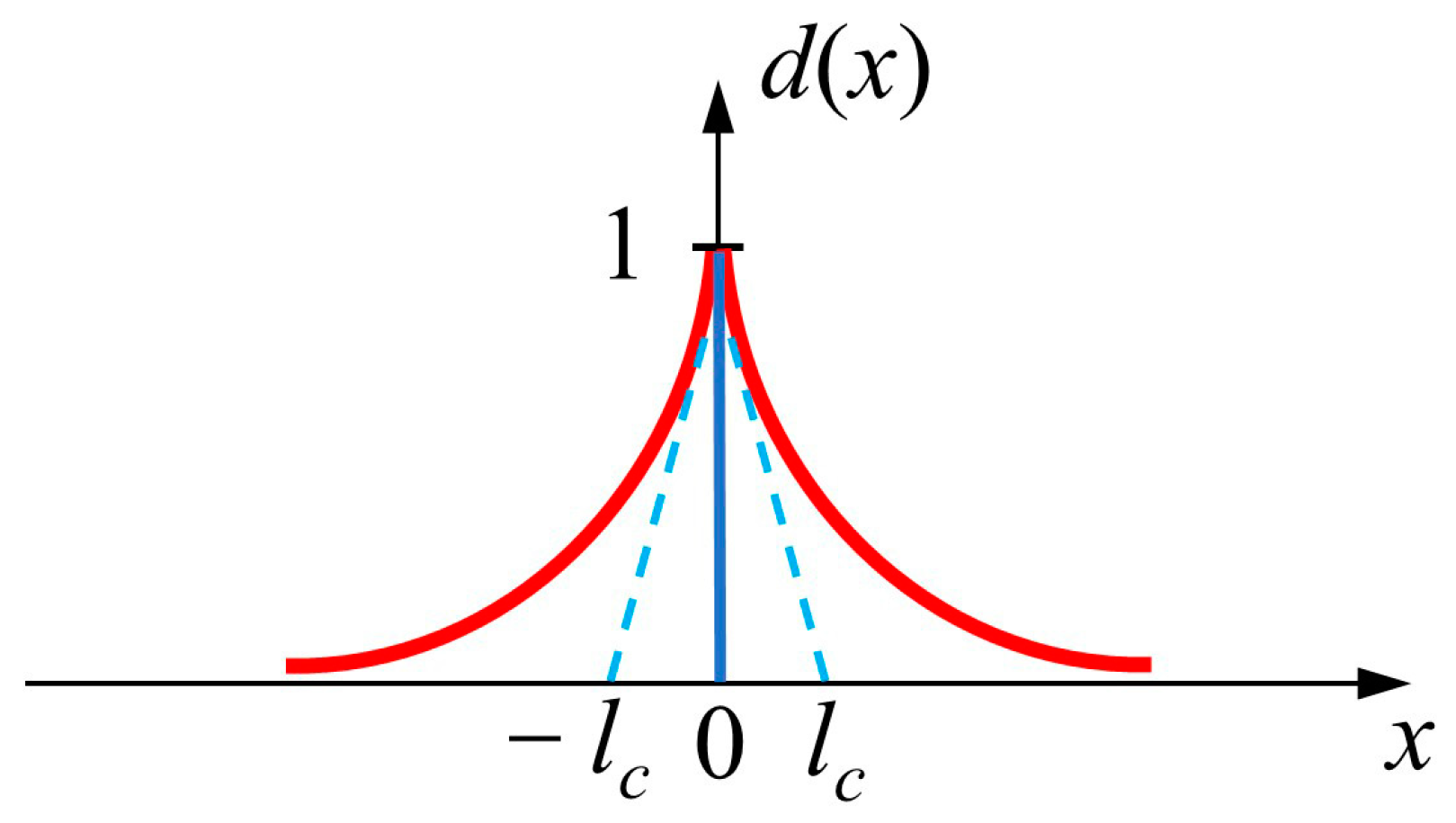
2.1. Phase-Field Approximation of Cracks
2.2. Fracture Variational Formula of Thermo-Mechanical Coupling Phase Field
2.3. Thermal-Mechanical Coupling Fracture Phase Field Model with a Fracture Energy Threshold
2.4. Governing Equation of Temperature-Dependent Fracture Energy Threshold
3. Numerical Implementation of the PFM
3.1. The Discretization of Finite Elements
3.2. Numerical Implementation of the Finite Element Method
4. Results and Discussions
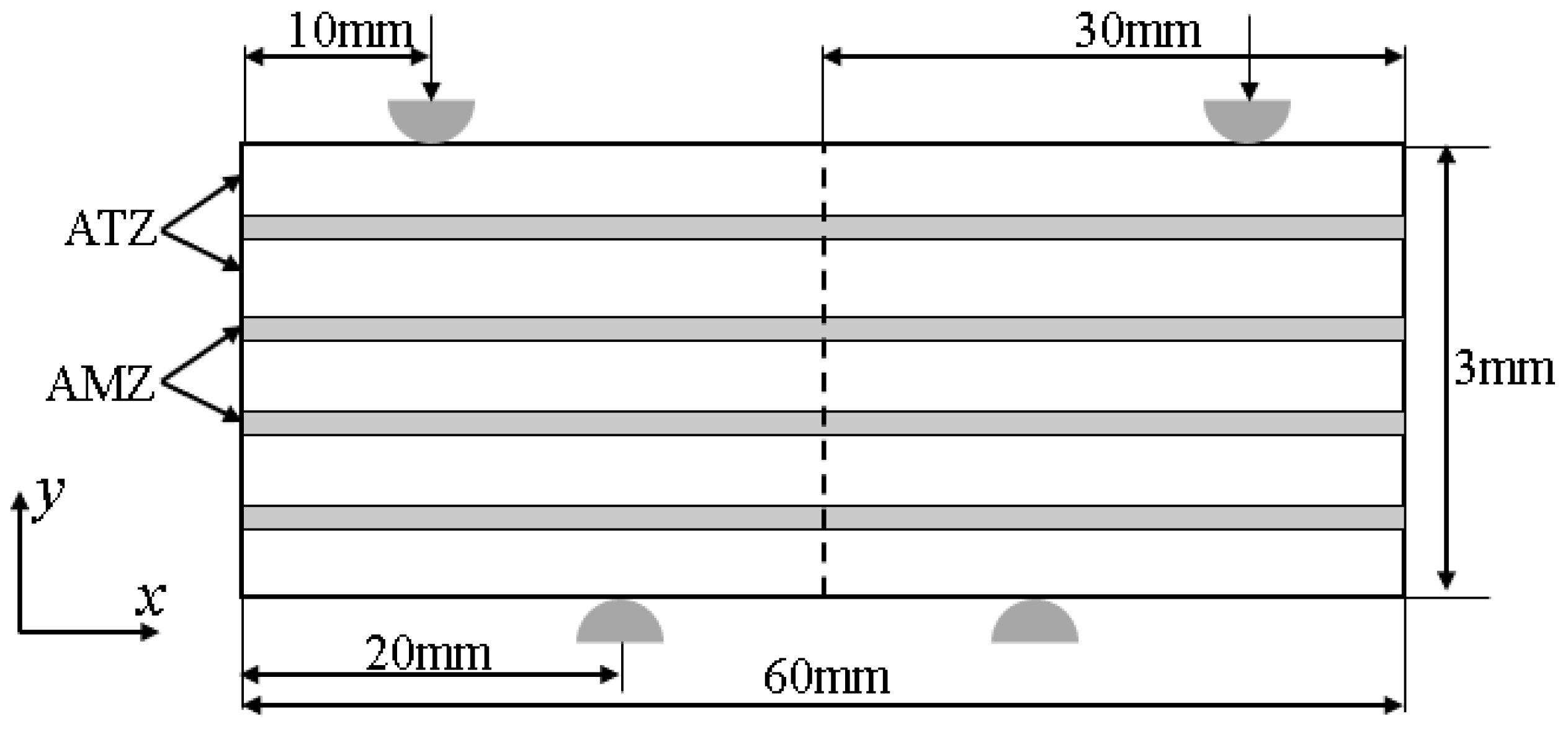
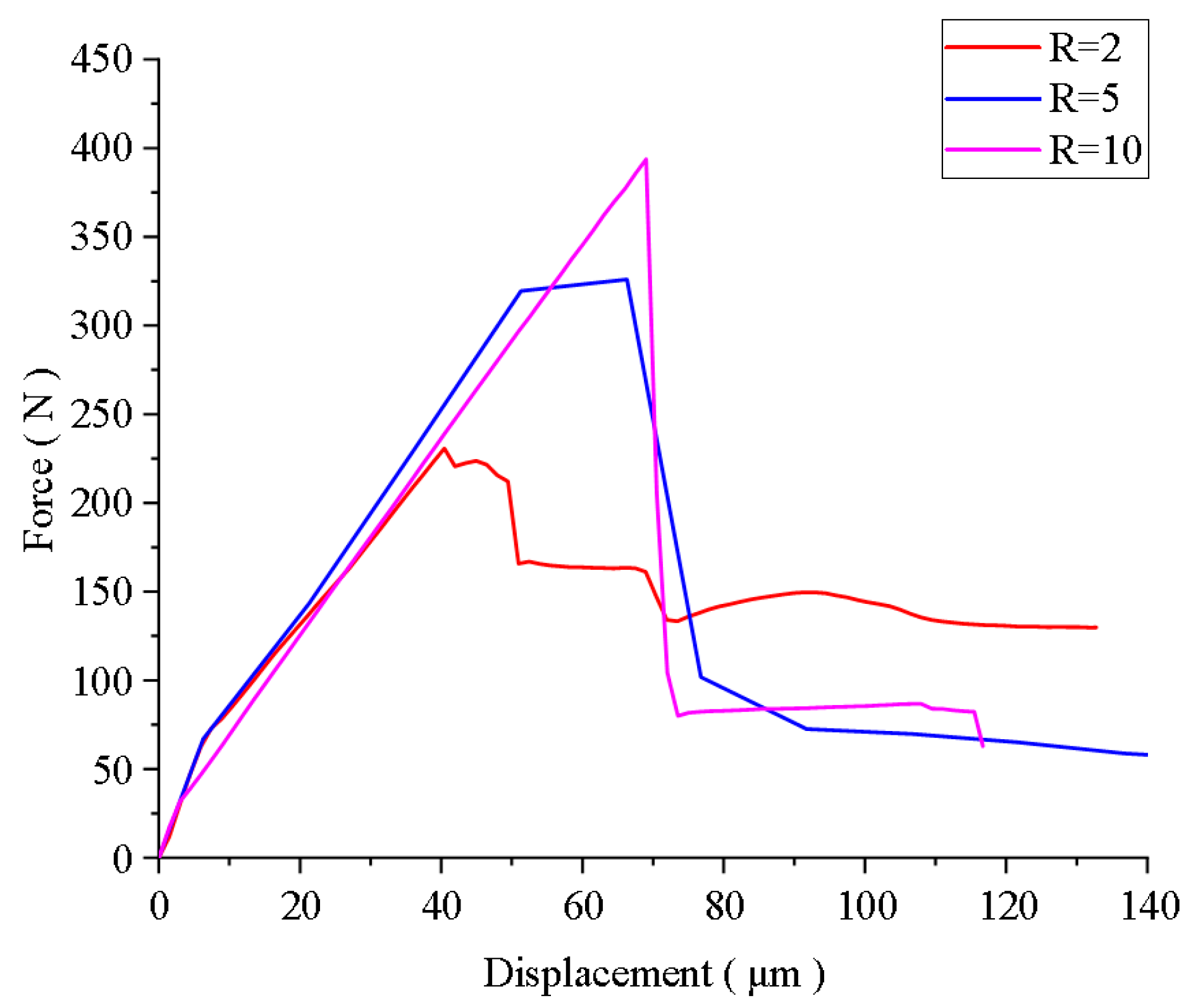
4.1. PFM Simulation of the Four-Point Bending Test of Al2O3/ZrO2-Layered Ceramics
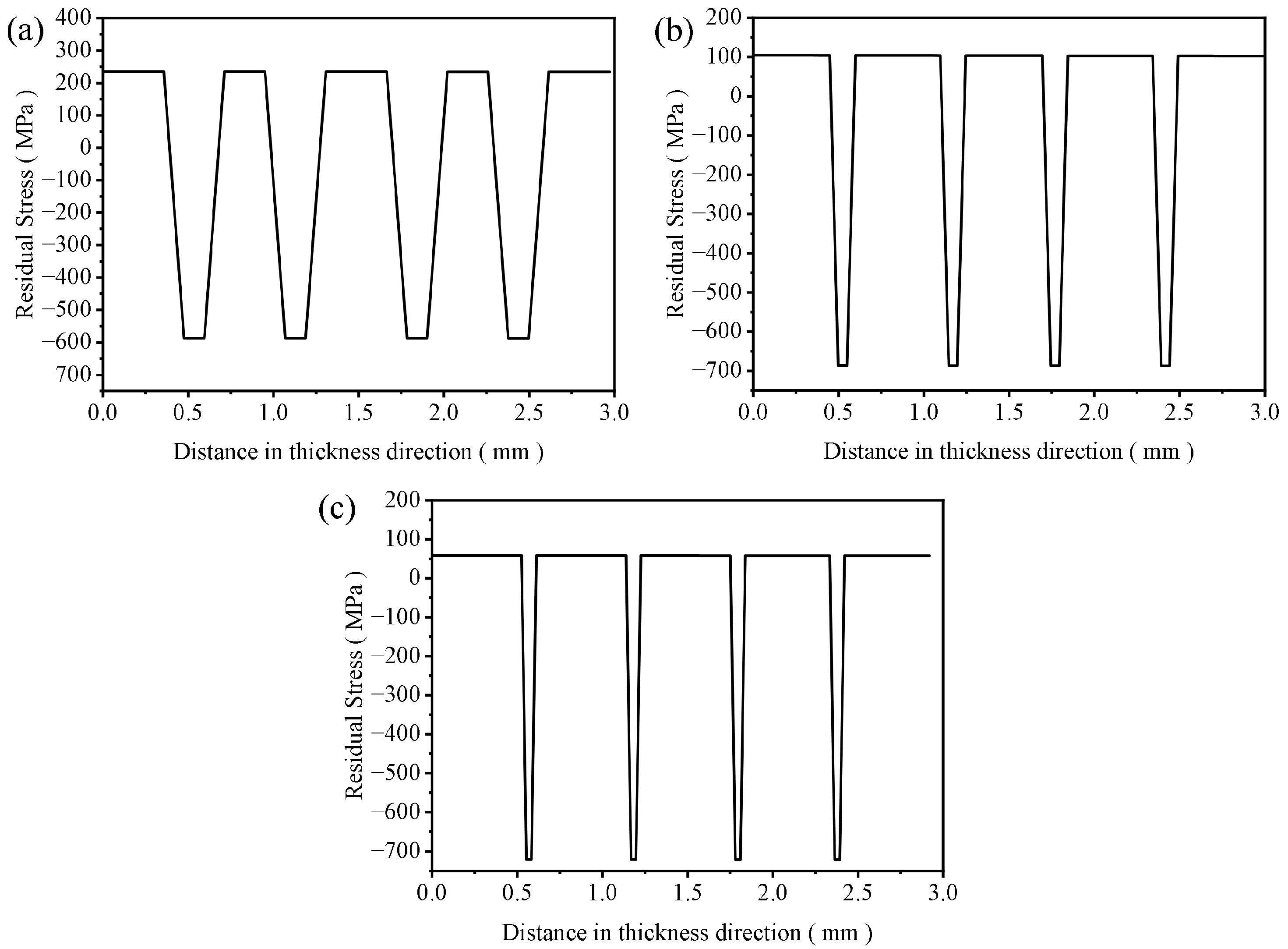
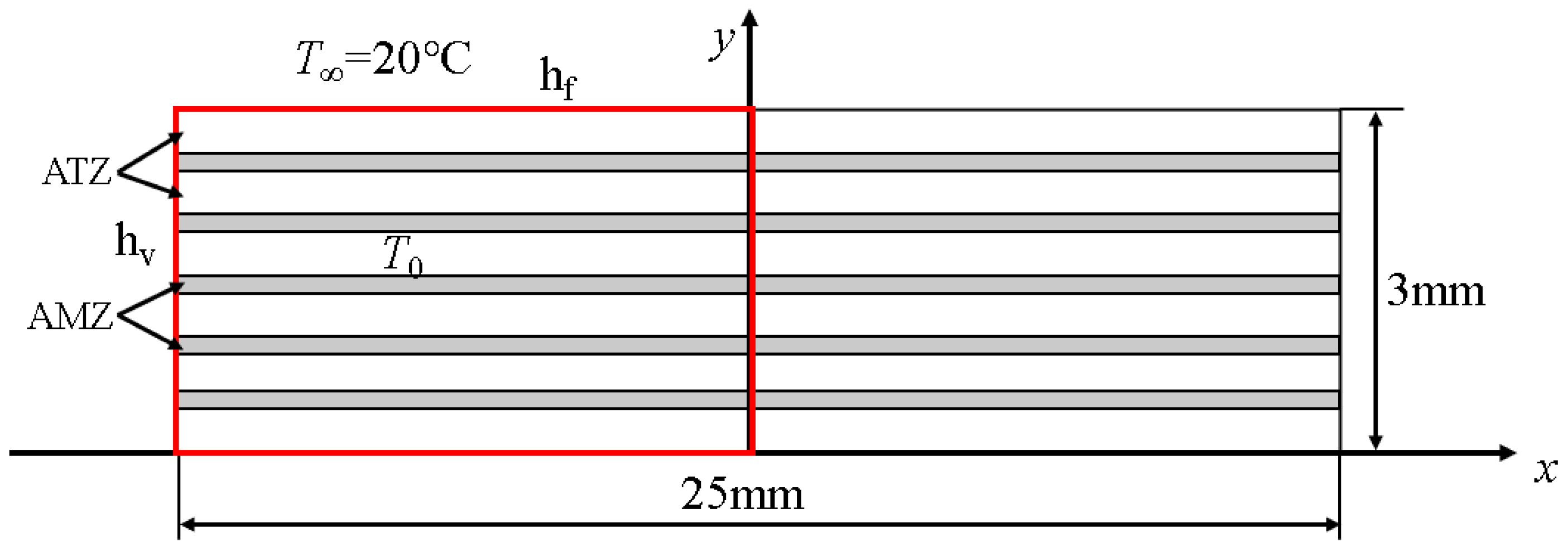
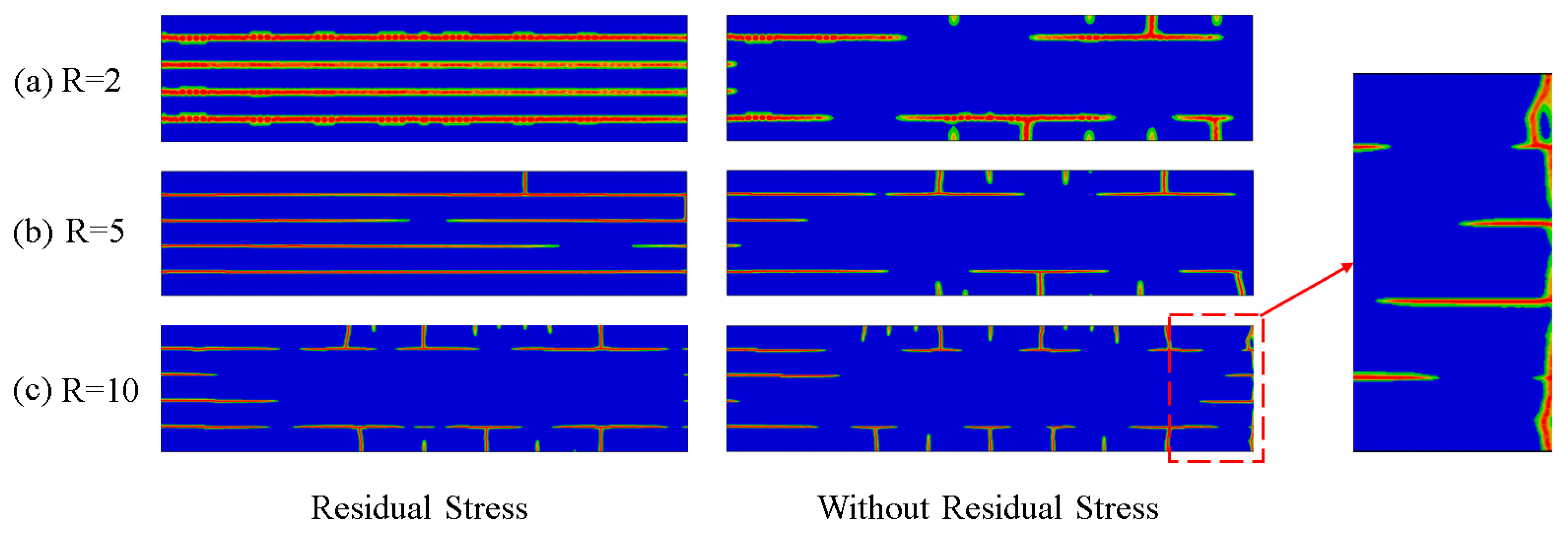
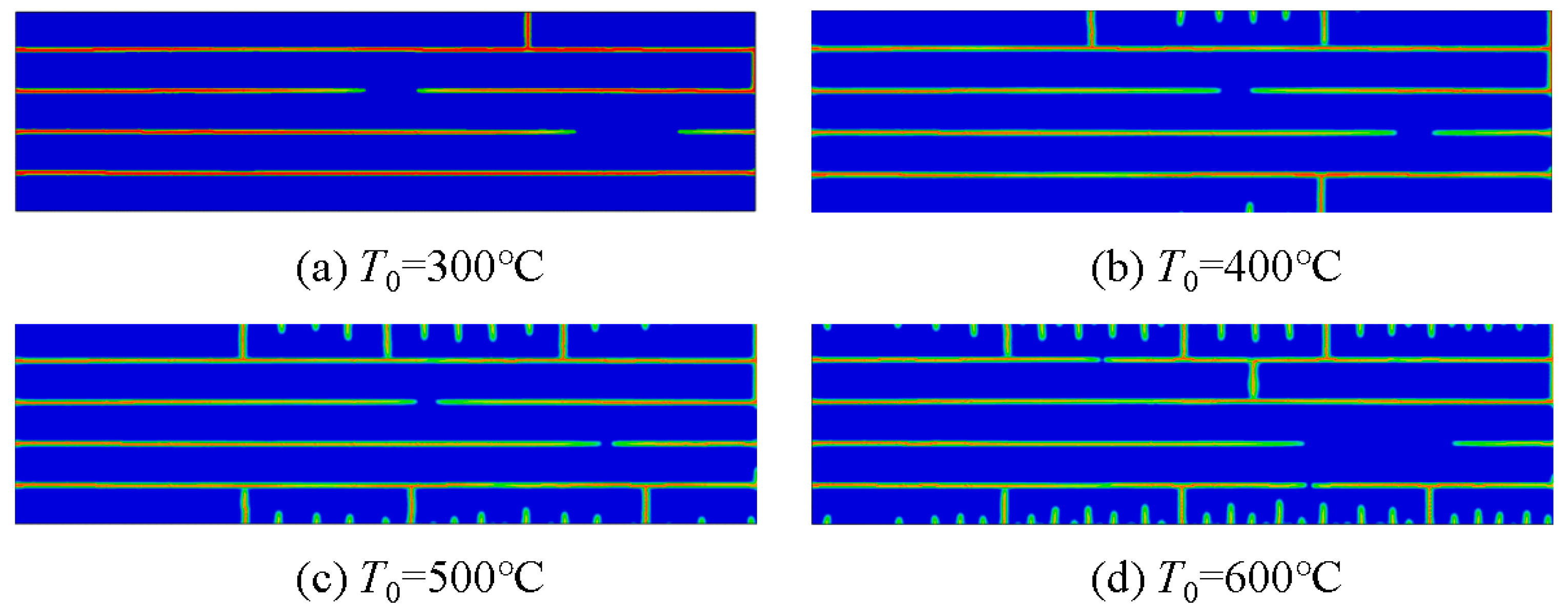
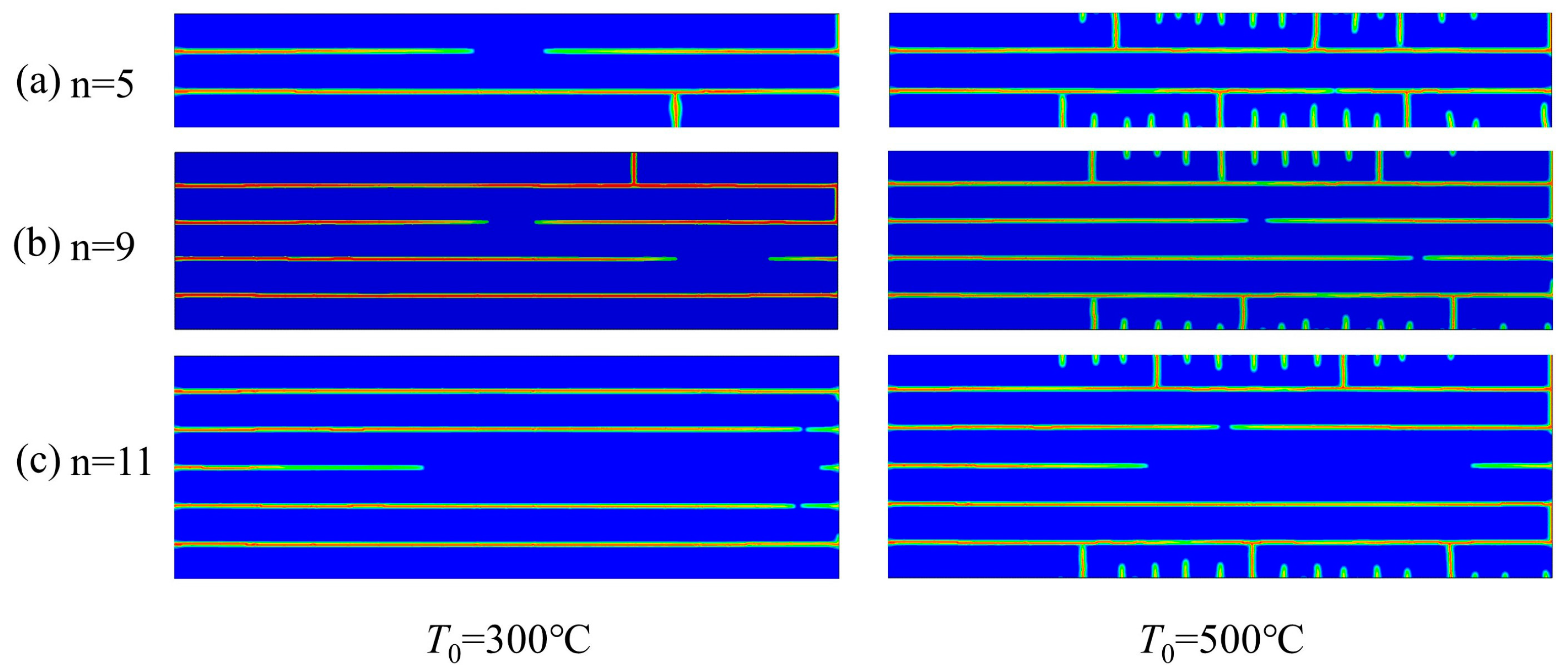
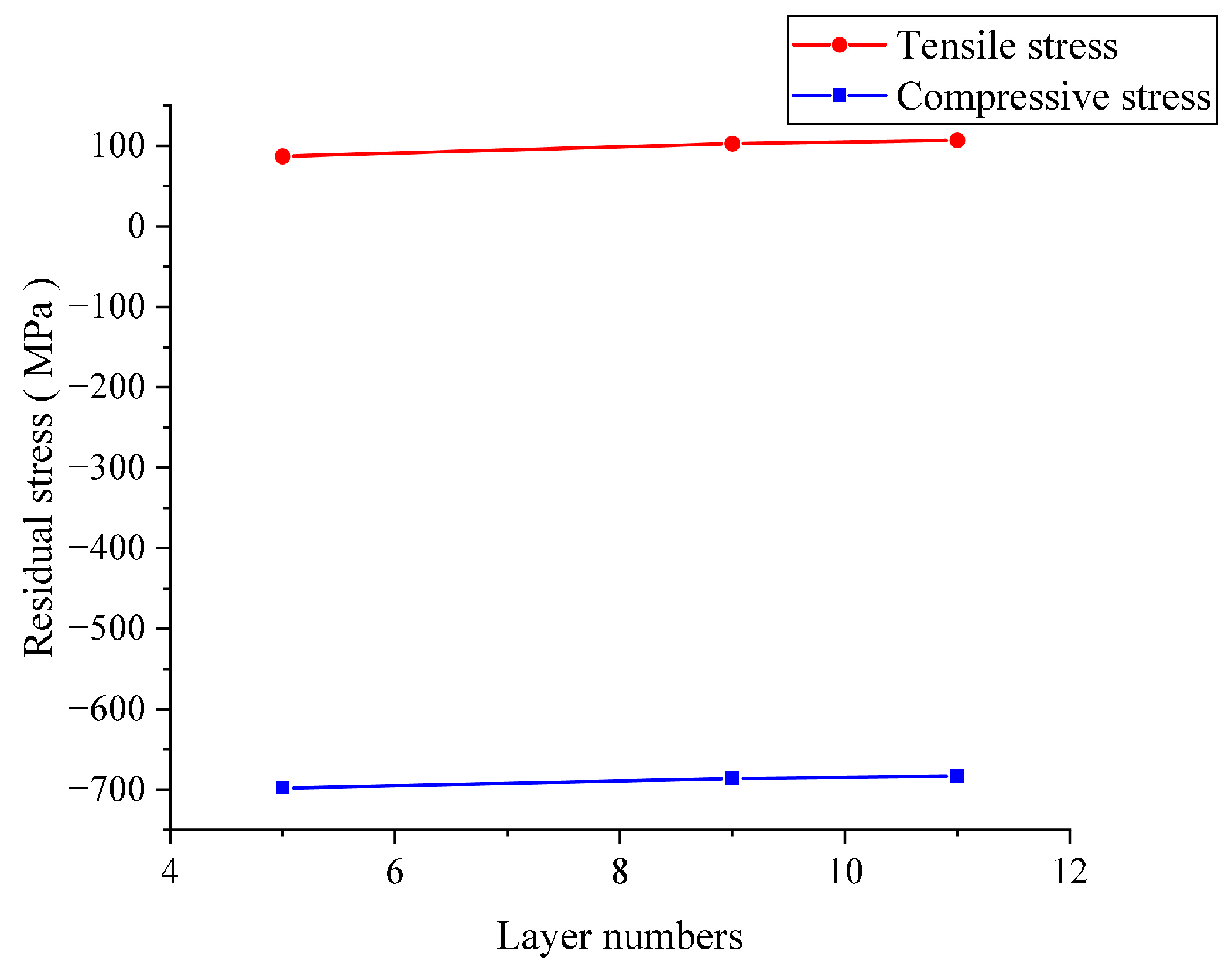
4.2. PFM Simulation of the Thermal Shock Fracture of Al2O3/ZrO2-Laminated Ceramic Specimens under Water Quenching
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Collin, M.; Rowcliffe, D. Analysis and prediction of thermal shock in brittle materials. Acta Mater. 2000, 48, 1655–1665. [Google Scholar] [CrossRef]
- Wei, Z.; Xu, X. FEM simulation on impact resistance of surface gradient and periodic layered bionic composites. Compos. Struct. 2020, 247, 112428. [Google Scholar] [CrossRef]
- Sun, M.; Bai, Y.; Li, M.; Fan, S.; Cheng, L. Structural design of laminated B4C/TiC composite fabricated by reactive melt infiltration. J. Alloys Compd. 2018, 765, 913–920. [Google Scholar] [CrossRef]
- Wei, C.; Ye, C. Mechanical properties and thermal shock behavior of bionic laminated ZrB2–SiC–G ceramics. Int. J. Refract. Met. Hard Mater. 2015, 51, 233–238. [Google Scholar] [CrossRef]
- Zhou, P.; Fan, Y.; Wang, P.; Chen, J. The indentation thermal shock behavior of laminated ZrB2–SiC ceramics with strong interfaces. Ceram. Int. 2016, 42, 17489–17496. [Google Scholar] [CrossRef] [Green Version]
- Zhou, P.; Wang, Z.; Fan, Y.; Hu, P.; Zhang, X.; Han, W. Thermal shock resistance of laminated ZrB2–SiC ceramic evaluated by indentation technique. J. Am. Ceram. Soc. 2015, 98, 2866–2872. [Google Scholar] [CrossRef]
- Bermejo, R.; Supancic, P.; Lube, T. Geometry effect on the thermal shock response of Al2O3/ZrO2 multilayered ceramics. Key Eng. Mater. 2007, 333, 251–254. [Google Scholar] [CrossRef]
- Bermejo, R.; Llanes, L.; Anglada, M.; Supancic, P.; Lube, T. Thermal shock behavior of an Al2O3/ZrO2 multilayered ceramic with residual stresses due to phase transformations. Key Eng. Mater. 2005, 290, 191–198. [Google Scholar] [CrossRef]
- Bermejo, R.; Torres, Y.; Sánchez-Herencia, A.J. Fracture Behavior of an Al2O3-5% tZrO2/Al2O3-30% mZrO2 multilayer system fabricated by slip casting. Fatigue Fract. Engng. Mater. Struct. 2006, 29, 71–78. [Google Scholar] [CrossRef]
- Ananchenko, D.V.; Nikiforov, S.V.; Sobyanin, K.V.; Konev, S.F.; Dauletbekova, A.K.; Akhmetova-Abdik, G.; Popov, A.I. Paramagnetic Defects and Thermoluminescence in Irradiated Nanostructured Monoclinic Zirconium Dioxide. Materials 2022, 15, 8624. [Google Scholar] [CrossRef]
- Antuzevics, A.; Elsts, E.; Kemere, M.; Lushchik, A.; Moskina, A.; Scherer, T.A.; Popov, A.I. Thermal annealing of neutron irradiation generated paramagnetic defects in transparent Al2O3 ceramics. Opt Mater. 2023, 135, 113250. [Google Scholar] [CrossRef]
- Vandeperre, L.J.; Kristofferson, A.; Carlström, E.; Clegg, W.J. Thermal shock of layered ceramic structures with crack-deflecting interfaces. J. Am. Ceram. Soc. 2001, 84, 104–110. [Google Scholar] [CrossRef]
- Elices, M.; Guinea, G.V.; Gomez, J.; Planas, J. The cohesive zone model: Advantages, limitations and challenges. Eng. Fract. Mech. 2002, 69, 137–163. [Google Scholar] [CrossRef]
- Moës, N.; Belytschko, T. Extended finite element method for cohesive crack growth. Eng. Fract. Mech. 2002, 69, 813–833. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, C.; Müller, R. A continuum phase field model for fracture. Eng. Fract. Mech. 2010, 77, 3625–3634. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Carollo, V.; Reinoso, J.; Paggi, M. Modeling complex crack paths in ceramic laminates: A novel variational framework combining the phase field method of fracture and the cohesive zone model. Eur. Ceram. Soc. 2018, 38, 2994–3003. [Google Scholar] [CrossRef]
- Borden, M.J.; Verhoosel, C.V.; Scott, M.A.; Hughes, T.J.; Landis, C.M. A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 2012, 217, 77–95. [Google Scholar] [CrossRef]
- Borden, M.J.; Hughes, T.J.; Landis, C.M.; Verhoosel, C.V. A higher-order phase-field model for brittle fracture: Formulation and analysis within the isogeometric analysis framework. Comput. Methods Appl. Mech. Eng. 2014, 273, 100–118. [Google Scholar] [CrossRef]
- Hakim, V.; Karma, A. Crack path prediction in anisotropic brittle materials. Phys. Rev. Lett. 2005, 95, 235501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, S.; Jiang, W.; Tonks, M.R. A new phase field fracture model for brittle materials that accounts for elastic anisotropy. Comput. Methods Appl. Mech. Eng. 2020, 358, 112643. [Google Scholar] [CrossRef]
- Zhang, S.; Kim, D.U.; Jiang, W.; Tonk, M.R. A phase field model of crack propagation in anisotropic brittle materials with preferred fracture planes. Comp. Mater. Sci. 2021, 193, 110400. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Yvonnet, J.; Zhu, Q.Z.; Bornert, M.; Chateau, C. A phase-field method for computational modeling of interfacial damage interacting with crack propagation in realistic microstructures obtained by microtomography. Comput. Methods Appl. Mech. Eng. 2016, 312, 567–595. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.T.; Waldmann, D.; Bui, T.Q. Role of interfacial transition zone in phase field modeling of fracture in layered heterogeneous structures. J. Comput. Phys. 2019, 386, 585–610. [Google Scholar] [CrossRef] [Green Version]
- Bourdin, B.; Marigo, J.J.; Maurini, C.; Sicsic, P. Morphogenesis and propagation of complex cracks induced by thermal shocks. Phys. Rev. Lett. 2014, 112, 014301. [Google Scholar] [CrossRef] [Green Version]
- Miehe, C.; Schaenzel, L.M.; Ulmer, H. Phase field modeling of fracture in multi-physics problems. Part I. Balance of crack surface and failure criteria for brittle crack propagation in thermo-elastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 449–485. [Google Scholar] [CrossRef]
- Chu, D.; Li, X.; Liu, Z. Study the dynamic crack path in brittle material under thermal shock loading by phase field modeling. Int. J. Fract. 2017, 208, 115–130. [Google Scholar] [CrossRef]
- Wang, T.; Ye, X.; Liu, Z.; Liu, X.; Chu, D.; Zhuang, Z. A phase-field model of thermo-elastic coupled brittle fracture with explicit time integration. Comput. Mech. 2020, 65, 1305–1321. [Google Scholar] [CrossRef]
- Molnár, G.; Gravouil, A. 2D and 3D Abaqus implementation of a robust staggered phase-field solution for modeling brittle fracture. Finite Elem. Anal. Des. 2017, 130, 27–38. [Google Scholar] [CrossRef]
- Miehe, C.; Kienle, D.; Aldakheel, F.; Teichtmeister, S. Phase field modeling of fracture in porous plasticity: A variational gradient-extended Eulerian framework for the macroscopic analysis of ductile failure. Comput. Methods Appl. Mech. Eng. 2016, 312, 3–50. [Google Scholar] [CrossRef]
- Li, D.; Li, P.; Li, W.; Li, W.; Zhou, K. Three-dimensional phase-field modeling of temperature-dependent thermal shock-induced fracture in ceramic materials. Eng. Fract. Mech. 2022, 268, 108444. [Google Scholar] [CrossRef]
- Fang, J.; Wu, C.; Rabczuk, T.; Wu, C.; Ma, C.; Sun, G.; Li, Q. Phase field fracture in elasto-plastic solids: Abaqus implementation and case studies. Theor. Appl. Fract. Mech. 2019, 103, 102252. [Google Scholar] [CrossRef]
- Mandal, T.K.; Nguyen, V.P.; Wu, J.Y.; Nguyen-Thanh, C.; de Vaucorbeil, A. Fracture of thermo-elastic solids: Phase-field modeling and new results with an efficient monolithic solver. Comput. Methods Appl. Mech. Eng. 2021, 376, 113648. [Google Scholar] [CrossRef]
- Klym, H.; Karbovnyk, I.; Piskunov, S.; Popov, A.I. Positron annihilation lifetime spectroscopy insight on free volume conversion of nanostructured MgAl2O4 ceramics. Nanomaterials 2021, 11, 3373. [Google Scholar] [CrossRef] [PubMed]
- Náhlík, L.; Šestáková, L.; Hutař, P.; Bermejo, R. Prediction of crack propagation in layered ceramics with strong interfaces. Eng. Fract. Mech. 2010, 77, 2192–2199. [Google Scholar] [CrossRef]
- Bermejo, R.; Torres, Y.; Sanchez-Herencia, A.J.; Baudín, C.; Anglada, M.; Llanes, L. Residual stresses, strength and toughness of laminates with different layer thickness ratios. Acta Mater. 2006, 54, 4745–4757. [Google Scholar] [CrossRef]
- Li, D.; Pang, Y.; Lu, T.; Liu, Z.; Chen, S. Numerical analysis of thermal shock cracking behaviors of ceramics based on the force-heat equivalence energy density principle. Front. Mater. 2022, 8, 641. [Google Scholar] [CrossRef]
- Xu, X.; Tian, C.; Sheng, S.; Lin, Z.; Song, F. Characterization of thermal-shock cracks in ceramic bars. Sci. China Phys. Mech. 2014, 57, 2205–2208. [Google Scholar] [CrossRef]




| Property | AMZ | ATZ |
|---|---|---|
| E (GPa) | 310 | 390 |
| ν | 0.22 | 0.22 |
| ρ (g/cm3) | 4.48 | 4.03 |
| α (10−6 °C−1) | 8.02 | 9.8 |
| k (W/(m·°C)) | 24.2 | 30.9 |
| Cp (J/(kg·°C)) | 687 | 762 |
| σ (MPa) | 110 | 392 |
| Layer Thickness Ratio, R (ATZ/AMZ) | 2 | 5 | 10 |
|---|---|---|---|
| ATZ | 0.429 | 0.530 | 0.556 |
| AMZ | 0.214 | 0.100 | 0.056 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, Y.; Li, D.; Li, X.; Wang, R.; Ao, X. Phase-Field Simulation of Temperature-Dependent Thermal Shock Fracture of Al2O3/ZrO2 Multilayer Ceramics with Phase Transition Residual Stress. Materials 2023, 16, 734. https://doi.org/10.3390/ma16020734
Pang Y, Li D, Li X, Wang R, Ao X. Phase-Field Simulation of Temperature-Dependent Thermal Shock Fracture of Al2O3/ZrO2 Multilayer Ceramics with Phase Transition Residual Stress. Materials. 2023; 16(2):734. https://doi.org/10.3390/ma16020734
Chicago/Turabian StylePang, Yong, Dingyu Li, Xin Li, Ruzhuan Wang, and Xiang Ao. 2023. "Phase-Field Simulation of Temperature-Dependent Thermal Shock Fracture of Al2O3/ZrO2 Multilayer Ceramics with Phase Transition Residual Stress" Materials 16, no. 2: 734. https://doi.org/10.3390/ma16020734
APA StylePang, Y., Li, D., Li, X., Wang, R., & Ao, X. (2023). Phase-Field Simulation of Temperature-Dependent Thermal Shock Fracture of Al2O3/ZrO2 Multilayer Ceramics with Phase Transition Residual Stress. Materials, 16(2), 734. https://doi.org/10.3390/ma16020734




