Theoretical and Experimental Investigation on the Flexural Behaviour of Prestressed NC-UHPC Composite Beams
Abstract
:1. Introduction
2. Theory and Calculation
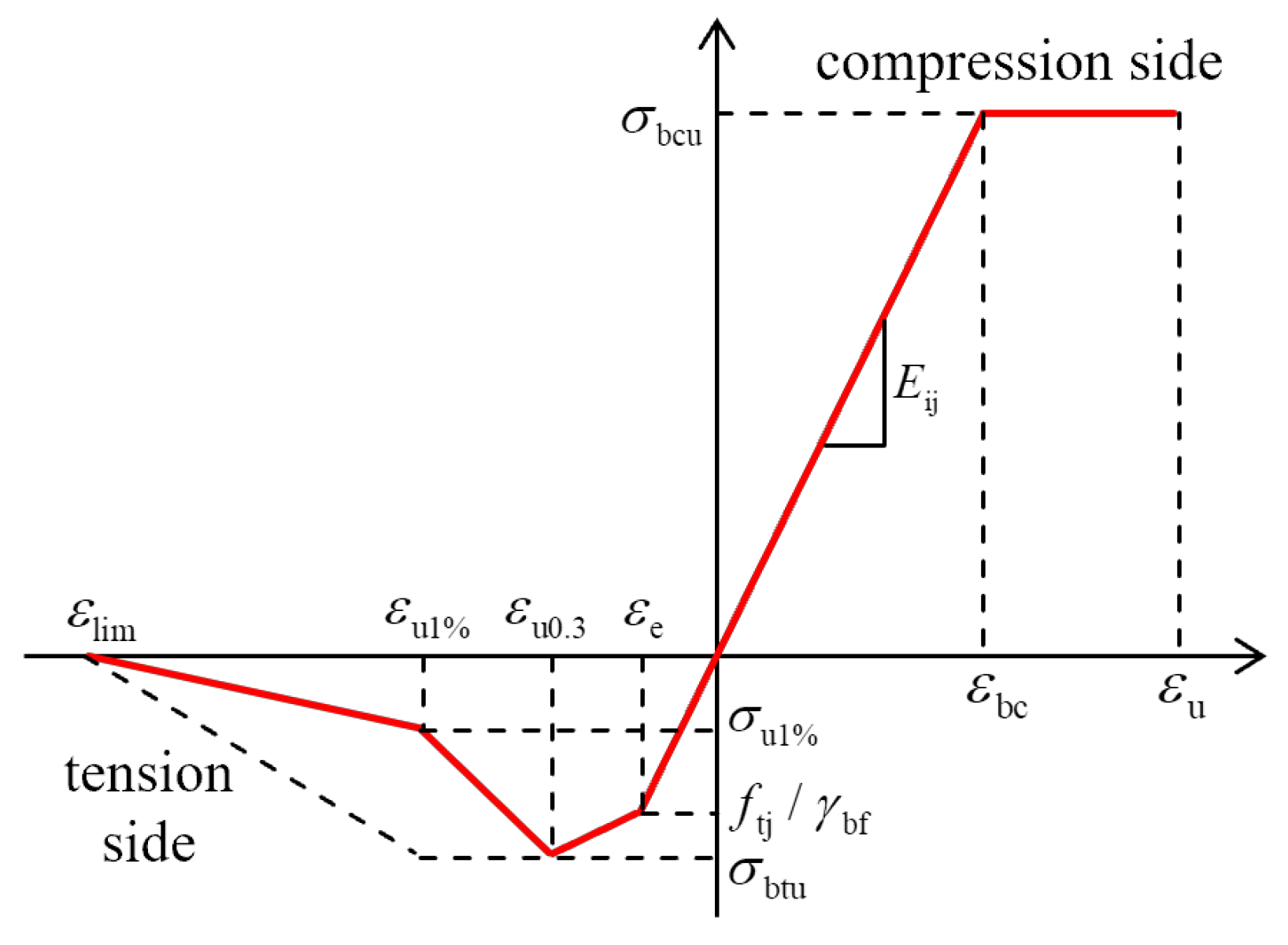
2.1. Calculation Method of UHPC Tensile Strength
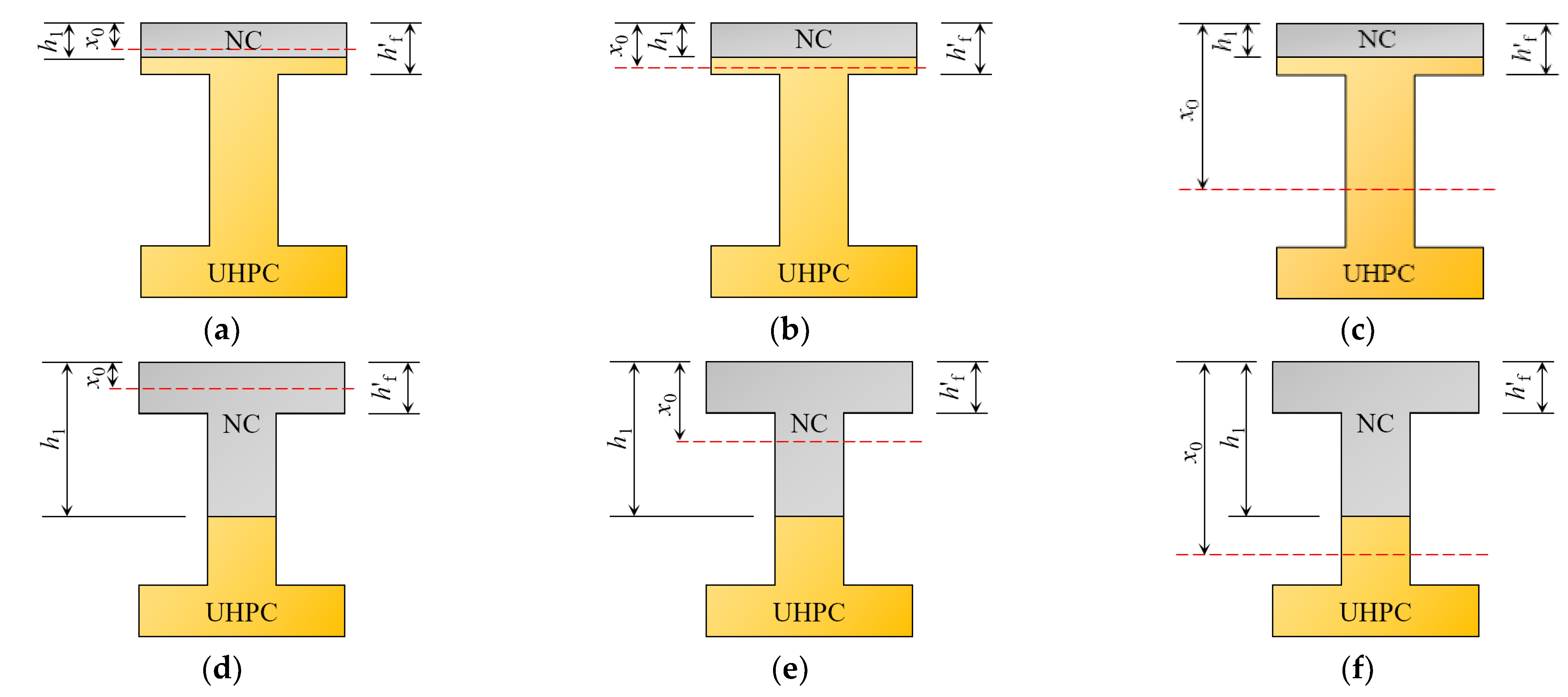
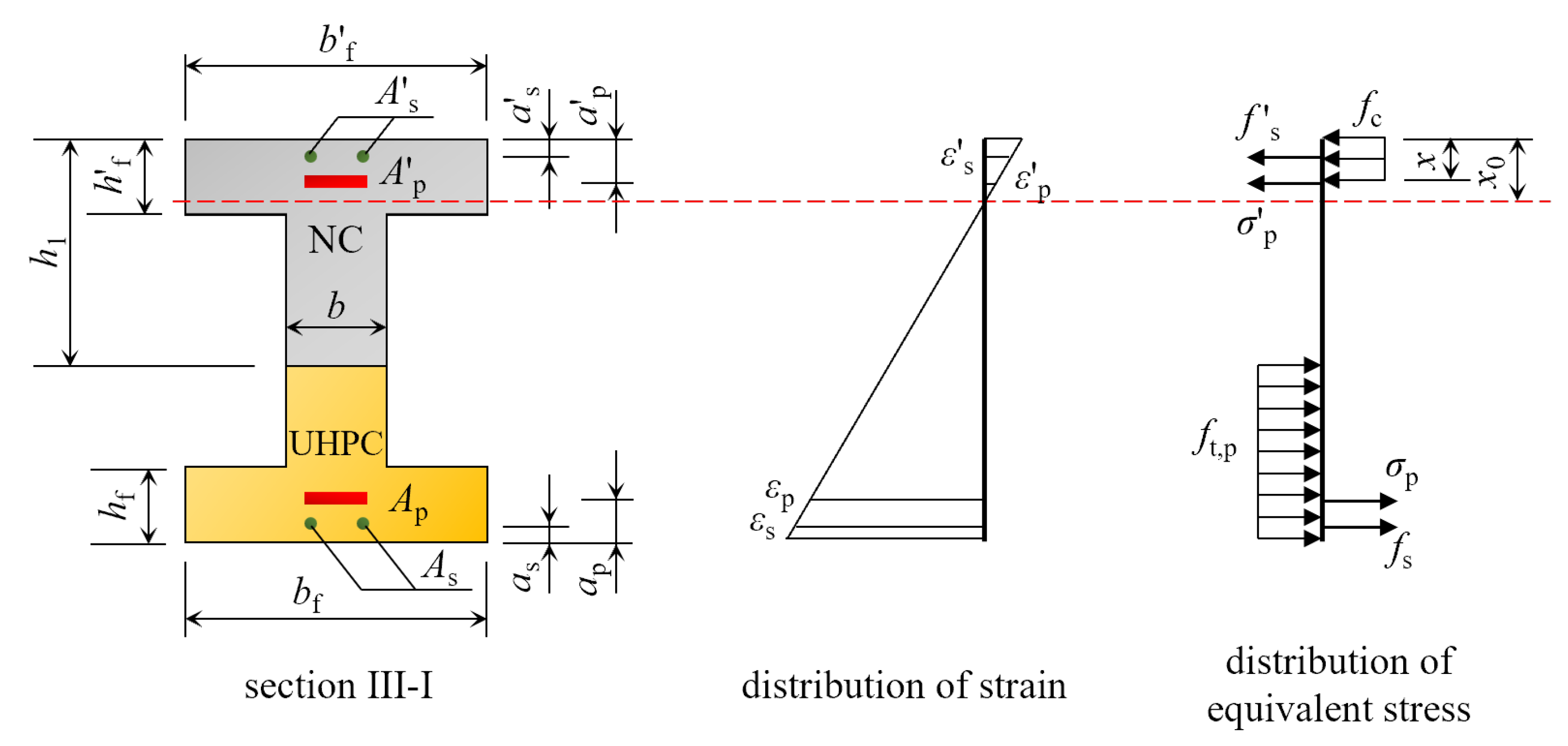
2.2. Normal Section Strength of Prestressed NC-UHPC Composite Bridge
2.3. Cracking Moments of NC-UHPC Composite Beams
3. Experimental Methods
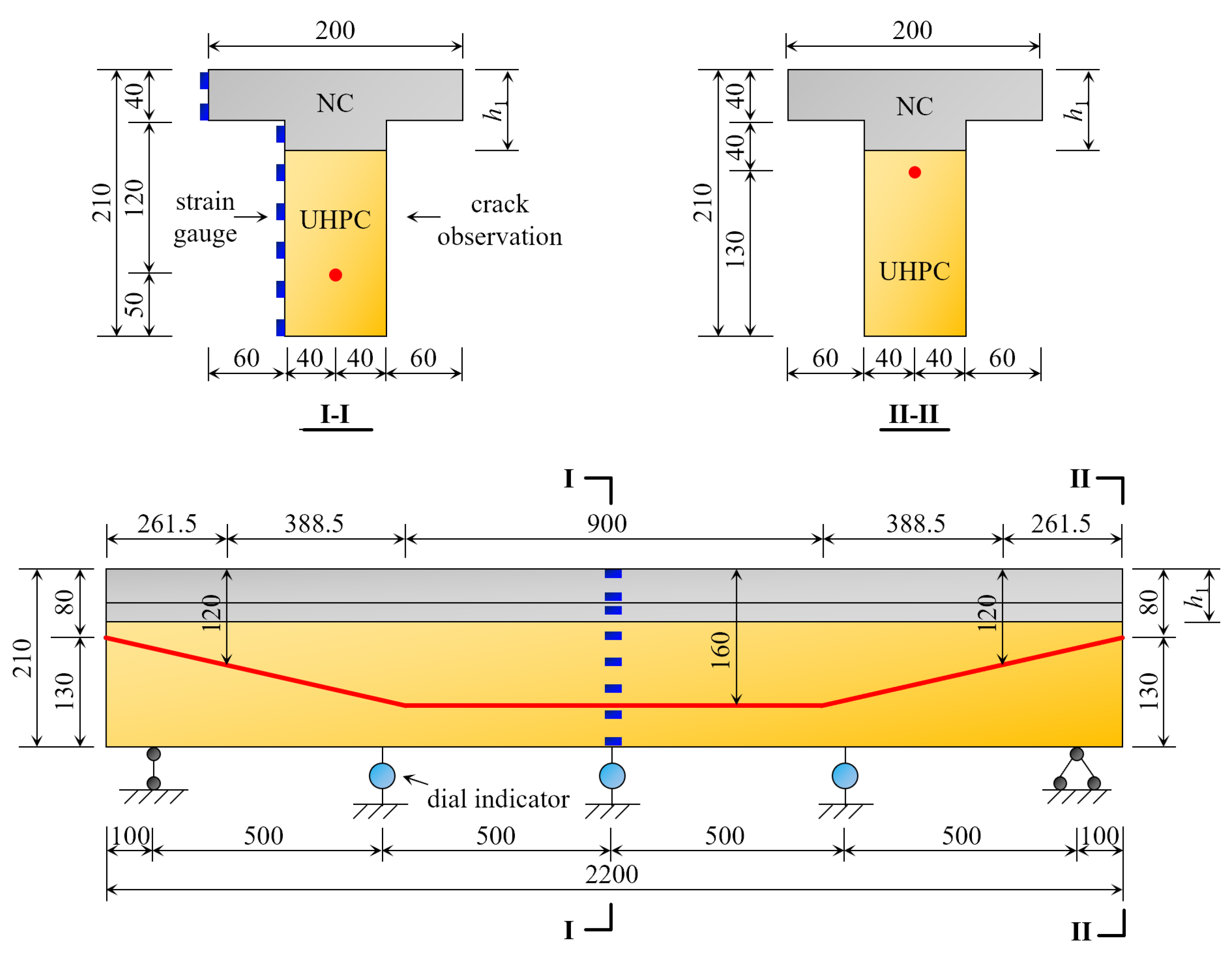
3.1. Design of NC-UHPC Composite Beam
3.2. Test Content and Measured Points Layout
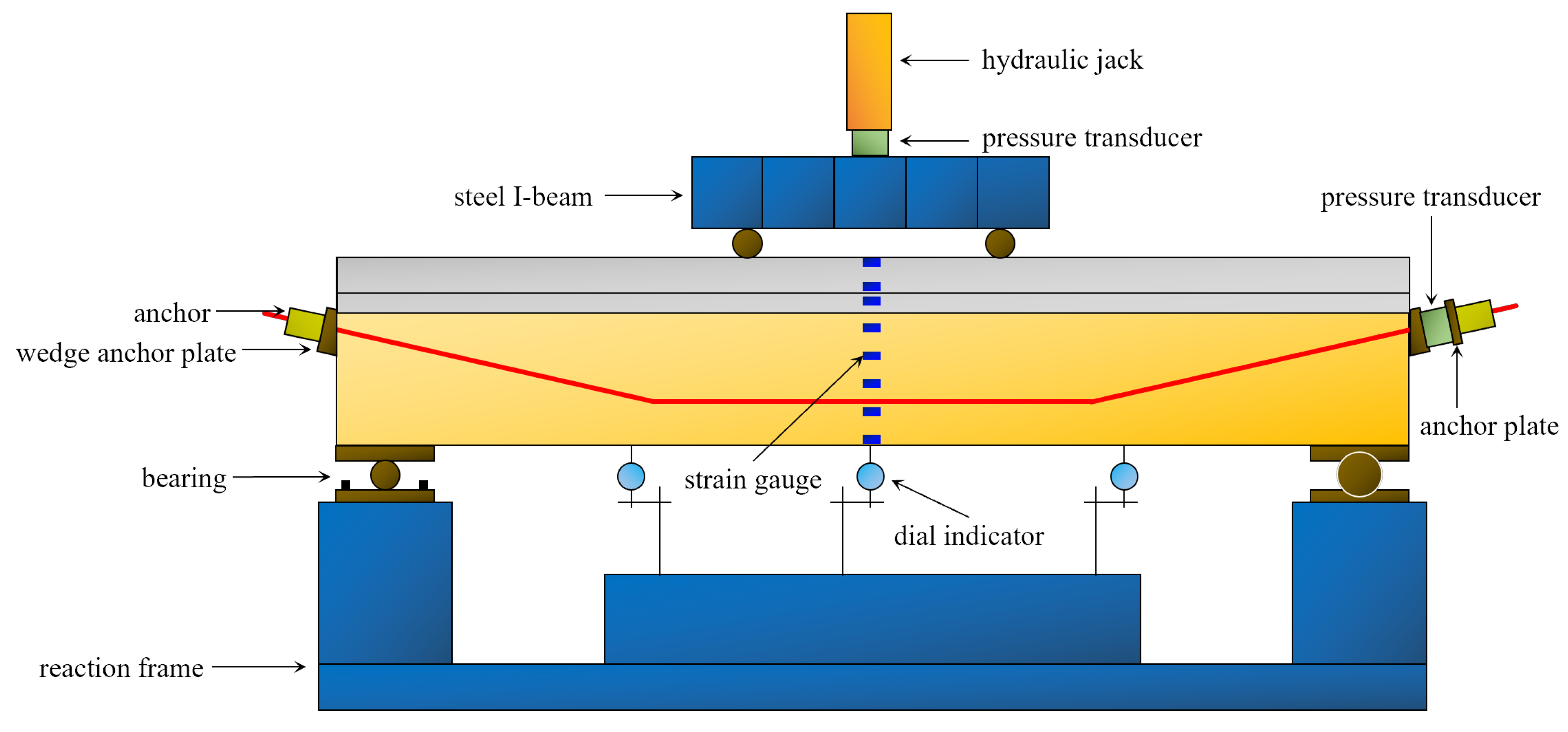
3.3. Tensioning
3.4. Static Bending Test
4. Results and Discussion
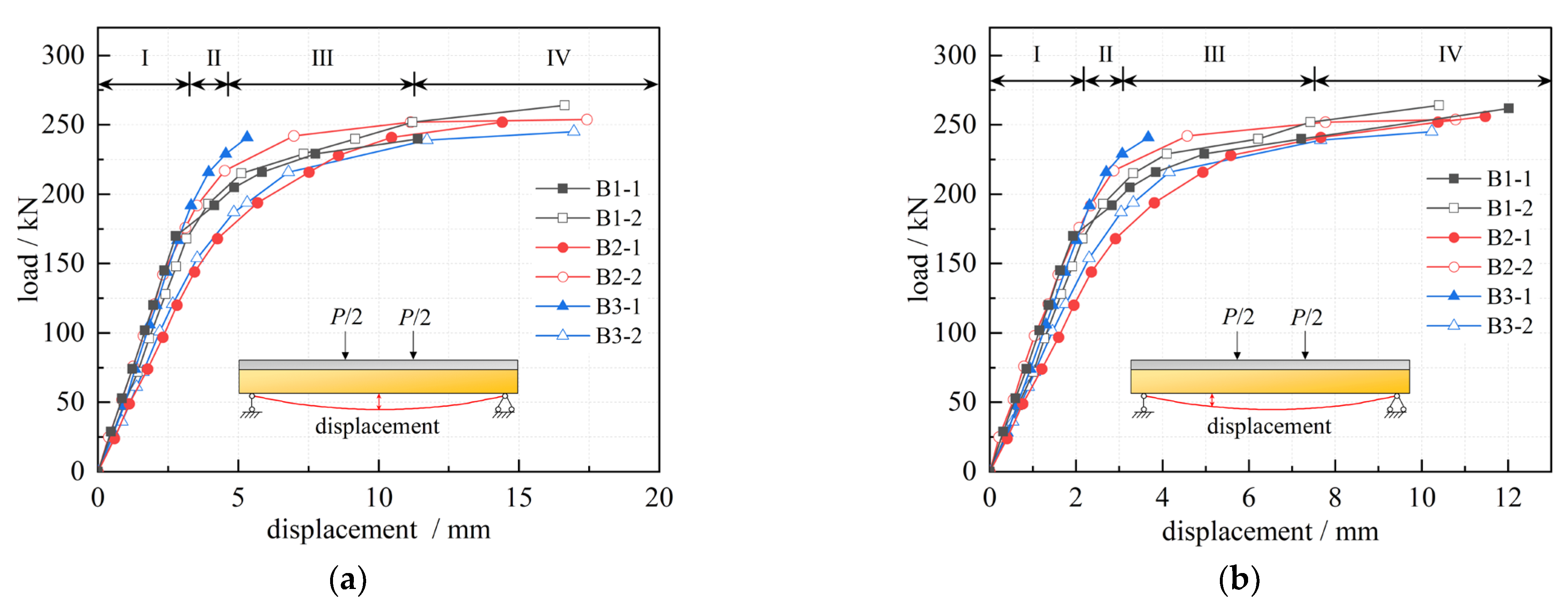
4.1. Load-Deflection Curves and the Failure Process
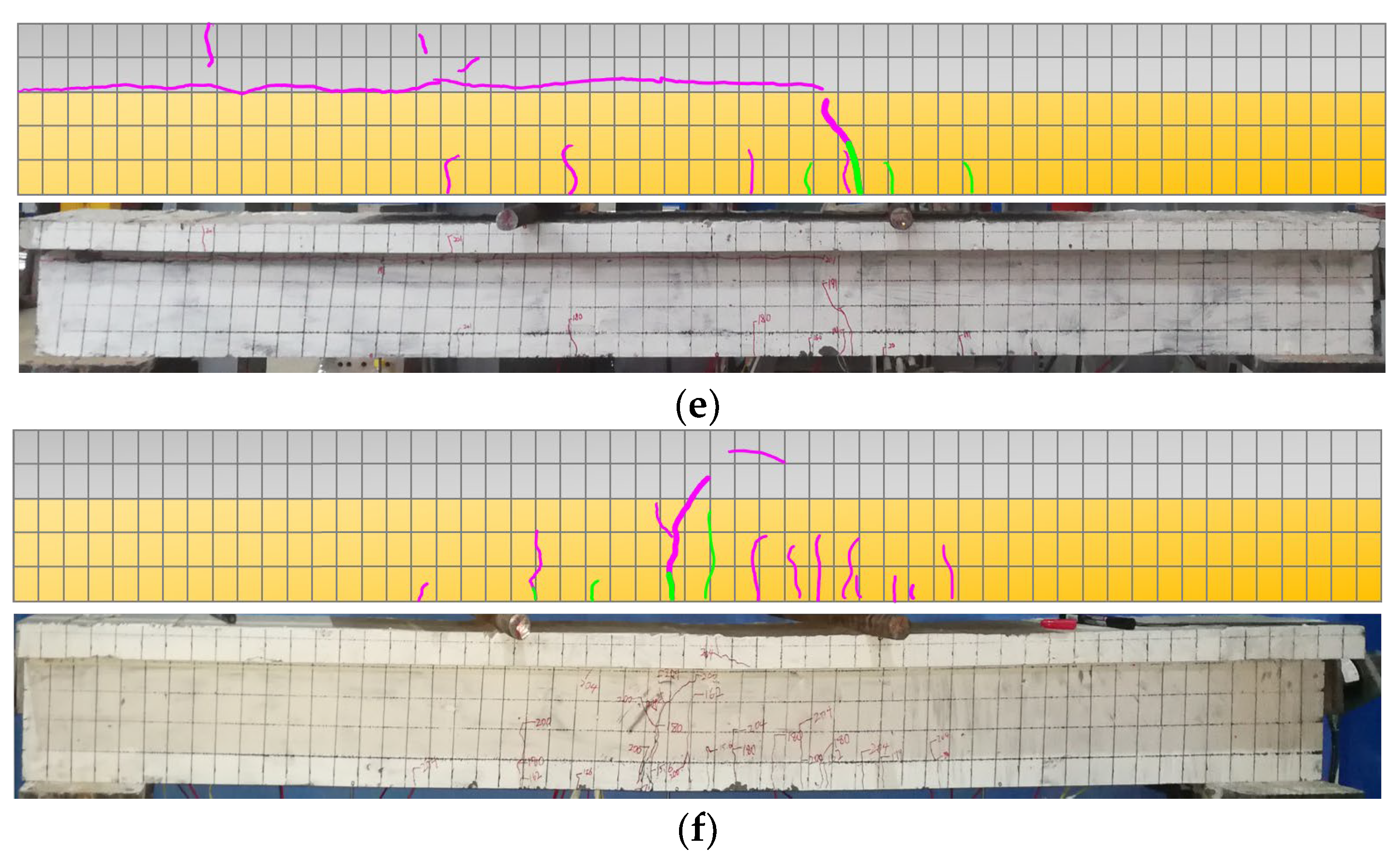
4.2. The Development of Cracks
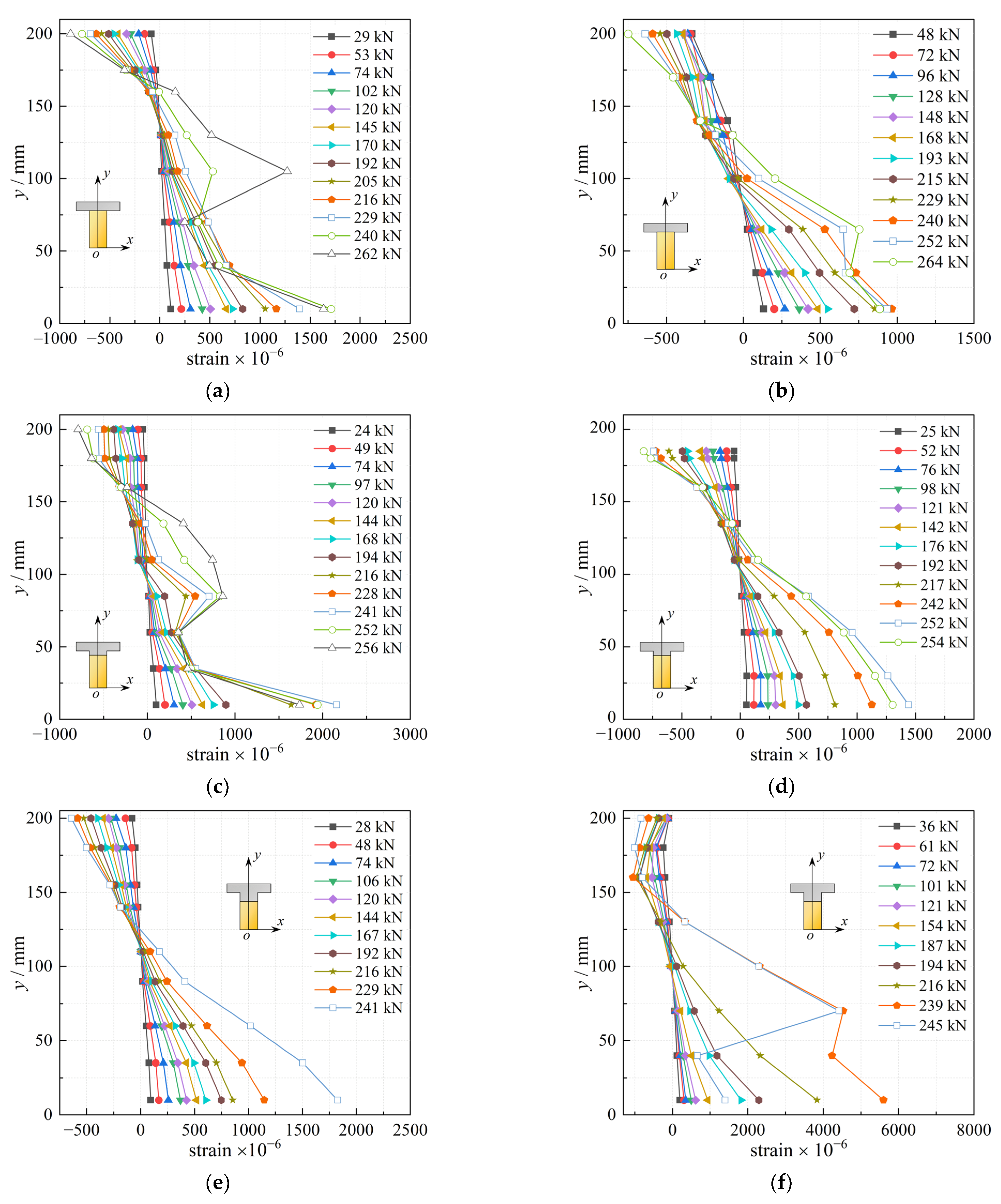
4.3. Strain of Concrete
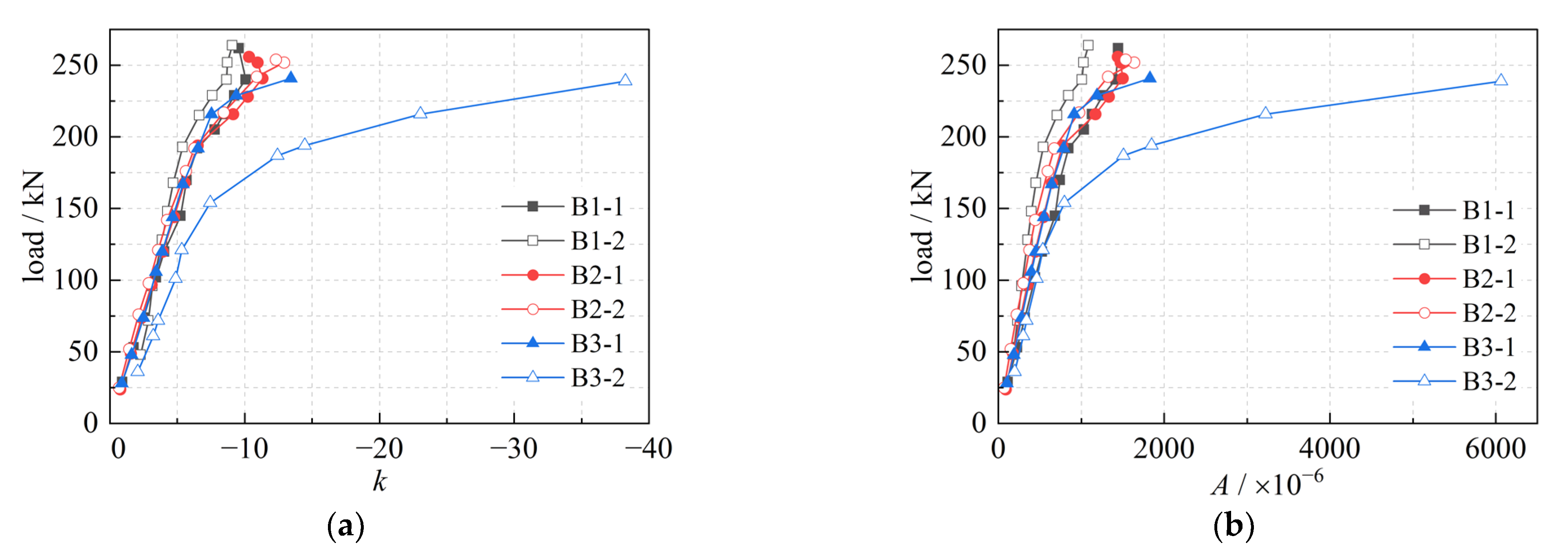
4.4. Normal Section Strength and Cracking Moment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, M.; Lu, W.; Song, J.; Lee, G.C. Application of ultra-high performance concrete in bridge engineering. Construct. Build. Mater. 2018, 186, 1256–1267. [Google Scholar] [CrossRef]
- Xue, J.; Briseghella, B.; Huang, F.; Nuti, C.; Tabatabai, H.; Chen, B. Review of ultra-high performance concrete and its application in bridge engineering. Construct. Build. Mater. 2020, 260, 119844. [Google Scholar] [CrossRef]
- Li, H.; Li, L.; Fan, X.; Ye, M.; Shao, X.; Yi, L. Experimental and numerical investigation on the flexural behavior of a large-scale prestressed UHPC T-Shaped girder. Eng. Struct. 2022, 272, 115027. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, C.; He, W.; Wu, L. Effects of steel fiber content and shape on mechanical properties of ultra high performance concrete. Construct. Build. Mater. 2016, 103, 8–14. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, C.; He, W.; Wang, D. Static and dynamic compressive properties of ultra-high performance concrete (UHPC) with hybrid steel fiber reinforcements. Cem. Concr. Compos. 2017, 79, 148–157. [Google Scholar] [CrossRef] [Green Version]
- Abbas, S.; Soliman, A.M.; Nehdi, M.L. Exploring mechanical and durability properties of ultra-high performance concrete incorporating various steel fiber lengths and dosages. Construct. Build. Mater. 2015, 75, 429–441. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, C.; Khayat, K.H. Investigation of mechanical properties and shrinkage of ultra-high performance concrete: Influence of steel fiber content and shape. Compos. Part B Eng. 2019, 174, 107021. [Google Scholar] [CrossRef]
- Shah, H.A.; Yuan, Q.; Photwichai, N. Use of materials to lower the cost of ultra-high-performance concrete–A review. Construct. Build. Mater. 2022, 327, 127045. [Google Scholar] [CrossRef]
- Feng, Z.; Li, C.; Yoo, D.Y.; Pan, R.; He, J.; Ke, L. Flexural and cracking behaviors of reinforced UHPC beams with various reinforcement ratios and fiber contents. Eng. Struct. 2021, 248, 113266. [Google Scholar] [CrossRef]
- Mahmud, G.H.; Yang, Z.; Hassan, A.M. Experimental and numerical studies of size effects of Ultra High Performance Steel Fibre Reinforced Concrete (UHPFRC) beams. Construct. Build. Mater. 2013, 48, 1027–1034. [Google Scholar] [CrossRef]
- Graybeal, B.A. Flexural behavior of an ultrahigh-performance concrete I-girder. J. Bridge Eng. 2008, 13, 602–610. [Google Scholar] [CrossRef]
- Yang, I.H.; Joh, C.; Kim, B.S. Structural behavior of ultra high performance concrete beams subjected to bending. Eng. Struct. 2010, 32, 3478–3487. [Google Scholar] [CrossRef]
- Shao, Y.; Billington, S.L. Utilizing full UHPC compressive strength in steel reinforced UHPC beams. In Proceedings of the International Interactive Symposium on Ultra-High Performance Concrete, New York, NY, USA, 2–5 June 2019. [Google Scholar] [CrossRef]
- Hussein, L.; Amleh, L. Structural behavior of ultra-high performance fiber reinforced con-crete-normal strength concrete or high strength concrete composite members. Construct. Build. Mater. 2015, 93, 1105–1116. [Google Scholar] [CrossRef]
- Yalçınkaya, Ç. A preliminary study on the development of the normal concrete-UHPC composite beam via wet casting. J. Struct. Eng. 2021, 4, 46–56. [Google Scholar] [CrossRef]
- Li, S.L.; Zhang, L.G.; Guo, P.; Zhang, P.; Wang, C.; Sun, W.C.; Han, S.L. Characteristic analysis of acoustic emission monitoring parameters for crack propagation in UHPC-NC composite beam under bending test. Construct. Build. Mater. 2021, 278, 122401. [Google Scholar] [CrossRef]
- Tong, T.; Yuan, S.; Wang, J.; Liu, Z. The role of bond strength in structural behaviors of UHPC-NC composite beams: Experimental investigation and finite element modeling. Compos. Struct. 2021, 255, 112914. [Google Scholar] [CrossRef]
- He, J.; Chao, L. Numerical analysis on shear resistance of ultra-high performance concrete-normal strength concrete composite beam. Struct. Concr. 2021, 22, 1128–1146. [Google Scholar] [CrossRef]
- Zhu, J.; Guo, X.; Kang, J.; Duan, M.; Wang, Y. Numerical and theoretical research on flexural behavior of steel-UHPC composite beam with waffle-slab system. J. Construct. Steel Res. 2020, 171, 106141. [Google Scholar] [CrossRef]
- Shafieifar, M.; Farzad, M.; Azizinamini, A. Experimental and numerical study on mechanical properties of Ultra High Performance Concrete (UHPC). Construct. Build. Mater. 2017, 156, 402–411. [Google Scholar] [CrossRef]
- De Maio, U.; Fantuzzi, N.; Greco, F.; Leonetti, L.; Pranno, A. Failure Analysis of Ultra High-Performance Fiber-Reinforced Concrete Structures Enhanced with Nanomaterials by Using a Diffuse Cohesive Interface Approach. Nanomaterials 2020, 10, 1792. [Google Scholar] [CrossRef]
- NF P18-470; Concrete-Ultra-High Performance Fiber-Reinforced Concrete-Specifications, Performance, Production and Conformity. AFNOR-French Standard Institute: Paris, France, 2016.
- De Domenico, D.; Messina, D.; Recupero, A. Quality control and safety assessment of prestressed concrete bridge decks through combined field tests and numerical simulation. Structures 2022, 39, 1135–1157. [Google Scholar] [CrossRef]
- Steinberg, E. Structural reliability of prestressed UHPC flexure models for bridge girders. J. Bridge Eng. 2010, 15, 65–72. [Google Scholar] [CrossRef]
- Lanwer, J.P.; Höper, S.; Gietz, L.; Kowalsky, U.; Empelmann, M.; Dinkler, D. Fundamental Investigations of Bond Behaviour of High-Strength Micro Steel Fibres in Ultra-High Performance Concrete under Cyclic Tensile Loading. Materials 2021, 15, 120. [Google Scholar] [CrossRef] [PubMed]
- Switek-Rey, A.; Denarié, E.; Brühwiler, E. Early age creep and relaxation of uhpfrc under low to high tensile stresses. Cem. Concr. Res. 2016, 83, 57–69. [Google Scholar] [CrossRef] [Green Version]
- Kang, S.T.; Choi, J.I.; Koh, K.T.; Lee, K.S.; Lee, B.Y. Hybrid effects of steel fiber and microfiber on the tensile behavior of ultra-high performance concrete. Compos. Struct. 2016, 145, 37–42. [Google Scholar] [CrossRef]
- Qi, J.; Wang, J.; Ma, Z.J. Flexural response of highstrength steel-ultra-high-performance fiber reinforced concrete beams based on a mesoscale constitutive model: Experiment and theory. Struct. Concr. 2018, 19, 719–734. [Google Scholar] [CrossRef]
- Abrishambaf, A.; Pimentel, M.; Nunes, S. Influence of fiber orientation on the tensile behaviour of ultra-high performance fiber reinforced cementitious composites. Cem. Concr. Res. 2017, 97, 28–40. [Google Scholar] [CrossRef]
- Xu, M.X.; Liang, X.W.; Wang, P.; Wang, Z.Y. Theoretical investigation on normal section flexural capacity of UHPC beams. Eng. Mech. 2019, 36, 70–78. (In Chinese) [Google Scholar] [CrossRef]
- Ali, H.M.; Hamad, L.N.T. First Diagonal Cracking and Ultimate Shear of Reactive Powder Concrete T-Beams without Stirrups. J. Eng. Dev. 2014, 18, 149–164. Available online: https://jeasd.uomustansiriyah.edu.iq/index.php/jeasd/article/view/955. (accessed on 1 September 2014).
- Meng, W.; Yao, Y.; Mobasher, B.; Khayat, K.H. Effects of loading rate and notch-to-depth ratio of notched beams on flexural performance of ultra-high-performance concrete. Cem. Concr. Compos. 2017, 83, 349–359. [Google Scholar] [CrossRef]
- Cao, Y.Y.Y.; Li, P.P.; Brouwers, H.J.H.; Sluijsmans, M.; Yu, Q.L. Enhancing flexural performance of ultra-high performance concrete by an optimized layered-structure concept. Compos. Part B Eng. 2019, 171, 154–165. [Google Scholar] [CrossRef]
- Huang, B.T.; Dai, J.G.; Weng, K.F.; Zhu, J.X.; Shah, S.P. Flexural performance of UHPC–concrete–ECC composite member reinforced with perforated steel plates. J. Struct. Eng. 2021, 147, 04021065. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, R.; Jia, L.J.; Wang, J.Y. Flexural behaviour of rebar-reinforced ultra-high-performance concrete beams. Mag. Concr. Res. 2018, 70, 997–1015. [Google Scholar] [CrossRef]
- Yoo, D.Y.; Yoon, Y.S. Structural performance of ultra-high-performance concrete beams with different steel fibers. Eng. Struct. 2015, 102, 409–423. [Google Scholar] [CrossRef]
- Aaleti, S.; Sritharan, S. Quantifying bonding characteristics between UHPC and normal-strength concrete for bridge deck application. J. Bridge Eng. 2019, 24, 04019041. [Google Scholar] [CrossRef] [Green Version]
- Pannell, F.N. The ultimate moment of resistance of unbonded prestressed concrete beams. Mag. Concr. Res. 1969, 21, 43–54. [Google Scholar] [CrossRef]
- Liu, S.; He, Z.; Hu, L. Interfacial microstructure between ultrahigh-performance concrete–normal concrete in fresh-on-fresh casting. Construct. Build. Mater. 2022, 322, 126476. [Google Scholar] [CrossRef]
- Al-Kamal, M.K. Nominal flexural strength of high-strength concrete beams. Adv. Concr. Construct. 2019, 7, 1–9. [Google Scholar] [CrossRef]
- Hu, R.; Fang, Z.; Jiang, R.; Xiang, Y.; Liu, C. Fatigue prediction model of ultra-high-performance concrete beams prestressed with CFRP tendons. Adv. Struct. Eng. 2022, 25, 611–624. [Google Scholar] [CrossRef]
- Chen, C.; Yang, C.; Pan, Y.; Zhang, H.; De Backer, H. Parameters analysis and design of transverse connection strengthening prestressed concrete T-girder bridge. Struct. Concr. 2021, 22, 3385–3395. [Google Scholar] [CrossRef]
- Grubb, M.A.; Corven, J.A.; Wilson, K.E.; Bouscher, J.W.; Volle, L.E. Load and Resistance Factor Design (LRFD) for Highway Bridge Superstructures; Federal Highway Administration: Arlington, VA, USA, 2002. [Google Scholar]
- Yoo, D.Y.; Banthia, N.; Kang, S.T.; Yoon, Y.S. Size effect in ultra-high-performance concrete beams. Eng. Fract. Mech. 2016, 157, 86–106. [Google Scholar] [CrossRef]




| Value | UHPC | NC | |
|---|---|---|---|
| Compressive | Tensile | ||
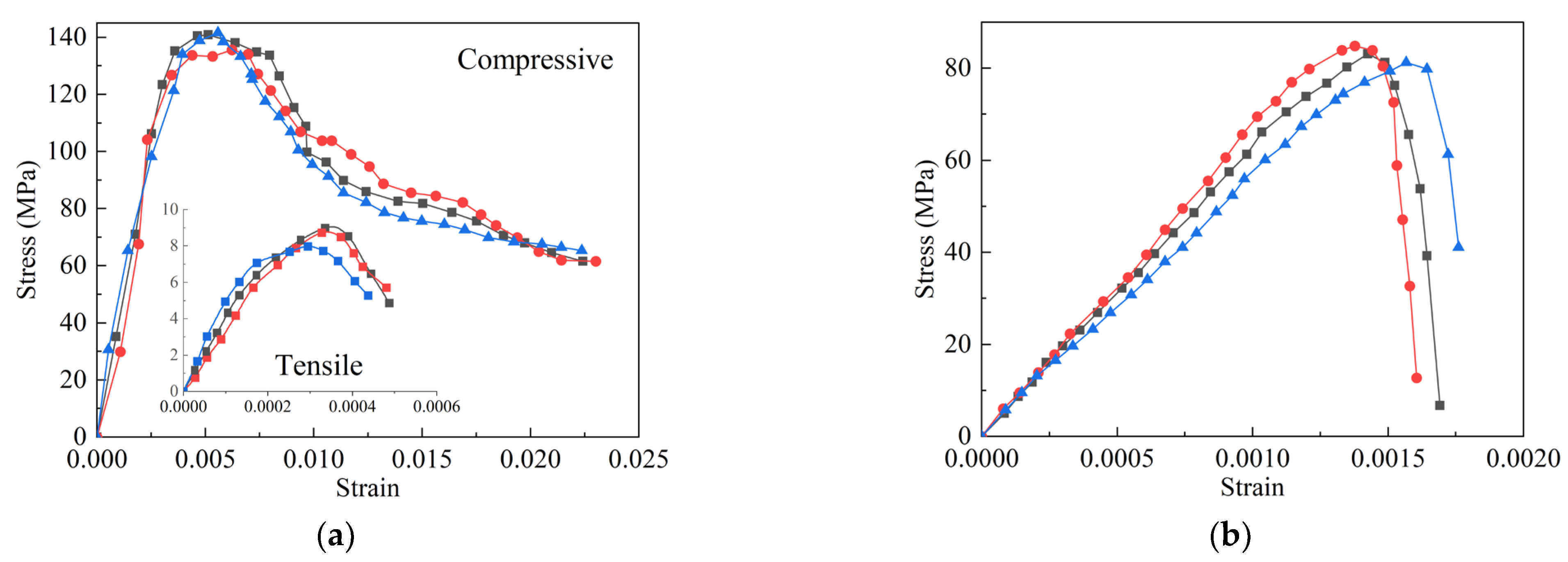
| Tested value/MPa | 140.79 | 8.97 | 83.15 |
| 135.56 | 8.72 | 84.88 | |
| 141.55 | 7.97 | 81.26 | |
| Mean value/MPa | 139.30 | 8.55 | 83.10 |
| Coefficient of variation | 2.34% | 6.09% | 2.18% |
| Number of Beams | Tensioning Stress/MPa | Strain/×10−6 | Reversed Deflection/mm | |||
|---|---|---|---|---|---|---|
| Control Value | Actual Value | Loss Value | Upper Edge | Lower Edge | ||
| B1-1 | 1300 | 1158.57 | 141.43 | 45.06 | −498.07 | 1.13 |
| B1-2 | 1300 | 1153.57 | 146.43 | 52.50 | −458.75 | 0.97 |
| B2-1 | 1300 | 1159.29 | 140.71 | 48.94 | −490.91 | 1.08 |
| B2-2 | 1300 | 1180.71 | 119.29 | −1.01 | −479.19 | 0.95 |
| B3-1 | 1300 | 1153.57 | 146.43 | 50.00 | −518.18 | 1.10 |
| B3-2 | 1300 | 1238.57 | 61.43 | −849.96 | −854.13 | 1.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, P.; Yan, W.; Zhao, H.; Ma, J. Theoretical and Experimental Investigation on the Flexural Behaviour of Prestressed NC-UHPC Composite Beams. Materials 2023, 16, 879. https://doi.org/10.3390/ma16020879
Lin P, Yan W, Zhao H, Ma J. Theoretical and Experimental Investigation on the Flexural Behaviour of Prestressed NC-UHPC Composite Beams. Materials. 2023; 16(2):879. https://doi.org/10.3390/ma16020879
Chicago/Turabian StyleLin, Pengzhen, Weiyi Yan, Hongwei Zhao, and Junjun Ma. 2023. "Theoretical and Experimental Investigation on the Flexural Behaviour of Prestressed NC-UHPC Composite Beams" Materials 16, no. 2: 879. https://doi.org/10.3390/ma16020879
APA StyleLin, P., Yan, W., Zhao, H., & Ma, J. (2023). Theoretical and Experimental Investigation on the Flexural Behaviour of Prestressed NC-UHPC Composite Beams. Materials, 16(2), 879. https://doi.org/10.3390/ma16020879






