Testing and Analysis of Uniaxial Mechanical Fatigue, Charpy Impact Fracture Energy and Microhardness of Two Low-Carbon Steels
Abstract
:1. Introduction
2. Basic Data on Experimental Research
3. Experimental Results and Discussion
3.1. Parameters Defining the Strength of the Material
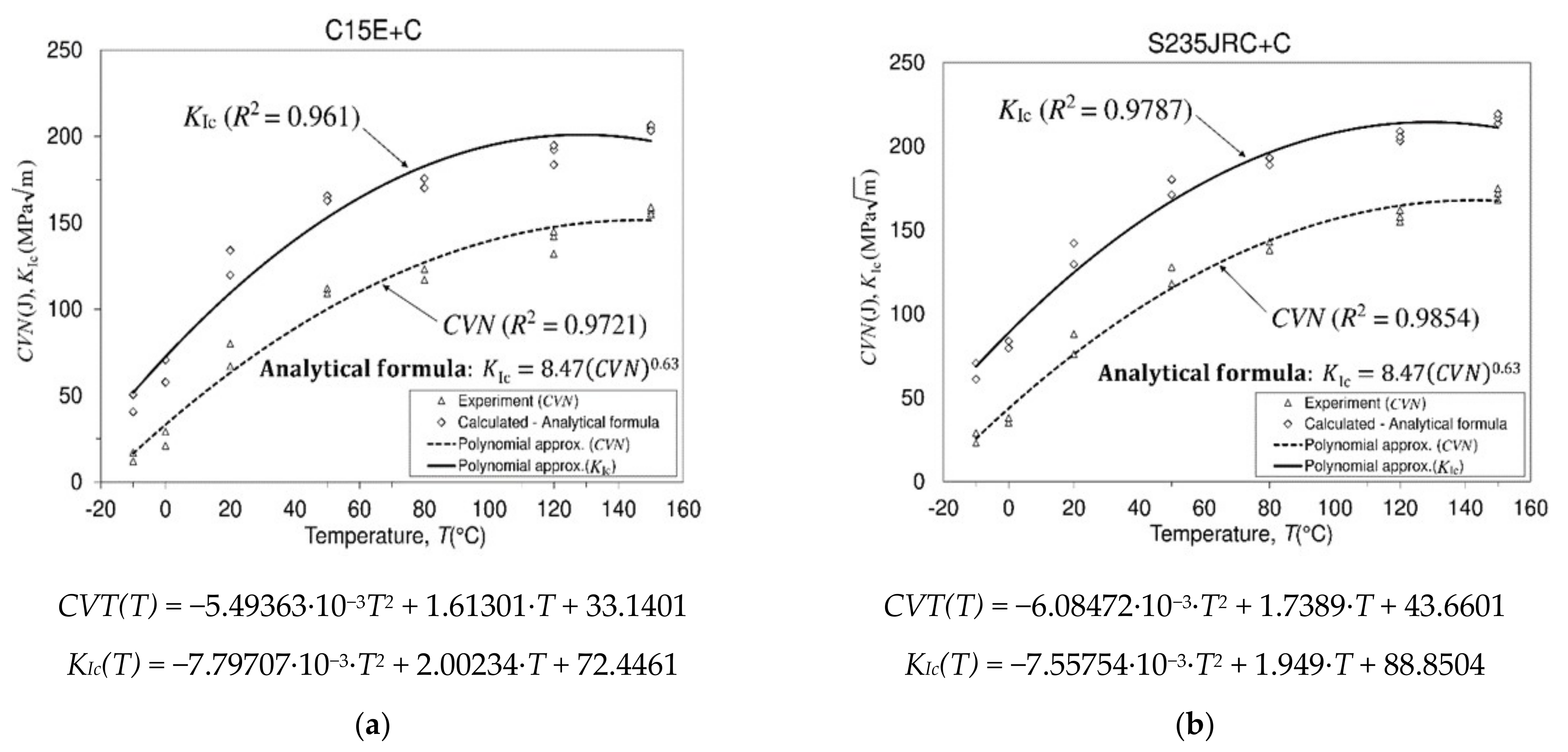
3.2. Impact Fracture Testing of a Material Using Charpy Machine
3.3. Uniaxial Fatigue Testing of Materials
3.3.1. General Consideration
3.3.2. Uniaxial Mechanical High-Cyclic Fatigue Testing of Materials at Different Stress Ratios
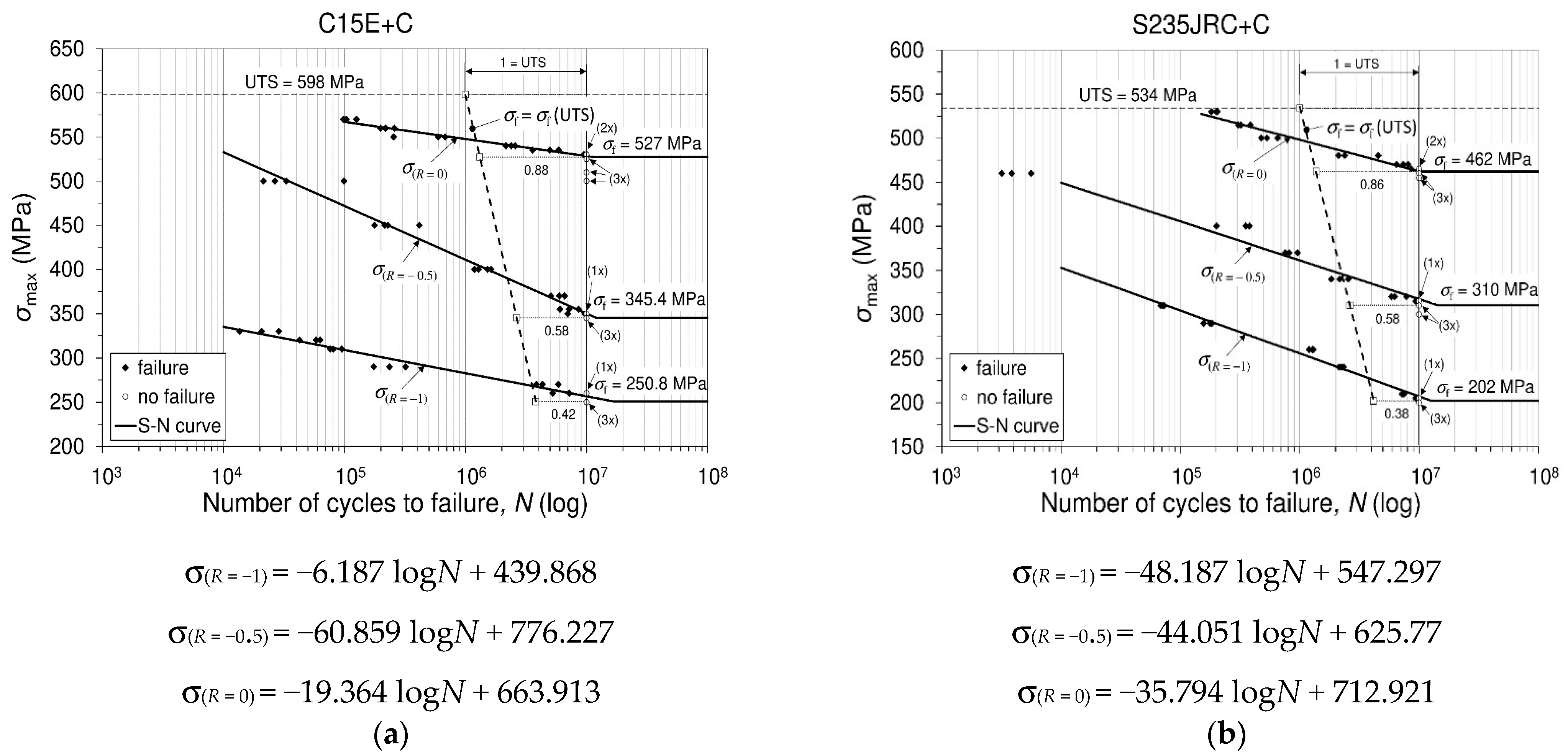
3.3.3. Stress Life (S − N) Diagram and Fatigue Limit Calculation
- -
- the ratio of the fatigue limit to the monotonic tensile strength of the material for a particular stress ratio at which the fatigue test was conducted;
- -
- an increase in the fatigue limit of an individual material with an increase in the stress ratio for an individual material, as well as an increase in the ratio between the fatigue limit and monotonic tensile strength, as stress ratio increases; and
- -
- relationship of the levels of fatigue limits obtained for the tested materials at certain stress ratios.
3.4. Microhardness Testing
3.5. Microstructure Analysis of Tested Materials
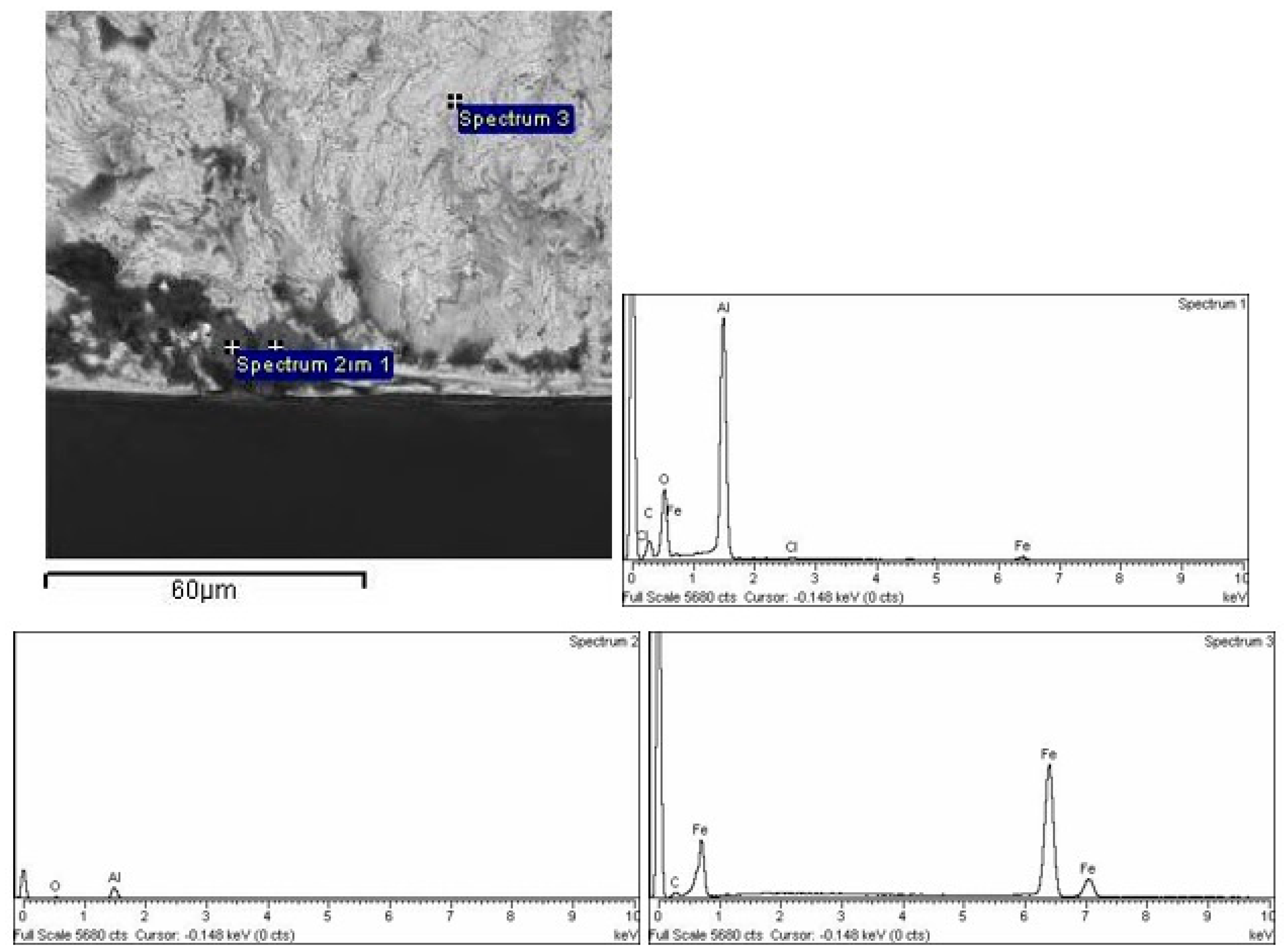
3.6. Fracture Surfaces
3.7. EDS Analysis
4. Conclusions
- Both investigated materials were tested for Charpy V-notch impact fracture energy in the temperature range from (−10 °C) to (+150 °C). For both tested materials, experimental results on the absorbed impact fracture energy as a function of test temperature are presented. Based on these data, curves were plotted that approximately outline the trend of absorbed fracture energy due to temperature change. These approximate curves simultaneously indicate that both considered materials belong to the BCC crystal structure. For this structure, if the unit cell edge length is “a” and the atomic radius “R”, then the measure “a =.”
- Both investigated materials were tested for uniaxial high-cyclic mechanical fatigue at room temperature and at several stress ratios ( For each of the tested materials, a stress-life (S-N) diagram is shown and the fatigue limit is calculated using the modified staircase method.
- The microhardness of both materials was tested and referenced in the text of the paper.
5. Summaries
- The average measured impact fracture energy in C15E+C steel, for example, at these two temperatures, is (−10 °C→14.5 J and +150 °C→157 J), respectively, and in the case of S235JRC+C steel, it is (−10 °C→26 J and +150 °C→171.6 J), respectively. The behavior of both considered materials is similar, and the obtained values are also slightly different.
- For each of the tested materials at each stress ratio (), the fatigue limit () as a function of ultimate tensile strength (designated as is defined in the form In this sense, for both tested materials the following results are obtained:
- The average value of microhardness is:C15E+C: 186.8 HV0.025; S235JRC+C: 181.4 HV0.025
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dowling, N.E. Mechanical Behavior of Materials, Engineering Methods for Deformation, Fracture and Fatigue, 4th ed.; Pearson: New York, NY, USA, 2013; pp. 1–20. [Google Scholar]
- Christensen, P.W.; Klarbring, A. An Introduction to Structural Optimization; Springer Science + Buisness Media BV: Linkoping, Sweden, 2009; pp. 1–7. [Google Scholar]
- Collins, H.A. Failure of Materials in Mechanical Design, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1993; pp. 6–15. [Google Scholar]
- Brnic, J.; Turkalj, G.; Niu, J.; Canadija, M.; Lanc, D. Analysis of experimental data on the behavior of steel S275JR—Reliability of modern design. Mater. Des. 2013, 47, 497–504. [Google Scholar] [CrossRef]
- Brnic, J.; Brcic, M.; Krscanski, S.; Lanc, D.; Chen, S. Uniaxial fatigue, creep and stress-strain responses of steel 30CrNiMo8. Steel Compos. Struct. 2019, 31, 409–417. [Google Scholar] [CrossRef]
- Brnic, J.; Brcic, M.; Krscanski, S.; Niu, J.; Chen, S.; Gao, Z. Deformation behavior of C15E + C steel under different uniaxial stress tests. Metals 2020, 10, 1445. [Google Scholar] [CrossRef]
- Brnic, J.; Brcic, M.; Balos, S.; Vukelic, G.; Krscanski, S.; Milutinovic, M.; Dramicanin, M. S235JRC+C steel response analysis subjected to uniaxial stress tests in the area of high temperatures and material fatigue. Sustainability 2021, 13, 5675. [Google Scholar] [CrossRef]
- Mayer, H. Fatigue damage of low amplitude cycles in low carbon steel. J. Mater. Sci. 2020, 44, 4919–4929. [Google Scholar] [CrossRef]
- Essa, K.; Kacmarcik, I.; Hartley, P.; Plancak, M.; Vilotic, D. Upsetting of bi-metallic ring billets. J. Mater. Process. Technol. 2012, 212, 817–824. [Google Scholar] [CrossRef]
- Wang, J.; Langlois, I.; Rafiq, M.; Bigot, R.; Lu, H. Study of the hot forging of weld cladded work pieces using upsetting tests. J. Mater. Process. Technol. 2014, 214, 365–379. [Google Scholar] [CrossRef] [Green Version]
- Bach, J.; Göken, M.; Höppel, H.W. Fatigue of low-alloyed carbon steels in the HCF/VHCF-regimes. In Fatige of Materials at Very High Numbers of Loading Cycles; Christ, H.J., Ed.; Springer Fachmedien, Wiesbaden GmbH: Wiesbaden, Germany, 2018; pp. 1–23. [Google Scholar]
- Simsek, T.; Baris, M.; Akkurt, A. Laser surface treatment of S235JRC carbon steel with Co2B nanocrystals. Inter. J. Mater. Res. 2017, 108, 486–494. [Google Scholar] [CrossRef]
- Bachmann, M.; Avilov, V.; Gumenyuk, A.; Rethmeier, M. Experimental and numerical investigation of an electromagnetic weld pool support system for high power laser beam welding of austenitic stainless steel. J. Mater. Process. Technol. 2014, 214, 578–591. [Google Scholar] [CrossRef]
- Sas-Boca, I.M.; Tintelecan, M.; Ilutiu-Varvara, D.A.; Pop, M.; Frunza, D.; Popa, F. Research on the mechanical properties of C45/S235JR multilayer steel systems. Procedia Manuf. 2019, 32, 8–14. [Google Scholar] [CrossRef]
- Nikolov, N.; Tsonev, V.; Penkov, K.; Kuzmanov, N.; Borisov, B. Machine for accelerated cyclic corrosion tests through alternate immersion in salt solution. IOP Conf. Ser. Mater. Sci. Eng. 2019, 664, 012016. [Google Scholar] [CrossRef]
- ASTM International. Annual Book of ASTM Standards, Volume 3, Metals—Mechanical Testing; Elevated and Low-Temperature Tests; Metallography; ASTM International: Baltimore, MD, USA, 2015. [Google Scholar]
- ISO 12107:2012 (E); Metallic Materials—Fatigue Testing—Statistical Planning and Analysis of Data. ISO Copyright Office: Geneva, Switzerland, 2012.
- Bramfit, B.L. Effects of composition, processing, and structure on properties of iron and steels. In ASM Handbook, Volume 20, Materials Selection and Design; Dieter, G.E., Ed.; ASM International: Novelty, OH, USA, 1997; pp. 357–382. [Google Scholar]
- Brnic, J.; Turkalj, G.; Canadija, M.; Krscanski, S.; Brcic, M.; Lanc, D. Deformation behavior and material properties of austenitic heat-resistant steel X15CrNiSi25-20 subjected to high temperatures and creep. Mater. Des. 2015, 69, 219–229. [Google Scholar] [CrossRef]
- Cubides-Herrera, C.S.; Villalba-Rondon, D.A.; Rodriguez-Baracaldo, R. Charpy impact toughness and transition temperature in ferrite-pearlite steel. Sci. Tech. 2019, 24, 200–204. [Google Scholar] [CrossRef]
- Courtney, T.H. Fundamental structure- property relationships in engineering materials. In ASM Handbook, Volume 20, Materials Selection and Design; Dieter, G.E., Ed.; ASM International: Novelty, OH, USA, 1997; pp. 336–356. [Google Scholar]
- Blinn, M.P.; Williams, R.A. Design for fracture toughness. In ASM Handbook, Volume 20, Materials Selection and Design; Dieter, G.E., Ed.; ASM International: Novelty, OH, USA, 1997; pp. 533–544. [Google Scholar]
- Brnic, J. Analysis of Engineering Structures and Material Behavior; John Wiley & Sons: Chichster, UK, 2018; pp. 239–318. [Google Scholar]
- Kannienen, M.F.; Popelar, C.H. Advanced Fracture Mechanics; Oxford University Press: New York, NY, USA, 1985; pp. 281–391. [Google Scholar]
- Farahmand, B.; Bockraft, G.; Glassco, J. Fatigue and Fracture Mechanics of High Risk Parts; International Thomson Publishing, Chapman & Hall: New York, NY, USA, 1997; pp. 1–12. [Google Scholar]
- Anderson, T.L. Fracture Mechanics, Fundamentals and Applications, 2nd ed.; CRC Press: New York, NY, USA, 1995; pp. 117–201. [Google Scholar]
- Chao, Y.J.; Ward, J.D.; Sands, R.G. Charpy impact energy, fracture toughness and ductile–brittle transition temperature of dual-phase 590 steel. Mater. Des. 2007, 28, 551–557. [Google Scholar] [CrossRef]
- Barbosa, V.S.; de Godois, L.A.C.; Bianchi, K.E.; Ruggieri, C. Charpy impact energy correlation with fracture toughness for low alloy structural steel welds. Theor. Appl. Fract. Mech. 2021, 113, 102934. [Google Scholar] [CrossRef]
- Yu, M.; Luo, Z.; Chao, Y.J. Correlations between Charpy V-notch impact energy and fracture toughness of nuclear reactor pressure vessel (RPV) steels. Eng. Fract. Mech. 2015, 147, 187–202. [Google Scholar] [CrossRef]
- Brnic, J.; Turkalj, G.; Lanc, D.; Canadija, M.; Brcic, M.; Vukelic, G.; Munjas, N. Testing and analysis of X39CrMo17-1 steel properties. Constr. Build. Mater. 2013, 44, 293–301. [Google Scholar] [CrossRef]
- Suresh, S. Fatigue of Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 2003; pp. 1–35. [Google Scholar]
- Brnic, J.; Krscanski, S.; Brcic, M.; Geng, L.; Niu, J.; Ding, B. Reliable experimental data as a key factor for design of mechanical structures. Struct. Eng. Mech. 2019, 72, 245. [Google Scholar] [CrossRef]
- McEvily, A.J. Metal Failures; John Wiley& Sons: New York, NY, USA, 2002; pp. 181–218. [Google Scholar]
- Susmel, L.; Wang, Y. The modified Manson-Coffin curve method to estimate fatigue lifetime under complex constant and variable amplitude multiaxial fatigue loading. Int. J. Fatigue 2016, 83, 135–149. [Google Scholar] [CrossRef] [Green Version]
- Angelova, D.; Yordanova, R.; Yankova, S. Fatigue crack development in a low-carbon steel. Microstructure influence. Modelling. Procedia Struct. Integr. 2016, 2, 2726–2733. [Google Scholar] [CrossRef]
- Goo, B.C.; Mun, H.S.; Cho, I.-S. Very-high-cycle fatigue and Charpy impact characteristics of manganese steel for railway axle at low temperatures. Appl. Sci. 2020, 10, 5042. [Google Scholar] [CrossRef]
- Ke, L.; Li, C.; He, J.; Lu, Y.; Jiao, Y.; Liu, Y. Fatigue evaluation and CFRP strengthening of diaphragm cutouts in orthotropic steel decks. Steel Compos. Struct. 2021, 39, 453–469. [Google Scholar] [CrossRef]
- Yang, H.; Qian, H.; Wang, P. Fatigue property analysis of U rib-to-crossbeam connections under heavy traffic vehicle load considering in-plane shear stress. Steel Compos. Struct. 2021, 38, 271–280. [Google Scholar] [CrossRef]
- Brnic, J.; Canadija, M.; Turkalj, G.; Krscanski, S.; Lanc, D.; Brcic, M.; Gao, Z. Short-time creep, fatigue and mechanical properties of 42CrMo4—Low alloy structural steel. Steel Compos. Struct. 2016, 22, 875–888. [Google Scholar] [CrossRef]
- Li, C.; Pan, H.; Tian, L.; Bi, W. Lifetime multi-hazard fragility analysis of transmission towers under earthquake and wind considering wind-induced fatigue effect. Struct. Saf. 2022, 99, 102266. [Google Scholar] [CrossRef]
- Sonsino, C.C.M. Course of SN—Curves especially in the high-cycle fatigue regime with regard tocomponent design and safety. Intern. J. Fatigue 2007, 29, 2246–2258. [Google Scholar] [CrossRef]
- Cherolis, N. E Facets on fatigue fractures. Microsc. Microanal. 2013, 19 (Suppl. S2), 1838. [Google Scholar] [CrossRef] [Green Version]
- Verma, N.; Pistorius, P.C.; Fruehan, R.J.; Potter, M.; Lind, M.; Story, S.R. Transient inclusion evolution during modification of alumina inclusions by calcium in liquid steel: Part II. Results and Discussion. Metall. Mater. Trans. B 2011, 42, 720–729. [Google Scholar] [CrossRef]








| Chemical Element | C | Cr | Si | Mn | P | S | Mo | Cu | Al | W | Sn | Nb | Co |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mat. 1.1141 | 0.135 | 0.084 | 0.233 | 0.38 | 0.01 | 0.009 | 0.019 | 0.027 | 0.035 | 0.006 | 0.007 | - | - |
| Mat. 1.0122 | 0.162 | 0.158 | 0.237 | 0.534 | 0.011 | 0.012 | 0.009 | 0.039 | 0.027 | 0.003 | 0.008 | 0.003 | 0.002 |
| Mat. 1.1141 | Fe | 98.995 | |||||||||||
| Mat. 1.0122 | Fe | 98.767 |
Room Temp., Specimen Failed(◆), Specimen Unfailed (○) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Stress Ratio | Specimen | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| C15E+C/S235JRC+C | ||||||||
| (A) | ||||||||
| −270/270 | −210/210 | ♦ | ♦ | ♦ | ||||
| −260/260 | −205/205 | ♦/○ | ♦ | ○ | ||||
| −250/250 | −200/200 | ○ | ||||||
| (B) | ||||||||
| −175/350 | −160/320 | ♦ | ♦ | ♦ | ||||
| −172.5/345 | −157.5/315 | ○ | ♦ | ♦ | ||||
| −170/340 | −155/310 | ○ | ||||||
| (C) | ||||||||
| 0/535 | 0/470 | ♦ | ♦ | ♦ | ||||
| 0/530 | 0/465 | ○ | ♦ | ○ | ||||
| 0/525 | 0/460 | ○ | ||||||
Room Temp., f-Specimen Failed | |||||
|---|---|---|---|---|---|
| Stress Ratio | fi | ifi | i2fi | ||
| C15E+C/S235JRC+C | |||||
| (A) | |||||
| −270/270 | −210/210 | 2 | 3 | 6 | 12 |
| −260/260 | −205/205 | 1 | 2/1 | 2/1 | 2/1 |
| −250/250 | −200/200 | 0 | 0 | 0 | 0 |
| 5/4 | 8/7 | 14/13 | |||
| (B) | |||||
| −175/350 | −160/320 | 2 | 3 | 6 | 12 |
| −172.5/345 | −157.5/315 | 1 | 2 | 2 | 2 |
| −170/340 | −155/310 | 0 | 0 | 0 | 0 |
| 5 | 8 | 14 | |||
| (C) | |||||
| 0/535 | 0/470 | 2 | 3 | 6 | 12 |
| 0/530 | 0/465 | 1 | 1 | 1 | 1 |
| 0/525 | 0/460 | 0 | 0 | 0 | 0 |
| 4 | 7 | 13 | |||
| Formula | |||
|---|---|---|---|
| C15E+C/S235JRC+C | |||
| 8/7 | 8 | 7 | |
| 14/13 | 14 | 13 | |
| 3/4 | 5 | 4 | |
| 0.24/0.1875 | 0.24 | 0.1875 | |
| The Value To Be Determined | Formula (Equation) ISO Standard [17] | Equation Number |
|---|---|---|
| Fatigue limit | (2) | |
| Mean fatigue strength | (3) | |
| Estimated standard deviation of the fatigue strength ( | (4) | |
| In Equations (2)–(4) there are: | - | |
| Items: ν, ) | In accordance with the recommendation of the mentioned ISO standard, the value ν, where is the number of items in a considered group. In addition, if a desired probability is , and a confidence level = 90%, according to the table B1, given in ISO standard [17], it is:= 2.333 | - |
| Materials | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| C15E+C UTS = 598 MPa [6] | S235JRC+C UTS = 534 MPa [7] | ||||||||
| Used Table 2, Table 3 and Table 4 | |||||||||
| Calculated value, Table 5 | Equation Number | 0 | |||||||
| Values (MPa) | |||||||||
| Mean fatigue strength | 3 | 261 | 346 | 531 | 206 | 316 | 466 | ||
| Estimated standard deviation ( | 4 | 4.36 | 1.75 | 1.75 | 1.75 | 2.18 | 1.75 | ||
| Fatigue limit ( | 2 | 250.8 | 345.4 | 527 | 202 | 310 | 462 | ||
| Ratio: | 0.42 | 0.58 | 0.88 | 0.38 | 0.58 | 0.86 | |||
| Type of Load | Type of Testing | Possible Failure (Damage) | Test Result |
|---|---|---|---|
| Repeated (cyclic) load | Uniaxial mechanical fatigue testing | Fracture of engineering component | Fatigue strength Fatigue limit (room temp.) |
| Impact load | Charpy V-notch impact testing | Fracture (separation) of considered element | Impact fracture energy (different temp.) |
| Applied load by diamond pyramid (indenter) | Vickers microhardness testing | Plastic deformation | Average Vickers microhardness values(room temp.) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brnic, J.; Balos, S.; Brcic, M.; Dramicanin, M.; Krscanski, S.; Milutinovic, M.; Ding, B.; Gao, Z. Testing and Analysis of Uniaxial Mechanical Fatigue, Charpy Impact Fracture Energy and Microhardness of Two Low-Carbon Steels. Materials 2023, 16, 884. https://doi.org/10.3390/ma16020884
Brnic J, Balos S, Brcic M, Dramicanin M, Krscanski S, Milutinovic M, Ding B, Gao Z. Testing and Analysis of Uniaxial Mechanical Fatigue, Charpy Impact Fracture Energy and Microhardness of Two Low-Carbon Steels. Materials. 2023; 16(2):884. https://doi.org/10.3390/ma16020884
Chicago/Turabian StyleBrnic, Josip, Sebastian Balos, Marino Brcic, Miroslav Dramicanin, Sanjin Krscanski, Mladomir Milutinovic, Biao Ding, and Zeng Gao. 2023. "Testing and Analysis of Uniaxial Mechanical Fatigue, Charpy Impact Fracture Energy and Microhardness of Two Low-Carbon Steels" Materials 16, no. 2: 884. https://doi.org/10.3390/ma16020884
APA StyleBrnic, J., Balos, S., Brcic, M., Dramicanin, M., Krscanski, S., Milutinovic, M., Ding, B., & Gao, Z. (2023). Testing and Analysis of Uniaxial Mechanical Fatigue, Charpy Impact Fracture Energy and Microhardness of Two Low-Carbon Steels. Materials, 16(2), 884. https://doi.org/10.3390/ma16020884



.JPG)




