Fracture Toughness Testing of Brittle Laminated Geomaterials Using Hollow Double-Wing Slotted Specimens
Abstract
:1. Introduction
2. Numerical Calibration of f for Mode I Fracture of HDWS Specimens
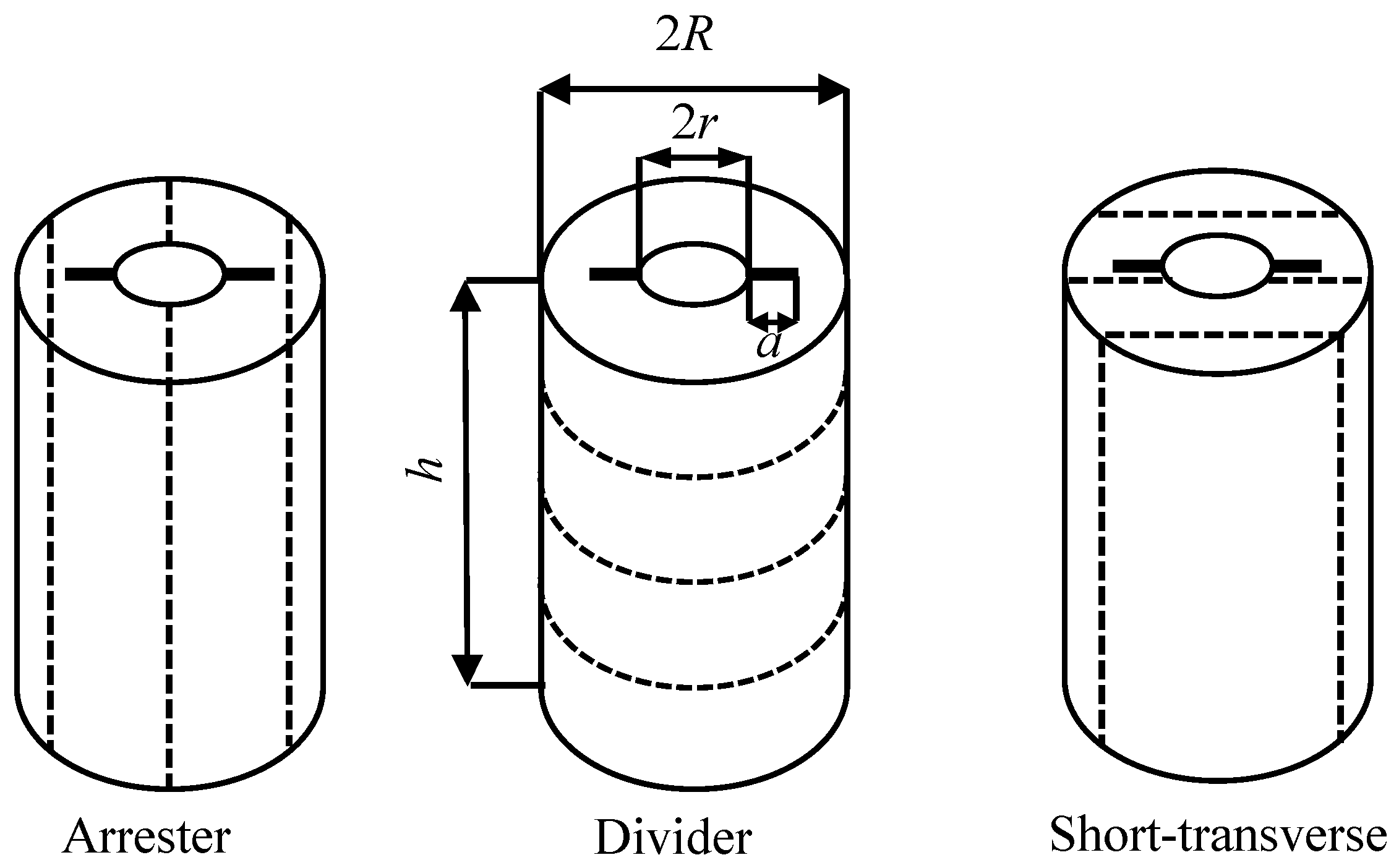
2.1. HDWS Specimens
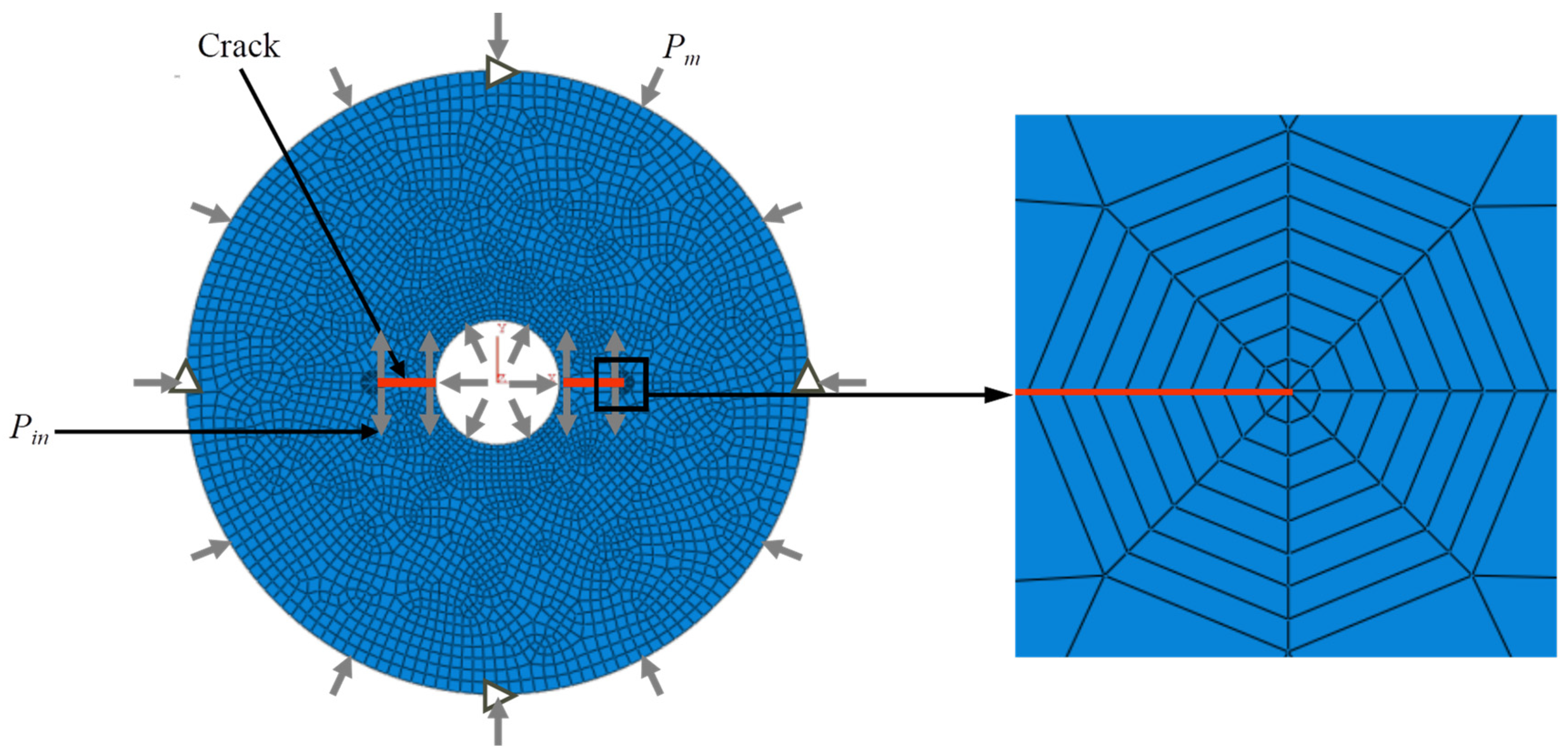
2.2. Procedure for the Numerical Calibration of f
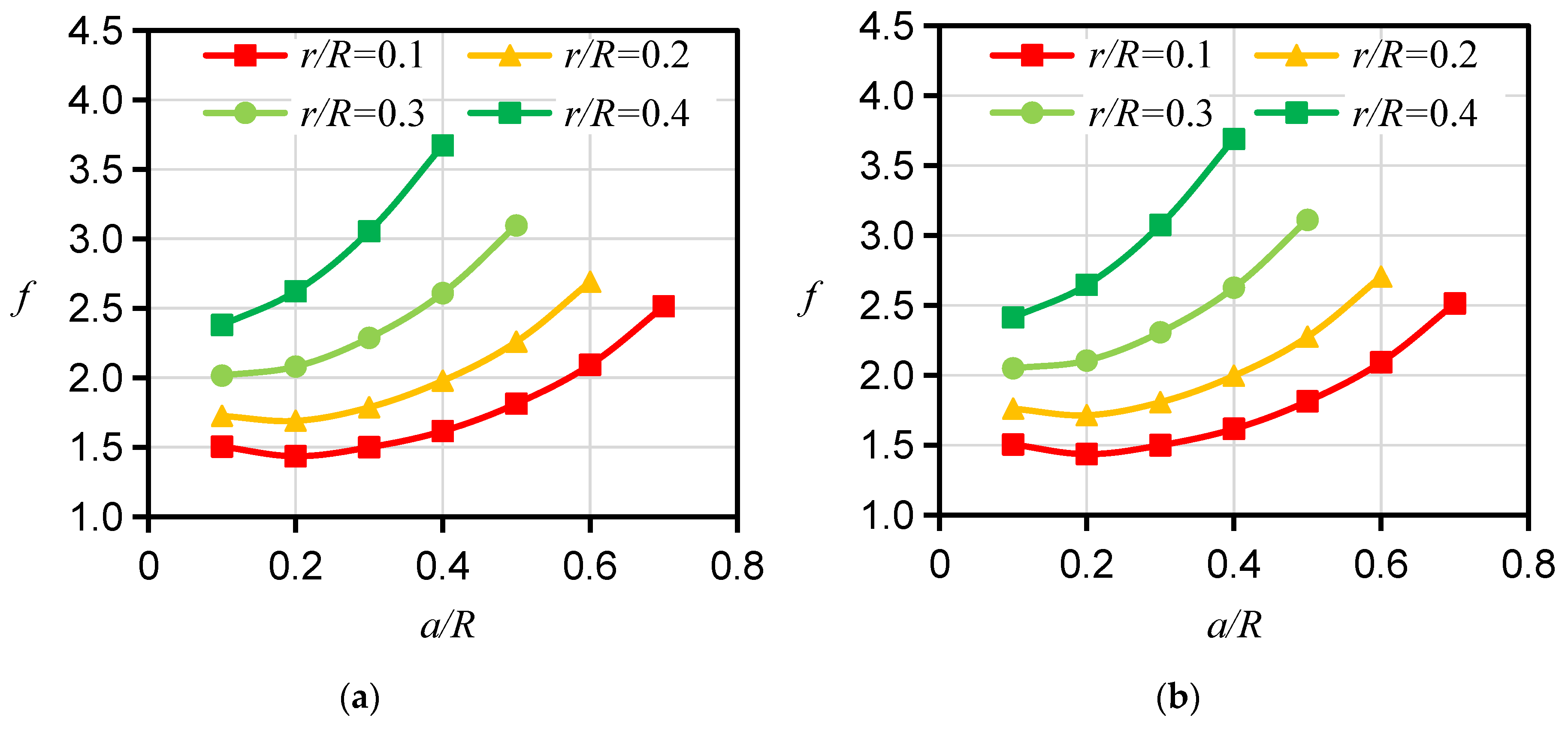
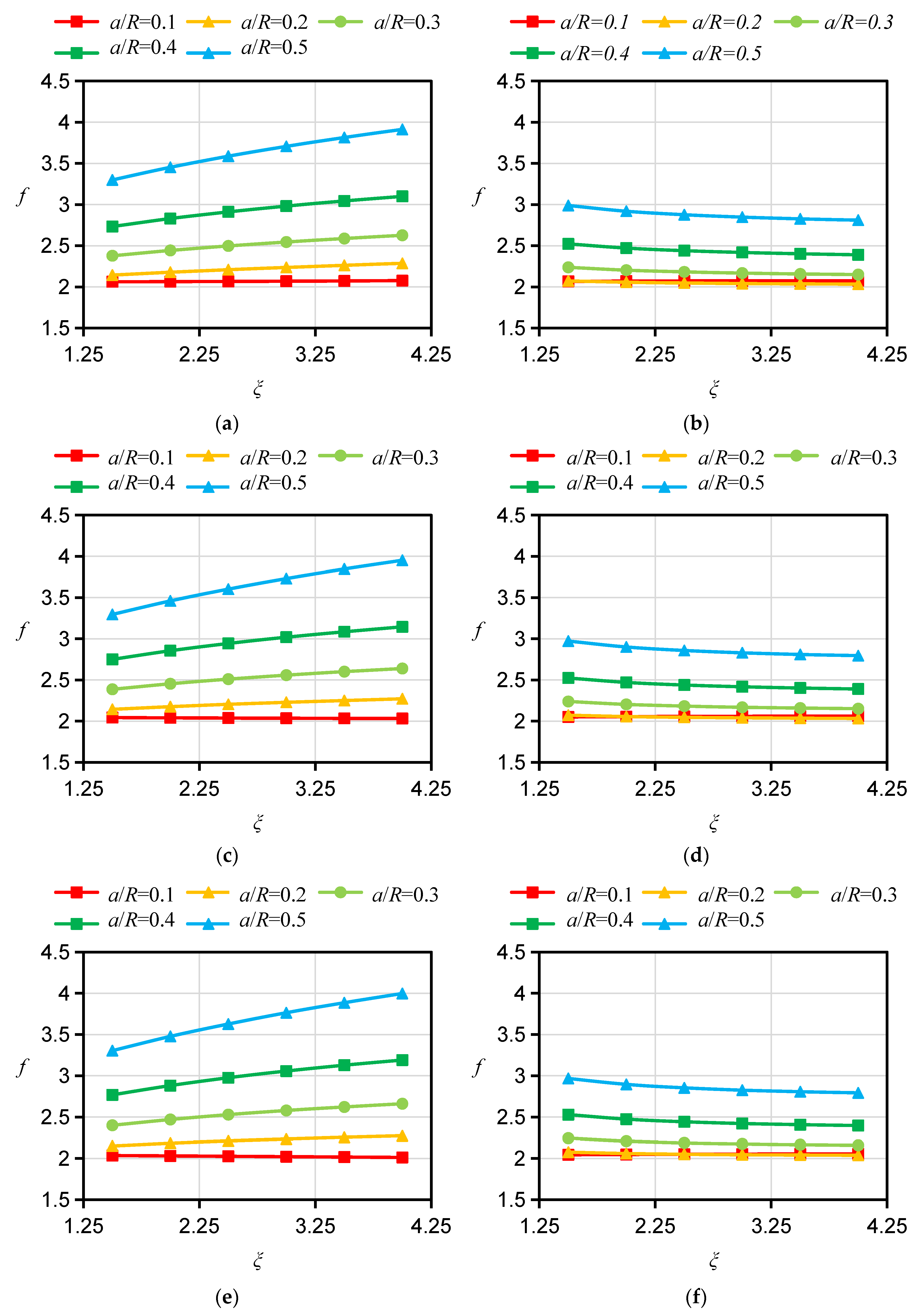
2.3. Influences of Loading Condition and Geometrical Dimension on f
2.4. Influences of Bedding Angle on f
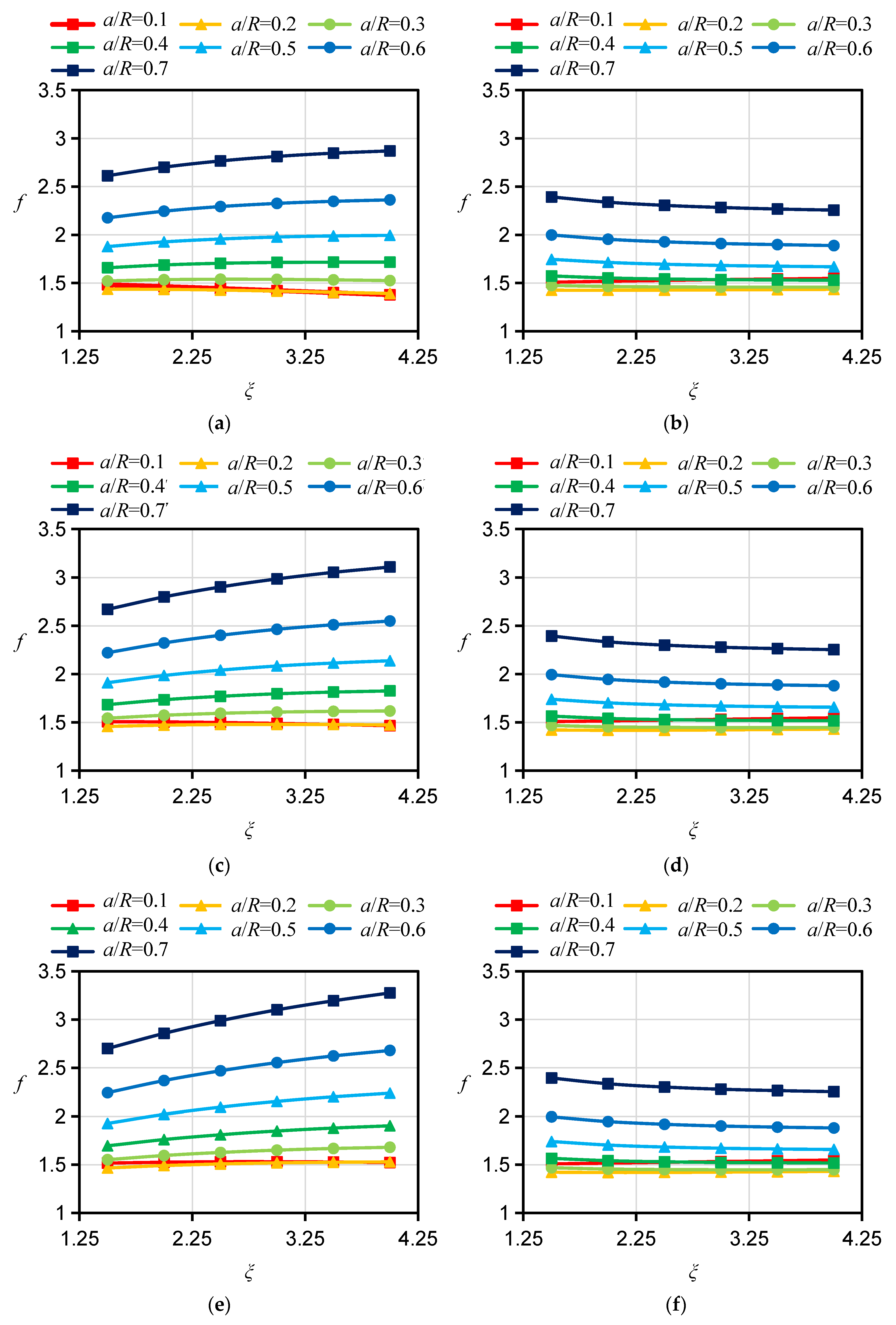
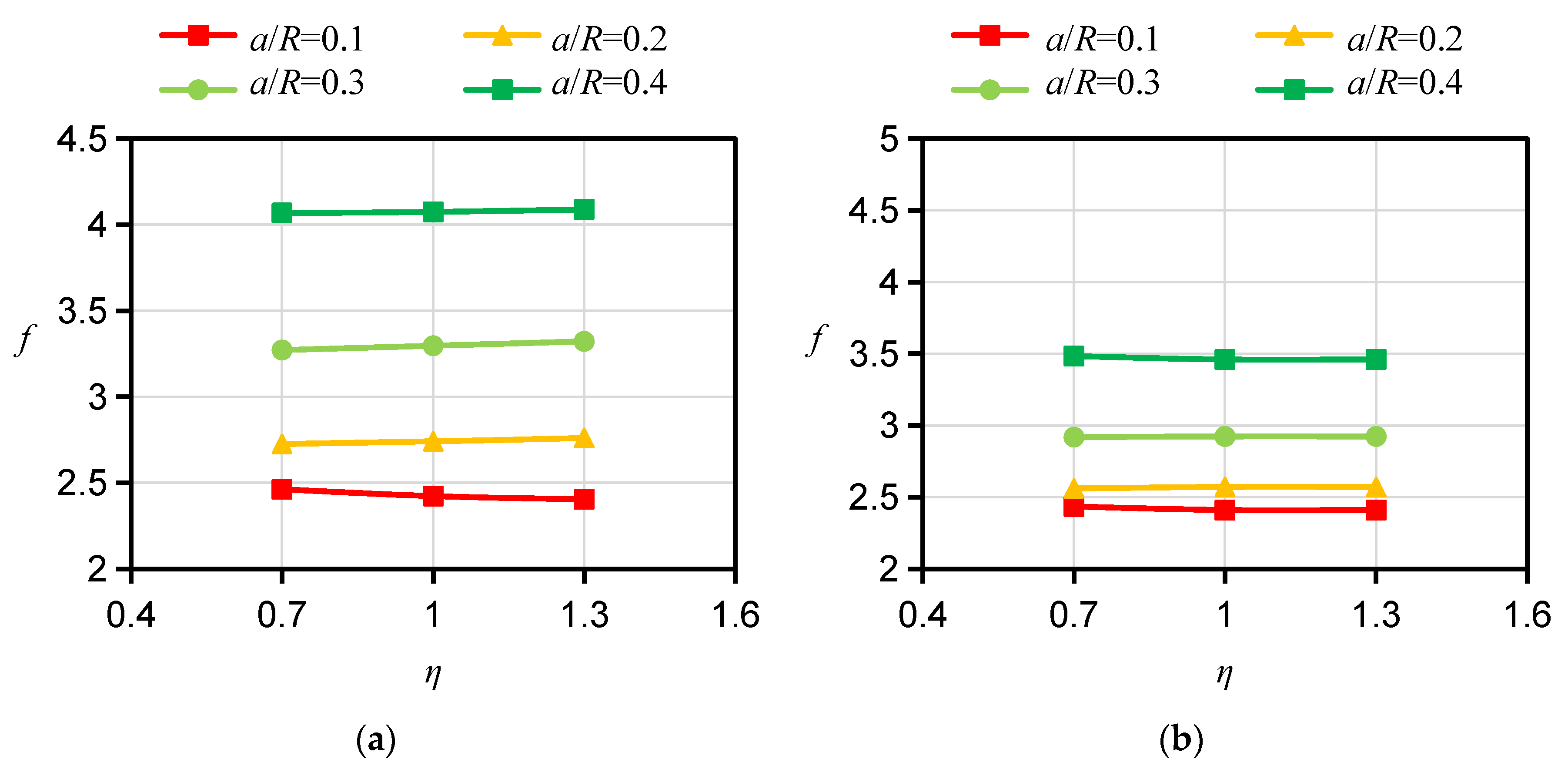
2.5. Influences of ξ and ƞ on f
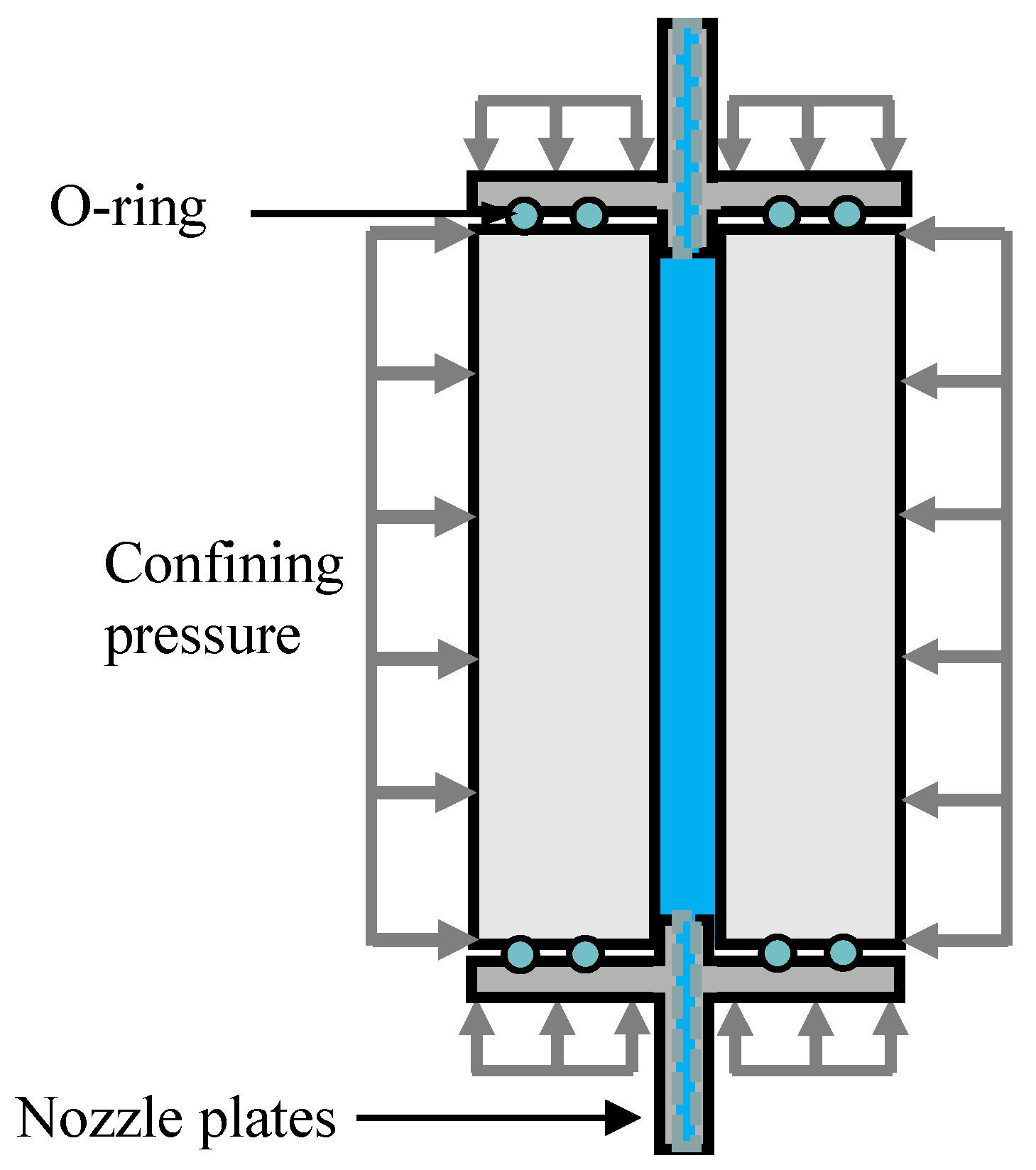
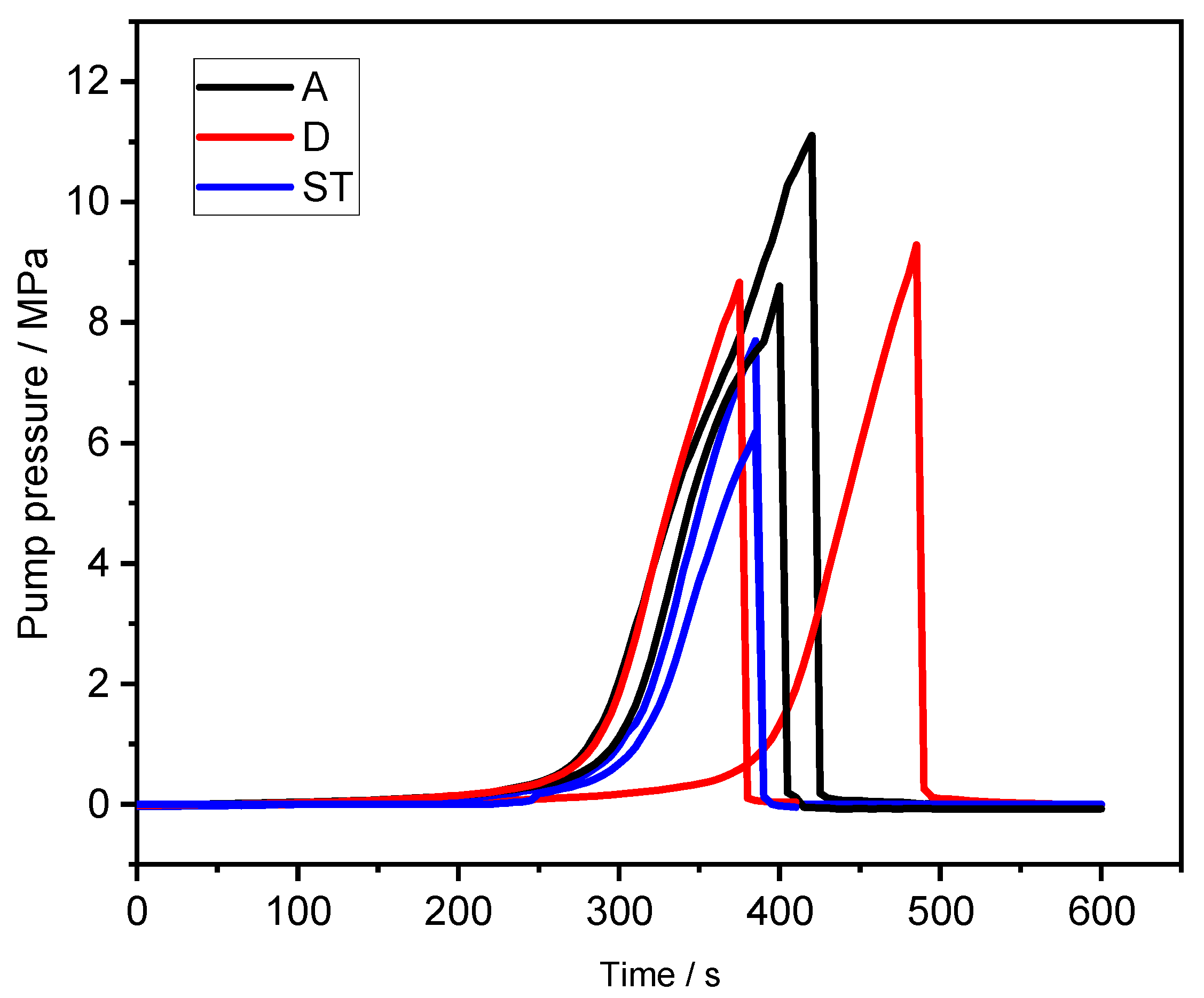
3. Hydraulic Fracturing Experiment of HDWS Specimens
4. Conclusions
- (1)
- Numerical simulation results show that the mode I f of the HDWS specimen increases monotonically with the increase in hole size. The pattern of variation in f with crack length is affected by the size of the hole. Furthermore, as the crack length increases, f increases at an accelerated rate.
- (2)
- There is clear anisotropy in f. With all other parameters being the same, f is the largest for specimens with an A orientation and the smallest for specimens with an ST orientation. A larger hole and a longer crack lead to more significant anisotropy in f.
- (3)
- The degree of anisotropy in elastic parameters has an important impact on f. A higher Young’s modulus ratio E/E′ results in a larger f for specimens with an A orientation, while it leads to a smaller f for specimens with an ST orientation. The apparent shear modulus ratio G′sv/G′ has relatively little impact on f.
- (4)
- The results from the hydraulic fracturing experiments indicate anisotropy in the peak pressure of specimens with different bedding orientations, with the peak pressure and fracture toughness of the samples in the ST direction being the lowest and those in the A direction being the highest.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shawaf, A.; Rasouli, V.; Dehdouh, A. The Impact of Formation Anisotropy and Stresses on Fractural Geometry—A Case Study in Jafurah’s Tuwaiq Mountain Formation (TMF), Saudi Arabia. Processes 2023, 11, 1545. [Google Scholar] [CrossRef]
- Adachi, J.; Siebrits, E.; Peirce, A.; Desroches, J. Computer simulation of hydraulic fractures. Int. J. Rock Mech. Min. Sci. 2007, 44, 739–757. [Google Scholar] [CrossRef]
- Tang, Y.; Zheng, H.; Xiang, H.; Nie, X.; Liao, R. Experimental Simulation on the Stress Disturbance Mechanism Caused by Hydraulic Fracturing on the Mechanical Properties of Shale Formation. Processes 2023, 11, 2931. [Google Scholar] [CrossRef]
- Ren, L.; Xie, H.P.; Sun, X.; Zhang, R.; Li, C.B.; Xie, J.; Zhang, Z.T. Characterization of Anisotropic Fracture Properties of Silurian Longmaxi Shale. Rock Mech. Rock Eng. 2021, 54, 665–678. [Google Scholar] [CrossRef]
- Chen, B.; Barboza, B.R.; Sun, Y.; Bai, J.; Thomas, H.R.; Dutko, M.; Cottrell, M.; Li, C. A Review of Hydraulic Fracturing Simulation. Arch. Comput. Methods Eng. 2021, 29, 1–58. [Google Scholar] [CrossRef]
- Fowell, R.J. Suggested method for determining mode I fracture toughness using Cracked Chevron Notched Brazilian Disc (CCNBD) specimens. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 57–64. [Google Scholar] [CrossRef]
- Kuruppu, M.D.; Obara, Y.; Ayatollahi, M.R.; Chong, K.P.; Funatsu, T. ISRM-Suggested Method for Determining the Mode I Static Fracture Toughness Using Semi-Circular Bend Specimen. Rock Mech. Rock Eng. 2014, 47, 267–274. [Google Scholar] [CrossRef]
- Awaji, H.; Sato, S. Combined Mode Fracture Toughness Measurement by the Disk Test. J. Eng. Mater. Technol. 1978, 100, 175–182. [Google Scholar] [CrossRef]
- Aliha, M.R.M.; Pakzad, R.; Ayatollahi, M.R. Numerical Analyses of a Cracked Straight-Through Flattened Brazilian Disk Specimen under Mixed-Mode Loading. J. Eng. Mech. 2014, 140, 219–224. [Google Scholar] [CrossRef]
- Luo, Y.; Ren, L.; Xie, L.Z.; Ai, T.; He, B. Fracture Behavior Investigation of a Typical Sandstone Under Mixed-Mode I/II Loading Using the Notched Deep Beam Bending Method. Rock Mech. Rock Eng. 2017, 50, 1987–2005. [Google Scholar] [CrossRef]
- Zhang, A.; Xie, H.; Zhang, R.; Ren, L.; Zhou, J.; Gao, M.; Tan, Q. Dynamic failure behavior of Jinping marble under various preloading conditions corresponding to different depths. Int. J. Rock Mech. Min. Sci. 2021, 148, 104959. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, K.; Zhang, B.; Yin, G.; Wang, H.; Wang, Z.; Li, C.; Lai, S.; Qian, Z. Influence of Stress Anisotropy on Petrophysical Parameters of Deep and Ultradeep Tight Sandstone. Appl. Sci. 2022, 12, 11543. [Google Scholar] [CrossRef]
- Ma, X.; Xie, J.; Yong, R.; Zhu, Y. Geological characteristics and high production control factors of shale gas reservoirs in Silurian Longmaxi Formation, southern Sichuan Basin, SW China. Pet. Explor. Dev. 2020, 47, 901–915. [Google Scholar] [CrossRef]
- Sun, C.; Nie, H.; Dang, W.; Chen, Q.; Zhang, G.; Li, W.; Lu, Z. Shale Gas Exploration and Development in China: Current Status, Geological Challenges, and Future Directions. Energy Fuels 2021, 35, 6359–6379. [Google Scholar] [CrossRef]
- Zhou, Q.; Xie, H.; Zhu, Z.; He, R.; Lu, H.; Fan, Z.; Nie, X.; Ren, L. Fracture Toughness Anisotropy in Shale Under Deep In Situ Stress Conditions. Rock Mech. Rock Eng. 2023, 56, 7535–7555. [Google Scholar] [CrossRef]
- Fan, Z.; Xie, H.; Ren, L.; Ru, Z.; He, R.; Li, C.-b.; Zhang, Z.; Wang, J.; Xie, J. Anisotropy in shear-sliding fracture behavior of layered shale under different normal stress conditions. J. Cent. South Univ. 2022, 29, 3678–3694. [Google Scholar] [CrossRef]
- Sui, W.; Wang, Y.; Li, J. Microscopic Study of Shale Anisotropy with SEM In Situ Compression and Three-Point Bending Experiments. Energies 2023, 16, 2440. [Google Scholar] [CrossRef]
- Antinao Fuentealba, F.J.; Bianchi, L.N.; Otegui, J.L.; Bianchi, G.L. Accurate experimental determination of rock fracture toughness under simulated reservoir confining pressures. Theor. Appl. Fract. Mech. 2022, 120, 103425. [Google Scholar] [CrossRef]
- Kataoka, M.; Mahdavi, E.; Funatsu, T.; Takehara, T.; Obara, Y.; Fukui, K.; Hashiba, K. Estimation of Mode I Fracture Toughness of Rock by Semi-Circular Bend Test under Confining Pressure Condition. Procedia Eng. 2017, 191, 886–893. [Google Scholar] [CrossRef]
- Al-Shayea, N.A.; Khan, K.; Abduljauwad, S.N. Effects of confining pressure and temperature on mixed-mode (I–II) fracture toughness of a limestone rock. Int. J. Rock Mech. Min. Sci. 2000, 37, 629–643. [Google Scholar] [CrossRef]
- Li, J.-L.; Wei, X.-D.; Zhao, G.-F. An integrated experimental and numerical study of size effect on the mode I fracture toughness of rock. Eng. Fract. Mech. 2023, 287, 109327. [Google Scholar] [CrossRef]
- Iqbal, M.J.; Mohanty, B. Experimental Calibration of ISRM Suggested Fracture Toughness Measurement Techniques in Selected Brittle Rocks. Rock Mech. Rock Eng. 2007, 40, 453–475. [Google Scholar] [CrossRef]
- Khan, K.; Al-Shayea, N.A. Effect of Specimen Geometry and Testing Method on Mixed Mode I–II Fracture Toughness of a Limestone Rock from Saudi Arabia. Rock Mech. Rock Eng. 2000, 33, 179–206. [Google Scholar] [CrossRef]
- Mohammed Shafeeque, K.K.; Surendra, K.V.N. Analysis of a Double Edge Cracked Circular Ring Under Diametrical Compression. In Recent Advances in Computational and Experimental Mechanics, Vol II; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2022; pp. 409–420. [Google Scholar]
- Nejati, M.; Aminzadeh, A.; Saar, M.O.; Driesner, T. Modified semi-circular bend test to determine the fracture toughness of anisotropic rocks. Eng. Fract. Mech. 2019, 213, 171. [Google Scholar] [CrossRef]
- Jin, Y.; Lu, Y.; Chen, M. Shale gas development: Opportunities and challenges for rock mechanics. Sci. Sin. Phys. Mech. Astron. 2017, 47, 114601. [Google Scholar] [CrossRef]
- Amadei, B. Importance of anisotropy when estimating and measuring in situ stresses in rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1996, 33, 293–325. [Google Scholar] [CrossRef]
- Shi, X.; Zhao, Y.; Gong, S.; Wang, W.; Yao, W. Co-effects of bedding planes and loading condition on Mode-I fracture toughness of anisotropic rocks. Theor. Appl. Fract. Mech. 2022, 117, 103158. [Google Scholar] [CrossRef]
- Feng, Y.; Tang, H.; Tang, H.; Leng, Y.; Shi, X.; Liu, J. Experimental Investigation of Stress Sensitivity of Elastic Wave Velocities for Anisotropic Shale in Wufeng–Longmaxi Formation. Processes 2023, 11, 2607. [Google Scholar] [CrossRef]
- Gehne, S. A Laboratory Study of Fluid-Driven Tensile Fracturing in Anisotropic Rocks. Ph.D. Thesis, University of Portsmouth, Portsmouth, UK, 2018. [Google Scholar]
- Chong, K.P.; Kuruppu, M.D.; Kuszmaul, J.S. Fracture toughness determination of layered materials. Eng. Fract. Mech. 1987, 28, 43–54. [Google Scholar] [CrossRef]
- Jing, L. A review of techniques, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering. Int. J. Rock Mech. Min. Sci. 2003, 40, 283–353. [Google Scholar] [CrossRef]
- He, R.; Ren, L.; Zhang, R.; Zhu, Z.; Sun, X. Anisotropy characterization of the elasticity and energy flow of Longmaxi shale under uniaxial compression. Energy Rep. 2022, 8, 1410–1424. [Google Scholar] [CrossRef]
- Sun, X.; Li, S.; Li, X.; Li, G.; Zheng, B.; Mao, T. The Mechanical Properties and Fracture Characteristics of Shale Layered Samples from the Lucaogou Formation Considering Natural Crack and Mineral Distribution. Materials 2023, 16, 5881. [Google Scholar] [CrossRef]
- Zhang, A.; Xie, H.; Zhang, R.; Gao, M.; Xie, J.; Jia, Z.; Ren, L.; Zhang, Z. Mechanical properties and energy characteristics of coal at different depths under cyclic triaxial loading and unloading. Int. J. Rock Mech. Min. Sci. 2023, 161, 105271. [Google Scholar] [CrossRef]
- Brenne, S.; Molenda, M.; Stockhert, F.; Alber, M. Hydraulic and Sleeve Fracturing Laboratory Experiments on 6 Rock Types. In Effective and Sustainable Hydraulic Fracturing; IntechOpen: London, UK, 2013. [Google Scholar]
- Tada, H. The Stress Analysis of Cracks Handbook; ASME Press: New York, NY, USA, 2000. [Google Scholar]
- Sarmadivaleh, M.; Joodi, B.; Nabipour, A. Steps to conducting a valid hydraulic-fracturing laboratory test. APPEA J. 2013, 53, 347. [Google Scholar] [CrossRef]
- Heng, S.; Li, X.; Liu, X.; Chen, Y. Experimental study on the mechanical properties of bedding planes in shale. J. Nat. Gas Sci. Eng. 2020, 76, 103161. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Z.; Fan, Z.; Zhou, Q.; Nie, X.; Ren, L. Fracture Toughness Testing of Brittle Laminated Geomaterials Using Hollow Double-Wing Slotted Specimens. Materials 2023, 16, 6754. https://doi.org/10.3390/ma16206754
Yao Z, Fan Z, Zhou Q, Nie X, Ren L. Fracture Toughness Testing of Brittle Laminated Geomaterials Using Hollow Double-Wing Slotted Specimens. Materials. 2023; 16(20):6754. https://doi.org/10.3390/ma16206754
Chicago/Turabian StyleYao, Zilong, Zidong Fan, Qin Zhou, Xiaofang Nie, and Li Ren. 2023. "Fracture Toughness Testing of Brittle Laminated Geomaterials Using Hollow Double-Wing Slotted Specimens" Materials 16, no. 20: 6754. https://doi.org/10.3390/ma16206754




