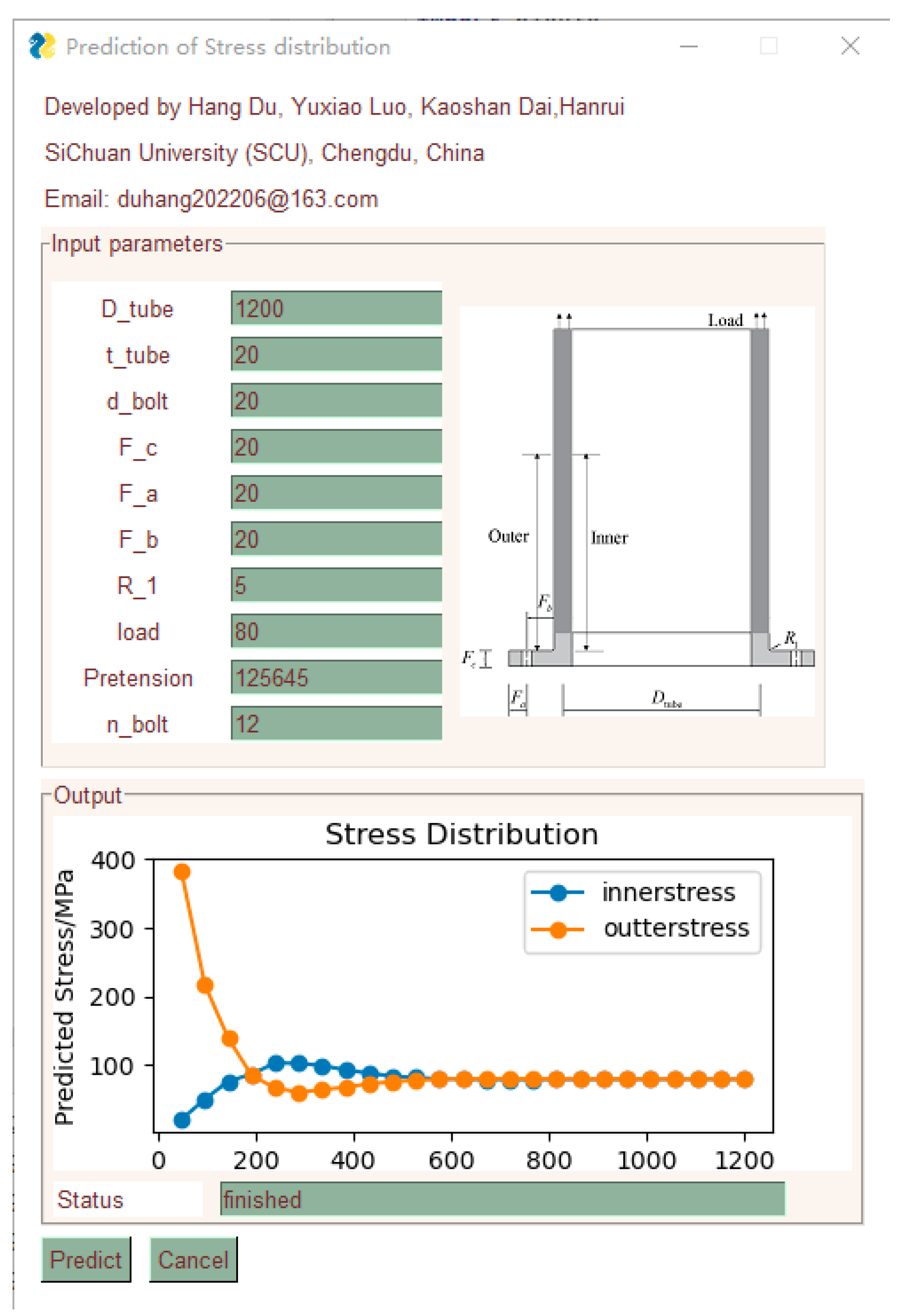
Stress Distribution Prediction of Circular Hollow Section Tube in Flexible High-Neck Flange Joints Based on the Hybrid Machine Learning Model
Abstract
:1. Introduction
1.1. Research Background
1.2. State-of-the-Art Review
1.2.1. The Design and Calculation Methodology for Flexible Flange Joints
1.2.2. Application of Machine Learning Models in Structural Design Area
1.3. Existing Research Gaps
1.4. Contribution of the Work
2. Theoretical Overview
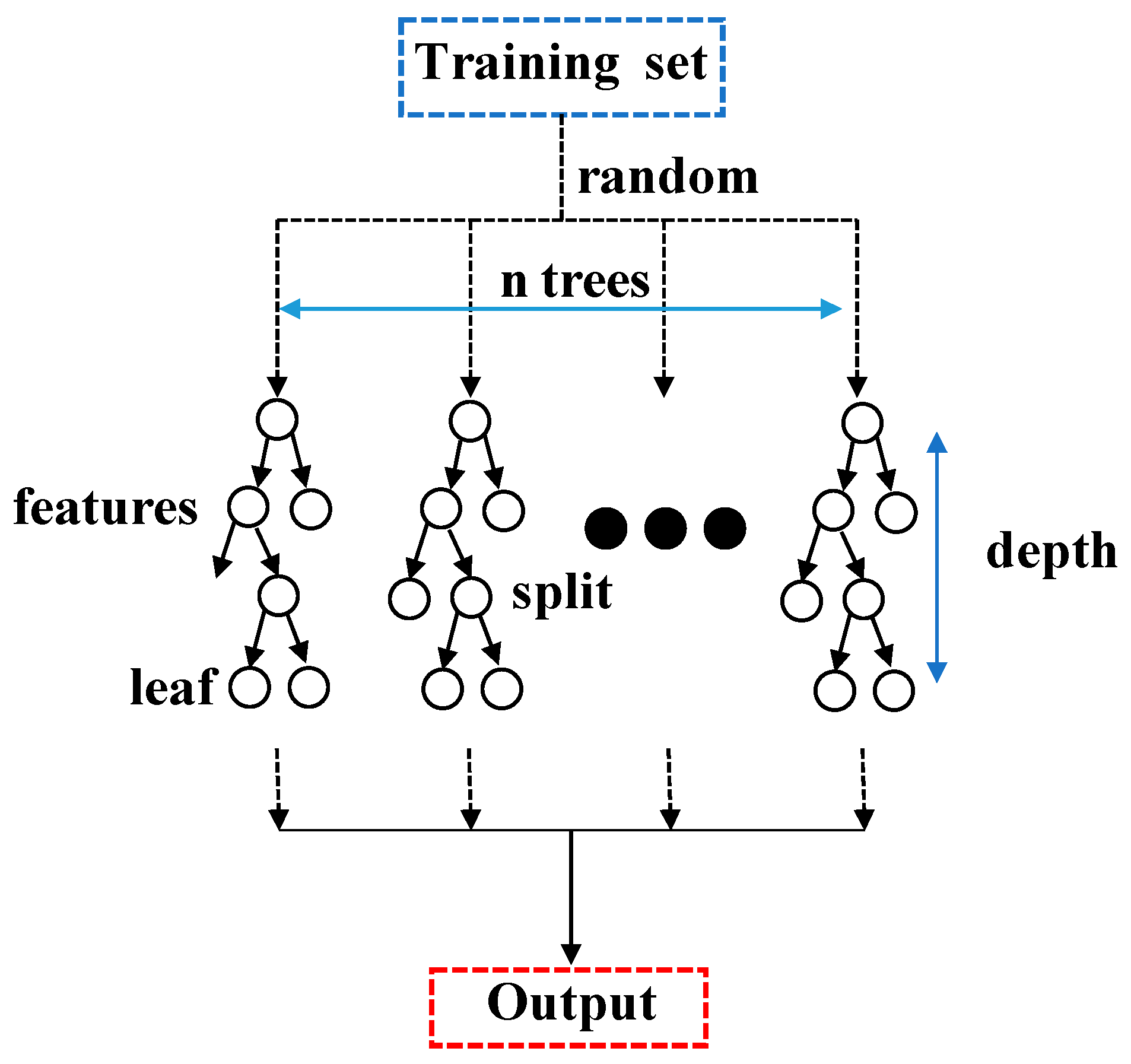
2.1. Random Forest Model and Parameters
2.2. Hybrid RF Model
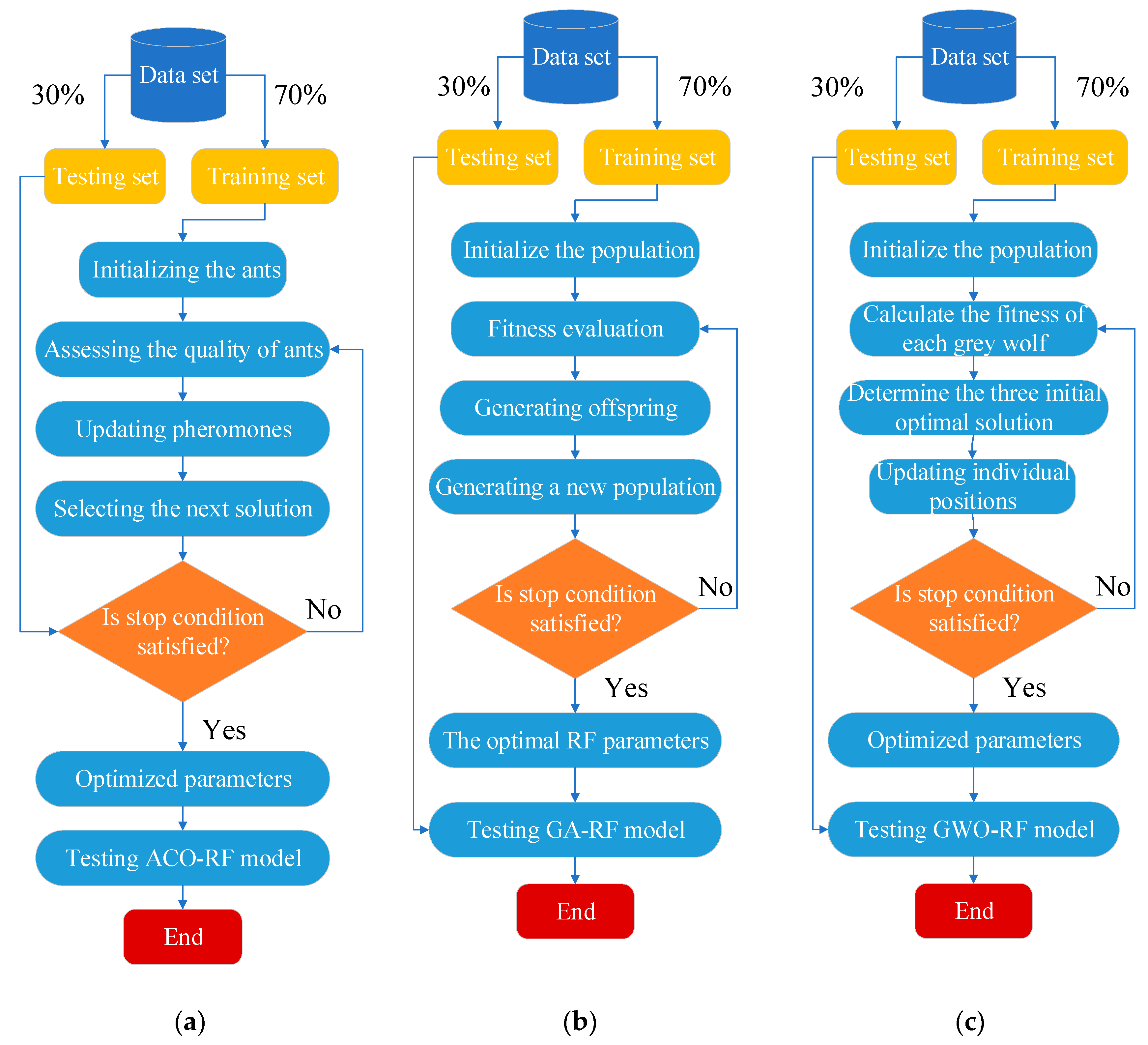
2.2.1. ACO-Base RF Model (ACO-RF)
2.2.2. GA-Based RF Model (GA-RF)
2.2.3. GWO-Based RF Model (GWO-RF)
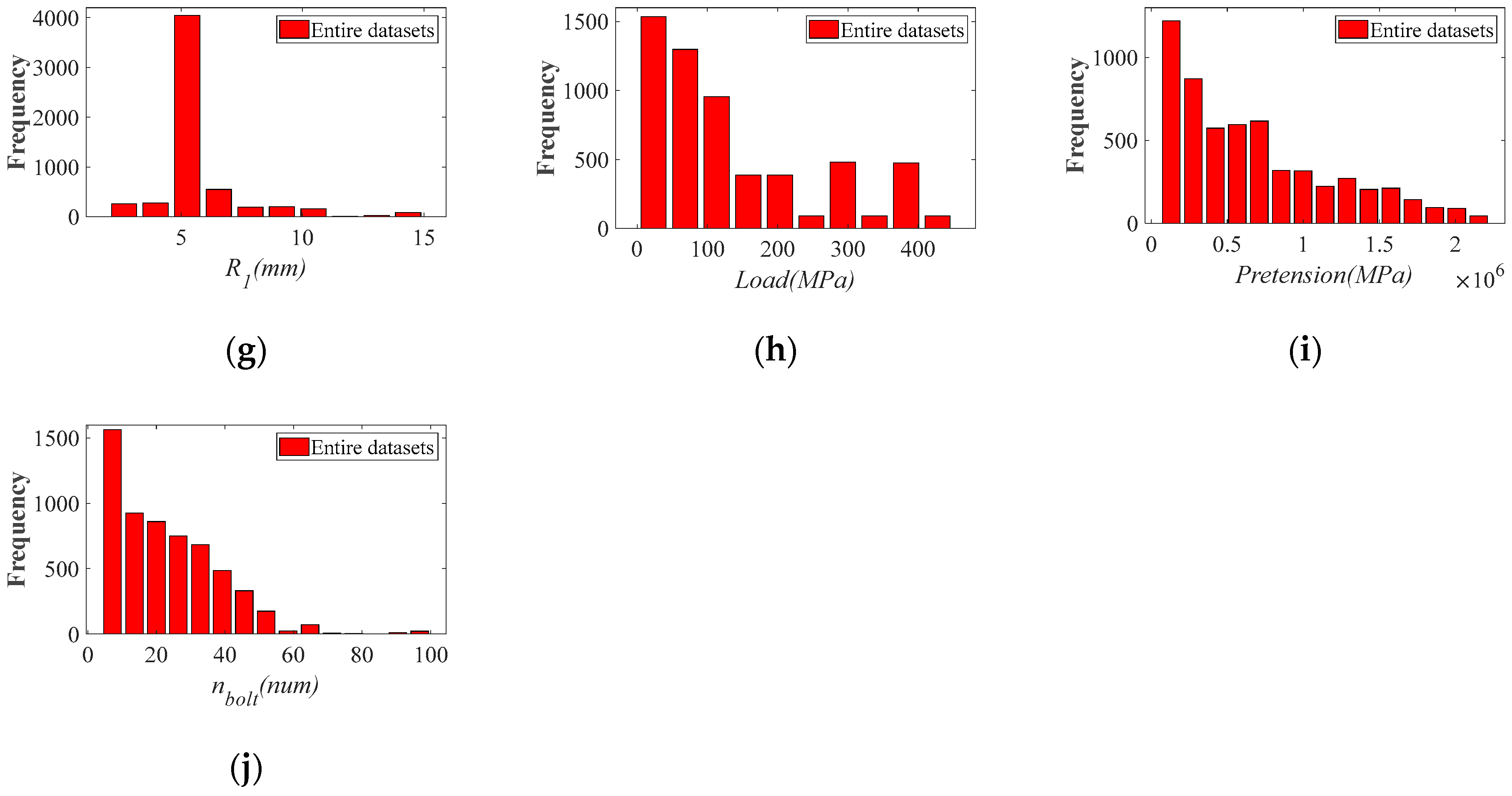
3. Data Generation
3.1. Parameter Ranges for the Geometric Model of Flange Joints
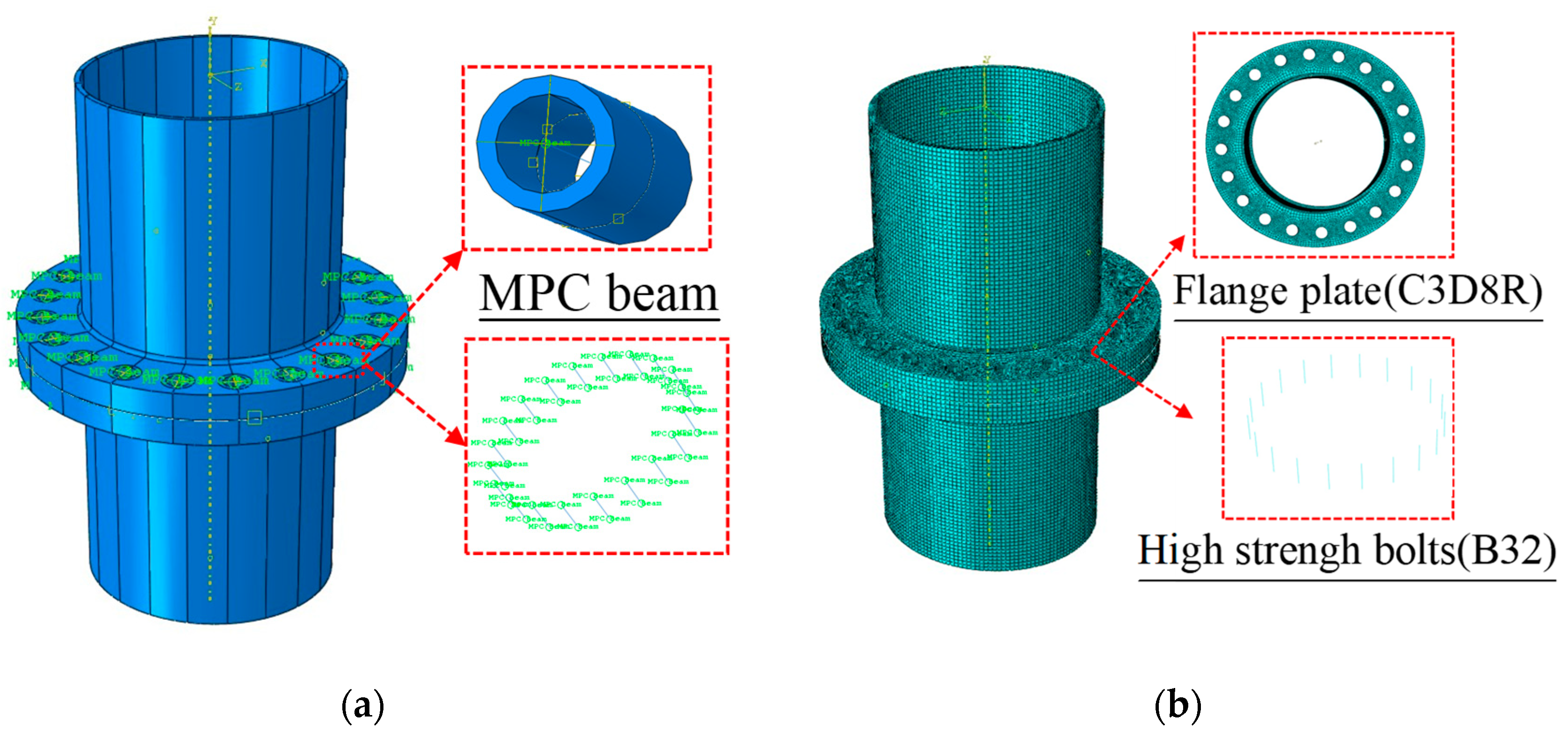
3.2. Numerical Analysis and Data Processing
4. Developing Machine Learning Models
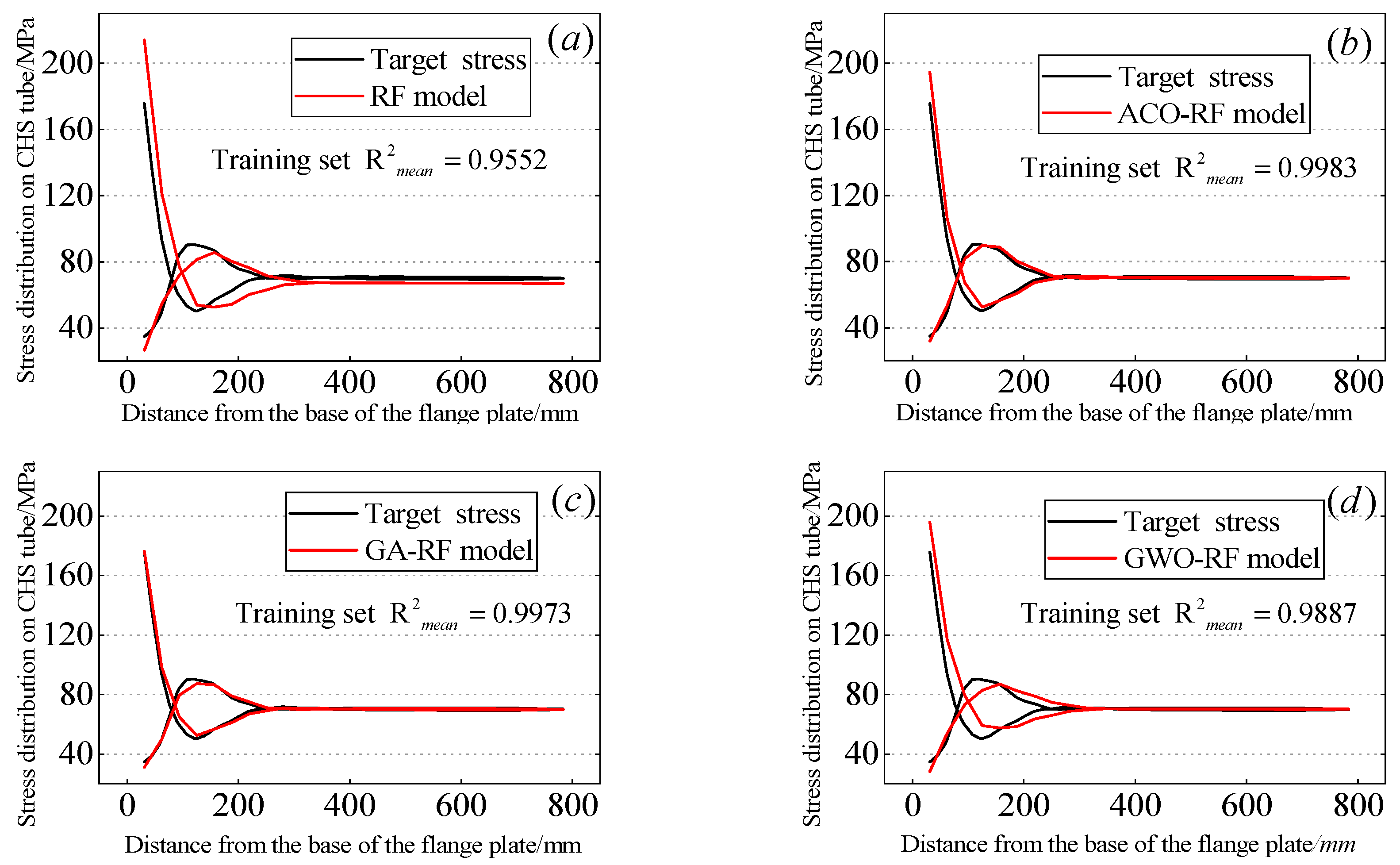
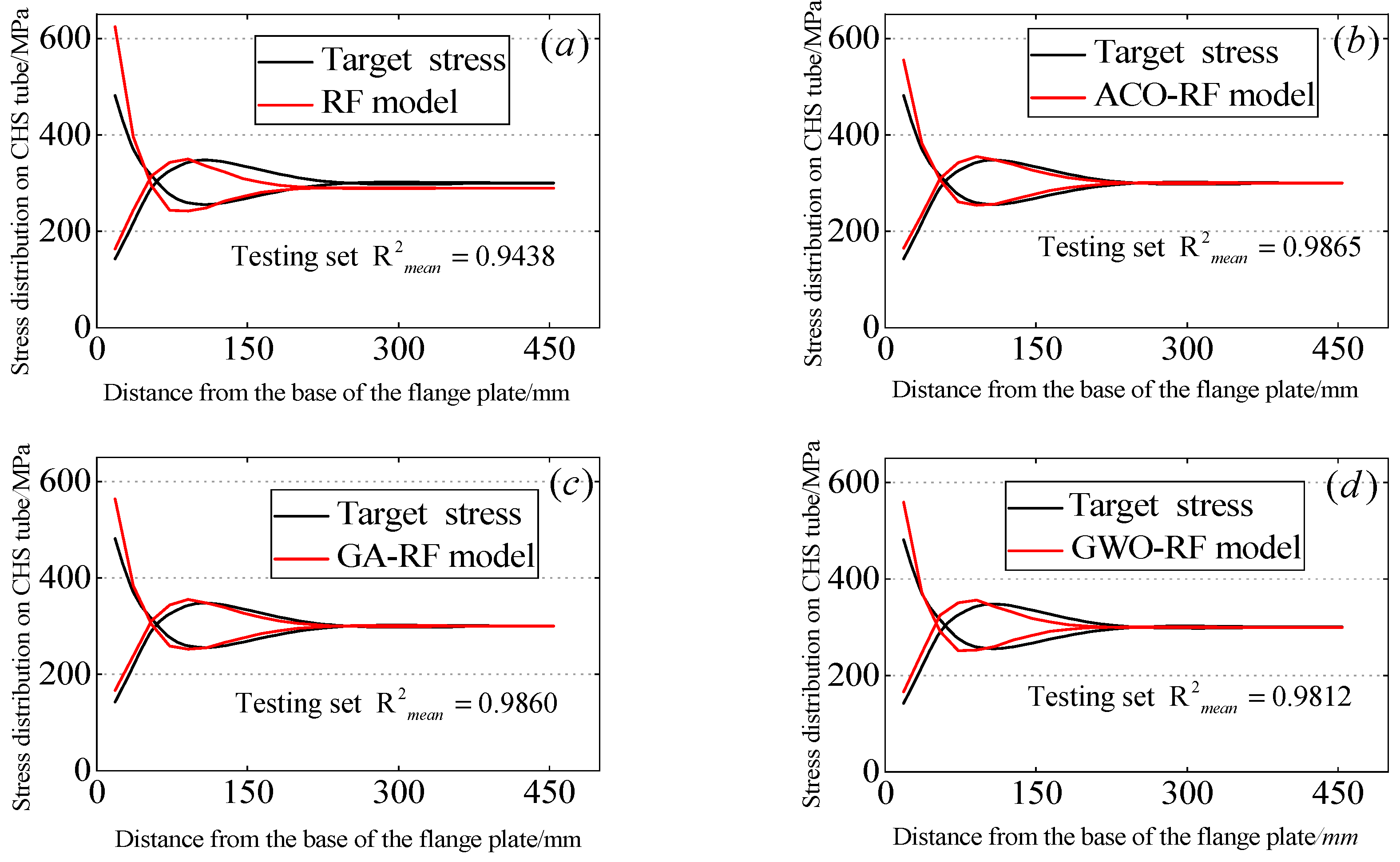
4.1. The Performance of the Three Hybrid Models
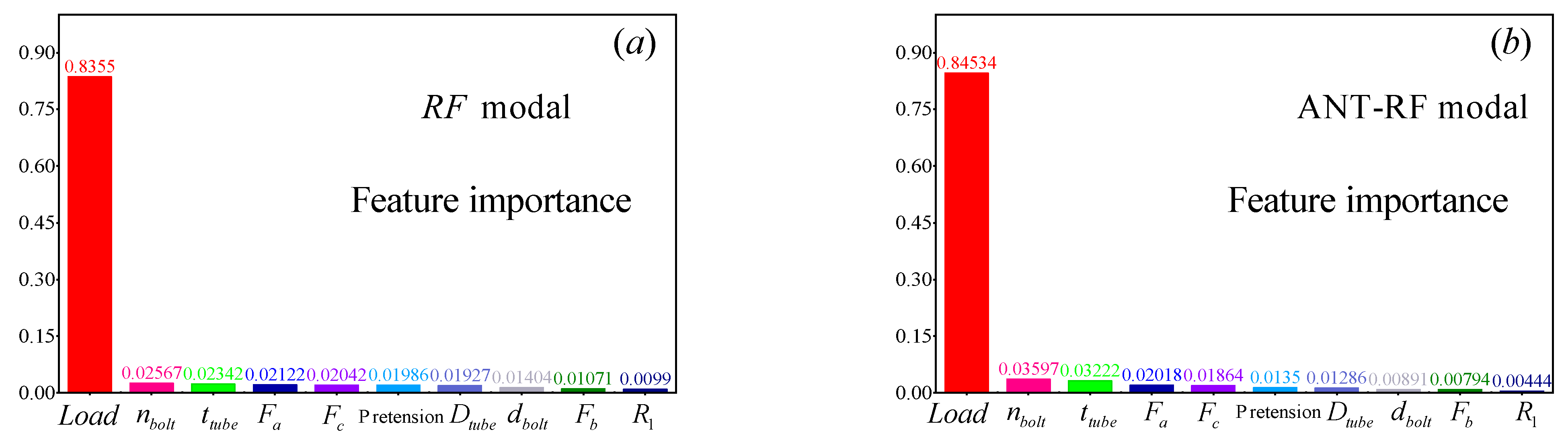
4.2. Feature Importance Analysis
5. Application of the Proposed GA-RF Model
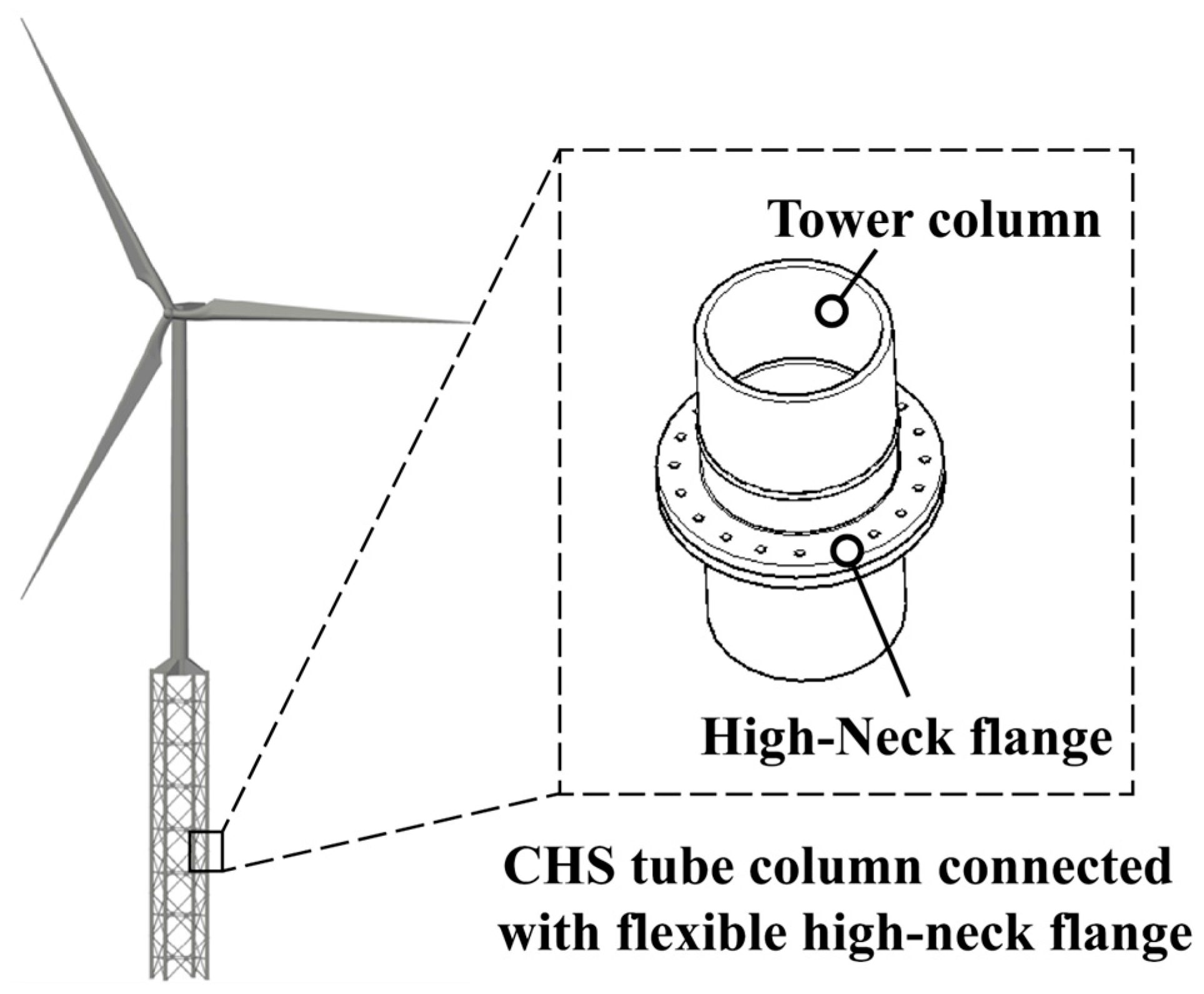
5.1. Engineering Background
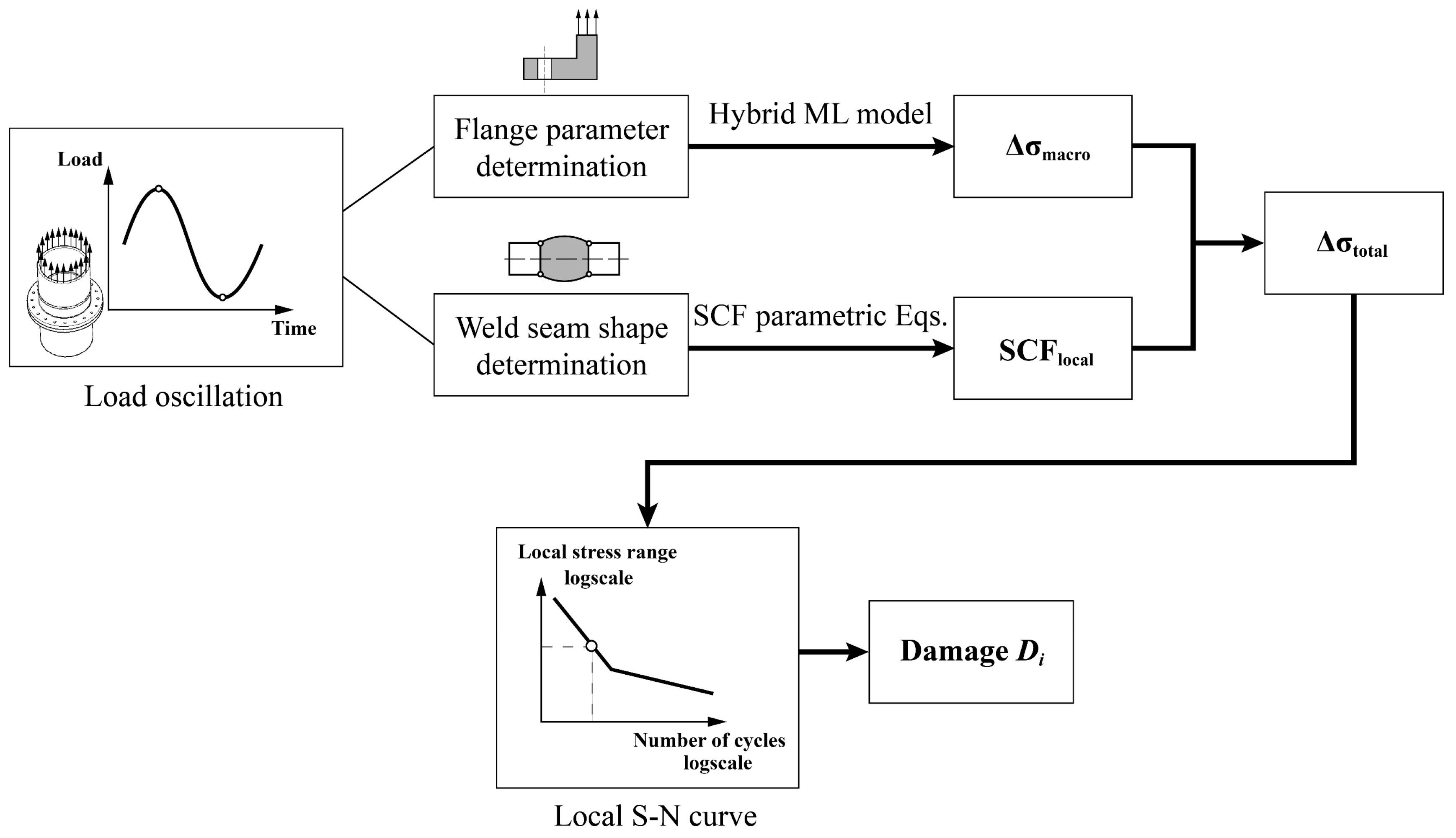
5.2. Fatigue Assessment Process
5.3. Damage Calculation of Flange Joint
6. Conclusions
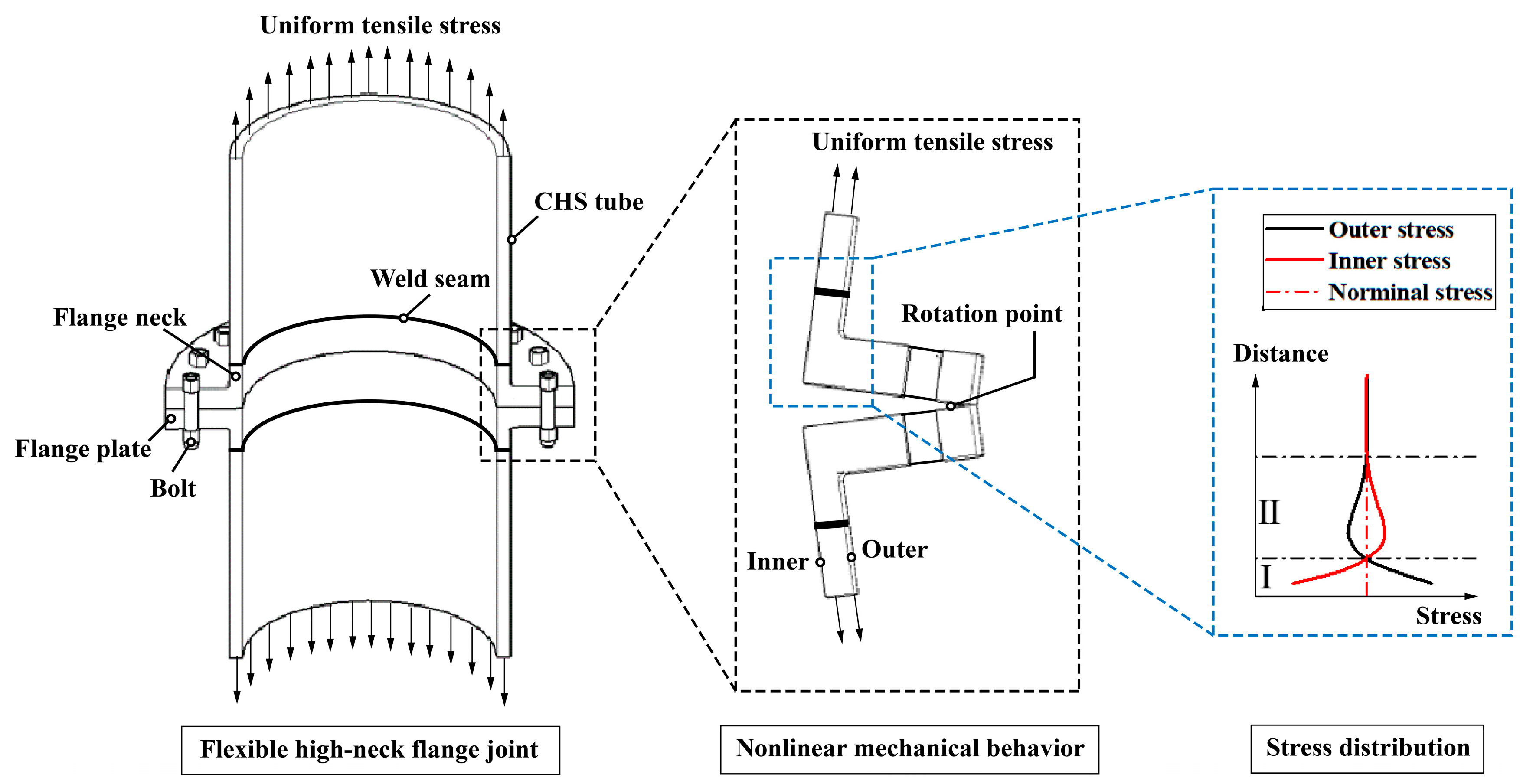
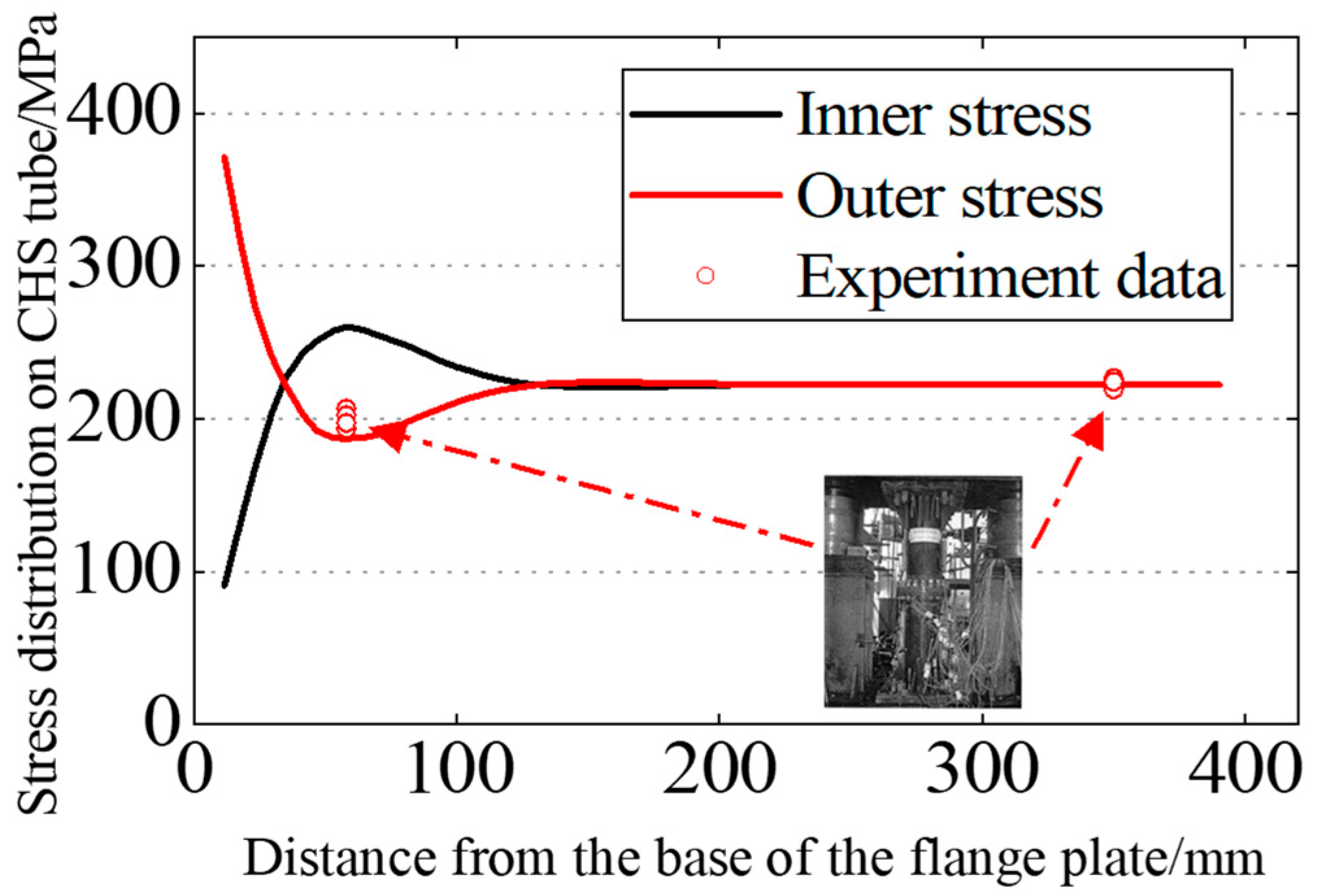
- Under tensile stress, the flexible high-neck flange exhibits significant nonlinear mechanical behavior, resulting in bending tensile stress on the outer surface of the CHS tube. Near the flange, high stress peaks can be detected. As the distance from the flange root increases, the stress level rapidly decreases to below the nominal stress, and then returns to the nominal stress level. On the inner surface of the tube, bending compressive stress is formed under tensile stress, resulting in an opposite trend compared to the outer surface.
- Feature importance analysis reveals that the most influential parameter on the stress distribution in the tube of flange joint is the magnitude of the tensile force. In addition to this, the number of bolts, wall thickness of the tube, and the positioning dimensions of the bolt holes follow in terms of their respective levels of impact, each playing a non-negligible role in the stress distribution.
- For the specific case discussed in this study, the performance of the ACO-RF model stands out as the most outstanding among the three hybrid models with an average coefficient of determination () of 0.9865 on the test dataset.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Dataset | Output | Parameters | RF | ACO-RF | GA-RF | GWO-RF |
|---|---|---|---|---|---|---|
| Training | Inner stress1 | 0.8694 | 0.9877 | 0.9781 | 0.9032 | |
| 29.317 | 8.0435 | 10.6888 | 21.9770 | |||
| 0.9324 | 0.9938 | 0.9890 | 0.9504 | |||
| 0.7971 | 0.9467 | 0.9374 | 0.9369 | |||
| Training | Inner stress2 | 0.9083 | 0.9930 | 0.9873 | 0.9441 | |
| 39.2002 | 9.2257 | 12.3288 | 25.5521 | |||
| 0.9530 | 0.9965 | 0.9936 | 0.9716 | |||
| 0.8181 | 0.9448 | 0.9575 | 0.9607 | |||
| Training | Inner stress3 | 0.9384 | 0.9958 | 0.9925 | 0.9702 | |
| 42.249 | 8.8295 | 11.6865 | 23.1952 | |||
| 0.9687 | 0.9979 | 0.9963 | 0.9850 | |||
| 0.8395 | 0.9891 | 0.9867 | 0.9838 | |||
| Training | Inner stress4 | 0.9492 | 0.9969 | 0.9947 | 0.9807 | |
| 45.1662 | 8.5487 | 11.1194 | 21.2575 | |||
| 0.9743 | 0.9985 | 0.9974 | 0.9903 | |||
| 0.8393 | 0.9933 | 0.9916 | 0.9885 | |||
| Training | Inner stress5 | 0.9524 | 0.9977 | 0.9967 | 0.9868 | |
| 47.5791 | 7.8710 | 9.4064 | 18.9266 | |||
| 0.9759 | 0.9989 | 0.9984 | 0.9934 | |||
| 0.8379 | 0.9946 | 0.9932 | 0.9903 | |||
| Training | Inner stress6 | 0.9581 | 0.9985 | 0.9977 | 0.9907 | |
| 43.6960 | 6.1540 | 7.4928 | 15.1826 | |||
| 0.9788 | 0.9992 | 0.9989 | 0.9953 | |||
| 0.8397 | 0.9962 | 0.9948 | 0.9925 | |||
| Training | Inner stress7 | 0.9610 | 0.9988 | 0.9981 | 0.9922 | |
| 41.3426 | 5.2536 | 6.5508 | 13.3918 | |||
| 0.9803 | 0.9994 | 0.9991 | 0.9961 | |||
| 0.8401 | 0.9971 | 0.9956 | 0.9932 | |||
| Training | Inner stress8 | 0.9622 | 0.9990 | 0.9982 | 0.9923 | |
| 38.6814 | 4.6124 | 6.0639 | 12.5662 | |||
| 0.9809 | 0.9995 | 0.9991 | 0.9962 | |||
| 0.8409 | 0.9974 | 0.9957 | 0.9933 | |||
| Training | Inner stress9 | 0.9649 | 0.9992 | 0.9986 | 0.9940 | |
| 36.5458 | 3.9847 | 5.1691 | 10.7202 | |||
| 0.9823 | 0.9996 | 0.9993 | 0.9970 | |||
| 0.8417 | 0.9982 | 0.9968 | 0.9938 | |||
| Training | Inner stress10 | 0.9663 | 0.9993 | 0.9988 | 0.9947 | |
| 34.9192 | 3.6221 | 4.6894 | 9.7043 | |||
| 0.9830 | 0.9996 | 0.9994 | 0.9974 | |||
| 0.8424 | 0.9986 | 0.9973 | 0.9943 | |||
| Training | Inner stress11 | 0.9680 | 0.9994 | 0.9990 | 0.9958 | |
| 33.7760 | 3.2470 | 4.1320 | 8.4678 | |||
| 0.9839 | 0.9997 | 0.9995 | 0.9979 | |||
| 0.8430 | 0.9991 | 0.9980 | 0.9948 | |||
| Training | Inner stress12 | 0.9691 | 0.9995 | 0.9992 | 0.9965 | |
| 32.9709 | 2.9536 | 3.7419 | 7.6019 | |||
| 0.9845 | 0.9997 | 0.9996 | 0.9983 | |||
| 0.8433 | 0.9993 | 0.9983 | 0.9950 | |||
| Training | Inner stress13 | 0.9699 | 0.9995 | 0.9993 | 0.9971 | |
| 32.5265 | 2.7246 | 3.4444 | 6.9611 | |||
| 0.9849 | 0.9998 | 0.9996 | 0.9985 | |||
| 0.8435 | 0.9994 | 0.9985 | 0.9951 | |||
| Training | Inner stress14 | 0.9705 | 0.9996 | 0.9994 | 0.9974 | |
| 32.210 | 2.5262 | 3.1935 | 6.4518 | |||
| 0.9852 | 0.9998 | 0.9997 | 0.9987 | |||
| 0.8436 | 0.9994 | 0.9985 | 0.9951 | |||
| Training | Inner stress15 | 0.9708 | 0.9996 | 0.9994 | 0.9977 | |
| 32.0628 | 2.3954 | 3.0280 | 6.1406 | |||
| 0.9853 | 0.9998 | 0.9997 | 0.9988 | |||
| 0.8436 | 0.9993 | 0.9985 | 0.9951 | |||
| Training | Inner stress16 | 0.9710 | 0.9997 | 0.9995 | 0.9978 | |
| 31.9702 | 2.3019 | 2.9121 | 5.9312 | |||
| 0.9854 | 0.9998 | 0.9997 | 0.9989 | |||
| 0.8436 | 0.9993 | 0.9985 | 0.9951 | |||
| Training | Inner stress17 | 0.9711 | 0.9997 | 0.9995 | 0.9979 | |
| 31.9338 | 2.2476 | 2.8450 | 5.8154 | |||
| 0.9855 | 0.9998 | 0.9997 | 0.9990 | |||
| 0.8435 | 0.9992 | 0.9985 | 0.9951 | |||
| Training | Inner stress18 | 0.9712 | 0.9997 | 0.9995 | 0.9979 | |
| 31.9240 | 2.2190 | 2.8136 | 5.7599 | |||
| 0.9855 | 0.9998 | 0.9998 | 0.9990 | |||
| 0.8435 | 0.9991 | 0.9984 | 0.9951 | |||
| Training | Inner stress19 | 0.9712 | 0.9997 | 0.9995 | 0.9980 | |
| 31.9227 | 2.2032 | 2.7985 | 5.7287 | |||
| 0.9855 | 0.9998 | 0.9998 | 0.9990 | |||
| 0.8435 | 0.9989 | 0.9983 | 0.9951 | |||
| Training | Inner stress20 | 0.9712 | 0.9997 | 0.9995 | 0.9980 | |
| 31.9397 | 2.2094 | 2.8096 | 5.7390 | |||
| 0.9855 | 0.9998 | 0.9998 | 0.9990 | |||
| 0.8434 | 0.9988 | 0.9983 | 0.9951 | |||
| Training | Inner stress21 | 0.9712 | 0.9997 | 0.9995 | 0.9980 | |
| 31.9447 | 2.2096 | 2.8113 | 5.7320 | |||
| 0.9855 | 0.9998 | 0.9998 | 0.9990 | |||
| 0.8434 | 0.9988 | 0.9983 | 0.9951 | |||
| Training | Inner stress22 | 0.9711 | 0.9997 | 0.9995 | 0.9979 | |
| 31.972 | 2.2493 | 2.8520 | 5.7864 | |||
| 0.9854 | 0.9998 | 0.9997 | 0.9990 | |||
| 0.8434 | 0.9987 | 0.9983 | 0.9951 | |||
| Training | Inner stress23 | 0.9711 | 0.9997 | 0.9995 | 0.9979 | |
| 31.9700 | 2.2451 | 2.8413 | 5.7580 | |||
| 0.9854 | 0.9998 | 0.9998 | 0.9990 | |||
| 0.8434 | 0.9987 | 0.9983 | 0.9952 | |||
| Training | Inner stress24 | 0.9710 | 0.9997 | 0.9995 | 0.9979 | |
| 32.006 | 2.3232 | 2.9121 | 5.8588 | |||
| 0.9854 | 0.9998 | 0.9997 | 0.9989 | |||
| 0.8435 | 0.9991 | 0.9986 | 0.9951 | |||
| Training | Inner stress25 | 0.9711 | 0.9997 | 0.9995 | 0.9980 | |
| 31.9666 | 2.1928 | 2.7747 | 5.6582 | |||
| 0.9854 | 0.9999 | 0.9998 | 0.9990 | |||
| 0.8436 | 0.9993 | 0.9987 | 0.9951 | |||
| Training | Outer stress1 | 0.8794 | 0.9915 | 0.9898 | 0.9616 | |
| 228.0632 | 54.0403 | 57.7710 | 113.0485 | |||
| 0.9377 | 0.9957 | 0.9949 | 0.9806 | |||
| 0.8033 | 0.9828 | 0.9812 | 0.9729 | |||
| Training | Outer stress2 | 0.8963 | 0.9941 | 0.9930 | 0.9724 | |
| 123.5416 | 25.5785 | 27.5240 | 55.2532 | |||
| 0.9468 | 0.9971 | 0.9965 | 0.9861 | |||
| 0.8141 | 0.9879 | 0.9863 | 0.9788 | |||
| Training | Outer stress3 | 0.8910 | 0.9946 | 0.9922 | 0.9686 | |
| 84.7124 | 16.5371 | 19.4731 | 39.5922 | |||
| 0.9439 | 0.9973 | 0.9961 | 0.9842 | |||
| 0.8224 | 0.9897 | 0.9875 | 0.9817 | |||
| Training | Outer stress4 | 0.8902 | 0.9947 | 0.9913 | 0.9619 | |
| 55.7043 | 10.7272 | 13.5501 | 28.3224 | |||
| 0.9435 | 0.9974 | 0.9956 | 0.9808 | |||
| 0.8328 | 0.9797 | 0.9787 | 0.9803 | |||
| Training | Outer stress5 | 0.9095 | 0.9955 | 0.9928 | 0.9699 | |
| 42.8242 | 8.1437 | 10.1963 | 20.7499 | |||
| 0.9537 | 0.9977 | 0.9964 | 0.9848 | |||
| 0.8406 | 0.9747 | 0.9674 | 0.9823 | |||
| Training | Outer stress6 | 0.9331 | 0.9967 | 0.9946 | 0.9781 | |
| 35.2476 | 6.3658 | 8.0538 | 16.2047 | |||
| 0.9660 | 0.9983 | 0.9973 | 0.9890 | |||
| 0.8444 | 0.9765 | 0.9837 | 0.9856 | |||
| Training | Outer stress7 | 0.9465 | 0.9975 | 0.9960 | 0.9836 | |
| 34.2433 | 5.7277 | 7.2509 | 14.6532 | |||
| 0.9729 | 0.9988 | 0.9980 | 0.9918 | |||
| 0.8444 | 0.9822 | 0.8932 | 0.9887 | |||
| Training | Outer stress8 | 0.9550 | 0.9982 | 0.9971 | 0.9880 | |
| 33.5105 | 4.9753 | 6.3458 | 12.9147 | |||
| 0.9772 | 0.9991 | 0.9986 | 0.9940 | |||
| 0.8441 | 0.9848 | 0.9809 | 0.9892 | |||
| Training | Outer stress9 | 0.9591 | 0.9986 | 0.9977 | 0.9902 | |
| 33.9730 | 4.6722 | 5.9011 | 12.1572 | |||
| 0.9793 | 0.9993 | 0.9988 | 0.9951 | |||
| 0.8434 | 0.9679 | 0.9892 | 0.9909 | |||
| Training | Outer stress10 | 0.9631 | 0.9989 | 0.9983 | 0.9928 | |
| 33.5021 | 4.0937 | 5.1244 | 10.6128 | |||
| 0.9814 | 0.9995 | 0.9992 | 0.9964 | |||
| 0.8435 | 0.9906 | 0.9901 | 0.9921 | |||
| Training | Outer stress11 | 0.9655 | 0.9991 | 0.9986 | 0.9942 | |
| 33.3807 | 3.7771 | 4.6846 | 9.6466 | |||
| 0.9826 | 0.9996 | 0.9993 | 0.9971 | |||
| 0.8434 | 0.9957 | 0.9943 | 0.9929 | |||
| Training | Outer stress12 | 0.9673 | 0.9993 | 0.9989 | 0.9953 | |
| 33.0116 | 3.4241 | 4.2419 | 8.6729 | |||
| 0.9835 | 0.9996 | 0.9994 | 0.9977 | |||
| 0.8436 | 0.9979 | 0.9964 | 0.9935 | |||
| Training | Outer stress13 | 0.9685 | 0.9994 | 0.9991 | 0.9961 | |
| 32.7939 | 3.1800 | 3.9217 | 7.9358 | |||
| 0.9841 | 0.9997 | 0.9995 | 0.9981 | |||
| 0.8437 | 0.9985 | 0.9971 | 0.9938 | |||
| Training | Outer stress14 | 0.9693 | 0.9995 | 0.9992 | 0.9967 | |
| 32.5636 | 2.9670 | 3.6536 | 7.3535 | |||
| 0.9846 | 0.9997 | 0.9996 | 0.9983 | |||
| 0.8438 | 0.9990 | 0.9976 | 0.9940 | |||
| Training | Outer stress15 | 0.9699 | 0.9995 | 0.9993 | 0.9970 | |
| 32.4160 | 2.8173 | 3.4571 | 6.9347 | |||
| 0.9848 | 0.9998 | 0.9996 | 0.9985 | |||
| 0.8439 | 0.9993 | 0.9979 | 0.9941 | |||
| Training | Outer stress16 | 0.9702 | 0.9996 | 0.9993 | 0.9973 | |
| 32.2930 | 2.7007 | 3.3075 | 6.6378 | |||
| 0.9850 | 0.9998 | 0.9997 | 0.9986 | |||
| 0.8440 | 0.9994 | 0.9980 | 0.9941 | |||
| Training | Outer stress17 | 0.9705 | 0.9996 | 0.9994 | 0.9974 | |
| 32.2087 | 2.6226 | 3.2109 | 6.4521 | |||
| 0.9851 | 0.9998 | 0.9997 | 0.9987 | |||
| 0.8440 | 0.9994 | 0.9981 | 0.9941 | |||
| Training | Outer stress18 | 0.9706 | 0.9996 | 0.9994 | 0.9975 | |
| 32.1475 | 2.5650 | 3.1434 | 6.3283 | |||
| 0.9852 | 0.9998 | 0.9997 | 0.9988 | |||
| 0.8440 | 0.9994 | 0.9981 | 0.9941 | |||
| Training | Outer stress19 | 0.9707 | 0.9996 | 0.9994 | 0.9976 | |
| 32.0967 | 2.5220 | 3.0993 | 6.2485 | |||
| 0.9852 | 0.9998 | 0.9997 | 0.9988 | |||
| 0.8440 | 0.9994 | 0.9981 | 0.9940 | |||
| Training | Outer stress20 | 0.9708 | 0.9996 | 0.9994 | 0.9976 | |
| 32.0650 | 2.4856 | 3.0634 | 6.1844 | |||
| 0.9853 | 0.9998 | 0.9997 | 0.9988 | |||
| 0.8441 | 0.9994 | 0.9980 | 0.9940 | |||
| Training | Outer stress21 | 0.9708 | 0.9996 | 0.9994 | 0.9977 | |
| 32.0285 | 2.4421 | 3.0235 | 6.1126 | |||
| 0.9853 | 0.9998 | 0.9997 | 0.9988 | |||
| 0.8440 | 0.9994 | 0.9980 | 0.9940 | |||
| Training | Outer stress22 | 0.9709 | 0.9996 | 0.9995 | 0.9978 | |
| 32.0028 | 2.3828 | 2.9627 | 6.0044 | |||
| 0.9854 | 0.9998 | 0.9997 | 0.9989 | |||
| 0.8440 | 0.9994 | 0.9980 | 0.9939 | |||
| Training | Outer stress23 | 0.9711 | 0.9997 | 0.9995 | 0.9979 | |
| 31.9624 | 2.2926 | 2.8705 | 5.8425 | |||
| 0.9854 | 0.9998 | 0.9997 | 0.9989 | |||
| 0.8440 | 0.9994 | 0.9980 | 0.9940 | |||
| Training | Outer stress24 | 0.9713 | 0.9997 | 0.9995 | 0.9981 | |
| 31.9216 | 2.1632 | 2.7335 | 5.6057 | |||
| 0.9855 | 0.9999 | 0.9998 | 0.9990 | |||
| 0.8439 | 0.9994 | 0.9979 | 0.9938 | |||
| Training | Outer stress25 | 0.9715 | 0.9998 | 0.9996 | 0.9982 | |
| 31.8719 | 1.9911 | 2.5583 | 5.3340 | |||
| 0.9856 | 0.9999 | 0.9998 | 0.9991 | |||
| 0.8438 | 0.9993 | 0.9980 | 0.9939 |
| Dataset | Output | Parameters | RF | ACO-RF | GA-RF | GWO-RF |
|---|---|---|---|---|---|---|
| Testing | Inner stress1 | 0.8333 | 0.9011 | 0.8957 | 0.8495 | |
| 30.0074 | 20.6258 | 21.2353 | 25.4910 | |||
| 0.9128 | 0.9493 | 0.9464 | 0.9217 | |||
| 0.7923 | 0.9478 | 0.9307 | 0.9394 | |||
| Testing | Inner stress2 | 0.8836 | 0.9389 | 0.9394 | 0.9113 | |
| 43.3498 | 26.3288 | 26.3931 | 31.8236 | |||
| 0.9400 | 0.9690 | 0.9692 | 0.9546 | |||
| 0.8032 | 0.9362 | 0.9197 | 0.9422 | |||
| Testing | Inner stress3 | 0.9215 | 0.9678 | 0.9678 | 0.9540 | |
| 48.5299 | 24.3547 | 24.4654 | 29.1799 | |||
| 0.9599 | 0.9838 | 0.9838 | 0.9767 | |||
| 0.8367 | 0.9849 | 0.9668 | 0.9788 | |||
| Testing | Inner stress4 | 0.9298 | 0.9751 | 0.9748 | 0.9658 | |
| 52.1086 | 24.0963 | 24.3433 | 28.2712 | |||
| 0.9643 | 0.9875 | 0.9873 | 0.9827 | |||
| 0.8340 | 0.9912 | 0.9697 | 0.9843 | |||
| Testing | Inner stress5 | 0.9347 | 0.9814 | 0.9804 | 0.9747 | |
| 53.3165 | 21.9952 | 22.6736 | 25.6728 | |||
| 0.9668 | 0.9907 | 0.9902 | 0.9873 | |||
| 0.8300 | 0.9909 | 0.9672 | 0.9844 | |||
| Testing | Inner stress6 | 0.9436 | 0.9874 | 0.9861 | 0.9826 | |
| 47.7223 | 17.1131 | 18.0405 | 20.1384 | |||
| 0.9714 | 0.9937 | 0.9930 | 0.9913 | |||
| 0.8320 | 0.9937 | 0.9681 | 0.9883 | |||
| Testing | Inner stress7 | 0.9488 | 0.9906 | 0.9894 | 0.9867 | |
| 44.5806 | 14.2618 | 15.2075 | 17.0074 | |||
| 0.9740 | 0.9953 | 0.9947 | 0.9933 | |||
| 0.8330 | 0.9960 | 0.9676 | 0.9912 | |||
| Testing | Inner stress8 | 0.9517 | 0.9924 | 0.9910 | 0.9880 | |
| 41.1745 | 12.1184 | 13.1978 | 15.1982 | |||
| 0.9755 | 0.9962 | 0.9955 | 0.9940 | |||
| 0.8344 | 0.9963 | 0.9654 | 0.9925 | |||
| Testing | Inner stress9 | 0.9556 | 0.9946 | 0.9935 | 0.9912 | |
| 38.9538 | 9.8531 | 10.7713 | 12.5363 | |||
| 0.9775 | 0.9973 | 0.9968 | 0.9956 | |||
| 0.8363 | 0.9980 | 0.9647 | 0.9941 | |||
| Testing | Inner stress10 | 0.9577 | 0.9956 | 0.9948 | 0.9927 | |
| 37.2435 | 8.5667 | 9.3696 | 11.0404 | |||
| 0.9786 | 0.9978 | 0.9974 | 0.9964 | |||
| 0.8378 | 0.9986 | 0.9637 | 0.9947 | |||
| Testing | Inner stress11 | 0.9598 | 0.9966 | 0.9961 | 0.9946 | |
| 36.2926 | 7.3965 | 7.9909 | 9.3966 | |||
| 0.9797 | 0.9983 | 0.9980 | 0.9973 | |||
| 0.8390 | 0.9992 | 0.9634 | 0.9948 | |||
| Testing | Inner stress12 | 0.9611 | 0.9972 | 0.9969 | 0.9956 | |
| 35.5853 | 6.6028 | 7.0655 | 8.3446 | |||
| 0.9803 | 0.9986 | 0.9984 | 0.9978 | |||
| 0.8398 | 0.9992 | 0.9629 | 0.9946 | |||
| Testing | Inner stress13 | 0.9619 | 0.9977 | 0.9974 | 0.9963 | |
| 35.2565 | 6.0549 | 6.4021 | 7.5898 | |||
| 0.9808 | 0.9988 | 0.9987 | 0.9982 | |||
| 0.8401 | 0.9989 | 0.9625 | 0.9940 | |||
| Testing | Inner stress14 | 0.9626 | 0.9980 | 0.9978 | 0.9968 | |
| 34.9817 | 5.6354 | 5.9180 | 7.0750 | |||
| 0.9811 | 0.9990 | 0.9989 | 0.9984 | |||
| 0.8402 | 0.9986 | 0.9621 | 0.9936 | |||
| Testing | Inner stress15 | 0.9630 | 0.9981 | 0.9980 | 0.9970 | |
| 34.8404 | 5.3932 | 5.6272 | 6.7780 | |||
| 0.9813 | 0.9991 | 0.9990 | 0.9985 | |||
| 0.8400 | 0.9982 | 0.9617 | 0.9931 | |||
| Testing | Inner stress16 | 0.9632 | 0.9982 | 0.9981 | 0.9971 | |
| 34.7398 | 5.2758 | 5.4786 | 6.6374 | |||
| 0.9814 | 0.9991 | 0.9990 | 0.9986 | |||
| 0.8399 | 0.9979 | 0.9615 | 0.9929 | |||
| Testing | Inner stress17 | 0.9634 | 0.9982 | 0.9981 | 0.9972 | |
| 34.6737 | 5.2354 | 5.4115 | 6.5781 | |||
| 0.9815 | 0.9991 | 0.9991 | 0.9986 | |||
| 0.8397 | 0.9975 | 0.9613 | 0.9926 | |||
| Testing | Inner stress18 | 0.9634 | 0.9982 | 0.9981 | 0.9972 | |
| 34.6493 | 5.2507 | 5.4101 | 6.5832 | |||
| 0.9815 | 0.9991 | 0.9991 | 0.9986 | |||
| 0.8396 | 0.9974 | 0.9613 | 0.9926 | |||
| Testing | Inner stress19 | 0.9635 | 0.9982 | 0.9981 | 0.9972 | |
| 34.6228 | 5.2743 | 5.4211 | 6.5955 | |||
| 0.9816 | 0.9991 | 0.9990 | 0.9986 | |||
| 0.8395 | 0.9972 | 0.9613 | 0.9926 | |||
| Training | Inner stress20 | 0.9634 | 0.9982 | 0.9981 | 0.9972 | |
| 34.6354 | 5.3047 | 5.4504 | 6.6210 | |||
| 0.9816 | 0.9991 | 0.9990 | 0.9986 | |||
| 0.8394 | 0.9972 | 0.9613 | 0.9926 | |||
| Training | Inner stress21 | 0.9634 | 0.9982 | 0.9981 | 0.9972 | |
| 34.6333 | 5.3122 | 5.4636 | 6.6256 | |||
| 0.9815 | 0.9991 | 0.9990 | 0.9986 | |||
| 0.8393 | 0.9971 | 0.9613 | 0.9926 | |||
| Training | Inner stress22 | 0.9634 | 0.9982 | 0.9981 | 0.9972 | |
| 34.6692 | 5.3070 | 5.4776 | 6.6240 | |||
| 0.9815 | 0.9991 | 0.9990 | 0.9986 | |||
| 0.8393 | 0.9971 | 0.9613 | 0.9926 | |||
| Training | Inner stress23 | 0.9633 | 0.9982 | 0.9981 | 0.9972 | |
| 34.6816 | 5.2596 | 5.4559 | 6.5837 | |||
| 0.9815 | 0.9991 | 0.9990 | 0.9986 | |||
| 0.8394 | 0.9971 | 0.9614 | 0.9928 | |||
| Training | Inner stress24 | 0.9633 | 0.9982 | 0.9981 | 0.9972 | |
| 34.7238 | 5.2050 | 5.4311 | 6.5364 | |||
| 0.9815 | 0.9991 | 0.9990 | 0.9986 | |||
| 0.8394 | 0.9972 | 0.9615 | 0.9925 | |||
| Training | Inner stress25 | 0.9633 | 0.9983 | 0.9981 | 0.9973 | |
| 34.7004 | 5.1365 | 5.3591 | 6.4637 | |||
| 0.9815 | 0.9991 | 0.9991 | 0.9986 | |||
| 0.8396 | 0.9976 | 0.9619 | 0.9929 | |||
| Training | Outer stress1 | 0.8626 | 0.9310 | 0.9377 | 0.9216 | |
| 228.5337 | 139.2439 | 134.0324 | 149.4037 | |||
| 0.9288 | 0.9649 | 0.9683 | 0.9600 | |||
| 0.7988 | 0.9959 | 0.9637 | 0.9871 | |||
| Training | Outer stress2 | 0.8772 | 0.9524 | 0.9541 | 0.9441 | |
| 125.7301 | 66.8862 | 66.7746 | 73.0712 | |||
| 0.9366 | 0.9759 | 0.9768 | 0.9717 | |||
| 0.8086 | 0.9966 | 0.9677 | 0.9873 | |||
| Training | Outer stress3 | 0.8754 | 0.9614 | 0.9590 | 0.9467 | |
| 84.0521 | 40.0646 | 42.1035 | 47.4426 | |||
| 0.9356 | 0.9805 | 0.9793 | 0.9730 | |||
| 0.8170 | 0.9984 | 0.9691 | 0.9913 | |||
| Training | Outer stress4 | 0.8695 | 0.9606 | 0.9548 | 0.9363 | |
| 56.2323 | 26.6666 | 29.0192 | 33.9125 | |||
| 0.9324 | 0.9801 | 0.9771 | 0.9676 | |||
| 0.8314 | 0.9956 | 0.9647 | 0.9960 | |||
| Training | Outer stress5 | 0.8951 | 0.9657 | 0.9627 | 0.9504 | |
| 43.6513 | 20.9249 | 22.0404 | 25.1714 | |||
| 0.9461 | 0.9827 | 0.9812 | 0.9749 | |||
| 0.8424 | 1.0033 | 0.9608 | 1.0019 | |||
| Training | Outer stress6 | 0.9147 | 0.9685 | 0.9675 | 0.9589 | |
| 38.1363 | 18.8254 | 19.2575 | 21.5230 | |||
| 0.9564 | 0.9841 | 0.9836 | 0.9793 | |||
| 0.8472 | 0.9915 | 0.9544 | 1.0037 | |||
| Training | Outer stress7 | 0.9297 | 0.9756 | 0.9756 | 0.9693 | |
| 38.2698 | 17.6189 | 17.7062 | 19.7856 | |||
| 0.9642 | 0.9877 | 0.9877 | 0.9845 | |||
| 0.8463 | 0.9964 | 0.9550 | 0.9949 | |||
| Training | Outer stress8 | 0.9398 | 0.9825 | 0.9822 | 0.9775 | |
| 37.7454 | 15.3956 | 15.6351 | 17.5188 | |||
| 0.9694 | 0.9912 | 0.9911 | 0.9887 | |||
| 0.8445 | 0.9965 | 0.9559 | 0.9942 | |||
| Training | Outer stress9 | 0.9454 | 0.9866 | 0.9861 | 0.9822 | |
| 38.2383 | 14.0717 | 14.4067 | 16.2491 | |||
| 0.9723 | 0.9933 | 0.9930 | 0.9910 | |||
| 0.8425 | 0.9902 | 0.9566 | 0.9899 | |||
| Training | Outer stress10 | 0.9513 | 0.9906 | 0.9899 | 0.9872 | |
| 37.3270 | 11.9179 | 12.4167 | 13.9183 | |||
| 0.9754 | 0.9953 | 0.9949 | 0.9936 | |||
| 0.8414 | 0.9952 | 0.9587 | 0.9908 | |||
| Training | Outer stress11 | 0.9547 | 0.9927 | 0.9920 | 0.9900 | |
| 36.9708 | 10.6362 | 11.1501 | 12.4684 | |||
| 0.9771 | 0.9963 | 0.9960 | 0.9950 | |||
| 0.8406 | 0.9965 | 0.9599 | 0.9909 | |||
| Training | Outer stress12 | 0.9576 | 0.9944 | 0.9938 | 0.9923 | |
| 36.2671 | 9.2766 | 9.8119 | 10.9439 | |||
| 0.9786 | 0.9972 | 0.9969 | 0.9961 | |||
| 0.8403 | 0.9975 | 0.9609 | 0.9913 | |||
| Training | Outer stress13 | 0.9595 | 0.9956 | 0.9951 | 0.9938 | |
| 35.8826 | 8.3239 | 8.8035 | 9.8354 | |||
| 0.9796 | 0.9978 | 0.9975 | 0.9969 | |||
| 0.8401 | 0.9978 | 0.9612 | 0.9913 | |||
| Training | Outer stress14 | 0.9609 | 0.9964 | 0.9960 | 0.9949 | |
| 35.5053 | 7.4623 | 7.9044 | 8.8854 | |||
| 0.9803 | 0.9982 | 0.9980 | 0.9975 | |||
| 0.8402 | 0.9983 | 0.9617 | 0.9917 | |||
| Training | Outer stress15 | 0.9618 | 0.9970 | 0.9967 | 0.9957 | |
| 35.2867 | 6.8290 | 7.2204 | 8.1810 | |||
| 0.9807 | 0.9985 | 0.9983 | 0.9978 | |||
| 0.8402 | 0.9984 | 0.9619 | 0.9918 | |||
| Training | Outer stress16 | 0.9624 | 0.9974 | 0.9972 | 0.9962 | |
| 35.1262 | 6.3195 | 6.6799 | 7.6498 | |||
| 0.9810 | 0.9987 | 0.9986 | 0.9981 | |||
| 0.8404 | 0.9986 | 0.9621 | 0.9921 | |||
| Training | Outer stress17 | 0.9627 | 0.9977 | 0.9975 | 0.9966 | |
| 35.0213 | 5.9656 | 6.2997 | 7.2877 | |||
| 0.9812 | 0.9989 | 0.9987 | 0.9983 | |||
| 0.8404 | 0.9985 | 0.9620 | 0.9920 | |||
| Training | Outer stress18 | 0.9630 | 0.9979 | 0.9977 | 0.9968 | |
| 34.9611 | 5.7150 | 6.0330 | 7.0471 | |||
| 0.9813 | 0.9989 | 0.9988 | 0.9984 | |||
| 0.8405 | 0.9985 | 0.9621 | 0.9922 | |||
| Training | Outer stress19 | 0.9631 | 0.9980 | 0.9978 | 0.9969 | |
| 34.9034 | 5.5474 | 5.8534 | 6.8920 | |||
| 0.9814 | 0.9990 | 0.9989 | 0.9985 | |||
| 0.8405 | 0.9985 | 0.9620 | 0.9921 | |||
| Training | Outer stress20 | 0.9632 | 0.9981 | 0.9979 | 0.9970 | |
| 34.8780 | 5.4398 | 5.7353 | 6.7971 | |||
| 0.9814 | 0.9990 | 0.9989 | 0.9985 | |||
| 0.8405 | 0.9985 | 0.9620 | 0.9921 | |||
| Training | Outer stress21 | 0.9632 | 0.9981 | 0.9980 | 0.9971 | |
| 34.8325 | 5.3598 | 5.6459 | 6.7275 | |||
| 0.9814 | 0.9991 | 0.9990 | 0.9985 | |||
| 0.8405 | 0.9984 | 0.9620 | 0.9921 | |||
| Training | Outer stress22 | 0.9633 | 0.9982 | 0.9980 | 0.9971 | |
| 34.8105 | 5.3006 | 5.5712 | 6.6697 | |||
| 0.9815 | 0.9991 | 0.9990 | 0.9986 | |||
| 0.8405 | 0.9984 | 0.9619 | 0.9921 | |||
| Training | Outer stress23 | 0.9634 | 0.9982 | 0.9981 | 0.9972 | |
| 34.7570 | 5.2292 | 5.4848 | 6.5962 | |||
| 0.9815 | 0.9991 | 0.9990 | 0.9986 | |||
| 0.8404 | 0.9982 | 0.9618 | 0.9920 | |||
| Training | Outer stress24 | 0.9634 | 0.9983 | 0.9981 | 0.9972 | |
| 34.7314 | 5.1838 | 5.4132 | 6.5320 | |||
| 0.9815 | 0.9991 | 0.9991 | 0.9986 | |||
| 0.8402 | 0.9980 | 0.9615 | 0.9916 | |||
| Training | Outer stress25 | 0.9634 | 0.9983 | 0.9982 | 0.9973 | |
| 34.6875 | 5.1162 | 5.3313 | 6.4471 | |||
| 0.9815 | 0.9992 | 0.9991 | 0.9987 | |||
| 0.8400 | 0.9974 | 0.9612 | 0.9912 |
References
- Couchaux, M.; Hjiaj, M.; Ryan, I.; Bureau, A. Bolted circular flange connections under static bending moment and axial force. J. Constr. Steel Res. 2019, 157, 314–336. [Google Scholar] [CrossRef]
- Q GDW 391-2009; Technical Regulation for Conformation Design of Steel Tubular Towers of Transmission Lines. State Grid Corporation: Beijing, China, 2009. (In Chinese)
- GB 50135-2017; Standard for Design of High-Rising Structures. Ministry of Housing and Urban-Rural Development: Beijing, China, 2009. (In Chinese)
- IIW-2259-15; Recommendations for Fatigue Design of Welded Joints and Components. International Institute of Welding: Genoa, Italy, 2016.
- DNVGL-ST-0126; Design Standard—Support Structures for Wind Turbines. DNV: Bærum, Norway, 2016.
- Luo, Y.; Ma, R.; Tsutsumi, S. Parametric formulae for elastic stress concentration factor at the weld toe of distorted butt-welded joints. Materials 2020, 13, 169. [Google Scholar] [CrossRef]
- Luo, Y.; Tsutsumi, S.; Han, R.; Ma, R.; Dai, K. Parametric formulae for stress concentration factor and clamping-induced stress of butt-welded joints under fatigue test condition. Weld. World 2022, 66, 1897–1913. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, Y.; Tsutsumi, S. Parametric formula for stress concentration factor of fillet weld joints with spline bead profile. Materials 2020, 13, 4639. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, Y.; Kotani, Y.; Tsutsumi, S. Generalized SCF formula of out-of-plane gusset welded joints and assessment of fatigue life extension by additional weld. Materials 2021, 14, 1249. [Google Scholar] [CrossRef]
- Mangalathu, S.; Jeon, J.S. Machine learning–based failure mode recognition of circular reinforced concrete bridge columns: Comparative study. J. Struct. Eng. 2019, 145, 04019104. [Google Scholar] [CrossRef]
- Rahman, J.; Ahmed, K.S.; Khan, N.I.; Islam, K.; Mangalathu, S. Data-driven shear strength prediction of steel fiber-reinforced concrete beams using a machine learning approach. Eng. Struct. 2021, 233, 111743. [Google Scholar] [CrossRef]
- Xie, Y.; Ebad Sichani, M.; Padgett, J.E.; DesRoches, R. The promise of implementing machine learning in earthquake engineering: A state-of-the-art review. Earthq. Spectra 2020, 36, 1769–1801. [Google Scholar] [CrossRef]
- Kameshwar, S.; Misra, S.; Padgett, J.E. Decision tree-based bridge restoration models for extreme event performance assessment of regional road networks. Struct. Infrastruct. Eng. 2020, 16, 431–445. [Google Scholar] [CrossRef]
- Karim, R.M.; Islam, K.; Ahmed, K.S.; Zhang, Q. Application of machine learning in bridge engineering: A state-of-the-art review. In Proceedings of the IABSE-JSCE Advances in Bridge Engineering-IV Conference, Dhaka, Bangladesh, 26–27 August 2020. [Google Scholar]
- He, S.; Chen, J.; Chen, Z.; Song, G. An exploratory study of underwater bolted connection looseness detection using percussion and a shallow machine learning algorithm. Acta Mech. Sin. 2023, 39, 722360. [Google Scholar] [CrossRef]
- Nguyen, H.D.; LaFave, J.M.; Lee, Y.J.; Shin, M. Rapid seismic damage-state assessment of steel moment frames using machine learning. Eng. Struct. 2022, 252, 113737. [Google Scholar] [CrossRef]
- Bolandi, H.; Li, X.; Salem, T.; Boddeti, V.N.; Lajnef, N. Deep learning paradigm for prediction of stress distribution in damaged structural components with stress concentrations. Adv. Eng. Softw. 2022, 173, 103240. [Google Scholar] [CrossRef]
- Liang, L.; Liu, M.; Martin, C.; Sun, W. A deep learning approach to estimate stress distribution: A fast and accurate surrogate of finite-element analysis. J. R. Soc. Interface 2018, 15, 20170844. [Google Scholar] [CrossRef]
- Sepasdar, R.; Karpatne, A.; Shakiba, M. A data-driven approach to full-field nonlinear stress distribution and failure pattern prediction in composites using deep learning. Comput. Methods Appl. Mech. Eng. 2022, 397, 115126. [Google Scholar] [CrossRef]
- Nguyen, N.V.; Nguyen, H.D.; Dao, N.D. Machine Learning Models for Predicting Maximum Displacement of Triple Pendulum Isolation Systems//Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 36, pp. 404–415. [Google Scholar]
- Nguyen, H.D.; Dao, N.D.; Shin, M. Machine learning-based prediction for maximum displacement of seismic isolation systems. J. Build. Eng. 2022, 51, 104251. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, S.; Zhou, T.; Armaghani, D.J.; Qiu, Y. Employing a genetic algorithm and grey wolf optimizer for optimizing RF models to evaluate soil liquefaction potential. Artif. Intell. Rev. 2022, 55, 5673–5705. [Google Scholar] [CrossRef]
- Leleń, M.; Biruk-Urban, K.; Józwik, J.; Tomiło, P. Modeling and Machine Learning of Vibration Amplitude and Surface Roughness after Waterjet Cutting. Materials 2023, 16, 6474. [Google Scholar] [CrossRef]
- Ahmed, A.; Song, W.; Zhang, Y.; Haque, M.A.; Liu, X. Hybrid BO-XGBoost and BO-RF Models for the Strength Prediction of Self-Compacting Mortars with Parametric Analysis. Materials 2023, 16, 4366. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, L.; Wu, Y. Research on transformer fault diagnosis based on GWO-RF algorithm. J. Phys. Conf. Ser. 2021, 1952, 032054. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Amit, Y.; Geman, D. Shape quantization and recognition with randomized trees. Neural Comput. 1997, 9, 1545–1588. [Google Scholar] [CrossRef]
- Dorigo, M. Optimization, Learning and Natural Algorithms. Ph.D. Thesis, Dipartimento di Elettronica, Politecnico di Milano, Milan, Italy, 1992. (In Italian). [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Positive Feedback as a Search Strategy; Technical Report 91-016; Dipartimento di Elettronica, Politecnicodi Milano: Milan, Italy, 1991. [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant System: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybernet Part B 1996, 26, 29–41. [Google Scholar] [CrossRef]
- Hole, K.R.; Gulhane, V.S.; Shellokar, N.D. Application of Genetic Algorithm for Image Enhancement and Segmentation. Int. J. Adv. Res. Comput. Eng. Technol. 2013, 2, 1342. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; A Bradford Book; The MIT Press: Cambridge, MA, USA; London, UK, 1999. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- GB50017-2017; Standard for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2017. (In Chinese)
- VDI 2230; Systematic Calculation of Highly Stressed Bolted Joints, Joints with One Cylindrical Bolt. Verein Deutscher the German Engineers Association: Harzgerode, Germany, 2015.
- Wen, X. Experimental Study on Fatigue Performance of Q460 High-Strength Steel Pipe Tower Joint. Master’s Thesis, Nanjing University of Technology, Nanjing, China, 2013. (In Chinese). [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- IEC-61400-1; Part 1: Design Requirements. International Electrotechnical Commission: London, UK, 2005.
- Miner, M.A. Cumulative damage in Fatigue. J. Appl. Mech. 1945, 12, A159–A164. [Google Scholar] [CrossRef]








| Authors | Machine Learning Model Used | Application Scenario |
|---|---|---|
| Mangalathu [10] | Artificial Neural Network (ANN) | Failure model prediction of a round reinforced concrete bridge column |
| Rahman [11] | eXtreme Gradient Boosting (XGboost) | Prediction of shear strength of steel fiber reinforced concrete beams |
| Kameshwar [13] | Decision Tree (DT) | Earthquake recovery model of a bridge |
| He [15] | K-Nearest Neighbor (KNN) | Prediction of loosening state of underwater bolt connection |
| Nguyen [16] | Random Forest (RF) | Damage assessment of buildings after an earthquake |
| Bolandi [17] | Convolutional Neural Networks (CNN) | Stress distribution of damaged structural components with stress concentration |
| Liang [18] | Deep Learning Model (DL) | Stress distribution in human aorta |
| Sepasdar [19] | Convolutional Neural Networks (CNN) | Nonlinear stress distribution and failure modes in microstructure characterization of composite materials |
| Nguyen [20] | Random Forest (RF) | Maximum displacement of three pendulum isolation system |
| Nguyen [21] | Random Forest (RF) | Peak lateral displacement of an isolation system under earthquake action |
| Zhou [22] | Random Forest (RF) | Assess the liquefaction potential of soil |
| Leleń [23] | Linear Regression (LR) | Prediction of vibration amplitude and surface roughness after water jet cutting |
| Ahmed [24] | Random Forest (RF) | Predict the strength of self-compacting mortar samples |
| Notation | Unit | Range of Variable | Description |
|---|---|---|---|
| mm | 6–46 | Thickness of steel pipe | |
| mm | 173–2555 | Steel pipe diameter | |
| Pretension | N | 59,886–2,034,355 | The pretension force applied by the bolt |
| mm | 14–64 | Diameter of bolt | |
| mm | 17.45–174.17 | Flange thickness | |
| mm | 17.92–157.87 | Distance from hole center to flange edge | |
| mm | 21.38–150.8 | Distance from hole center to root | |
| num | 4–96 | Number of bolts | |
| mm | 2–13 | Flange fillet | |
| Load | MPa | 0–450 | A uniform load applied to a steel pipe |
| Model | n_Estimators | Max_Features | Min_Samples_Leaf | Max_Depth | Min_Samples_Split |
|---|---|---|---|---|---|
| RF | 100 | 0.2 | 10 | 200 | 2 |
| ACO-RF | 110 | 1.0 | 2 | 91 | 4 |
| GR-RF | 133 | 0.7 | 1 | 14 | 3 |
| GWO-RF | 161 | 0.6 | 3 | 15 | 4 |
| Dataset | Parameters | Model | |||
|---|---|---|---|---|---|
| RF | ACO-RF | GA-RF | GWO-RF | ||
| Training | 0.9552 | 0.9983 | 0.9973 | 0.9887 | |
| 41.4376 | 5.6718 | 6.8446 | 13.8133 | ||
| 0.9773 | 0.9991 | 0.9986 | 0.9943 | ||
| 0.8396 | 0.9929 | 0.9905 | 0.9901 | ||
| Testing | 0.9438 | 0.9865 | 0.9860 | 0.9812 | |
| 44.3442 | 14.6456 | 14.9875 | 17.1670 | ||
| 0.9713 | 0.9932 | 0.9929 | 0.9903 | ||
| 0.8358 | 0.9946 | 0.9608 | 0.9900 | ||
| Pretension | ||||||||
|---|---|---|---|---|---|---|---|---|
| 20 mm | 977 mm | 339,500 N | 36 mm | 50 mm | 60 mm | 75 mm | 22 | 5 mm |
| 37.5 mm | 30° | 6.125 mm | 25 mm | 1 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, K.; Du, H.; Luo, Y.; Han, R.; Li, J. Stress Distribution Prediction of Circular Hollow Section Tube in Flexible High-Neck Flange Joints Based on the Hybrid Machine Learning Model. Materials 2023, 16, 6815. https://doi.org/10.3390/ma16206815
Dai K, Du H, Luo Y, Han R, Li J. Stress Distribution Prediction of Circular Hollow Section Tube in Flexible High-Neck Flange Joints Based on the Hybrid Machine Learning Model. Materials. 2023; 16(20):6815. https://doi.org/10.3390/ma16206815
Chicago/Turabian StyleDai, Kaoshan, Hang Du, Yuxiao Luo, Rui Han, and Ji Li. 2023. "Stress Distribution Prediction of Circular Hollow Section Tube in Flexible High-Neck Flange Joints Based on the Hybrid Machine Learning Model" Materials 16, no. 20: 6815. https://doi.org/10.3390/ma16206815
APA StyleDai, K., Du, H., Luo, Y., Han, R., & Li, J. (2023). Stress Distribution Prediction of Circular Hollow Section Tube in Flexible High-Neck Flange Joints Based on the Hybrid Machine Learning Model. Materials, 16(20), 6815. https://doi.org/10.3390/ma16206815






