Estimating the Slope Safety Factor Using Simple Kinematically Admissible Solutions
Abstract
:1. Introduction
2. Materials and Methods
- ▪ Two equilibrium equations
- ▪ a limit state condition, e.g., Mohr–Coulomb;
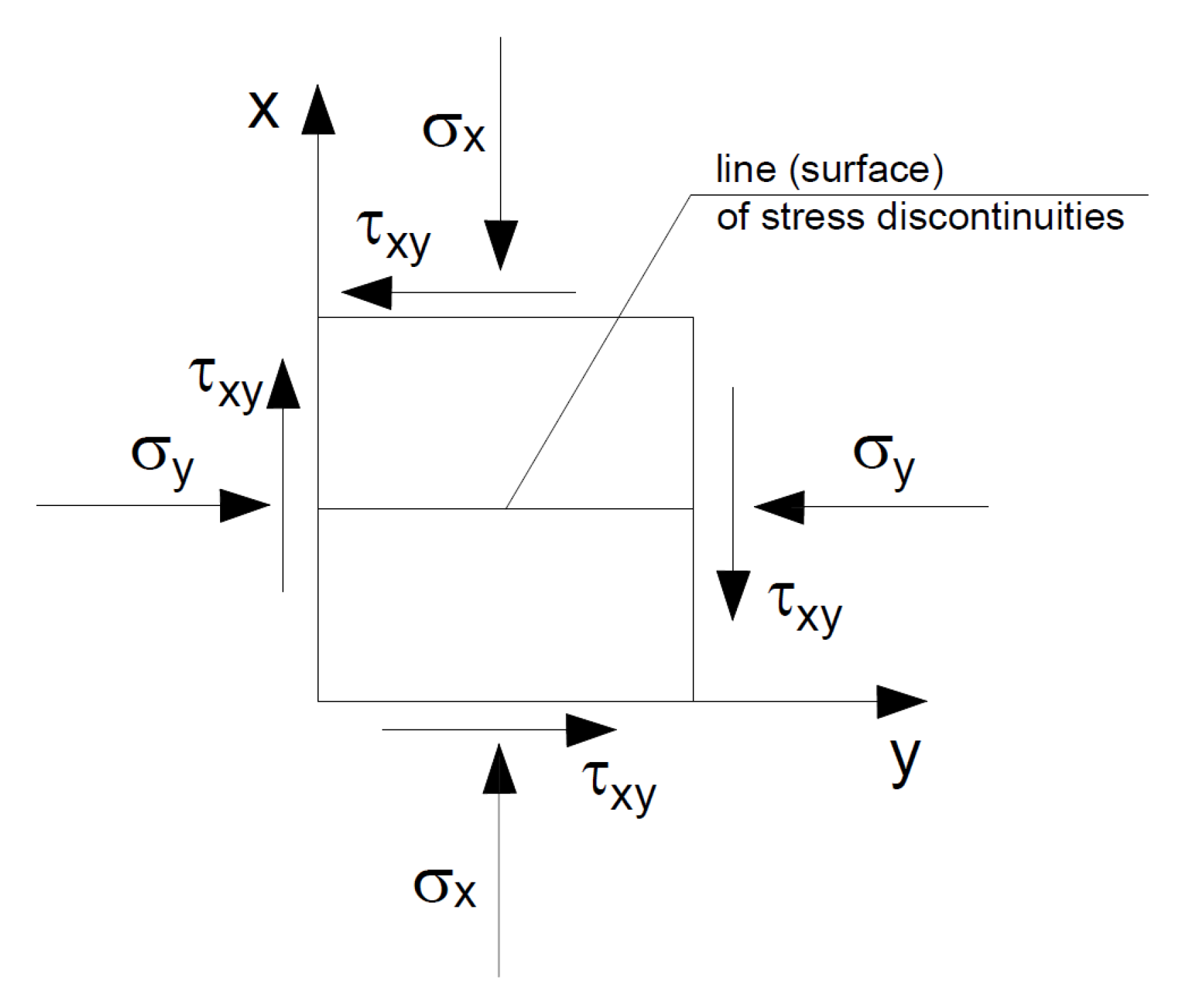
- ▪ The relationships between the components of the stress vector and tensor, which take the form:
- The continuity of the medium must be achieved.
- The rule of flow must be assumed.
- Boundary conditions [30] must be met.
3. Results
3.1. Statically and Kinematically Admissible Solution—Simple Example
3.1.1. Statically Admissible Solution—Lower Bound
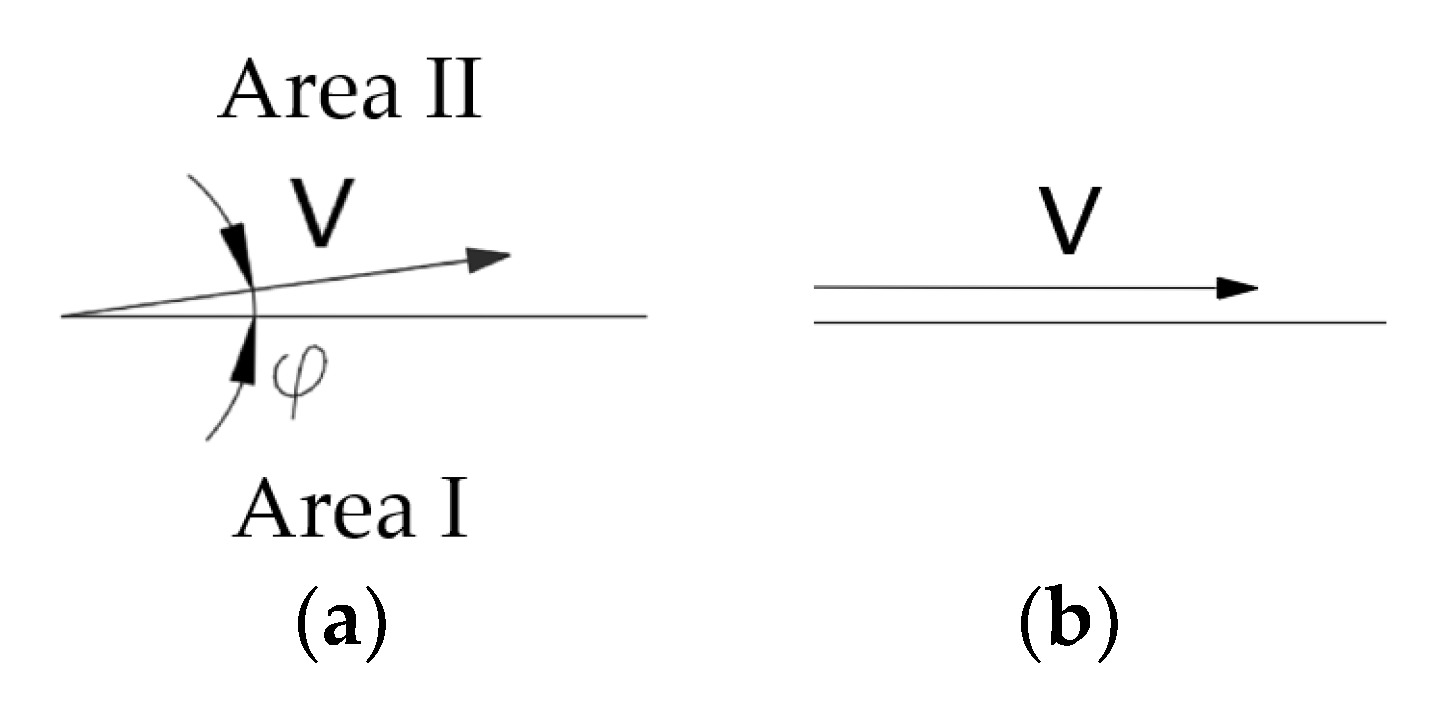
3.1.2. Kinematically Admissible Solution—Associated Flow Rule—Upper Bound
3.1.3. Kinematically Admissible Solution—Non-Associated Flow Rule—Lower Bound
3.2. Simple Kinematically Admissible Solutions for the Slope Stability Problem—Comparison with the Classical Fellenius Method
3.2.1. Slope Stability—The Fellenius Method
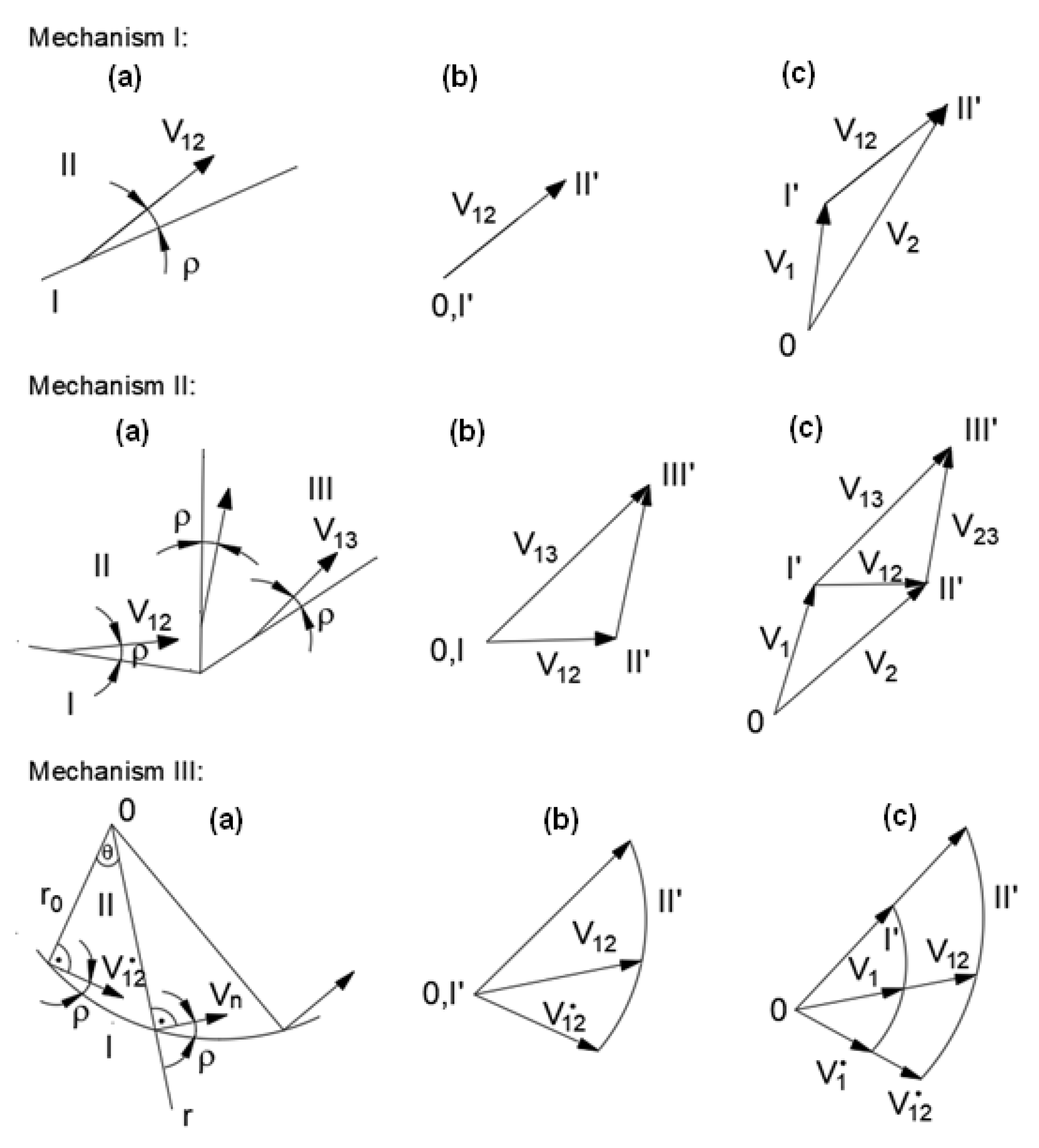
3.2.2. Kinematically Admissible Solution—One Slip Line Associated Flow Rule
3.2.3. Kinematically Admissible Solution—One Slip Line (Non-Associated Flow Rule)
3.2.4. Kinematically Admissible Solution for an Associated Flow Rule
3.2.5. Kinematically Admissible Solution for a Non-Associated Flow Rule
3.2.6. Kinematically Admissible Solution—Associated Flow Rule
3.2.7. The Kinematically Admissible Solution—The Associate Flow Rule
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, C.; Huang, Y.; Zhan, L.-T. SPH-based simulation of flow process of landslide AT Hongao landfill in China. Nat. Hazards 2018, 93, 1113–1126. [Google Scholar] [CrossRef]
- Zhu, C.; Huang, Y. Numerical simulation of earthquake-induced landslide run-out. Jpn. Geotech. Soc. Spec. Publ. 2016, 2, 938–941. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, C. Simulation of flow slides in municipal solid waste dumps using a modified MPS method. Nat. Hazards 2014, 74, 491–508. [Google Scholar] [CrossRef]
- PN-EN 1997-1; Eurocode 7: Geotechnical Design—Part 1: General Rules. SAI: Warsaw, Poland, 1997.
- Bond, A.J.; Shuppener, B.; Scarpelli, G.; Orr, T.L.L. Eurocode 7: Geotechnical Design Worked examples. In Proceedings of the JRC Scientific and Policy Reports, Dublin, Ireland, 13–14 June 2013; pp. 59–63. [Google Scholar]
- Pantelidis, L.; Griffiths, D.V. Integrating Eurocode 7 (load and resistance factor design) using non-conventional factoring strategies in slope stability analysis. Can. Geotech. J. 2004, 51, 208–216. [Google Scholar]
- Länsivaara, T.; Poutanen, T. Slope stability with partial safety factor method. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013. [Google Scholar]
- Papić, J.; Dimitrievski, L.; Prolović, V. Value of partial factors for EC 7 slope stability analysis: Solved “mystery”? In Proceedings of the 3rd International Conference on New Developments in Soil Mechanics and Geotechnical Engineering, Nicosia, North Cyprus, 28–30 June 2012; Near East University: Nicosia, North Cyprus, 2012. [Google Scholar]
- Konderla, H. Stability of slopes and slopes according to Eurocode 7 [Stateczność skarp i zboczy w ujęciu Eurokodu 7—In polish]. Geoinżynieria 2008, 32, 197–204. [Google Scholar]
- Martins, F.F.; Valente, B.D.S.S.; Vieira, C.F.S.; Martins, J.B. Slope Stability Of Embankments. In Proceedings of the ISRM International Symposium, Melbourne, Australia, 19–24 November 2000. [Google Scholar]
- Martins, F.F.; Vieira, C.F.S.; Martins, J.B. Slope Stability of Embankments on Soft Clay. In Application of Numerical Methods to Geotechnical Problems; Springer: Vienna, Austria, 1998. [Google Scholar]
- Agam, M.W.; Hashim, M.H.M.; Murad, M.I.; Zabidi, H. Slope Sensitivity Analysis Using Spencer’s Method in Comparison with General Limit Equilibrium Method. Procedia Chem. 2016, 19, 651–658. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, W.; Zhang, F.; Gao, Y.; Lü, Q. Reliability analysis on permanent displacement of earth slopes using the simplified Bishop method. Comput. Geotech. 2020, 117, 103286. [Google Scholar] [CrossRef]
- Zekaj, L.; Anamali, E.; Capo, E.; Xhemalaj, M. Comparison of Probability Based Design and Eurocode 7 in Slope Stability Analysis. In Proceedings of the International Balkans Conference on Challenges of Civil Engineering, BCCCE, Tirana, Albania, 19–21 May 2011; EPOKA University: Tirana, Albania, 2011. [Google Scholar]
- Rossi, M.; Bacic, M.; Kovacevic, M.S.; Libric, L. Development of Fragility Curves for Piping and Slope Stability of River Levees. Water 2021, 13, 738. [Google Scholar] [CrossRef]
- Nilsen, B. New trends in rock slope stability analyses. Bull. Eng. Geol. Environ. 2000, 58, 173–178. [Google Scholar] [CrossRef]
- Kavvadas, M.; Karlaftis, M.; Fortsakis, P.; Stylianidi, E. Probabilistic analysis in slope stability. In Proceedings of the 17th International Conference on Soil Mechanics and Geotechnical Engineering, Alexandria, Egypt, 5–9 October 2009; IOS Press: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Low, B.K.; Phoon, K.-K. Reliability-based design and its complementary role to Eurocode 7 design approach. Comput. Geotech. 2015, 65, 30–44. [Google Scholar] [CrossRef]
- Budetta, P. Some Remarks on the Use of Deterministic and Probabilistic Approaches in the Evaluation of Rock Slope Stability. Geosciences 2020, 10, 163. [Google Scholar] [CrossRef]
- Florin, B. Comparative Study Of Semi-Probabilistic and Probabilistic Approaches for Slope Stability Assessment. Study Case. Bul. Institutului Politeh. Din Iaşi Univ. Teh. Gheorghe Asachi Din Iaşi 2019, 65, 4. [Google Scholar]
- Daryani, E.; Bahadori, H.; Daryani, K.E. Soil Probabilistic Slope Stability Analysis Using Stochastic Finite Difference Method. Mod. Appl. Sci. 2017, 11, 23–29. [Google Scholar] [CrossRef]
- Bogusz, W. Application of partial factors to geotechnical parameters according to Eurocode 7 in stability calculations using the finite element method [Stosowanie współczynników częściowych do parametrów geotechnicznych według Eurokodu 7 w obliczeniach stateczności metodą elementów skończonych—In polish]. Acta Sci. Pol. Archit. 2013, 3, 12. [Google Scholar]
- Maciejewski, J.; Jarzębowski, A. Application of kinematically admissible solution to passive earth pressure problems. Int. J. Geomech. 2004, 4, 127–136. [Google Scholar] [CrossRef]
- Izbicki, R.; Mróz, Z. Limit load methods in soil and rock mechanics [Metody nośności granicznej w mechanice gruntów i skał—In Polish]; Polish Scientific Publishers PWN: Warsaw, Poland, 1976. [Google Scholar]
- Trąmpczyński, W. Automation of Mechanical Excavation of Soil Machine Tools; IPPT PAN: Warsaw, Poland, 1996. (In Polish) [Google Scholar]
- Trąmpczyński, W.; Szyba, D. Kinematically admissible solutions for the incipient stage of earth moving processes in the cases of various pushing wall forms. Eng. Trans. 1991, 39, 123–134. [Google Scholar]
- Jarzębowski, A.; Maciejewski, J.A.; Szyba, D.; Trąmpczyński, W. The optimisation on heavy machine tools filling proces and tool shapes. In Proceedings of the 12th International Symposium on Automation and Robotics in Construction (ISARC), Warsaw, Poland, 30 May–1 June 1995. [Google Scholar]
- Maciejewski, J.; Jarzębowski, A.; Trąmpczyński, W. Study of the efficiency of the digging process using the model of excavator bucket. J. Terr. 2003, 40, 221–233. [Google Scholar] [CrossRef]
- Trąmpczyński, W.; Maciejewski, J. On the kinematically admissible solutions for soil-tool interaction description in the case of heavy machine working processes. In Proceedings of the 5th ISTVS European Conference, Budapest, Hungary, 4–6 September 1991. [Google Scholar]
- Trąmpczyński, W.; Sokołowski, K. Introduction to Soil Mechanics [Wstęp do Mechaniki Gruntów—In polish]; Publishing House of the Kielce University of Technology: Kielce, Poland, 2000. [Google Scholar]
- Zhao, L.-H.; Li, L.; Yang, F.; Luo, Q.; Liu, X. Upper bound analysis of slope stability with nonlinear failure criterion based on strength reduction technique. J. Cent. South Univ. 2010, 17, 836–844. [Google Scholar] [CrossRef]
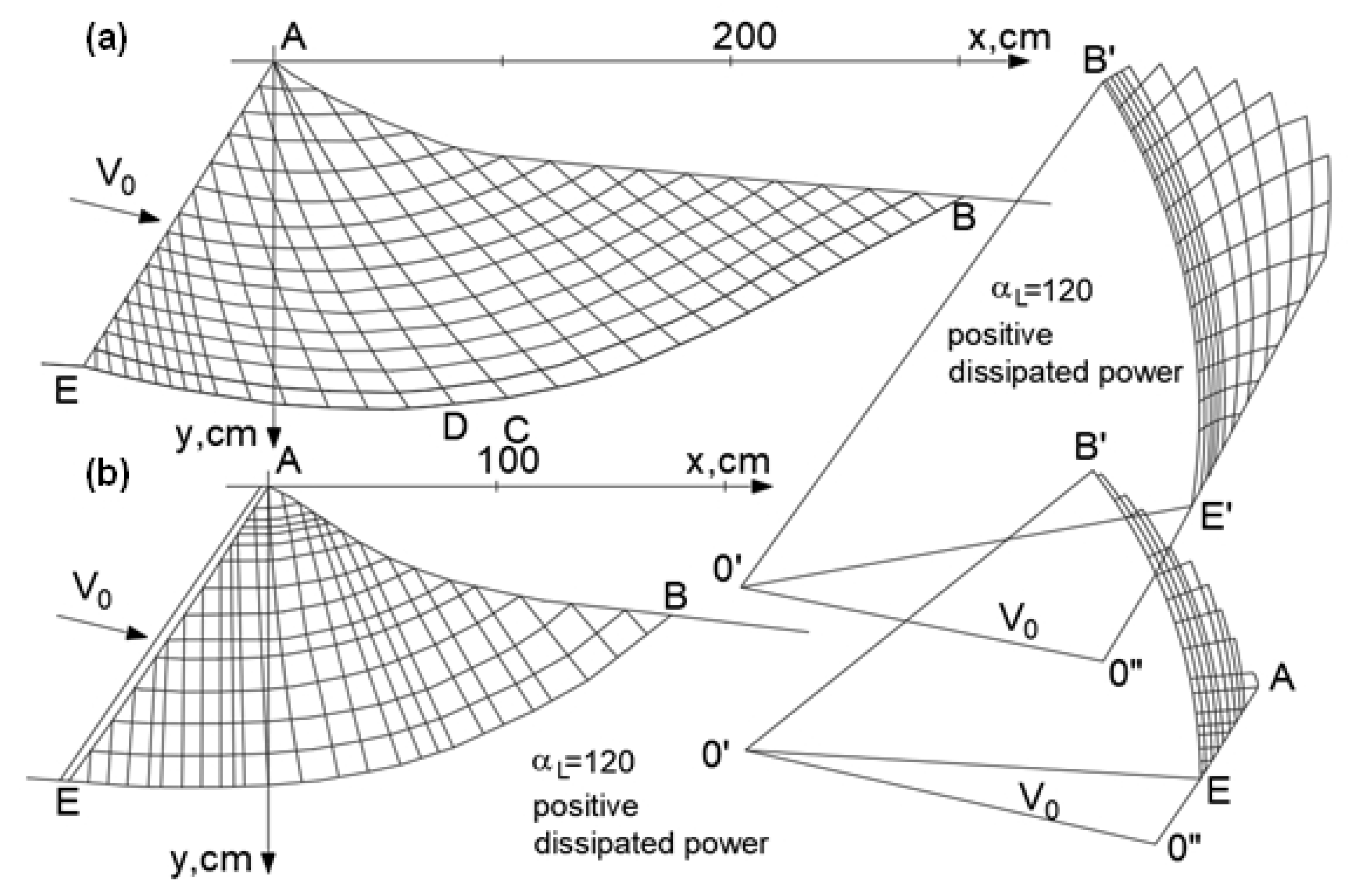
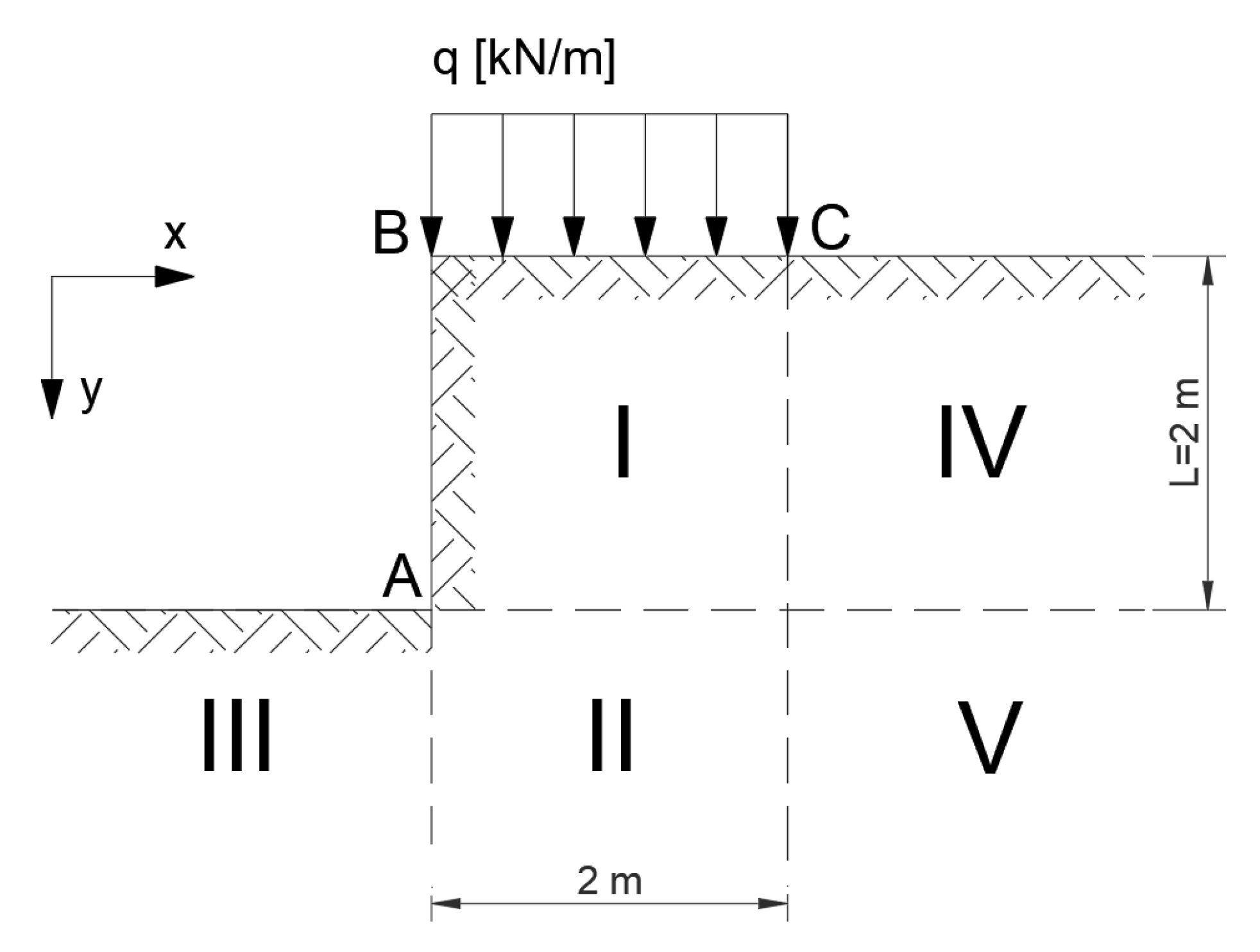

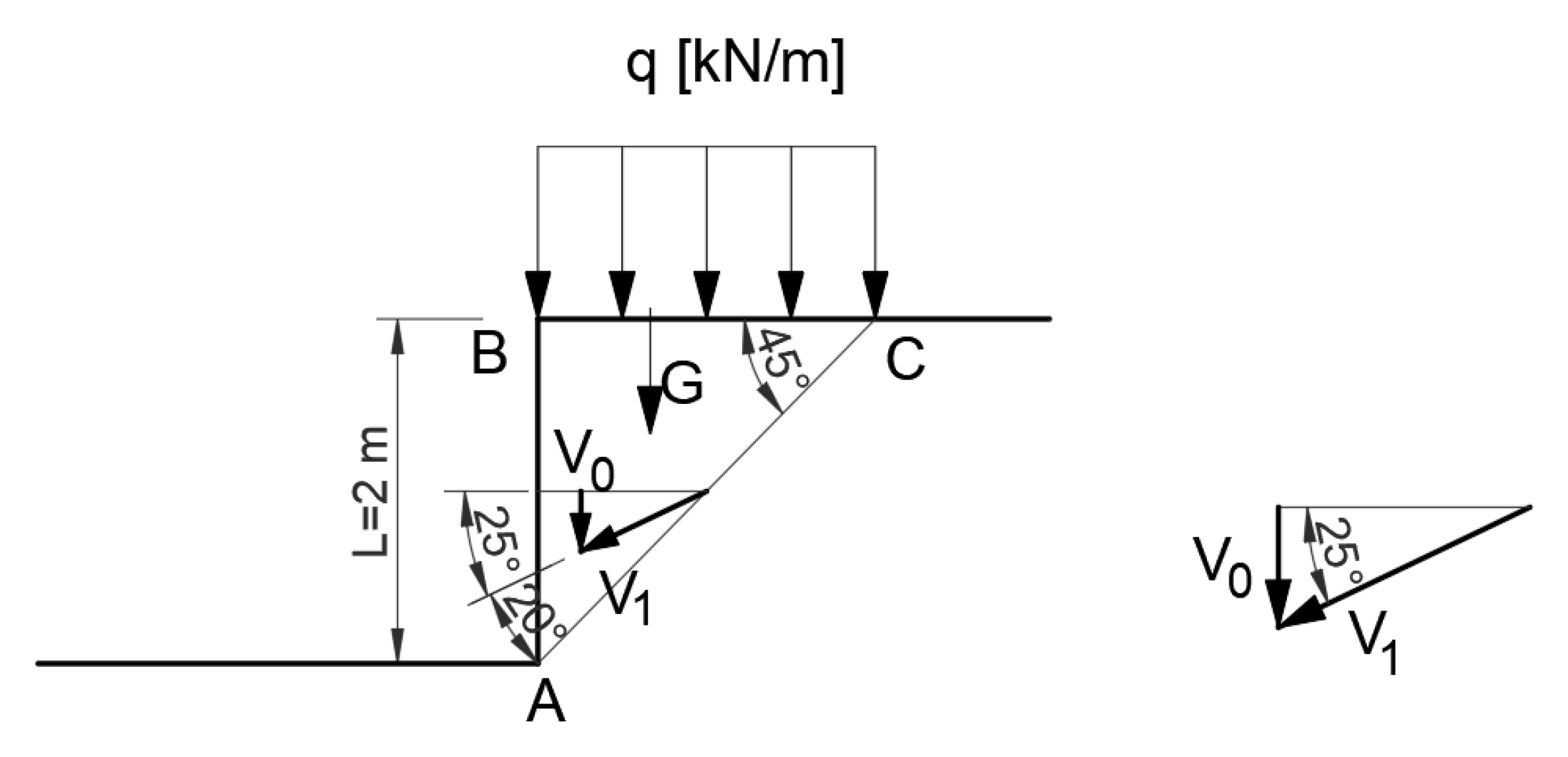

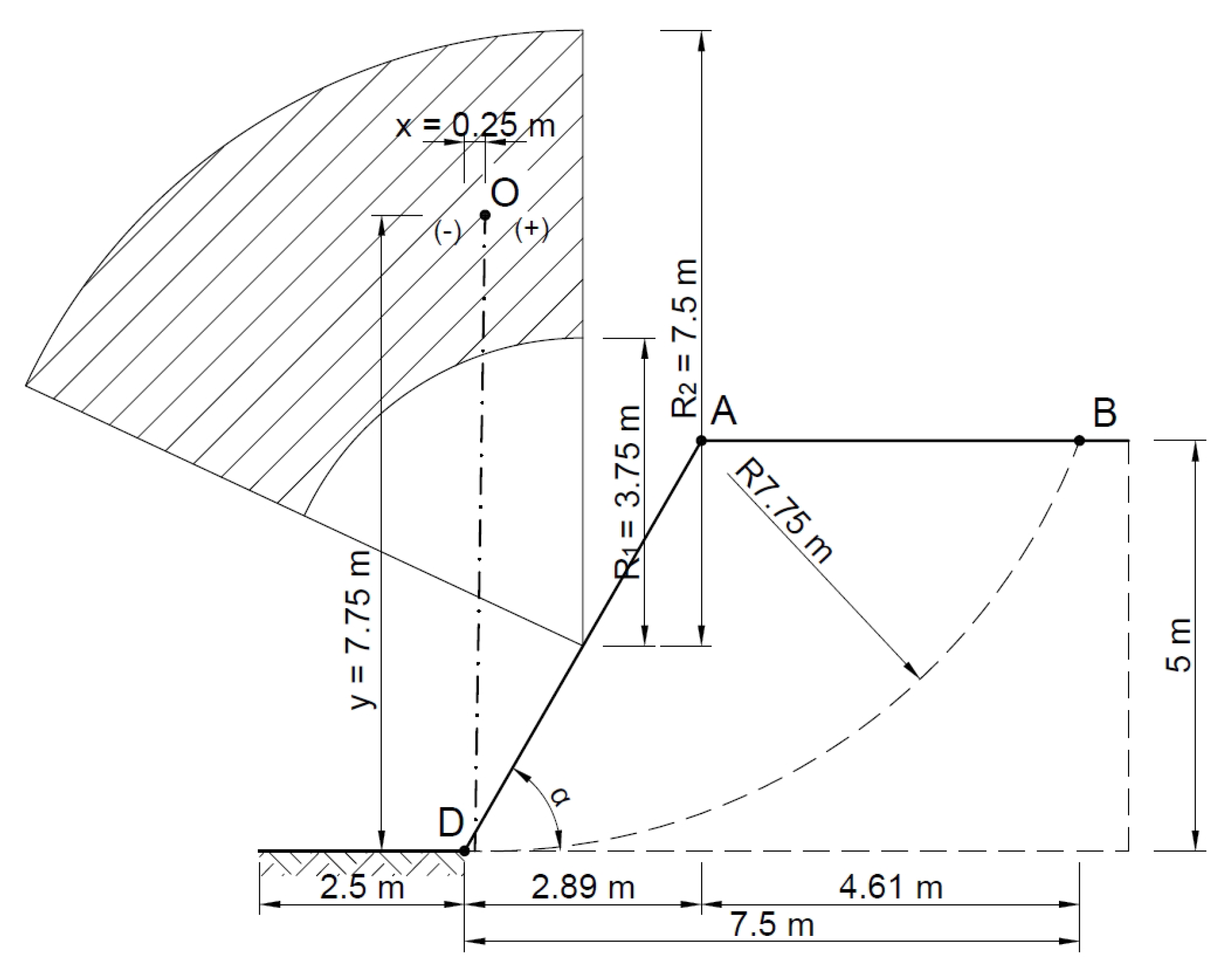
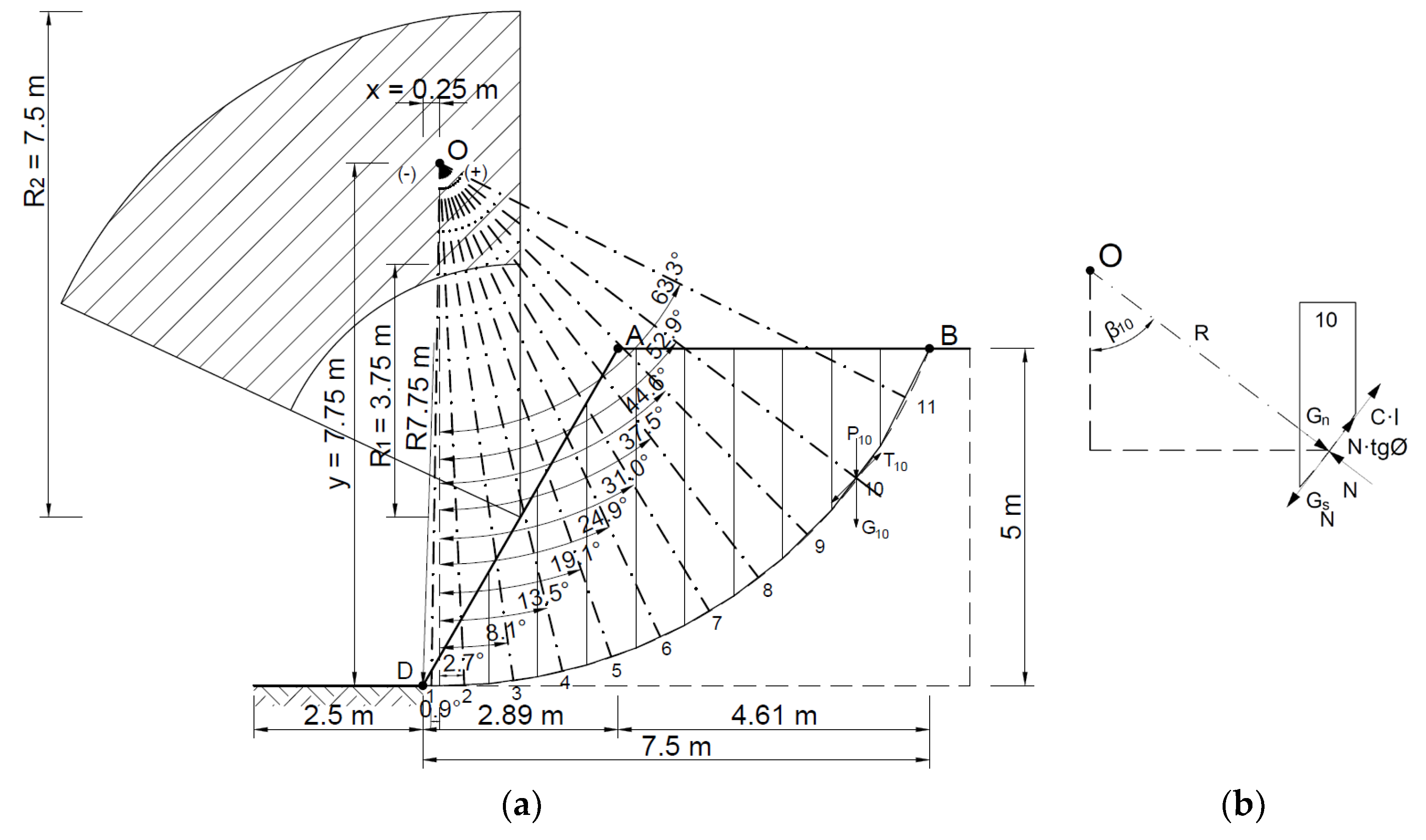
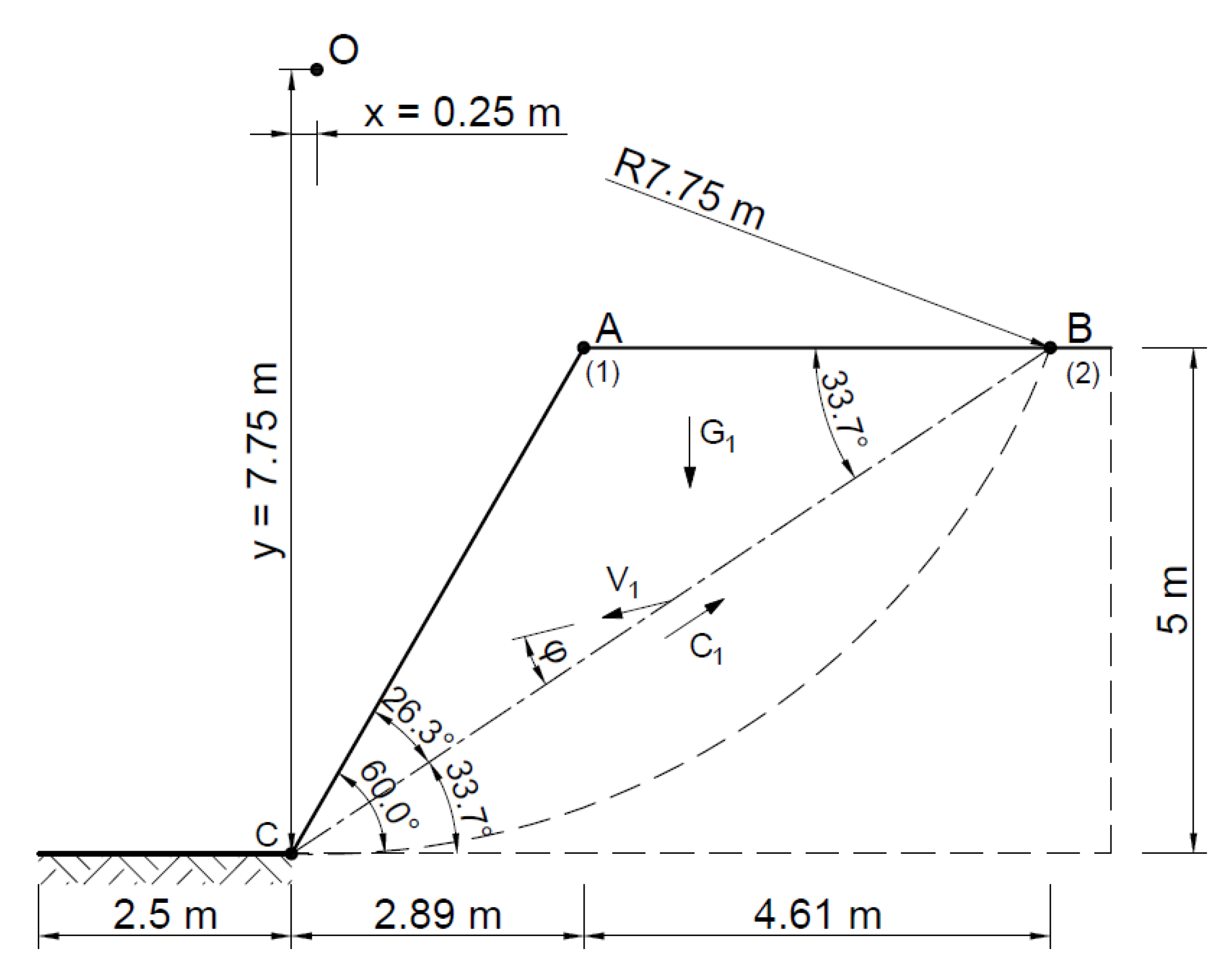
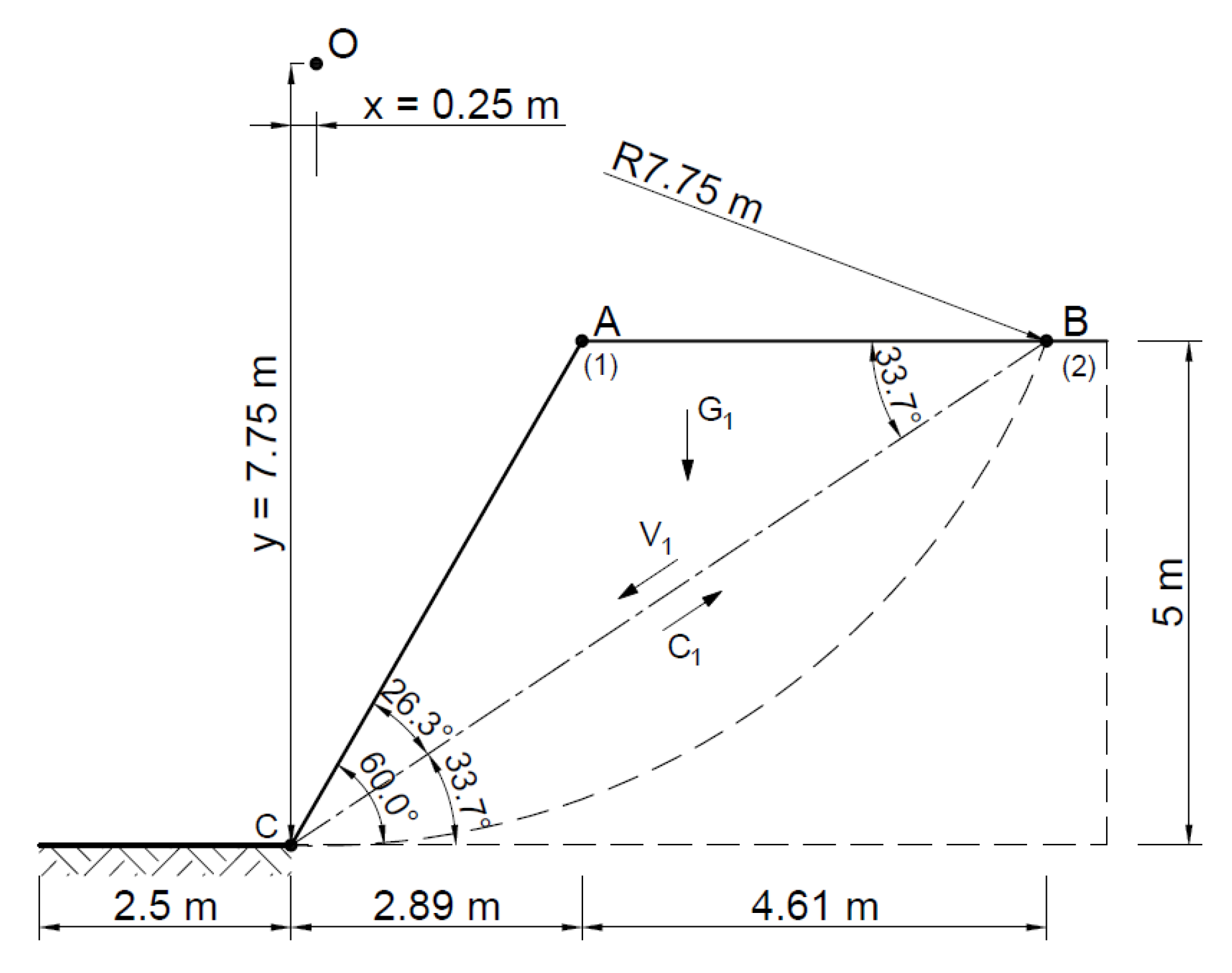
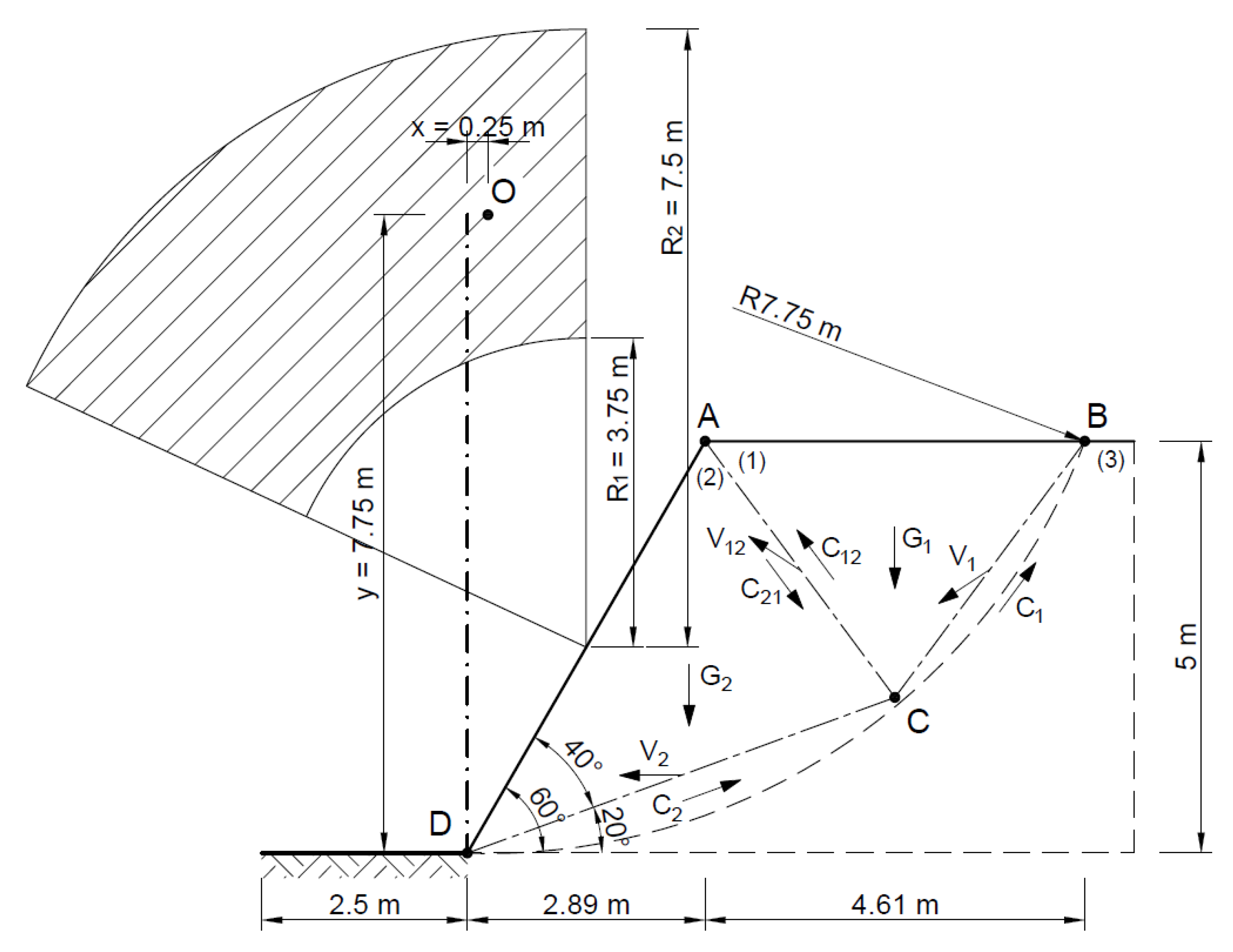
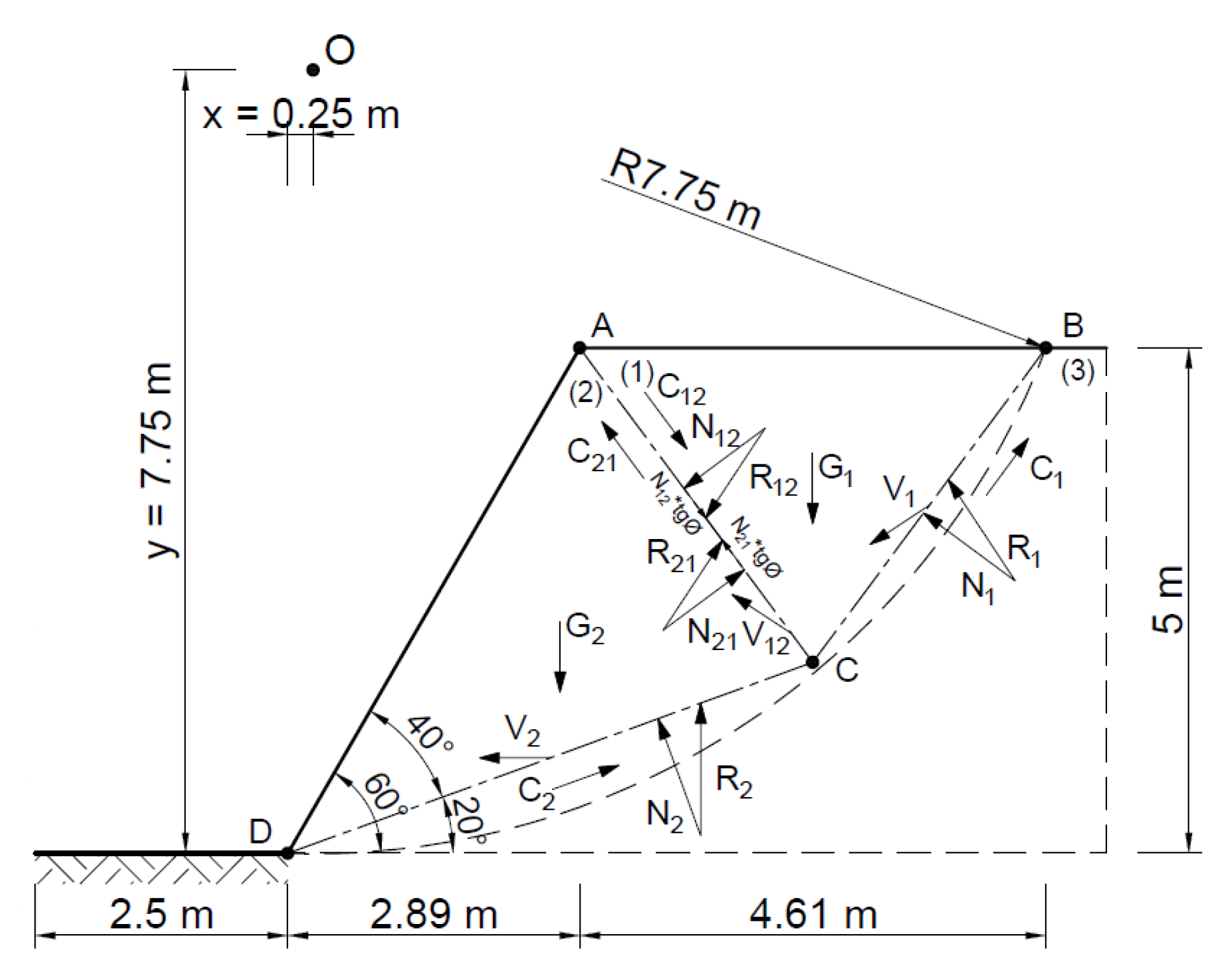
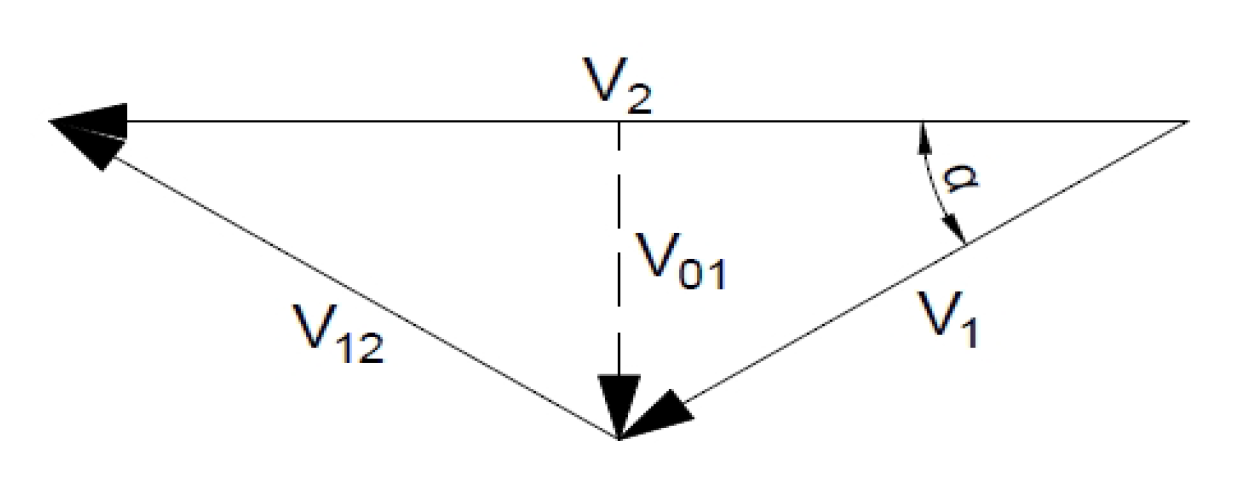
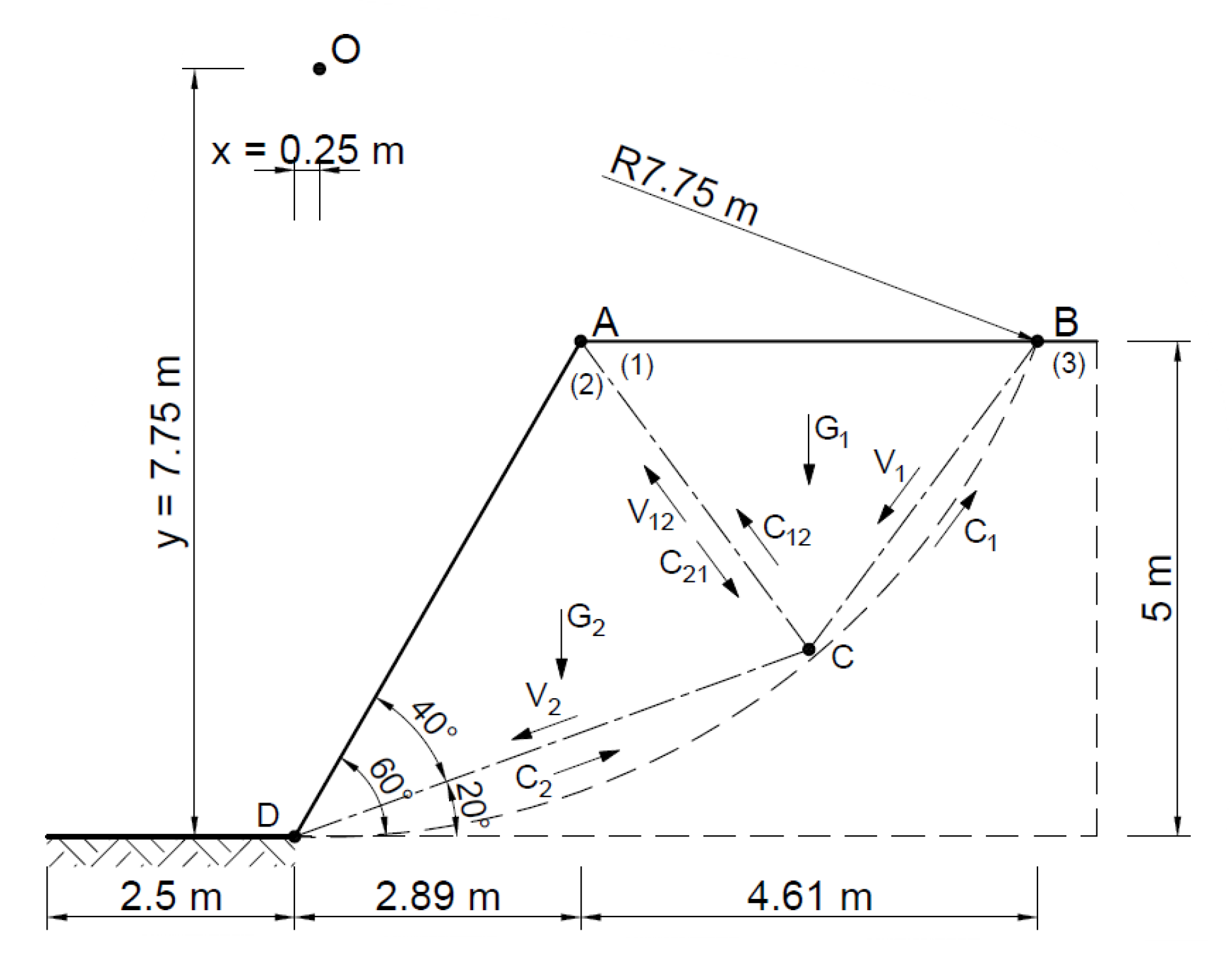
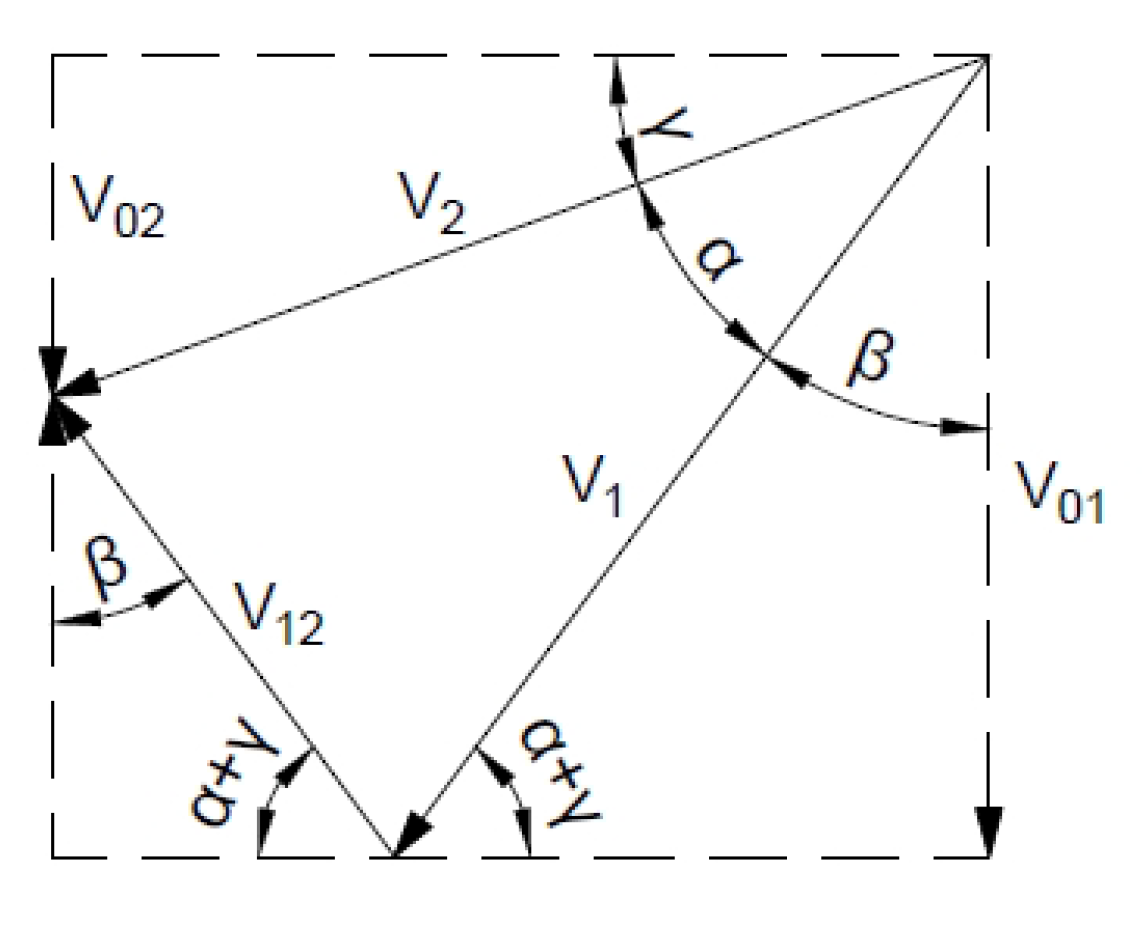
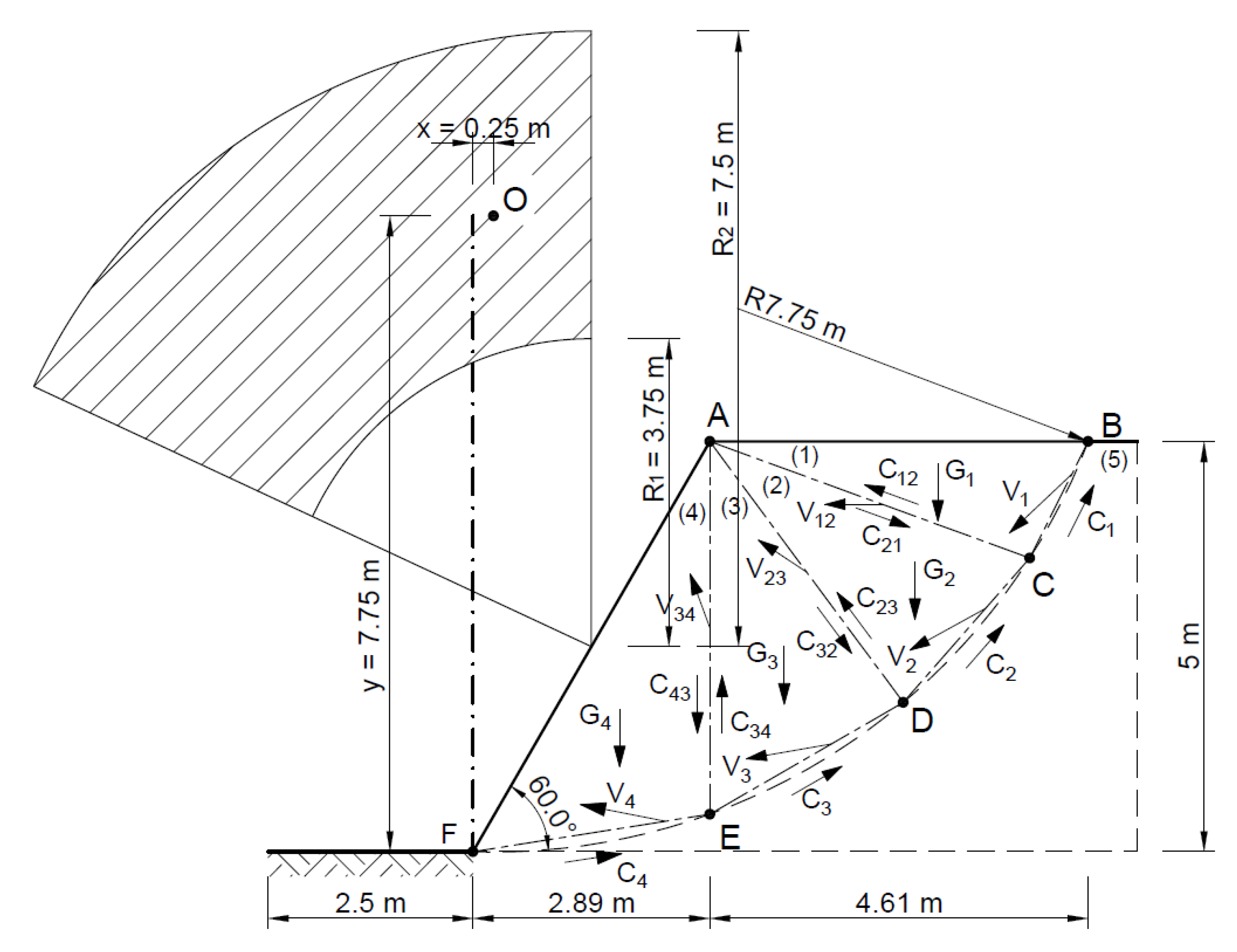
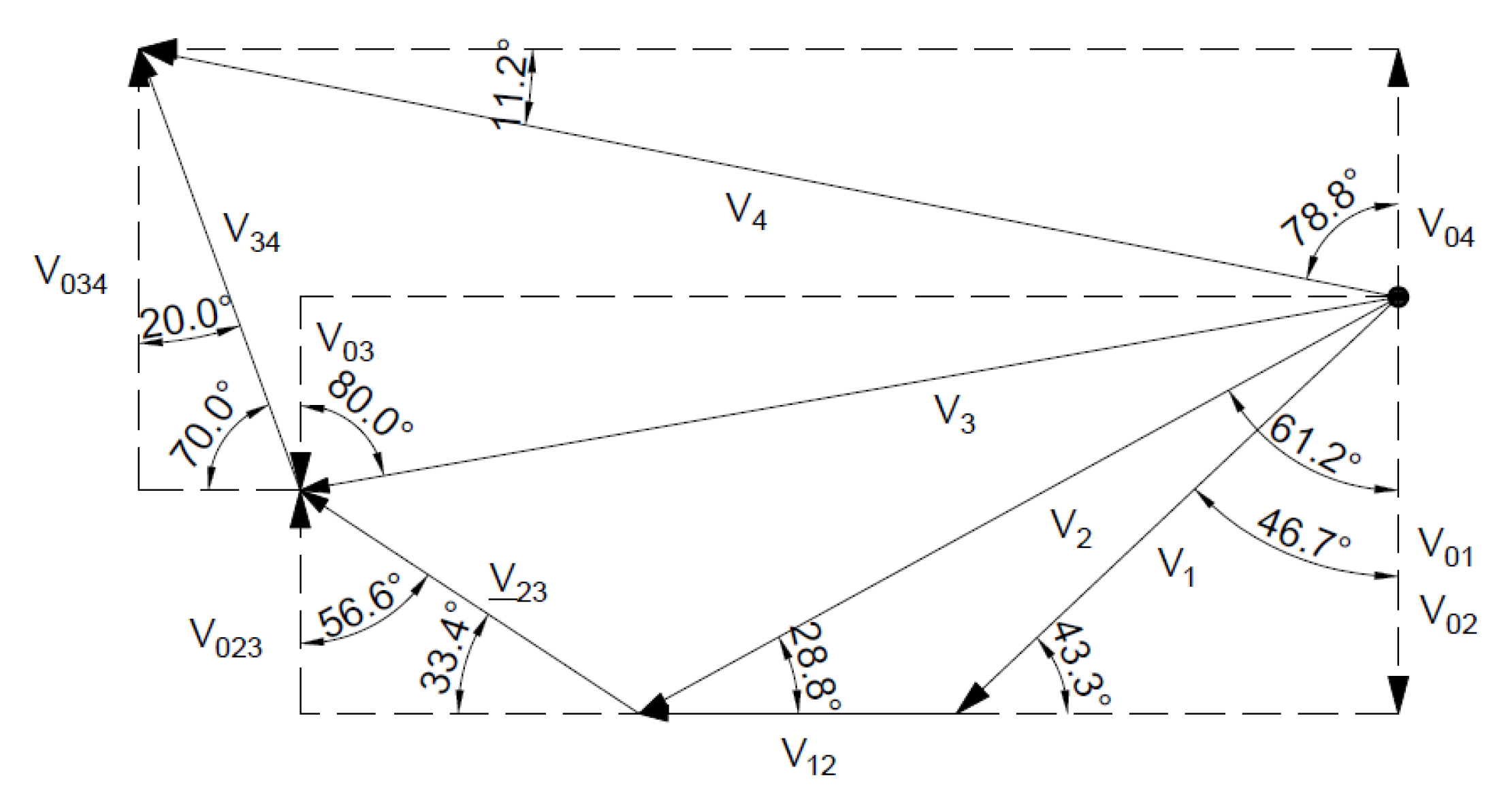
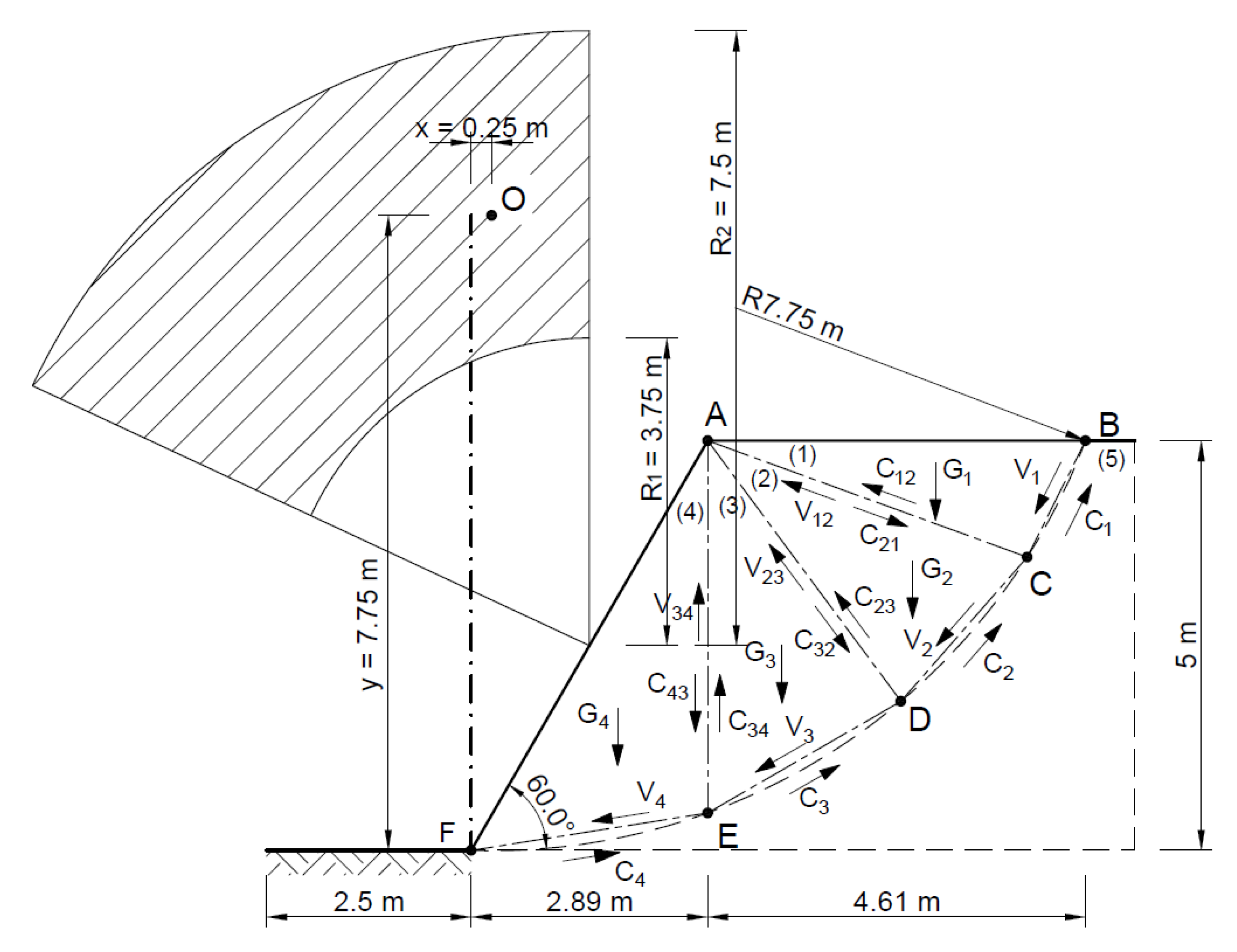

| Method | A Statically Admissible Solution—Lower Bound | Associated Flow Rule—Upper Bound | Non-Associated Flow Rule—Upper Bound |
|---|---|---|---|
| Safety factor | 1.33 | 2.93 | 1.86 |
| Block | Area Pi (m2) | Side lengths Li (m) | γ (kN) | Tangential Component Li (kN) | ||
|---|---|---|---|---|---|---|
| ABC | 11.5 | |AB| = 4.6 | |AC| = 5.8 | |BC| = 9.0 | 248 | |BC| = 180 kN |
| Block | Area Pi (m2) | Side Lengths Li (m) | γ (kN) | Tangential Component Li (kN) | ||
|---|---|---|---|---|---|---|
| ABC | 7.17 | |AB| = 4.61 | |AC| = 3.87 | |BC| = 3.87 | 154.2 | |BC|= 77.4 kN |
| ACD | 10.25 | |AD| = 5.77 | |AC| = 3.87 | |CD| = 5.52 | 220.4 | |CD|= 110.4 kN |
| Block | Field Pi (m2) | Side Lengths Li (m) | γ (kN) | Tangential Component Li (kN) | ||
|---|---|---|---|---|---|---|
| ABC | 3.27 | |AB| = 4.61 | |AC| = 4.15 | |BC| = 1.59 | 70.3 | c|AC| = 83.0 kN c|BC| = 31.8 kN |
| ACD | 4.53 | |AC| = 4.15 | |AD| = 3.96 | |CD| = 2.34 | 97.4 | c|AD| = 79.2 kN c|CD| = 46.8 kN |
| ADE | 5.36 | |AD| = 3.96 | |AE| = 4.54 | |DE| = 2.72 | 115.2 | c|AE| = 90.8 kN c|DE| = 54.4 kN |
| AEF | 6.56 | |AE| = 4.54 | |AF| = 5.77 | |EF| = 2.92 | 141.0 | c|EF| = 58.4 kN c|AE| = 90.8 kN |
| Used Method | Safety Factor | |
|---|---|---|
| Fellenius Method | ||
| Kinematically admissible solution—one block | non-associated flow rule | |
| associated flow rule | ||
| Kinematically admissible solution—two blocks | non-associated flow rule | |
| associated flow rule | ||
| Kinematically admissible solution—four blocks | non-associated flow rule | |
| associated flow rule | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bacharz, K.; Bacharz, M.; Trąmpczyński, W. Estimating the Slope Safety Factor Using Simple Kinematically Admissible Solutions. Materials 2023, 16, 7074. https://doi.org/10.3390/ma16227074
Bacharz K, Bacharz M, Trąmpczyński W. Estimating the Slope Safety Factor Using Simple Kinematically Admissible Solutions. Materials. 2023; 16(22):7074. https://doi.org/10.3390/ma16227074
Chicago/Turabian StyleBacharz, Kamil, Magdalena Bacharz, and Wiesław Trąmpczyński. 2023. "Estimating the Slope Safety Factor Using Simple Kinematically Admissible Solutions" Materials 16, no. 22: 7074. https://doi.org/10.3390/ma16227074





