Numerical Modeling of Residual Stresses and Fracture Strengths of Ba0.5Sr0.5Co0.8Fe0.2O3−δ in Reactive Air Brazed Joints
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Production and Characterization
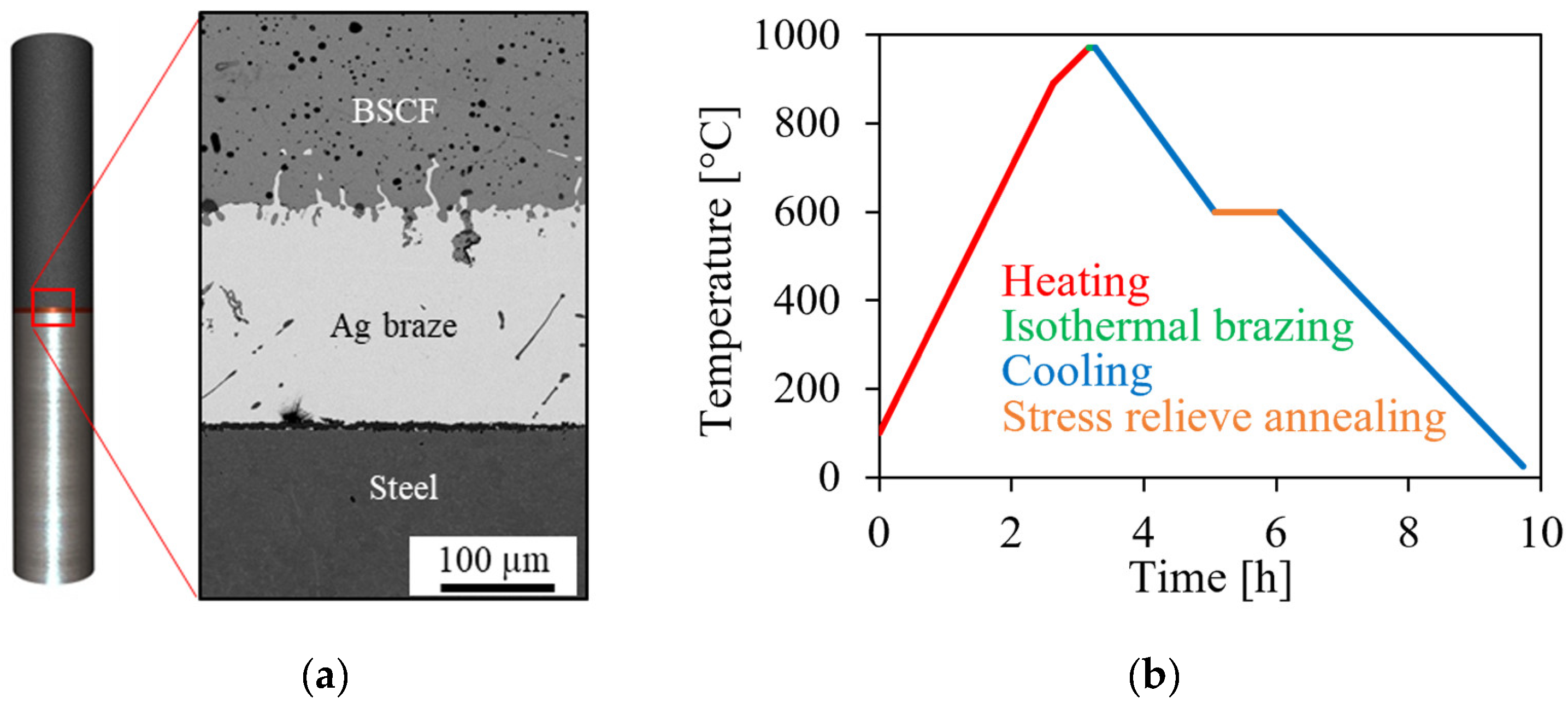
2.1.1. Brazed Joint Sample
2.1.2. Wetting Sample
2.1.3. TPP Reference Samples
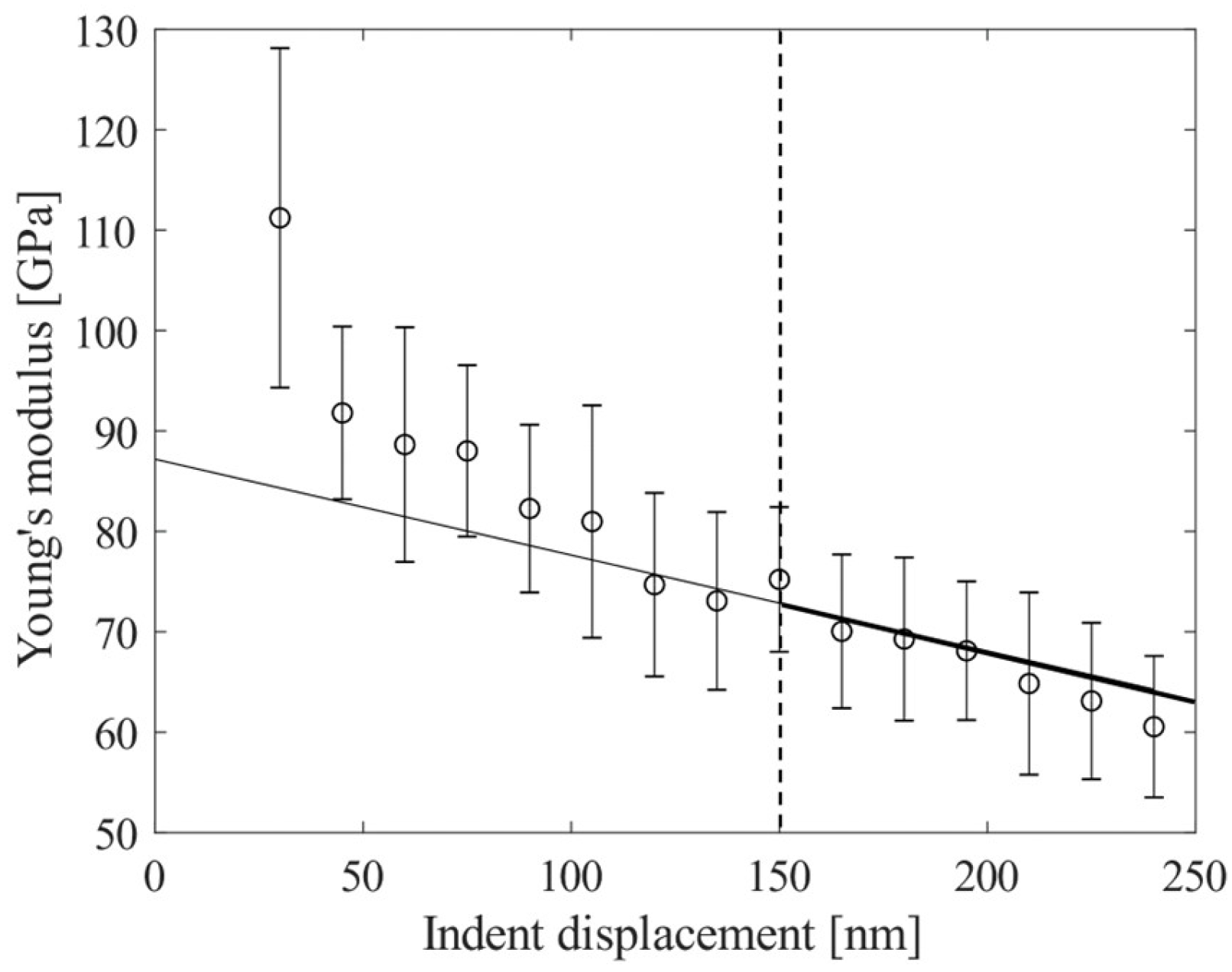
2.1.4. Nanoindentation
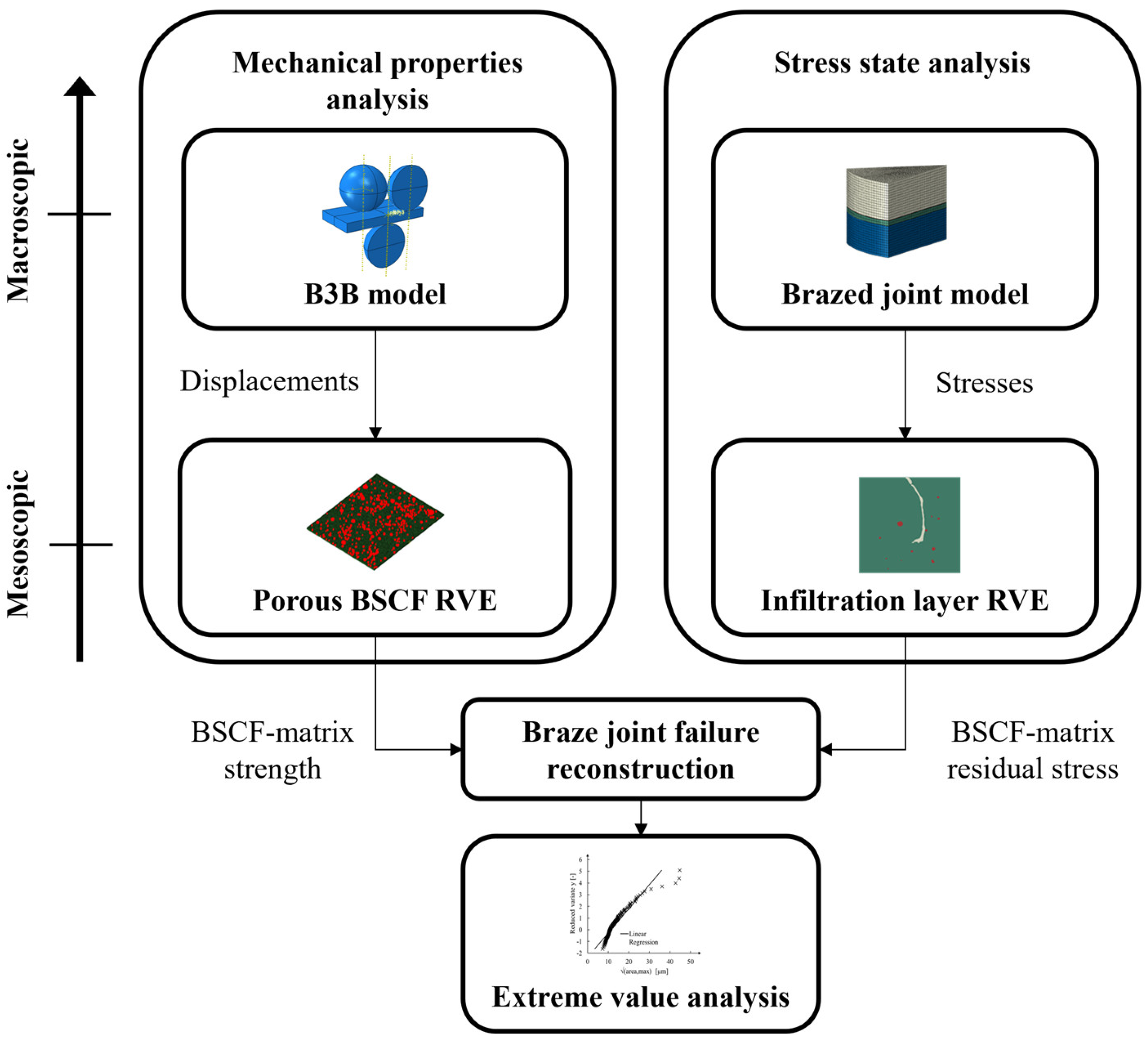
2.2. Numerical Methods
2.2.1. Multiscale Modeling
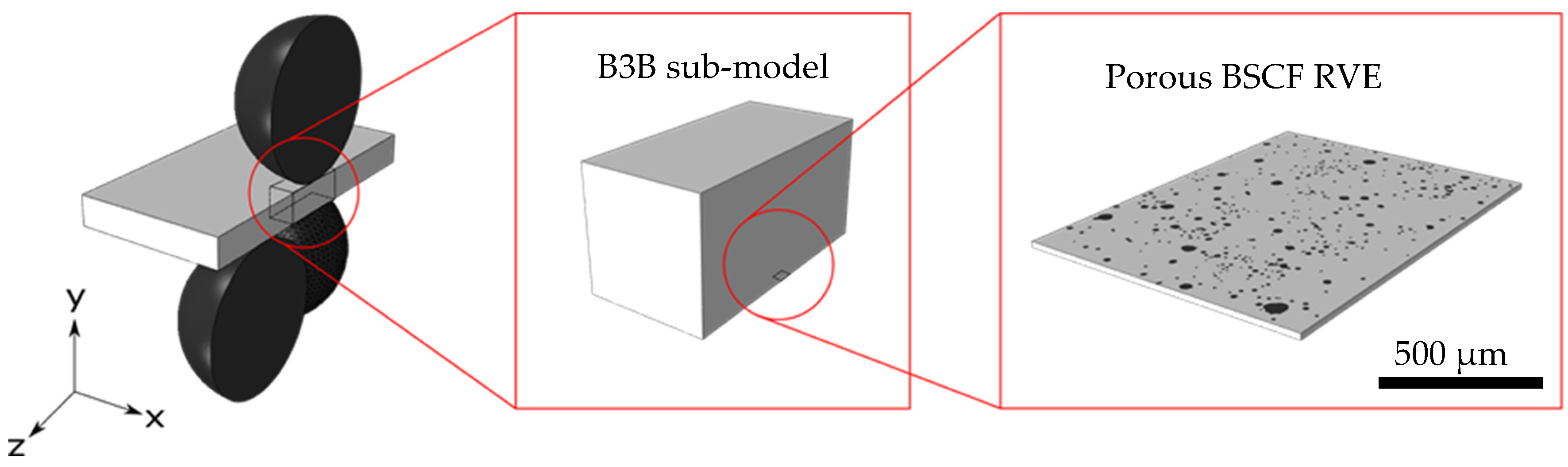
2.2.2. Generation of Representative Volume Elements
2.2.3. Ball-on-Three-Balls Virtual Experiment
- The displacement of the single ball on the top side was calibrated using the experimentally determined fracture stresses. Therefore, the displacement in the B3B macroscopic model was varied until the maximum principal stress obtained in the B3B sub-model was equal to the experimental value.
- The displacements of the calibrated B3B sub-model were mapped to the BSCF RVE as described above.
- The maximum principal stress value within the BSCF matrix was extracted from the BSCF RVE and considered a strength of the BSCF matrix.
2.2.4. Extreme Value Analysis
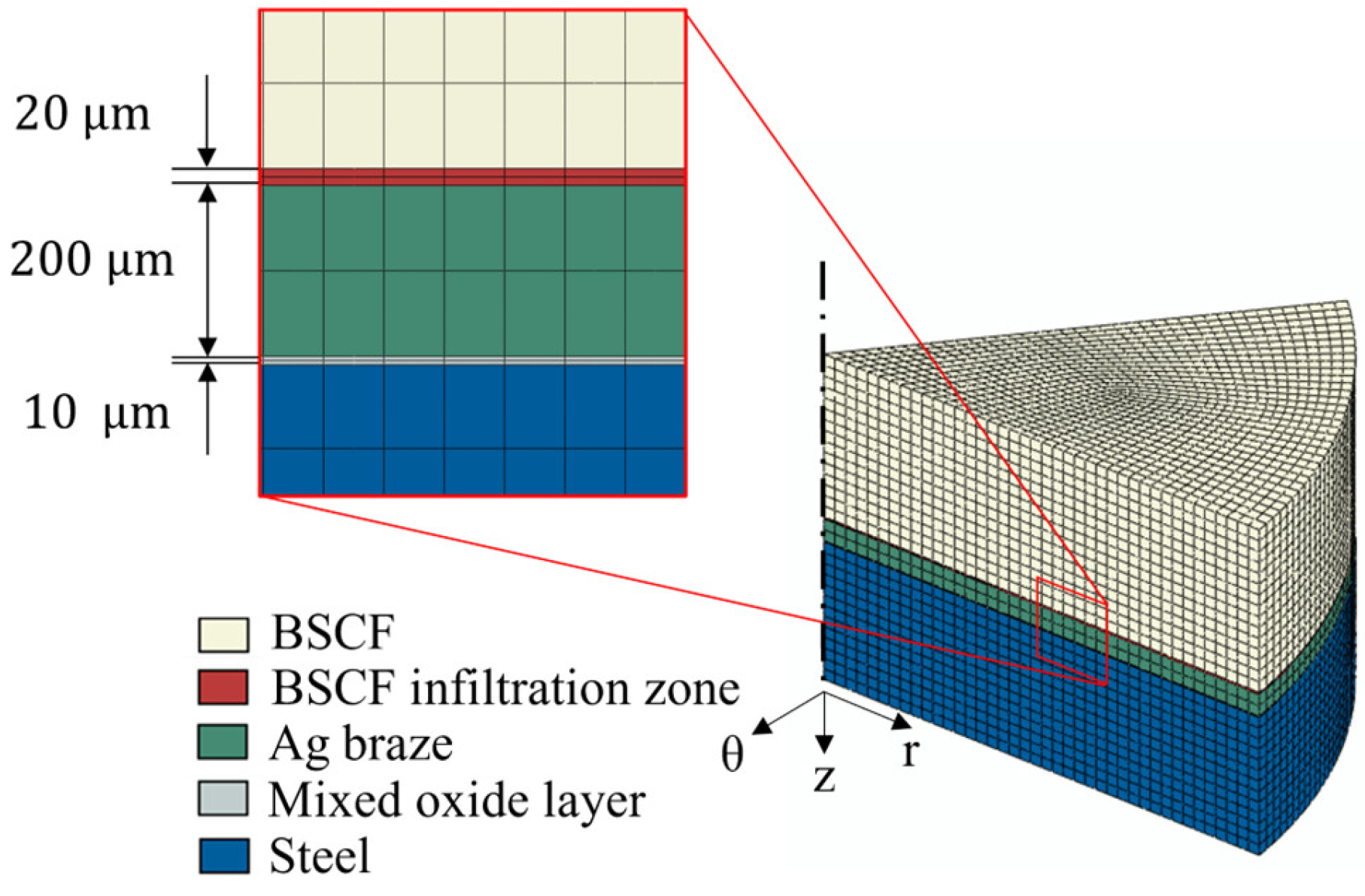
2.2.5. Brazed Joint Modeling
3. Results and Discussion
3.1. Experimental Determination of Model Parameters
3.1.1. Infiltration Zone Microstructural Analysis
3.1.2. BSCF and TPP Material Properties
3.2. Numerical Results
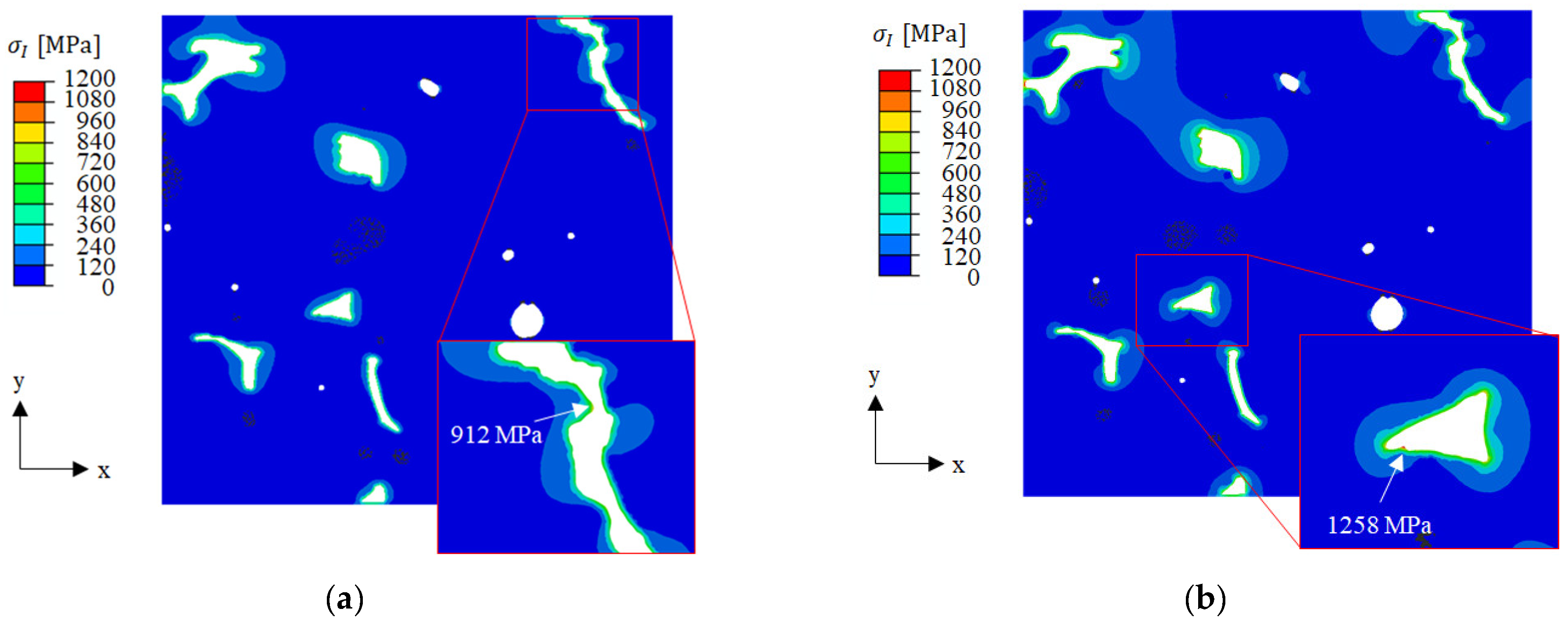
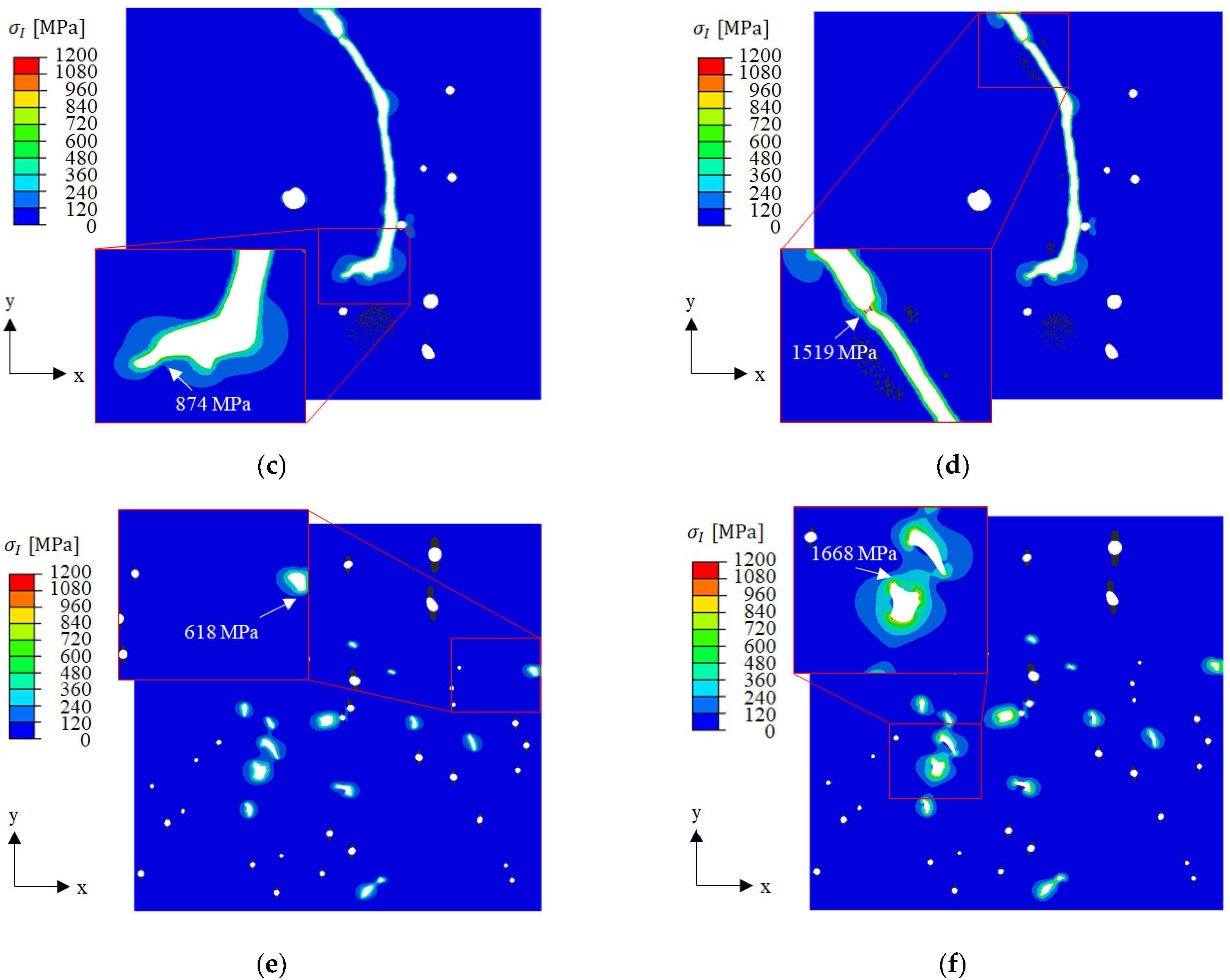
3.2.1. BSCF Bulk Material Strength
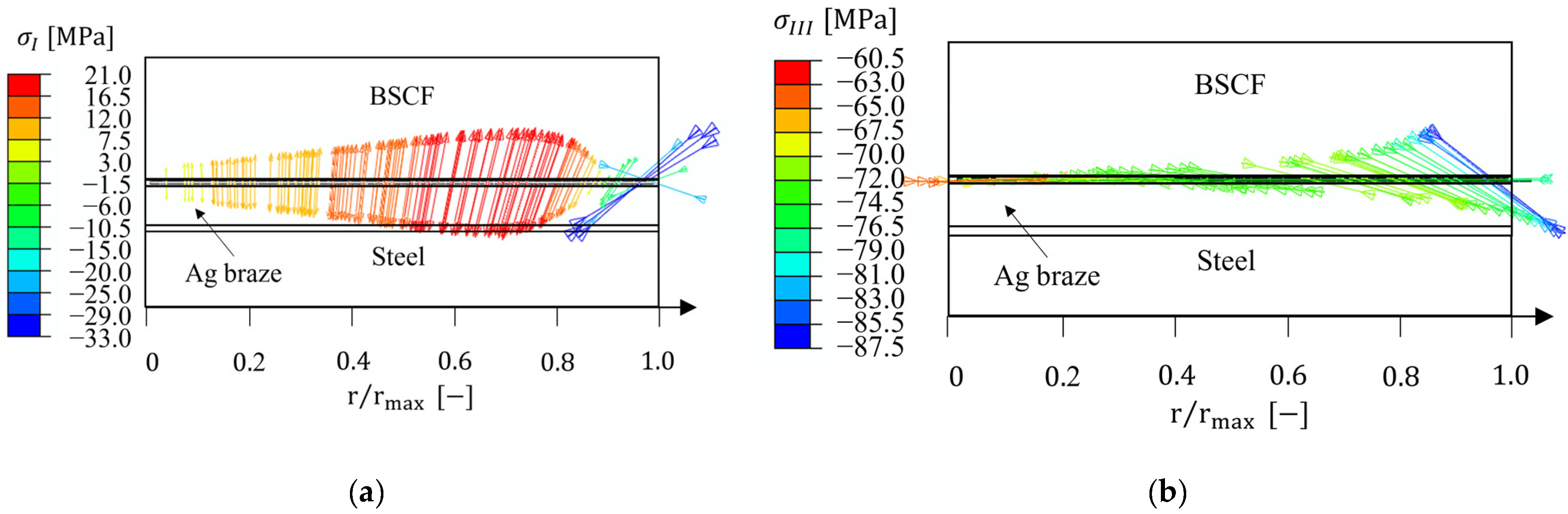
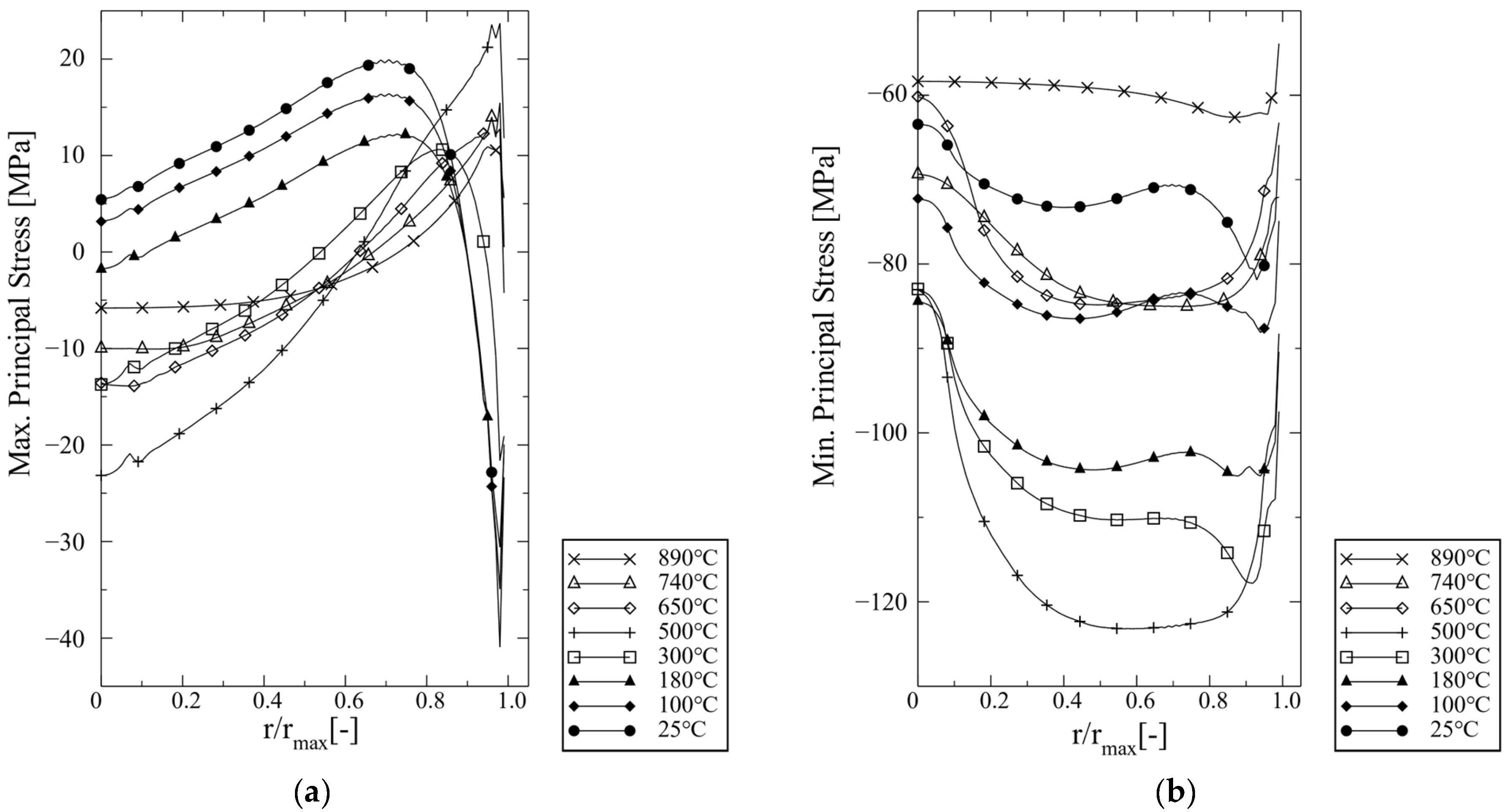
3.2.2. Macroscopic Internal Stresses in Brazed Joint
3.2.3. Thermally Induced Stresses in BSCF
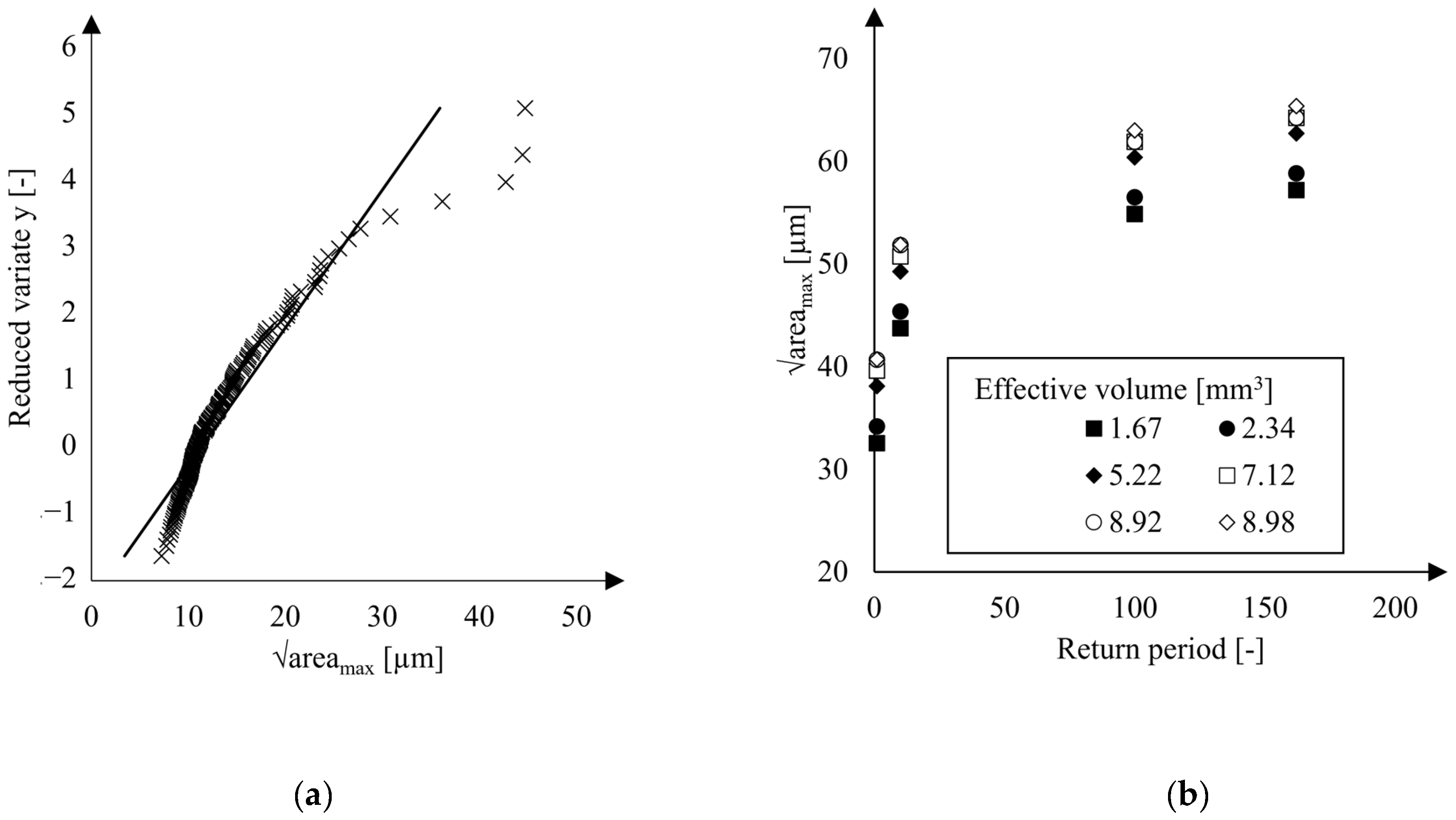
3.2.4. Extreme Value Analysis
4. Conclusions and Outlook
- Microstructural residual stresses in BSCF-steel joints and temperature-dependent critical stress of bulk BSCF were predicted through the hierarchical multiscale finite element model.
- Mechanical and physical material properties of precipitating triple point phases (TPP) associated with BSCF damage, which were not available in existing literature, were effectively obtained through nanoindentation and dilatometry.
- Mesoscale RVE simulations were used to reconstruct the failure mechanisms. Two material models of TTPs were explored, including multi-phase TPP (CuO, Co3O4, CoO, and BSCF in equal parts) and single-phase TPP (CuO only).
- Mesoscale cooling simulations revealed that small single-phase TPPs are more likely to cause damage in BSCF compared to larger single-phase TPPs or multi-phase TPPs. Damage in the BSCF occurs during the cooling phase after brazing, typically at temperatures between 100 °C and room temperature. It was observed that crack initiation sites are consistently located at BSCF/TPP phase boundaries.
- To statistically validate the temperature-dependent BSCF fracture stresses, an extreme value analysis based on the weakest link theory was conducted. This analysis revealed that the calibrated fracture strengths obtained from the inverse FEA were underestimated, likely due to limited microstructural information derived directly from a single micrograph.
- Future improvements in the brazing process should focus on promoting the formation of advantageous multi-phase precipitations in the BSCF matrix, thereby enhancing its structural integrity. It is suggested that future work include a 3D microstructure reconstruction to map spatial correlations of precipitation phases and gain better knowledge of the fracture behavior and damage mechanisms of BSCF.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BSCF | Ba0.5Sr0.5Co0.8Fe0.2O3−δ—Oxygen transport membrane material |
| TPP | Triple point phase |
| RAB | Reactive Air Brazing |
| B3B | ball-on-three-balls (test) |
| 2D/3D | Two dimensional/three dimensional |
| RVE | representative volume element |
| FEA | finite element analysis |
| SEM | Scanning electron microscope |
Mathematical Symbols
| critical defect size according to Murakami | |
| linear regression coefficient | |
| maximal Feret diameter in the whole image | |
| Feret diameter of a pore | |
| cumulative distribution of maximum pore sizes | |
| estimated height of the inspected micrographs | |
| number of micrographs | |
| Weibull modulus | |
| total number of micrographs inspected | |
| number of finite elements | |
| relative radial position of in a brazed joint | |
| total inspected area of micrographs | |
| return period | |
| maximum principal stress in the volume element i | |
| maximal principal stress in the whole model | |
| medium principal stress in the volume element i | |
| minimal principal stress in the volume element i | |
| inspection volume | |
| effective volume | |
| volume of each finite element | |
| reduced variate |
References
- Singh, M.; Ohji, T.; Asthana, R.; Mathur, S. Ceramic Integration and Joining Technologies: From Macro to Nanoscale; Singh, M., Ed.; Online-Ausg; Wiley-American Ceramic Society: Hoboken, NJ, USA, 2011; ISBN 9781283282666. [Google Scholar]
- Srivastava, A.K.; Sharma, A. Advances in Joining and Welding Technologies for Automotive and Electronic Applications. Materials 2017, 5, 7–13. [Google Scholar] [CrossRef]
- Moret, F.; Eustathopolous, N. Ceramic to metal direct brazing. J. Phys. IV Fr. 1993, 03, C7-1043–C7-1052. [Google Scholar] [CrossRef]
- Weil, K.S.; Kim, J.Y.; Hardy, J.S. Reactive Air Brazing: A Novel Method of Sealing SOFCs and Other Solid-State Electrochemical Devices. Electrochem. Solid-State Lett. 2005, 8, A133. [Google Scholar] [CrossRef]
- Darsell, J.T.; Weil, K.S. The effect of palladium additions on the solidus/liquidus temperatures and wetting properties of Ag-CuO based air brazes. J. Alloys Compd. 2007, 433, 184–192. [Google Scholar] [CrossRef]
- Friant, J.R.; Meier, A.; Darsell, J.T.; Weil, K.S. Transitions in Wetting Behavior Between Liquid Ag-CuO Alloys and Al2O3 Substrates. J. Am. Ceram. Soc. 2012, 95, 1549–1555. [Google Scholar] [CrossRef]
- Kim, J.Y.; Hardy, J.S.; Scott Weil, K. Effects of CuO Content on the Wetting Behavior and Mechanical Properties of a Ag-CuO Braze for Ceramic Joining. J. Am. Ceram. Soc. 2005, 88, 2521–2527. [Google Scholar] [CrossRef]
- Tillmann, W.; Anar, N.B.; Wojarski, L. Mechanical behavior of reactive air brazed (RAB) Crofer 22 APU-Al2O3 joints at ambient temperature. SN Appl. Sci. 2020, 2, 809. [Google Scholar] [CrossRef]
- Cao, J.; Si, X.; Li, W.; Song, X.; Feng, J. Reactive air brazing of YSZ-electrolyte and Al2O3-substrate for gas sensor sealing: Interfacial microstructure and mechanical properties. Int. J. Hydrogen Energy 2017, 42, 10683–10694. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, T.; Zhang, J.; Wu, C.; Lu, X.; Ding, W. Induction brazing BaCo0.7 Fe0.2Nb0.1O3−δ membrane tubes to steel supports with Ag-based filler in air. J. Membr. Sci. 2017, 533, 19–27. [Google Scholar] [CrossRef]
- Hardy, J.S.; Kim, J.Y.; Weil, K.S. Joining Mixed Conducting Oxides Using an Air-Fired Electrically Conductive Braze. J. Electrochem. Soc. 2004, 151, J43. [Google Scholar] [CrossRef]
- Bobzin, K.; Öte, M.; Wiesner, S.; Kaletsch, A.; Broeckmann, C. Characterization of Reactive Air Brazed Ceramic/Metal Joints with Unadapted Thermal Expansion Behavior. Adv. Eng. Mater. 2014, 16, 1490–1497. [Google Scholar] [CrossRef]
- Erskine, K.M.; Meier, A.M.; Pilgrim, S.M. Brazing perovskite ceramics with silver/copper oxide braze alloys. J. Mater. Sci. 2002, 37, 1705–1709. [Google Scholar] [CrossRef]
- Han, N.; Shen, Z.; Zhao, X.; Chen, R.; Thakur, V.K. Perovskite oxides for oxygen transport: Chemistry and material horizons. Sci. Total Environ. 2022, 806, 151213. [Google Scholar] [CrossRef]
- Ehle, L.C.; Richter, S.; Herzog, S.; Broeckmann, C.; Mayer, J. Identification of Cu-Co-oxide phases of reactive air brazed Ba0.5Sr0.5Co0.8Fe0.2O3−δ-Ag-14CuO joints by EBSD, EPMA and TEM diffraction. IOP Conf. Ser. Mater. Sci. Eng. 2020, 891, 12012. [Google Scholar] [CrossRef]
- Kaletsch, A. Reaktivlöten von Perowskit-Stahl-Verbunden und deren Alterungsbeständigkeit in oxidierender Atmosphäre; Shaker Verlag: Düren, Germany, 2016; ISBN 978-3-8440-4257-3. [Google Scholar]
- Kaletsch, A.; Bezold, A.; Pfaff, E.M.; Broeckmann, C. Effects of Copper Oxide Content in AgCuO Braze Alloy on Microstructure and Mechanical Properties of Reactive-Air-Brazed Ba0.5Sr0.5Co0.8Fe0.2O3−δ (BSCF). J. Ceram. Sci. Technol. 2012, 3, 95–104. [Google Scholar] [CrossRef]
- Budarapu, P.R.; Zhuang, X.; Rabczuk, T.; Bordas, S.P. Multiscale modeling of material failure: Theory and computational methods. In Advances in Crystals and Elastic Metamaterials, Part 2; Elsevier: Amsterdam, The Netherlands, 2019; pp. 1–103. ISBN 9780128174791. [Google Scholar]
- Kiebach, R.; Engelbrecht, K.; Kwok, K.; Molin, S.; Søgaard, M.; Niehoff, P.; Schulze-Küppers, F.; Kriegel, R.; Kluge, J.; Hendriksen, P.V. Joining of ceramic Ba0.5Sr0.5Co0.8Fe0.2O3 membranes for oxygen production to high temperature alloys. J. Membr. Sci. 2016, 506, 11–21. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, J.; Li, L.; Zhang, C.; Zhang, Y.; Lu, X. Stress analysis of the brazing joints of tubular ceramic oxygen-permeable membranes and metal supports. Ceram. Int. 2019, 45, 1545–1553. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. In Collected Works of J. D. Eshelby; Markenscoff, X., Gupta, A., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 209–229. ISBN 978-1-4020-4416-8. [Google Scholar]
- Liu, Y.; Steven Greene, M.; Chen, W.; Dikin, D.A.; Liu, W.K. Computational microstructure characterization and reconstruction for stochastic multiscale material design. Comput. Aided Des. 2013, 45, 65–76. [Google Scholar] [CrossRef]
- Bostanabad, R.; Zhang, Y.; Li, X.; Kearney, T.; Brinson, L.C.; Apley, D.W.; Liu, W.K.; Chen, W. Computational microstructure characterization and reconstruction: Review of the state-of-the-art techniques. Prog. Mater. Sci. 2018, 95, 1–41. [Google Scholar] [CrossRef]
- Swaminathan, S.; Ghosh, S.; Pagano, N.J. Statistically Equivalent Representative Volume Elements for Unidirectional Composite Microstructures: Part I—Without Damage. J. Compos. Mater. 2006, 40, 583–604. [Google Scholar] [CrossRef]
- Chen, Q.; Zhao, F.; Jia, J.; Zhu, C.; Bai, S.; Ye, Y. Multiscale simulation of elastic response and residual stress for ceramic particle reinforced composites. Ceram. Int. 2022, 48, 2431–2440. [Google Scholar] [CrossRef]
- Horny, D.; Schukraft, J.; Weidenmann, K.A.; Schulz, K. Numerical and Experimental Characterization of Elastic Properties of a Novel, Highly Homogeneous Interpenetrating Metal Ceramic Composite. Adv. Eng. Mater. 2020, 22, 1901556. [Google Scholar] [CrossRef]
- Carneiro, P.M.; Maceiras, A.; Nunes-Pereira, J.; Silva, P.D.; Silva, A.P.; Baudín, C. Property characterization and numerical modelling of the thermal conductivity of CaZrO3-MgO ceramic composites. J. Eur. Ceram. Soc. 2021, 41, 7241–7252. [Google Scholar] [CrossRef]
- Gong, Z.; Guan, K.; Rao, P.; Zeng, Q.; Liu, J.; Feng, Z. Numerical Study of Thermal Shock Damage Mechanism of Polycrystalline Ceramics. Front. Mater. 2021, 8, 724377. [Google Scholar] [CrossRef]
- Zimina, V.A.; Smolin, I.Y. The Modeling of the Fracture of Three-Phase Ceramic Composite. Procedia Struct. Integr. 2022, 35, 188–195. [Google Scholar] [CrossRef]
- Kayser, W.; van Kempen, S.; Bezold, A.; Boin, M.; Wimpory, R.; Broeckmann, C. Numerical investigation of the WC re-precipitation impact on the residual stress state in WC20 wt.-%Co hardmetal. Int. J. Refract. Met. Hard Mater. 2019, 84, 105003. [Google Scholar] [CrossRef]
- Raju, K.; Tay, T.-E.; Tan, V.B.C. A review of the FE2 method for composites. Multiscale Multidiscip. Model. Exp. Des. 2021, 4, 1–24. [Google Scholar] [CrossRef]
- Pirkelmann, S.; Raether, F.; Seifert, G. Top-down material design of multi-phase ceramics. Open Ceram. 2022, 9, 100211. [Google Scholar] [CrossRef]
- Gebhardt, C.; Trimborn, T.; Weber, F.; Bezold, A.; Broeckmann, C.; Herty, M. Simplified ResNet approach for data driven prediction of microstructure-fatigue relationship. Mech. Mater. 2020, 151, 103625. [Google Scholar] [CrossRef]
- Börger, A.; Supancic, P.; Danzer, R. The ball on three balls test for strength testing of brittle discs: Stress distribution in the disc. J. Eur. Ceram. Soc. 2002, 22, 1425–1436. [Google Scholar] [CrossRef]
- Pfaff, E.M.; Oezel, M.; Eser, A.; Bezold, A. Reliability of Ceramic Membranes of BSCF for Oxygen Separation in a Pilot Membrane Reactor. In Ceramics for Environmental and Energy Applications II: A Collection of Papers Presented at the 10th Pacific Rim Conference on Ceramic and Glass Technology, Coronado, CA, USA, 2–6 June 2013; Pyzik, A.J., Boccaccini, A.R., Dogan, F., Lin, H.-T., Belharouak, I., Marra, J.C., Tritt, T.M., Sekino, T., Katoh, Y., Eds.; American Ceramic Society: Westerville, OH, USA; Hoboken, NJ, USA, 2014; pp. 153–163. ISBN 9781118771327. [Google Scholar]
- Huang, B.X.; Malzbender, J.; Steinbrech, R.W.; Singheiser, L. Discussion of the complex thermo-mechanical behavior of Ba0.5Sr0.5Co0.8Fe0.2O3−δ. J. Membr. Sci. 2010, 359, 80–85. [Google Scholar] [CrossRef]
- Munz, D.; Fett, T. Mechanisches Verhalten Keramischer Werkstoffe; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Murakami, Y. Metal Fatigue: Effects of Small Defects and Nonmetallic Inclusions, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2002; ISBN 0080440649. [Google Scholar]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Herzog, S.; Boussinot, G.; Kaletsch, A.; Apel, M.; Broeckmann, C. Microstructure coarsening in Ba0.5Sr0.5Co0.8Fe0.2O3−δ during reactive air brazing. J. Eur. Ceram. Soc. 2022, 42, 5842–5850. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, X.; Bhakhri, V.; Giuliani, F.; Atkinson, A. Nanoindentation of porous bulk and thin films of La0.6Sr0.4Co0.2Fe0.8O3−δ. Acta Mater. 2013, 61, 5720–5734. [Google Scholar] [CrossRef]
- Yao, B.; Zhou, X.; Liu, M.; Yu, J.; Cao, J.; Wang, L. First-principles calculations on phase transformation and elastic properties of CuO under pressure. J. Comput. Electron. 2018, 17, 1450–1456. [Google Scholar] [CrossRef]
- Wachtman, J.B.; Cannon, W.R.; Matthewson, M.J. Mechanical Properties of Ceramics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; ISBN 9780470451519. [Google Scholar]
- Bargmann, S.; Klusemann, B.; Markmann, J.; Schnabel, J.E.; Schneider, K.; Soyarslan, C.; Wilmers, J. Generation of 3D representative volume elements for heterogeneous materials: A review. Prog. Mater. Sci. 2018, 96, 322–384. [Google Scholar] [CrossRef]
- Seibert, P.; Ambati, M.; Raßloff, A.; Kästner, M. Reconstructing random heterogeneous media through differentiable optimization. Comput. Mater. Sci. 2021, 196, 110455. [Google Scholar] [CrossRef]
- Robertson, A.E.; Kalidindi, S.R. Efficient generation of anisotropic N-field microstructures from 2-point statistics using multi-output Gaussian random fields. Acta Mater. 2022, 232, 117927. [Google Scholar] [CrossRef]


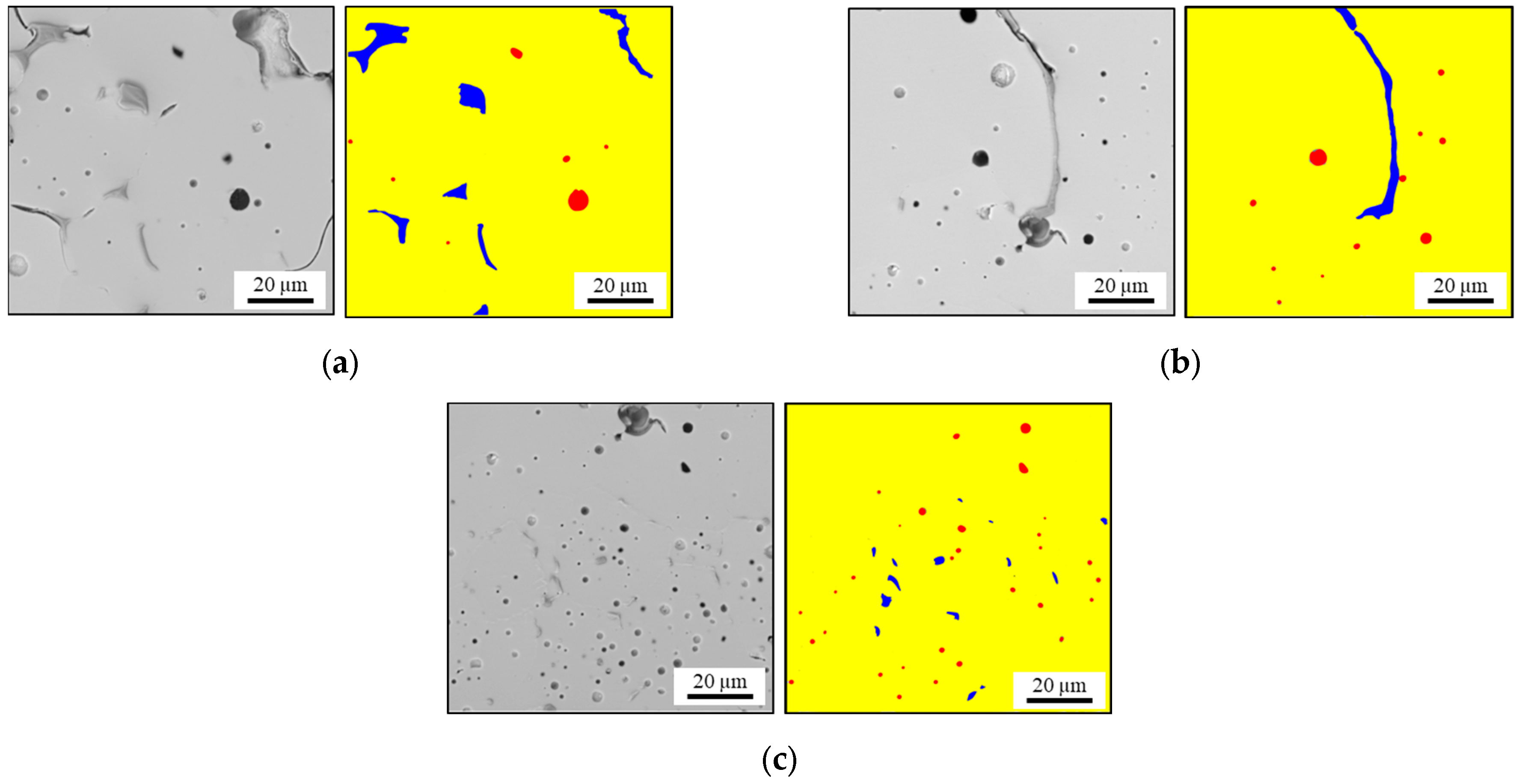
| BSCF | Multi-Phase TPP | Single-Phase TPP (CuO) | |||||
|---|---|---|---|---|---|---|---|
| Temperature [°C] | Young’s Modulus [GPa] | Young’s Modulus [GPa] | CTE [10−6 K−1] | Young’s Modulus [GPa] | CTE [10−6 K−1] | Young’s Modulus [GPa] | CTE [10−6 K−1] |
| 24 | 119.4 | 230.5 | 9.44 | 230.5 | 9.44 | 86.7 | 4.9 |
| 100 | 99.6 | 191.7 | 9.81 | 191.7 | 9.81 | 86.0 | 5.45 |
| 200 | 88.4 | 170.3 | 9.77 | 170.3 | 9.77 | 85.0 | 6.04 |
| 300 | 84.1 | 161.9 | 9.65 | 161.9 | 9.65 | 84.0 | 6.56 |
| 400 | 96.9 | 186.6 | 9.97 | 186.6 | 9.97 | 83.0 | 6.9 |
| 500 | 99.9 | 192.5 | 10.43 | 192.5 | 10.43 | 82.0 | 718 |
| 600 | 100.7 | 193.9 | 11.30 | 193.9 | 11.30 | 81.0 | 7.61 |
| 700 | 95.4 | 183.7 | 12.36 | 183.7 | 12.36 | 80.0 | 8.39 |
| 800 | 91.8 | 176.8 | 13.19 | 176.8 | 13.19 | 79.0 | 10.19 |
| 900 | - | - | - | - | - | 78.0 | - |
| 1000 | - | - | - | - | - | 77.0 | - |
| Temperature [°C] | BSCF Matrix [MPa] | Porous BSCF [MPa] [35] |
|---|---|---|
| 24 | 1599 | 188 |
| 100 | 1620 | 169 |
| 200 | 732 | 75 |
| 300 | 708 | 69 |
| 400 | 674 | 71 |
| 600 | 895 | 87 |
| 800 | 1210 | 108 |
| Temperature [°C] | Weibull Modulus [-] [35] | Effective Volume [mm³] |
|---|---|---|
| 24 | 8.5 | 1.67 |
| 100 | 5.4 | 5.22 |
| 200 | 4.8 | 7.12 |
| 300 | 4.4 | 8.92 |
| 400 | 4.8 | 7.12 |
| 600 | 4.1 | 8.98 |
| 800 | 7.4 | 2.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rudenskiy, D.; Herzog, S.; Horbach, L.; Gebhardt, N.C.; Weber, F.; Kaletsch, A.; Broeckmann, C. Numerical Modeling of Residual Stresses and Fracture Strengths of Ba0.5Sr0.5Co0.8Fe0.2O3−δ in Reactive Air Brazed Joints. Materials 2023, 16, 7265. https://doi.org/10.3390/ma16237265
Rudenskiy D, Herzog S, Horbach L, Gebhardt NC, Weber F, Kaletsch A, Broeckmann C. Numerical Modeling of Residual Stresses and Fracture Strengths of Ba0.5Sr0.5Co0.8Fe0.2O3−δ in Reactive Air Brazed Joints. Materials. 2023; 16(23):7265. https://doi.org/10.3390/ma16237265
Chicago/Turabian StyleRudenskiy, Donat, Simone Herzog, Lutz Horbach, Nils Christian Gebhardt, Felix Weber, Anke Kaletsch, and Christoph Broeckmann. 2023. "Numerical Modeling of Residual Stresses and Fracture Strengths of Ba0.5Sr0.5Co0.8Fe0.2O3−δ in Reactive Air Brazed Joints" Materials 16, no. 23: 7265. https://doi.org/10.3390/ma16237265
APA StyleRudenskiy, D., Herzog, S., Horbach, L., Gebhardt, N. C., Weber, F., Kaletsch, A., & Broeckmann, C. (2023). Numerical Modeling of Residual Stresses and Fracture Strengths of Ba0.5Sr0.5Co0.8Fe0.2O3−δ in Reactive Air Brazed Joints. Materials, 16(23), 7265. https://doi.org/10.3390/ma16237265







