Enhancing/Improving Forming Limit Curve and Fracture Height Predictions in the Single-Point Incremental Forming of Al1050 Sheet Material
Abstract
:1. Introduction
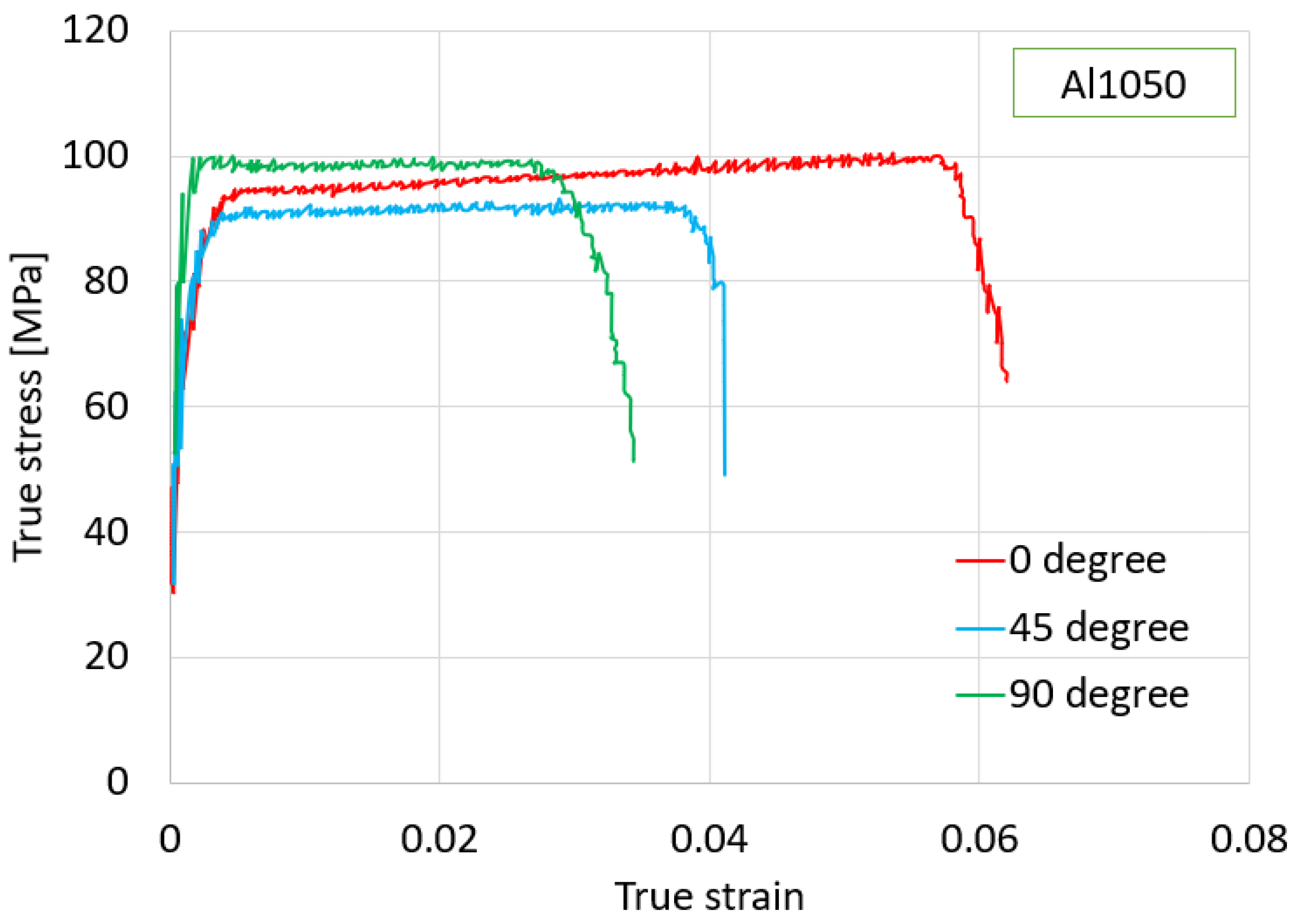
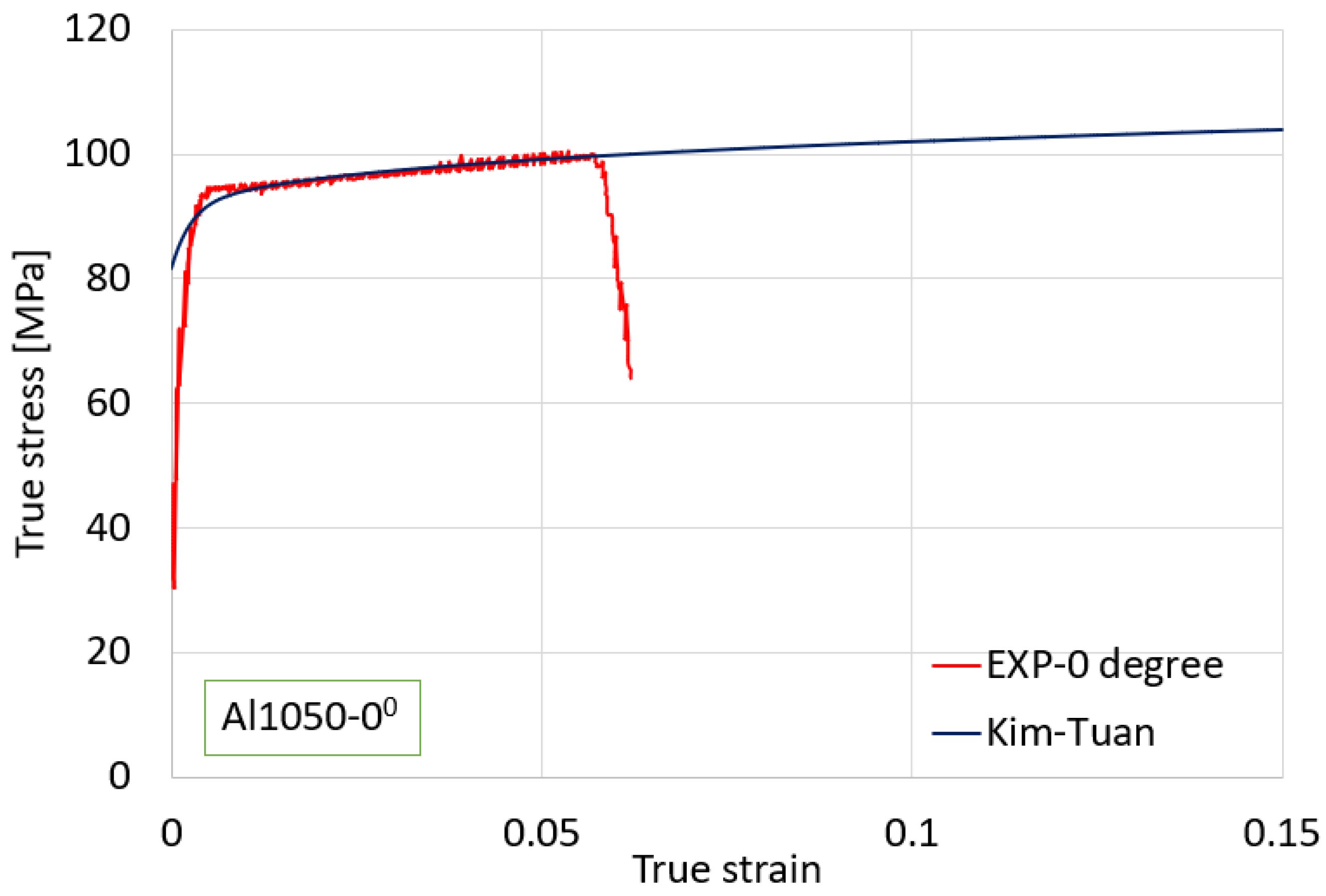
2. Material Properties
3. Prediction of the Forming Limit Curve (FLC)
3.1. Modified Maximum Force Criterion Method
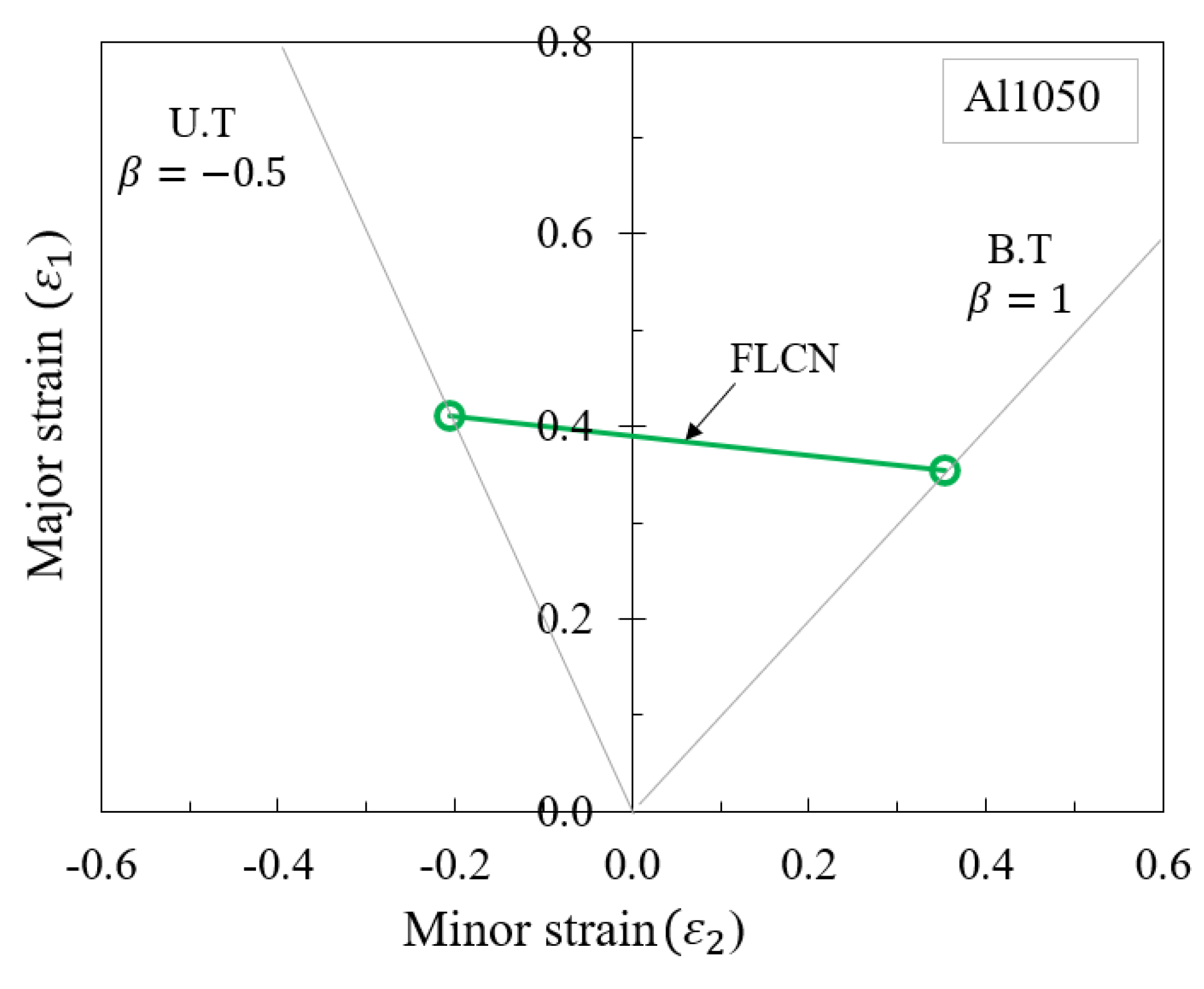
3.2. Graphical Method for Al1050 Material
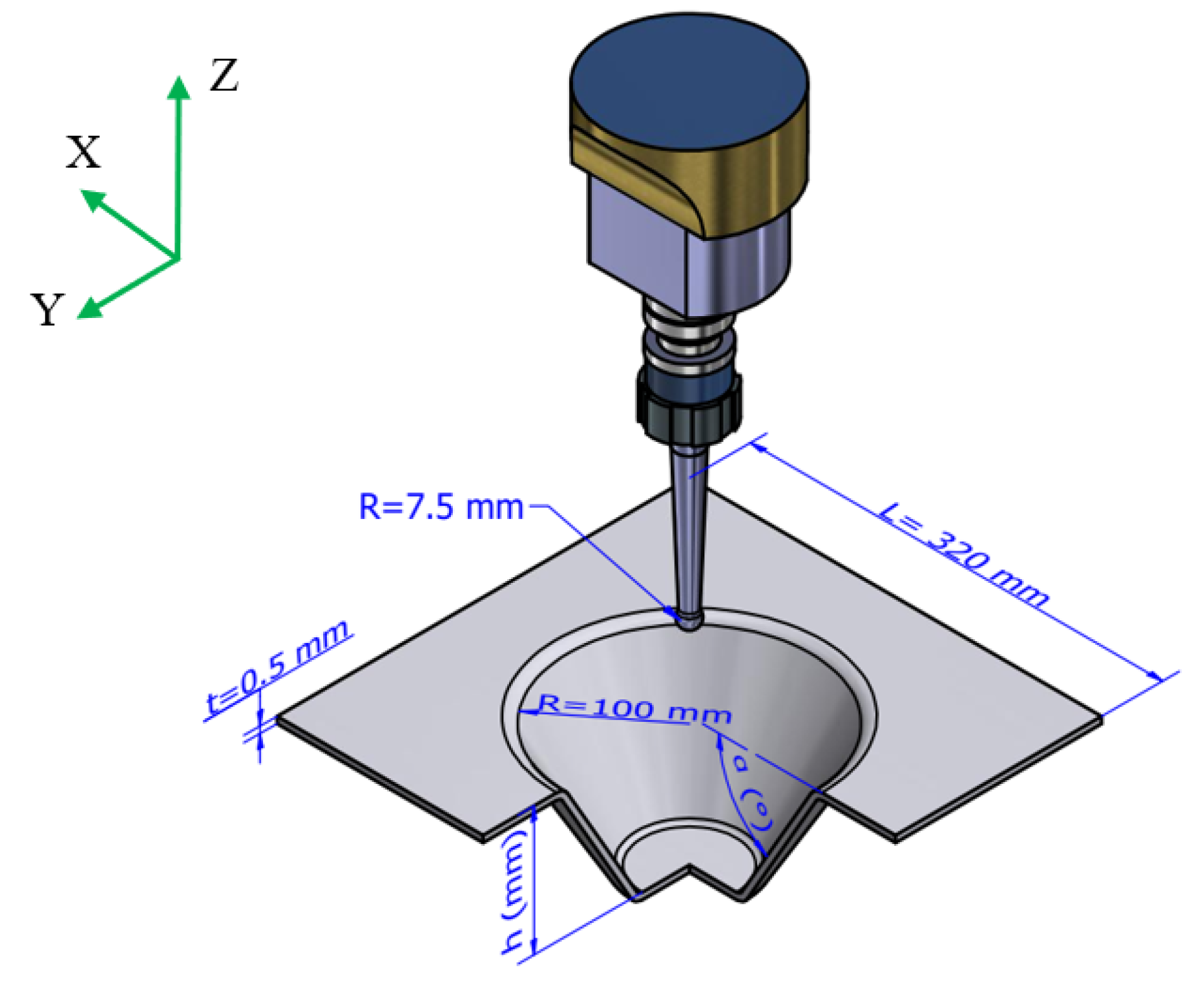
4. Experiment and Finite Element (FE) Simulation
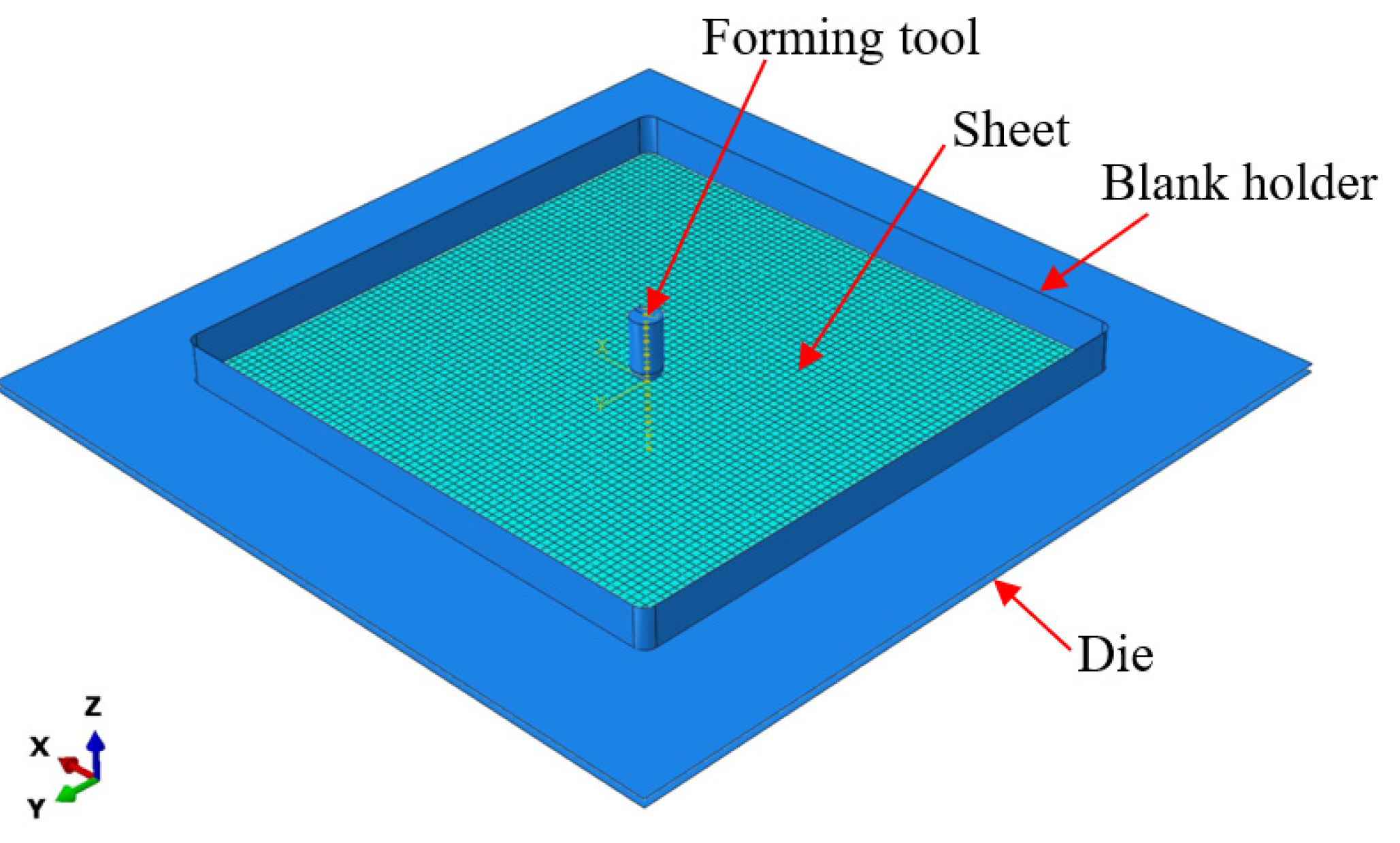
4.1. Finite Element Simulation
4.2. SPIF Experiment
5. Results and Discussion
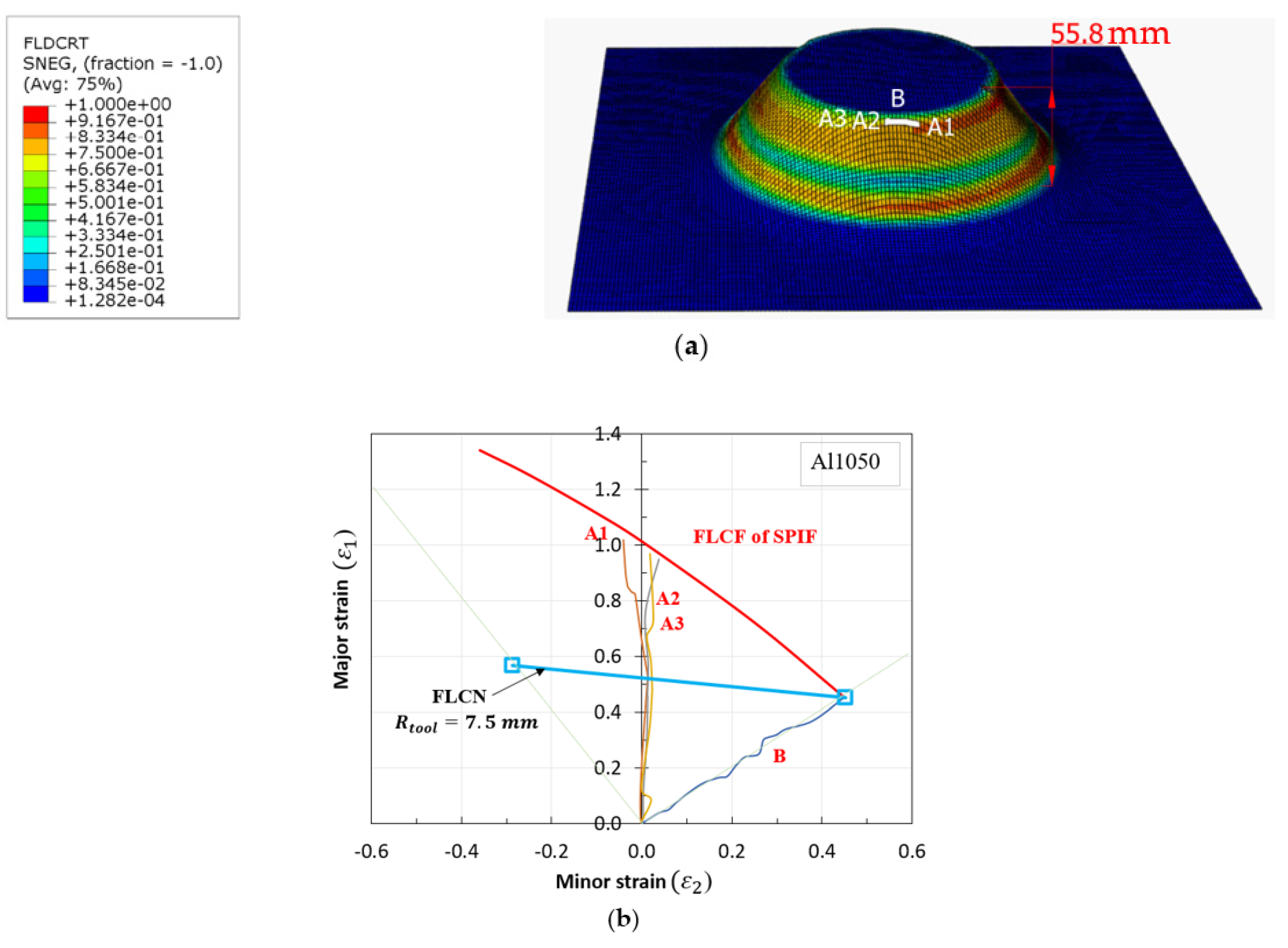
5.1. Comparison of Fracture Height in SPIF Simulation and Experiment
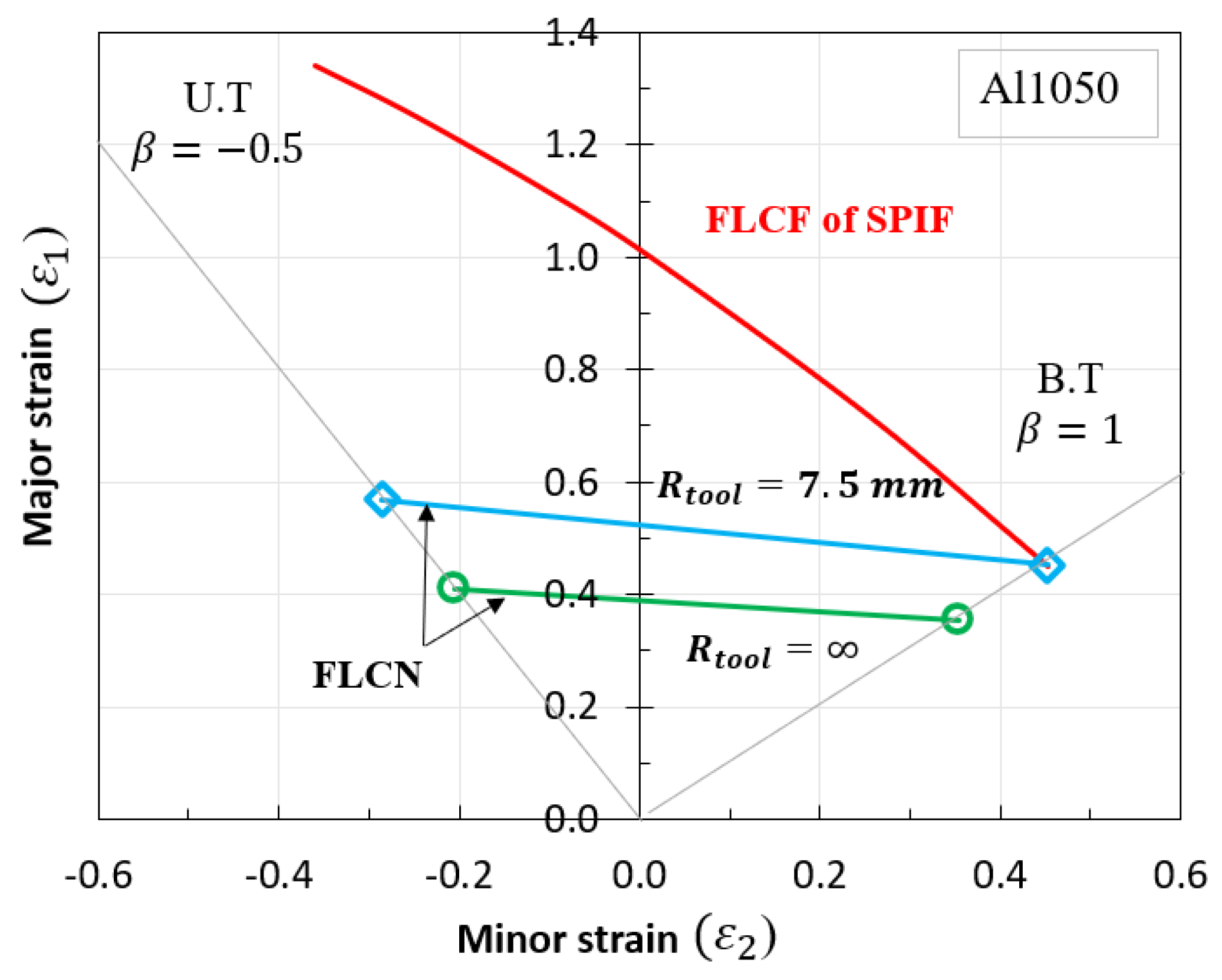
5.2. Proposed Forming Limit Curves at Fracture (FLCF) in SPIF
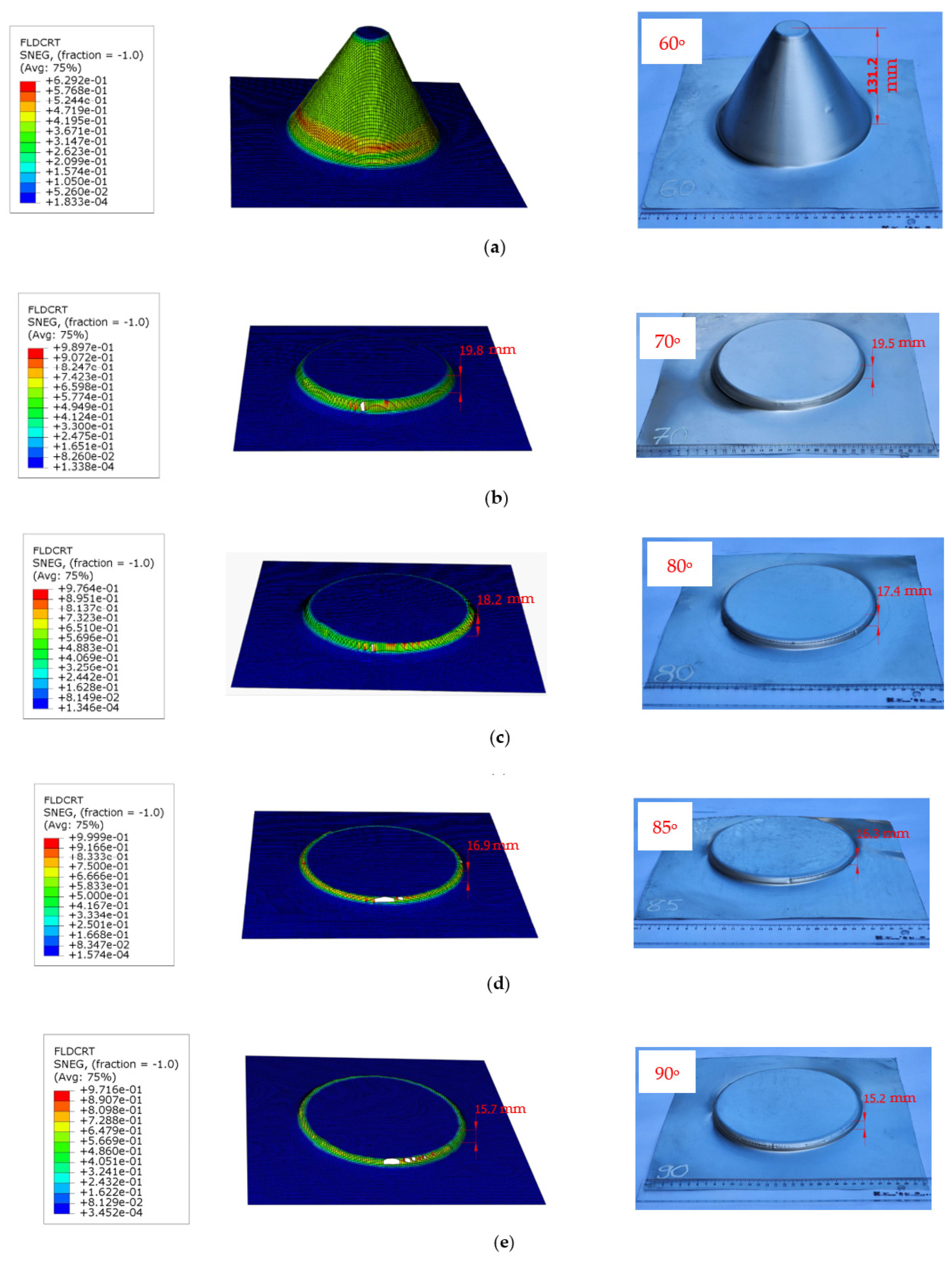
5.3. Verification of the Proposed FLCF with Varying Forming Angles
6. Conclusions
- Graphical method for FLC construction: a FLC is methodically constructed using the graphical approach and employed in numerical simulations to predict the variation in fracture height during SPIF. The results show a notable deviation between the simulated and experimental outcomes, particularly when forming the truncated cone with a 62° wall angle. The deviation, amounting to 15.97%, underscores the challenge in accurately modeling the SPIF process.
- Proposed forming limit curve at fracture in SPIF (FLCF): To enhance accuracy, a new FLCF is introduced based on the relationship between major and minor strains, drawing on the simulation results for truncated cone shaping with varying tool radii. The FLCF aligns remarkably well with experimental observations, especially for a 62° forming tilt angle, where the deviation is significantly reduced to 3.13%. This highlights the potential of the proposed FLCF in improving SPIF simulations.
- Validation across varied forming wall angles: To assess the reliability of the newly proposed FLCF, this study explores its effectiveness in predicting failure and forming fracture heights across a range of forming wall angles, spanning from 60° to 90°. The results are promising: for a 60° wall angle, the samples reach their maximum height without encountering fractures, with an FLDCRT value of 0.6292. With increasing forming wall angles (70°, 80°, 85°, 90°), the forming fracture height of the truncated cone tends to decrease, aligning closely with FLDCRT values approaching 1.0. The deviation in the forming fracture height between the simulations and experiments remains within acceptable limits, with the largest discrepancy observed at 4.6% in most cases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, S.P.; Elangovan, S.; Mohanraj, R.; Boopathi, S. Real-time applications and novel manufacturing strategies of incremental forming: An industrial perspective. Mater. Today Proc. 2021, 46, 8153–8164. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Najm, S.M.; Pepelnjak, T.; Bensaid, K.; Szpunar, M. Incremental Sheet Forming of Metal-Based Composites Used in Aviation and Automotive Applications. J. Compos. Sci. 2022, 6, 295. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Oleksik, V.; Pepelnjak, T.; Najm, S.M.; Paniti, I.; Maji, K. Emerging trends in single point incremental sheet forming of lightweight metals. Metals 2021, 11, 1188. [Google Scholar] [CrossRef]
- Trzepiecinski, T.; Lemu, H.G. Recent developments and trends in the friction testing for conventional sheet metal forming and incremental sheet forming. Metals 2020, 10, 47. [Google Scholar] [CrossRef]
- Romero, P.E.; Rodriguez-Alabanda, O.; Molero, E.; Guerrero-Vaca, G. Use of the support vector machine (SVM) algorithm to predict geometrical accuracy in the manufacture of molds via single point incremental forming (SPIF) using aluminized steel sheets. J. Mater. Res. Technol. 2021, 15, 1562–1571. [Google Scholar] [CrossRef]
- Araújo, R.; Teixeira, P.; Montanari, L.; Reis, A.; Silva, M.B.; Martins, P.A.F. Single point incremental forming of a facial implant. Prosthet. Orthot. Int. 2014, 38, 369–378. [Google Scholar] [CrossRef]
- Rosa-Sainz, A.; Silva, M.B.; Beltrán, A.M.; Centeno, G.; Vallellano, C. Assessing Formability and Failure of UHMWPE Sheets through SPIF: A Case Study in Medical Applications. Polymers 2023, 15, 3560. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, Y.; Xu, C.; Liu, Y.; Ghafoor, S.; Li, F. Incremental sheet forming towards biomedical implants: A review. J. Mater. Res. Technol. 2020, 9, 7225–7251. [Google Scholar] [CrossRef]
- Chadha, K.; Dubor, A.; Puigpinos, L.; Rafols, I. Space Filling Curves for Optimising Single Point Incremental Sheet Forming using Supervised Learning Algorithms. Proc. Int. Conf. Educ. Res. Comput. Aided Archit. Des. Eur. 2020, 1, 555–562. [Google Scholar] [CrossRef]
- Nicholas, P.; Chiujdea, R.S.; Sonne, K.; Scaffidi, A. Design and Fabrication Methodologies for Repurposing End of Life Metal via Robotic Incremental Sheet Metal Forming. Proc. Int. Conf. Educ. Res. Comput. Aided Archit. Des. Eur. 2021, 2, 171–180. [Google Scholar] [CrossRef]
- Mezher, M.T.; Khazaal, S.M.; Namer, N.S.M.; Shakir, R.A. A comparative analysis study of hole flanging by incremental sheet forming process of AA1060 and DC01 sheet metals. J. Eng. Sci. Technol. 2021, 16, 4383–4403. [Google Scholar]
- Naranjo, J.; Miguel, V.; Martínez, A.; Coello, J.; Manjabacas, M.C. Analysis of material behavior models for the Ti6Al4V alloy to simulate the Single Point Incremental Forming process. Procedia Manuf. 2017, 13, 307–314. [Google Scholar] [CrossRef]
- Mezher, M.T.; Kovács, B. An Investigation of the Impact of Forming Process Parameters in Single Point Incremental Forming Using Experimental and Numerical Verification. Period. Polytech. Mech. Eng. 2022, 66, 183–196. [Google Scholar] [CrossRef]
- Al-Obaidi, A.; Kräusel, V.; Kroll, M. FE Simulation of Hot Single Point Incremental Forming Assisted by Induction Heating. In Proceedings of the XIX International UIE Congress on Evolution and New Trends in Electrothermal Processes, Pilsen, Czech Republic, 3 January 2021; pp. 27–28. Available online: http://dspace5.zcu.cz/handle/11025/45782 (accessed on 10 November 2021).
- Popp, M.-O.; Rusu, G.-P.; Popp, I.-O.; Gîrjob, C.-E. Numerical Study of a Variable Wall Angle Made of DC01 Steel by Incremental Forming Process. Acta Univ. Cibiniensis. Tech. Ser. 2022, 74, 21–25. [Google Scholar] [CrossRef]
- Gupta, P.; Jeswiet, J. Parameters for the FEA simulations of single point incremental forming. Prod. Manuf. Res. 2019, 7, 161–177. [Google Scholar] [CrossRef]
- Saidi, B.; Moreau, L.G.; Cherouat, A.; Nasri, R. Experimental and numerical study on warm single-point incremental sheet forming (WSPIF) of titanium alloy Ti–6Al–4V, using cartridge heaters. J. Brazilian Soc. Mech. Sci. Eng. 2020, 42, 534. [Google Scholar] [CrossRef]
- Bouhamed, A.; Jrad, H.; Said, L.B.; Wali, M.; Dammak, F. A non-associated anisotropic plasticity model with mixed isotropic–kinematic hardening for finite element simulation of incremental sheet metal forming process. Int. J. Adv. Manuf. Technol. 2019, 42, 929–940. [Google Scholar] [CrossRef]
- Han, H.N.; Kim, K.H. A ductile fracture criterion in sheet metal forming process. J. Mater. Process. Technol. 2003, 142, 231–238. [Google Scholar] [CrossRef]
- Rusu, R.-E.; Breaz, G.-P.; Popp, S.-G.; Oleksik, M.-O.; Racz, V. Experimental Research on Wolfram Inert Gas AA1050 Aluminum Alloy Tailor Welded Blanks Processed by Single Point Incremental Forming Process. Materials 2023, 16, 6408. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Oh, S.-H.; Kim, S.-H.; Kim, Y.-S. Effects of Low-Frequency Vibrations on Single Point Incremental Sheet Forming. Metals 2022, 12, 346. [Google Scholar] [CrossRef]
- Shang, M.; Li, Y.; Yang, M.; Chen, Y.; Bai, L.; Li, P. Wall Thickness Uniformity in ISF of Hydraulic Support: System Design, Finite Element Analysis and Experimental Verification. Machines 2023, 11, 353. [Google Scholar] [CrossRef]
- Abe, H.; Chung, J.C.; Mori, T.; Hosoi, A.; Jespersen, K.M. Kawada The effect of nanospike structures on direct bonding strength properties between aluminum and carbon fiber reinforced thermoplastics. Compos. Part B 2019, 172, 26–32. [Google Scholar] [CrossRef]
- ISO 6892-1; Metallic Materials Tensile Testing Part 1: Method of Test at Room Temperature. International Organization for Standardization: Geneva, Switzerland, 2019. Available online: https://www.iso.org/standard/78322.html (accessed on 17 October 2023).
- Luyen, T.-T.; Pham, Q.-T.; Kim, Y.-S.; Nguyen, D.-T. Application/Comparison Study of a Graphical Method of Forming Limit Curve Estimation for DP590 Steel Sheets. J. Korean Soc. Precis. Eng. 2019, 36, 883–890. [Google Scholar] [CrossRef]
- Luyen, T.T.; Mac, T.B.; Banh, T.L.; Nguyen, D.T. Investigating the impact of yield criteria and process parameters on fracture height of cylindrical cups in the deep drawing process of SPCC sheet steel. Int. J. Adv. Manuf. Technol. 2023, 128, 2059–2073. [Google Scholar] [CrossRef]
- Pham, Q.T.; Kim, J.; Luyen, T.; Nguyen, D.T.; Kim, Y.S. Application of a graphical method on estimating forming limit curve of automotive sheet metals. Int. J. Automot. Technol. 2019, 20, 3–8. [Google Scholar] [CrossRef]
- Hill, R. A Theory of the Yielding and Plastic Flow of Anisotropic Metals. Proc. R. Soc. A Math. Phys. Eng. Sci. 1948, 193, 281–297. [Google Scholar] [CrossRef]
- Swift, H.W. Plastic instability under plane stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Hora, P.; Tong, L.; Berisha, B. Modified maximum force criterion, a model for the theoretical prediction of forming limit curves. Int. J. Mater. Form. 2013, 6, 267–279. [Google Scholar] [CrossRef]
- Bouffioux, C.H.C.; Sol, P.E.H.; Van Bael, J.R.D.P.V.H.A.; Habraken, L.D.A.M. Forming forces in single point incremental forming: Prediction by finite element simulations, validation and sensitivity. Comput. Mech. 2011, 47, 573–590. [Google Scholar] [CrossRef]
- Park, N.; Huh, H.; Lim, S.J.; Lou, Y.; Kang, Y.S.; Seo, M.H. Fracture-based forming limit criteria for anisotropic materials in sheet metal forming. Int. J. Plast. 2017, 96, 1–35. [Google Scholar] [CrossRef]
- Hibbitt, D.; Karlsson, B.; Sorensen, P. ABAQUS/CAE User’s Manual, Version 6.10.1; ABAQUS Inc.: Palo Alto, CA, USA, 2001; pp. 1–847. [Google Scholar]
- Clift, S.E.; Hartley, P.; Sturgess, C.E.N.; Rowe, G.W. Fracture prediction in plastic deformation processes. Int. J. Mech. Sci. 1990, 32, 1–17. [Google Scholar] [CrossRef]
- Shi, M.F.; Gerdeen, J.C. Effect of strain gradient and curvature on forming limit diagrams for anisotropic sheets. J. Mater. Shap. Technol. 1991, 9, 253–268. [Google Scholar] [CrossRef]
- Son, H.S.; Kim, Y.S. Prediction of forming limits for anisotropic sheets containing prolate ellipsoidal voids. Int. J. Mech. Sci. 2003, 45, 1625–1643. [Google Scholar] [CrossRef]








| Material | Al1050 | ||
|---|---|---|---|
| Rolling direction | 0° | 45° | 90° |
| Yield strength (MPa) | 81.6 | 79.7 | 89.8 |
| Anisotropy coefficient (r) | 0.62 | 0.38 | 0.85 |
| Density (ρ, kg/mm3) | 2.7 × 10−6 | ||
| Elastic modulus (E, kN/mm2) | 69 | ||
| Poisson coefficient | 0.33 | ||
| Value | F | G | H | L | M | N |
|---|---|---|---|---|---|---|
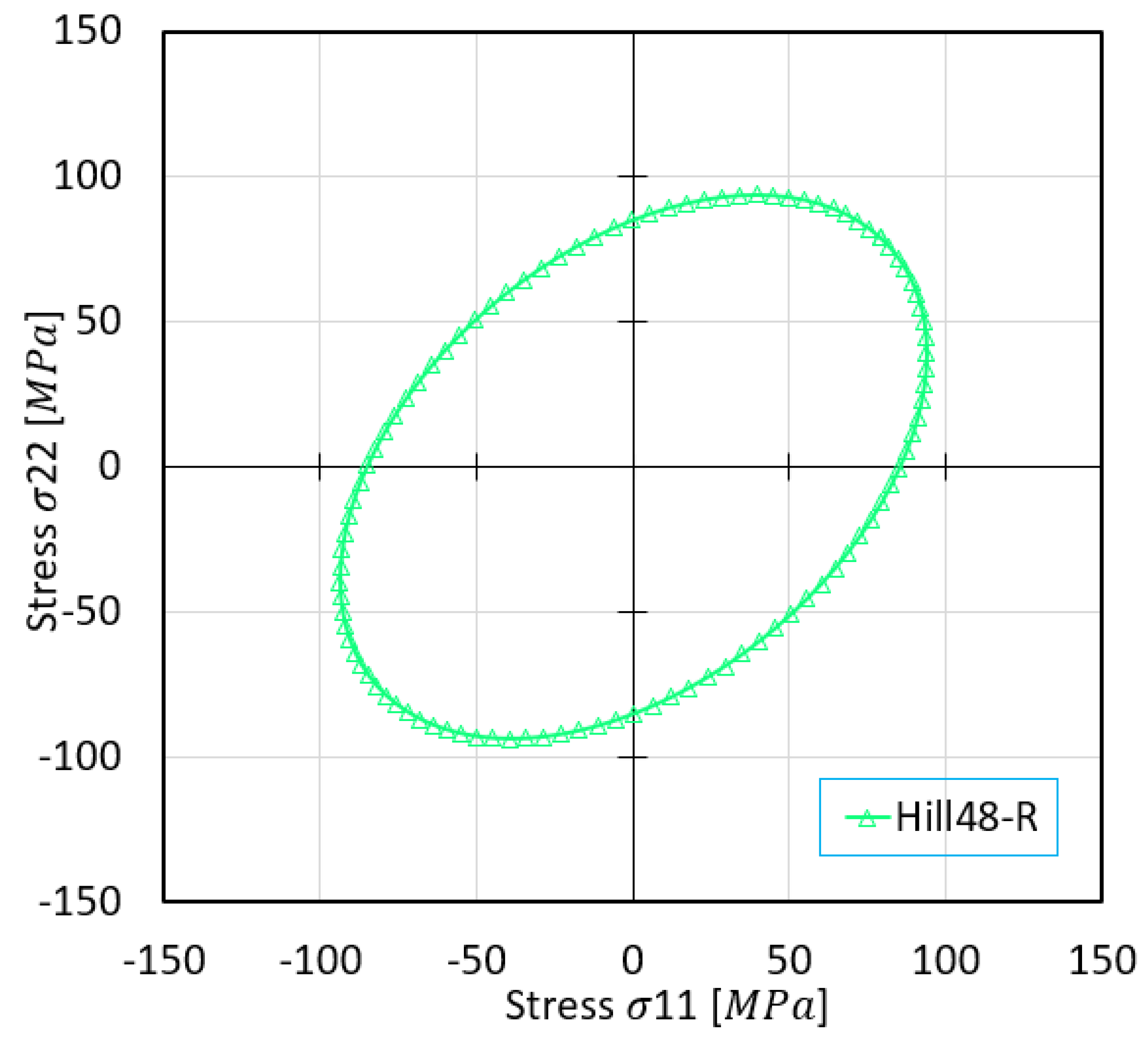
| Hill’48R | 0.4503 | 0.6173 | 0.3827 | 1.5 | 1.5 | 0.9394 |
| Coefficient | R11 | R22 | R33 | R12 | R13 | R23 |
|---|---|---|---|---|---|---|
| Hill’48R | 1 | 1.0957 | 0.9679 | 1.2636 | 1 | 1 |
| Coefficient | Tensile Strain (U.T) | Bi-Axial Tensile (B.T) | |
|---|---|---|---|
| Hill’48R | 0 | 1 | |
| −0.5 | 1 | ||
| 1 | 0.597 | ||
| 0.213 | 0.171 | ||
| Coefficient | U.T | B.T | |
|---|---|---|---|
| Kim–Tuan | 0.415 | 0.625 | |
| 0.410 | 0.354 | ||
| −0.205 | 0.354 | ||
| Fracture Height | Experiment | Simulation | Deviation |
|---|---|---|---|
| Wall angle (o) | he (mm) | (mm) | (%) |
| 62 | 57.6 | 48.4 | 15.97% |
| Wall Angle (o) | 60 | 70 | 80 | 85 | 90 |
|---|---|---|---|---|---|
| Simulation, hs (mm) | 131.2 (No failure) | 19.8 | 18.2 | 16.9 | 15.7 |
| Experiment, he (mm) | 19.5 | 17.4 | 16.3 | 15.2 | |
| 1.54% | 4.60% | 3.68% | 3.29% | ||
| FLDCRT value | 0.6292 | 1 | 1 | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoang, T.-K.; Luyen, T.-T.; Nguyen, D.-T. Enhancing/Improving Forming Limit Curve and Fracture Height Predictions in the Single-Point Incremental Forming of Al1050 Sheet Material. Materials 2023, 16, 7266. https://doi.org/10.3390/ma16237266
Hoang T-K, Luyen T-T, Nguyen D-T. Enhancing/Improving Forming Limit Curve and Fracture Height Predictions in the Single-Point Incremental Forming of Al1050 Sheet Material. Materials. 2023; 16(23):7266. https://doi.org/10.3390/ma16237266
Chicago/Turabian StyleHoang, Trung-Kien, The-Thanh Luyen, and Duc-Toan Nguyen. 2023. "Enhancing/Improving Forming Limit Curve and Fracture Height Predictions in the Single-Point Incremental Forming of Al1050 Sheet Material" Materials 16, no. 23: 7266. https://doi.org/10.3390/ma16237266
APA StyleHoang, T.-K., Luyen, T.-T., & Nguyen, D.-T. (2023). Enhancing/Improving Forming Limit Curve and Fracture Height Predictions in the Single-Point Incremental Forming of Al1050 Sheet Material. Materials, 16(23), 7266. https://doi.org/10.3390/ma16237266







