Simulation of the Influence of the Radial Graded Porosity Distribution on Elastic Modulus of γ/β Phase Ti-Based Alloy Foams for Bone Implant
Abstract
:1. Introduction
2. Materials and Methods
2.1. Metallurgical Design of Alloys
- (a)
- Microstructure: The Ti-based alloys must be composed with a high γ/β phase ratio.
- (b)
- Synthesis method: As the γ-phase is a metastable phase, a non-equilibrium method was used to synthesize it. In this context, mechanical alloying exhibited some advantages: (i) it is a simple and versatile technique, (ii) it has very large departures from equilibrium, with the maximum departure from equilibrium being ~30 kJ/mol, and (iii) there is a possibility of obtaining materials with nanocrystalline grain size and high deformation, which are two of the characteristics required to synthesize Ti-based alloy with γ-phase, through mechanical alloying.
- (c)
- Ti-based alloys: Three Ti-based alloys were chosen according to previous studies completed by our group and reported by other works where the γ-phase was obtained by mechanical alloying. The alloys selected were Ti-13Ta-6Mn (TTM), Ti-13Ta-(TT) and Ti-13Ta-6Sn (TTS) (all in at.%).
- (d)
- Consolidated samples: Only consolidated samples were obtained since synthesizing foams with α γ/β-phase ratio is very complex when using traditional processes.
2.2. Consolidated Sample Production
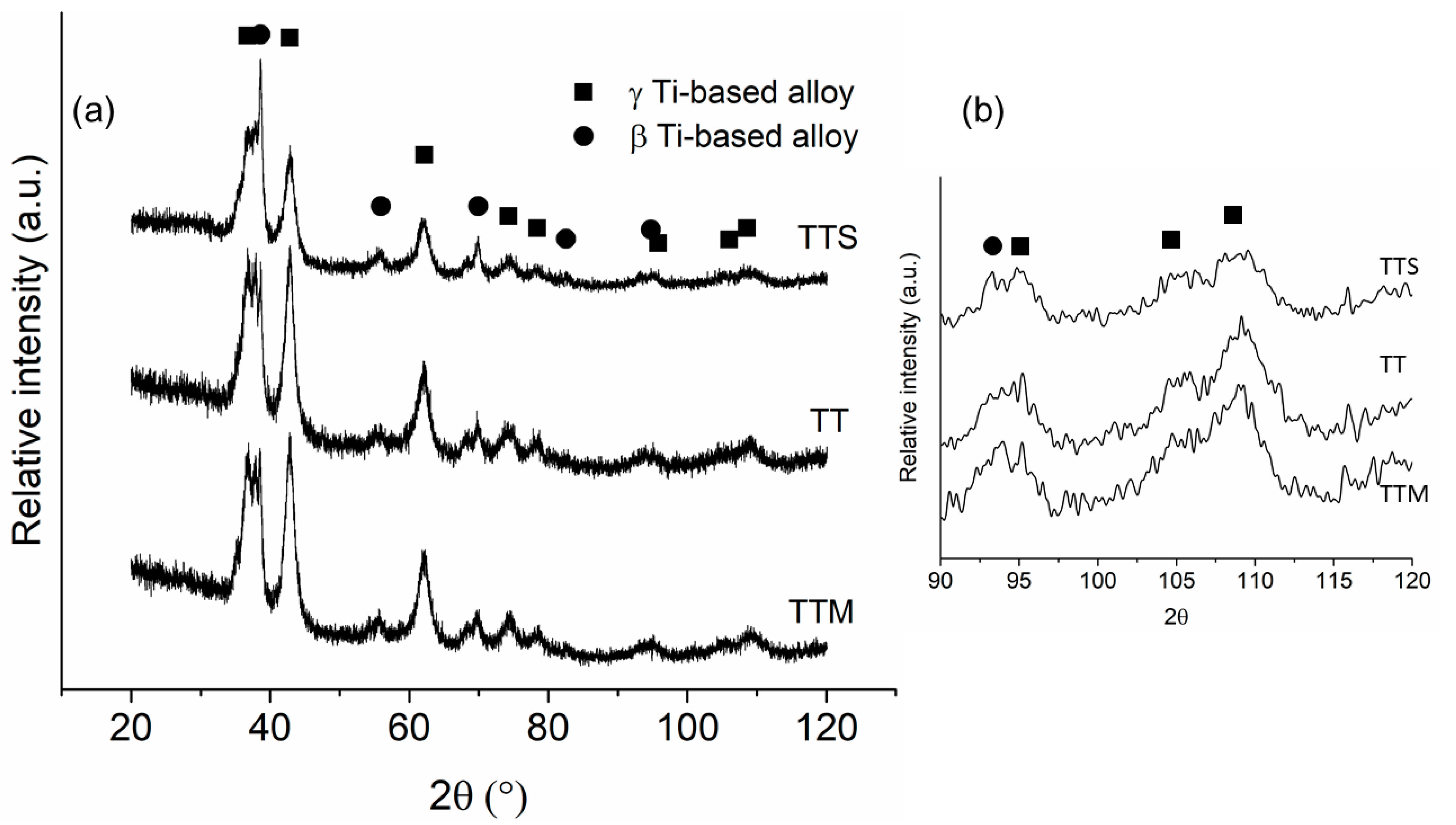
2.3. Sample Characterization
3. Modelling and Simulation
3.1. RVE-FEM Method
3.2. Simplified Theoretical Model to Estimate Young’s Modulus
4. Results and Discussion
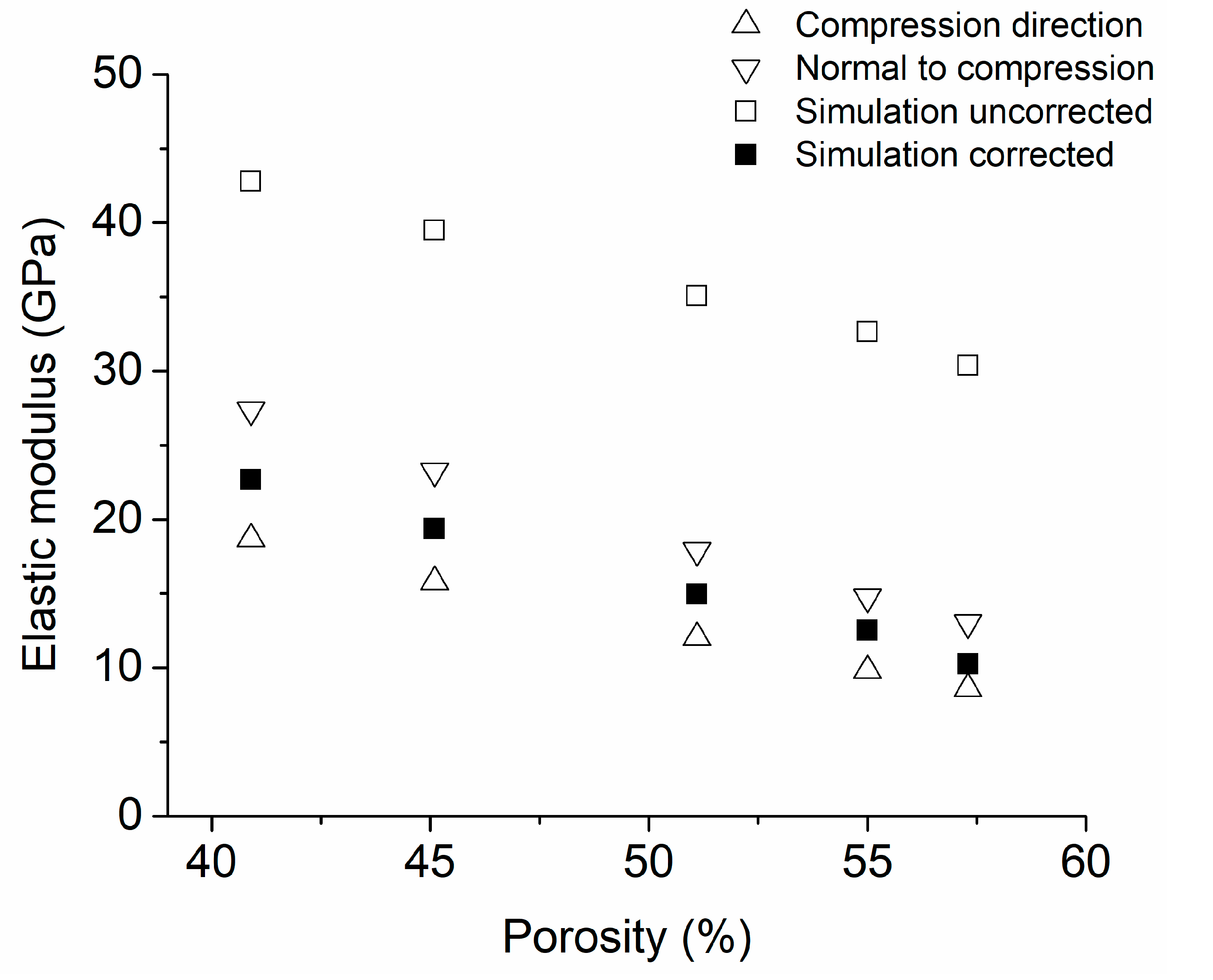
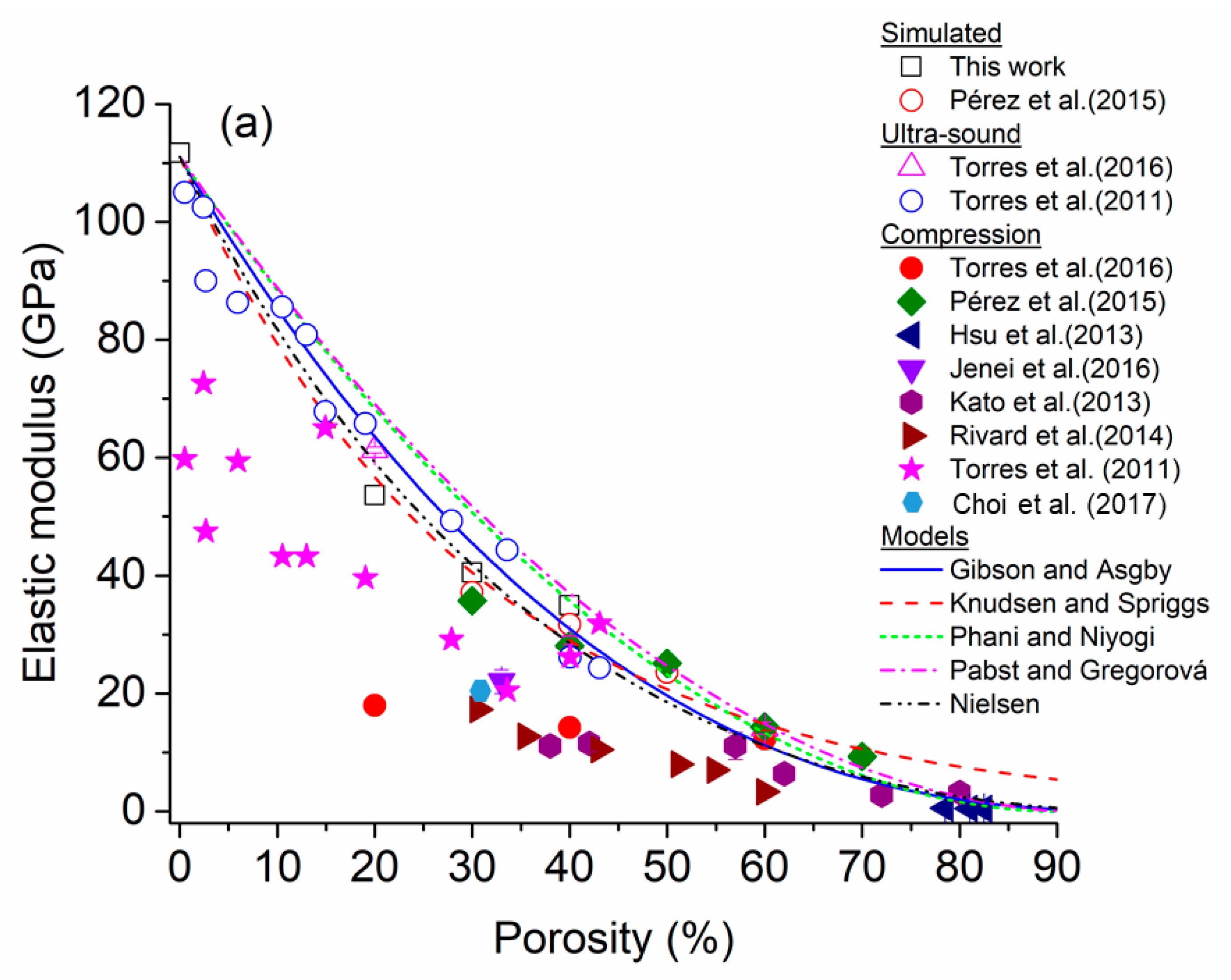
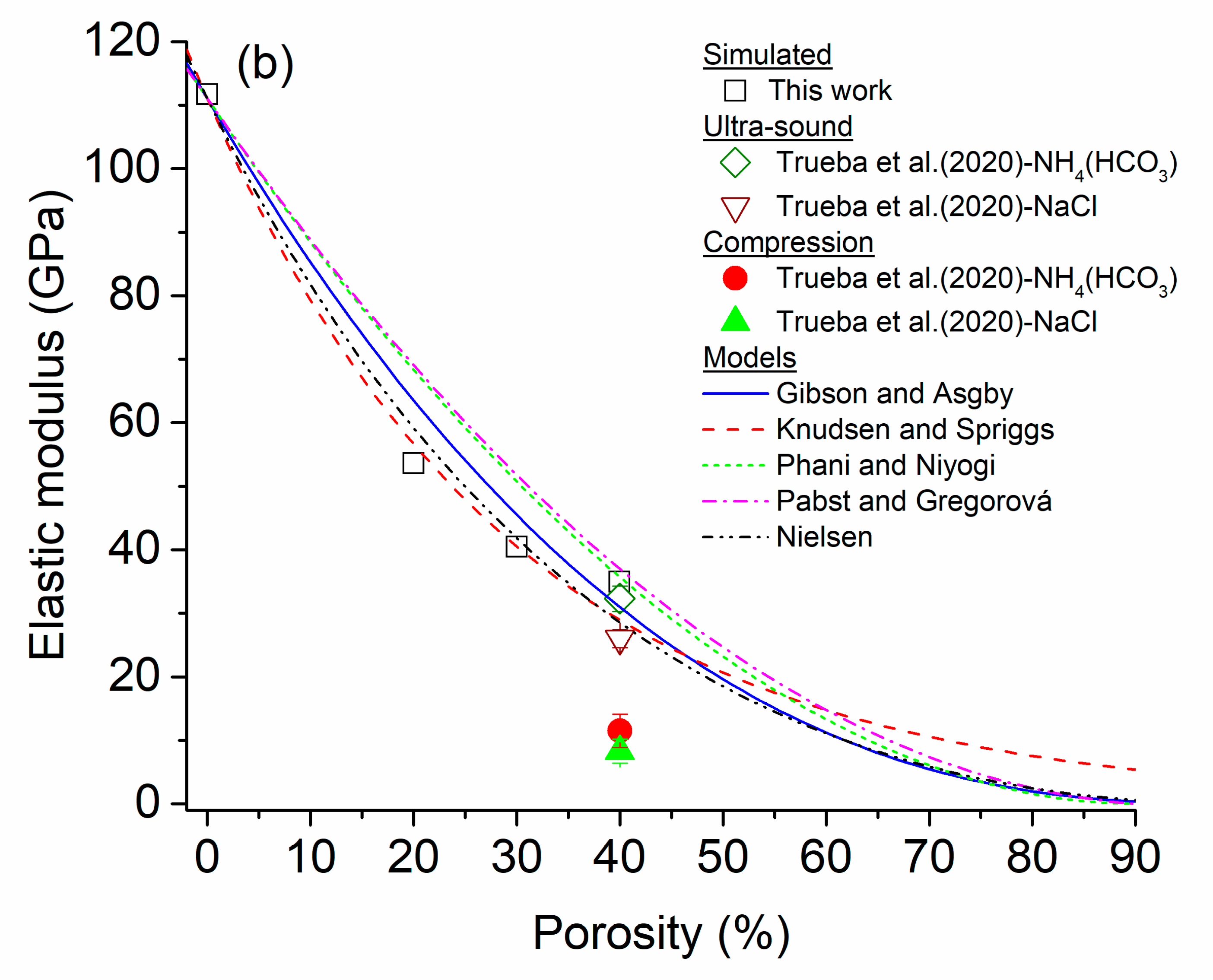
4.1. Validation of Method Using cp-Ti Foams
4.2. Ti-Based Alloy Foams
- (a)
- Comparison with binary Ti-based alloy foams
- (b)
- Comparison with ternary Ti-based alloy foams
- (c)
- Comparison with multicomponent Ti-based alloy foams

- (d)
- Brief analysis of obtained results using theoretical models
| Alloy | Synthesis Method | Matrix Phase | Pore Size Range, μm | Pore Shape | Porosity Range, % | Young’s Modulus Range, GPa | Method to Measure Young’s Modulus | Theoretical Model | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| Binary alloys | |||||||||
| Ni-Ti (at.%) | Space-holder NaCl | 70–400 μm | Blocky | 32–36 | 10–25 | CT 0.05 mm/min | [99] | ||
| Ti–10Mg (wt.%) | Space-holder NH4HCO3 | 100–400 μm | Irregular | 13.8–54.8 | 7.12–1.5 | CT 0.5 mm/min | [90] | ||
| Ti-51Ni (at.%) | Space-holder Mg | Austenite + quite small MgO | 250–600 μm | Equiaxial | 49–64 | 8.7–2.9 | CT 0.1 mm/min | [89] | |
| Ti-5Al (wt.%) | Space-holder NH4HCO3 | α-phase | Promedio = 225 μm | Equiaxial | 57–85 | 13–3.5 | CT 1 × 10−2 s−1 | [17] | |
| Ti-5W (wt.%) | freeze-cast | β-phase + Widmanstätten α/β structure | Lamellar equiaxed | 39 | 25.4 | CT (1) RT (2) 1.0 × 10−3 s−1 | G-A α = 1 n = 2 | [85] | |
| Ti-Zr (at.%) | Space-holder ammonium hydrogen carbonate | 200–500 μm | Irregular | 70 | 15.3 | CT RT 1 × 10−3 s−1 | [91] | ||
| Ti-13Ta | Dealloying method adding Mg | β-phase | 0.1–90 μm | Irregular | 60–76 | 0.65–0.53 | CT 1 × 10−3 s−1 | [88] | |
| Ternary alloys | |||||||||
| Ti-18Nb-4Sn (wt.%) | Space-holder NH4HCO3 | β-phase | 50–450 | Irregular | 0–60 | 75.8–10.9 | CT 1.0 × 10−4 s−1 | G-A α = 1 n = 2 | [7] |
| Ti-22Nb-6Ta (at.%) | Space-holder pmmc (3) | β-phase and small quantities of α-phase, α’’ + TiC, (Nb,Ti)C + NbC | ~100–3200 μm | Irregular | 33–57.4 | 14.6–3.7 | CT 2.0 × 10−3 s−1 | [81] | |
| Ti-30Nb-13Ta (at.%) | α-phase + y-phase (4) | 0 | 49 | CT 0.05 mm/min | K-S m = 3.95 | [57] | |||
| Ti-22Nb-(2-8)Zr (at.%) | Space-holder pmmc | β-phase and small quantities of α-phase, α’’ + TiC, (Nb,Ti)C + NbC | 100–3100 μm | Irregular | 24.8–66.8 | 15.5–1.5 | CT 2.0 × 10−3 s−1 | [81] | |
| Ti-35-Zr-28Nb | Space-holder NH4HCO3 | β-phase | 100 to 500 μm | Irregular | 35–55 | 6.9–1.8 | CT 2 × 10−3 s−1 | [93,94] | |
| Ti-13Ta-12Sn (at.%) | Space-holder (NH4)2CO3 | β-phase with bimodal microstructure | 200 to 500 μm | Blocky Irregular | 24–55 | 39.4–11.8 | Ultra-sound, transmission technique | G-A α = 0.98 n = 2.9 | [92] |
| Ti-13Ta-12Sn (at.%) | Space-holder (NH4)2CO3 | β-phase | 200–500 μm | Blocky Irregular | 24–52 | 56.1–13.4 | Ultra-sound, transmission technique | G-A α = 1.01 n = 1.96 | [92] |
| Ti-6Al-4V (wt.%) | Space-holder NaCl | α-phase + β-phase | 150–250 μm | 44.7–70 | 33–9.5 | CT 0.5mm/min | G-A α = 1.0 n = 2.0 | [98] | |
| Ti-6Al-4V (wt.%) | Selective laser melting | α-phase + β-phase | 559–777 μm (top view) 783–1014 μm (side view) | Cylindrical | 43–71 | 55–9.7 | CT RT 1 × 10−4 s−1 | G-A α = 1.5 n = 2.0 | [96] |
| Ti-6Al-4V (wt.%) | Selective laser melting | 401–801 μm | Cylindrical | 44.9–56.2 | 7.5–5.0 | CT 1.5 mm/min | [95] | ||
| Ti-6Al-4V | Space-holder (NH4)2CO3 | α-phase + β-phase | Irregular | 31–42 | 5.6–3.2 | Ultra-sound, transmission technique | [19] | ||
| Ti-6Al-4V | Electron beam melting | α-phase + β-phase | 2.5–4 mm | Diamond unit cell | 80.1–81.5 | 2.6–2.0 | CT RT 1 × 10−4 s−1 | G-A α = 1.5 n = 2.0 | [20] |
| Multicomponent alloys | |||||||||
| Ti-34Nb-29Ta-xMn (x = 2, 4 and 6 wt.%). | Space-holder NH4HCO3 | α-phase + β-phase + TiO | 100–600 μm <20 μm | Irregular | 50 | 27–33 | CT 0.125 mm/min | K-N b = 3.36 P-N m = 1.93 pc = 83% P-G a = 1 Pc = 83% G-A α = 1 n = 2 N Ff = 0.7 | [4] |
| Ti-20Nb-11Ta-16Fe-1Mn (at.%) | Space-holder NH4HCO3 | α-phase + β-phase | 10 μm | Irregular | 25–37 | 11.7–4.5 | Ultra-sound, transmission technique | [97] | |
| Ti-20Nb-11Ta-16Fe-1Mn (at.%) | Arc-melting | α-phase + β-phase | 3.5 | 84.3 | Ultra-sound, transmission technique | [97] | |||
| Ti-13Zr-13Ta-3Nb (wt.%) | Space-holder NaCl | β-phase | 100 to 600 μm | Equiaxial–Irregular | 40–60 | 9–4.5 | Ultra-sound, transmission technique | K-N b = 6.4 G-A α = 0.5 n = 2.1 | [13] |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Z.; Asghar, M.M.; Zaidi, S.A.H.; Nawaz, K.; Wang, B.; Zhao, W.; Xu, F. The Dynamic Relationship between Economic Growth and Life Expectancy: Contradictory Role of Energy Consumption and Financial Development in Pakistan. Struct. Chang. Econ. Dyn. 2020, 53, 257–266. [Google Scholar] [CrossRef]
- Roser, M.; Ortiz-Ospina, E.; Ritchie, H. Our World in Data, Life Expectancy. 2019. Available online: https://ourworldindata.org/life-expectancy#all-charts-preview (accessed on 15 July 2021).
- Geetha, M.; Singh, A.K.; Asokamani, R.; Gogia, A.K. Ti based biomaterials, the ultimate choice for orthopaedic implants—A review. Prog. Mater. Sci. 2009, 54, 397–425. [Google Scholar] [CrossRef]
- Aguilar, C.; Guerra, C.; Lascano, S.; Guzman, D.; Rojas, P.A.; Thirumurugan, M.; Bejar, L.; Medina, A. Synthesis and characterization of Ti–Ta–Nb–Mn foams. Mater. Sci. Eng. C 2016, 58, 420–431. [Google Scholar] [CrossRef] [PubMed]
- Tyagi, S.A.; Manjaiah, M. Additive manufacturing of titanium-based lattice structures for medical applications—A review. Bioprinting 2023, 30, e00267. [Google Scholar] [CrossRef]
- Leyens, C.; Peters, M. Titanium and Titanium Alloys: Fundamentals and Applications; Wiley-VCH: Hoboken, NJ, USA, 2003; ISBN 3527305343. [Google Scholar]
- Xiong, J.; Li, Y.; Wang, X.; Hodgson, P.; Wen, C. Mechanical properties and bioactive surface modification via alkali-heat treatment of a porous Ti–18Nb–4Sn alloy for biomedical applications. Acta Biomater. 2008, 4, 1963–1968. [Google Scholar] [CrossRef] [PubMed]
- Abhash, A.; Singh, P.; Ch, V.A.N.; Sathaiah, S.; Kumar, R.; Gupta, G.K.; Mondal, D.P. Study of newly developed Ti–Al–Co alloys foams for bioimplant application. Mater. Sci. Eng. A 2020, 774, 138910. [Google Scholar] [CrossRef]
- Peters, M.; Kumpfert, J.; Ward, C.H.; Leyens, C. Titanium alloys for aerospace applications. Adv. Eng. Mater. 2003, 5, 419–427. [Google Scholar] [CrossRef]
- Nomura, N.; Kohama, T.; Oh, I.H.; Hanada, S.; Chiba, A.; Kanehira, M.; Sasaki, K. Mechanical properties of porous Ti–15Mo–5Zr–3Al compacts prepared by powder sintering. Mater. Sci. Eng. C 2005, 25, 330–335. [Google Scholar] [CrossRef]
- Cai, X.; Follet, H.; Peralta, L.; Gardegaront, M.; Farlay, D.; Gauthier, R.; Yu, B.; Gineyts, E.; Olivier, C.; Langer, M.; et al. Anisotropic elastic properties of human femoral cortical bone and relationships with composition and microstructure in elderly. Acta Biomater. 2019, 90, 254–266. [Google Scholar] [CrossRef]
- Lopes, E.S.N.; Contieri, R.J.; Button, S.T.; Caram, R. Femoral hip stem prosthesis made of graded elastic modulus metastable b Ti Alloy. Mater. Des. 2015, 69, 30–36. [Google Scholar] [CrossRef]
- Aguilar, C.; Arancibia, M.; Alfonso, I.; Sancy, M.; Tello, K.; Salinas, V.; De Las Cuevas, F. Influence of Porosity on the Elastic Modulus of Ti-Zr-Ta-Nb Foams with a Low Nb Content. Metals 2019, 9, 176. [Google Scholar] [CrossRef]
- Pérez, L.; Lascano, S.; Aguilar, C.; Domancic, D.; Alfonso, I. Simplified fractal FEA model for the estimation of the Young’s modulus of Ti foams obtained by powder metallurgy. Mater. Des. 2015, 83, 276–283. [Google Scholar] [CrossRef]
- Zhu, K.; Li, C.; Zhu, Z.; Liu, C.S. Measurement of the dynamic Young ’ s modulus of porous titanium and Ti6Al4V. J. Mater. Sci. 2007, 42, 7348–7353. [Google Scholar] [CrossRef]
- Aguilar, C.; San Martín, F.; Martínez, C.; Cámara, B.; Claverías, F.; Undabarrena, A.; Sancy, M.; Salinas, V.; Muñoz, L. Improving mechanical properties and antibacterial response of α/β ternary Ti–Ta alloy foams for biomedical uses. J. Mater. Res. Technol. 2023, 24, 8735–8753. [Google Scholar] [CrossRef]
- Singh, P.; Singh, I.B.; Mondal, D.P. A comparative study on compressive deformation and corrosion behaviour of heat treated Ti4wt % Al foam of di ff erent porosity made of milled and unmilled powders. Mater. Sci. Eng. C 2019, 98, 918–929. [Google Scholar] [CrossRef] [PubMed]
- Jenei, P.; Choi, H.; Tóth, A.; Choe, H.; Gubicza, J. Mechanical behavior and microstructure of compressed Ti foams synthesized via freeze casting. J. Mech. Behav. Biomed. Mater. 2016, 63, 407–416. [Google Scholar] [CrossRef] [PubMed]
- Martínez, C.; Guerra, C.; Silva, D.; Cubillos, M.; Briones, F.; Muñoz, L.; Páez, M.A.; Aguilar, C.; Sancy, M. Effect of porosity on mechanical and electrochemical properties of Ti–6Al–4V alloy. Electrochim. Acta 2020, 338, 2–11. [Google Scholar] [CrossRef]
- Chen, S.Y.; Kuo, C.N.; Su, Y.L.; Huang, J.C.; Wu, Y.C.; Lin, Y.H.; Chung, Y.C.; Ng, C.H. Microstructure and fracture properties of open-cell porous Ti-6Al-4V with high porosity fabricated by electron beam melting. Mater. Charact. 2018, 138, 255–262. [Google Scholar] [CrossRef]
- Nawaz, A.; Rani, S. Fabrication methods and property analysis of metal foams—A technical overview. Mater. Sci. Technol. 2023, 39, 1877–1902. [Google Scholar] [CrossRef]
- Guler, K.A.; Acar, S. Lost Foam Casting of Metallic Parts and Structures. Encycl. Mater. Met. Alloys 2022, 4, 73–86. [Google Scholar]
- Fan, Y.; Li, S.; Yin, B.; Li, Y.; Tu, Z.; Cai, Z. Preparation and microstructure evolution of novel ultra-low thermal conductivity calcium silicate-based ceramic foams. Ceram. Int. 2022, 48, 21602–21611. [Google Scholar] [CrossRef]
- Ronca, D.; Langella, F.; Chierchia, M.; D’Amora, U.; Russo, T.; Domingos, M.; Gloria, A.; Bartolo, P.; Ambrosio, L. Bone Tissue Engineering: 3D PCL-based Nanocomposite Scaffolds with Tailored Properties. Procedia CIRP 2016, 49, 51–54. [Google Scholar] [CrossRef]
- Maietta, S.; Gloria, A.; Improta, G.; Richetta, M.; De Santis, R.; Martorelli, M. A further analysis on Ti6Al4V lattice structures manufactured by selective laser melting. J. Healthc. Eng. 2019, 2019, 3212594. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.; Ashcroft, I.A.; Hague, R.J.M.; Kennedy, A.R.; Clare, A.T. Salt-metal feedstocks for the creation of stochastic cellular structures with controlled relative density by powder bed fabrication. Mater. Des. 2018, 149, 63–72. [Google Scholar] [CrossRef]
- Shbeh, M.M.; Goodall, R. Open Celled Porous Titanium. Adv. Eng. Mater. 2017, 19, 1600664. [Google Scholar] [CrossRef]
- Guo, A.X.Y.; Cheng, L.; Zhan, S.; Zhang, S.; Xiong, W.; Wang, Z.; Wang, G.; Cao, S.C. Biomedical applications of the powder-based 3D printed titanium alloys: A review. J. Mater. Sci. Technol. 2022, 125, 252–264. [Google Scholar] [CrossRef]
- Gibson, L.; Ashby, M. Cellular Solids: Structure and Properties; Cambridge University Press: New York, NY, USA, 1997. [Google Scholar]
- Pabst, W.; Gregorová, E. New relation for the porosity dependence of the effective tensile modulus of brittle materials. J. Mater. Sci. 2004, 39, 3501. [Google Scholar] [CrossRef]
- Spriggs, R. Expression for Effect of Porosity on Elastic Modulus of Polycrystalline Refractory Materials, Particularly Aluminum Oxide. J. Am. Ceram. Soc. 1961, 44, 628–629. [Google Scholar] [CrossRef]
- Phani, K.; Niyogi, S. Young’s modulus of porous brittle solids. J. Mater. Sci. 1987, 22, 257–263. [Google Scholar] [CrossRef]
- Warren, W.E.; Kraynik, A.M. The Linear Elastic Properties of Open-Cell Foams. J. Appl. Mech. 2013, 55, 341–346. [Google Scholar] [CrossRef]
- Knudsen, F. Dependence of Mechanical Strength of Brittle Polycrystalline Specimens on Porosity and Grain Size. J. Am. Ceram. Soc. 1959, 42, 373–397. [Google Scholar] [CrossRef]
- Nielsen, L. Elasticity and Damping of Porous Materials and Impregnated Materials. J. Am. Ceram. Soc. 1984, 67, 93–98. [Google Scholar] [CrossRef]
- Zhu, H.X.; Mills, N.J.; Knott, J.F. Analysis of the high strain compression open-cell foams. J. Mech. Phys. Solids 1997, 45, 1875–1904. [Google Scholar] [CrossRef]
- Ryan, G.; Pandit, A.; Apatsidis, D.P. Fabrication methods of porous metals for use in orthopaedic applications. Biomaterials 2006, 27, 2651–2670. [Google Scholar] [CrossRef]
- Pérez, L.; Lascano, S.; Aguilar, C.; Estay, D.; Messner, U.; Figueroa, I.A.; Alfonso, I. DEM-FEA estimation of pores arrangement effect on the compressive Young’s modulus for Mg foams. Comput. Mater. Sci. 2015, 110, 281–286. [Google Scholar] [CrossRef]
- Trueba, P.; Chicardi, E.; Torres, Y. Development and implementation of a sequential compaction device to obtain radial graded porosity cylinders. J. Manuf. Process. 2020, 50, 142–153. [Google Scholar] [CrossRef]
- Carvalho, O.; Buciumeanu, M.; Miranda, G.; Madeira, S.; Silva, F.S. Development of a method to produce FGMs by controlling the reinforcement distribution. Mater. Des. 2016, 92, 233–239. [Google Scholar] [CrossRef]
- Oh, I.; Segawa, H.; Nomura, N.; Hanada, S. Microstructures and Mechanical Properties of Porosity-Graded Pure Titanium Compacts. Mater. Trans. 2003, 44, 657–660. [Google Scholar] [CrossRef]
- Traini, T.; Mangano, C.; Sammons, R.L.; Mangano, F.; Macchi, A.; Piattelli, A. Direct laser metal sintering as a new approach to fabrication of an isoelastic functionally graded material for manufacture of porous titanium dental implants. Dent. Mater. 2008, 24, 1525–1533. [Google Scholar] [CrossRef]
- Torres, Y.; Trueba, P.; Pavón, J.J.; Chicardi, E.; Kamm, P.; García-Moreno, F.; Rodríguez-Ortiz, J.A. Design, processing and characterization of titanium with radial graded porosity for bone implants. Mater. Des. 2016, 110, 179–187. [Google Scholar] [CrossRef]
- Salvo, C.; Aguilar, C.; Cardoso-Gil, R.; Medina, A.; Bejar, L.; Mangalaraja, R.V. Study on the microstructural evolution of Ti-Nb based alloy obtained by high-energy ball milling. J. Alloys Compd. 2017, 720, 254–263. [Google Scholar] [CrossRef]
- Hanawa, T. Recent Development of New Alloys for Biomedical Use Takao Hanawa. Mater. Sci. Forum 2006, 512, 243–248. [Google Scholar] [CrossRef]
- Chandrasekaran, M.; Xia, Z.S. Effect of alloying time and composition on the mechanical properties of Ti alloy. Mater. Sci. Eng. A 2005, 394, 220–228. [Google Scholar] [CrossRef]
- Niinomi, M.; Nakai, M.; Hieda, J. Development of new metallic alloys for biomedical applications. Acta Biomater. 2012, 8, 3888–3903. [Google Scholar] [CrossRef] [PubMed]
- Chinnappan, R.; Panigrahi, B.K.; van de Walle, A. First-principles study of phase equilibrium in Ti–V, Ti–Nb, and Ti–Ta alloys. Calphad 2016, 54, 125–133. [Google Scholar] [CrossRef]
- Yu, Q.; Kacher, J.; Gammer, C.; Traylor, R.; Samanta, A.; Yang, Z.; Minor, A.M. In situ TEM observation of FCC Ti formation at elevated temperatures. Scr. Mater. 2017, 140, 9–12. [Google Scholar] [CrossRef]
- Van Heerden, D.; Josell, D.; Shechtman, D. The formation of f.c.c. Titanium in titanium-aluminum multilayers. Acta Mater. 1996, 44, 297–306. [Google Scholar] [CrossRef]
- Prasanthi, T.N.; Sudha, C.; Ravikirana, S.S. Formation and reversion of metastable fcc phase in a Ti-5Ta-2Nb explosive clad. Mater. Charact. 2016, 116, 24–32. [Google Scholar] [CrossRef]
- Zhang, D.L.; Ying, D.Y. Formation of fcc titanium during heating high energy ball milled Al-Ti powders. Mater. Lett. 2002, 52, 329–333. [Google Scholar] [CrossRef]
- Ahuja, R.; Fraser, H.L. Structure and mechanical properties of nanolaminated Ti-Al thin films. JOM 1994, 46, 35–39. [Google Scholar] [CrossRef]
- Ren, J.; Sun, Q.; Xiao, L.; Ding, X.; Sun, J. Size-dependent of compression yield strength and deformation mechanism in titanium single-crystal nanopillars orientated [0001] and [112−0]. Mater. Sci. Eng. A 2014, 615, 22–28. [Google Scholar] [CrossRef]
- Lindemann, I.; Schmidt, R.; Pilz, S.; Gebel, B.; Teresiak, A.; Gebert, A. Ultrafine-grained Ti-40Nb prepared by reactive milling of the elements in hydrogen. J. Alloys Compd. 2017, 729, 1244–1249. [Google Scholar] [CrossRef]
- Chicardi, E.; García-Garrido, C.; Sayagués, M.J.; Torres, Y.; Amigó, V.; Aguilar, C. Development of a novel fcc structure for an amorphous-nanocrystalline Ti-33Nb-4Mn (at.%) ternary alloy. Mater. Charact. 2018, 135, 46–56. [Google Scholar] [CrossRef]
- Chicardi, E.; Gutiérrez-gonzález, C.F.; Sayagués, M.J.; García-garrido, C. Development of a novel TiNbTa material potentially suitable for bone replacement implants. Mater. Des. 2018, 145, 88–96. [Google Scholar] [CrossRef]
- Wu, H.C.; Kumar, A.; Wang, J.; Bi, X.F.; Tomé, C.N.; Zhang, Z.; Mao, S.X. Rolling-induced Face Centered Cubic Titanium in Hexagonal Close Packed Titanium at Room Temperature. Sci. Rep. 2016, 6, 24370. [Google Scholar] [CrossRef]
- Bolokang, A.S.; Phasha, M.J.; Motaung, D.E.; Cummings, F.R.; Muller, T.F.G.; Arendse, C.J. Microstructure and phase transformation on milled and unmilled Ti induced by water quenching. Mater. Lett. 2014, 132, 157–161. [Google Scholar] [CrossRef]
- Aguilar, C.; Pio, E.; Medina, A.; Martínez, C.; Sancy, M.; Guzman, D. Evolution of synthesis of FCC nanocrystalline solid solution and amorphous phase in the Ti-Ta based alloy by high milling energy. J. Alloys Compd. 2021, 854, 155980. [Google Scholar] [CrossRef]
- ASTM D2845-08; Standard Test Method for Laboratory Determination of Pulse Velocities and Ultrasonic Elastic Constants of Rock. ASTM International: West Conshohocken, PA, USA, 2013.
- Lutterotti, L.; Matthies, S.; Wenk, H.R. MAUD: A friendly Java program for material analysis using diffraction. Newsl. CDP 1999, 21, 14–15. [Google Scholar]
- Lutterotti, L.; Scardi, P. Simultaneous structure and size–strain refinement by the Rietveld method. J. Appl. Crystallogr. 1990, 23, 246–252. [Google Scholar] [CrossRef]
- Scardi, P.; Lutterotti, L.; Maistrelli, P. Experimental determination of the instrumental broadening in the Bragg–Brentano geometry. Powder Diffr. 1994, 9, 180–186. [Google Scholar] [CrossRef]
- Delhez, R.; de Keijser Th, H.; Langford, J.I.; Louër, D.; Mittemeijer, E.J.; Sonneveld, E.J. Crystal imperfection broadening and peak shape in the Rietveld method. In The Rietveld Method; Young, R.A., Ed.; Oxford University: Oxford, UK, 1993. [Google Scholar]
- de Keijser, T.H.; Langford, J.I.; Mittemeijer, E.J.; Vogels, A.B.P. Use of the Voigt function in a single-line method for the analysis of X-ray diffraction line broadening. J. Appl. Crystallogr. 1982, 15, 308–314. [Google Scholar] [CrossRef]
- Chapter 3: Theory Documentation. Material Designer Feature 2020 R2. 2020. Available online: www.ansys.com (accessed on 15 July 2021).
- Imwinkelried, T. Mechanical properties of open-pore titanium foamMechanical properties of open-pore titanium foam. J. Biomed. Mater. Res. A 2007, 81, 964–970. [Google Scholar] [CrossRef]
- Tanwongwan, W.; Carmai, J. Finite Element Modelling of Titanium Foam Behaviour for Dental Application. In Proceedings of the World Congress on Engineering, London, UK, 6–8 July 2011; Volume III, pp. 4–9. [Google Scholar]
- Aguilar, C.; Castro, F.; Martínez, V.; Guzmán, D.; de las Cuevas, F.; Lozada, L.; Vielma, N. Structural study of nanocrystalline solid solution of Cu–Mo obtained by mechanical alloying. Mater. Sci. Eng. A 2012, 548, 189–194. [Google Scholar] [CrossRef]
- Chakraborty, J.; Kumar, K.; Ranjan, R.; Chowdhury, S.G.; Singh, S.R. Thickness-dependent fcc-hcp phase transformation in polycrystalline titanium thin films. Acta Mater. 2011, 59, 2615–2623. [Google Scholar] [CrossRef]
- Chatterjee, P.; Gupta, S.P. Sen An X-ray diffraction study of nanocrystalline titanium prepared by high-energy vibrational ball milling. Appl. Surf. Sci. 2001, 182, 372–376. [Google Scholar] [CrossRef]
- Chatterjee, P.; Gupta, S.P. Sen An X-ray diffraction study of strain localization and anisotropic dislocation contrast in nanocrystalline titanium. Philos. Mag. A 2001, 81, 49–60. [Google Scholar] [CrossRef]
- Aguayo, A.; Murrieta, G.; de Coss, R. Elastic stability and electronic structure of fcc Ti, Zr, and Hf: A first-principles study. Phys. Rev. B 2002, 65, 092106. [Google Scholar] [CrossRef]
- Manna, I.; Chattopadhyay, P.P.; Nandi, P.; Banhart, F.; Fecht, H.J. Formation of face-centered-cubic titanium by mechanical attrition. J. Appl. Phys. 2003, 93, 1520–1524. [Google Scholar] [CrossRef]
- Jing, R.; Liu, C.Y.; Ma, M.Z.; Liu, R.P. Microstructural evolution and formation mechanism of FCC titanium during heat treatment processing. J. Alloys Compd. 2013, 552, 202–207. [Google Scholar] [CrossRef]
- Rhodes, C.G.; Williams, J.C. Observations of an interface phase in the alpha/beta boundaries in titanium alloys. Metall. Trans. A 1975, 6, 1670–1671. [Google Scholar] [CrossRef]
- Xiong, S.; Qi, W.; Huang, B.; Wang, M.; Li, Z.; Liang, S. Size-temperature phase diagram of titanium nanosolids. J. Phys. Chem. C 2012, 116, 237–241. [Google Scholar] [CrossRef]
- Torres, Y.; Pavón, J.J.; Nieto, I.; Rodríguez, J.A. Conventional powder metallurgy process and characterization of porous titanium for biomedical applications. Metall. Mater. Trans. B 2011, 42, 891–900. [Google Scholar] [CrossRef]
- Kato, K.; Ochiai, S.; Yamamoto, A.; Daigo, Y.; Honma, K.; Matano, S.; Omori, K. Novel multilayer Ti foam with cortical bone strength and cytocompatibility. Acta Biomater. 2013, 9, 5802–5809. [Google Scholar] [CrossRef]
- Rivard, J.; Brailovski, V.; Dubinskiy, S.; Prokoshkin, S. Fabrication, morphology and mechanical properties of Ti and metastable Ti-based alloy foams for biomedical applications. Mater. Sci. Eng. C 2014, 45, 421–433. [Google Scholar] [CrossRef]
- Hsu, H.-C.; Wu, S.; Hsu, S.; Syu, J.; Ho, W. The structure and mechanical properties of as-cast Ti–25Nb–xSn alloys for biomedical applications. Mater. Sci. Eng. A 2013, 568, 1–7. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. The mechanics of three-dimensional cellular materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 1982, 382, 43–59. [Google Scholar] [CrossRef]
- Ashby, M.F.; Evans, T.; Fleck, N.A.; Hutchinson, J.W.; Wadley, H.N.G.; Gibson, L.J. Metal Foams: A Design Guide; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Choi, H.; Shil, S.; Choe, H. Study of the compression and wear-resistance properties of freeze-cast Ti and Ti–5W alloy foams for biomedical applications. J. Mech. Behav. Biomed. Mater. 2017, 72, 66–73. [Google Scholar] [CrossRef]
- Manonukul, A.; Srikudvien, P.; Tange, M. Microstructure and mechanical properties of commercially pure titanium foam with varied cell size fabricated by replica impregnation method. Mater. Sci. Eng. A 2016, 650, 432–437. [Google Scholar] [CrossRef]
- Torres, Y.; Lascano, S.; Bris, J.; Pavón, J.; Rodriguez, J. Development of porous titanium for bi-omedical applications: A comparison between loose sintering and space-holder techniques. Mater. Sci. Eng. C 2014, 37, 148–155. [Google Scholar] [CrossRef]
- Adamek, G.; Kozlowski, M.; Jurczyk, M.; Wirstlein, P.; Zurawski, J.; Jakubowicz, J. Formation and properties of biomedical ti-ta foams prepared from nanoprecursors by thermal dealloying process. Materials 2019, 12, 2668. [Google Scholar] [CrossRef]
- Ipek Nakas, G.; Dericioglu, A.F.; Bor, S. Fatigue behavior of TiNi foams processed by the magnesium space holder technique. J. Mech. Behav. Biomed. Mater. 2011, 4, 2017–2023. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Tao, J.; Zhang, J.L.; Wang, T. Effects of addition of NH4HCO3 on pore characteristics and compressive properties of porous Ti-10%Mg composites. Trans. Nonferrous Met. Soc. China (Engl. Ed.) 2011, 21, 1074–1079. [Google Scholar] [CrossRef]
- Wen, C.E.; Yamada, Y.; Hodgson, P.D. Fabrication of novel TiZr alloy foams for biomedical applications. Mater. Sci. Eng. C 2006, 26, 1439–1444. [Google Scholar] [CrossRef]
- Aguilar, C.; Aguirre, T.; Martínez, C.; De Barbieri, F.; Martín, F.S.; Salinas, V.; Alfonso, I. Improving the mechanical strength of ternary beta titanium alloy (Ti-Ta-Sn) foams, using a bimodal microstructure. Mater. Des. 2020, 195, 108945. [Google Scholar] [CrossRef]
- Xu, W.; Tian, J.; Liu, Z.; Lu, X.; Hayat, M.D.; Yan, Y.; Li, Z.; Qu, X.; Wen, C. Novel porous Ti35Zr28Nb scaffolds fabricated by powder metallurgy with excellent osteointegration ability for bone-tissue engineering applications. Mater. Sci. Eng. C 2019, 105, 110015. [Google Scholar] [CrossRef]
- Li, Y.; Ding, Y.; Munir, K.; Lin, J.; Brandt, M.; Atrens, A.; Xiao, Y.; Kanwar, J.R.; Wen, C. Novel β-Ti35Zr28Nb alloy scaffolds manufactured using selective laser melting for bone implant applications. Acta Biomater. 2019, 87, 273–284. [Google Scholar] [CrossRef]
- Ran, Q.; Yang, W.; Hu, Y.; Shen, X.; Yu, Y.; Xiang, Y.; Cai, K. Osteogenesis of 3D printed porous Ti6Al4V implants with different pore sizes. J. Mech. Behav. Biomed. Mater. 2018, 84, 1–11. [Google Scholar] [CrossRef]
- Chen, S.Y.; Huang, J.C.; Pan, C.T.; Lin, C.H.; Yang, T.L.; Huang, Y.S.; Ou, C.H.; Chen, L.Y.; Lin, D.Y.; Lin, H.K.; et al. Microstructure and mechanical properties of open-cell porous Ti-6Al-4V fabricated by selective laser melting. J. Alloys Compd. 2017, 713, 248–254. [Google Scholar] [CrossRef]
- Guerra, C.; Sancy, M.; Walczak, M.; Martínez, C.; Ringuedé, A.; Cassir, M.; Han, J.; Ogle, K.; de Melo, H.G.; Salinas, V.; et al. Effect of added porosity on a novel porous Ti-Nb-Ta-Fe-Mn alloy exposed to simulated body fluid. Mater. Sci. Eng. C 2020, 111, 110758. [Google Scholar] [CrossRef]
- Quan, Y.; Zhang, F.; Rebl, H.; Nebe, B.; Keßler, O.; Burkel, E. Ti6Al4V foams fabricated by spark plasma sintering with post-heat treatment. Mater. Sci. Eng. A 2013, 565, 118–125. [Google Scholar] [CrossRef]
- Bansiddhi, A.; Dunand, D.C. Shape-memory NiTi foams produced by replication of NaCl space-holders. Acta Biomater. 2008, 4, 1996–2007. [Google Scholar] [CrossRef] [PubMed]
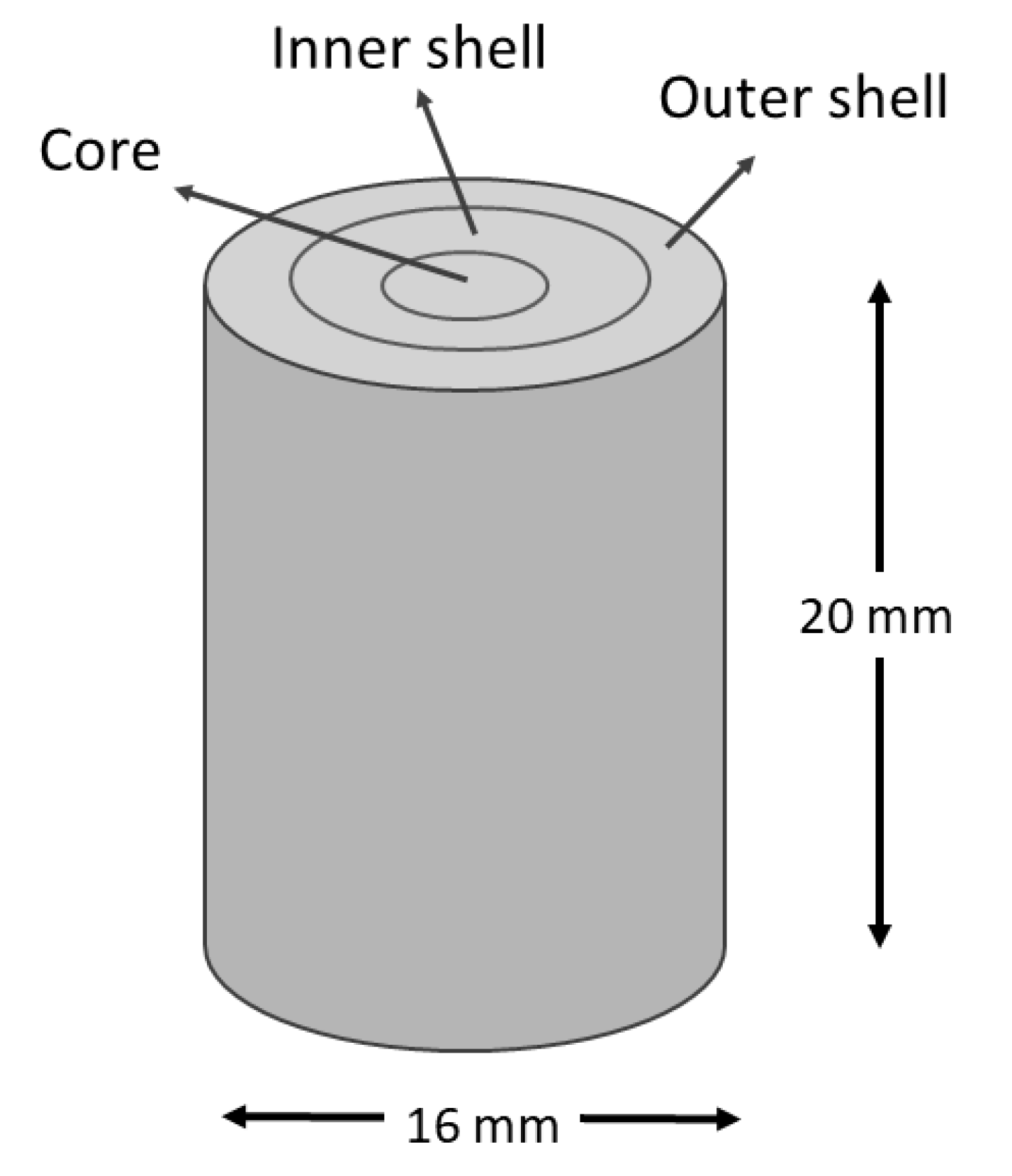
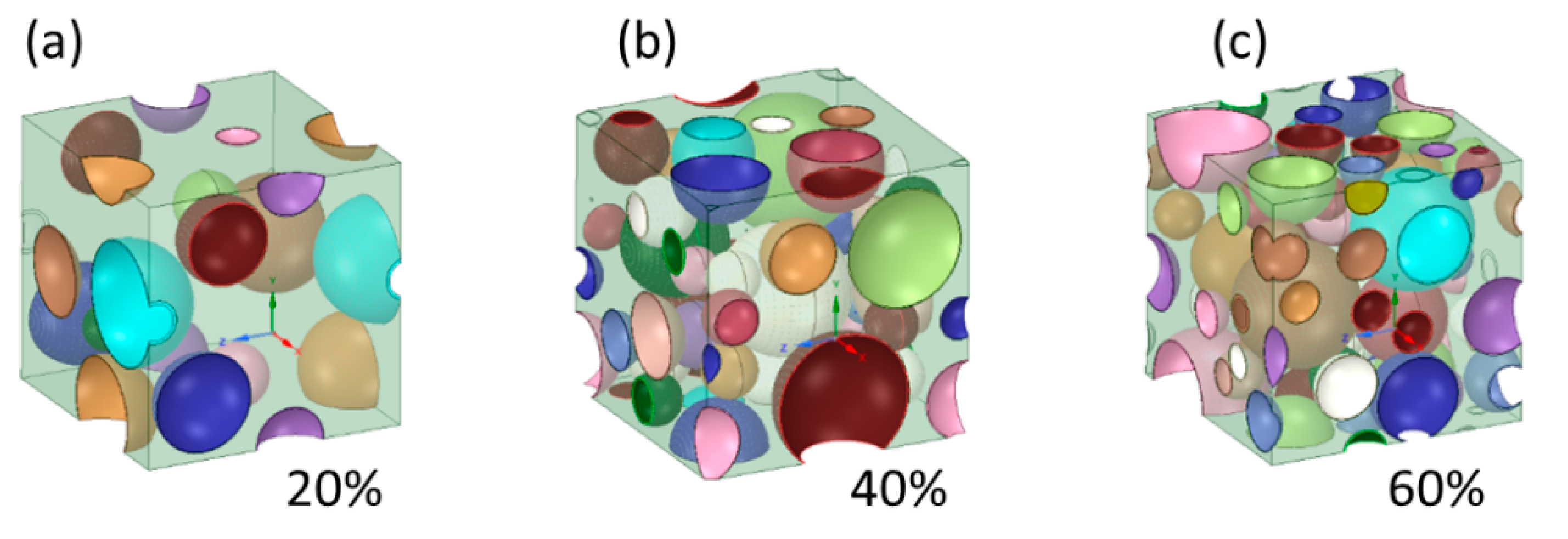



| Porosity (v/v%) | ||||
|---|---|---|---|---|
| Radial Graded Porosity Configuration (pc) | Core | Inner Shell | Outer Shell | Average Porosity (ap) |
| pc-1 | CS | CS | CS | 0 |
| pc-2 | CS | 20 | 40 | 20 |
| pc-3 | CS | 30 | 60 | 30 |
| pc-4 | 20 | 40 | 60 | 40 |
| Material | Young’s Modulus, GPa | Poisson Coefficient | Density, g/m3 |
|---|---|---|---|
| cp-Ti (grade 4) | 110 | 0.31 | 4.51 |
| Ti-13Ta-6Mn (TTM) | 69 | 0.31 | 5.96 |
| Ti-13Ta-(TT) | 61 | 0.31 | 7.30 |
| Ti-13Ta-6Sn (TTS) | 65 | 0.31 | 6.24 |
| Alloy | Lattice Parameter, nm | Crystallite Size, nm | Microstrain, <ε2>1/2 | Amount, wt.% | GofF | Rwp |
|---|---|---|---|---|---|---|
| TTM | 0.42292 | 7.6 | 6.9 × 10−3 | 76 | 1.0 | 8.8 |
| TT | 0.42247 | 7.3 | 5.8 × 10−3 | 77.8 | 1.0 | 10.0 |
| TTS | 0.42302 | 7.0 | 7.6 × 10−3 | 73.5 | 1.1 | 10.5 |
| Material | Properties | Gibson and Ashby | Knudsen and Spriggs | Phani and Niyogi | Pabst and Gregorová | Nielsen |
|---|---|---|---|---|---|---|
| cp-Ti | E = 111 GPa d = 4.50 g/cc | α = 1 n = 2.5 | b = 3.36 | m = 1.93 pc = 90% | a = 1 pc = 90% | Ff = 0.5 |
| Alloy | Properties | Gibson–Ashby | Knudsen–Spriggs | Phani–Niyogi | Pabst–Gregorová | Nielsen |
|---|---|---|---|---|---|---|
| Ti-13Ta-6Mn | E = 70 GPa d = 5.96 g/cc | R-square = 0.96 α = 1.23 n = 2.57 | R-square = 0.99 b = 3.06 | R-square = 0.56 m = 1.45 pc = 90% | R-square = 0.94 a = 1.1 pc = 78% | R-square = 0.98 Ff = 0.52 |
| Ti-13Ta | E = 57 GPa d = 7.30 g/cc | R-square = 0.96 α = 1.0 n = 2.51 | R-square = 0.99 b = 3.01 | R-square = 0.89 m = 2.05 pc = 90% | R-square = 0.95 a = 1.1 pc = 82% | R-square = 0.98 Ff = 0.58 |
| Ti-13Ta-6Sn | E = 51 GPa d = 6.24 g/cc | R-square = 0.97 α = 0.98 n = 2.49 | R-square = 0.99 b = 3.05 | R-square = 0.90 m = 2.46 pc = 90% | R-square = 0.95 a = 1.1 pc = 81% | R-square = 0.98 Ff = 0.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar, C.; Alfonso, I.; González, D.; Pio, E.; Neves, G.O.; De Barbieri, F.; Sancy, M.; Muñoz, L. Simulation of the Influence of the Radial Graded Porosity Distribution on Elastic Modulus of γ/β Phase Ti-Based Alloy Foams for Bone Implant. Materials 2023, 16, 7320. https://doi.org/10.3390/ma16237320
Aguilar C, Alfonso I, González D, Pio E, Neves GO, De Barbieri F, Sancy M, Muñoz L. Simulation of the Influence of the Radial Graded Porosity Distribution on Elastic Modulus of γ/β Phase Ti-Based Alloy Foams for Bone Implant. Materials. 2023; 16(23):7320. https://doi.org/10.3390/ma16237320
Chicago/Turabian StyleAguilar, Claudio, Ismelí Alfonso, Daniel González, Edgar Pio, Guilherme Oliveira Neves, Flavio De Barbieri, Mamie Sancy, and Lisa Muñoz. 2023. "Simulation of the Influence of the Radial Graded Porosity Distribution on Elastic Modulus of γ/β Phase Ti-Based Alloy Foams for Bone Implant" Materials 16, no. 23: 7320. https://doi.org/10.3390/ma16237320
APA StyleAguilar, C., Alfonso, I., González, D., Pio, E., Neves, G. O., De Barbieri, F., Sancy, M., & Muñoz, L. (2023). Simulation of the Influence of the Radial Graded Porosity Distribution on Elastic Modulus of γ/β Phase Ti-Based Alloy Foams for Bone Implant. Materials, 16(23), 7320. https://doi.org/10.3390/ma16237320








