General Planar Ideal Flow Solutions with No Symmetry Axis
Abstract
:1. Introduction
2. Statement of the Problem
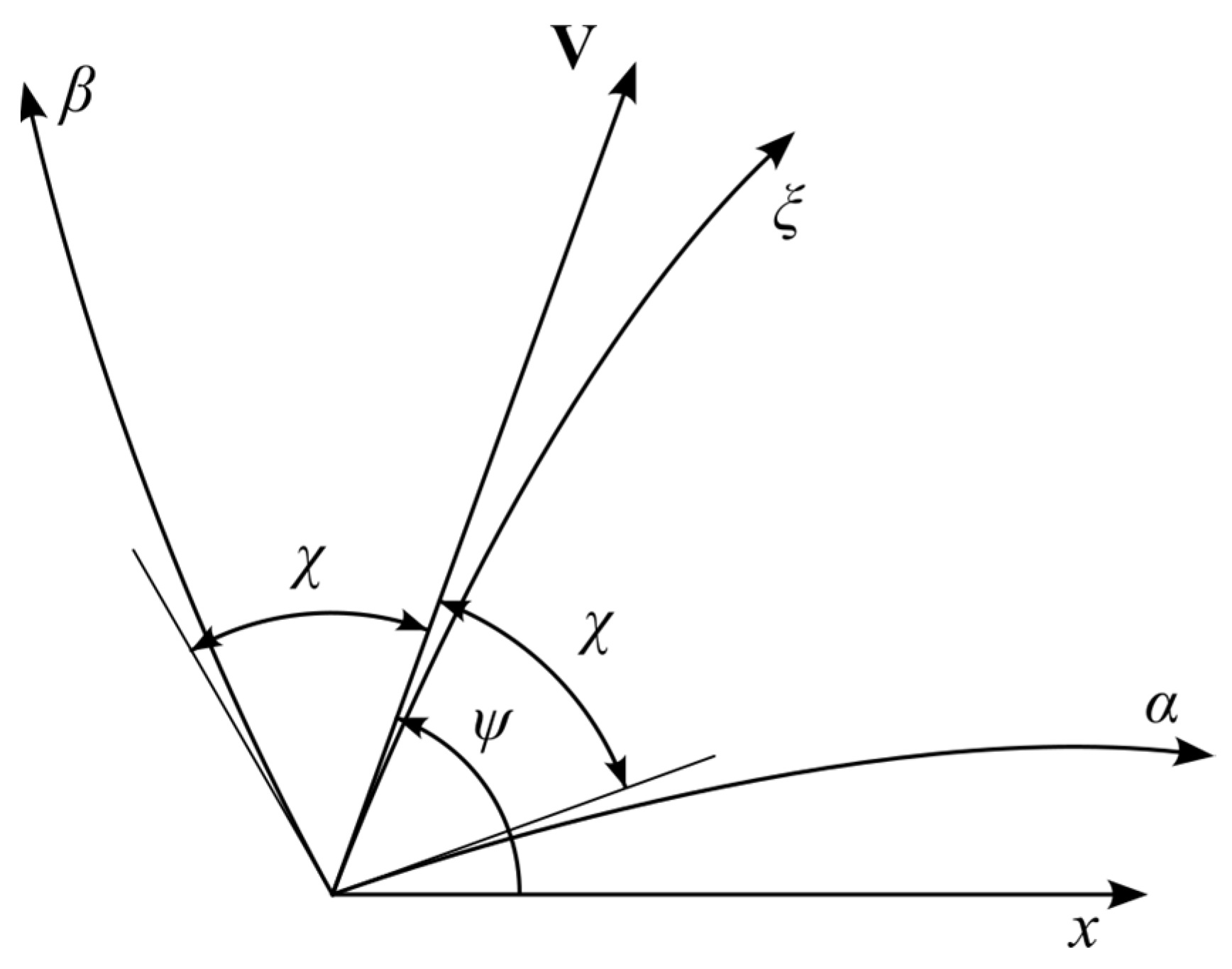
3. System of Equations in Characteristic Coordinates
4. Characteristic Network and Ideal Die Shapes
4.1. Special Solutions near the Die’s Exit
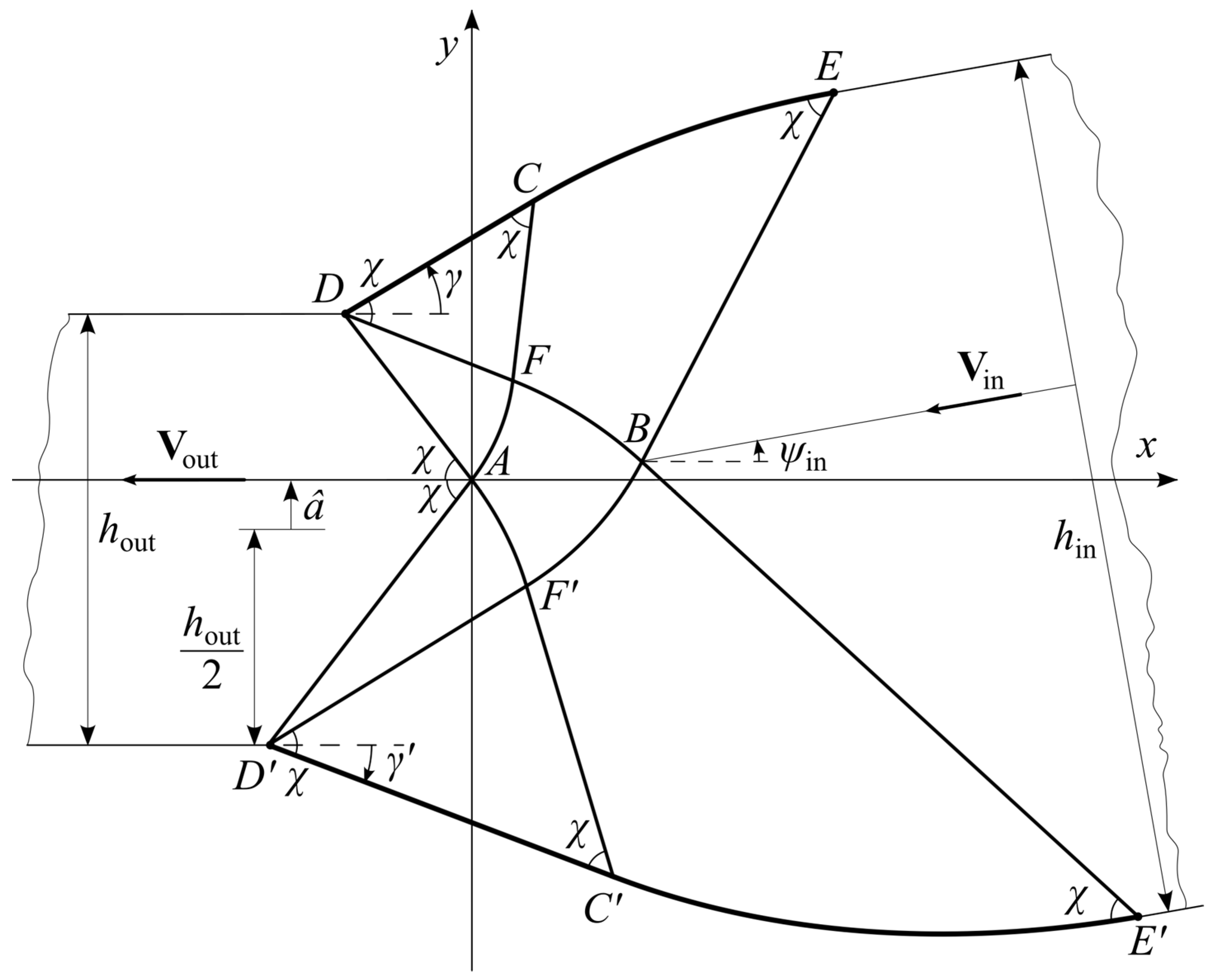
4.2. Region AFBF’ (Figure 3)
4.3. Regions FCEB and F’C’E’B (Figure 3)
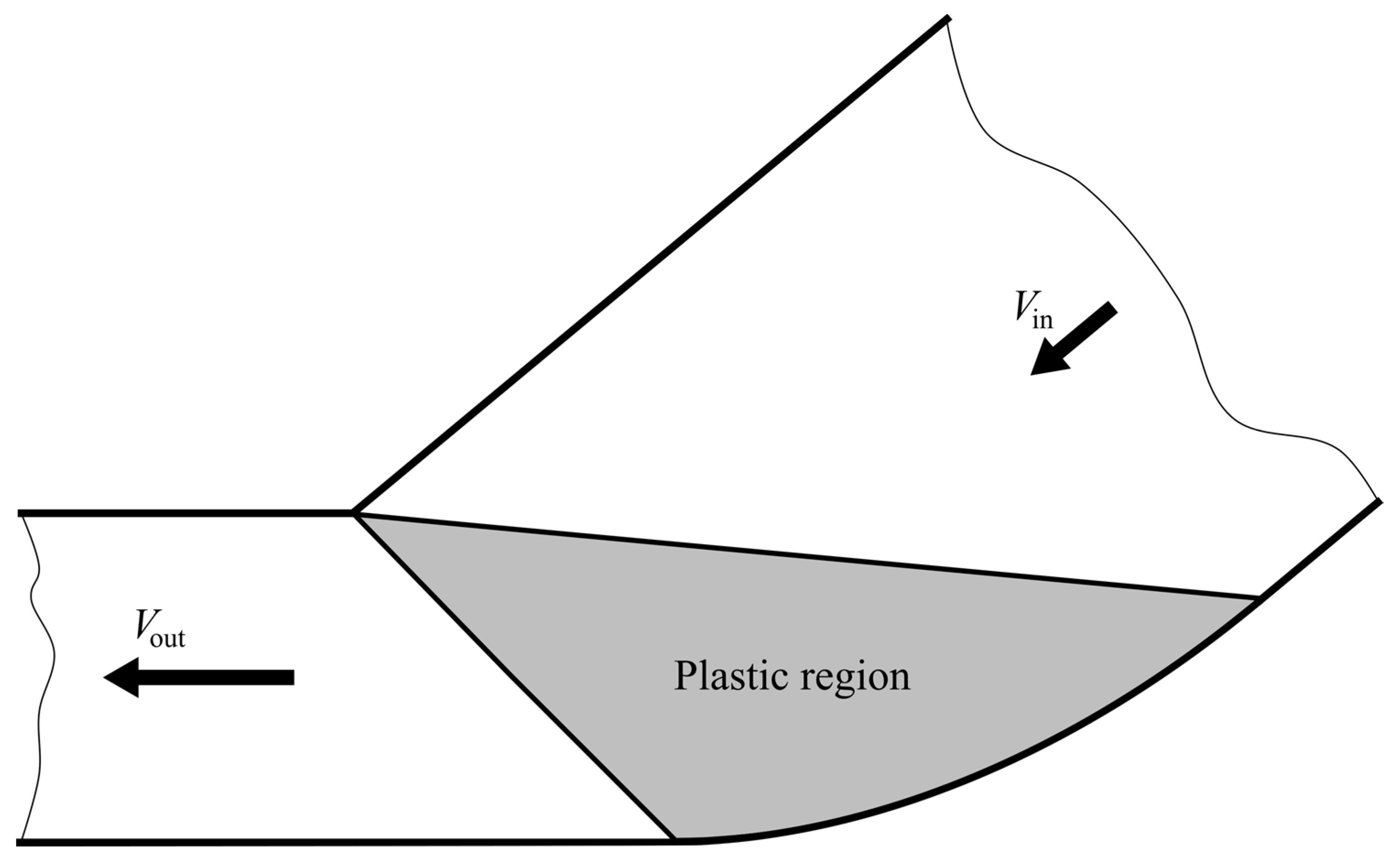
4.4. Ideal Die Shapes
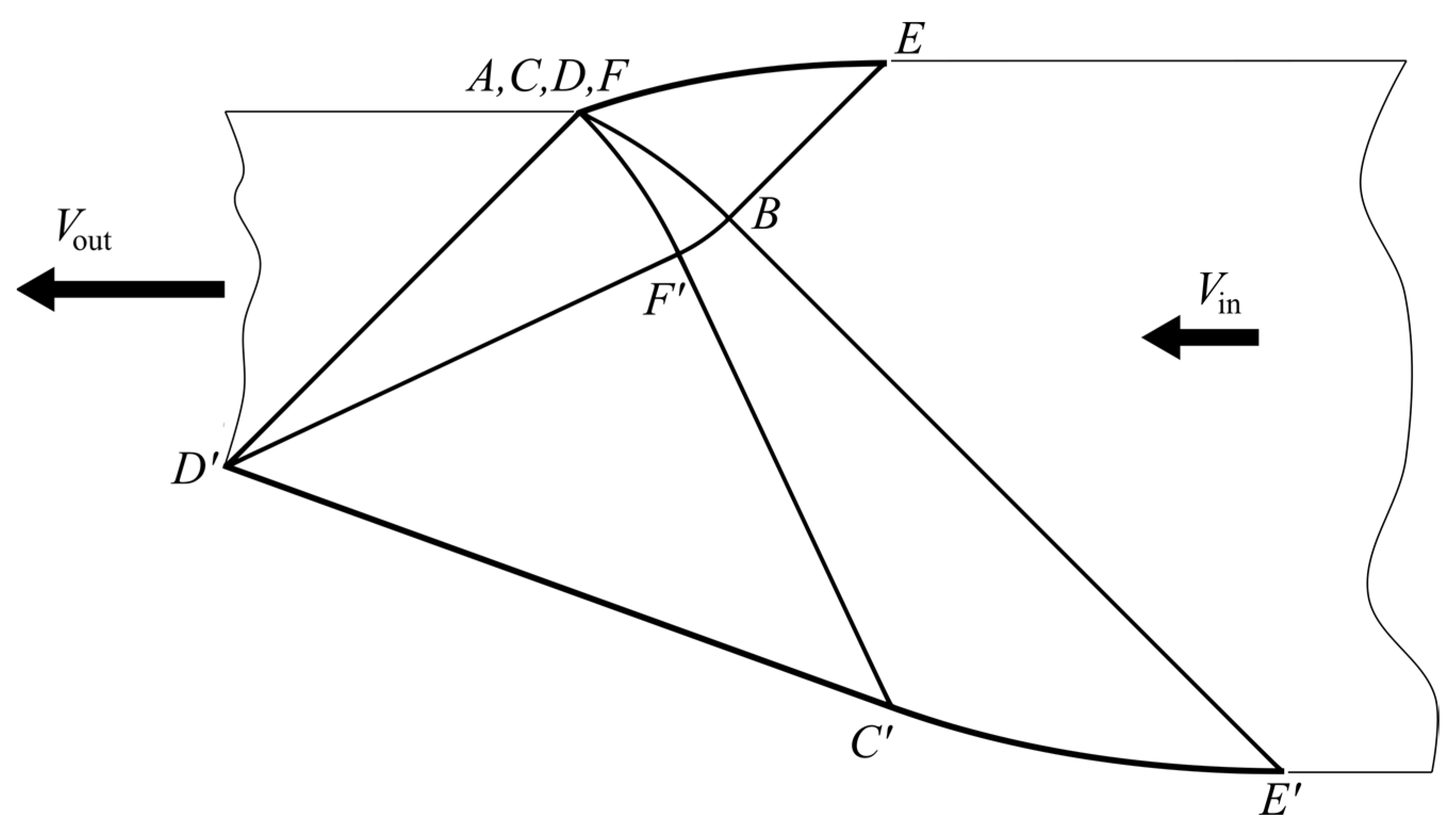
4.5. Special Solutions
5. Pressure on the Die’s Walls
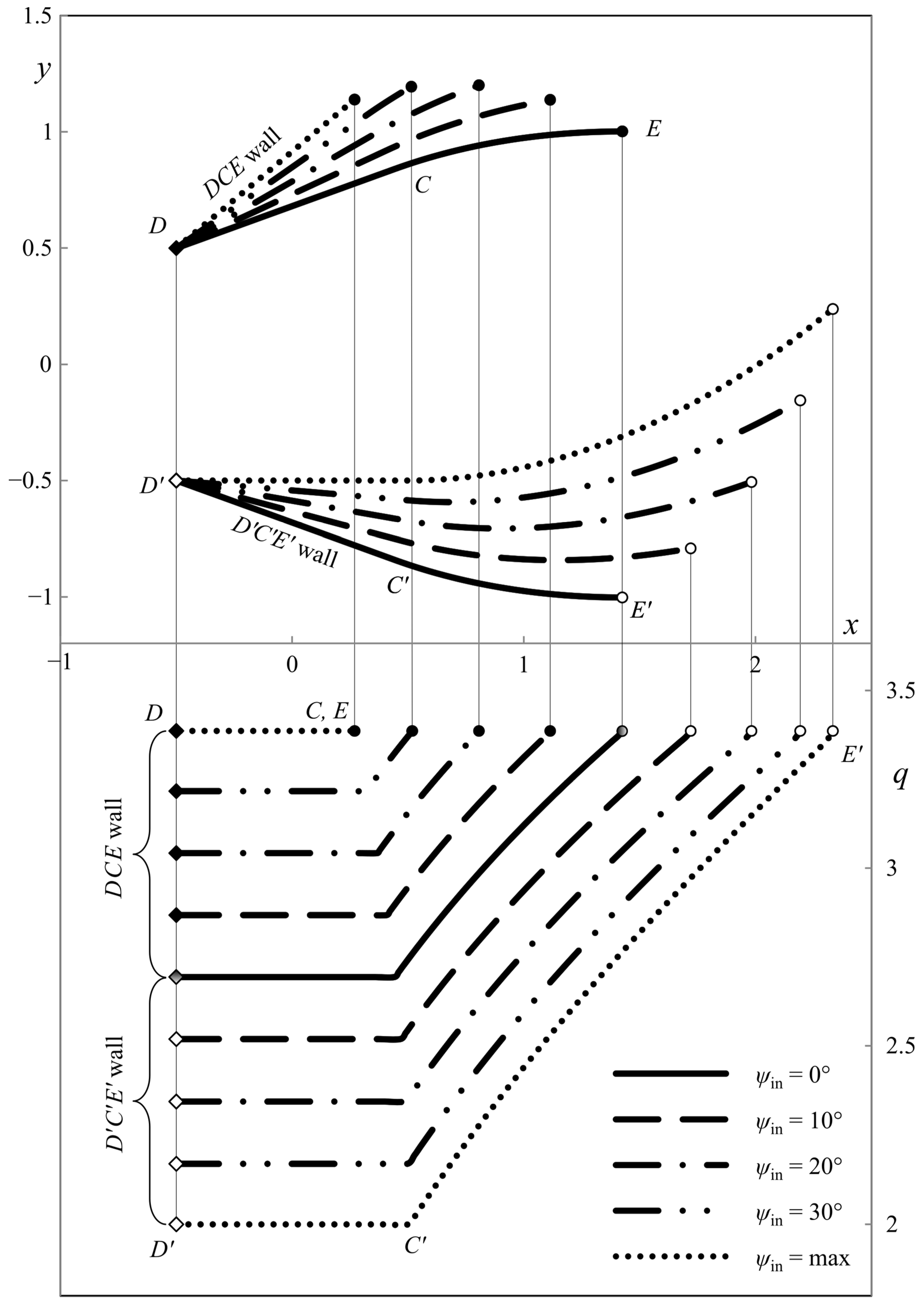
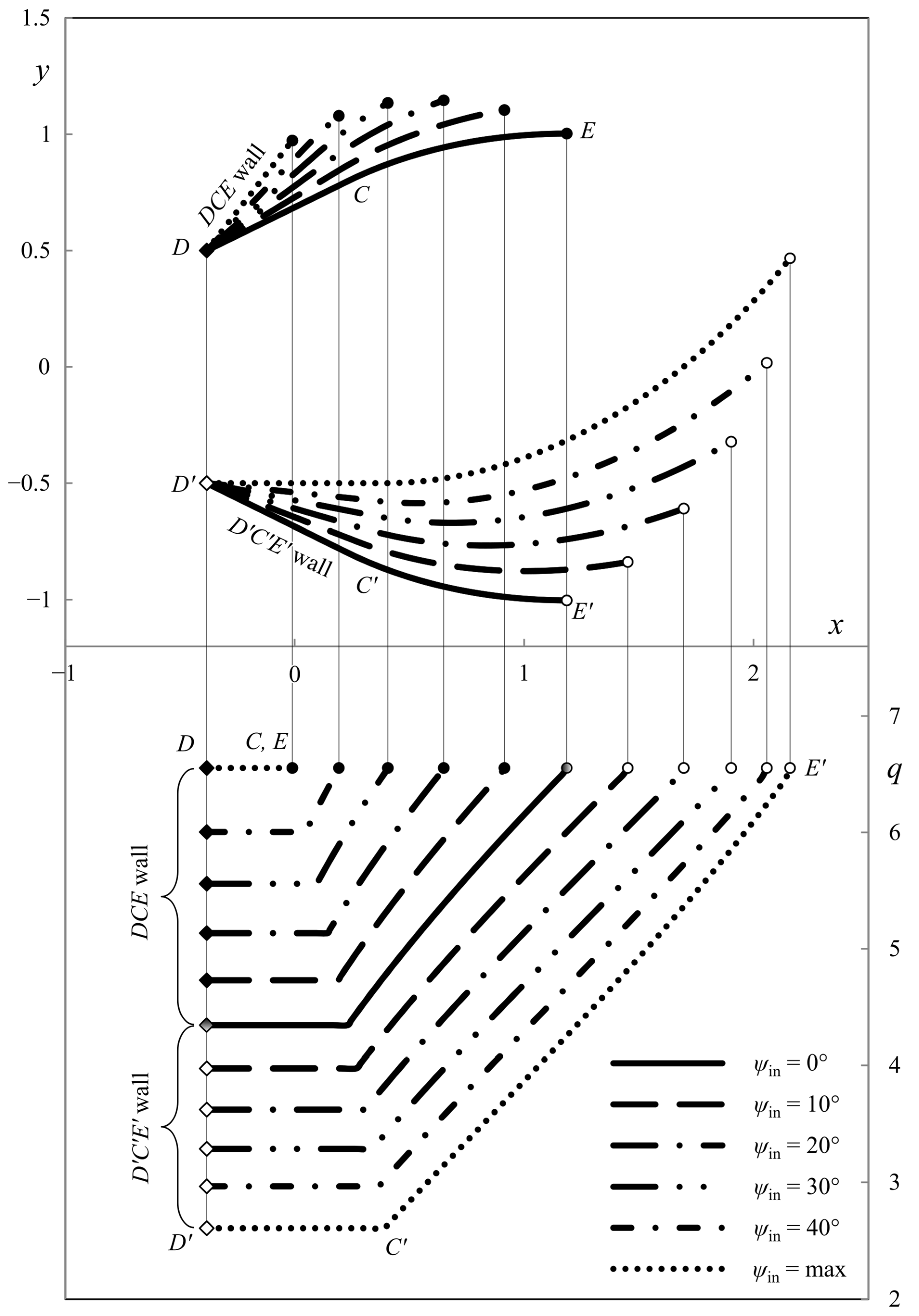
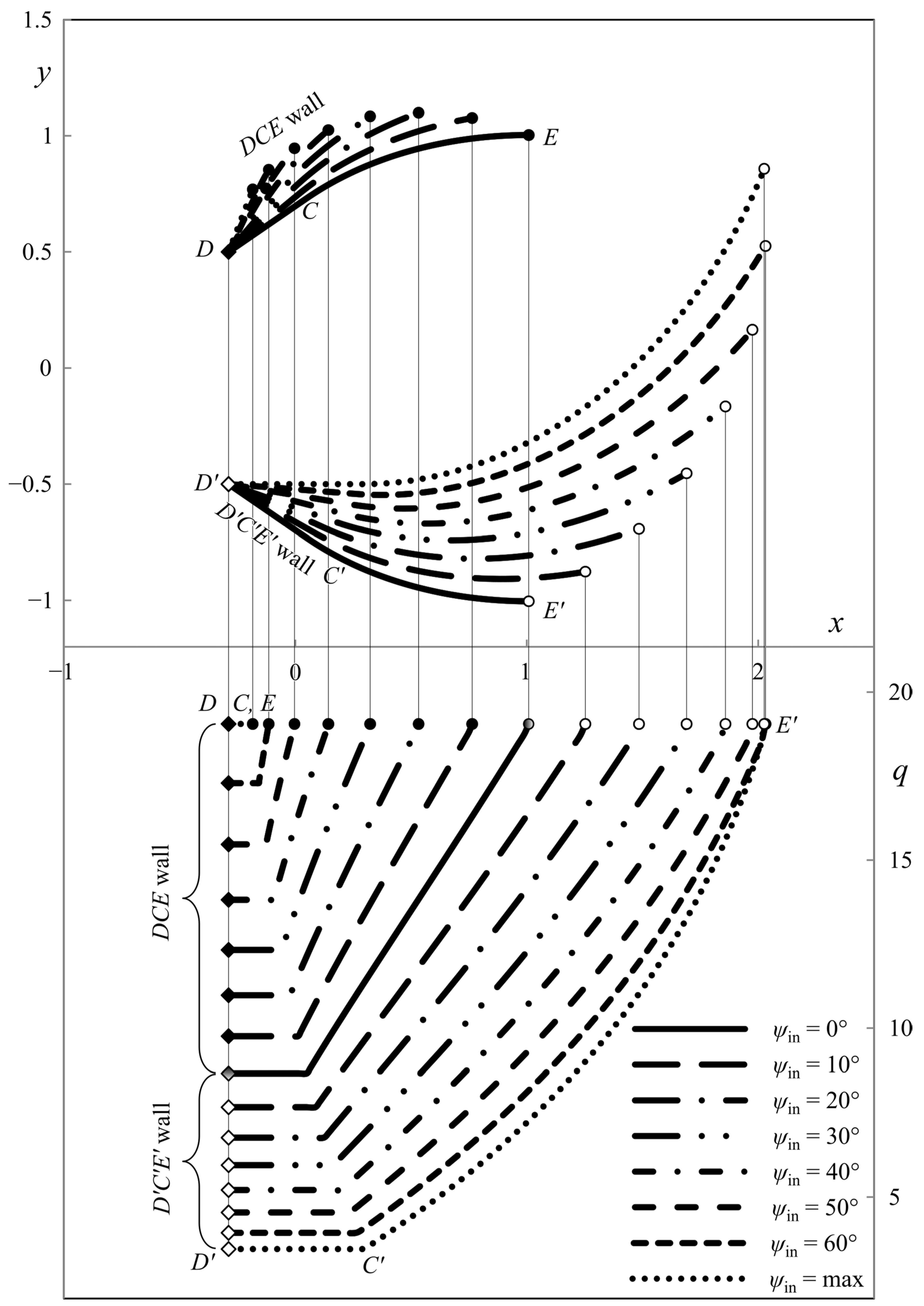
6. Illustrative Examples
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chung, K.; Alexandrov, S. Ideal Flow in Plasticity. Appl. Mech. Rev. 2007, 60, 316–335. [Google Scholar] [CrossRef]
- Richmond, O.; Devenpeck, M.L. A die profile for maximum efficiency in strip drawing. In Proceedings of the 4th U.S. National Congress of Applied Mechanics, Berkeley, CA, USA, 18–21 June 1962; pp. 1053–1057. [Google Scholar]
- Devenpeck, M.L.; Richmond, O. Strip-Drawing Experiments with a Sigmoidal Die Profile. J. Manuf. Sci. Eng. 1965, 87, 425–428. [Google Scholar] [CrossRef]
- Richmond, O.; Morrison, H.L. Streamlined wire drawing dies of minimum length. J. Mech. Phys. Solids 1967, 15, 195–203. [Google Scholar] [CrossRef]
- Hill, R. Ideal forming operations for perfectly plastic solids. J. Mech. Phys. Solids 1967, 15, 223–227. [Google Scholar] [CrossRef]
- Richmond, O.; Alexandrov, S. The theory of general and ideal plastic deformations of Tresca solids. Acta Mech. 2002, 158, 33–42. [Google Scholar] [CrossRef]
- Cox, A.D.; Eason, G.; Hopkins, H.G. Axially symmetric plastic deformations in soils. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1961, 254, 1–45. [Google Scholar] [CrossRef]
- Cox, G.M.; Thamwattana, N.; McCue, S.W.; Hill, J.M. Coulomb–Mohr Granular Materials: Quasi-static Flows and the Highly Frictional Limit. Appl. Mech. Rev. 2008, 61, 060802. [Google Scholar] [CrossRef]
- Coombs, W.M.; Crouch, R.S.; Heaney, C.E. Observations on Mohr-Coulomb Plasticity under Plane Strain. J. Eng. Mech. 2013, 139, 1218. [Google Scholar] [CrossRef]
- Lomakin, E.; Beliakova, T. Spherically symmetric deformation of solids with nonlinear stress-state-dependent properties. Contin. Mech. Thermodyn. 2023, 35, 1721–1733. [Google Scholar] [CrossRef]
- Mehrabadi, M.M.; Cowin, S.C. Initial planar deformation of dilatant granular materials. J. Mech. Phys. Solids 1978, 26, 269–284. [Google Scholar] [CrossRef]
- Kruyt, N.P. An analysis of the generalized double-sliding models for cohesionless granular materials. J. Mech. Phys. Solids 1990, 38, 27–35. [Google Scholar] [CrossRef]
- Spencer, A.J.M. A theory of the kinematics of ideal soils under plane strain conditions. J. Mech. Phys. Solids 1964, 12, 337–351. [Google Scholar] [CrossRef]
- Marshall, E.A. The compression of a slab of ideal soil between rough plates. Acta Mech. 1967, 3, 82–92. [Google Scholar] [CrossRef]
- Pemberton, C.S. Flow of imponderable granular materials in wedge-shaped channels. J. Mech. Phys. Solids 1965, 13, 351–360. [Google Scholar] [CrossRef]
- Spencer, A.J.M. Deformation of ideal granular materials. In Mechanics of Solids, The Rodney Hill 60th Anniversary Volume; Hopkins, H.G., Sewell, M.J., Eds.; Pergamon Press: Oxford, UK, 1982; pp. 607–652. [Google Scholar]
- Spitzig, W.A.; Sober, R.J.; Richmond, O. The effect of hydrostatic pressure on the deformation behavior of maraging and HY-80 steels and its implications for plasticity theory. Metall Trans A 1976, 7, 1703–1710. [Google Scholar] [CrossRef]
- Brownrigg, A.; Spitzig, W.A.; Richmond, O.; Teirlinck, D.; Embury, J.D. The influence of hydrostatic pressure on the flow stress and ductility of a spherodized 1045 steel. Acta Metallurg. 1983, 31, 1141–1150. [Google Scholar] [CrossRef]
- Spitzig, W.A.; Richmond, O. The effect of pressure on the flow stress of metals. Acta Metallurg. 1984, 32, 457–463. [Google Scholar] [CrossRef]
- Savage, J.C.; Lockner, D.A. A test of the double-shearing model of flow for granular materials. J. Geophys. Res. 1997, 102, 12287–12294. [Google Scholar] [CrossRef]
- Jiang, M.J.; Liu, J.D.; Arroyo, M. Numerical evaluation of three non-coaxial kinematic models using the distinct element method for elliptical granular materials. Int. J. Numer. Anal. Methods Geomech. 2016, 40, 2468–2488. [Google Scholar] [CrossRef]
- Harris, D. Double shearing and double rotation: A generalisation of the plastic potential model in the mechanics of granular materials. Int. J. Eng. Sci. 2009, 47, 1208–1215. [Google Scholar] [CrossRef]
- Alexandrov, S.; Mokryakov, V. Design of Dies of Minimum Length Using the Ideal Flow Theory for Pressure-Dependent Materials. Mathematics 2023, 11, 3726. [Google Scholar] [CrossRef]
- Hill, R. A remark on diagonal streaming in plane plastic strain. J. Mech. Phys. Solids 1966, 14, 245–248. [Google Scholar] [CrossRef]
- Alexandrov, S.; Pirumov, A. A Die Profile for Maximum Efficiency in Strip Drawing of Anisotropic Materials. Procedia Manuf. 2018, 21, 60–67. [Google Scholar] [CrossRef]
- Alexandrov, S.; Mokryakov, V.; Date, P. Ideal Flow Theory of Pressure-Dependent Materials for Design of Metal Forming Processes. Mater. Sci. Forum 2018, 920, 193–198. [Google Scholar] [CrossRef]
- Min, F.; Liu, H.; Zhu, G.; Chang, Z.; Guo, N.; Song, J. The streamlined design of self-bending extrusion die. Int. J. Adv. Manuf. Technol. 2021, 116, 363–373. [Google Scholar] [CrossRef]
- Harris, D. Some Properties of a New Model for Slow Flow of Granular Materials. Meccanica 2006, 41, 351–362. [Google Scholar] [CrossRef]
- Alexandrov, S. Geometry of plane strain characteristic fields in pressure-dependent plasticity. ZAMM-J. Appl. Math. Mech. Z. Angew. Math. Mech. 2015, 95, 1296–1301. [Google Scholar] [CrossRef]
- Lindqvist, M.; Evertsson, C.M. Development of wear model for cone crushers. Wear 2006, 261, 435–442. [Google Scholar] [CrossRef]
- Popov, V. Generalized Archard law of wear based on Rabinowicz criterion of wear particle formation. Mech. Eng. 2019, 17, 39–45. [Google Scholar] [CrossRef]
- Farzad, H.; Ebrahimi, R. An investigation of die profile effect on die wear of plane strain extrusion using incremental slab method and finite element analysis. Int. J. Adv. Manuf. Technol. 2020, 111, 627–644. [Google Scholar] [CrossRef]
- Bang, J.; Kim, M.; Bae, G.; Kim, H.-G.; Lee, M.-G.; Song, J. Efficient Wear Simulation Methodology for Predicting Nonlinear Wear Behavior of Tools in Sheet Metal Forming. Materials 2022, 15, 4509. [Google Scholar] [CrossRef] [PubMed]
- Hill, R.; Lee, E.H.; Tupper, S.J. A Method of Numerical Analysis of Plastic Flow in Plane Strain and Its Application to the Compression of a Ductile Material Between Rough Plates. J. Appl. Mech. 1951, 18, 46–52. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alexandrov, S.; Mokryakov, V. General Planar Ideal Flow Solutions with No Symmetry Axis. Materials 2023, 16, 7378. https://doi.org/10.3390/ma16237378
Alexandrov S, Mokryakov V. General Planar Ideal Flow Solutions with No Symmetry Axis. Materials. 2023; 16(23):7378. https://doi.org/10.3390/ma16237378
Chicago/Turabian StyleAlexandrov, Sergei, and Vyacheslav Mokryakov. 2023. "General Planar Ideal Flow Solutions with No Symmetry Axis" Materials 16, no. 23: 7378. https://doi.org/10.3390/ma16237378
APA StyleAlexandrov, S., & Mokryakov, V. (2023). General Planar Ideal Flow Solutions with No Symmetry Axis. Materials, 16(23), 7378. https://doi.org/10.3390/ma16237378






