3.1. The Influence of Temperature Differential Cycling on Compressive Strength of Concrete
By observing the changes in color in the fracture surfaces of the cement concrete specimens, it can be found that the color changed gradually from the dark gray of the un-cycled specimens to the lighter gray after 120 cycles, and then to gray–white after 300 cycles (as shown in
Figure 5).
To analyze and discuss the impact of temperature differential cycling on the performance of concrete specimens further, the experimental research on the compressive performance of concrete was also conducted in this study as well as observing the apparent characteristics of the specimens after temperature differential cycling. The failure surfaces of the cement concrete specimens under uniaxial compressive stress after temperature differential cycling are shown in
Figure 6.
It was observed that after a fewer number of temperature differential cycling (60 and 120 cycles), there were no obvious through cracks in the concrete specimens before loading. However, when the load reached a certain level, cracks rapidly developed and extended in a short time until they penetrated the entire specimen. After a greater number of thermal cycles (180, 240, and 300 cycles), cracks could be observed in the early stages of loading, and the specimens showed a denser pattern of cracks at the center.
Furthermore, it can be seen from the morphology of the fracture surface in
Figure 6 that without temperature differential cycling, there were 10 fracture occurrences at the interface between the coarse aggregate and cement paste with a maximum diameter of 21.2 mm; after 120 thermal cycles, there were 11 occurrences with a maximum diameter of 25.5 mm; and after 300 thermal cycles, there were 18 occurrences with a maximum diameter of 28.3 mm.
This indicates that with the continuous progression of temperature differential cycling, the number of damaged points on the interface between coarse aggregates and cement paste increases gradually. This phenomenon may stem from the differing thermal effects between coarse aggregates and the cementitious matrix when subjected to temperature fluctuations, leading to distinct deformations between them. These deformation disparities could trigger the formation of microcracks in the transitional area of the interface between coarse aggregates and cement paste. These microcracks continue to propagate and extend under the influence of temperature cycling, progressively compromising the overall integrity of the interface transitional zone and deteriorating its performance. Additionally, we have observed that with the ongoing temperature differential cycles, the points of damage gradually extend from the edge region of the specimen towards the central area. This suggests that the impact of temperature cycling on the specimen’s surface is more significant than its internal regions.
The failure loads and compressive strengths of the cement concrete specimens after different temperature differential cyclin measured by the axial compression tests are shown in
Table 4. It is worth mentioning that, according to GB/T 50081-2019 “Standard for Test Method of Mechanical Properties on Ordinary Concrete” [
28], the compressive strength of the non-standard specimens used in this study (100 mm × 100 mm × 300 mm) must be converted using Formula (1).
where, a is the size conversion coefficient, a = 0.95;
ft is the compressive strength of the specimen obtained from the test.
It can be found from
Table 4 that comparing the specimens at the reference temperature (20 °C), those subjected to temperature differential cycling initially exhibit an increase in compressive strength. However, after 60 cycles of temperature variation, the compressive strength begins to decrease. Furthermore, as the number of temperature differential cycling increases, the reduction in compressive strength of the cement concrete specimens becomes more pronounced. That is, for cement concrete, the compressive strength shows an overall trend of “first increasing and then decreasing” during the process of temperature differential cycling.
To observe the impact of temperature differential cycling on the strength of cement concrete more intuitively, a graph has been plotted to show the change in the average compressive strength of each group of specimens with the number of temperature differential cycling, as shown in
Figure 7. The slopes and intercepts of each segment of the curve can be found in
Table 5.
It can be seen from
Figure 7 and
Table 5 that the strength of the concrete specimens improved after the initial 60 cycles, but when reaching 120 cycles, the strength falls back to near the compressive strength values at the baseline temperature, and it continues to decline with an increasing number of temperature cycles. On one hand, due to the different thermal effects among the various components of the concrete specimens, the size and rate of thermal deformation varies during the changes in temperature, leading to the formation of microcracks between components, thus affecting the integrity and degrading the strength of the specimens. On the other hand, considering the actual experimental conditions, the specimens in the temperature control chamber experience a temperature difference between their surface and interior during the changes in the temperature control chamber, leading to thermal stress and promoting the formation of microcracks, further degrading the strength of the concrete specimens.
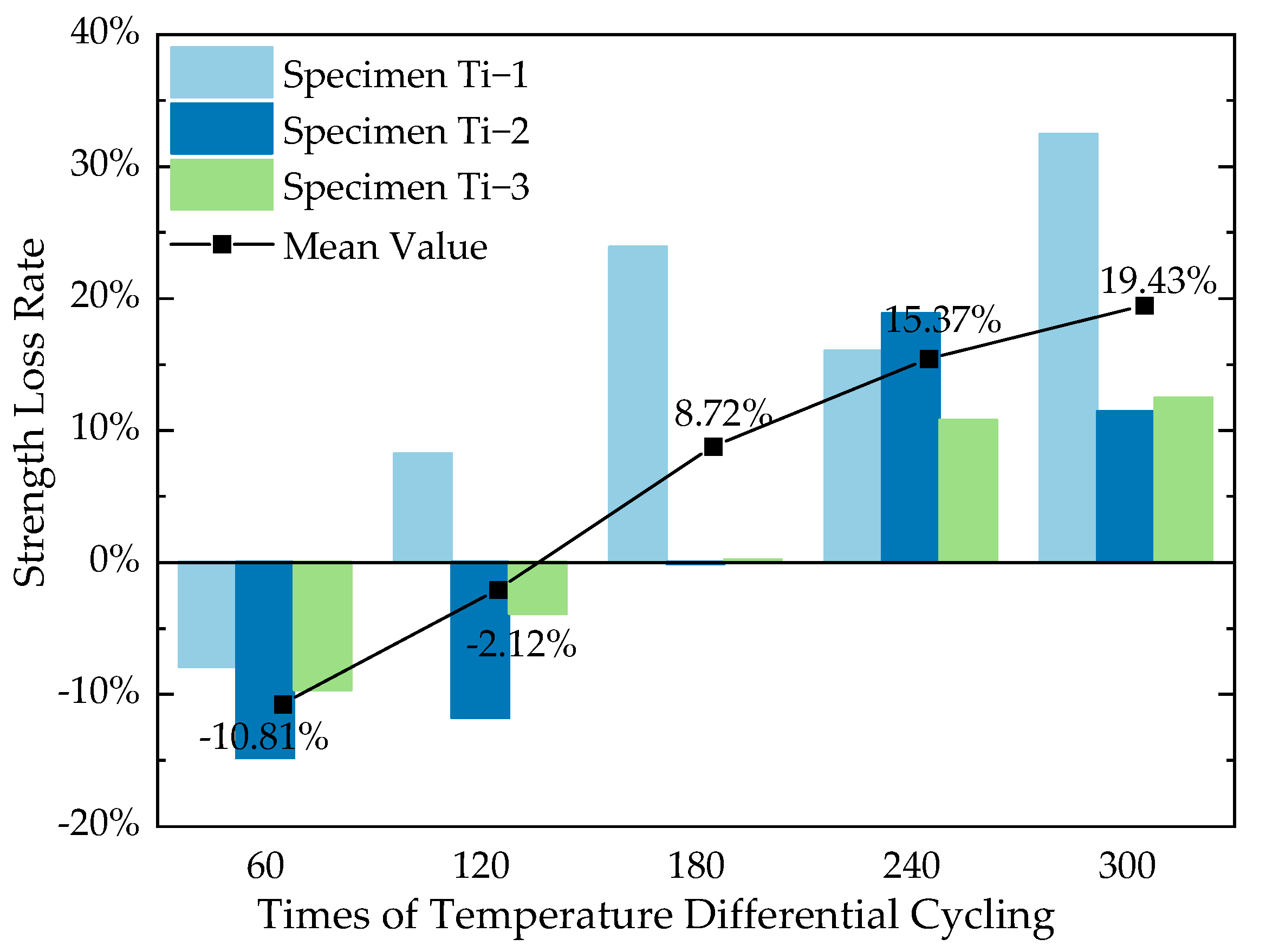
The strength loss rate
Rs (Equation (2)) was selected in this study to characterize the strength degradation of cement concrete specimens after different temperature differential cycling quantitatively. The strength loss rate of the concrete specimens obtained from the axial compression test is shown in
Table 6, and a graph depicting the average compressive strength loss rate as a function of the number of temperature cycles is presented in
Figure 8.
where
fcpT is the compressive strength of the concrete specimens after different temperature differential cycling, and
fcp is the compressive strength of the concrete specimens at the baseline temperature (20 °C).
It is observed that comparing concrete that has not undergone temperature differential cycling, the strength loss of concrete specimens shows negative values in the early stages of cycling, indicating an upward trend in strength. However, after 180 cycles, some specimens begin to show a significant decrease in strength, by more than 20%. After 240 cycles, the loss in compressive strength of the specimens reaches 10–20%, and after 240 cycles, the compressive strength loss even reaches 10–30%.
By observing the curve of the average compressive strength loss rate of concrete specimens in
Figure 8, it can be found that in the first 120 cycles, the strength loss rate of concrete specimens shows as a negative value, meaning the strength of the specimens has generally increased compared to that at the baseline temperature, and it reaches its maximum value at the 60 cycles. During 120–180 cycles, the strength loss rate gradually increases to a positive value, indicating that the strength of the specimens gradually decreases to below that at the baseline temperature and continues to diminish. At the same time, it can be found from the rate of the curve that the increase in the strength loss rate is gradual relatively during 60–120 cycles; and grows significantly during 120–180 cycles; then returns to a gradual pace during 180–300 cycles.
The possible reasons are as follows: in the early stages of temperature differential cycling (first 120 cycles), the rise in temperature promotes the hydration of some cement particles that have not yet fully hydrated, which could enhance the internal density of the concrete and thus increase the strength of the concrete specimens. Within the first 60 cycles, the strength increase caused by the hydration of the cement is greater than the deterioration caused by the temperature differential cycling on the strength of the concrete specimens, hence showing an increase in strength. During 120–180 cycles, as the number of temperature differential cycling increases, the unhydrated cement and fly ash particles decrease gradually, the hydration process slows down, the enhancement effect on strength weakens, and the impact of temperature cycling becomes the dominant factor, thus showing a strength loss rate rising from a negative to a positive value, with a relatively large rate of increase. In the later stages of temperature cycling (180–300 cycles), there are some microcracks inside the concrete specimens already, and the existence of those weakens the thermal stress caused by the different thermal properties between the concrete components, thus having a smaller impact on strength, which is reflected in the slowing rate of increase in the strength loss rate of the concrete specimens.
3.2. Effect of Temperature Differential Cycling on the Fatigue Performance of Concrete
The fatigue life of concrete specimens subjected to different temperature differential cycling under various stress levels is measured by axial compression fatigue tests as shown in
Table 7.
The fatigue life of concrete, which means the maximum number of load cycles a concrete can withstand before failure under cyclic loading conditions, is one of the important characteristics for evaluating the service performance of concrete. In fact, the fatigue life of concrete is closely related to its own heterogeneity, the number of temperature differential cycling, and the level of the load, and thus typically exhibits a large degree of variability. Therefore, it is necessary to introduce probabilistic statistical methods to describe the distribution of fatigue life of concrete more accurately.
It is well known that the distribution of fatigue life of concrete usually follows both a two-parameter Weibull distribution and a log-normal distribution. The two-parameter Weibull distribution is a continuous distribution that describes the distribution of fatigue life of materials through two parameters: shape and scale. Due to its convenience and straightforward derivation, it is widely used in the statistical analysis of material life [
31,
32,
33,
34]. However, the two-parameter Weibull distribution model often cannot avoid the use of mathematical methods such as the maximum likelihood method or the moment estimation method, which involve multiple dimensions of equations and large amounts of computation, thus limiting its practical application. Therefore, based on the premise that the concrete fatigue life conforms to both the log-normal distribution and the two-parameter Weibull distribution, the assumption of the log-normal distribution’s approximation was used in this study to estimate the distribution parameters of the two-parameter Weibull distribution to improve calculation efficiency.
Assume the target variable
x follows a two-parameter Weibull distribution, the density function of which can be describe as [
35]:
where
β is the shape parameter;
η is the scale parameter.
Assume the target variable
x follows a log-normal distribution at the same time, the density function of which can be describe as [
36]:
where
EX is the logarithmic mean of the sample variables, and
σ2 is the variance between the sample variables.
Then, the characteristic functions of the two distribution functions are:
Performing a Taylor expansion on the characteristic functions:
According to the continuity theorem, when the two functions are approximate, it holds that:
By combining Equations (7)–(9) and approximating the first three terms of the Taylor expansion, it can be obtained that:
For n = 0, the left and right sides of Equation (10) are equal;
For
n = 1, 2, there are additional equations derived:
where
E(·) is the expected value of the sample.
It can be obtained from Equations (3), (4), (11) and (12):
where Γ(·)is the gamma function.
For ease of calculation, let:
Performing calculations of ω(
β) within the range
β = [1, 3.175], we can obtain a corresponding table as shown in
Table 8.
According to Equation (15), Equations (13) and (14) can be further simplified:
Thus, we can calculate the value of ω(
β) using Equation (16), then refer to
Table 8 to find the shape parameter
β, and obtain the scale parameter
η using Equation (17), thereby achieving the estimation of the two-parameter Weibull distribution parameters through the assumption of the log-normal distribution’s approximation. The calculated values of the Weibull distribution parameters for the compressive fatigue life of the cement concrete in this study are shown in
Table 9.
The Kolmogorov–Smirnov (K–S) test method was used in this study to evaluate the goodness of fit between the experimental distribution of the fatigue life of cement concrete and the two-parameter Weibull distribution model determined by the calculated distribution parameters [
37,
38]. As one of the most commonly used non-parametric methods, the essence of the K–S test method’s evaluation of the goodness of fit is to describe the distance between the empirical function of the sample distribution and the distribution function of the reference distribution quantitatively. The size of the distance reflects the goodness of fit between the sample and the reference distribution.
Let
Fn(
x) be the empirical distribution function of the sample:
where n is the sample size, and
i is the sample index.
Let
Pn(
x) be the cumulative probability distribution function of the reference distribution, then calculate the distance
Di between the two distributions:
According to the significance of the K–S test, the maximum deviation between
Fn(
x) and
Pn(
x), denoted as
Dmax, is the statistic of K–S test:
For this study, the empirical cumulative probability distribution function
Fn(
x) corresponds to the cumulative probability distribution function of the compressive fatigue life of the cement concrete obtained from the experiment, and
Pn(
x) corresponds to the cumulative probability distribution function of the two-parameter Weibull model:
Taking the distribution of compressive fatigue life of cement concrete specimens under stress level S = 0.70 without temperature differential cycling (T = 0) as an example, the K–S test for the goodness of fit of the two-parameter Weibull distribution is shown in
Table 10.
It can be seen that the value of test statistic calculated out is
Dmax = 0.3656, and the standard value of which, according to the critical value table of the K–S test standard, is
DC = 0.734 (at the significance level of 5%, on 3 test repetitions) [
25]. Since
Dmax <
DC, the goodness of fit between the distribution of fatigue life and the two-parameter Weibull distribution can pass the K–S test, meaning that the distribution of compressive fatigue life of cement concrete under the condition of S = 0.70, T = 0 conforms to the two-parameter Weibull distribution. Using this method, the goodness of fit between the fatigue life distribution of cement concrete under all working conditions and the two-parameter Weibull distribution is tested, the results are shown in
Table 11.
It can be seen that for all stress levels and temperature cycling conditions in this study, the goodness of fit of the two-parameter Weibull distribution of concrete specimen fatigue life can pass the K–S test, which means that at a 5% significance level, the fatigue life distribution of cement concrete can be well described by the two-parameter Weibull distribution.
To characterize the impact of temperature cycling frequency on concrete life quantitatively, an exponential function was applied in this study to fit the variation in fatigue life with temperature cycling frequency, as shown in Equation (22):
where a, b, c are coefficient constants related to stress levels.
The specific values are shown in
Table 12, the fitting curve is shown in
Figure 9.
To verify the fit of the exponential fitting formula used in this study for compressive fatigue life of concrete, calculations were made using Equation (22) for the fatigue life of concrete under different temperature differential cycling and different stress levels. The calculated fatigue life values were then compared with the experimental values, as shown in
Table 13.
It can be found in
Table 13 that in 74.7% of the cases, the relative deviation between the calculated value of fatigue life and the experimental value is less than 40%. Therefore, it is considered that Equation (22) can reflect the compressive fatigue life of cement concrete under the effect of temperature differential cycling, providing a reference for practical engineering applications.
Figure 9 reveals that for every incremental increase of 60 cycles in temperature difference, the fatigue life of concrete specimens at the same stress level decreases by approximately 22.23–22.46%; while for the same temperature cycling conditions, an increase in stress level from S
1 = 0.70 to S
2 = 0.80, and from S
2 = 0.80 to S
3 = 0.90, results in a reduction in the fatigue life of the concrete specimens by 71.50–73.32% and 96.72–96.92%, respectively. Therefore, we believe that both temperature differential cycling and fatigue loading have a significant impact on the compressive fatigue life of cement concrete, with the influence of the stress level being more pronounced. At the same time, it is also noted that, unlike the change in compressive strength of specimens with temperature cycling frequency, the fatigue life of the specimens shows a consistent downward trend. A possible reason is that although the compressive strength of the specimens may increase after 60 cycles of temperature differential cycling, the internal micro-cracks and other defects continue to accumulate under the influence of fatigue loading. At this stage, both the number and width of internal micro-cracks in the specimens are greater than those before the temperature differential cycling, and the speed of propagation of micro-cracks increases with the load during the fatigue loading process, indicating that the overall integrity of the specimens continues to deteriorate, resulting in a reduction in fatigue life.
For a more intuitive description of the relationship between stress level, temperature differential cycling, and fatigue life of concrete, a linear regression analysis was performed on the fatigue life of cement concrete after different temperature differential cycling. The equation of fatigue life for cement concrete after temperature differential cycling (Equation (23)) was obtained and the S-N curve was plotted (
Figure 10).
where k and b are coefficient constants related to the number of temperature cycles, the specific values are as shown in
Table 14.
It can be found clearly from
Figure 10 that as the number of temperature cycles increases, the S-N curve for cement concrete shifts to the left overall, signifying a significant reduction in fatigue life. At a stress level of S = 0.80, the fatigue life of concrete (lgN) after 300 cycles (T = 300) is even reduced by up to 11.34% compared to T = 0, which confirms the non-negligible impact of temperature cycling on the compressive fatigue life of cement concrete once again. Therefore, to design and predict the fatigue life of cement concrete more scientifically and accurately in actual engineering, it is important to consider not only the environmental stress level but also the effects of temperature differential cycling.
3.3. Microstructure of Concrete after Temperature Differential Cycling
The deterioration of compressive strength and the decrease in compressive fatigue life of concrete specimens after temperature differential cycling both, fundamentally, come down to changes in the microstructure. Hence, we approached the issue from the perspective of the microscopic level, employing ultrasonic testing methods to analyze the velocity of sound through concrete specimens after temperature differential cycling statistically.
As is widely known, ultrasonics, as a form of mechanical wave, exhibit different phenomena such as reflection and refraction when passing through various media, which could result in different characteristics such as sound speed and amplitude. While the concrete material, which is a heterogeneous medium, undergoes dissimilar thermal strains in its components under the action of temperature differential cycling. This could lead to internal defects such as micro-cracks and voids in the concrete material, which inevitably affect the propagation path of sound waves, thus manifesting as a loss in wave speed. Therefore, we believe that the change in ultrasonic speed after temperature differential cycling can serve as a statistical measure for characterizing the internal damage patterns of concrete.
The results of the ultrasonic test on concrete specimens after different numbers of temperature differential cycling in this study are shown in
Table 15, and the curve of the average ultrasonic velocity of three measuring points is drawn as
Figure 11.
It can be found from
Figure 11 that the ultrasonic velocity of the cement concrete specimen exhibits a gradual decreasing trend with the increase in the number of temperature differential cycles, and the phenomenon of which also indicates, to some extent, that as the temperature differential cycling progresses, damages such as microcracks and pores within the concrete specimen increase, leading to more ultrasonic waves being absorbed, and consequently, a reduction in ultrasonic velocity is observed.
The reducing rate of ultrasonic velocity is calculated as shown in
Figure 12.
Similar to the trend of strength loss with increasing number of temperature differential cycling, the reducing rate of ultrasonic velocity also shows a trend of gradual increasing. However, it is noted that during the early stages of the temperature differential cycling, there was no negative value in the reducing rate of ultrasonic velocity of the specimen. The possible reason is that in the early process of temperature differential cycling (first 120 cycles), although the hydration of some cement particles increased the hardness of the cement stone, thus improving the strength of the concrete specimen, it could not fully compensate for the microcracks continuously forming and developing at the interface between coarse aggregate and cement paste due to the effect of temperature differential cycling. It is precisely because of the presence of these microcracks that there is a certain degree of loss when ultrasonic waves penetrate the specimen. During the mid-process of temperature differential cycling (120–240 cycles), the cement particles are mostly hydrated, and the effects of temperature differential cycling become the predominant factor, causing a large number of internal microcracks to form in the specimen, which is then reflected in the rapid increase in the reducing rate of ultrasonic velocity. In the later process of the temperature differential cycling (240–300 cycles), the thermal stress between the coarse aggregate and the cement paste is reduced due to the presence of a large number of internal microcracks, resulting in a decreased rate of new microcrack formation. Although the existing cracks continue to absorb energy and gradually expand, the rate of expansion has become stable, so they have no longer a significant impact on the sound velocity, which is also reflected in the gradual leveling off of the rate of increase in the reducing rate of velocity.
Considering that the trend in the reducing rate of ultrasonic velocity of the concrete specimen has a strong correlation with the rate of loss in compressive strength after the temperature differential cycling, a linear fitting analysis of the relationship between the strength loss rate (
Rs) and the velocity loss rate (
RU) of the concrete specimen was also conducted in this study. The fitting formula is as shown in Equation (24), and the fitting curve is shown in
Figure 13.
where k and b are coefficient constants, which are calculated to be k = 0.47 and b = 0.06, respectively. The degree of fit
R2 reached 0.963, indicating a strong linear relationship between the strength loss rate and the velocity loss rate of the concrete specimen, which also verifies that the ultrasonic velocity loss rate of the concrete specimen can quantitatively characterize the deterioration of concrete strength.