Computer-Aided Structural Diagnosis of Bridges Using Combinations of Static and Dynamic Tests: A Preliminary Investigation
Abstract
:1. Introduction
2. Materials and Methods
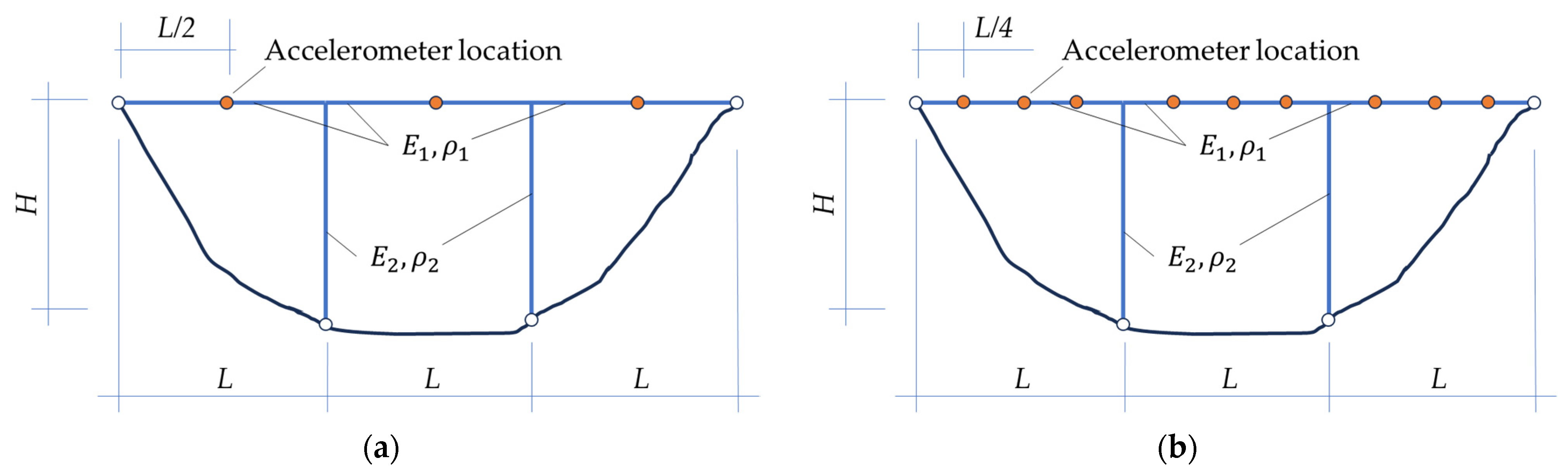
2.1. Concrete Bridges—Conceptual Examples
2.2. Inverse Procedure
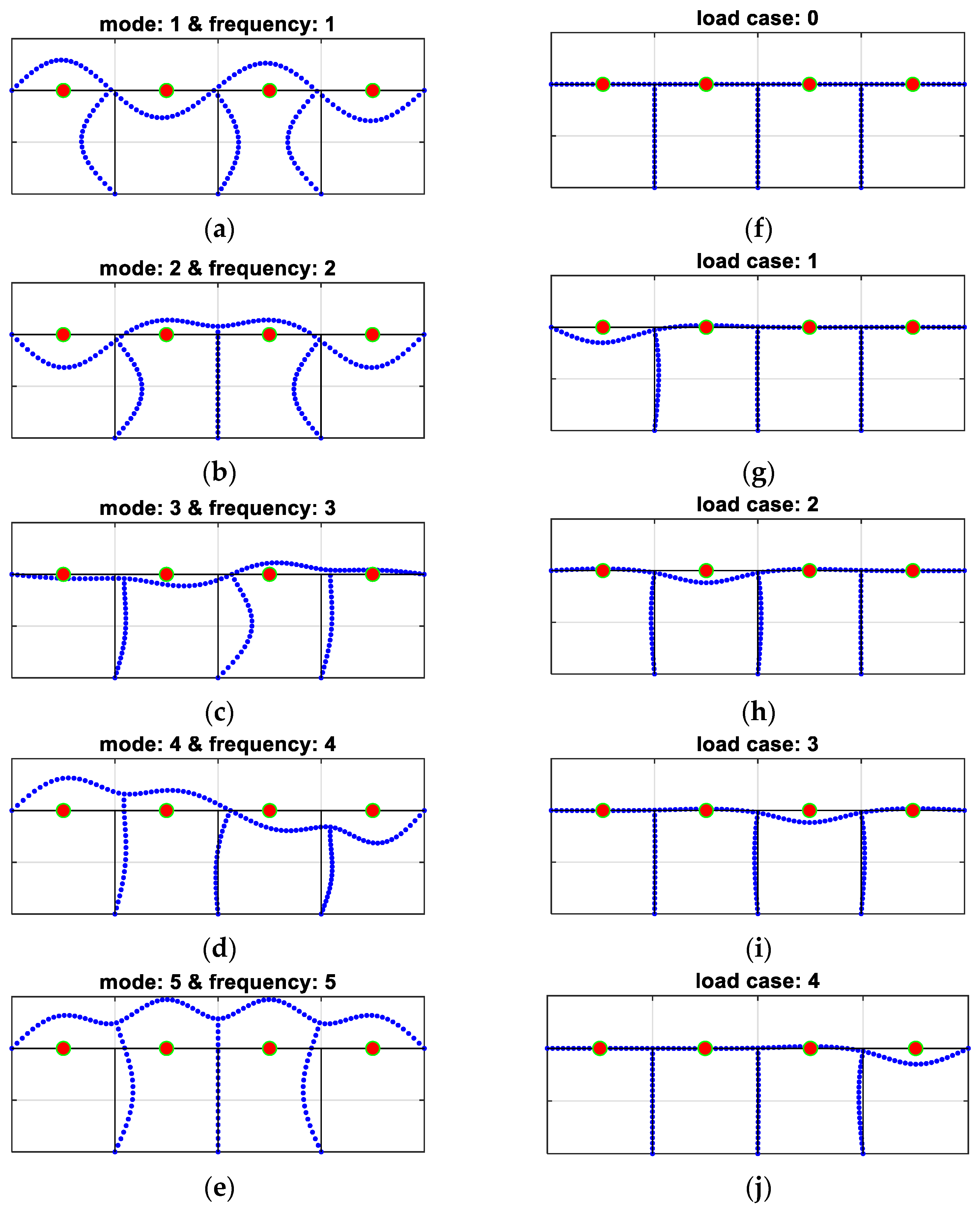
- variant 1: the discrepancy between the eigenfrequencies of the pseudo-experimental model and the numerical twin only (for few selected first eigenfrequencies);
- variant 2: in addition to the set of natural frequencies, the discrepancy between modes of natural vibration in both models (again, for few selected first modes);
- variant 3: in addition to the set of natural frequencies, the discrepancy in structure deflections in selected locations of the bridge due to static loads in several load cases;
- variant 4: in addition to the set of natural frequencies and eigenmodes, the discrepancy in structure deflections in selected locations of the bridge due to static loads in several load cases.
2.3. Objective Function
2.4. Minimization Algorithm
2.5. Numerical and Pseudo-Experimental Models
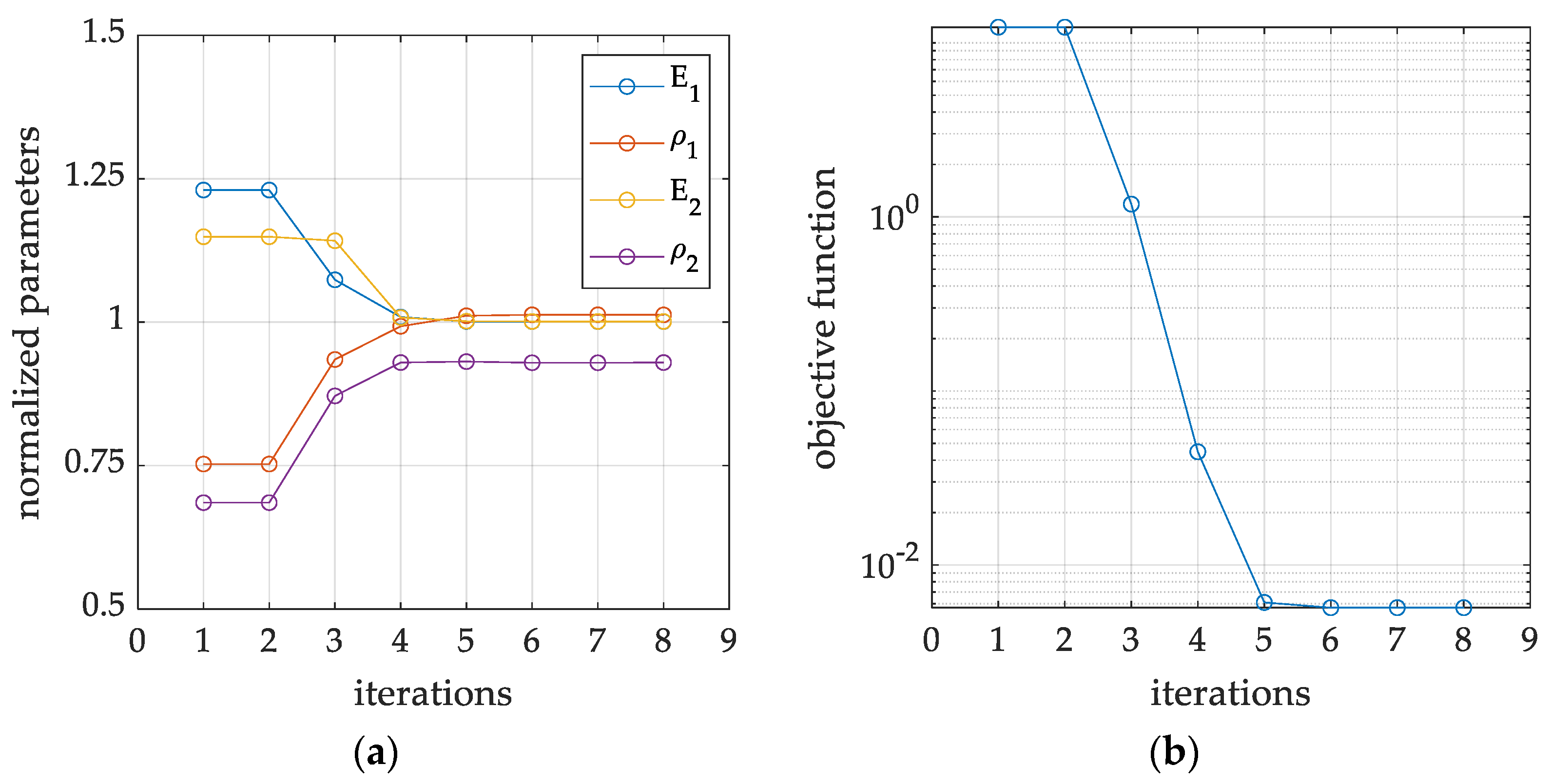
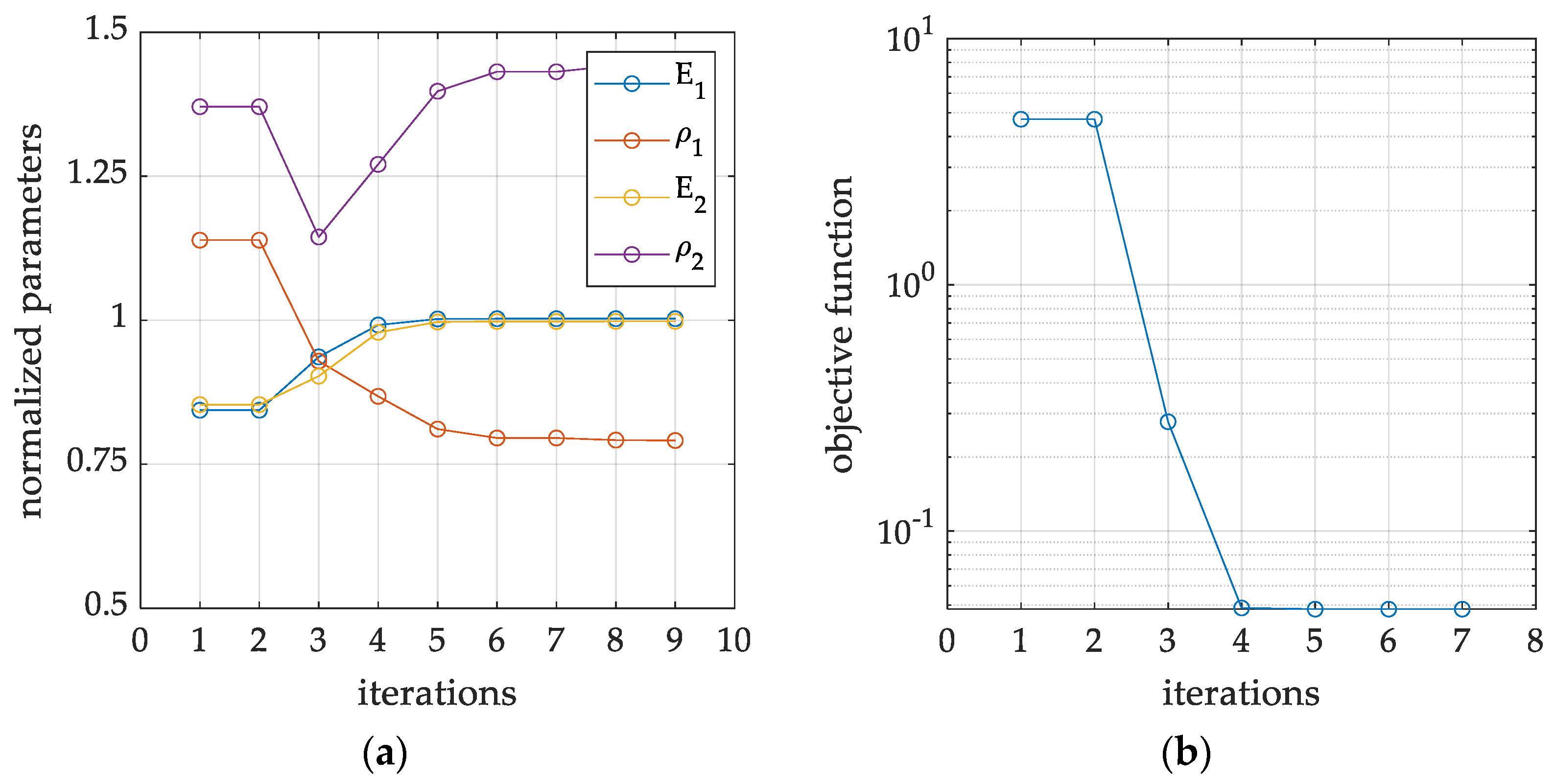
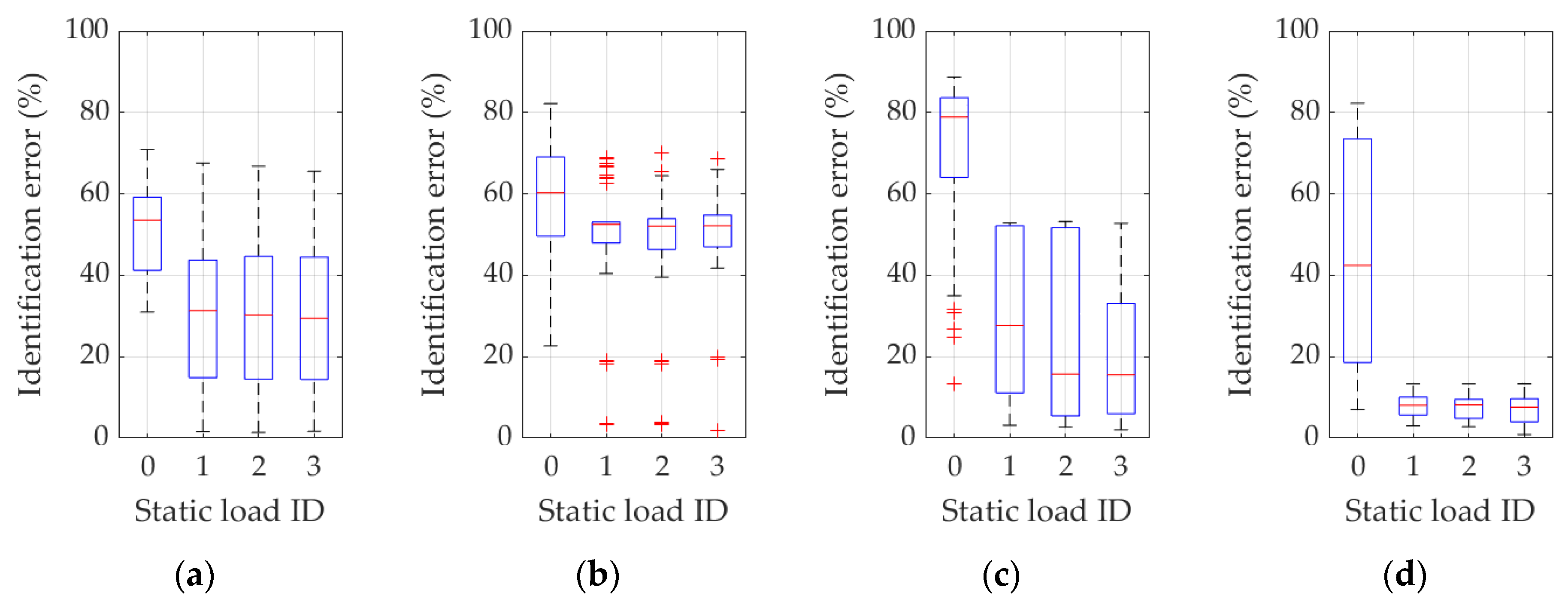
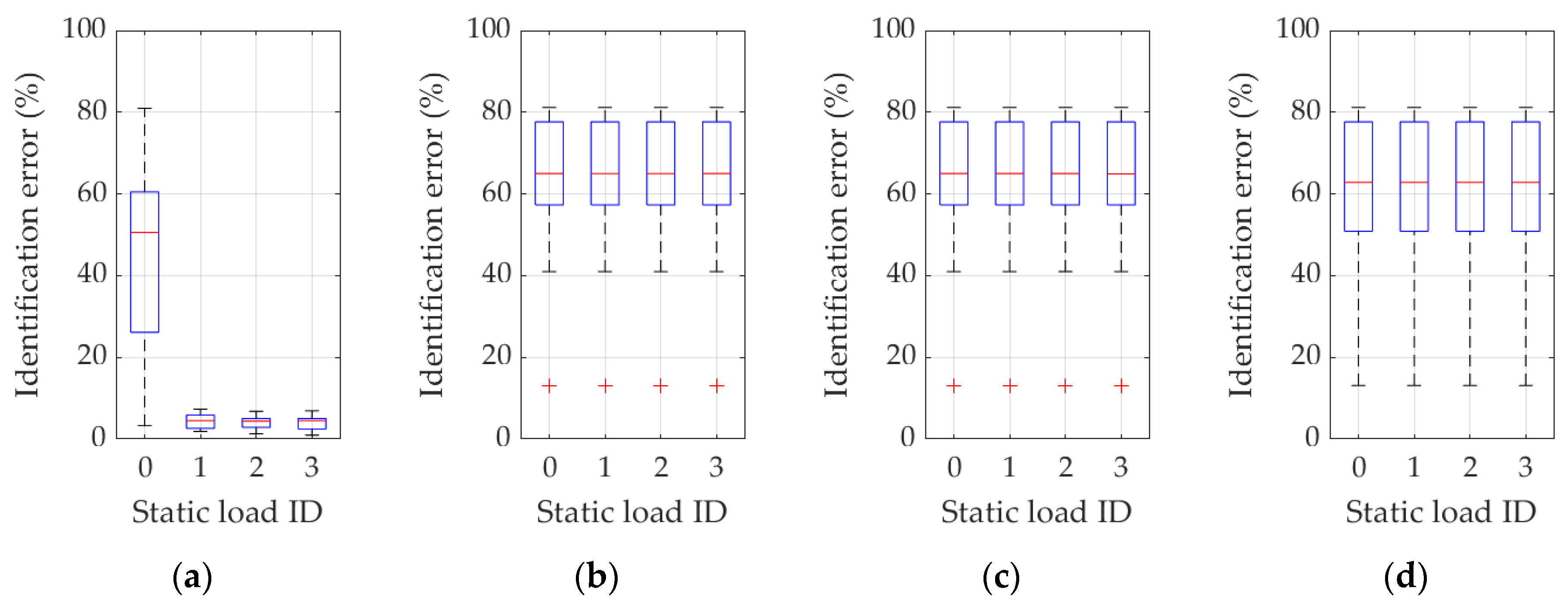
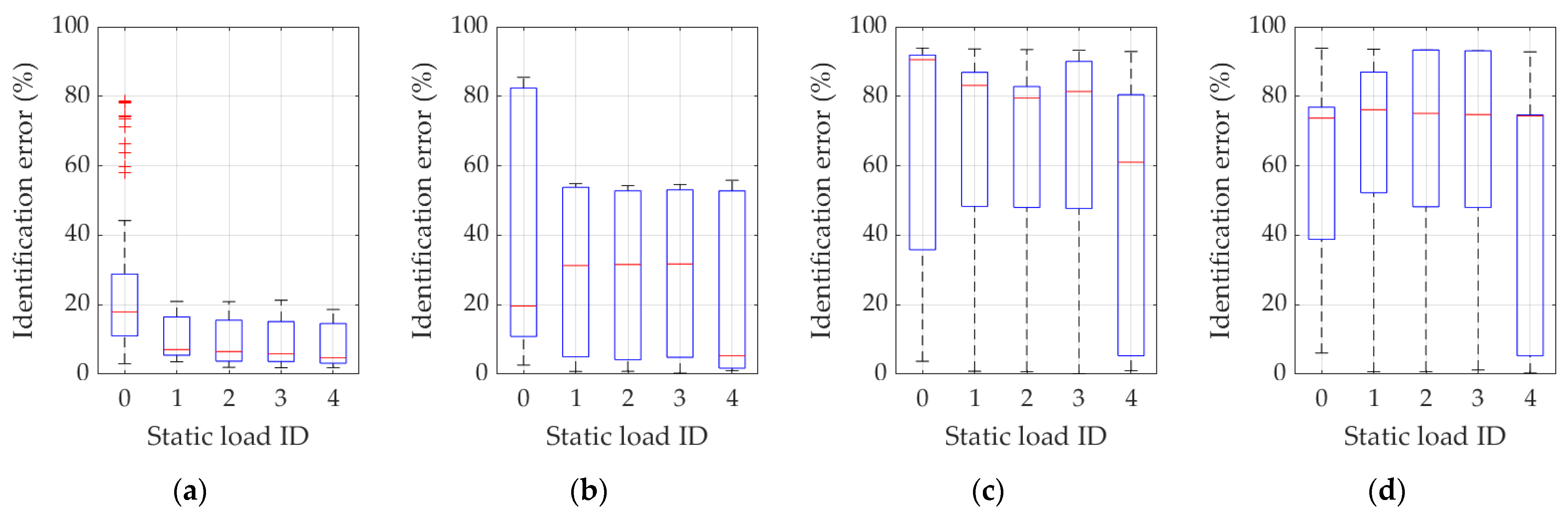
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description |
| Vector of sought parameters | |
| Young’s modulus of the i-th structural component | |
| Mass density of the i-th structural component | |
| Discrepancy term for the i-th natural vibration frequency | |
| Numerical i-th natural vibration frequency | |
| Pseudo-experimental i-th natural vibration frequency | |
| Discrepancy term for the i-th natural vibration mode shape, at the j-th measurement location | |
| Numerical j-th vertical component of the i-th natural vibration mode shape | |
| Pseudo-experimental j-th vertical component of the i-th natural vibration mode shape | |
| Discrepancy term for the k-th static load case, at the j-th measurement location | |
| Numerical j-th vertical displacement component for the k-th static load case | |
| Pseudo-experimental j-th vertical displacement component for the k-th static load case | |
| Discrepancy (or objective) function | |
| Discrepancy vector for the natural vibration frequencies | |
| Discrepancy vector of the vertical components of the natural vibration mode shapes | |
| Discrepancy vector of the vertical displacement components for the static load cases |
References
- Scalbi, A.; Zani, G.; di Prisco, M.; Mannella, P. The role of maintenance plans on serviceability and life extension of existing bridges. Struct. Concr. 2023, 24, 127–142. [Google Scholar] [CrossRef]
- Gattulli, V.; Chiaramonte, L. Condition Assessment by Visual Inspection for a Bridge Management System. Comput.-Aided Civ. Inf. 2005, 20, 95–107. [Google Scholar] [CrossRef]
- di Prisco, M.; Scola, M.; Zani, G. On site assessment of Azzone Visconti bridge in Lecco: Limits and reliability of current techniques. Constr. Build. Mater. 2019, 209, 269–282. [Google Scholar] [CrossRef]
- Ferrari, R.; Cocchetti, G.; Rizzi, E. Reference Structural Investigation on a 19th-Century Arch Iron Bridge Loyal to Design-Stage Conditions. Int. J. Archit. Herit. 2020, 14, 1425–1455. [Google Scholar] [CrossRef]
- Cornaggia, A.; Ferrari, R.; Zola, M.; Rizzi, E.; Gentile, C. Signal Processing Methodology of Response Data from a Historical Arch Bridge toward Reliable Modal Identification. Infrastructures 2022, 7, 74. [Google Scholar] [CrossRef]
- Sun, L.; Shang, Z.; Xia, Y.; Bhowmick, S.; Nagarajaiah, S. Review of Bridge Structural Health Monitoring Aided by Big Data and Artificial Intelligence: From Condition Assessment to Damage Detection. J. Struct. Eng. 2020, 146, 04020073. [Google Scholar] [CrossRef]
- Flah, M.; Nunez, I.; Chaabene, W.B.; Nehdi, M.L. Machine Learning Algorithms in Civil Structural Health Monitoring: A Systematic Review. Arch. Comput. Method E 2021, 28, 2621–2643. [Google Scholar] [CrossRef]
- Du, C.; Dutta, S.; Kurup, P.; Yu, T.; Wang, X. A review of railway infrastructure monitoring using fiber optic sensors. Sensor Actuat. A-Phys. 2020, 303, 111728. [Google Scholar] [CrossRef]
- Rashidi, M.; Mohammadi, M.; Kivi, S.S.; Abdolvand, M.M.; Truong-Hong, L.; Samali, B. A decade of modern bridge monitoring using terrestrial laser scanning: Review and future directions. Remote Sens. 2020, 12, 3796. [Google Scholar] [CrossRef]
- Bado, M.F.; Casas, J.R. A review of recent distributed optical fiber sensors applications for civil engineering structural health monitoring. Sensors 2021, 21, 1818. [Google Scholar] [CrossRef]
- Ahmed, H.; La, H.M.; Gucunski, N. Review of non-destructive civil infrastructure evaluation for bridges: State-of-the-art robotic platforms, sensors and algorithms. Sensors 2020, 20, 3954. [Google Scholar] [CrossRef]
- Assad, R.; El-Adaway, I.H. Bridge Infrastructure Asset Management System: Comparative Computational Machine Learning Approach for Evaluating and Predicting Deck Deterioration Conditions. J. Infrastruct. Syst. 2020, 26, 04020032. [Google Scholar] [CrossRef]
- Mousavi, A.A.; Zhang, C.; Masri, S.F.; Gholipour, G. Structural damage detection method based on the complete ensemble empirical mode decomposition with adaptive noise: A model steel truss bridge case study. Struct. Health Monit. 2022, 21, 887–912. [Google Scholar] [CrossRef]
- Tonelli, D.; Luchetta, M.; Rossi, F.; Migliorino, P.; Zonta, D. Structural health monitoring based on acoustic emissions: Validation on a prestressed concrete bridge tested to failure. Sensors 2020, 20, 7272. [Google Scholar] [CrossRef]
- Bien, J.; Kuzawa, M.; Kaminski, T. Strategies and tools for the monitoring of concrete bridges. Struct. Concr. 2020, 21, 1227–1239. [Google Scholar] [CrossRef]
- Aloisio, A.; Alaggio, R.; Fragiacomo, M. Dynamic identification and model updating of full-scale concrete box girders based on the experimental torsional response. Constr. Build. Mater. 2020, 264, 120146. [Google Scholar] [CrossRef]
- Pereira, S.; Magalhaes, F.; Gomes, J.P.; Cunha, A.; Lemos, J.V. Vibration-based damage detection of a concrete arch dam. Eng. Struct. 2021, 235, 112032. [Google Scholar] [CrossRef]
- Fang, J.; Ishida, T.; Fathalla, E.; Tsuchiya, S. Full-scale fatigue simulation of the deterioration mechanism of reinforced concrete road bridge slabs under dry and wet conditions. Eng. Struct. 2021, 245, 112988. [Google Scholar] [CrossRef]
- Gode, K.; Paeglitis, A. Concrete bridge deterioration caused by de-icing salts in high traffic volume road environment in Latvia. Balt. J. Road Bridge E 2014, 9, 200–207. [Google Scholar] [CrossRef]
- Kanjee, J.P.; Ballim, Y.; Otieno, M. A visual condition assessment of a reinforced concrete railway bridge subject to alkali silica reaction (ASR) deterioration in Johannesburg. MRS Adv. 2023, 8, 570–576. [Google Scholar] [CrossRef]
- Rao, A.S.; Lepech, M.D.; Kiremidjian, A.S.; Sun, X.-Y. Simplified structural deterioration model for reinforced concrete bridge piers under cyclic loading. Struct. Infr. Eng. 2017, 13, 55–66. [Google Scholar] [CrossRef]
- Ghosh, J.; Padgett, J.E. Impact of multiple component deterioration and exposure conditions on seismic vulnerability of concrete bridges. Earthq. Struct. 2012, 3, 649–673. [Google Scholar] [CrossRef]
- Alonso Medina, P.; Leon Gonzalez, J. Reinforced concrete long-term deterioration prediction for the implementation of a Bridge Management System. Mater. Today Proc. 2022, 58, 1265–1271. [Google Scholar] [CrossRef]
- Fang, I.-K.; Chen, C.-R.; Chang, I.-S. Field static load test on Kao-Ping-Hsi cable-stayed bridge. J. Bridge Eng. 2004, 9, 531–540. [Google Scholar] [CrossRef]
- Bayraktar, A.; Turker, T.; Tadla, J.; Kursun, A.; Erdis, A. Static and dynamic field load testing of the long span Nissibi cable-stayed bridge. Soil Dyn. Earthq. Eng. 2017, 94, 136–157. [Google Scholar] [CrossRef]
- Pandey, A.K.; Biswas, M. Damage detection in structures using changes in flexibility. J. Sound Vib. 1994, 169, 3–17. [Google Scholar] [CrossRef]
- Farrar, C.R.; Jauregui, D.A. Comparative study of damage identification algorithms applied to a bridge: I. Experiment. Smart Mater. Struct. 1998, 7, 704–719. [Google Scholar] [CrossRef]
- Farrar, C.R.; Jauregui, D.A. Comparative study of damage identification algorithms applied to a bridge: II. Numerical study. Smart Mater. Struct. 1998, 7, 720–731. [Google Scholar] [CrossRef]
- Mottershead, J.E.; Friswell, M.I. Model updating in structural dynamics: A survey. J. Sound Vib. 1993, 167, 347–375. [Google Scholar] [CrossRef]
- Reynders, E. System identification methods for (Operational) Modal Analysis: Review and comparison. Archiv. Comput. Method. Eng. 2012, 19, 51–124. [Google Scholar] [CrossRef]
- Pioldi, F.; Ferrari, R.; Rizzi, E. Output–only modal dynamic identification of frames by a refined FDD algorithm at seismic input and high damping. Mech. Syst. Signal Proc. 2016, 68–69, 265–291. [Google Scholar] [CrossRef]
- Pioldi, F.; Ferrari, R.; Rizzi, E. Earthquake structural modal estimates of multi-storey frames by a refined Frequency Domain Decomposition algorithm. J. Vib. Control 2017, 23, 2037–2063. [Google Scholar] [CrossRef]
- Pioldi, F.; Ferrari, R.; Rizzi, E. Seismic FDD modal identification and monitoring of building properties from real strong–motion structural response signals. Struct. Control Health Monitor. 2017, 24, e1982. [Google Scholar] [CrossRef]
- Cardoso, R.; Cury, A.; Barbosa, F. A robust methodology for modal parameters estimation applied to SHM. Mech. Syst. Signal Proc. 2017, 95, 24–41. [Google Scholar] [CrossRef]
- Sohn, H.; Czarnecki, J.A.; Farrar, C.R. Structural health monitoring using statistical process control. J. Struct. Eng. 2000, 126, 1356–1363. [Google Scholar] [CrossRef]
- Magalhāes, F.; Cunha, A.; Caetano, E. Vibration based structural health monitoring of an arch bridge: From automated OMA to damage detection. Mech. Syst. Signal Proc. 2012, 28, 212–228. [Google Scholar] [CrossRef]
- Song, G.; Gu, H.; Mo, Y.L.; Hsu, T.T.C.; Dhonde, H. Concrete structural health monitoring using embedded piezoceramic transducers. Smart Mater. Struct. 2007, 16, 959–968. [Google Scholar] [CrossRef]
- Xu, L.; Qu, Z.; Zheng, J.; Liu, Y. Concrete cracks monitoring of a practical bridge by using structural health monitoring technique. Key Eng. Mater. 2015, 648, 1–8. [Google Scholar] [CrossRef]
- Kulprapha, N.; Warnitchai, P. Structural health monitoring of continuous prestressed concrete bridges using ambient thermal responses. Eng. Struct. 2012, 40, 20–38. [Google Scholar] [CrossRef]
- Breccolotti, M. On the Evaluation of Prestress Loss in PRC Beams by Means of Dynamic Techniques. Int. J. Concr. Struct. Mater. 2018, 12, 1. [Google Scholar] [CrossRef]
- Hu, W.-H.; Tang, D.-H.; Teng, J.; Said, S.; Rohrmann, R.G. Structural health monitoring of a prestressed concrete bridge based on statistical pattern recognition of continuous dynamic measurements over 14 years. Sensors 2018, 18, 4117. [Google Scholar] [CrossRef]
- Bonopera, M.; Chang, K.-C. Novel method for identifying residual prestress force in simply supported concrete girder-bridges. Adv. Struct. Eng. 2021, 24, 3238–3251. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory; Siam: New York, NY, USA, 2005. [Google Scholar]
- Aster, R.C.; Bochers, B.; Thurber, C.H. Parameter Estimation and Inverse Analysis; Elsevier: Oxford, UK, 2013. [Google Scholar]
- Bui, H.D. Inverse Problems in the Mechanics of Materials: An Introduction; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Mroz, Z.; Stavroulakis, G.E. (Eds.) Parameter Identification of Materials and Structures; Springer: Wien, Austria, 2005. [Google Scholar] [CrossRef]
- Buljak, V.; Cocchetti, G.; Cornaggia, A.; Garbowski, T.; Maier, G.; Novati, G. Materials Mechanical Characterizations and Structural Diagnoses by Inverse Analyses. In Handbook of Damage Mechanics; Voyiadjis, G.Z., Ed.; Springer: New York, NY, USA, 2015; pp. 619–642. [Google Scholar] [CrossRef]
- Garbowski, T.; Maier, G.; Novati, G. Diagnosis of concrete dams by flat–jack tests and inverse analyses based on proper orthogonal decomposition. J. Mech. Mater. Struct. 2011, 6, 181–202. [Google Scholar] [CrossRef]
- Gajewski, T.; Garbowski, T. Calibration of concrete parameters based on digital image correlation and inverse analysis. Archiv. Civ. Mech. Eng. 2014, 14, 170–180. [Google Scholar] [CrossRef]
- Bocciarelli, M.; Buljak, V.; Moy, C.K.S.; Ringer, S.P.; Ranzi, G. An inverse analysis approach based on POD direct model for the mechanical characterization of metallic materials. Comput. Mater. Sci. 2014, 95, 302–308. [Google Scholar] [CrossRef]
- Arizzi, F.; Rizzi, E. Elastoplastic parameter identification by simulation of static and dynamic indentation tests. Model. Sim. Mater. Sci. Eng. 2014, 22, 035017. [Google Scholar] [CrossRef]
- Buljak, V.; Cocchetti, G.; Cornaggia, A.; Maier, G. Assessment of residual stresses and mechanical characterization of materials by “hole drilling” and indentation tests combined and by inverse analysis. Mech. Res. Comm. 2015, 68, 18–24. [Google Scholar] [CrossRef]
- Buljak, V.; Cocchetti, G.; Cornaggia, A.; Maier, G. Estimation of residual stresses by inverse analysis based on experimental data from sample removal for “small punch” tests. Eng. Struct. 2017, 136, 77–86. [Google Scholar] [CrossRef]
- Buljak, V.; Cocchetti, G.; Cornaggia, A.; Maier, G. Parameter identification in elastoplastic material models by Small Punch Tests and inverse analysis with model reduction. Meccanica 2018, 53, 3815–3829. [Google Scholar] [CrossRef]
- Cocchetti, G.; Mahini, M.R.; Maier, G. Mechanical characterization of foils with compression in their planes. Mech. Adv. Mater. Struct. 2014, 21, 853–870. [Google Scholar] [CrossRef]
- Buljak, V.; Bavier-Romero, S.; Kallel, A. Calibration of Drucker–Prager cap constitutive model for ceramic powder compaction through inverse analysis. Materials 2021, 14, 4044. [Google Scholar] [CrossRef]
- Miller, B. Application of neural networks for structure updating. Comput. Assist. Mech. Eng. Sci. 2011, 18, 191–203. [Google Scholar]
- Ribeiro, D.; Calcada, R.; Delgado, R.; Brehm, M.; Zabel, V. Finite element model updating of a bowstring–arch railway bridge based on experimental modal parameters. Eng. Struct. 2012, 40, 413–435. [Google Scholar] [CrossRef]
- Bendon, C.; Dilena, M.; Morassi, A. Ambient vibration testing and structural identification of a cable–stayed bridge. Meccanica 2016, 51, 2777–2796. [Google Scholar] [CrossRef]
- Shabbir, F.; Omenzetter, P. Model updating using genetic algorithms with sequential technique. Eng. Struct. 2016, 120, 166–182. [Google Scholar] [CrossRef]
- Crognale, M.; De Iuliis, M.; Rinaldi, C.; Gattulli, V. Damage detection with image processing: A comparative study. Earthq. Eng. Eng. Vib. 2023, 22, 333–345. [Google Scholar] [CrossRef]
- dell’Isola, F.; Vestroni, F.; Vidoli, S. Structural-damage detection by distributed piezoelectric transducers and tuned electric circuits. Res. Nondestruct. Eval. 2005, 16, 101–118. [Google Scholar] [CrossRef]
- Capecchi, D.; Ciambella, J.; Pau, A.; Vestroni, F. Damage identification in a parabolic arch by means of natural frequencies, modal shapes and curvatures. Meccanica 2016, 51, 2847–2859. [Google Scholar] [CrossRef]
- Gattulli, V.; Potenza, F.; Piccirillo, G. Multiple Tests for Dynamic Identification of a Reinforced Concrete Multi-Span Arch Bridge. Buildings 2022, 12, 833. [Google Scholar] [CrossRef]
- Buljak, V. Inverse Analysis with Model Reduction; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Kleiber, M.; Antunez, H.; Hien, T.D.; Kowalczyk, P. Parameter Sensitivity in Nonlinear Mechanics; Wiley: Chichester, UK, 1997. [Google Scholar]
- Leonhardt, F. Vorlesungen über Massivbau. Sechster Teil. Grundlag des Massivbrückenbaues; Springer: Berlin, Germany, 1979. [Google Scholar] [CrossRef]
- Billington, D.P. Robert Maillart’s Bridges. The Art of Engineering; Princeton University Press: Princeton, UK, 1979. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using Frequency Domain Decomposition. Smart Mater. Struct. 2001, 10, 441–445. [Google Scholar] [CrossRef]
- Malekjafarian, A.; Obrien, E.J. Identification of bridge mode shapes using Short Time Frequency Domain Decomposition of the responses measured in a passing vehicle. Eng. Struct. 2014, 81, 386–397. [Google Scholar] [CrossRef]
- Peeters, B.; De Roeck, G. Reference-based stochastic subspace identification for output-only modal analysis. Mech. Syst. Sign. Proc. 1999, 13, 855–878. [Google Scholar] [CrossRef]
- Peters, B.; De Roeck, G. Reference based stochastic subspace identification in Civil Engineering. Inv. Prob. Eng. 2000, 8, 47–74. [Google Scholar] [CrossRef]
- Reynders, E.; De Roeck, G. Reference-based combined deterministic-stochastic subspace identification for experimental and operational modal analysis. Mech. Syst. Sign. Proc. 2008, 22, 617–637. [Google Scholar] [CrossRef]
- Reynders, E.; Pintelon, R.; De Roeck, G. Uncertainty bounds on modal parameters obtained from stochastic subspace identification. Mech. Syst. Sign. Proc. 2008, 22, 948–969. [Google Scholar] [CrossRef]
- Dohler, M.; Mevel, L. Efficient multi-order uncertainty computation for stochastic subspace identification. Mech. Syst. Sign. Proc. 2013, 38, 346–366. [Google Scholar] [CrossRef]
- Reynders, E.; Maes, K.; Lombaert, G.; De Roeck, G. Uncertainty quantification in operational modal analysis with stochastic subspace identification: Validation and applications. Mech. Syst. Sign. Proc. 2016, 66–67, 13–30. [Google Scholar] [CrossRef]
- Ferrari, R.; Froio, D.; Rizzi, E.; Gentile, C.; Chatzi, E. Model updating of a historic concrete bridge by sensitivity and global optimization–based Latin hypercube sampling. Eng. Struct. 2019, 1, 139–160. [Google Scholar] [CrossRef]
- Qin, S.; Han, S.; Li, S. In-situ testing and finite element model updating of a long-span cable-stayed bridge with ballastless track. Structures 2022, 45, 1412–1423. [Google Scholar] [CrossRef]
- Bai, Y.; Peng, Z.; Wang, Z. A finite element model updating method based on the trust region and adaptive surrogate model. J. Sound Vib. 2023, 555, 117701. [Google Scholar] [CrossRef]
- Vasuki, A. Nature-Inspired Optimization Algorithms; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- MathWorks. Matlab User’s Guide—Release 2022a; The MathWorks Inc.: Natick, MA, USA, 2014. [Google Scholar]
- Tang, G.; Yan, X.; Wang, X. Chaotic Signal Denoising Based on Adaptive Smoothing Multiscale Morphological Filtering. Complexity 2020, 2020, 7242943. [Google Scholar] [CrossRef]
- Ravizza, G.; Ferrari, R.; Rizzi, E.; Dertimanis, V. On the denoising of structural vibration response records from low-cost sensors: A critical comparison and assessment. J. Civ. Struct. Health Monitor. 2021, 11, 1201–1224. [Google Scholar] [CrossRef]
- Greś, S.; Tatsis, K.E.; Dertimanis, V.; Chatzi, E. Low-rank approximation of Hankel matrices in denoising applications for statistical damage diagnosis of wind turbine blades. Mech. Syst. Sign. Proc. 2023, 197, 110391. [Google Scholar] [CrossRef]




| Load ID | Load Cases | |||
|---|---|---|---|---|
| 0 | 1 | 2 | 3 | |
| 0 | + | |||
| 1 | + | |||
| 2 | + | + | ||
| 3 | + | + | + | |
| Name | Frequency | Load Case | ||||
|---|---|---|---|---|---|---|
| ID | 0 | 1 | 1 and 2 | 1–3 | 1–4 | |
| Example 1a | 1 | 51.43 11.20 | 30.28 18.14 | 30.61 18.46 | 30.29 18.66 | - |
| 1 and 2 | 58.96 13.93 | 49.88 15.52 | 49.66 15.42 | 49.77 15.57 | - | |
| 1–3 | 72.28 17.27 | 28.81 20.76 | 24.30 20.64 | 22.93 19.24 | - | |
| 1–4 | 44.36 26.74 | 7.99 3.02 | 7.86 3.29 | 7.24 3.79 | - | |
| 1–5 | 35.15 22.91 | 7.40 9.42 | 2.32 | 2.45 | - | |
| 1–6 | 29.23 23.02 | 7.16 9.25 | 2.05 | 2.10 | - | |
| Example 1b | 1 | 45.44 14.27 | 16.69 13.62 | 16.73 13.76 | 16.65 13.74 | - |
| 1 and 2 | 41.42 15.24 | 25.21 14.67 | 25.13 14.75 | 24.98 14.81 | - | |
| 1–3 | 40.84 17.58 | 13.75 5.80 | 13.72 5.56 | 13.66 5.71 | - | |
| 1–4 | 30.01 12.94 | 8.62 4.13 | 8.48 4.14 | 8.44 4.06 | - | |
| 1–5 | 24.93 17.50 | 3.98 | 4.16 | .19 | ||
| Example 2 | 1 | 49.55 14.37 | 21.45 12.06 | 22.09 12.67 | 22.30 13.15 | 13.19 9.69 |
| 1 and 2 | 47.63 19.87 | 22.05 16.51 | 22.05 16.65 | 21.91 16.76 | 29.32 20.41 | |
| 1–3 | 48.40 19.61 | 15.79 14.44 | 15.55 14.55 | 15.44 14.70 | 11.27 11.36 | |
| 1–4 | 39.47 21.38 | 3.11 | 3.26 | 3.28 | 4.55 | |
| Name | Frequency | Load Case | ||||
|---|---|---|---|---|---|---|
| ID | 0 | 1 | 1 and 2 | 1–3 | 1–4 | |
| Example 1a | 1 | 15.34 | 3.29 | 2.56 | 2.28 | - |
| 1 and 2 | 13.30 | 13.30 | 13.30 | 13.30 | - | |
| 1–3 | 13.30 | 13.30 | 13.30 | 13.30 | - | |
| 1–4 | 15.23 | 15.23 | 15.23 | 15.23 | - | |
| Example 1b | 1 | 21.26 | 1.63 | 1.47 | 1.69 | - |
| 1 and 2 | 19.94 | 19.94 | 19.94 | 19.94 | - | |
| 1–3 | 19.94 | 19.94 | 19.94 | 19.94 | - | |
| 1–4 | 20.14 | 30.14 | 20.14 | 20.14 | - | |
| Example 2 | 1 | 20.98 | 5.78 | 6.04 | 5.90 | 5.93 |
| 1 and 2 | 32.74 | 24.88 | 24.30 | 24.18 | 24.65 | |
| 1–3 | 32.84 | 28.42 | 27.88 | 28.39 | 34.02 | |
| 1–4 | 27.30 | 25.35 | 24.98 | 23.44 | 34.49 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garbowski, T.; Cornaggia, A.; Zaborowicz, M.; Sowa, S. Computer-Aided Structural Diagnosis of Bridges Using Combinations of Static and Dynamic Tests: A Preliminary Investigation. Materials 2023, 16, 7512. https://doi.org/10.3390/ma16247512
Garbowski T, Cornaggia A, Zaborowicz M, Sowa S. Computer-Aided Structural Diagnosis of Bridges Using Combinations of Static and Dynamic Tests: A Preliminary Investigation. Materials. 2023; 16(24):7512. https://doi.org/10.3390/ma16247512
Chicago/Turabian StyleGarbowski, Tomasz, Aram Cornaggia, Maciej Zaborowicz, and Sławomir Sowa. 2023. "Computer-Aided Structural Diagnosis of Bridges Using Combinations of Static and Dynamic Tests: A Preliminary Investigation" Materials 16, no. 24: 7512. https://doi.org/10.3390/ma16247512
APA StyleGarbowski, T., Cornaggia, A., Zaborowicz, M., & Sowa, S. (2023). Computer-Aided Structural Diagnosis of Bridges Using Combinations of Static and Dynamic Tests: A Preliminary Investigation. Materials, 16(24), 7512. https://doi.org/10.3390/ma16247512










