Fermat Principle, Ramsey Theory and Metamaterials
Abstract
:1. Introduction
2. Results
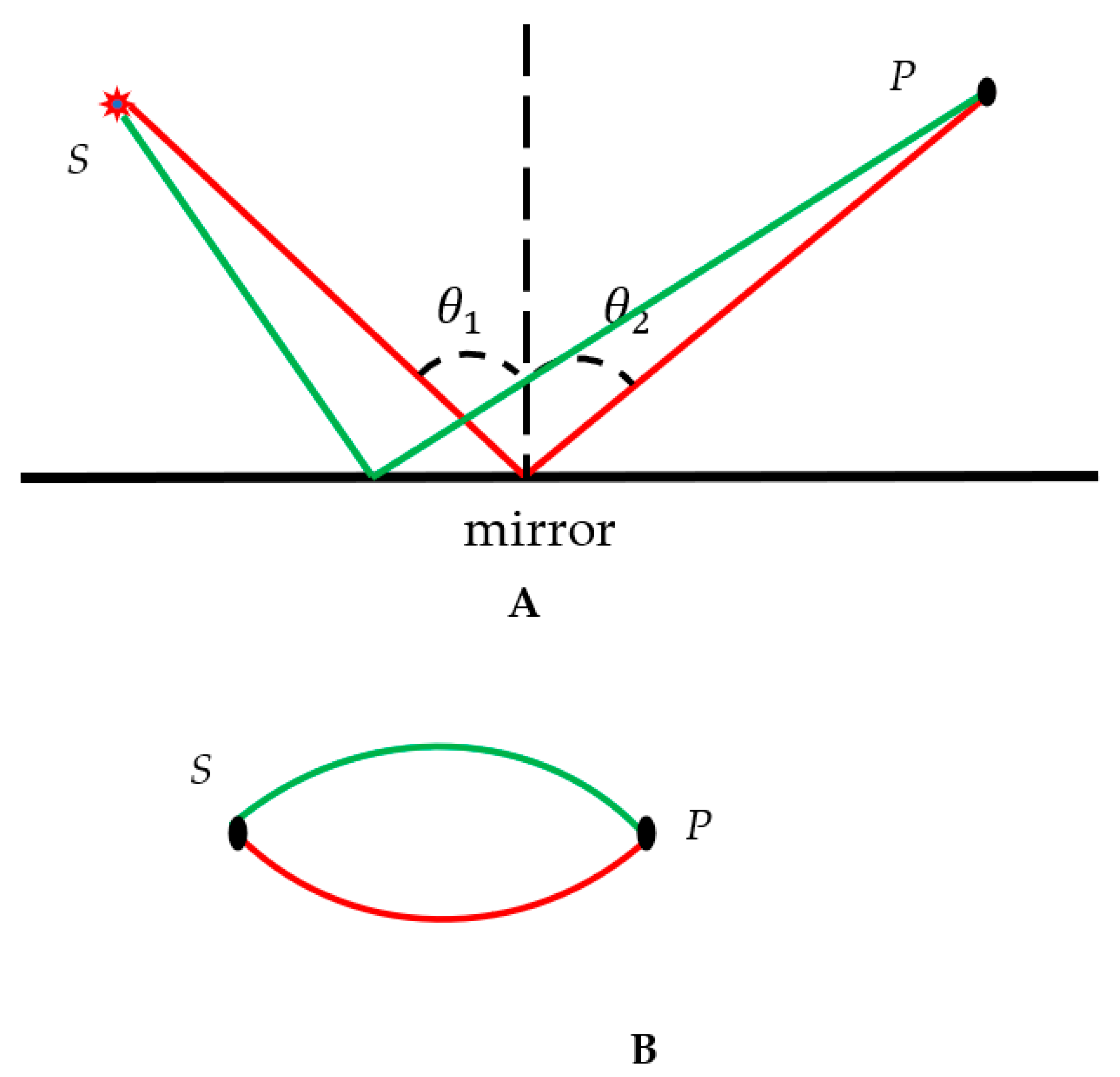
2.1. Ramsey Approach to Optical Systems: From Real Optical System to a Graph
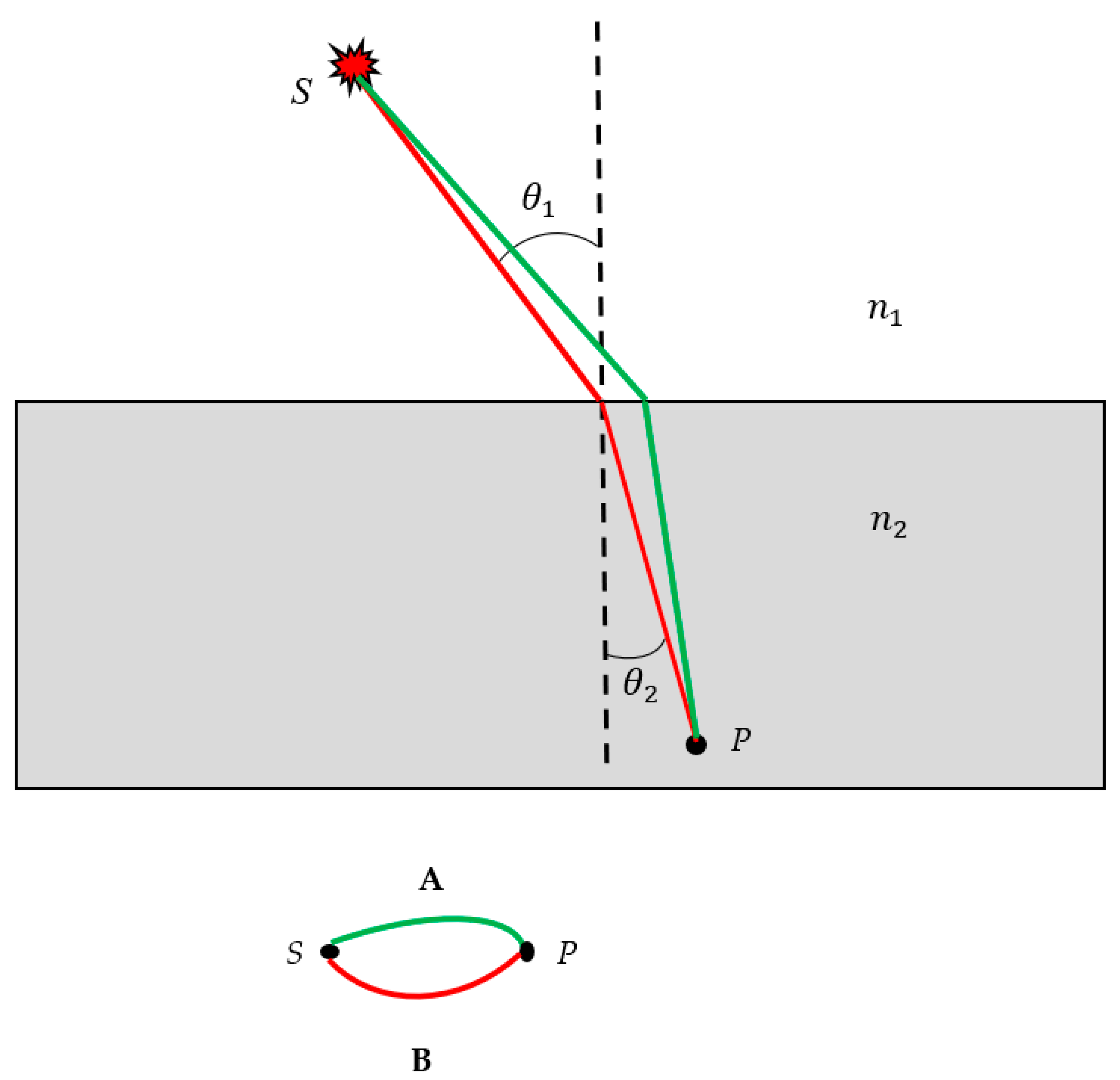
2.2. Ramsey Approach to Metamaterials
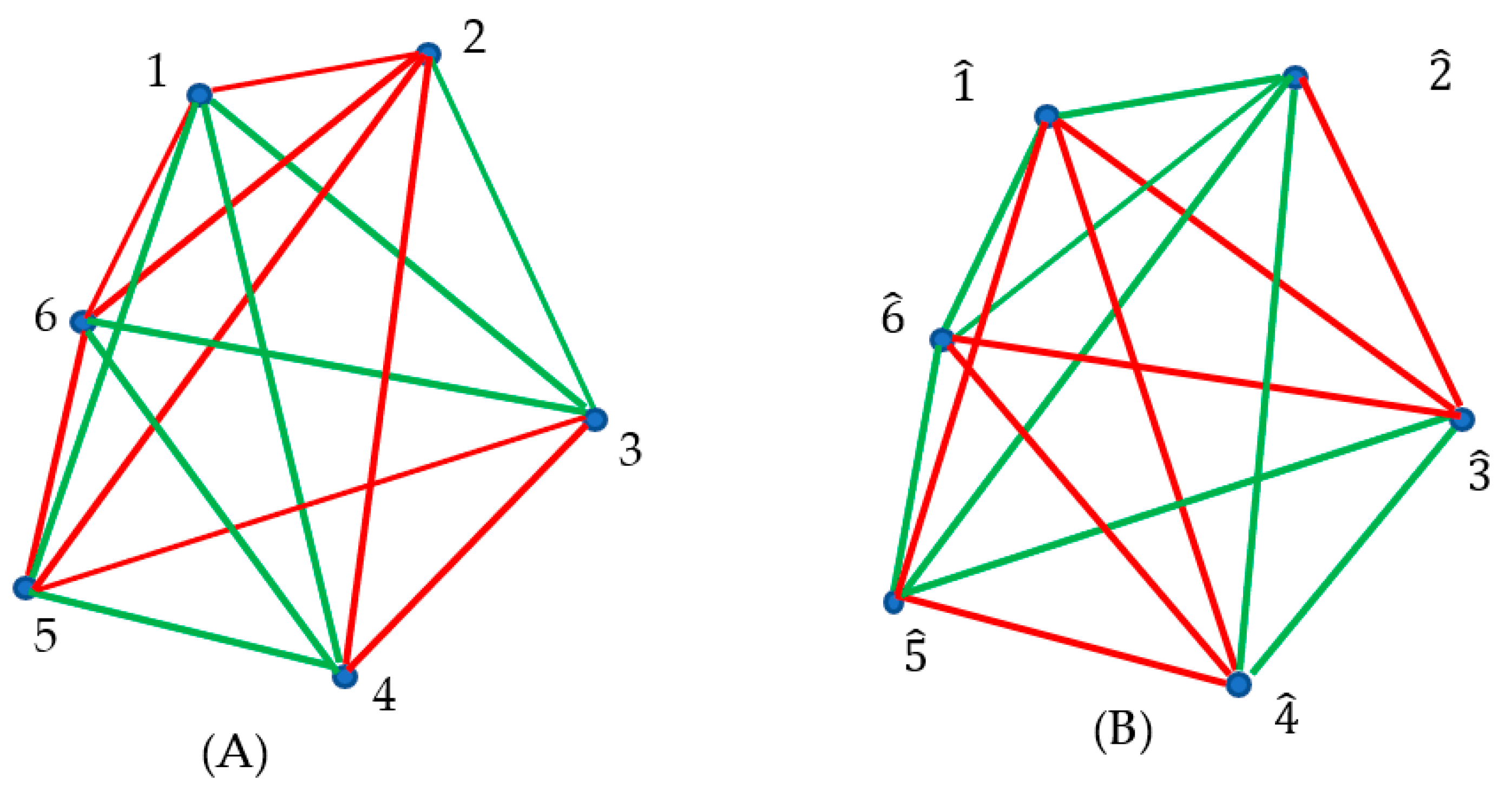
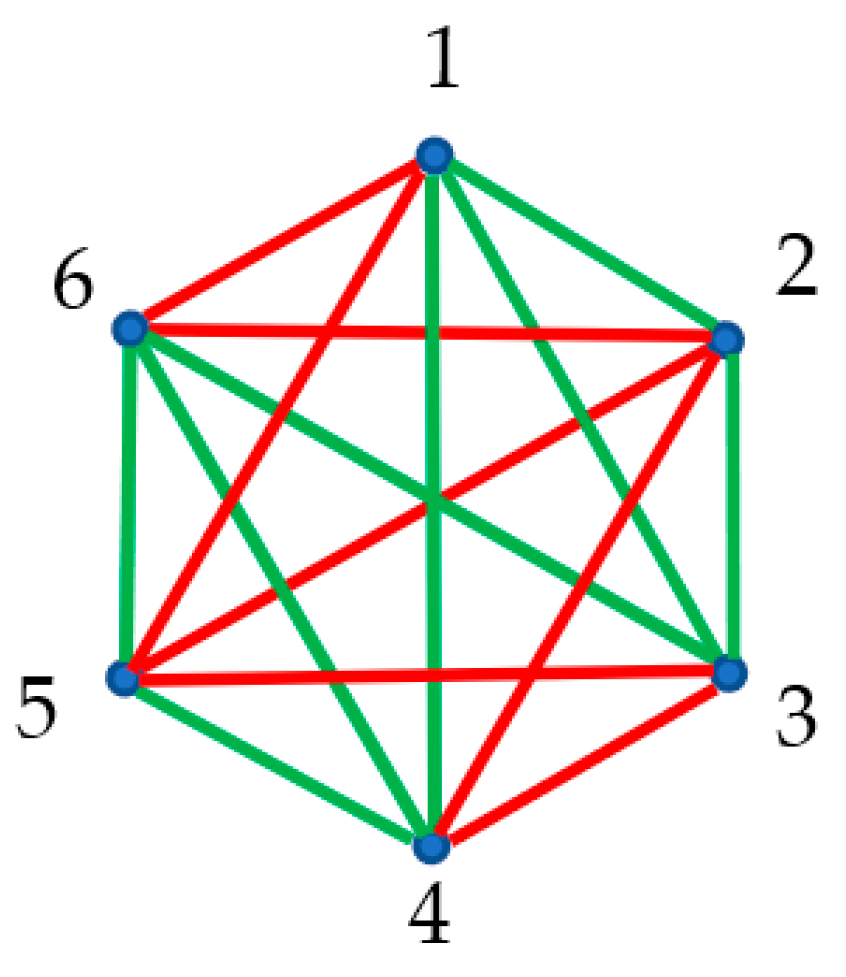
2.3. Optical Interpretation of the Infinite Ramsey Theorem
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hecht, E. Section 4.5—Fermat’s Principle. In Optics, 4th ed.; Addison-Wesley: Reading, MA, USA, 2002; pp. 106–111. [Google Scholar]
- Ceccarelli, M. Distinguished Figures in Mechanism and Machine Science: Their Contributions and Legacies; Springer: Dodrecht, The Netherlands, 2007; pp. 217–247. [Google Scholar]
- Adamson, P. Philosophy in the Islamic World: A History of Philosophy without Any Gaps; Oxford University Press: Oxford, UK, 2016; p. 77. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Veselago, V.G. Some remarks regarding electrodynamics of materials with negative refraction. Appl. Phys. B 2005, 81, 403–407. [Google Scholar] [CrossRef]
- Veselago, V.G. Formulating Fermat’s principle for light traveling in negative refraction materials. Physics-Uspekhi 2002, 45, 1097. [Google Scholar] [CrossRef]
- Smith, D.R.; Kroll, N.K. Negative Refractive Index in Left-Handed Materials. Phys. Rev. Lett. 2000, 85, 2933. [Google Scholar] [CrossRef] [PubMed]
- Shalaev, V. Optical negative-index metamaterials. Nat. Photon 2007, 1, 41–48. [Google Scholar] [CrossRef]
- Pokrovsky, A.L.; Efros, A.L. Lens based on the use of left-handed materials. Appl. Opt. 2003, 42, 5701–5705. [Google Scholar] [CrossRef] [PubMed]
- Wilson, R.J. Introduction to Graph Theory, 4th ed.; Addison Wesley Longman Limited, Edinburgh Gate: Harlow, UK, 1996; pp. 8–21. [Google Scholar]
- Trudeau, R.J. Introduction to Graph Theory; Corrected, enlarged republication. ed.; Dover Pub.: New York, NY, USA, 1993; pp. 19–64. [Google Scholar]
- Katz, M.; Reimann, J. An Introduction to Ramsey Theory: Fast Functions, Infinity, and Metamathematics, Student Mathematical Library; American Mathematical Society: Providence, RI, USA, 2018; Volume 87, pp. 1–34. [Google Scholar]
- Graham, R.L.; Spencer, J.H. Ramsey Theory. Sci. Am. 1990, 7, 112–117. [Google Scholar] [CrossRef]
- Li, Y.; Lin, Q. Elementary Methods of the Graph Theory, Applied Mathematical Sciences; Springer: Cham, Switzerland, 2020; pp. 3–44. [Google Scholar]
- Graham, R.; Butler, S. Rudiments of Ramsey Theory, 2nd ed.; American Mathematical Society: Providence, RI, USA, 2015; pp. 7–46. [Google Scholar]
- Landman, B.M.; Robertson, A. Ramsey Theory on the Integers; Student Mathematical Library, AMS: Providence, RI, USA, 2004; Volume 24. [Google Scholar]
- Chartrand, G.; Zhang, P. New directions in Ramsey theory. Discret. Math. Lett. 2021, 6, 84–96. [Google Scholar]
- Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth; Hyperion: New York, NY, USA, 1998; p. 52. [Google Scholar]
- Roberts, F.S. Applications of Ramsey theory. Discret. Appl. Math. 1984, 9, 251–261. [Google Scholar] [CrossRef]
- Bassetto, M.; Cui, W. A Ramsey Theory of Financial Distortions; IFS Working Papers; IFS Working Paper No. W21/05; Institute for Fiscal Studies (IFS): London, UK, 2021. [Google Scholar]
- Shvalb, N.; Frenkel, M.; Shoval, S.; Bormashenko, E. Dynamic Ramsey Theory of Mechanical Systems Forming a Complete Graph and Vibrations of Cyclic Compounds. Dynamics 2023, 3, 272–281. [Google Scholar] [CrossRef]
- Shvalb, N.; Frenkel, M.; Shoval, S.; Bormashenko, E. Ramsey theory and thermodynamics. Heliyon 2023, 9, e13561. [Google Scholar] [CrossRef]
- Kar, S. Metamaterials and Metasurfaces: Basics and Trends; Series in Electromagnetics and Metamaterials; IOP Publishing: Bristol, UK, 2023; Chapter 1; pp. 1–46. [Google Scholar]
- Cai, W.; Shalaev, V. Optical Metamaterials: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2010; Chapter 6; pp. 101–120. [Google Scholar]
- Engheta, N.; Ziolkowski, R.W. Metamaterials: Physics and Engineering Explorations; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [PubMed]
- Dudek, A.; Prałat, P. On some Multicolor Ramsey Properties of Random Graphs. SIAM J. Discret. Math. 2017, 31, 2079–2092. [Google Scholar] [CrossRef]
- Masic, I. Ibn al-Haitham--father of optics and describer of vision theory. Medical Arhiv. 2008, 62, 183–188. [Google Scholar]
- Choudum, S.A.; Ponnusamy, B. Ramsey numbers for transitive tournaments. Discret. Math. 1999, 206, 119–129. [Google Scholar] [CrossRef]
- Nehra, R.; Sekine, R.; Ledezma, L.; Guo, Q.; Gray, R.M. Few-cycle vacuum squeezing in nanophotonics. Science 2022, 377, 1333–1337. [Google Scholar] [CrossRef]
- Leblond, H.; Mihalache, D. Models of few optical cycle solitons beyond the slowly varying envelope approximation. Phys. Rep. 2013, 523, 61–126. [Google Scholar] [CrossRef]
- Shuman, E.S.; Barry, J.F.; Glenn, D.R.; DeMill, D. Radiative Force from Optical Cycling on a Diatomic Molecule. Phys. Rev. Lett. 2009, 103, 223001. [Google Scholar] [CrossRef]
- Gao, P.; Yao, B.; Rupp, R.; Min, J.; Guo, R.; Ma, B.; Zheng, J.; Lei, M.; Yan, S.; Dan, D.; et al. Autofocusing based on wavelength dependence of diffraction in two-wavelength digital holographic microscopy. Opt. Lett. 2012, 37, 1172–1174. [Google Scholar] [CrossRef]
- Wen, Y.; Wang, H.; Anand, A.; Qu, W.; Cheng, H.; Dong, Z.; Wu, Y. A fast autofocus method based on virtual differential optical path in digital holography: Theory and applications. Opt. Lasers Eng. 2019, 121, 133–142. [Google Scholar] [CrossRef]
- Kiaei, M.S.; Assi, C. A Survey on the p-Cycle Protection Method. IEEE Commun. Surv. Tutor. 2009, 11, 53–70. [Google Scholar] [CrossRef]
- Mitra, D.; Lasner, Z.D.; Zhu, G.-Z.; Dickerson, C.E.; Augenbraun, B.L.; Bailey, A.D.; Alexandrova, A.N.; Campbell, W.C.; Caram, J.R.; Hudson, E.R.; et al. Pathway toward Optical Cycling and Laser Cooling of Functionalized Arenes. J. Phys. Chem. Lett. 2022, 13, 7029–7035. [Google Scholar] [CrossRef] [PubMed]
- Hofsäss, S.; Doppelbauer, M.; Wright, S.C.; Kray, S.; Sartakov, B.G.; P´erez-Ríos, J.; Meijer, G.; Truppe, S. Optical cycling of AlF molecules. New J. Phys. 2021, 23, 075001. [Google Scholar] [CrossRef]
- Shvalb, N.; Frenkel, M.; Shoval, S.; Bormashenko, E. Universe as a Graph (Ramsey Approach to Analysis of Physical Systems). World J. Phys. 2023, 1, 1–24. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frenkel, M.; Shoval, S.; Bormashenko, E. Fermat Principle, Ramsey Theory and Metamaterials. Materials 2023, 16, 7571. https://doi.org/10.3390/ma16247571
Frenkel M, Shoval S, Bormashenko E. Fermat Principle, Ramsey Theory and Metamaterials. Materials. 2023; 16(24):7571. https://doi.org/10.3390/ma16247571
Chicago/Turabian StyleFrenkel, Mark, Shraga Shoval, and Edward Bormashenko. 2023. "Fermat Principle, Ramsey Theory and Metamaterials" Materials 16, no. 24: 7571. https://doi.org/10.3390/ma16247571






