Mechanical Properties of AISI 316L Lattice Structures via Laser Powder Bed Fusion as a Function of Unit Cell Features
Abstract
:1. Introduction
2. Materials and Methods
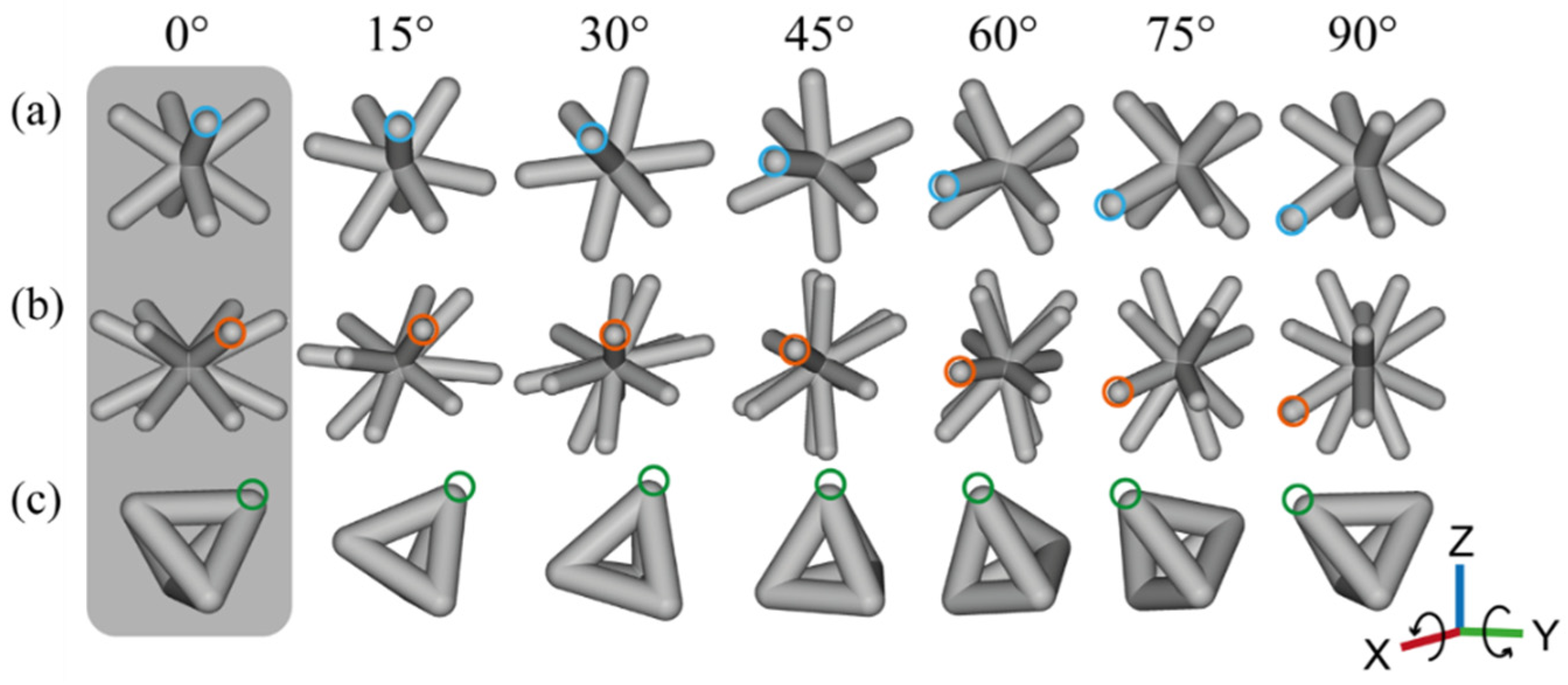
2.1. Design of the Lattice Structures and Samples for Compression Test
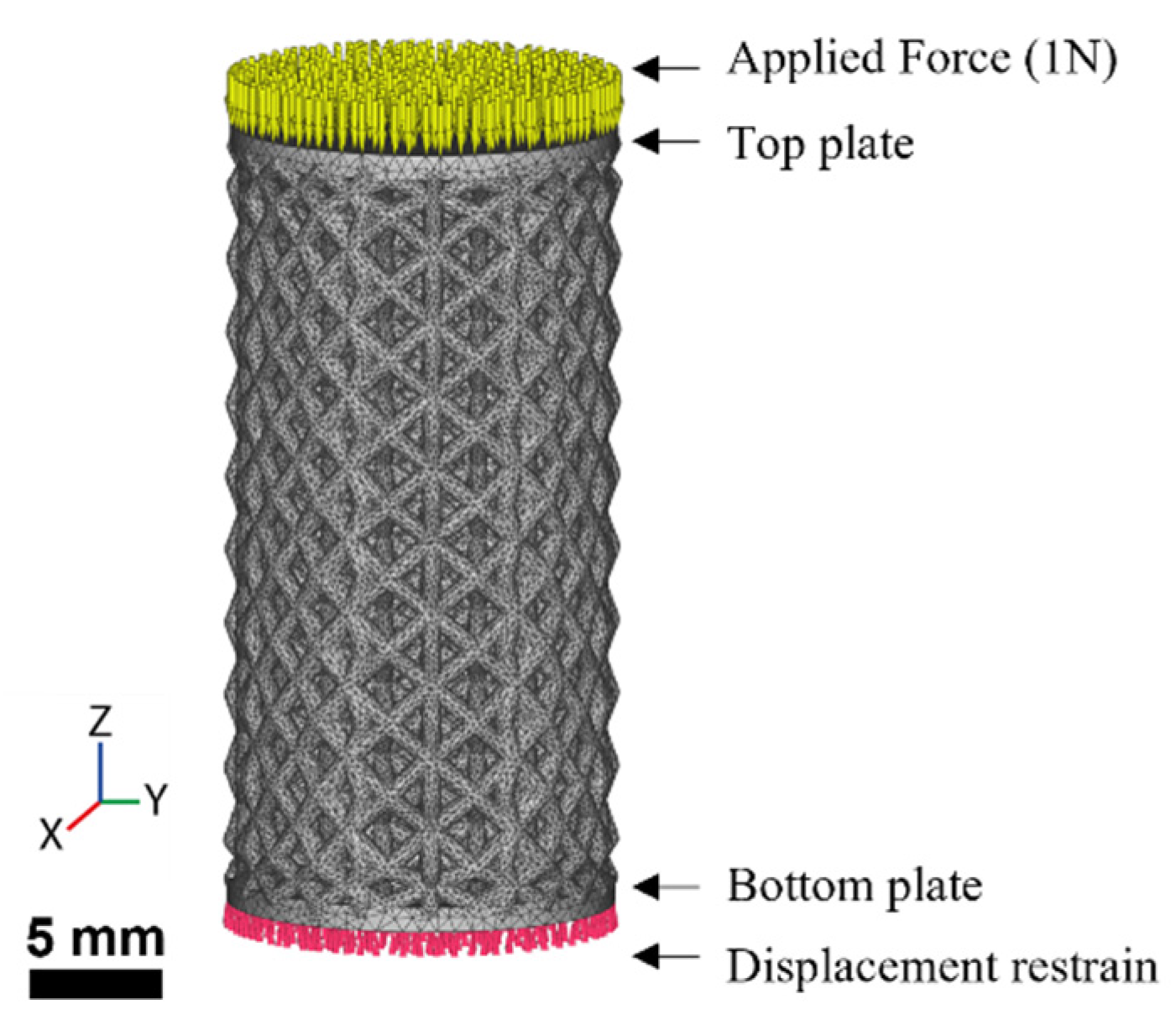
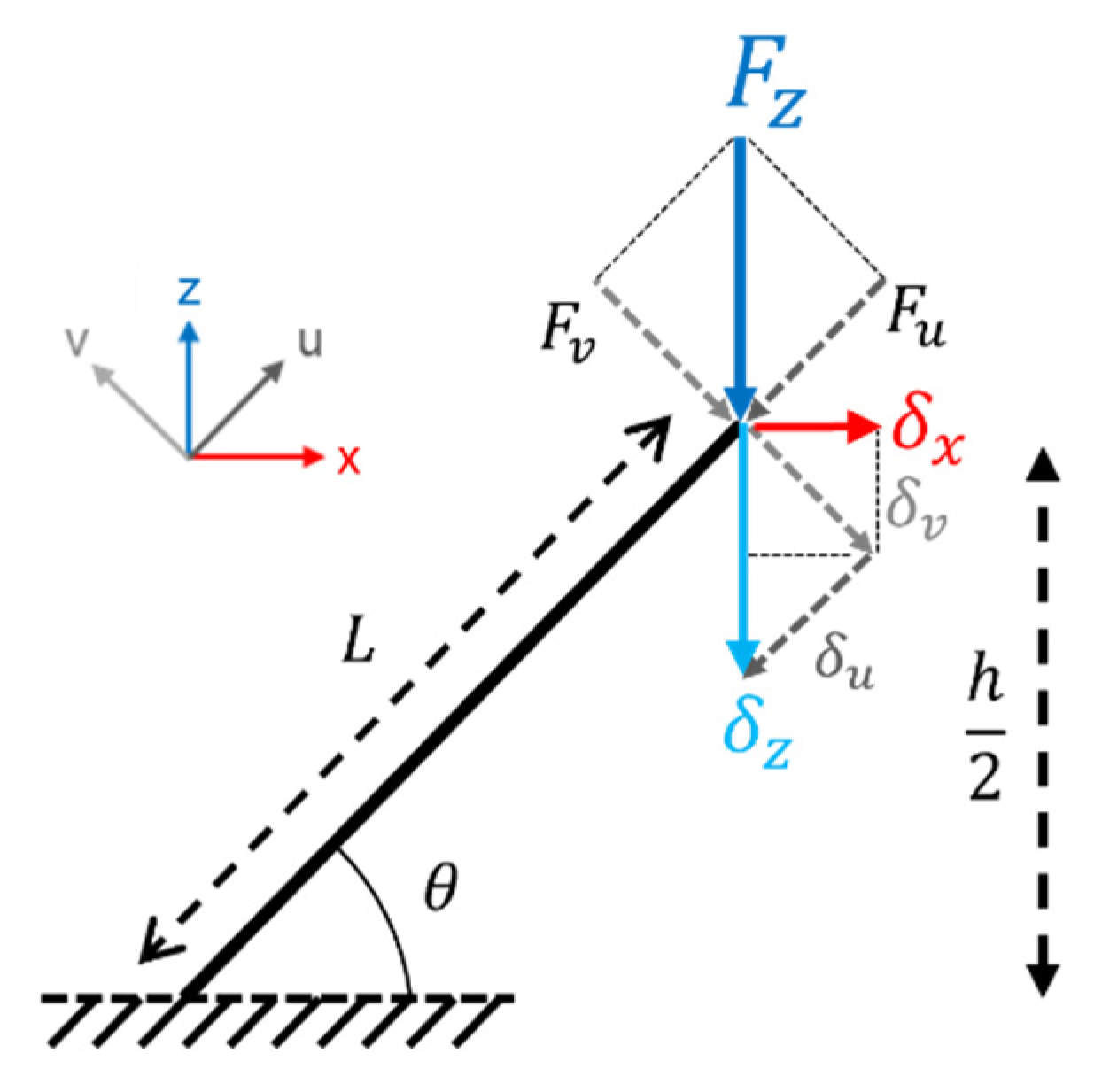
2.2. Mechanical Computational Characterization via Finite Element Modeling (FEM)
2.3. Additive Manufacturing via the Laser Powder Bed Fusion (LPBF) Process
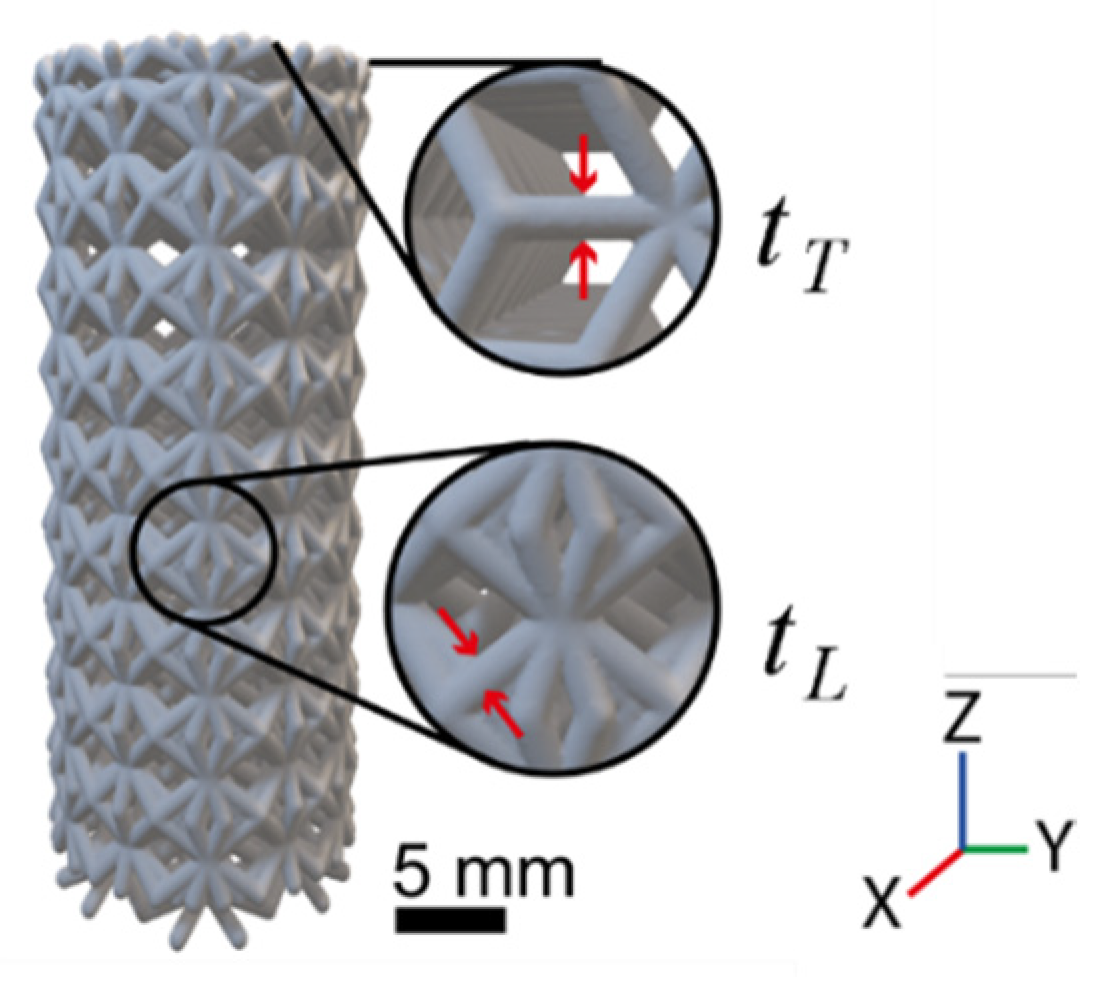
2.4. Morphological Characterization
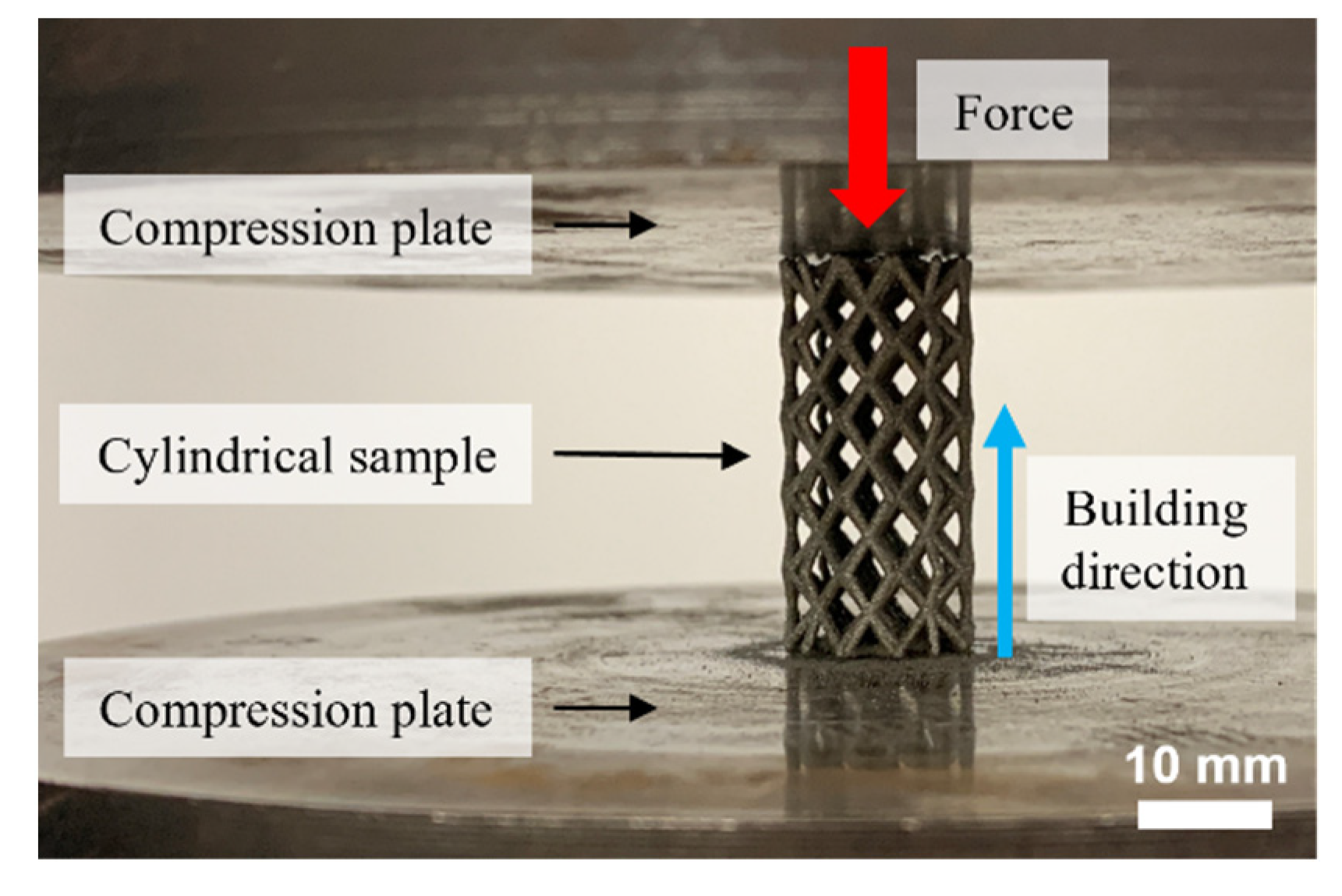
2.5. Mechanical Characterization via Compression Tests
3. Results
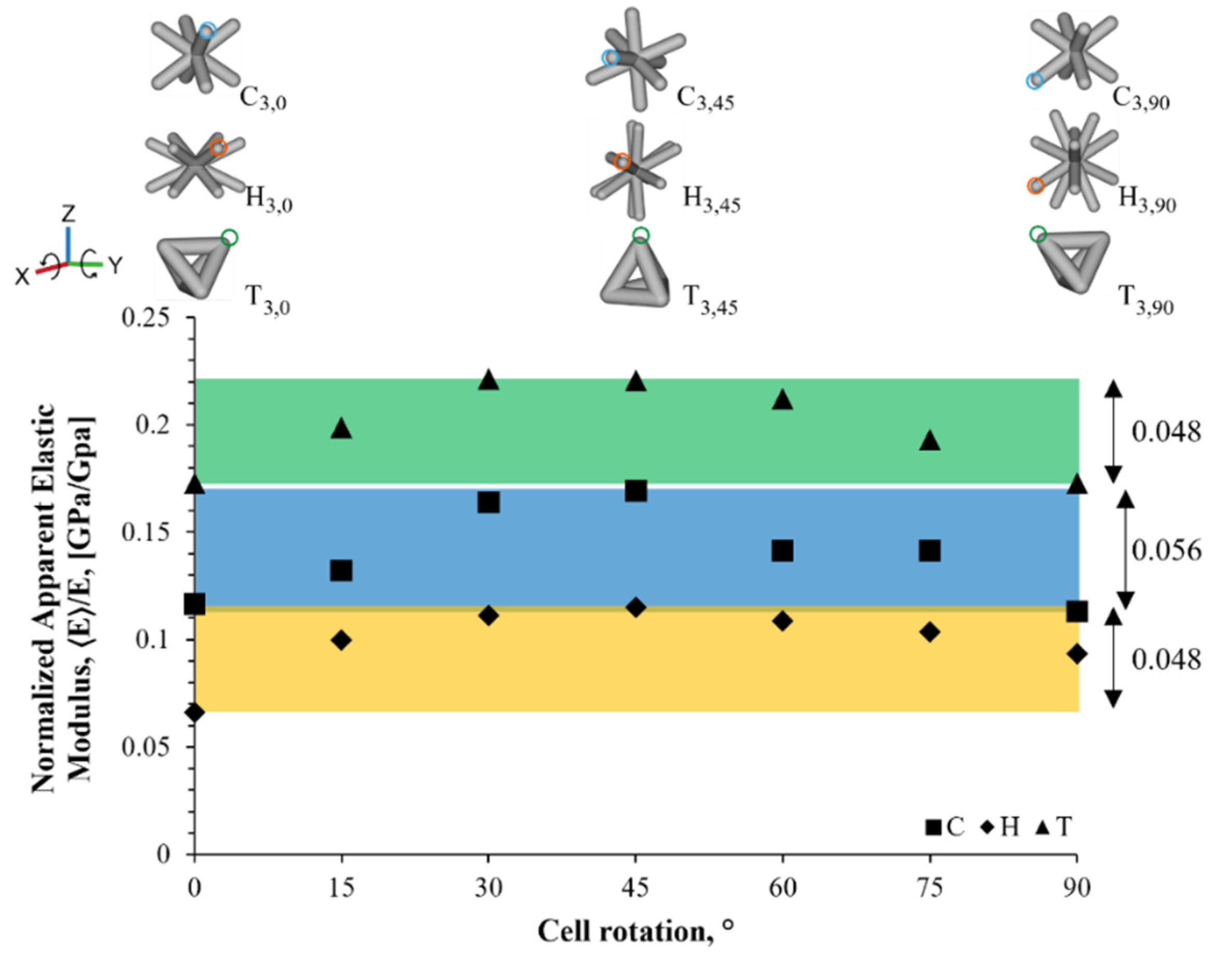
3.1. Computational Characterization via Finite Element Modeling
3.2. Morphological Characterization
3.3. Mechanical Characterization via Compression Tests
4. Discussion
5. Conclusions
- The LPBF process tended to generate a strut diameter larger than intended, resulting in larger relative densities compared to the nominal values. Moreover, these deviations were dependent on the component direction according to the printing direction;
- It was found that the angle between the strut and the plane normal to the loading directions had a direct impact on the structural stiffness by shifting the deformation from bending to stretching dominated;
- The LPBF parts with different types of lattice geometries and unit cell size reduced the SS316L bulk elastic modulus between 47% and 93% by imposing a porosity that resulted in an experimental density in the range of 23% to 69%;
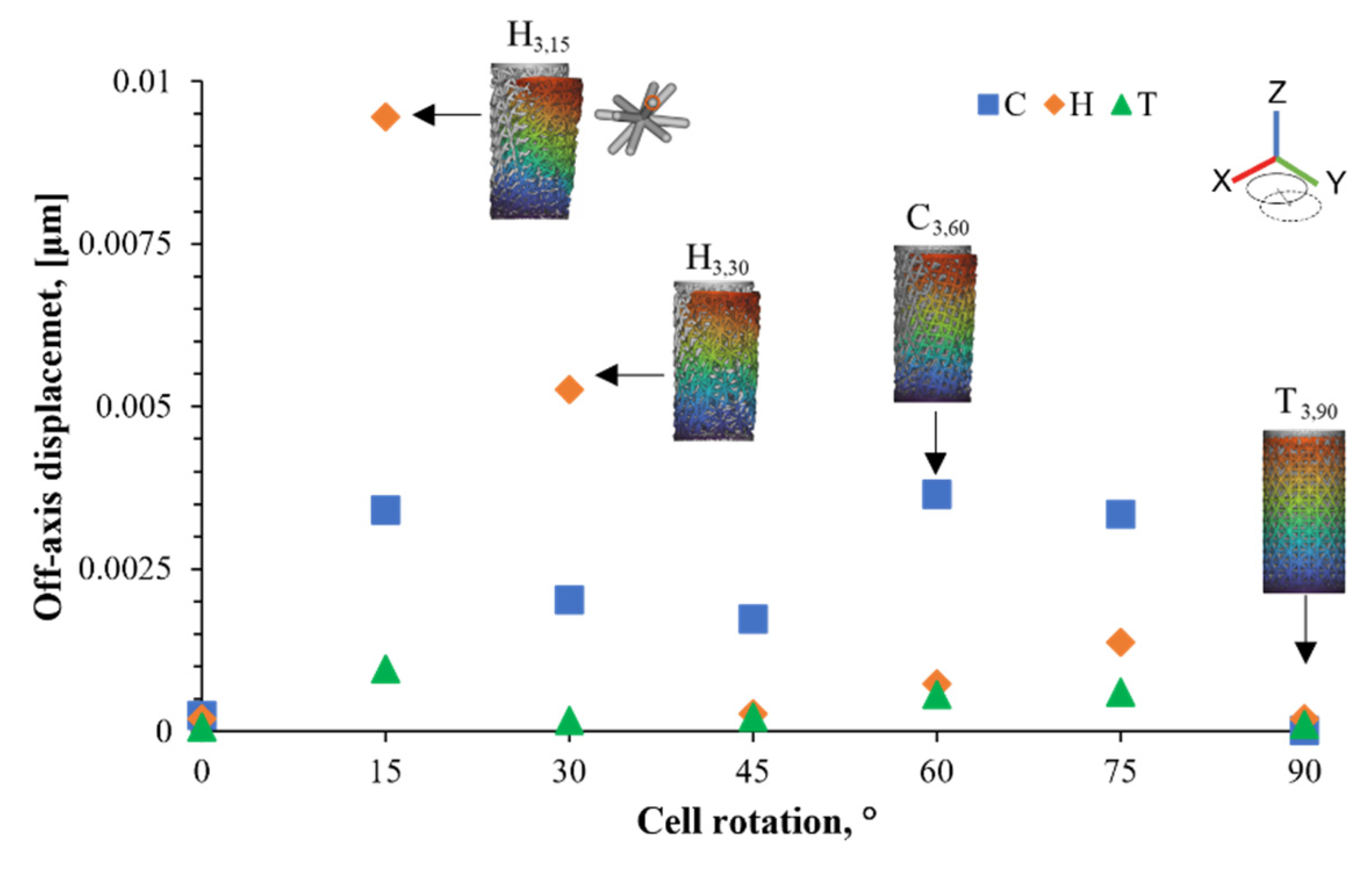
- Off-axis displacement was also observed for all of the unit cell types at different levels, attributed to axial motion provoked by the external stress and the presence of twisting deformation manner. The H cell performed the greatest movement, while the T cell had almost none;
- The simulation results indicate that the tetrahedron unit cell had the smallest Emax/Emin ratio and off-axis displacement due to the fact of its stretch-dominating deformation. Additionally, the steady mechanical behavior was further seen in the experimental results, featuring desirable elastic modulus despite the resulting dimensional variation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Murr, L.E. Additive Manufacturing of Biomedical Devices: An Overview. Mater. Technol. 2018, 33, 57–70. [Google Scholar] [CrossRef]
- Munir, K.S.; Li, Y.; Wen, C. Metallic Scaffolds Manufactured by Selective Laser Melting for Biomedical Applications. In Metallic Foam Bone; Elsevier: Amsterdam, The Netherlands, 2017; pp. 1–23. ISBN 978-0-08-101289-5. [Google Scholar]
- Munir, K.; Biesiekierski, A.; Wen, C.; Li, Y. Selective Laser Melting in Biomedical Manufacturing. In Metallic Biomaterials Processing and Medical Device Manufacturing; Elsevier: Amsterdam, The Netherlands, 2020; pp. 235–269. ISBN 978-0-08-102965-7. [Google Scholar]
- Vock, S.; Klöden, B.; Kirchner, A.; Weißgärber, T.; Kieback, B. Powders for Powder Bed Fusion: A Review. Prog. Addit. Manuf. 2019, 4, 383–397. [Google Scholar] [CrossRef] [Green Version]
- Yue, M.; Li, M.; An, N.; Yang, K.; Wang, J.; Zhou, J. Modeling SEBM Process of Tantalum Lattices. Rapid Prototyp. J. 2022, 29, 232–245. [Google Scholar] [CrossRef]
- Chekotu, J.; Groarke, R.; O’Toole, K.; Brabazon, D. Advances in Selective Laser Melting of Nitinol Shape Memory Alloy Part Production. Materials 2019, 12, 809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khorasani, A.; Gibson, I.; Veetil, J.K.; Ghasemi, A.H. A Review of Technological Improvements in Laser-Based Powder Bed Fusion of Metal Printers. Int. J. Adv. Manuf. Technol. 2020, 108, 191–209. [Google Scholar] [CrossRef]
- Mahyar Khorasani, A.; Gibson, I.; Goldberg, M.; Littlefair, G. Characterizing the Effect of Cutting Condition, Tool Path, and Heat Treatment on Cutting Forces of Selective Laser Melting Spherical Component in Five-Axis Milling. J. Manuf. Sci. Eng. 2018, 140, 051011. [Google Scholar] [CrossRef]
- Chmielewska, A.; Jahadakbar, A.; Wysocki, B.; Elahinia, M.; Święszkowski, W.; Dean, D. Chemical Polishing of Additively Manufactured, Porous, Nickel–Titanium Skeletal Fixation Plates. 3d Print Addit. Manuf. 2021, 9, 269–277. [Google Scholar] [CrossRef]
- Khorasani, M.; Ghasemi, A.H.; Farabi, E.; Leary, M.; Gibson, I.; Rolfe, B. A Comprehensive Investigation of Abrasive Barrel Finishing on Hardness and Manufacturability of Laser-Based Powder Bed Fusion Hollow Components. Int. J. Adv. Manuf. Technol. 2022, 120, 3471–3490. [Google Scholar] [CrossRef]
- Walker, J.M.; Haberland, C.; Taheri Andani, M.; Karaca, H.E.; Dean, D.; Elahinia, M. Process Development and Characterization of Additively Manufactured Nickel–Titanium Shape Memory Parts. J. Intell. Mater. Syst. Struct. 2016, 27, 2653–2660. [Google Scholar] [CrossRef]
- Kadic, M.; Milton, G.W.; van Hecke, M.; Wegener, M. 3D Metamaterials. Nat. Rev. Phys. 2019, 1, 198–210. [Google Scholar] [CrossRef]
- Kanaujia, P.K.; bin Ramezan, M.A.; Yap, X.Y.; Song, Y.; Du, Z.; Gan, C.L.; Lam, Y.C.; Lai, C.Q. Mechanical Response of Lightweight Hollow Truss Metal Oxide Lattices. Materialia 2019, 8, 100439. [Google Scholar] [CrossRef]
- Chen, X.; Ji, Q.; Wei, J.; Tan, H.; Yu, J.; Zhang, P.; Laude, V.; Kadic, M. Light-Weight Shell-Lattice Metamaterials for Mechanical Shock Absorption. Int. J. Mech. Sci. 2020, 169, 105288. [Google Scholar] [CrossRef]
- Arabnejad, S.; Johnston, B.; Tanzer, M.; Pasini, D. Fully Porous 3D Printed Titanium Femoral Stem to Reduce Stress-Shielding Following Total Hip Arthroplasty. J. Orthop. Res. 2017, 35, 1774–1783. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, J.; Zhang, L.; Wei, S.; Zhang, Z.; Choi, S.-K.; Song, B.; Shi, Y. A Review of Additive Manufacturing of Metamaterials and Developing Trends. Mater. Today 2021, 50, 303–328. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, MA, USA, 1997; ISBN 9780521499118. [Google Scholar]
- Graziosi, S.; Ballo, F.M.; Libonati, F.; Senna, S. 3D Printing of Bending-Dominated Soft Lattices: Numerical and Experimental Assessment. Rapid Prototyp. J. 2022, 28, 51–64. [Google Scholar] [CrossRef]
- Gümrük, R.; Mines, R.A.W.; Karadeniz, S. Static Mechanical Behaviours of Stainless Steel Micro-Lattice Structures under Different Loading Conditions. Mater. Sci. Eng. A 2013, 586, 392–406. [Google Scholar] [CrossRef]
- McKown, S.; Shen, Y.; Brookes, W.K.; Sutcliffe, C.J.; Cantwell, W.J.; Langdon, G.S.; Nurick, G.N.; Theobald, M.D. The Quasi-Static and Blast Loading Response of Lattice Structures. Int. J. Impact. Eng. 2008, 35, 795–810. [Google Scholar] [CrossRef]
- Neff, C.; Hopkinson, N.; Crane, N.B. Experimental and Analytical Investigation of Mechanical Behavior of Laser-Sintered Diamond-Lattice Structures. Addit. Manuf. 2018, 22, 807–816. [Google Scholar] [CrossRef]
- Wauthle, R.; Ahmadi, S.M.; Amin Yavari, S.; Mulier, M.; Zadpoor, A.A.; Weinans, H.; van Humbeeck, J.; Kruth, J.-P.; Schrooten, J. Revival of Pure Titanium for Dynamically Loaded Porous Implants Using Additive Manufacturing. Mater. Sci. Eng. C 2015, 54, 94–100. [Google Scholar] [CrossRef]
- Dadbakhsh, S.; Speirs, M.; Kruth, J.-P.; van Humbeeck, J. Influence of SLM on Shape Memory and Compression Behaviour of NiTi Scaffolds. CIRP Ann. 2015, 64, 209–212. [Google Scholar] [CrossRef] [Green Version]
- Tsai, P.-I.; Hsu, C.-C.; Chen, S.-Y.; Wu, T.-H.; Huang, C.-C. Biomechanical Investigation into the Structural Design of Porous Additive Manufactured Cages Using Numerical and Experimental Approaches. Comput. Biol. Med. 2016, 76, 14–23. [Google Scholar] [CrossRef] [PubMed]
- Choy, S.Y.; Sun, C.-N.; Leong, K.F.; Wei, J. Compressive Properties of Ti-6Al-4V Lattice Structures Fabricated by Selective Laser Melting: Design, Orientation and Density. Addit. Manuf. 2017, 16, 213–224. [Google Scholar] [CrossRef]
- Bai, L.; Zhang, J.; Xiong, Y.; Chen, X.; Sun, Y.; Gong, C.; Pu, H.; Wu, X.; Luo, J. Influence of Unit Cell Pose on the Mechanical Properties of Ti6Al4V Lattice Structures Manufactured by Selective Laser Melting. Addit. Manuf. 2020, 34, 101222. [Google Scholar] [CrossRef]
- Weißmann, V.; Bader, R.; Hansmann, H.; Laufer, N. Influence of the Structural Orientation on the Mechanical Properties of Selective Laser Melted Ti6Al4V Open-Porous Scaffolds. Mater. Des. 2016, 95, 188–197. [Google Scholar] [CrossRef]
- ISO 13314; International Organization for Standardization. ISO: Geneva, Switzerland, 2011.
- Onck, P.R.; Andrews, E.W.; Gibson, L.J. Size Effects in Ductile Cellular Solids. Part I: Modeling. Int. J. Mech. Sci. 2001, 43, 681–699. [Google Scholar] [CrossRef] [Green Version]
- Ramirez-Cedillo, E.; Sandoval-Robles, J.A.; Ruiz-Huerta, L.; Caballero-Ruiz, A.; Rodriguez, C.A.; Siller, H.R. Process Planning Guidelines in Selective Laser Melting for the Manufacturing of Stainless Steel Parts. Procedia Manuf. 2018, 26, 973–982. [Google Scholar] [CrossRef]
- Ashby, M.F.; Medalist, R.F.M. The Mechanical Properties of Cellular Solids. Metall. Trans. A 1983, 14, 1755–1769. [Google Scholar] [CrossRef]
- Roy, S.; Khutia, N.; Das, D.; Das, M.; Balla, V.K.; Bandyopadhyay, A.; Chowdhury, A.R. Understanding Compressive Deformation Behavior of Porous Ti Using Finite Element Analysis. Mater. Sci. Eng. C 2016, 64, 436–443. [Google Scholar] [CrossRef] [PubMed]
- Torres-Sanchez, C.; al Mushref, F.R.A.; Norrito, M.; Yendall, K.; Liu, Y.; Conway, P.P. The Effect of Pore Size and Porosity on Mechanical Properties and Biological Response of Porous Titanium Scaffolds. Mater. Sci. Eng. C 2017, 77, 219–228. [Google Scholar] [CrossRef] [Green Version]
- Taheri Andani, M.; Haberland, C.; Walker, J.M.; Karamooz, M.; Sadi Turabi, A.; Saedi, S.; Rahmanian, R.; Karaca, H.; Dean, D.; Kadkhodaei, M.; et al. Achieving Biocompatible Stiffness in NiTi through Additive Manufacturing. J. Intell. Mater. Syst. Struct. 2016, 27, 2661–2671. [Google Scholar] [CrossRef]
- Bartolomeu, F.; Costa, M.M.; Alves, N.; Miranda, G.; Silva, F.S. Engineering the Elastic Modulus of NiTi Cellular Structures Fabricated by Selective Laser Melting. J. Mech. Behav. Biomed. Mater. 2020, 110, 103891. [Google Scholar] [CrossRef] [PubMed]
- Liverani, E.; Toschi, S.; Ceschini, L.; Fortunato, A. Effect of Selective Laser Melting (SLM) Process Parameters on Microstructure and Mechanical Properties of 316L Austenitic Stainless Steel. J. Mater. Process. Technol. 2017, 249, 255–263. [Google Scholar] [CrossRef]
- Li, X.; Ghasri-Khouzani, M.; Bogno, A.-A.; Liu, J.; Henein, H.; Chen, Z.; Qureshi, A.J. Investigation of Compressive and Tensile Behavior of Stainless Steel/Dissolvable Aluminum Bimetallic Composites by Finite Element Modeling and Digital Image Correlation. Materials 2021, 14, 3654. [Google Scholar] [CrossRef]
- Lavery, N.P.; Cherry, J.; Mehmood, S.; Davies, H.; Girling, B.; Sackett, E.; Brown, S.G.R.; Sienz, J. Effects of Hot Isostatic Pressing on the Elastic Modulus and Tensile Properties of 316L Parts Made by Powder Bed Laser Fusion. Mater. Sci. Eng. A 2017, 693, 186–213. [Google Scholar] [CrossRef] [Green Version]
- Emmelmann, C.; Scheinemann, P.; Munsch, M.; Seyda, V. Laser Additive Manufacturing of Modified Implant Surfaces with Osseointegrative Characteristics. Phys. Procedia 2011, 12, 375–384. [Google Scholar] [CrossRef] [Green Version]
- Kozak, J.; Zakrzewski, T. Accuracy Problems of Additive Manufacturing Using SLS/SLM Processes; AIP Publishing: Bydgoszcz, Poland, 2018; p. 20010. [Google Scholar]
- Zhong, T.; He, K.; Li, H.; Yang, L. Mechanical Properties of Lightweight 316L Stainless Steel Lattice Structures Fabricated by Selective Laser Melting. Mater. Des. 2019, 181, 108076. [Google Scholar] [CrossRef]
- Alaña, M.; Cutolo, A.; Probst, G.; Ruiz de Galarreta, S.; van Hooreweder, B. Understanding Elastic Anisotropy in Diamond Based Lattice Structures Produced by Laser Powder Bed Fusion: Effect of Manufacturing Deviations. Mater. Des. 2020, 195, 108971. [Google Scholar] [CrossRef]
- Benedetti, M.; du Plessis, A.; Ritchie, R.O.; Dallago, M.; Razavi, S.M.J.; Berto, F. Architected Cellular Materials: A Review on Their Mechanical Properties towards Fatigue-Tolerant Design and Fabrication. Mater. Sci. Eng. R Rep. 2021, 144, 100606. [Google Scholar] [CrossRef]
- Ashby, M.F. The Properties of Foams and Lattices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 15–30. [Google Scholar] [CrossRef]
- Namdeo, A.; Bhandare, V.; Sahariah, B.J.; Khanikar, P. Tetrahedral and Strut-Reinforced Tetrahedral Microlattices: Selectively Laser Melted High-Strength and High-Stiffness Cellular Metamaterials. Mater. Sci. Eng. A 2022, 855, 143878. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Mohr, D. Stiffness and Specific Energy Absorption of Additively-Manufactured Metallic BCC Metamaterials Composed of Tapered Beams. Int. J. Mech. Sci. 2018, 141, 101–116. [Google Scholar] [CrossRef]
- Xiao, L.; Song, W.; Wang, C.; Liu, H.; Tang, H.; Wang, J. Mechanical Behavior of Open-Cell Rhombic Dodecahedron Ti–6Al–4V Lattice Structure. Mater. Sci. Eng. A 2015, 640, 375–384. [Google Scholar] [CrossRef]
- Ashby, M.F.; Evans, T.; Fleck, N.; Hutchinson, J.W.; Wadley, H.N.G.; Gibson, L.J. Metal Foams: A Design Guide; Elsevier, 2000. [Google Scholar]
- Bauer, J.; Meza, L.R.; Schaedler, T.A.; Schwaiger, R.; Zheng, X.; Valdevit, L. Nanolattices: An Emerging Class of Mechanical Metamaterials. Adv. Mater. 2017, 29, 1701850. [Google Scholar] [CrossRef] [PubMed]
- Iyer, S.; Alkhader, M.; Venkatesh, T.A. On the Relationships between Cellular Structure, Deformation Modes and Electromechanical Properties of Piezoelectric Cellular Solids. Int. J. Solids Struct. 2016, 80, 73–83. [Google Scholar] [CrossRef]






| Element | Fe | Cr | Ni | Mo | Mn | Si | N | O | P |
|---|---|---|---|---|---|---|---|---|---|
| Mass weight, (wt %) | Bal. | 16.00–18.00 | 10.00–14.00 | 2.00–3.00 | ≤2.00 | ≤1.00 | ≤0.10 | ≤0.10 | ≤0.045 |
| Parameter | Value |
|---|---|
| Laser power, P | 170 W |
| Exposure time, ET | 20 μs |
| Hatch distance, HD | 60 μm |
| Layer thickness, LT | 50 μm |
| Number of exposures, N | 2 |
| Point distance, PD | 80 μm |
| Hatch offset, HO | 60 μm |
| Strategy | Meander |
| ID | Cell Topology | Unit Cell Size | Cell Orientation |
|---|---|---|---|
| C3,0 | Body-centered cube | 3 mm | 0° |
| C3,45 | 45 | ||
| C6,0 | 6 mm | 0° | |
| C6,45 | 45 | ||
| H3,0 | Hexagonal prism vertex centroid | 3 mm | 0° |
| H3,45 | 45 | ||
| H6,0 | 6 mm | 0° | |
| H6,45 | 45 | ||
| T3,0 | Tetrahedron | 3 mm | 0° |
| T3,45 | 45 | ||
| T6,0 | 6 mm | 0° | |
| T6,45 | 45 |
| ID | Nominal | Experimental | Absolute Error | |||||
|---|---|---|---|---|---|---|---|---|
| Strut Thickness, t, (μm) | Engineering Density, 〈ρN〉, (%) | Strut Top Thickness, tT, (μm) | Strut Lateral Thickness, tL, (μm) | Engineering Density, 〈ρE〉, (%) | Strut Top Thickness, tT, (μm) | Strut Lateral Thickness, tL, (μm) | Engineering Density, 〈ρE〉, (%) | |
| C3,0 | 800 | 45.83 | 877.89 | 900.38 | 61.31 | 77.89 | 100.38 | 15.48 |
| C3,45 | 43.09 | 868.69 | 880.16 | 56.25 | 68.69 | 80.16 | 13.16 | |
| C6,0 | 17.27 | 883.74 | 914.34 | 23.54 | 83.74 | 114.34 | 6.27 | |
| C6,45 | 17.42 | 881.42 | 896.11 | 23.62 | 81.42 | 96.11 | 6.2 | |
| H3,0 | 38.23 | 920.33 | 921.21 | 51.02 | 120.33 | 121.21 | 12.79 | |
| H3,45 | 35.52 | 882.13 | 909.65 | 46.39 | 82.13 | 109.65 | 10.87 | |
| H6,0 | 18.48 | 940.63 | 932.34 | 25.56 | 140.63 | 132.34 | 7.08 | |
| H6,45 | 19.29 | 897.51 | 945.82 | 25.79 | 97.51 | 145.82 | 6.50 | |
| T3,0 | 38.6 | 898.37 | 954.98 | 51.71 | 98.37 | 154.98 | 13.11 | |
| T3,45 | 52.25 | 910.70 | 945.65 | 68.17 | 110.7 | 145.65 | 15.92 | |
| T6,0 | 22.63 | 928.79 | 953.88 | 31.07 | 128.79 | 153.88 | 8.44 | |
| T6,45 | 24.3 | 902.61 | 946.90 | 32.64 | 102.61 | 146.9 | 8.34 | |
| Bulk | 100.00 | 97.03 | −2.97 | |||||
| ID | 〈E〉/ESS316L | 〈σy〉/ σySS316L | ||||
|---|---|---|---|---|---|---|
| CE | nE | R2 | Cy | ny | R2 | |
| C 0° | 1.1227 | 1.8900 | 0.99 | 0.8097 | 2.4337 | 0.9702 |
| C 45° | 0.8506 | 0.8836 | 0.88 | 0.8647 | 2.0074 | 0.9773 |
| H 0° | 0.9372 | 1.6945 | 0.99 | 0.9469 | 3.135 | 0.9980 |
| H 45° | 0.9115 | 1.4150 | 0.98 | 1.0132 | 2.431 | 0.9991 |
| T 0° | 1.1586 | 1.5932 | 0.97 | 0.9416 | 2.3092 | 0.9925 |
| T 45° | 1.0471 | 1.7828 | 0.99 | 0.8489 | 2.1151 | 0.9945 |
| Unit Cell Rotation Angle | |||||||
|---|---|---|---|---|---|---|---|
| ID | 0° | 15° | 30° | 45° | 60° | 75° | 90° |
| C | 35.26 | 56.35 | 76.33 | 80.26 | 63.42 | 47.79 | 35.26 |
| H | 26.57 | 46.61 | 63.43 | 67.99 | 62.42 | 63.37 | 63.44 |
| T | 45.00 | 57.43 | 62.11 | 58.60 | 66.72 | 59.29 | 45.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olivas-Alanis, L.H.; Fraga-Martínez, A.A.; García-López, E.; Lopez-Botello, O.; Vazquez-Lepe, E.; Cuan-Urquizo, E.; Rodriguez, C.A. Mechanical Properties of AISI 316L Lattice Structures via Laser Powder Bed Fusion as a Function of Unit Cell Features. Materials 2023, 16, 1025. https://doi.org/10.3390/ma16031025
Olivas-Alanis LH, Fraga-Martínez AA, García-López E, Lopez-Botello O, Vazquez-Lepe E, Cuan-Urquizo E, Rodriguez CA. Mechanical Properties of AISI 316L Lattice Structures via Laser Powder Bed Fusion as a Function of Unit Cell Features. Materials. 2023; 16(3):1025. https://doi.org/10.3390/ma16031025
Chicago/Turabian StyleOlivas-Alanis, Luis H., Antonio Abraham Fraga-Martínez, Erika García-López, Omar Lopez-Botello, Elisa Vazquez-Lepe, Enrique Cuan-Urquizo, and Ciro A. Rodriguez. 2023. "Mechanical Properties of AISI 316L Lattice Structures via Laser Powder Bed Fusion as a Function of Unit Cell Features" Materials 16, no. 3: 1025. https://doi.org/10.3390/ma16031025
APA StyleOlivas-Alanis, L. H., Fraga-Martínez, A. A., García-López, E., Lopez-Botello, O., Vazquez-Lepe, E., Cuan-Urquizo, E., & Rodriguez, C. A. (2023). Mechanical Properties of AISI 316L Lattice Structures via Laser Powder Bed Fusion as a Function of Unit Cell Features. Materials, 16(3), 1025. https://doi.org/10.3390/ma16031025








