Process Parameter Selection for Production of Stainless Steel 316L Using Efficient Multi-Objective Bayesian Optimization Algorithm
Abstract
:1. Introduction
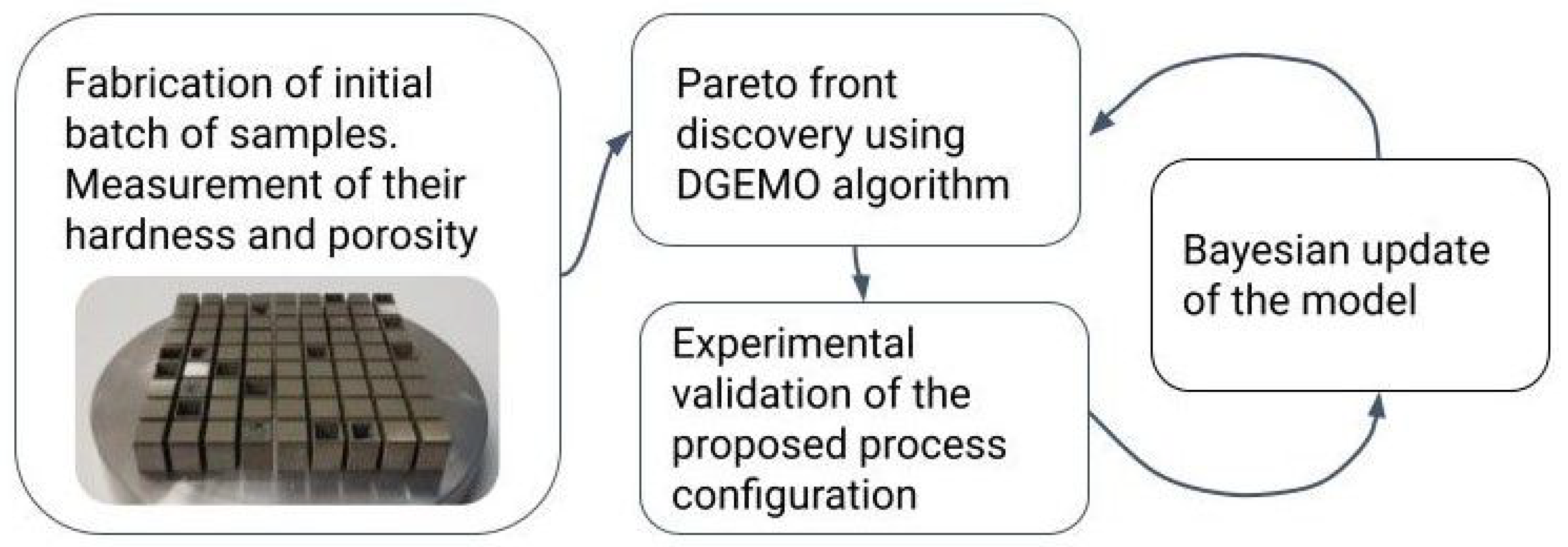
2. Materials and Methods
2.1. Gaussian Process
2.2. Bayesian Optimization: Pareto Front Approximation
2.3. Bayesian Update Procedure: Batch Selection Strategy
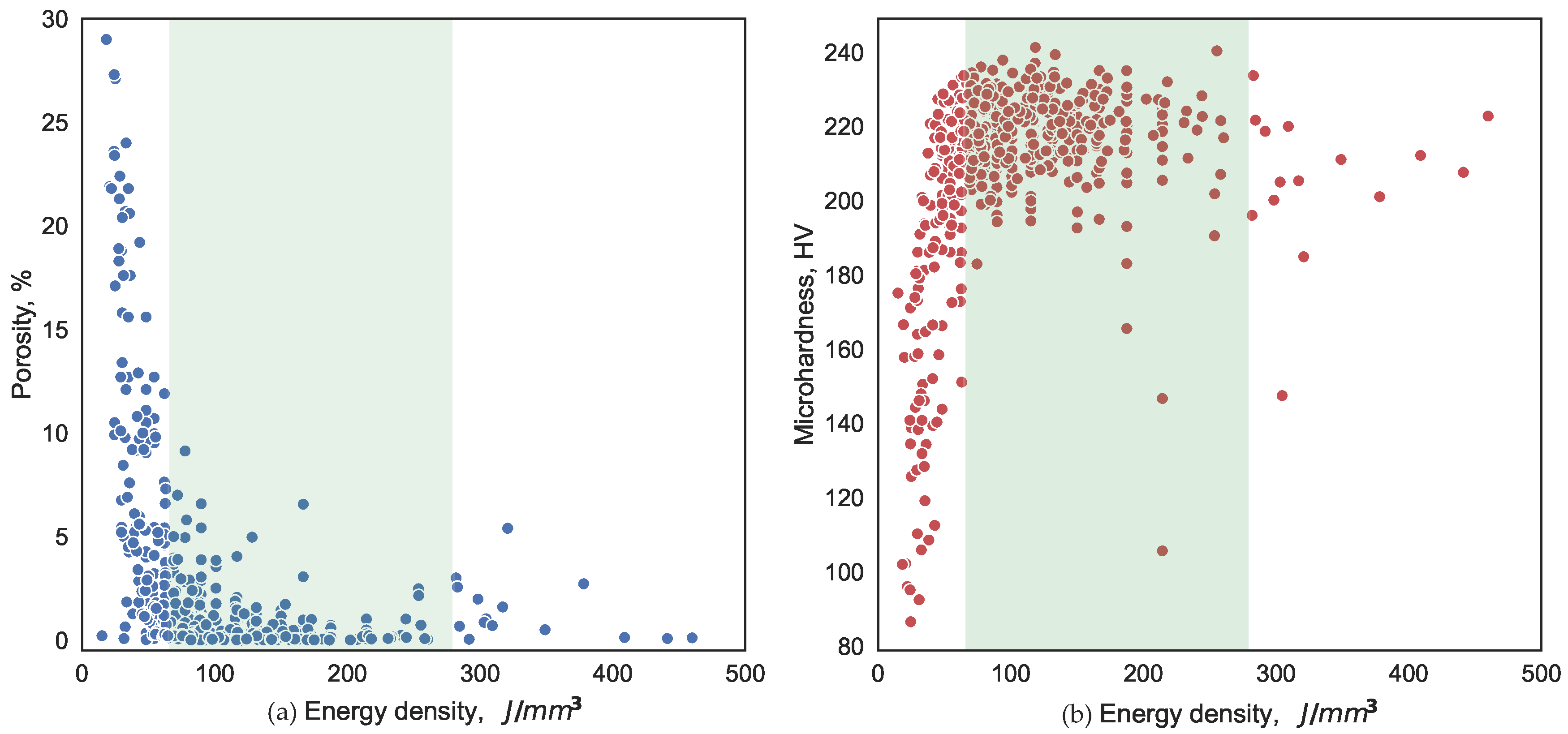
3. Results
4. Discussion
5. Conclusions
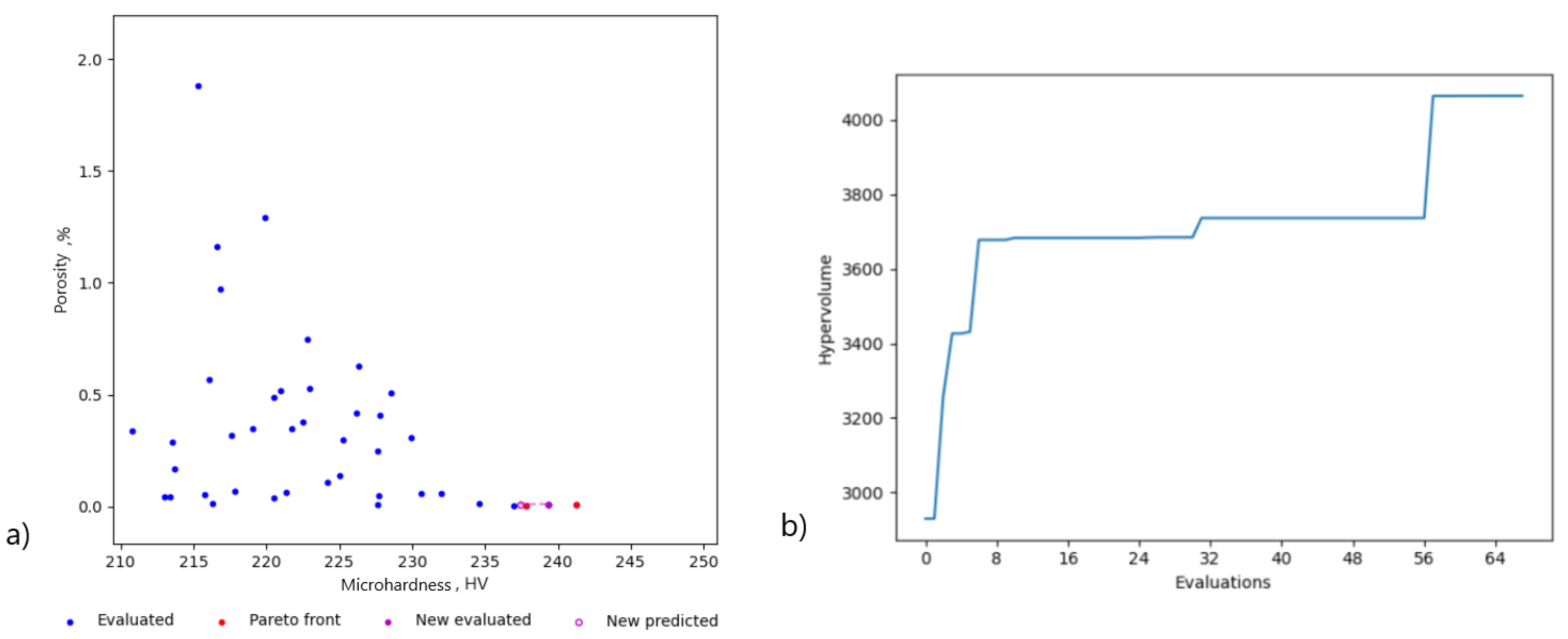
- The model trained on relatively small batch of data quickly found three points on the Pareto front in just six iterations.
- The highest value of the hardness obtained empirically was HV, corresponding to a VED of J/mm, with a power of 133 W, a scanning speed of 850 mm/s, and hatch spacing of 66 µm.
- The highest relative density part had a porosity of % and the following parameters: VED J/mm, power 108 W, scanning speed 465 mm/s, hatch spacing 97 µm.
- The VED that was explored by the algorithm lied in the range of 240–265 J/mm; the hardness of the produced parts was 224–235 HV, and the porosity was in the range of 0.2–0.37%.
- The recommended processing window corresponded to the parts manufactured with an energy density that lied in the range of 65–280 J/mm.
- The trained model prescribed the following parameters to ensure quality parts: 58 W, 257 mm/s, 45 µm, with a scan rotation angle of 131 degrees.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AM | Additive manufacturing |
| L-PBF | Laser powder bed fusion |
| MOBO | Multi-objective Bayesian optimization |
| ML | Machine learning |
| GP | Gaussian process |
References
- ISO/ASTM 52900:2021; Standard Terminology for Additive Manufacturing-General Principles- Terminology. ASTM International: West Conshohocken, PA, USA, 2021.
- Liu, R.; Wang, Z.; Sparks, T.; Liou, F.; Newkirk, J. Aerospace applications of laser additive manufacturing. Laser Additive Manufacturing: Materials, Design, Technologies, and Applications; Woodhead Publishing: Sawston, UK, 2017; pp. 351–371. [Google Scholar] [CrossRef]
- Bozkurt, Y.; Karayel, E. 3D printing technology methods, biomedical applications, future opportunities and trends. J. Mater. Res. Technol. 2021, 14, 1430–1450. [Google Scholar] [CrossRef]
- Pollock, T.M. Alloy design for aircraft engines. Nat. Publ. Group 2016, 15, 809–815. [Google Scholar] [CrossRef]
- Culmone, C.; Smit, G.; Breedveld, P. Additive manufacturing of medical instruments: A state-of-the-art review. Addit. Manuf. 2019, 27, 461–473. [Google Scholar] [CrossRef]
- Sundseth, J.; Berg-Johnsen, J. Prefabricated Patient-Matched Cranial Implants for Reconstruction of Large Skull Defects. J. Cent. Nerv. Syst. Dis. 2013, 5, JCNSD.S11106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, F.; Wei, M.; Viswanathan, V.V.; Swart, B.; Shao, Y.; Wu, G.; Zhou, C. 3D printing technologies for electrochemical energy storage. Nano Energy 2017, 40, 418–431. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components – Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Du Plessis, A.; Yadroitsava, I.; Yadroitsev, I. Effects of defects on mechanical properties in metal additive manufacturing: A review focusing on X-ray tomography insights. Mater. Des. 2020, 187, 108385. [Google Scholar] [CrossRef]
- Zhang, W.; Tong, M.; Harrison, N.M. Scanning strategies effect on temperature, residual stress and deformation by multi-laser beam powder bed fusion manufacturing. Addit. Manuf. 2020, 36, 101507. [Google Scholar] [CrossRef]
- Arısoy, Y.M.; Criales, L.E.; Özel, T.; Lane, B.; Moylan, S.; Donmez, A. Influence of scan strategy and process parameters on microstructure and its optimization in additively manufactured nickel alloy 625 via laser powder bed fusion. Int. J. Adv. Manuf. Technol. 2017, 90, 1393–1417. [Google Scholar] [CrossRef]
- Kumar, P.; Farah, J.; Akram, J.; Teng, C.; Ginn, J.; Misra, M. Influence of laser processing parameters on porosity in Inconel 718 during additive manufacturing. Int. J. Adv. Manuf. Technol. 2019, 103, 1497–1507. [Google Scholar] [CrossRef]
- Kuzminova, Y.; Firsov, D.; Konev, S.; Dudin, A.; Dagesyan, S.; Akhatov, I.; Evlashin, S. Structure control of 316L stainless steel through an additive manufacturing. Lett. Mater. 2019, 9, 551–555. [Google Scholar] [CrossRef] [Green Version]
- Liverani, E.; Toschi, S.; Ceschini, L.; Fortunato, A. Effect of selective laser melting (SLM) process parameters on microstructure and mechanical properties of 316L austenitic stainless steel. J. Mater. Process. Technol. 2017, 249, 255–263. [Google Scholar] [CrossRef]
- Gu, D.; Shen, Y. Balling phenomena in direct laser sintering of stainless steel powder: Metallurgical mechanisms and control methods. Mater. Des. 2009, 30, 2903–2910. [Google Scholar] [CrossRef]
- Cherry, J.A.; Davies, H.M.; Mehmood, S.; Lavery, N.P.; Brown, S.G.R.; Sienz, J. Investigation into the effect of process parameters on microstructural and physical properties of 316L stainless steel parts by selective laser melting. Int. J. Adv. Manuf. Technol. 2015, 76, 869–879. [Google Scholar] [CrossRef] [Green Version]
- Bertoli, U.S.; Wolfer, A.J.; Matthews, M.J.; Delplanque, J.P.R.; Schoenung, J.M. On the limitations of Volumetric Energy Density as a design parameter for Selective Laser Melting. Mater. Des. 2017, 113, 331–340. [Google Scholar] [CrossRef] [Green Version]
- King, W.E.; Barth, H.D.; Castillo, V.M.; Gallegos, G.F.; Gibbs, J.W.; Hahn, D.E.; Kamath, C.; Rubenchik, A.M. Observation of keyhole-mode laser melting in laser powder-bed fusion additive manufacturing. J. Mater. Process. Technol. 2014, 214, 2915–2925. [Google Scholar] [CrossRef]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef] [Green Version]
- Gongora, A.E.; Xu, B.; Perry, W.; Okoye, C.; Riley, P.; Reyes, K.G.; Morgan, E.F.; Brown, K.A. A Bayesian experimental autonomous researcher for mechanical design. Sci. Adv. 2020, 6, eaaz1708. [Google Scholar] [CrossRef] [Green Version]
- Aboutaleb, A.M.; Bian, L.; Elwany, A.; Shamsaei, N.; Thompson, S.M.; Tapia, G. Accelerated process optimization for laser-based additive manufacturing by leveraging similar prior studies. IISE Trans. 2017, 49, 31–44. [Google Scholar] [CrossRef]
- Burger, B.; Maffettone, P.M.; Gusev, V.V.; Aitchison, C.M.; Bai, Y.; Wang, X.; Li, X.; Alston, B.M.; Li, B.; Clowes, R.; et al. A mobile robotic chemist. Nature 2020, 583, 237–241. [Google Scholar] [CrossRef]
- Panahizadeh, V.; Ghasemi, A.H.; Asl, Y.D.; Davoudi, M. Optimization of LB-PBF process parameters to achieve best relative density and surface roughness for Ti6Al4V samples: Using NSGA-II algorithm. Rapid Prototyp. J. 2022, 28, 1821–1833. [Google Scholar] [CrossRef]
- Ye, J.; Yasin, M.S.; Muhammad, M.; Liu, J.; Vinel, A.; Slvia, D.; Shamsaei, N.; Shao, S. Bayesian Process Optimization for Additively Manufactured Nitinol. In Proceedings of the 2021 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 2–4 August 2021; University of Texas at Austin: Austin, TX, USA, 2021. [Google Scholar]
- Tapia, G.; Elwany, A.H.; Sang, H. Prediction of porosity in metal-based additive manufacturing using spatial Gaussian process models. Addit. Manuf. 2016, 12, 282–290. [Google Scholar] [CrossRef]
- Rankouhi, B.; Jahani, S.; Pfefferkorn, F.E.; Thoma, D.J. Compositional grading of a 316L-Cu multi-material part using machine learning for the determination of selective laser melting process parameters. Addit. Manuf. 2021, 38, 101836. [Google Scholar] [CrossRef]
- Bradford, E.; Schweidtmann, A.M.; Lapkin, A. Efficient multiobjective optimization employing Gaussian processes, spectral sampling and a genetic algorithm. J. Glob. Optim. 2018, 71, 407–438. [Google Scholar] [CrossRef] [Green Version]
- Belakaria, S.; Deshwal, A.; Jayakodi, N.K.; Doppa, J.R. Uncertainty-Aware Search Framework for Multi-Objective Bayesian Optimization. Proc. Aaai Conf. Artif. Intell. 2020, 34, 10044–10052. [Google Scholar] [CrossRef]
- Lukovic, M.K.; Tian, Y.; Matusik, W. Diversity-Guided Multi-Objective Bayesian Optimization with Batch Evaluations. Adv. Neural Inf. Process. Syst. 2020, 33, 17708–17720. [Google Scholar]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef] [Green Version]
- Emmerich, M.; Klinkenberg, J.w. The computation of the expected improvement in dominated hypervolume of Pareto front approximations. Rapp. Tech. Leiden Univ. 2008, 34, 1–8. [Google Scholar]
- Panov, D.; Oreshkin, O.; Voloskov, B.; Petrovskiy, V.; Shishkovsky, I. Pore healing effect of laser polishing and its influence on fatigue properties of 316L stainless steel parts fabricated by laser powder bed fusion. Opt. Laser Technol. 2022, 156, 108535. [Google Scholar] [CrossRef]
- Slotwinski, J.A.; Garboczi, E.J.; Hebenstreit, K.M. Porosity Measurements and Analysis for Metal Additive Manufacturing Process Control. J. Res. Natl. Inst. Stand. Technol. 2014, 119, 494. [Google Scholar] [CrossRef]
- Tian, Y.; Luković, M.K.; Erps, T.; Foshey, M.; Matusik, W. AutoOED: Automated Optimal Experiment Design Platform. arXiv 2021, arXiv:2104.05959. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2014. [Google Scholar] [CrossRef] [Green Version]
- Kamath, C.; El-Dasher, B.; Gallegos, G.F.; King, W.E.; Sisto, A. Density of additively-manufactured, 316L SS parts using laser powder-bed fusion at powers up to 400 W. Int. J. Adv. Manuf. Technol. 2014, 74, 65–78. [Google Scholar] [CrossRef] [Green Version]
- Linares, J.M.; Chaves-Jacob, J.; Lopez, Q.; Sprauel, J.M. Fatigue life optimization for 17-4Ph steel produced by selective laser melting. Rapid Prototyp. J. 2022, 28, 1182–1192. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016. [Google Scholar] [CrossRef] [Green Version]
- Karamov, R.; Akhatov, I.; Sergeichev, I.V. Prediction of Fracture Toughness of Pultruded Composites Based on Supervised Machine Learning. Polymers 2022, 14, 3619. [Google Scholar] [CrossRef]


| Parameters | Minimum Value | Maximum Value |
|---|---|---|
| Time (min) | 1 | 4 |
| Gas circulation speed (m/s) | 1.5 | 4 |
| Laser power (W) | 30 | 175 |
| Scan speed (mm/s) | 100 | 3000 |
| Hatch distance (µm) | 40 | 120 |
| Scan angle (degrees) | 0 | 150 |
| Time, min | Gas Feed, m/s | Power, W | Speed, mm/s | Hatch Spacing, µm | Energy Density, J/mm | Angle, ° | Hardness, HV |
|---|---|---|---|---|---|---|---|
| 2 | 3.5 | 133.0 | 850.0 | 66.0 | 118.5 | 44.0 | 241.3 |
| 2 | 3.5 | 154.0 | 335.0 | 90.0 | 255.4 | 48.0 | 240.3 |
| 2 | 3.5 | 123.0 | 583.0 | 79.0 | 133.5 | 18.0 | 239.3 |
| 2 | 3.5 | 159.0 | 1128.0 | 75.0 | 93.9 | 50.0 | 237.8 |
| 2 | 4.0 | 74.3 | 448.6 | 70.0 | 118.3 | 74.9 | 237.0 |
| 3 | 2.5 | 113.0 | 910.0 | 80.0 | 77.6 | 150.0 | 236.0 |
| 2 | 3.5 | 101.0 | 505.0 | 87.0 | 114.9 | 5.0 | 235.4 |
| 3 | 3.5 | 51.5 | 726.9 | 41.0 | 86.4 | 10.7 | 235.1 |
| 3 | 2.5 | 147.0 | 490.0 | 90.0 | 166.7 | 150.0 | 235.0 |
| 2 | 3.5 | 114.0 | 454.0 | 67.0 | 187.4 | 41.0 | 235.0 |
| Time, min | Gas Feed, m/s | Power, W | Speed, mm/s | Hatch Spacing, µm | Energy Density, J/mm | Angle, ° | Porosity, % |
|---|---|---|---|---|---|---|---|
| 2 | 3.5 | 108.0 | 465.0 | 97.0 | 119.72 | 77.0 | 0.0007 |
| 2 | 3.5 | 163.0 | 616.0 | 71.0 | 186.35 | 51.0 | 0.0013 |
| 2 | 3.5 | 131.0 | 955.0 | 77.0 | 89.07 | 83.0 | 0.0042 |
| 2 | 3.5 | 101.0 | 505.0 | 87.0 | 114.94 | 5.0 | 0.0043 |
| 2 | 3.5 | 159.0 | 1128.0 | 75.0 | 93.97 | 50.0 | 0.0058 |
| 2 | 3.5 | 146.0 | 606.0 | 88.0 | 136.89 | 8.0 | 0.0067 |
| 2 | 3.5 | 137.0 | 628.0 | 82.0 | 133.02 | 25.0 | 0.0071 |
| 2 | 3.5 | 138.0 | 914.0 | 92.0 | 82.06 | 30.0 | 0.0074 |
| 2 | 3.5 | 133.0 | 850.0 | 66.0 | 118.54 | 44.0 | 0.0075 |
| 2 | 3.5 | 163.0 | 1268.0 | 74.0 | 86.86 | 35.0 | 0.0083 |
| Time, min | Gas Feed, m/s | Power, W | Speed, mm/s | Hatch Spacing, µm | Energy Density, J/mm | Angle, ° |
|---|---|---|---|---|---|---|
| 3 | 3.5 | 59.0 | 254.0 | 45.0 | 258.1 | 123.0 |
| 3 | 3.5 | 58.0 | 257.0 | 47.0 | 240.1 | 131.0 |
| 3 | 3.5 | 60.0 | 257.0 | 44.0 | 265.3 | 123.0 |
| 2 | 3.5 | 59.0 | 256.0 | 45.0 | 256.1 | 123.0 |
| 2 | 3.5 | 59.0 | 258.0 | 45.0 | 254.1 | 124.0 |
| 2 | 3.5 | 59.0 | 259.0 | 44.0 | 258.9 | 123.0 |
| Predicted Hardness (Std.), HV | Actual Hardness, HV | Predicted Porosity (Std.), % | Actual Porosity. % |
|---|---|---|---|
| 248.0 ± 18.0 | 231.0 | 0.510 ± 2.918 | 0.200 |
| 248.0 ± 17.7 | 235.0 | 0.510 ± 2.854 | 0.310 |
| 248.0 ± 18.5 | 225.0 | 0.490 ± 2.980 | 0.370 |
| 248.0 ± 17.9 | 229.0 | 0.520 ± 2.916 | 0.260 |
| 248.0 ± 18.4 | 224.0 | 0.480 ± 2.930 | 0.200 |
| 249.0 ± 18.6 | 232.0 | 0.450 ± 2.948 | 0.210 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chepiga, T.; Zhilyaev, P.; Ryabov, A.; Simonov, A.P.; Dubinin, O.N.; Firsov, D.G.; Kuzminova, Y.O.; Evlashin, S.A. Process Parameter Selection for Production of Stainless Steel 316L Using Efficient Multi-Objective Bayesian Optimization Algorithm. Materials 2023, 16, 1050. https://doi.org/10.3390/ma16031050
Chepiga T, Zhilyaev P, Ryabov A, Simonov AP, Dubinin ON, Firsov DG, Kuzminova YO, Evlashin SA. Process Parameter Selection for Production of Stainless Steel 316L Using Efficient Multi-Objective Bayesian Optimization Algorithm. Materials. 2023; 16(3):1050. https://doi.org/10.3390/ma16031050
Chicago/Turabian StyleChepiga, Timur, Petr Zhilyaev, Alexander Ryabov, Alexey P. Simonov, Oleg N. Dubinin, Denis G. Firsov, Yulia O. Kuzminova, and Stanislav A. Evlashin. 2023. "Process Parameter Selection for Production of Stainless Steel 316L Using Efficient Multi-Objective Bayesian Optimization Algorithm" Materials 16, no. 3: 1050. https://doi.org/10.3390/ma16031050
APA StyleChepiga, T., Zhilyaev, P., Ryabov, A., Simonov, A. P., Dubinin, O. N., Firsov, D. G., Kuzminova, Y. O., & Evlashin, S. A. (2023). Process Parameter Selection for Production of Stainless Steel 316L Using Efficient Multi-Objective Bayesian Optimization Algorithm. Materials, 16(3), 1050. https://doi.org/10.3390/ma16031050







