Modified Compression Test of Corrugated Board Fruit Tray: Numerical Modeling and Global Sensitivity Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Global Sensitivity Calculations
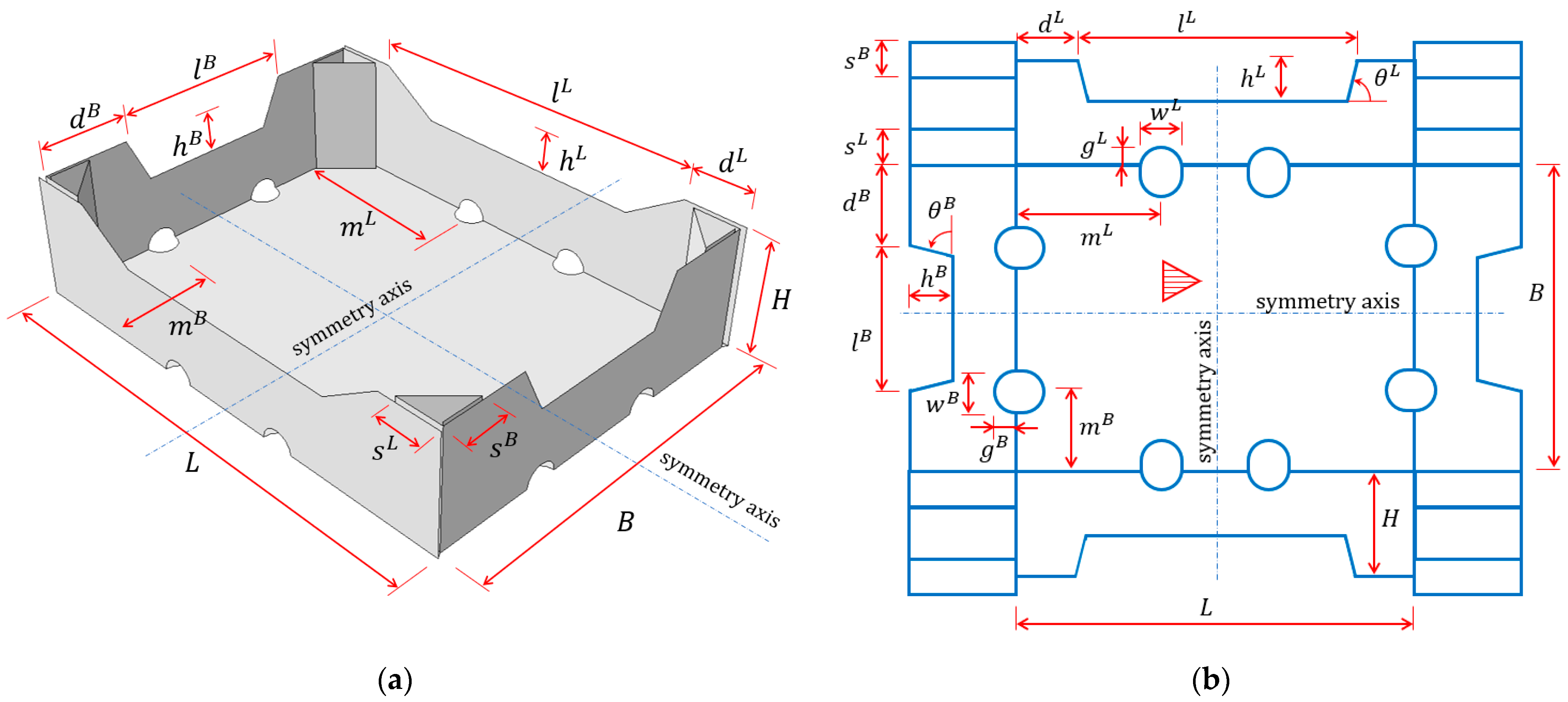
2.2. Parametric Model of Open-Top Cartons
- and —the length and width of the packaging, respectively;
- —the height of the stiffening triangles and the carton;
- and —half of the horizontal length of the non-folded part of the longer and shorter sidewalls, respectively;
- and —the width and height of the trapezoidal folds on the longer and shorter sidewalls, respectively;
- and —the length of the sides of the stiffening triangles on the longer and shorter sidewalls, respectively;
- and —the width and height of the ventilation holes on the longer sidewalls, respectively;
- —the distance of the ventilation holes on the longer sidewalls from the shorter sidewalls to its axis;
- and —the width and height of the ventilation holes on the shorter sidewalls, respectively;
- —the distance of the ventilation holes on the shorter sidewalls from the longer sidewalls to its axis;
- and —inclination of the arms of the trapezoidal folds on the longer and shorter sidewalls, respectively.
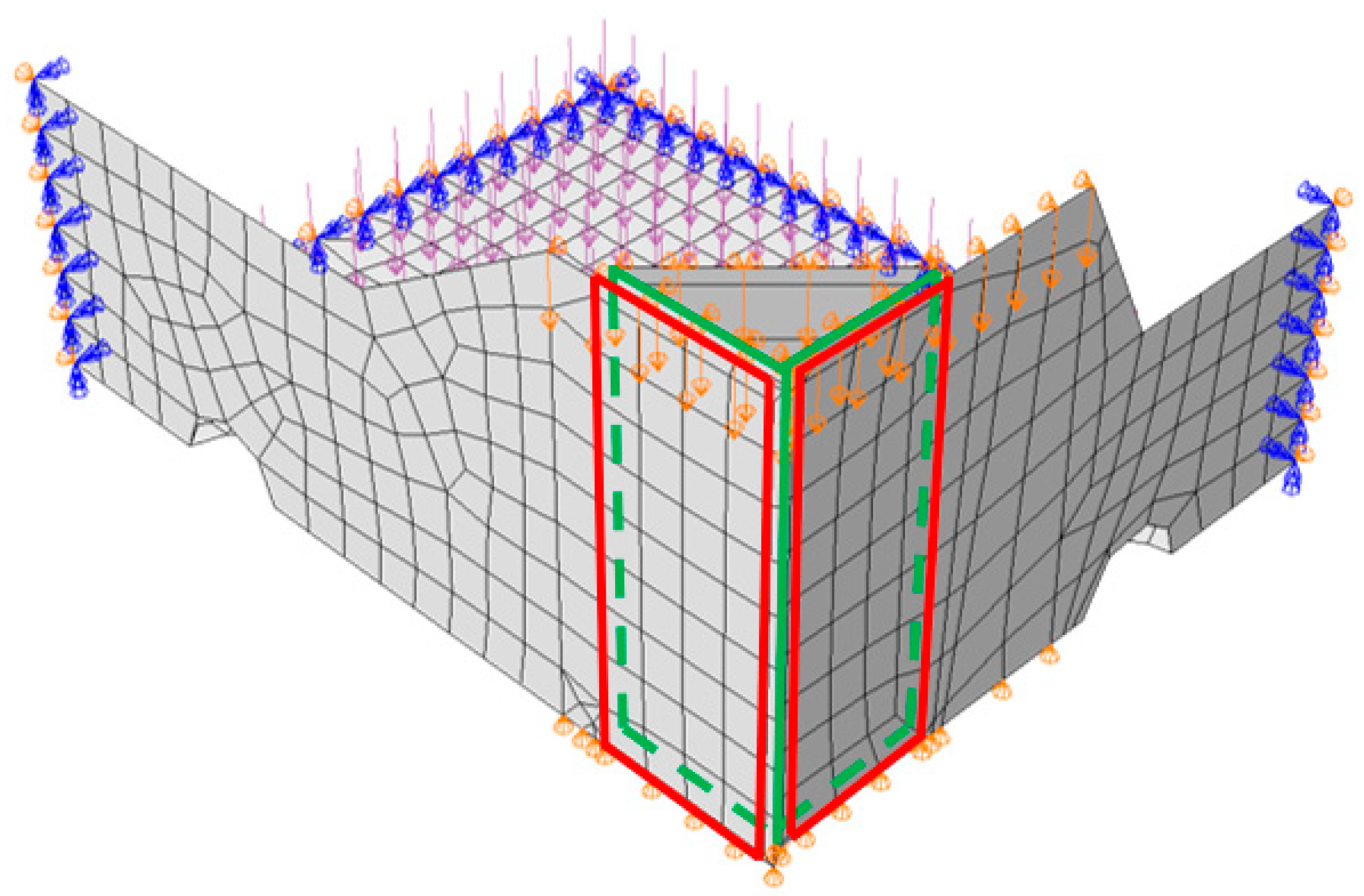
2.3. Numerical Model of Open-Top Boxes
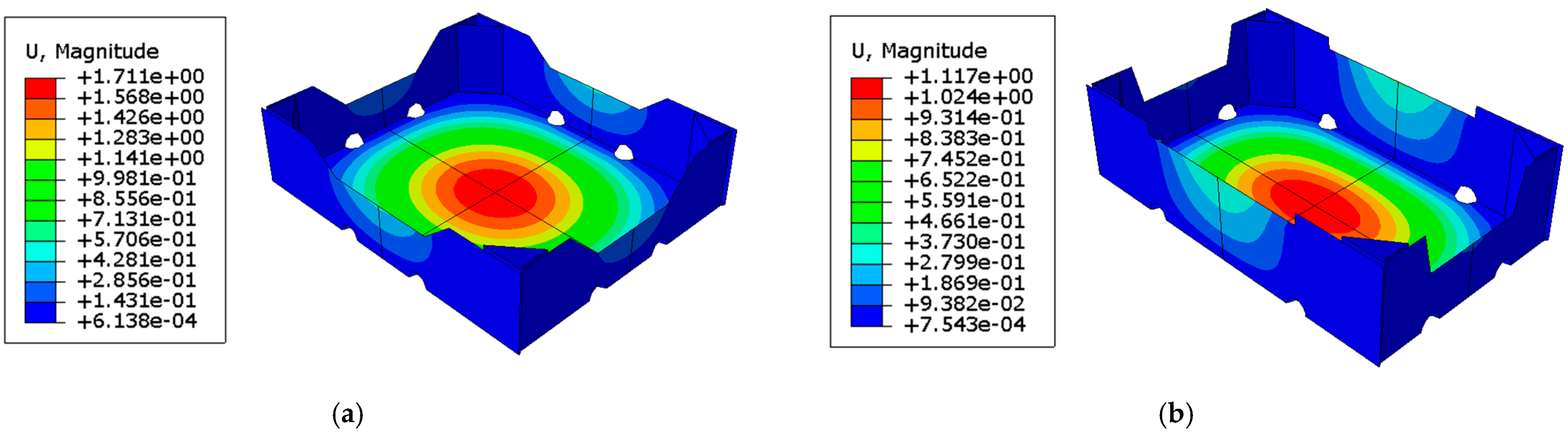
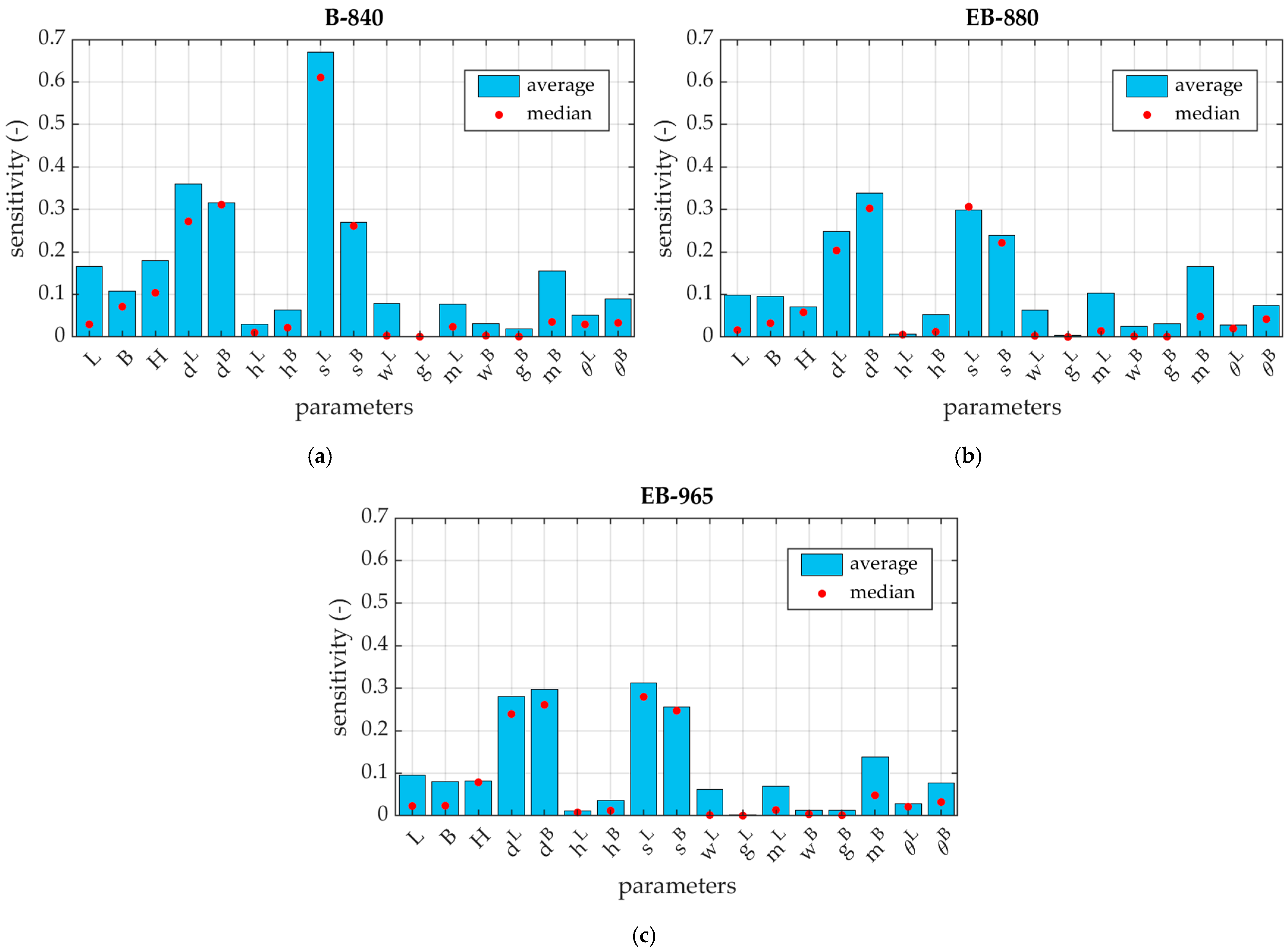
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAO. Banana Market Review 2020. 2021. Available online: https://agfstorage.blob.core.windows.net/misc/FP_com/2021/10/11/Ban.pdf (accessed on 8 January 2023).
- Singh, J.; Olsen, E.; Singh, S.P.; Manley, J.; Wallace, F. The Effect of Ventilation and Hand Holes on Loss of Compression Strength in Corrugated Boxes. J. Appl. Packag. Res. 2008, 2, 227–238. [Google Scholar]
- Lindh, H.; Olsson, A.; Williams, H. Consumer perceptions of food packaging: Contributing to or counteracting environmentally sustainable development? Packag. Technol. Sci. 2016, 29, 3–23. [Google Scholar] [CrossRef] [Green Version]
- Neill, C.; Williams, R. Consumer Preference for Alternative Milk Packaging: The Case of An Inferred Environmental Attribute. J. Agric. Appl. Econ. 2016, 48, 241–256. [Google Scholar] [CrossRef] [Green Version]
- Popovic, I.; Bossink, B.A.G.; van der Sijde, P.C. Factors Influencing Consumers’ Decision to Purchase Food in Environmentally Friendly Packaging: What Do We Know and Where Do We Go from Here? Sustainability 2019, 11, 7197. [Google Scholar] [CrossRef] [Green Version]
- Urbanik, T.J.; Saliklis, E.P. Finite element corroboration of buckling phenomena observed in corrugated boxes. Wood Fiber Sci. 2003, 35, 322–333. [Google Scholar]
- Nordstrand, T. Basic Testing and Strength Design of Corrugated Board and Containers. Ph.D. Thesis, Lund University, Lund, Sweden, 2003. [Google Scholar]
- Nordstrand, T.; Carlsson, L. Evaluation of transverse shear stiffness of structural core sandwich plates. Comp. Struct. 1997, 37, 145–153. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, R.; Subudhi, S. Numerical modeling of forced-air pre-cooling of fruits and vegetables: A review. Int. J. Refrig. 2022, 145, 217–232. [Google Scholar] [CrossRef]
- Nanga, R.; Curto, J.; Gaspar, P.D.; Silva, P.D.; Santos Cruz, J.M. Numerical parametric study of the influence of fruit packaging boxes arrangement on fluid flow and heat transfer. Int. J. Energy Clean Environ. 2023, 24, 45–59. [Google Scholar] [CrossRef]
- Ilangovan, A.; Curto, J.; Gaspar, P.D.; Silva, P.D.; Alves, N. CFD Modelling of the Thermal Performance of Fruit Packaging Boxes—Influence of Vent-Holes Design. Energies 2021, 14, 7990. [Google Scholar] [CrossRef]
- Han, J.; Park, J.M. Finite element analysis of vent/hand hole designs for corrugated fibreboard boxes. Packag. Technol. Sci. 2007, 20, 39–47. [Google Scholar] [CrossRef]
- Frank, B. Corrugated Box Compression—A Literature Survey. Packag. Technol. Sci. 2014, 27, 105–128. [Google Scholar] [CrossRef]
- Garbowski, T.; Knitter-Piątkowska, A.; Mrówczyński, D. Numerical Homogenization of Multi-Layered Corrugated Cardboard with Creasing or Perforation. Materials 2021, 14, 3786. [Google Scholar] [CrossRef] [PubMed]
- Fadiji, T.; Coetzee, C.J.; Berry, T.M.; Opara, U.L. Investigating the role of geometrical configurations of ventilated fresh produce packaging to improve the mechanical strength—Experimental and numerical approaches. Food Packag. Shelf Life. 2019, 20, 100312. [Google Scholar] [CrossRef]
- Berry, T.M.; Fadiji, T.S.; Defraeye, T.; Opara, U.L. The role of horticultural carton vent hole design on cooling efficiency and compression strength: A multi-parameter approach. Postharvest Biol. Technol. 2017, 124, 62–74. [Google Scholar] [CrossRef]
- Fadiji, T.; Coetzee, C.J.; Opara, U.L. Compression strength of ventilated corrugated paperboard packages: Numerical modelling, experimental validation and effects of vent geometric design. Biosyst. Eng. 2016, 151, 231–247. [Google Scholar] [CrossRef]
- Fadiji, T.; Ambaw, A.; Coetzee, C.J.; Berry, T.M.; Opara, U.L. Application of finite element analysis to predict the mechanical strength of ventilated corrugated paperboard packaging for handling fresh produce. Biosyst. Eng. 2018, 174, 260–281. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the Compressive Strength of Corrugated Cardboard Boxes with Various Openings. Energies 2021, 14, 155. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the Compressive Strength of Corrugated Cardboard Boxes with Various Perforations. Energies 2021, 14, 1095. [Google Scholar] [CrossRef]
- Mrówczyński, D.; Garbowski, T.; Knitter-Piątkowska, A. Estimation of the Compressive Strength of Corrugated Board Boxes with Shifted Creases on the Flaps. Materials 2021, 14, 5181. [Google Scholar] [CrossRef]
- McKee, R.C.; Gander, J.W.; Wachuta, J.R. Compression strength formula for corrugated boxes. Paperboard Packag. 1963, 48, 149–159. [Google Scholar]
- Buchanan, J.S.; Draper, J.; Teague, G.W. Combined board characteristics that determine box performance. Paperboard Packag. 1964, 49, 74–85. [Google Scholar]
- Shick, P.E.; Chari, N.C.S. Top-to-bottom compression for double wall corrugated boxes. Tappi J. 1965, 48, 423–430. [Google Scholar]
- Wolf, M. New equation helps pin down box specifications. Packag. Eng. 1972, 17, 66–67. [Google Scholar]
- Kellicutt, K.; Landt, E. Development of design data for corrugated fiberboard shipping containers. Tappi J. 1952, 35, 398–402. [Google Scholar]
- Maltenfort, G. Compression strength of corrugated containers. Fibre Contain. 1956, 41, 106–121. [Google Scholar]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. The Role of Buckling in the Estimation of Compressive Strength of Corrugated Cardboard Boxes. Materials 2020, 13, 4578. [Google Scholar] [CrossRef]
- Adamopoulos, S.; Karageorgos, A.; Rapti, E.; Birbilis, D. Predicting the properties of corrugated base papers using multiple linear regression and artificial neural networks. Drewno 2016, 59, 61–72. [Google Scholar] [CrossRef]
- Chaveesuk, R.; Santichiwasatiana, B.; Jinkarn, T. Prediction using artificial neural networks of edgewise compression strength of corrugated fiberboards. Agric. Nat. Resour. 2021, 55, 1062–1071. [Google Scholar] [CrossRef]
- Archaviboonyobul, T.; Chaveesuk, R.; Singh, J.; Jinkarn, T. An analysis of the influence of hand hole and ventilation hole design on compressive strength of corrugated fiberboard boxes by an artificial neural network model. Packag. Technol. Sci. 2020, 33, 171–181. [Google Scholar] [CrossRef]
- Boniecki, P.; Przybył, J.; Kuzimska, T.; Mueller, W.; Raba, B.; Lewicki, A.; Przybył, K.; Zaborowicz, M.; Koszela, K. Neural image analysis in the proces of quality assessment: Domestic pig oocytes. In Proceedings of the Sixth International Conference on Digital Image Processing (ICDIP 2014), Athens, Greece, 5–6 April 2014. [Google Scholar] [CrossRef]
- Stręk, A.M.; Dudzik, M.; Kwiecień, A.; Wańczyk, K.; Lipowska, B. Verification of application of ANN modelling in study of compressive behaviour of aluminium sponges. Eng. Trans. 2019, 67, 271–288. [Google Scholar] [CrossRef]
- Frankowski, J.; Zaborowicz, M.; Sieracka, D.; Łochyńska, M.; Czeszak, W. Prediction of the Hemp Yield Using Artificial Intelligence Methods. J. Nat. Fibers 2022, 19, 13725–13735. [Google Scholar] [CrossRef]
- Araujo, G.; Andrade, F.A.A. Post-Processing Air Temperature Weather Forecast Using Artificial Neural Networks with Measurements from Meteorological Stations. Appl. Sci. 2022, 12, 7131. [Google Scholar] [CrossRef]
- Jani, D.B.; Mishra, M.; Sahoo, P.K. Application of artificial neural network for predicting performance of solid desiccant cooling systems—A review. Renew. Sustain. Energ. Rev. 2017, 80, 352–366. [Google Scholar] [CrossRef]
- Funes, E.; Allouche, Y.; Beltrán, G.; Jiménez, A. A Review: Artificial Neural Networks as Tool for Control Food Industry Process. J. Sens. Technol. 2015, 5, 28–43. [Google Scholar] [CrossRef] [Green Version]
- Mrówczyński, D.; Gajewski, T.; Garbowski, T. Sensitivity Analysis of Open-Top Cartons in Terms of Compressive Strength Capacity. Materials 2023, 16, 412. [Google Scholar] [CrossRef] [PubMed]
- Mohite, A.M.; Sharma, N.; Aggarwal, S.; Sharma, S. Effect of tamarindus coating on post-harvest quality of apple and pears stored at different condition. Carpathian J. Food Sci. Technol. 2018, 10, 17–25. [Google Scholar]
- Mrówczyński, D.; Knitter-Piątkowska, A.; Garbowski, T. Non-Local Sensitivity Analysis and Numerical Homogenization in Optimal Design of Single-Wall Corrugated Board Packaging. Materials 2022, 15, 720. [Google Scholar] [CrossRef]
- Mrówczyński, D.; Knitter-Piątkowska, A.; Garbowski, T. Optimal Design of Double-Walled Corrugated Board Packaging. Materials 2022, 15, 2149. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Sudjianto, A. An efficient algorithm for constructing optimal design of computer experiments. J. Stat. Plan. Inference 2005, 134, 268–287. [Google Scholar] [CrossRef]
- Buljak, V.; Garbowski, T. Efficient methods for optimal space filling in model reduction techniques, Proceedings of XX International Conference on Computer Methods in Mechanics CMM2013. In Recent Advances in Computational Mechanics; Łodygowski, T., Rakowski, J., Litewka, P., Eds.; CRC Press: Boca Raton, FL, USA, 2014; pp. 285–292. [Google Scholar]
- Abaqus Unified FEA Software. Available online: https://www.3ds.com/products-services/simulia/products/abaqus (accessed on 14 January 2023).
- Hill, R. A theory of the yielding and plastic flow in anisotropic metals. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 193, 281–297. [Google Scholar] [CrossRef]
- FEMat BSE System. Available online: http://fematsystems.pl/bse-system_en/ (accessed on 14 January 2023).



| Box Case | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 366 | 282 | 94 | 46 | 70.5 | 30 | 37 | 36 | 31.5 | 25 | 12.5 | 134.5 | 25 | 12.5 | 91.5 | 33.5 | 65 |
| 2 | 330 | 282 | 94 | 46 | 70.5 | 30 | 37 | 36 | 31.5 | 25 | 12.5 | 134.5 | 30 | 15 | 91.5 | 33.5 | 65 |
| 3 | 366 | 254 | 94 | 46 | 70.5 | 30 | 37 | 36 | 31.5 | 30 | 15 | 134.5 | 25 | 12.5 | 91.5 | 33.5 | 65 |
| 4 | 366 | 282 | 85 | 46 | 70.5 | 30 | 37 | 36 | 31.5 | 25 | 12.5 | 90 | 25 | 12.5 | 70 | 33.5 | 65 |
| 5 | 366 | 282 | 94 | 76 | 70.5 | 30 | 37 | 36 | 31.5 | 20 | 10 | 114.5 | 20 | 10 | 111.5 | 90 | 90 |
| 6 | 366 | 282 | 94 | 73 | 70.5 | 30 | 37 | 50 | 40 | 32 | 16 | 134.5 | 36 | 18 | 91.5 | 33.5 | 65 |
| 7 | 386 | 282 | 94 | 83 | 70.5 | 30 | 37 | 30 | 40 | 32 | 16 | 134.5 | 25 | 12.5 | 91.5 | 45 | 45 |
| 8 | 386 | 302 | 94 | 83 | 80.5 | 40 | 40 | 30 | 40 | 32 | 16 | 134.5 | 25 | 12.5 | 91.5 | 75 | 60 |
| 9 | 391 | 262 | 104 | 85.5 | 60.5 | 40 | 40 | 25 | 25 | 28 | 14 | 125 | 25 | 12.5 | 91.5 | 75 | 60 |
| 11 | 396 | 262 | 90 | 88 | 60.5 | 40 | 40 | 45 | 32 | 35 | 14 | 125 | 30 | 12.5 | 91.5 | 80 | 85 |
| 12 | 401 | 265 | 98 | 80.5 | 52 | 20 | 20 | 38 | 40 | 34 | 17 | 125 | 28 | 14 | 91.5 | 55 | 45 |
| 13 | 386 | 268 | 98 | 100 | 83.5 | 20 | 20 | 38 | 32 | 20 | 10 | 125 | 20 | 10 | 91.5 | 55 | 45 |
| 14 | 388 | 271 | 98 | 91 | 75 | 15 | 25 | 42 | 45 | 20 | 10 | 155 | 20 | 10 | 111 | 55 | 45 |
| 15 | 392 | 252 | 94 | 93 | 65.5 | 15 | 25 | 30 | 27 | 20 | 10 | 92 | 20 | 10 | 85 | 55 | 45 |
| 16 | 396 | 252 | 81 | 48 | 41 | 15 | 25 | 30 | 27 | 20 | 10 | 135 | 20 | 10 | 111 | 20 | 35 |
| 17 | 398 | 252 | 81 | 49 | 41 | 35 | 35 | 30 | 27 | 20 | 10 | 135 | 20 | 10 | 111 | 37 | 35 |
| 18 | 396 | 252 | 83 | 67.5 | 51 | 25 | 35 | 36 | 36 | 35 | 10 | 135 | 35 | 10 | 85 | 65 | 55 |
| 19 | 310 | 290 | 85 | 68 | 70 | 25 | 35 | 30 | 28 | 16 | 8 | 95 | 16 | 8 | 85 | 65 | 55 |
| 20 | 320 | 271 | 81 | 73 | 55.5 | 25 | 35 | 40 | 28 | 22 | 11 | 115 | 22 | 11 | 95 | 40 | 45 |
| Grade | ||||||||
|---|---|---|---|---|---|---|---|---|
| (MPa) | (MPa) | (–) | (MPa) | (MPa) | (MPa) | (MPa) | (–) | |
| B-840 | 2032 | 1111 | 0.40 | 1184 | 7 | 11 | 3.05 | 0.95 |
| EB-880 | 1636 | 907 | 0.40 | 963 | 8 | 11 | 3.50 | 0.65 |
| EB-965 | 1616 | 750 | 0.44 | 898 | 7 | 11 | 3.01 | 0.74 |
| Load | BCT |
|---|---|
| (kg) | (%) |
| 5 | −0.30 |
| 10 | −0.57 |
| 15 | −1.05 |
| Case | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | −0.01 | −0.01 | −0.02 | 0.53 | 0.90 | 0 | 0 | 0.17 | 0.66 | −0.01 | 0 | 0.57 | 0 | 0 | 0.56 | 0.01 | 0.03 |
| 2 | 0.01 | −0.02 | 0.08 | −0.01 | 0.34 | 0.01 | 0.01 | 0.41 | 0.25 | 0 | 0 | 0 | 0 | 0 | 0 | 0.02 | 0.03 |
| 3 | 0 | 0 | 0.01 | −0.03 | 0.36 | 0.01 | 0.01 | 0.41 | 0.25 | 0 | 0 | 0.01 | 0 | 0.01 | 0.01 | 0.02 | 0.03 |
| 4 | 0 | −0.01 | 0.11 | −0.06 | 0.02 | 0.01 | −0.02 | 0.20 | 0.27 | 0 | 0 | 0.01 | −0.04 | −0.02 | 0.29 | 0.03 | 0 |
| 5 | −0.02 | −0.02 | 0.17 | 0.52 | 0.66 | 0.02 | −0.02 | 0.43 | 0.24 | 0 | 0 | 0 | 0 | 0 | 0 | 0.11 | 0.22 |
| 6 | −0.23 | 0.02 | 0 | 0.40 | 0.21 | 0.01 | 0 | 0.29 | 0.27 | 0 | 0 | −0.02 | −0.07 | 0 | −0.10 | 0.02 | 0.02 |
| 7 | 0 | −0.22 | −0.12 | 0.24 | 0.13 | 0.01 | −0.32 | 0.64 | 0.30 | 0 | 0 | −0.01 | −0.01 | 0.06 | −0.31 | 0.02 | −0.31 |
| 8 | 0.02 | −0.06 | 0.02 | 0.22 | 0.39 | 0 | 0.02 | 0.31 | 0.28 | −0.29 | 0 | −0.05 | 0.01 | −0.05 | 0.09 | 0.03 | 0.02 |
| 9 | 0 | 0.09 | −0.11 | 0.30 | 0.38 | 0 | 0.02 | 0.20 | 0.22 | 0 | 0 | 0 | 0 | 0 | 0 | 0.04 | 0.10 |
| 10 | −0.13 | 0 | −0.23 | 0.54 | 0.12 | 0.04 | −0.01 | 0.27 | 0.09 | 0 | 0 | 0.02 | 0.03 | 0 | 0.03 | 0.07 | 0.14 |
| 11 | −0.52 | −0.09 | −0.16 | 0.17 | 0 | 0.01 | −0.01 | −0.26 | 0.30 | −0.52 | 0 | −0.21 | 0 | 0 | −0.17 | 0.02 | 0 |
| 12 | −0.10 | 0 | −0.08 | 0.07 | 0.23 | 0.01 | 0.01 | 0.06 | 0.23 | −0.14 | 0 | −0.09 | 0 | 0 | −0.35 | 0.02 | 0.02 |
| 13 | 0.01 | −0.20 | −0.07 | 0.22 | 0.29 | 0.02 | 0.01 | 0.10 | 0.11 | −0.03 | 0 | 0.01 | 0 | 0 | 0.01 | 0.03 | 0.02 |
| 14 | 0.10 | 0.11 | 0.13 | 0.26 | 0.42 | −0.02 | 0 | 0.22 | 0.20 | −0.01 | 0 | 0.16 | 0 | 0 | 0.35 | 0.01 | −0.03 |
| 15 | 0.24 | −0.05 | −0.04 | 0.36 | 0.23 | 0.02 | 0 | 0.68 | 0.46 | 0 | 0 | 0 | 0 | −0.01 | 0.01 | 0.02 | 0.03 |
| 16 | 0.26 | 0.25 | 0.09 | 0.24 | 0.31 | 0.01 | 0.02 | 0.32 | 0.23 | 0 | 0 | 0.08 | 0.02 | 0 | 0.01 | 0.02 | 0.10 |
| 17 | 0 | 0 | 0.16 | 0.31 | 0.26 | −0.02 | 0.13 | 0.26 | 0.30 | 0 | 0 | 0 | 0.02 | 0.11 | 0 | 0 | 0.12 |
| 18 | −0.17 | 0.02 | −0.03 | 0.17 | 0.16 | 0 | −0.06 | −0.49 | 0.06 | −0.17 | 0.02 | −0.02 | 0.01 | 0 | 0.41 | 0.02 | 0.15 |
| 19 | 0 | 0.41 | 0.01 | 0.73 | 0.25 | 0.01 | 0.01 | 0.49 | 0.20 | 0 | −0.01 | −0.01 | 0 | 0 | 0 | 0.02 | 0.02 |
| 20 | −0.07 | 0.02 | −0.01 | 0.24 | 0.26 | 0 | 0.05 | 0.03 | 0.19 | −0.08 | 0 | −0.12 | 0 | 0 | 0.06 | 0.02 | 0.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garbowski, T.; Mrówczyński, D.; Grabski, J.K. Modified Compression Test of Corrugated Board Fruit Tray: Numerical Modeling and Global Sensitivity Analysis. Materials 2023, 16, 1121. https://doi.org/10.3390/ma16031121
Garbowski T, Mrówczyński D, Grabski JK. Modified Compression Test of Corrugated Board Fruit Tray: Numerical Modeling and Global Sensitivity Analysis. Materials. 2023; 16(3):1121. https://doi.org/10.3390/ma16031121
Chicago/Turabian StyleGarbowski, Tomasz, Damian Mrówczyński, and Jakub Krzysztof Grabski. 2023. "Modified Compression Test of Corrugated Board Fruit Tray: Numerical Modeling and Global Sensitivity Analysis" Materials 16, no. 3: 1121. https://doi.org/10.3390/ma16031121
APA StyleGarbowski, T., Mrówczyński, D., & Grabski, J. K. (2023). Modified Compression Test of Corrugated Board Fruit Tray: Numerical Modeling and Global Sensitivity Analysis. Materials, 16(3), 1121. https://doi.org/10.3390/ma16031121








