Electronic Structure of NdFeCoB Oxide Magnetic Particles Studied by DFT Calculations and XPS
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiment
2.2. Calculations
2.2.1. Methods
2.2.2. Molecular and Crystal Models
3. Results
3.1. Estimation of Concentrations According to XRD Data
3.2. Estimation of Concentrations According to XPS Data
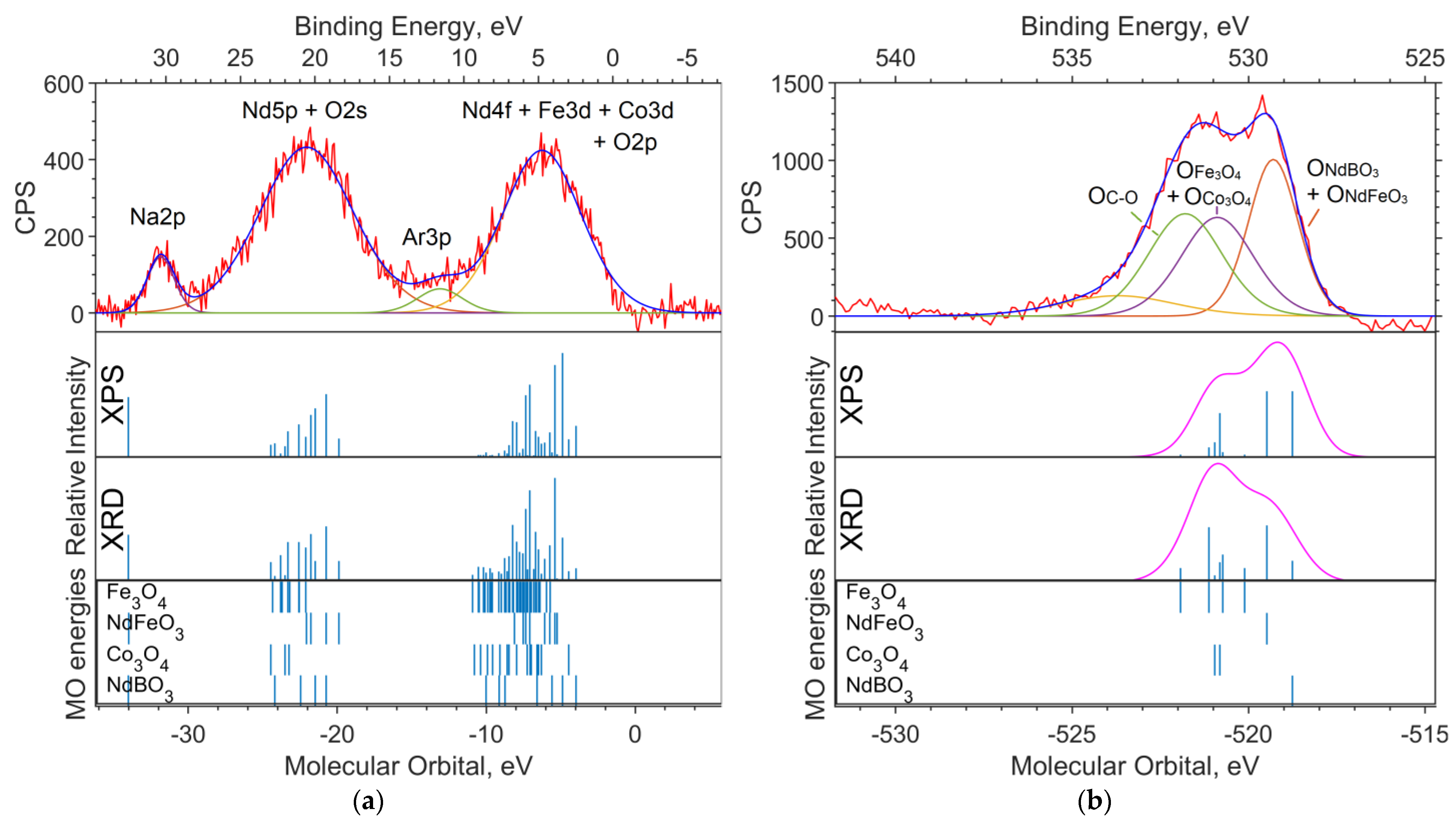
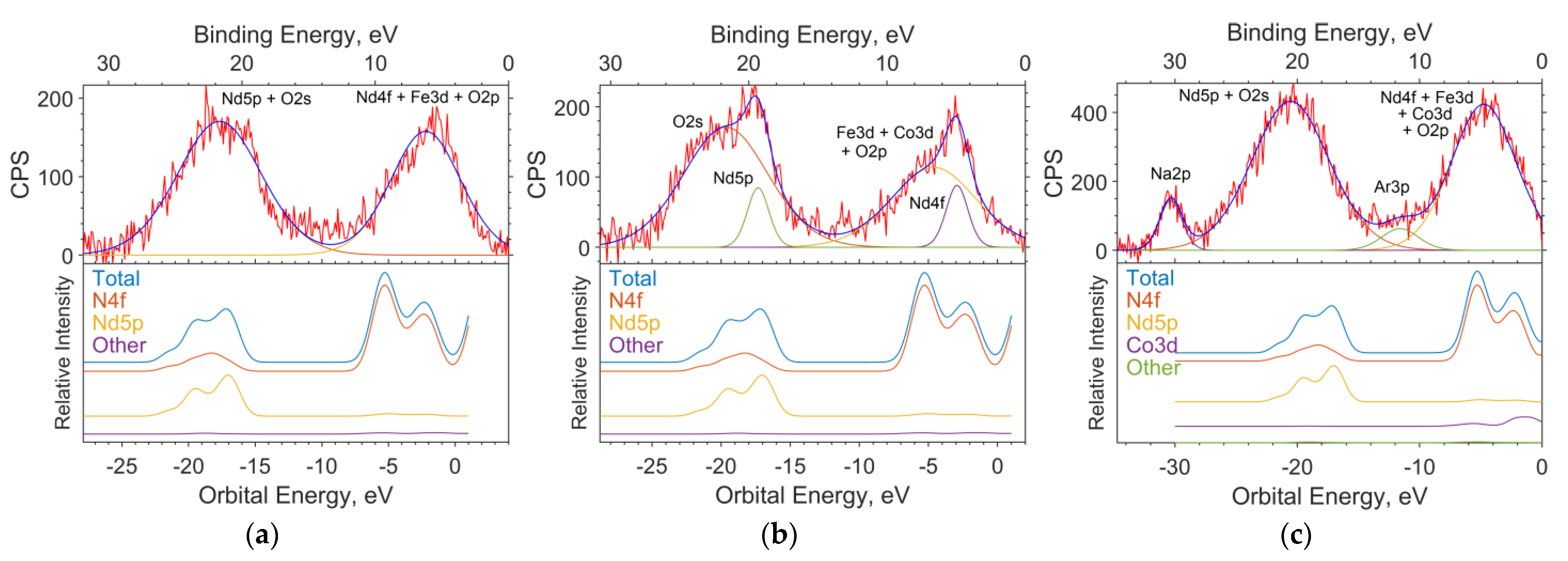
3.3. Spectra Modeling
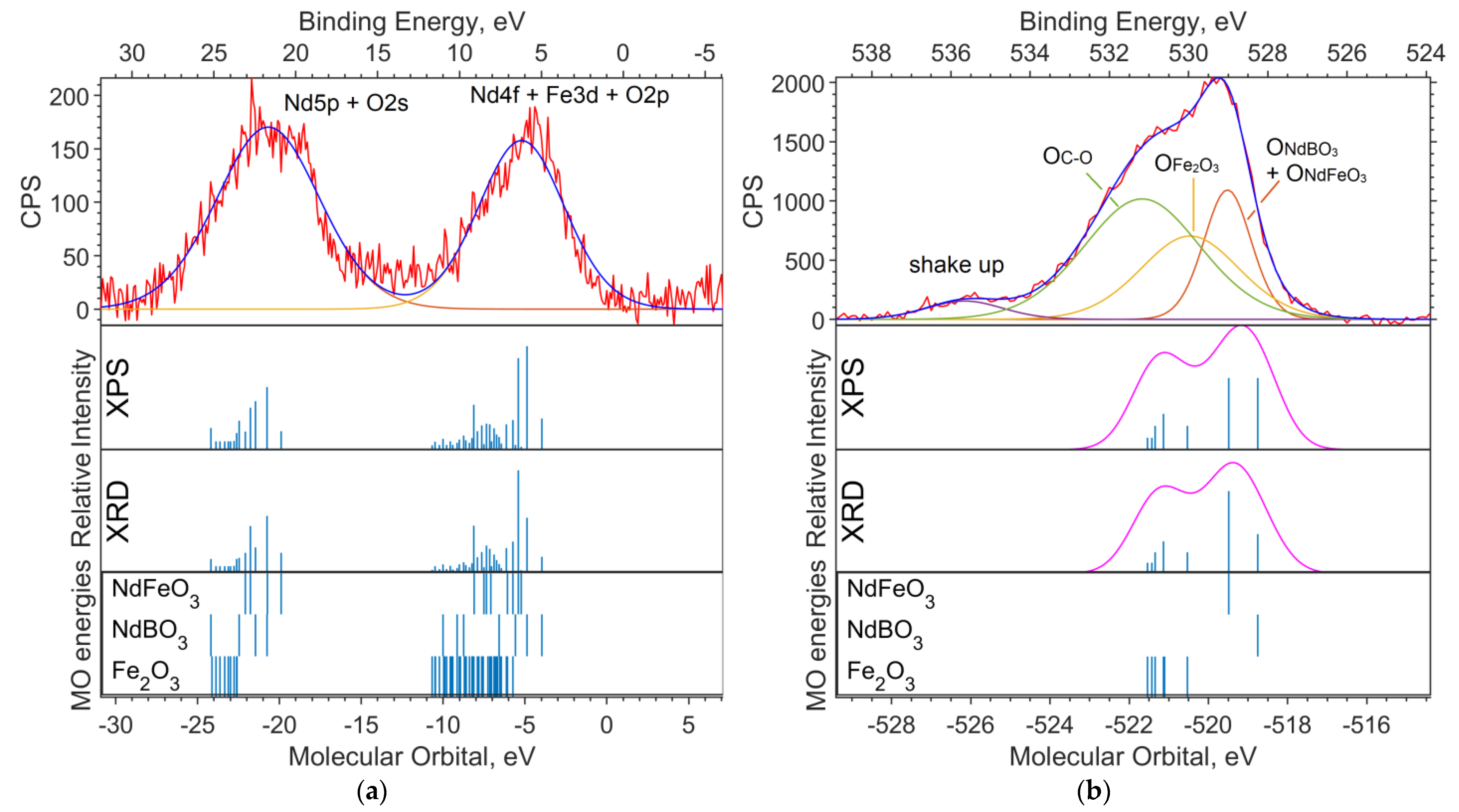
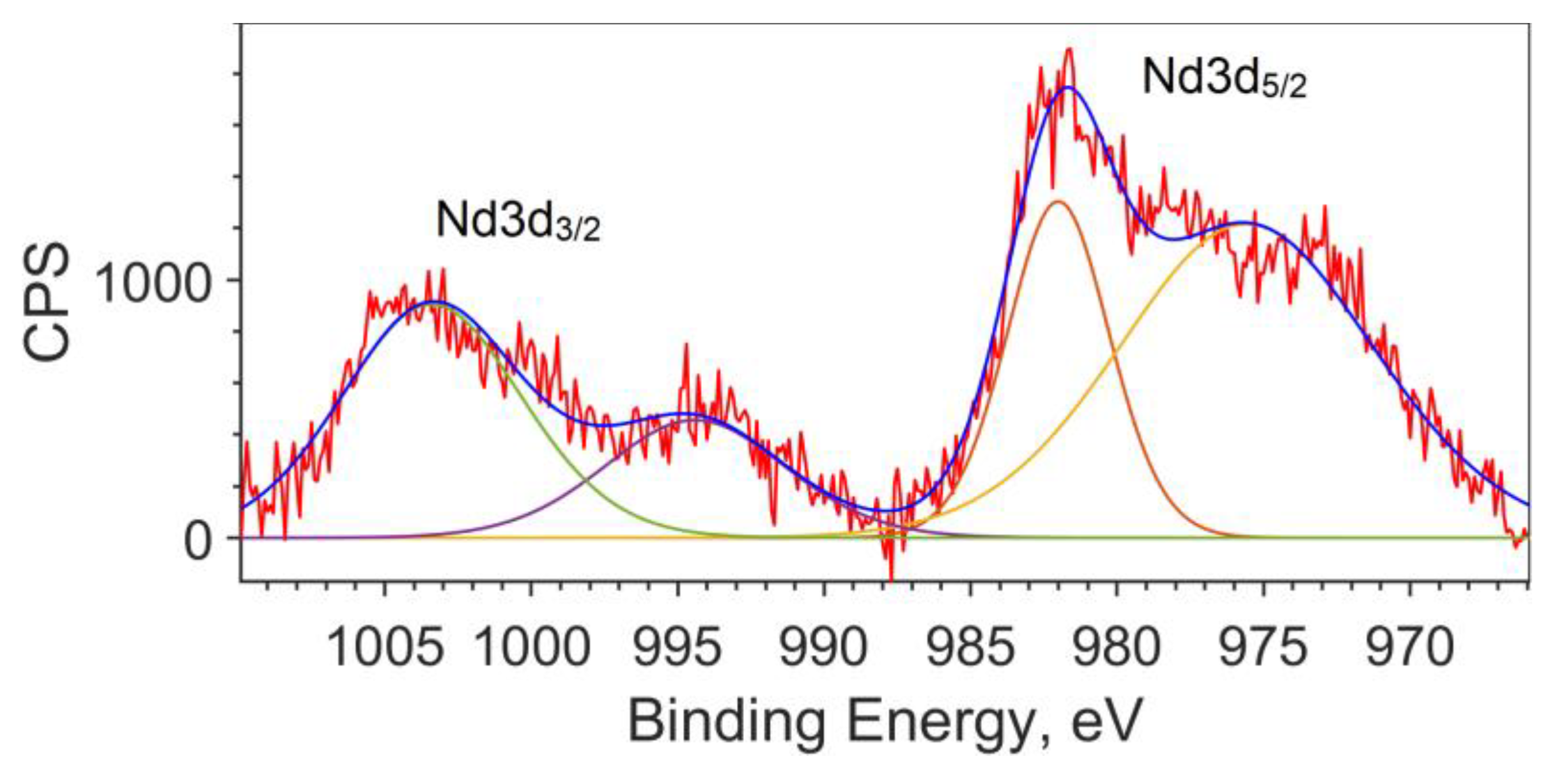
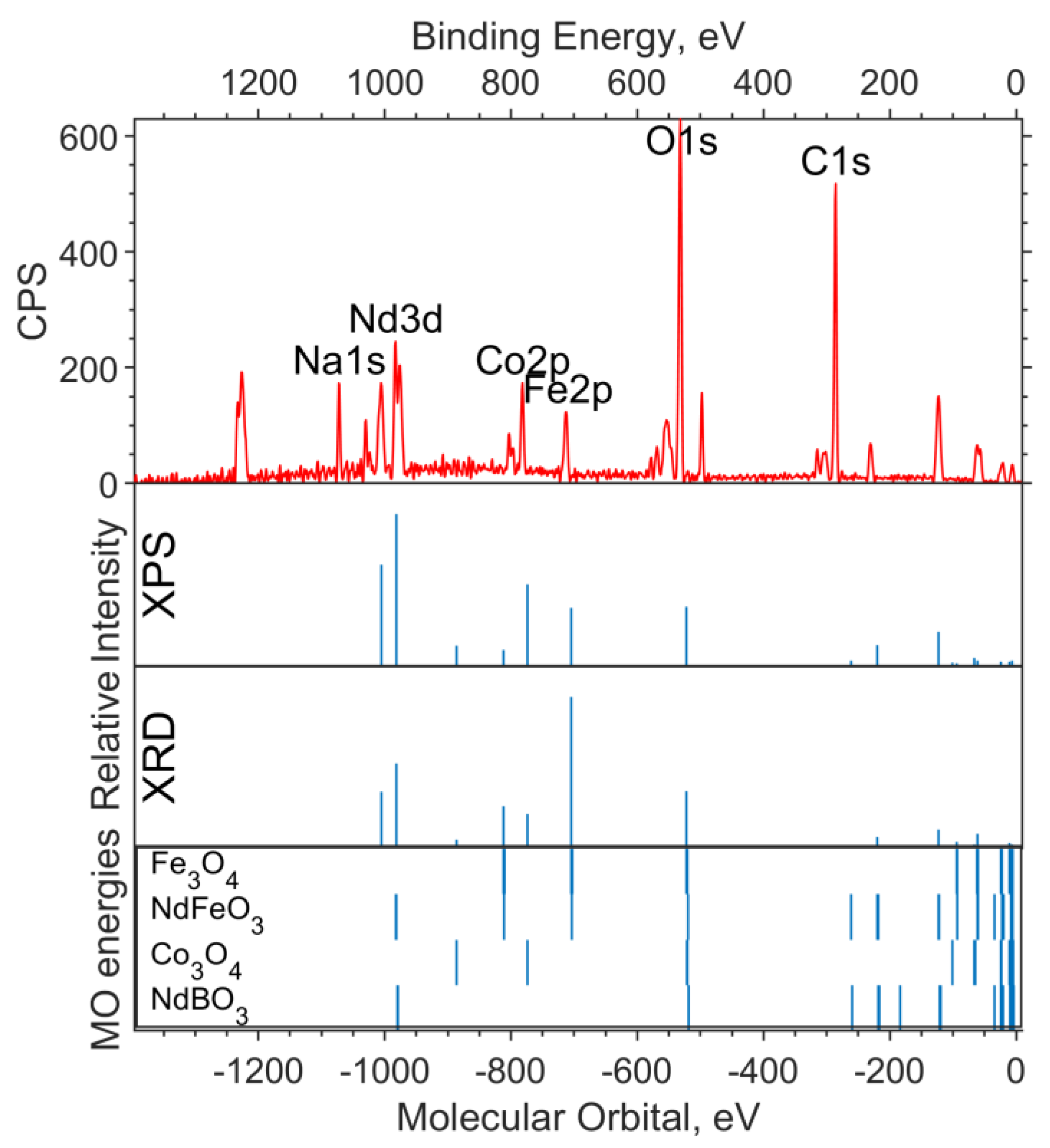
3.3.1. Oxide Sample with Co Concentration x = 0
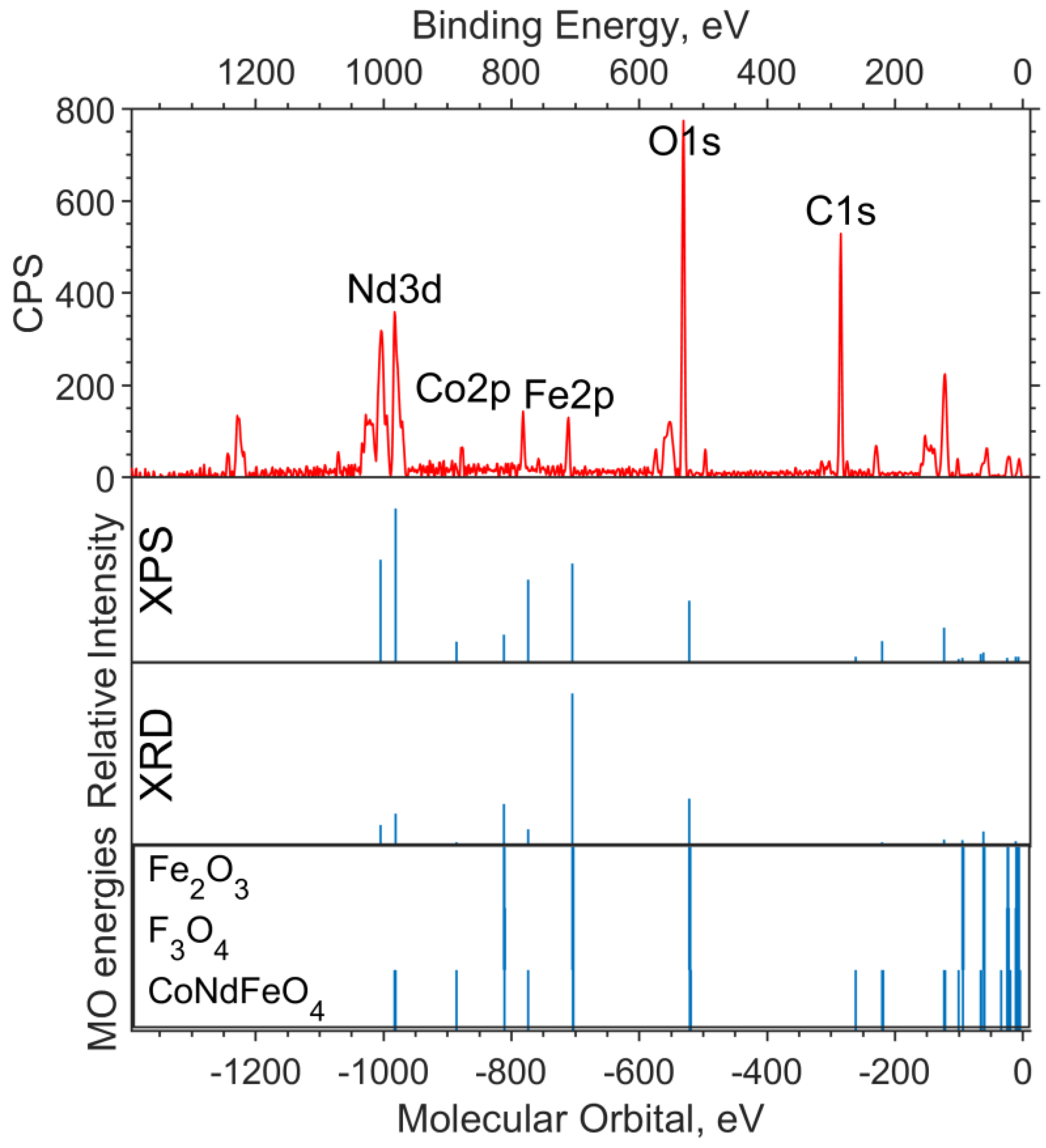
3.3.2. Oxide Sample with Co Concentration x = 0.05
3.3.3. Oxide Sample with Co Concentration x = 0.5
3.4. Modeling Spectra from Crystal Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Matsuura, Y. Recent development of Nd-Fe-B sintered magnets and their applications. J. Magn. Magn. Mater. 2006, 303, 344–347. [Google Scholar] [CrossRef]
- Gutfleisch, O.; Willard, M.A.; Brück, E.; Chen, C.H.; Sankar, S.G.; Liu, J.P. Magnetic materials and devices for the 21st century: Stronger, lighter, and more energy efficient. Adv. Mater. 2011, 23, 821–842. [Google Scholar] [CrossRef] [PubMed]
- Papynov, E.K.; Dran’kov, A.N.; Tkachenko, I.A.; Buravlev, I.Y.; Mayorov, V.Y.; Merkulov, E.B.; Fedorets, A.N.; Ognev, A.V.; Samardak, A.S.; Drenin, A.S.; et al. Synthesis and sorption characteristics of magnetic materials based on cobalt oxides and their reduced forms. Russ. J. Inorg. Chem. 2020, 65, 820–828. [Google Scholar] [CrossRef]
- Kolesnikova, V.G.; Makarova, L.A.; Omelyanchik, A.S.; Sobolev, K.V.; Isaev, D.A.; Alekhina, I.A.; Komlev, A.S.; Rodionova, V.V.; Perov, N.S. Magnetoactive elastomers based on ferromagnetic and ferroelectric particles: A FORC approach. J. Magn. Magn. Mater. 2022, 558, 169506. [Google Scholar] [CrossRef]
- Skomski, R.; Coey, J. Giant energy product in nanostructured two-phase magnets. Phys. Rev. B 1993, 48, 15812. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cui, B.; Zheng, L.; Li, W.; Liu, J.; Hadjipanayis, G. Single-crystal and textured polycrystalline Nd2Fe14B flakes with a submicron or nanosize thickness. Acta Mater. 2012, 60, 1721–1730. [Google Scholar] [CrossRef]
- Cui, B.Z.; Zheng, L.Y.; Marinescu, M.; Liu, J.F.; Hadjipanayis, G.C. Textured Nd2Fe14B flakes with enhanced coercivity. J. Appl. Phys. 2012, 111, 07A735. [Google Scholar] [CrossRef]
- Samardak, V.Y.; Kharitonov, V.N.; Belov, A.A.; ·Shichalin, O.O.; Papynov, E.K.; Protasov, A.V.; Stashkova, L.A.; Kuranova, N.N.; ·Pushin, V.G.; Samardak, A.S.; et al. V Structure, Composition and Magnetic Properties of Nd-(Fe,Co)-B Hard Magnetic Copper-Doped Powders. J. Supercond. Nov. Magn. 2022, 35, 1703–1708. [Google Scholar]
- Pal, A.; Gabay, A.; Hadjipanayis, G.C. Mechanochemical synthesis of Nd2Fe14B alloy with high coercivity. J. Alloy. Compd. 2012, 543, 31–33. [Google Scholar] [CrossRef]
- Ahmadpour, G.; Samardak, A.Y.; Korochentsev, V.V.; Osmushko, I.S.; Samardak, V.Y.; Komissarov, A.A.; Shtarev, D.S.; Samardak, A.S.; Ognev, A.V.; Nasirpouri, F. Microstructure, composition and magnetic properties of Nd-(Fe1-xCox)-B oxide magnetic particles synthesized by Pechini-type chemical method. Adv. Powder Technol. 2021, 32, 3964–3979. [Google Scholar] [CrossRef]
- Tan, X.; Parmar, H.; Zhong, Y.; Chaudhary, V.; Ramanujan, R.V. Effect of Dy substitution on the microstructure and magnetic properties of Thigh (BH)max Nd-Dy-Fe-Co-B nanoparticles prepared by microwave processing. J. Magn. Magn. Mater. 2019, 471i, 278–285. [Google Scholar] [CrossRef]
- Yu, L.; Yang, C.; Hou, Y. Controllable Nd2Fe14B/Fe nanocomposites: Chemical synthesis and magnetic properties. Nanoscale 2014, 6, 10638–10642. [Google Scholar] [CrossRef] [PubMed]
- Fairley, N. CasaXPS: Processing Software for XPS, AES, SIMS and More. Casa Sofwware Ltd. 2018. Available online: http://www.casaxps.com/ (accessed on 5 October 2022).
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. A New Basis Set Exchange: An Open, Up-to-date Resource for the Molecular Sciences. Community J. Chem. inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baseggio, O.; Bonfà, P.; Brunato, D.; Car, R.; Carnimeo, I.; Cavazzoni, C.; de Gironcoli, S.; Delugas, P.; Ruffino, F.F.; et al. Quantum ESPRESSO toward the exascale. J. Chem. Phys. 2020, 152, 154105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Leach, A.R. Molecular Modeling: Principles and Applications; Prentice Hall: Harlow, UK, 2001. [Google Scholar]


| Compound | Molecular Model | Crystal Model |
|---|---|---|
| Fe2O3 (molecular model—Fe6O9) |  |  |
| NdBO3 |  | 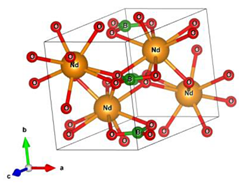 |
| NdFeO3 |  | 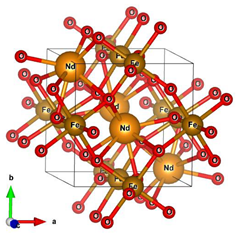 |
| Co3O4 | 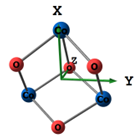 | 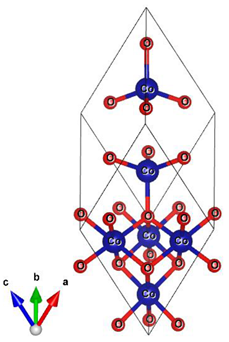 |
| CoNdFeO4 | 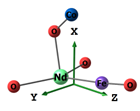 | - |
| Nd2Fe14B | - |  |
| x | Phase | Weight (%) |
|---|---|---|
| 0 | NdFeO3 | 37.9 (3) |
| NdBO3 | 18.0 (2) | |
| Fe2O3 | 44.1 (3) | |
| 0.05 | Fe2O3 | 72.0 (7) |
| Fe3O4 | 9.8 (8) | |
| CoNdFeO4 | 18.0 (4) | |
| 0.5 | NdFeO3 | 25.7 (3) |
| Fe3O4 | 55.8 (4) | |
| NdBO3 | 9.6 (2) | |
| Co3O4 | 8.9 (5) |
| Atomic Shell | Pos. | Area | at.% |
|---|---|---|---|
| x = 0 | |||
| Nd3d5/2 | 982 | 4117.0 | 6.3 |
| Fe2p3/2 | 710 | 1705.0 | 12.5 |
| O1s | 531 | 3807.5 | 36.6 |
| C1s | 285 | 1460.0 | 41.1 |
| Na1s | 1071 | 1054.0 | 3.5 |
| x = 0.05 | |||
| Nd3d5/2 | 982 | 5161.0 | 3.41 |
| Fe2p3/2 | 710 | 1260.5 | 2.64 |
| C1s | 285 | 2551.0 | 56.14 |
| O1s | 531 | 4340.0 | 32.60 |
| Co2p3/2 | 781 | 2343.7 | 2.78 |
| Na1s | 1071 | 939.0 | 2.43 |
| x = 0.5 | |||
| Nd3d5/2 | 982 | 8374.5 | 3.15 |
| Co2p3/2 | 781 | 2737.0 | 3.02 |
| Fe2p3/2 | 710 | 1462.0 | 2.95 |
| C1s | 285 | 3028.0 | 64.03 |
| O1s | 531 | 3386.5 | 24.44 |
| Na1s | 1071 | 972.0 | 2.41 |
| x = 0 | |
| NdFeO3 | 2 |
| NdBO3 | 2 |
| Fe2O3 | 3 |
| x = 0.05 | |
| Fe2O3 | 1 |
| Fe3O4 | 1 |
| CoNdFeO4 | 10 |
| x = 0.5 | |
| Fe3O4 | 1 |
| NdFeO3 | 3 |
| Co3O4 | 2 |
| NdBO3 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samardak, V.Y.; Komissarov, A.A.; Dotsenko, A.A.; Korochentsev, V.V.; Osmushko, I.S.; Belov, A.A.; Mushtuk, P.S.; Antonov, V.A.; Ahmadpour, G.; Nasirpouri, F.; et al. Electronic Structure of NdFeCoB Oxide Magnetic Particles Studied by DFT Calculations and XPS. Materials 2023, 16, 1154. https://doi.org/10.3390/ma16031154
Samardak VY, Komissarov AA, Dotsenko AA, Korochentsev VV, Osmushko IS, Belov AA, Mushtuk PS, Antonov VA, Ahmadpour G, Nasirpouri F, et al. Electronic Structure of NdFeCoB Oxide Magnetic Particles Studied by DFT Calculations and XPS. Materials. 2023; 16(3):1154. https://doi.org/10.3390/ma16031154
Chicago/Turabian StyleSamardak, Vadim Yu., Alexander A. Komissarov, Alexander A. Dotsenko, Vladimir V. Korochentsev, Ivan S. Osmushko, Anton A. Belov, Pavel S. Mushtuk, Valerii A. Antonov, Ghader Ahmadpour, Farzad Nasirpouri, and et al. 2023. "Electronic Structure of NdFeCoB Oxide Magnetic Particles Studied by DFT Calculations and XPS" Materials 16, no. 3: 1154. https://doi.org/10.3390/ma16031154
APA StyleSamardak, V. Y., Komissarov, A. A., Dotsenko, A. A., Korochentsev, V. V., Osmushko, I. S., Belov, A. A., Mushtuk, P. S., Antonov, V. A., Ahmadpour, G., Nasirpouri, F., Samardak, A. S., & Ognev, A. V. (2023). Electronic Structure of NdFeCoB Oxide Magnetic Particles Studied by DFT Calculations and XPS. Materials, 16(3), 1154. https://doi.org/10.3390/ma16031154







