Time-Varying Pattern and Prediction Model for Geopolymer Mortar Performance under Seawater Immersion
Abstract
:1. Introduction
2. Experimental Program
2.1. Raw Materials
2.2. Sample Preparation
2.3. Test Method
2.4. UCS Prediction Model of GPM
2.4.1. Support Vector Regression (SVR)
2.4.2. The SVR Prediction Model
3. Results and Discussion
3.1. Mass Change
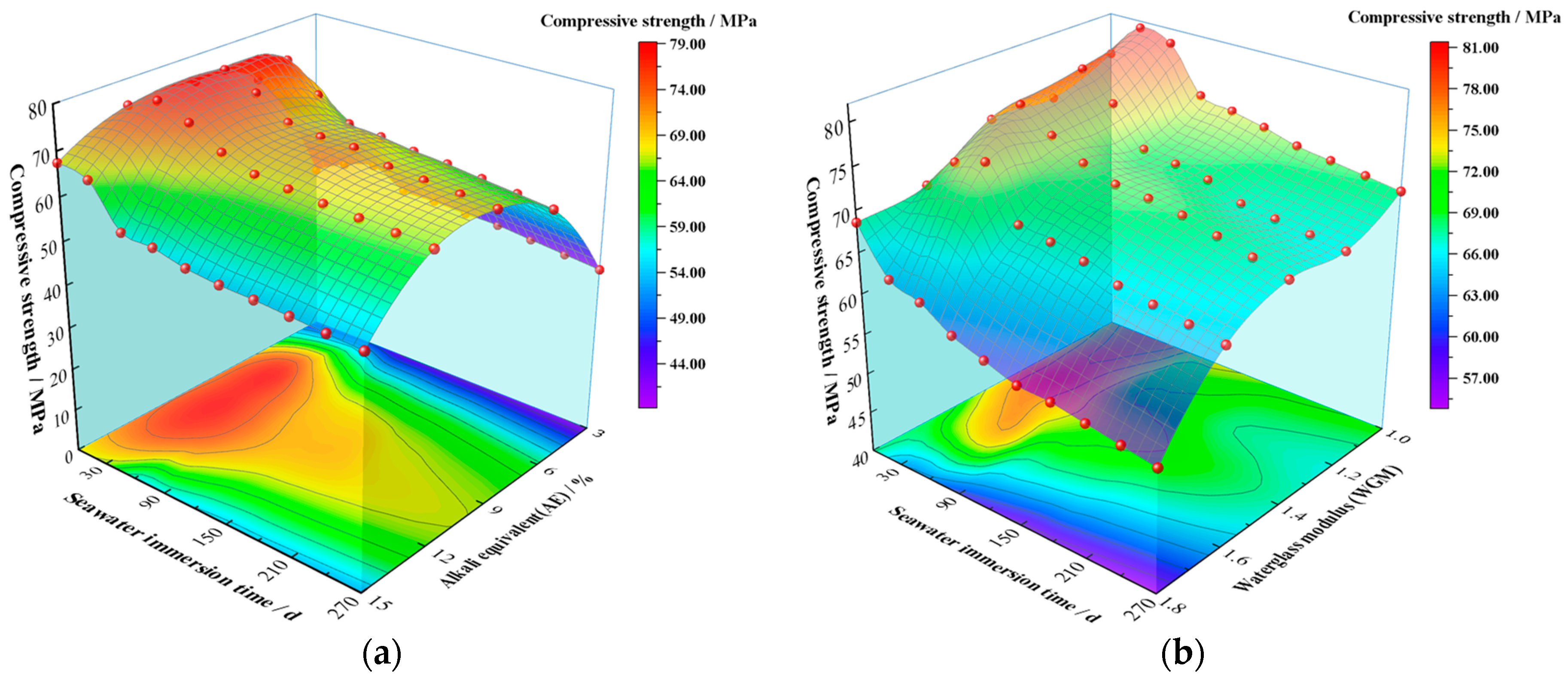
3.2. Time-Varying Law of Compressive Strength
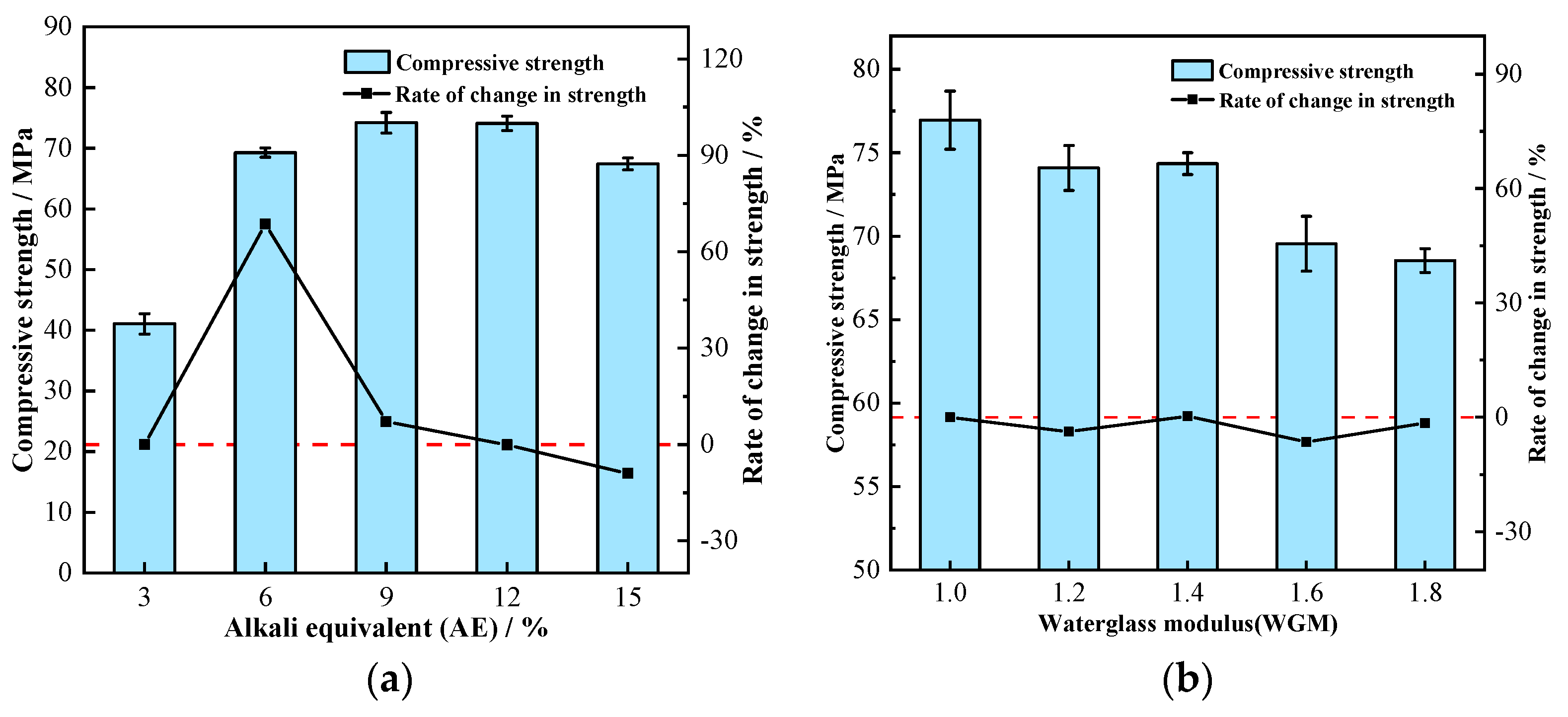
3.2.1. Initial Compressive Strength
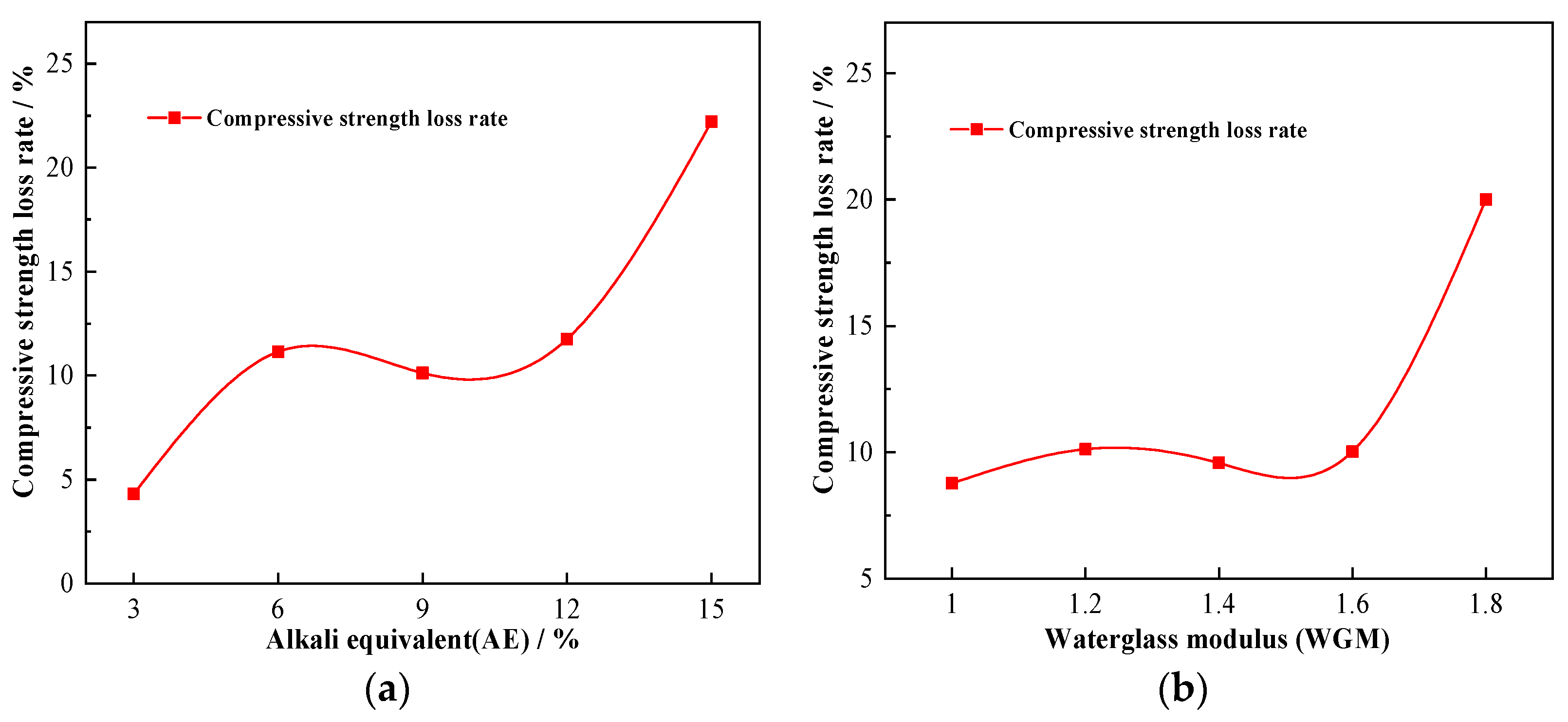
3.2.2. The Impact of AE
3.2.3. The Impact of WGM
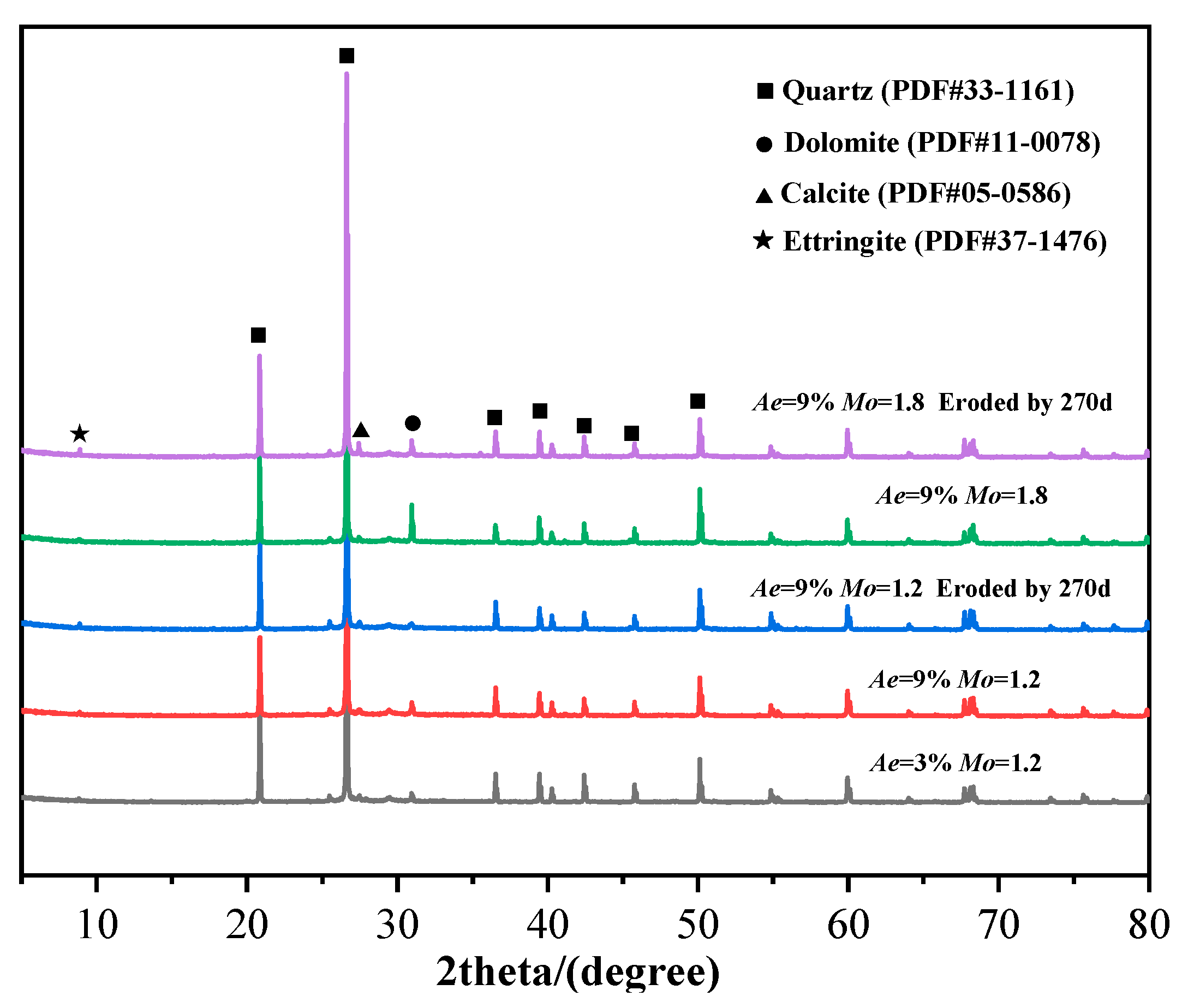
3.3. X-Ray Diffraction (XRD) Analysis
3.4. Scanning Electron Microscope (SEM) Analysis
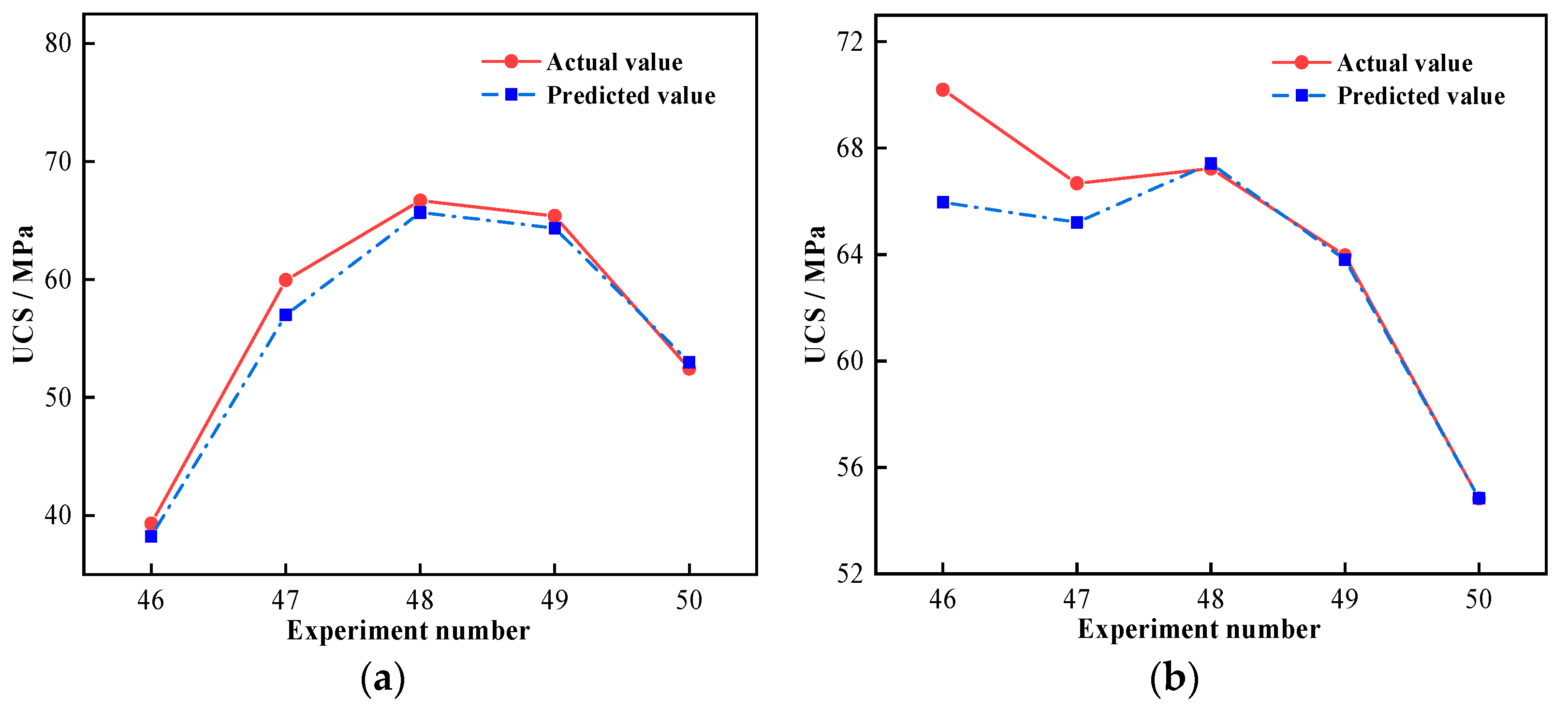
3.5. Predicted Results and Discussion of SVR Model
3.6. SVR Model Analysis
3.6.1. Parameter Analysis
3.6.2. Comparative Performance Evaluation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maage, M.; Helland, S.; Poulsen, E.; Vennesland, O.; Carl, J.E. Service life prediction of existing concrete structures exposed to marine environment. ACI Mater. J. 1996, 93, 602–608. [Google Scholar]
- Davidovits, J. Geopolymer Cement a review 2013. In Geopolymer Science and Technics; Geopolymer Institute: Saint-Quentin, France, 2013; pp. 1–11. [Google Scholar]
- Baščarević, Z.; Komljenović, M.; Miladinović, Z.; Nikolić, V.; Marjanović, N.; Petrović, R. Impact of sodium sulfate solution on mechanical properties and structure of fly ash based geopolymers. Mater. Struct. 2015, 48, 683–697. [Google Scholar] [CrossRef]
- Duxson, P.; Fernández-Jiménez, A.; Provis, J.L.; Lukey, G.C.; Palomo, A.; van Deventer, J.S. Geopolymer technology: The current state of the art. J. Mater. Sci. 2007, 42, 2917–2933. [Google Scholar] [CrossRef]
- Mengasini, L.; Mavroulidou, M.; Gunn, M.J. Alkali-activated concrete mixes with ground granulated blast furnace slag and paper sludge ash in seawater environments. Sustain. Chem. Pharm. 2021, 20, 100380. [Google Scholar] [CrossRef]
- Bondar, D.; Lynsdale, C.; Milestone, N. Simplified model for prediction of compressive strength of alkali-activated natural pozzolans. J. Mater. Civ. Eng. 2012, 24, 391–400. [Google Scholar] [CrossRef]
- Provis, J.L. Alkali-activated materials. Cem. Concr. Res. 2018, 114, 40–48. [Google Scholar] [CrossRef]
- Wang, H.; Li, H.; Yan, F. Synthesis and mechanical properties of metakaolinite-based geopolymer. Colloids Surf. Physicochem. Eng. Asp. 2005, 268, 1–6. [Google Scholar] [CrossRef]
- Qiu, T.S.; Kuang, J.Z.; Shi, F. Effect of alkali on the geopolymer strength. Adv. Build. Mater. 2011, 168–170, 1827–1832. [Google Scholar] [CrossRef]
- Dai, S.; Wang, H.; An, S.; Yuan, L. Mechanical Properties and Microstructural Characterization of Metakaolin Geopolymers Based on Orthogonal Tests. Materials 2022, 15, 2957. [Google Scholar] [CrossRef]
- Xie, J.; Wang, J.; Rao, R.; Wang, C.; Fang, C. Effects of combined usage of GGBS and fly ash on workability and mechanical properties of alkali activated geopolymer concrete with recycled aggregate. Compos. Part B Eng. 2019, 164, 179–190. [Google Scholar] [CrossRef]
- Bakharev, T.; Sanjayan, J.G.; Cheng, Y.-B. Resistance of alkali-activated slag concrete to acid attack. Cem. Concr. Res. 2003, 33, 1607–1611. [Google Scholar] [CrossRef]
- Bakharev, T.; Sanjayan, J.G.; Cheng, Y.B. Resistance of alkali-activated slag concrete to alkali–aggregate reaction. Cem. Concr. Res. 2001, 31, 331–334. [Google Scholar] [CrossRef]
- Pasupathy, K.; Sanjayan, J.; Rajeev, P.; Law, D.W. The effect of chloride ingress in reinforced geopolymer concrete exposed in the marine environment. J. Build. Eng. 2021, 39, 102281. [Google Scholar] [CrossRef]
- Li, W.; Shumuye, E.D.; Shiying, T.; Wang, Z.; Zerfu, K. Eco-friendly fibre reinforced geopolymer concrete: A critical review on the microstructure and long-term durability properties. Case Stud. Constr. Mater. 2022, 16, e00894. [Google Scholar] [CrossRef]
- Xiao, F.; Cui, H.T.; Wang, Y.W.; Lu, T.W. Study on Properties of High Performance Marine Concrete under Seawater Attack. Adv. Mater. Res. 2014, 838, 1791–1796. [Google Scholar] [CrossRef]
- Chindaprasirt, P.; Chalee, W. Effect of sodium hydroxide concentration on chloride penetration and steel corrosion of fly ash-based geopolymer concrete under marine site. Constr. Build. Mater. 2014, 63, 303–310. [Google Scholar] [CrossRef]
- Ouda, A.S.; Gharieb, M. Behavior of alkali-activated pozzocrete-fly ash paste modified with ceramic tile waste against elevated temperatures and seawater attacks. Constr. Build. Mater. 2021, 285, 122866. [Google Scholar] [CrossRef]
- Behnood, A.; Behnood, V.; Gharehveran, M.M.; Alyamac, K.E. Prediction of the compressive strength of normal and high-performance concretes using M5P model tree algorithm. Constr. Build. Mater. 2017, 142, 199–207. [Google Scholar] [CrossRef]
- Chou, J.S.; Pham, A.D. Smart artificial firefly colony algorithm-based support vector regression for enhanced forecasting in civil engineering. Copmut. Aided Civ. Infrastruct. Eng. 2015, 30, 715–732. [Google Scholar] [CrossRef]
- Omran, B.A.; Chen, Q.; Jin, R. Comparison of data mining techniques for predicting compressive strength of environmentally friendly concrete. J. Comput. Civ. Eng. 2016, 30, 04016029. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Thirukumaran, S.; Sumathi, A. Enhanced fuzzy C-means clustering with optimization of support vector regression for imputation of medical database. J. Med. Imaging Health Inform. 2016, 6, 1612–1616. [Google Scholar] [CrossRef]
- Peng, X.; Xu, D. Projection support vector regression algorithms for data regression. Knowl. Based. Syst. 2016, 112, 54–66. [Google Scholar] [CrossRef]
- Bakharev, T. Durability of geopolymer materials in sodium and magnesium sulfate solutions. Cem. Concr. Res. 2005, 35, 1233–1246. [Google Scholar] [CrossRef]
- Guo, L.; Wu, Y.; Xu, F.; Song, X.; Ye, J.; Duan, P.; Zhang, Z. Sulfate resistance of hybrid fiber reinforced metakaolin geopolymer composites. Compos. Part B Eng. 2020, 183, 107689. [Google Scholar] [CrossRef]
- Rowles, M.; O’Connor, B. Chemical Optimization of the Compressive Strength of Aluminosilicate Geopolymers Synthesis by Sodium Silicate Activation of Metakaolinite. J. Mater. Chem. 2003, 13, 1161–1165. [Google Scholar] [CrossRef]
- Sturm, P.; Gluth, G.J.G.; Jäger, C.; Brouwers, H.J.H.; Kühne, H.C. Sulfuric acid resistance of one-part alkali-activated mortars. Cem. Concr. Res. 2018, 109, 54–63. [Google Scholar] [CrossRef]
- Alonso, S.; Palomo, A. Alkaline activation of metakaolin and calcium hydroxide mixtures: Influence of temperature, activator concentration and solids ratio. Mater. Lett. 2001, 47, 55–62. [Google Scholar] [CrossRef]
- Zhu, C.; Lu, C. The progress to recognize the hardening mechanism of water glass. Inorg. Chem. Ind. 2001, 33, 22–25. [Google Scholar]
- Dombrowski, K.; Buchwald, A.; Weil, M. The influence of calcium content on the structure and thermal performance of fly ash based geopolymers. J. Mater. Sci. 2007, 42, 3033–3043. [Google Scholar] [CrossRef]
- Chi, M.; Huang, R. Binding mechanism and properties of alkali-activated fly ash/slag mortars. Constr. Build. Mater. 2013, 40, 291–298. [Google Scholar] [CrossRef]
- Wang, S.-D.; Scrivener, K.L.; Pratt, P.L. Factors affecting the strength of alkali-activated slag. Cem. Concr. Res. 1994, 24, 1033–1043. [Google Scholar] [CrossRef]
- Xie, Z.; Xi, Y. Hardening mechanisms of an alkaline-activated class F fly ash. Cem. Concr. Res. 2001, 31, 1245–1249. [Google Scholar] [CrossRef]
- Wang, Q.; Bian, H.; Li, M.; Dai, M.; Chen, Y.; Jiang, H.; Zhang, Q.; Dong, F.; Huang, J.; Ding, Z. Effects of a Water-Glass Module on Compressive Strength, Size Effect and Stress-Strain Behavior of Geopolymer Recycled Aggregate Concrete. Crystals 2022, 12, 218. [Google Scholar] [CrossRef]
- Davidovits, J. Geopolymers: Inorganic polymeric new materials. J. Therm. Anal. Calorim. 1991, 37, 1633–1656. [Google Scholar] [CrossRef]
- He, J.; Zhang, J.; Yu, Y.; Zhang, G. The strength and microstructure of two geopolymers derived from metakaolin and red mud-fly ash admixture: A comparative study. Constr. Build. Mater. 2012, 30, 80–91. [Google Scholar] [CrossRef]
- Murayama, N.; Yamamoto, H.; Shibata, J. Mechanism of zeolite synthesis from coal fly ash by alkali hydrothermal reaction. Int. J. Miner. Process. 2002, 64, 1–17. [Google Scholar] [CrossRef]
- Qiao, W.; Khishe, M.; Ravakhah, S. Underwater targets classification using local wavelet acoustic pattern and Multi-Layer Perceptron neural network optimized by modified Whale Optimization Algorithm. Ocean Eng. 2021, 219, 108415. [Google Scholar] [CrossRef]
- Qiao, W.; Moayedi, H.; Foong, L.K. Nature-inspired hybrid techniques of IWO, DA, ES, GA, and ICA, validated through a k-fold validation process predicting monthly natural gas consumption. Energy Build. 2020, 217, 110023. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]


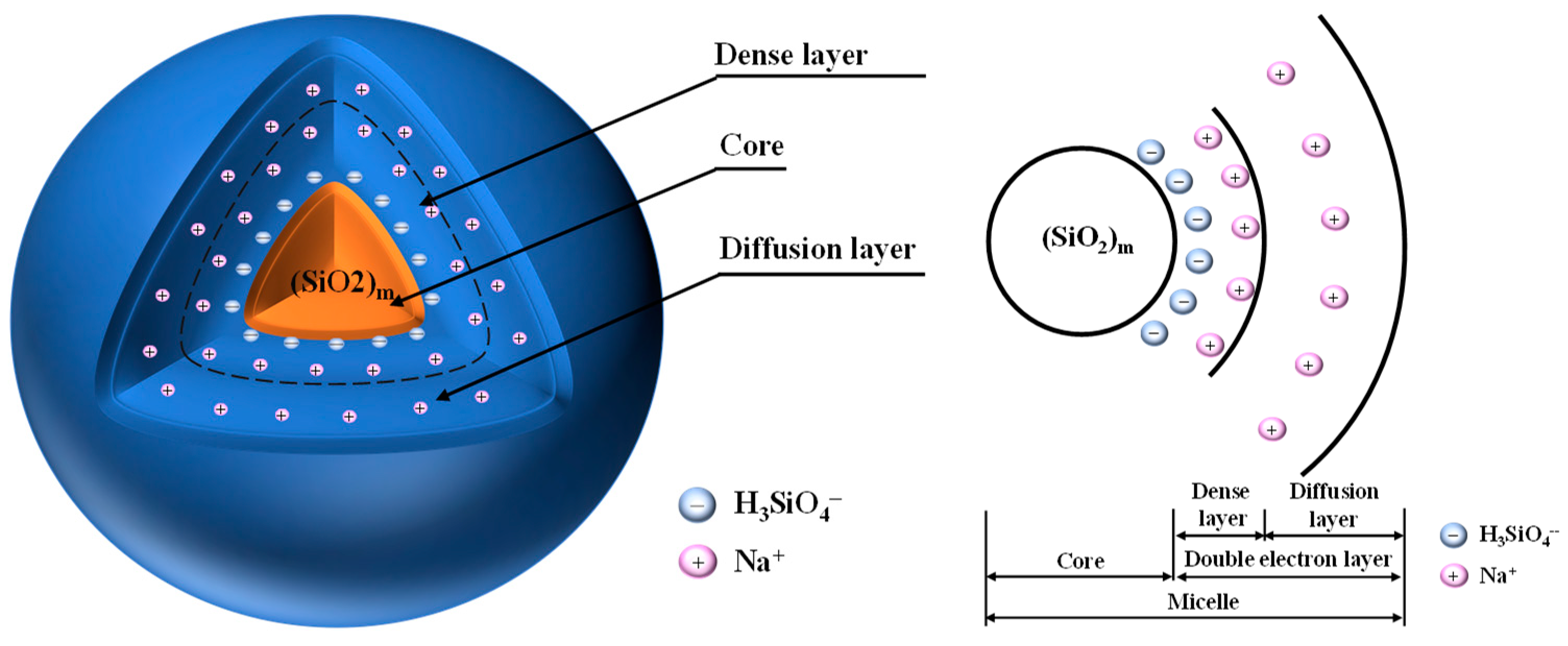


| Oxide Content | SiO2 | Al2O3 | Fe2O3 | CaO | TiO2 | SO3 | K2O | MgO | Na2O |
|---|---|---|---|---|---|---|---|---|---|
| FA (wt %) | 50.94 | 36.20 | 3.93 | 3.63 | 1.36 | 1.26 | 1.11 | 0.52 | 0.41 |
| Slag (wt %) | 32.73 | 14.61 | 0.27 | 36.50 | 0.68 | 2.45 | 0.43 | 7.87 | 0.28 |
| Materials | Density (g/cm3) | Specific Surface Area (m2/g) | Loss on Ignition /% |
|---|---|---|---|
| FA | 2.42 | 0.43 | 1.51 |
| Slag | 3.00 | 0.60 | 2.30 |
| SF | 2.35 | 17.00 | 2.43 |
| No. | Ae/% | FA | SF | Slag | Sand | NaOH | Waterglass | Water |
|---|---|---|---|---|---|---|---|---|
| A3 | 3 | 105 | 180 | 315 | 1200 | 14.90 | 75.06 | 209 |
| A6 | 6 | 29.79 | 150.11 | 179 | ||||
| A9 | 9 | 44.69 | 225.17 | 148 | ||||
| A12 | 12 | 59.59 | 300.22 | 117 | ||||
| A15 | 15 | 74.49 | 375.28 | 86 |
| No. | Mo | FA | SF | Slag | Sand | NaOH | Waterglass | Water |
|---|---|---|---|---|---|---|---|---|
| M10 | 1.0 | 105 | 180 | 315 | 1200 | 48.86 | 187.64 | 168 |
| M12 | 1.2 | 44.69 | 225.17 | 148 | ||||
| M14 | 1.4 | 40.53 | 262.69 | 128 | ||||
| M16 | 1.6 | 36.36 | 300.22 | 108 | ||||
| M18 | 1.8 | 32.20 | 337.75 | 88 |
| Compound | Standard Concentration | Artificial Seawater Concentration |
|---|---|---|
| NaCl | 24.53 | 73.59 |
| MgCl2·6H2O | 11.11 | 33.33 |
| Na2SO4 | 4.09 | 12.27 |
| CaCl2 | 1.16 | 3.48 |
| KCl | 0.695 | 2.09 |
| NaHCO3 | 0.201 | 0.60 |
| Experiment No. | Influencing Factors(xi) | Measured Compressive Strength (yi)/MPa | |
|---|---|---|---|
| Immersion Time/d | Ae/% | ||
| 1 | 0 | 3 | 41.08 |
| 2 | 0 | 6 | 69.27 |
| 3 | 0 | 9 | 74.19 |
| 4 | 0 | 12 | 74.09 |
| 5 | 0 | 15 | 67.41 |
| 6 | 30 | 3 | 44.90 |
| 7 | 30 | 6 | 75.83 |
| … | … | … | … |
| 48 | 270 | 9 | 66.68 |
| 49 | 270 | 12 | 65.38 |
| 50 | 270 | 15 | 52.44 |
| Experiment No. | Influencing Factors(xi) | Measured Compressive Strength (yi)/MPa | |
|---|---|---|---|
| Immersion Time/d | Mo | ||
| 1 | 0 | 1 | 76.95 |
| 2 | 0 | 1.2 | 74.19 |
| 3 | 0 | 1.4 | 74.35 |
| 4 | 0 | 1.6 | 69.55 |
| 5 | 0 | 1.8 | 68.54 |
| 6 | 30 | 1 | 81.18 |
| 7 | 30 | 1.2 | 78.73 |
| … | … | … | … |
| 48 | 270 | 1.4 | 67.23 |
| 49 | 270 | 1.6 | 62.57 |
| 50 | 270 | 1.8 | 54.83 |
| No. | Indicators | Seawater Immersion Time/d | |||||
|---|---|---|---|---|---|---|---|
| 0 | 30 | 60 | 120 | 180 | 270 | ||
| A3 | Mass/g | 754.22 | 763.52 | 765.67 | 769.50 | 760.10 | 762.80 |
| Loss rate/% | - | 1.23 | 0.28 | 0.50 | −1.22 | 0.36 | |
| A6 | Mass/g | 744.92 | 759.67 | 760.07 | 764.40 | 760.30 | 759.80 |
| Loss rate/% | - | 1.98 | 0.05 | 0.57 | −0.54 | −0.07 | |
| A9 | Mass/g | 746.20 | 750.45 | 768.42 | 769.70 | 762.60 | 763.40 |
| Loss rate/% | - | 0.57 | 2.39 | 0.17 | −0.92 | 0.10 | |
| A12 | Mass/g | 735.37 | 738.42 | 757.55 | 756.70 | 756.10 | 748.80 |
| Loss rate/% | - | 0.41 | 2.59 | −0.11 | −0.08 | −0.97 | |
| A15 | Mass/g | 738.98 | 744.80 | 754.68 | 754.30 | 742.60 | 738.92 |
| Loss rate/% | - | 0.79 | 1.33 | −0.05 | −1.55 | −0.50 | |
| No. | Indicators | Seawater Immersion Time/d | |||||
|---|---|---|---|---|---|---|---|
| 0 | 30 | 60 | 90 | 180 | 270 | ||
| M10 | Mass/g | 755.37 | 757.38 | 761.20 | 763.80 | 758.60 | 761.20 |
| Loss rate/% | - | 0.27 | 0.50 | 0.34 | −0.68 | 0.34 | |
| M12 | Mass/g | 746.20 | 750.45 | 768.42 | 769.70 | 762.60 | 763.40 |
| Loss rate/% | - | 0.57 | 2.39 | 0.17 | −0.92 | 0.10 | |
| M14 | Mass/g | 751.67 | 760.28 | 767.67 | 760.80 | 767.20 | 760.80 |
| Loss rate/% | - | 1.15 | 0.97 | −0.89 | 0.84 | −0.83 | |
| M16 | Mass/g | 743.35 | 754.28 | 760.47 | 755.80 | 760.50 | 761.70 |
| Loss rate/% | - | 1.47 | 0.82 | −0.61 | 0.62 | 0.16 | |
| M18 | Mass/g | 733.93 | 749.40 | 746.65 | 740.60 | 738.40 | 733.80 |
| Loss rate/% | - | 2.11 | −0.37 | −0.81 | −0.30 | −0.62 | |
| Sample | Training Set | Testing Set | ||
|---|---|---|---|---|
| MSE | R2 | MSE | R2 | |
| A | 0.00103 | 0.9709 | 0.00118 | 0.9974 |
| M | 0.00200 | 0.9919 | 0.00224 | 0.9966 |
| Sample | Penalty Factor C | Kernel Function Variance g |
|---|---|---|
| A | 1024 | 0.0884 |
| M | 90.5097 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Du, K.; Wu, C.; Tao, M.; Zhao, R. Time-Varying Pattern and Prediction Model for Geopolymer Mortar Performance under Seawater Immersion. Materials 2023, 16, 1244. https://doi.org/10.3390/ma16031244
Wu Y, Du K, Wu C, Tao M, Zhao R. Time-Varying Pattern and Prediction Model for Geopolymer Mortar Performance under Seawater Immersion. Materials. 2023; 16(3):1244. https://doi.org/10.3390/ma16031244
Chicago/Turabian StyleWu, Yingjie, Kun Du, Chengqing Wu, Ming Tao, and Rui Zhao. 2023. "Time-Varying Pattern and Prediction Model for Geopolymer Mortar Performance under Seawater Immersion" Materials 16, no. 3: 1244. https://doi.org/10.3390/ma16031244
APA StyleWu, Y., Du, K., Wu, C., Tao, M., & Zhao, R. (2023). Time-Varying Pattern and Prediction Model for Geopolymer Mortar Performance under Seawater Immersion. Materials, 16(3), 1244. https://doi.org/10.3390/ma16031244






