Application of the Improved POA-RF Model in Predicting the Strength and Energy Absorption Property of a Novel Aseismic Rubber-Concrete Material
Abstract
:1. Introduction
2. Research Significance
3. Experiment of a Novel Aseismic Concrete Material
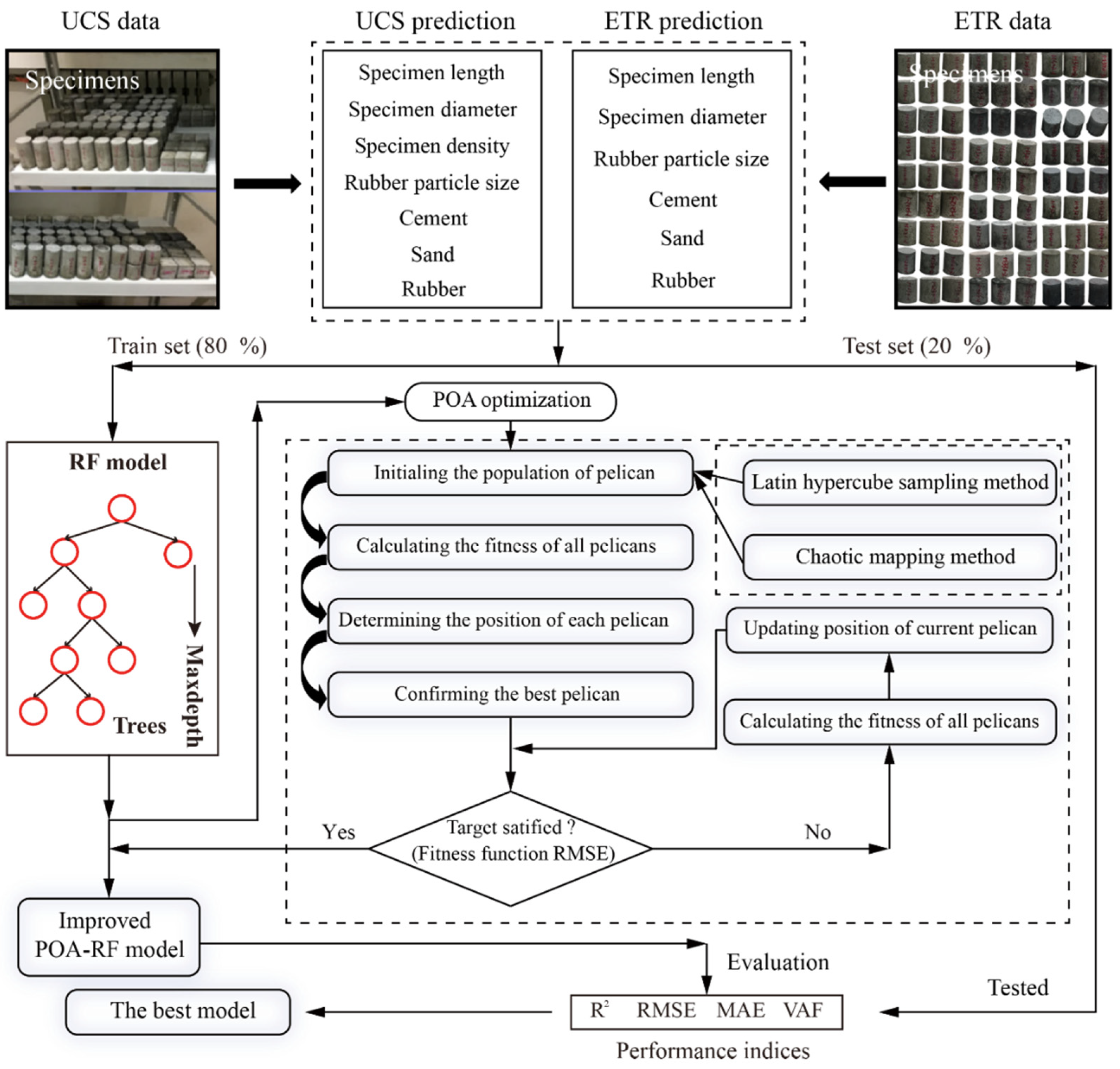
4. Methodologies
4.1. Random Forest
4.2. Improved Pelican Optimization Algorithm
4.2.1. Pelican Optimization Algorithm
4.2.2. Optimization Methods
Chaotic Mapping Method (CM)
Latin Hypercube Sampling Method (LHS)
4.3. A Novel Combination of the IPOA and RF Model
5. Performance Evaluation
6. Results and Discussion
6.1. The Development Results of the Proposed Models
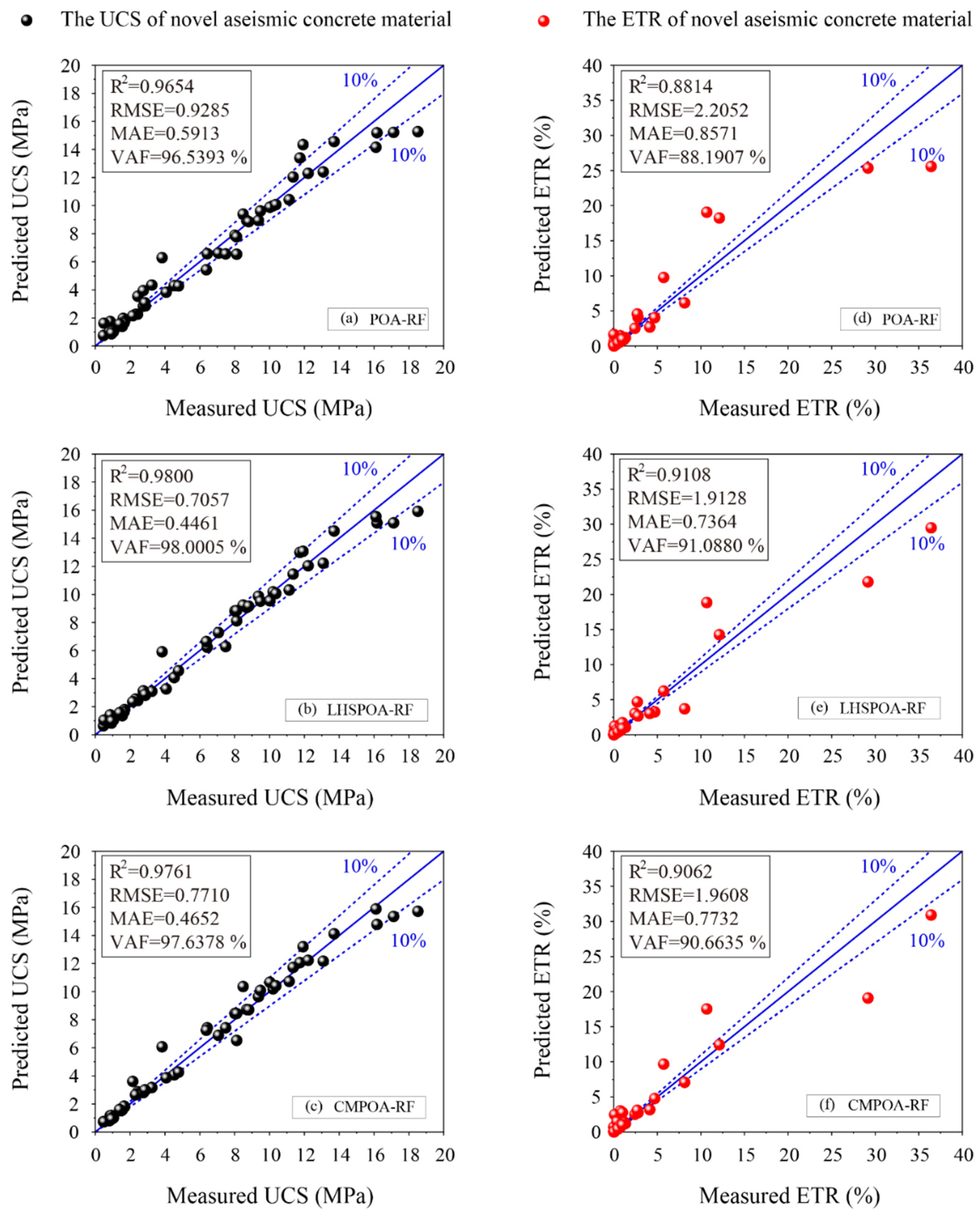
6.2. Performance Evaluation for the UCS and the ETR Prediction
6.3. Sensitively Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Dai, Q.; Si, R.; Guo, S. Investigation of properties and performances of Polyvinyl Alcohol (PVA) fiber-reinforced rubber concrete. Constr. Build. Mater. 2018, 193, 631–642. [Google Scholar] [CrossRef]
- Jokar, F.; Khorram, M.; Karimi, G.; Hataf, N. Experimental investigation of mechanical properties of crumbed rubber concrete containing natural zeolite. Constr. Build. Mater. 2019, 208, 651–658. [Google Scholar] [CrossRef]
- Pham, T.M.; Elchalakani, M.; Karrech, A.; Hao, H. Axial impact behavior and energy absorption of rubberized concrete with/without fiber-reinforced polymer confinement. Int. J. Prot. Struct. 2019, 10, 154–173. [Google Scholar] [CrossRef]
- Hu, S.; Tang, H.; Han, S. Energy absorption characteristics of PVC coarse aggregate concrete under impact load. Int. J. Concr. Struct. Mater. 2021, 15, 26. [Google Scholar] [CrossRef]
- Maho, B.; Sukontasukkul, P.; Jamnam, S.; Yamaguchi, E.; Fujikake, K.; Banthia, N. Effect of rubber insertion on impact behavior of multilayer steel fiber reinforced concrete bulletproof panel. Constr. Build. Mater. 2019, 216, 476–484. [Google Scholar] [CrossRef]
- Eisa, A.S.; Elshazli, M.T.; Nawar, M.T. Experimental investigation on the effect of using crumb rubber and steel fibers on the structural behavior of reinforced concrete beams. Constr. Build. Mater. 2020, 252, 119078. [Google Scholar] [CrossRef]
- Mei, X.; Sheng, Q.; Cui, Z.; Luo, Q. Experimental study on the energy absorption characteristics of viscoelastic damping layers. IOP Conf. Ser. Earth Environ. Sci. 2021, 861, 022026. [Google Scholar] [CrossRef]
- Gerges, N.N.; Issa, C.A.; Fawaz, S.A. Rubber concrete: Mechanical and dynamical properties. Case Stud. Constr. Mater. 2018, 9, e00184. [Google Scholar] [CrossRef]
- Huang, W.; Huang, X.; Xing, Q.; Zhou, Z. Strength reduction factor of crumb rubber as fine aggregate replacement in concrete. J. Build. Eng. 2020, 32, 101346. [Google Scholar] [CrossRef]
- Pham, T.M.; Chen, W.; Khan, A.M.; Hao, H.; Elchalakani, M.; Tran, T.M. Dynamic compressive properties of lightweight rubberized concrete. Constr. Build. Mater. 2020, 238, 117705. [Google Scholar] [CrossRef]
- Mei, X.; Li, C.; Sheng, Q.; Cui, Z.; Zhou, J.; Dias, D. Development of a hybrid artificial intelligence model to predict the uniaxial compressive strength of a new aseismic layer made of rubber-sand concrete. Mech. Adv. Mater. Struct. 2022, 1–18. [Google Scholar] [CrossRef]
- Bachir, R.; Mohammed, A.M.S.; Habib, T. Using artificial neural networks approach to estimate compressive strength for rubberized concrete. Period. Polytech. Civ. Eng. 2018, 62, 858–865. [Google Scholar] [CrossRef]
- Hadzima-Nyarko, M.; Nyarko, E.K.; Ademović, N.; Miličević, I.; Kalman Šipoš, T. Modelling the influence of waste rubber on compressive strength of concrete by artificial neural networks. Materials 2019, 12, 561. [Google Scholar] [CrossRef] [PubMed]
- Jalal, M.; Jalal, H. Behavior assessment, regression analysis and support vector machine (SVM) modeling of waste tire rubberized concrete. J. Clean. Prod. 2020, 273, 122960. [Google Scholar] [CrossRef]
- Gregori, A.; Castoro, C.; Venkiteela, G. Predicting the compressive strength of rubberized concrete using artificial intelligence methods. Sustainability 2021, 13, 7729. [Google Scholar] [CrossRef]
- Gupta, T.; Patel, K.A.; Siddique, S.; Sharma, R.K.; Chaudhary, S. Prediction of mechanical properties of rubberised concrete exposed to elevated temperature using ANN. Measurement 2019, 147, 106870. [Google Scholar] [CrossRef]
- Zhang, Y.; Aslani, F.; Lehane, B. Compressive strength of rubberized concrete: Regression and GA-BPNN approaches using ultrasonic pulse velocity. Constr. Build. Mater. 2021, 307, 124951. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, J.; Liu, C.; Zheng, J. Prediction of rubber fiber concrete strength using extreme learning machine. Front. Mater. 2021, 7, 582635. [Google Scholar] [CrossRef]
- Han, B.; Wu, Y.; Liu, L. Prediction and uncertainty quantification of compressive strength of high-strength concrete using optimized machine learning algorithms. Struct. Concr. 2022, 23, 3772–3785. [Google Scholar] [CrossRef]
- Dat, L.T.M.; Dmitrieva, T.L.; Duong, V.N.; Canh, D.T.N. An Artificial intelligence approach for predicting compressive strength of eco-friendly concrete containing waste tire rubber. IOP Conf. Ser. Earth Environ. Sci. 2020, 612, 012029. [Google Scholar] [CrossRef]
- Kovačević, M.; Lozančić, S.; Nyarko, E.K.; Hadzima-Nyarko, M. Modeling of compressive strength of self-compacting rubberized concrete using machine learning. Materials 2021, 14, 4346. [Google Scholar] [CrossRef]
- Hadzima-Nyarko, M.; Nyarko, E.K.; Lu, H.; Zhu, S. Machine learning approaches for estimation of compressive strength of concrete. Eur. Phys. J. Plus 2020, 135, 682. [Google Scholar] [CrossRef]
- Ahmad, A.; Ostrowski, K.A.; Maślak, M.; Farooq, F.; Mehmood, I.; Nafees, A. Comparative study of supervised machine learning algorithms for predicting the compressive strength of concrete at high temperature. Materials 2021, 14, 4222. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Li, C.; Zhang, S. Application of Six Metaheuristic Optimization Algorithms and Random Forest in the uniaxial compressive strength of rock prediction. Appl. Soft Comput. 2022, 131, 109729. [Google Scholar] [CrossRef]
- Farooq, F.; Nasir Amin, M.; Khan, K.; Rehan Sadiq, M.; Javed, M.F.; Aslam, F.; Alyousef, R. A comparative study of random forest and genetic engineering programming for the prediction of compressive strength of high strength concrete (HSC). Appl. Sci. 2020, 10, 7330. [Google Scholar] [CrossRef]
- Mai, H.V.T.; Nguyen, T.A.; Ly, H.B.; Tran, V.Q. Prediction compressive strength of concrete containing GGBFS using random forest model. Adv. Civ. Eng. 2021, 2021, 6671448. [Google Scholar] [CrossRef]
- Sun, Y.; Li, G.; Zhang, J.; Qian, D. Prediction of the strength of rubberized concrete by an evolved random forest model. Adv. Civ. Eng. 2019, 2019, 5198583. [Google Scholar] [CrossRef]
- Huang, X.Y.; Wu, K.Y.; Wang, S.; Lu, T.; Lu, Y.F.; Deng, W.C.; Li, H.M. Compressive Strength Prediction of Rubber Concrete Based on Artificial Neural Network Model with Hybrid Particle Swarm Optimization Algorithm. Materials 2022, 15, 3934. [Google Scholar] [CrossRef]
- Shariati, M.; Mafipour, M.S.; Ghahremani, B.; Azarhomayun, F.; Ahmadi, M.; Trung, N.T.; Shariati, A. A novel hybrid extreme learning machine–grey wolf optimizer (ELM-GWO) model to predict compressive strength of concrete with partial replacements for cement. Eng. Comput. 2020, 38, 757–779. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Cao, M.T. Estimating strength of rubberized concrete using evolutionary multivariate adaptive regression splines. J. Civ. Eng. Manag. 2016, 22, 711–720. [Google Scholar] [CrossRef]
- Cook, R.; Lapeyre, J.; Ma, H.; Kumar, A. Prediction of compressive strength of concrete: Critical comparison of performance of a hybrid machine learning model with standalone models. J. Mater. Civ. Eng. 2019, 31, 1–15. [Google Scholar] [CrossRef]
- Zhou, J.; Dai, Y.; Du, K.; Khandelwal, M.; Li, C.; Qiu, Y. COSMA-RF: New intelligent model based on chaos optimized slime mould algorithm and random forest for estimating the peak cutting force of conical picks. Transp. Geotech. 2022, 36, 100806. [Google Scholar] [CrossRef]
- Mhaya, A.M.; Huseien, G.F.; Abidin, A.R.Z.; Ismail, M. Long-term mechanical and durable properties of waste tires rubber crumbs replaced GBFS modified concretes. Constr. Build. Mater. 2020, 256, 119505. [Google Scholar] [CrossRef]
- Keerio, M.A.; Abbasi, S.A.; Kumar, A.; Bheel, N.; Tashfeen, M. Effect of silica fume as cementitious material and waste glass as fine aggregate replacement constituent on selected properties of concrete. Silicon 2020, 14, 165–176. [Google Scholar] [CrossRef]
- Adnan, H.M.; Dawood, A.O. Recycling of plastic box waste in the concrete mixture as a percentage of fine aggregate. Constr. Build. Mater. 2021, 284, 122666. [Google Scholar] [CrossRef]
- Arulmoly, B.; Konthesingha, C. Pertinence of alternative fine aggregates for concrete and mortar: A brief review on river sand substitutions. Aust. J. Civ. Eng. 2021, 20, 272–307. [Google Scholar] [CrossRef]
- Mei, X.; Sheng, Q.; Cui, Z.; Zhang, M.; Dias, D. Experimental investigation on the mechanical and damping properties of rubber-sand-concrete prepared with recycled waste tires for aseismic isolation layer. Soil Dyn. Earthq. Eng. 2023, 165, 107718. [Google Scholar] [CrossRef]
- Zhang, J.; Li, D.; Wang, Y. Predicting uniaxial compressive strength of oil palm shell concrete using a hybrid artificial intelligence model. J. Build. Eng. 2020, 30, 101282. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, S.; Qiu, Y. Optimization of random forest through the use of MVO, GWO and MFO in evaluating the stability of underground entry-type excavations. Tunn. Undergr. Space Technol. 2022, 124, 104494. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Pelican optimization algorithm: A novel nature-inspired algorithm for engineering applications. Sensors 2022, 22, 855. [Google Scholar] [CrossRef]
- Anderson, J.G. Foraging behavior of the American white pelican (Pelecanus erythrorhyncos) in western Nevada. Colon. Waterbirds 1991, 14, 166–172. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Abd Elaziz, M.; Lu, S. Chaotic opposition-based grey-wolf optimization algorithm based on differential evolution and disruption operator for global optimization. Expert Syst. Appl. 2018, 108, 1–27. [Google Scholar] [CrossRef]
- Long, W.; Cai, S.H.; Jiao, J.J. Hybrid grey wolf optimization algorithm for high-dimensional optimization. Control Decis. 2016, 31, 1991–1997. [Google Scholar]
- Pradhan, M.; Roy, P.K.; Pal, T. Oppositional based grey wolf optimization algorithm for economic dispatch problem of power system. Ain Shams Eng. J. 2018, 9, 2015–2025. [Google Scholar] [CrossRef]
- Muangkote, N.; Sunat, K.; Chiewchanwattana, S. An improved grey wolf optimizer for training q-Gaussian Radial Basis Functional-link nets. In Proceedings of the 2014 International Computer Science and Engineering Conference (ICSEC), Khon Kaen, Thailand, 30 July–1 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 209–214. [Google Scholar]
- Luo, J.; Chen, H.; Xu, Y.; Huang, H.; Zhao, X. An improved grasshopper optimization algorithm with application to financial stress prediction. Appl. Math. Modell. 2018, 64, 654–668. [Google Scholar] [CrossRef]
- Hu, G.; Xu, Z.; Wang, G.; Zeng, B.; Liu, Y.; Lei, Y. Forecasting energy consumption of long-distance oil products pipeline based on improved fruit fly optimization algorithm and support vector regression. Energy 2021, 224, 120153. [Google Scholar] [CrossRef]
- Zhang, Q.; Fang, L.; Zhao, Y. Double subgroups fruit fly optimization algorithm with characteristics of Levy flight. J. Comput. Appl. 2015, 35, 1348. [Google Scholar]
- Tian, D.; Zhao, X.; Shi, Z. Chaotic particle swarm optimization with sigmoid-based acceleration coefficients for numerical function optimization. Swarm Evolut. Comput. 2019, 51, 100573. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, C.; Zhang, M.; Yang, F.; Gao, L. A modified comprehensive learning particle swarm optimizer and its application in cylindricity error evaluation problem. Math. Biosci. Eng. 2019, 16, 1190–1209. [Google Scholar] [CrossRef] [PubMed]
- Kaur, G.; Arora, S. Chaotic whale optimization algorithm. J. Comput. Des. Eng. 2018, 5, 275–284. [Google Scholar] [CrossRef]
- Rosli, S.J.; Rahim, H.A.; Abdul Rani, K.N.; Ngadiran, R.; Ahmad, R.B.; Yahaya, N.Z.; Andrew, A.M. A hybrid modified method of the sine cosine algorithm using Latin hypercube sampling with the cuckoo search algorithm for optimization problems. Electronics 2020, 9, 1786. [Google Scholar] [CrossRef]
- Shukla, A.K.; Singh, P.; Vardhan, M. An adaptive inertia weight teaching-learning-based optimization algorithm and its applications. Appl. Math. Modell. 2020, 77, 309–326. [Google Scholar] [CrossRef]
- Yin, B.; Wang, C.; Abza, F. New brain tumor classification method based on an improved version of whale optimization algorithm. Biomed. Signal Process. Control 2020, 56, 101728. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J.; Khandelwal, M.; Zhang, X.; Monjezi, M.; Qiu, Y. Six novel hybrid extreme learning machine–swarm intelligence optimization (ELM–SIO) models for predicting backbreak in open-pit blasting. Nat. Resour. Res. 2022, 31, 3017–3039. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J.; Tao, M.; Du, K.; Wang, S.; Armaghani, D.J.; Mohamad, E.T. Developing hybrid ELM-ALO, ELM-LSO and ELM-SOA models for predicting advance rate of TBM. Transp. Geotech. 2022, 36, 100819. [Google Scholar] [CrossRef]
- Rebouh, R.; Boukhatem, B.; Ghrici, M.; Tagnit-Hamou, A. A practical hybrid NNGA system for predicting the compressive strength of concrete containing natural pozzolan using an evolutionary structure. Constr. Build. Mater. 2017, 149, 778–789. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J.; Dias, D.; Gui, Y. A Kernel Extreme Learning Machine-Grey Wolf Optimizer (KELM-GWO) Model to Predict Uniaxial Compressive Strength of Rock. Appl. Sci. 2022, 12, 8468. [Google Scholar] [CrossRef]
- Zhang, J.; Dias, D.; An, L.; Li, C. Applying a novel slime mould algorithm-based artificial neural network to predict the settlement of a single footing on a soft soil reinforced by rigid inclusions. Mech. Adv. Mater. Struct. 2022, 1–16. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, Y.; Armaghani, D.J.; Zhang, W.; Li, C.; Zhu, S.; Tarinejad, R. Predicting TBM penetration rate in hard rock condition: A comparative study among six XGB-based metaheuristic techniques. Geosci. Front. 2021, 12, 101091. [Google Scholar] [CrossRef]
- Zhou, J.; Li, C.; Arslan, C.A.; Hasanipanah, M.; Bakhshandeh Amnieh, H. Performance evaluation of hybrid FFA-ANFIS and GA-ANFIS models to predict particle size distribution of a muck-pile after blasting. Eng. Comput. 2021, 37, 265–274. [Google Scholar] [CrossRef]
- Nafees, A.; Khan, S.; Javed, M.F.; Alrowais, R.; Mohamed, A.M.; Mohamed, A.; Vatin, N.I. Forecasting the Mechanical Properties of Plastic Concrete Employing Experimental Data Using Machine Learning Algorithms: DT, MLPNN, SVM, and RF. Polymers 2022, 14, 1583. [Google Scholar] [CrossRef] [PubMed]
- Pianosi, F.; Wagener, T. A simple and efficient method for global sensitivity analysis based on cumulative distribution functions. Environ. Modell. Softw. 2015, 67, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Pianosi, F.; Wagener, T. Distribution-based sensitivity analysis from a generic input-output sample. Environ. Modell. Softw. 2018, 108, 197–207. [Google Scholar] [CrossRef] [Green Version]








| Procedures | Description |
|---|---|
| Step 1—Dosing | Mixing the rubber and river sand with the cement in pre-designed proportions and thoroughly stirring. |
| Step 2—Concreting | Stirring the mixture for five minutes and quickly pouring it into the mold. |
| Step 3—Demolding | After 24 h, separating the specimen and polishing it to the specified specification. |
| Step 4—Maintaining | Maintaining all specimens at required temperature (20 degrees) and humidity (95 %). |
| Step 5—Testing | After 28 days, testing 140 specimens in the laboratory. |
| RM (%) | SM (%) | CM (%) | RPS (mm) |
|---|---|---|---|
| 0 | 100 | 40 | / |
| 10 | 90 | 30 | 1~2 |
| 10 | 90 | 40 | 0.5~1 |
| 10 | 90 | 40 | 0.075~0.25 |
| 10 | 90 | 50 | 0.25~0.5 |
| 10 | 90 | 60 | 0.075~0.25 |
| 30 | 70 | 30 | 0.5~1 |
| 30 | 70 | 40 | 1~2 |
| 30 | 70 | 40 | 0.075~0.25 |
| 30 | 70 | 50 | 0.075~0.25 |
| 30 | 70 | 60 | 0.25~0.5 |
| 50 | 50 | 30 | 0.25~0.5 |
| 50 | 50 | 30 | 0.075~0.25 |
| 50 | 50 | 40 | 1~2 |
| 50 | 50 | 40 | 0.5~1 |
| 50 | 50 | 40 | 0.25~0.5 |
| 50 | 50 | 40 | 0.075~0.25 |
| 50 | 50 | 50 | 1~2 |
| 50 | 50 | 50 | 0.075~0.25 |
| 50 | 50 | 60 | 0.5~1 |
| 50 | 50 | 60 | 0.075~0.25 |
| 70 | 30 | 30 | 0.075~0.25 |
| 70 | 30 | 40 | 0.25~0.5 |
| 70 | 30 | 40 | 0.075~0.25 |
| 70 | 30 | 50 | 0.5~1 |
| 70 | 30 | 60 | 1~2 |
| 100 | 0 | 40 | 0.075~0.25 |
| Variables | Sign | Unit | Min | Max | Mean | Median | St. D |
|---|---|---|---|---|---|---|---|
| Rubber | R | g | 15.66 | 90.83 | 61.21 | 65.85 | 22.76 |
| River sand | S | g | 33.26 | 207.63 | 92.82 | 74.99 | 50.52 |
| Cement | C | g | 50.52 | 236.10 | 129.47 | 129.38 | 51.26 |
| Rubber particle size | RPS | mm | 0.16 | 1.50 | 0.56 | 0.38 | 0.48 |
| Specimen mass | M | g | 168.40 | 393.50 | 283.49 | 279.25 | 65.71 |
| Specimen density | r | g/cm3 | 0.98 | 50.59 | 16.09 | 1.72 | 22.42 |
| Specimen diameter | D | mm | 48.99 | 50.59 | 50.11 | 50.15 | 0.29 |
| Specimen length | L | mm | 95.52 | 102.67 | 99.05 | 99.27 | 1.20 |
| Uniaxial compressive strength | UCS | MPa | 0.47 | 18.52 | 5.82 | 4.11 | 5.02 |
| Variables | Sign | Unit | Min | Max | Mean | Median | St. D |
|---|---|---|---|---|---|---|---|
| Rubber | R | g | 7.28 | 42.53 | 29.11 | 30.38 | 10.91 |
| River sand | S | g | 16.60 | 97.96 | 44.35 | 36.90 | 23.64 |
| Cement | C | g | 24.36 | 111.48 | 62.84 | 60.59 | 23.65 |
| Rubber particle size | RPS | mm | 0.16 | 1.50 | 0.56 | 0.38 | 0.48 |
| Specimen mass | M | g | 81.20 | 186.70 | 136.29 | 138.00 | 29.59 |
| Specimen density | r | g/cm3 | 0.91 | 1.95 | 1.45 | 1.46 | 0.30 |
| Specimen diameter | D | mm | 48.47 | 49.98 | 49.48 | 49.48 | 0.30 |
| Specimen length | L | mm | 46.46 | 50.15 | 48.74 | 48.86 | 0.67 |
| Energy transmission rate | ETR | % | 0.00 | 36.43 | 2.32 | 0.13 | 6.37 |
| Population | Fitness (RMSE) | |||||
|---|---|---|---|---|---|---|
| UCS | ETR | |||||
| POA-RF | LHSPOA-RF | CMPOA-RF | POA-RF | LHSPOA-RF | CMPOA-RF | |
| 20 | 0.07503 | 0.06054 | 0.06338 | 0.16103 | 0.13669 | 0.14078 |
| 40 | 0.08197 | 0.06505 | 0.06265 | 0.16081 | 0.13484 | 0.14024 |
| 60 | 0.07419 | 0.06329 | 0.06277 | 0.16199 | 0.13340 | 0.14158 |
| 80 | 0.08340 | 0.05929 | 0.06154 | 0.16085 | 0.13294 | 0.14239 |
| 100 | 0.08368 | 0.06324 | 0.06159 | 0.16083 | 0.13671 | 0.14238 |
| Best hyperparameters combination | ||||||
| Nt | 15 | 22 | 17 | 18 | 13 | 14 |
| Maxdepth | 2 | 2 | 2 | 1 | 1 | 1 |
| Models | UCS Prediction | |||||||
| Performance Indices | ||||||||
| R2 | Score | RMSE | Score | MAE | Score | VAF (%) | Score | |
| POA-RF | 0.9654 | 1 | 0.9285 | 1 | 0.5913 | 1 | 96.5393 | 1 |
| LHSPOA-RF | 0.9800 | 3 | 0.7057 | 3 | 0.4461 | 3 | 98.0005 | 3 |
| CMPOA-RF | 0.9761 | 2 | 0.7710 | 2 | 0.4652 | 2 | 97.6378 | 2 |
| Models | ETR Prediction | |||||||
| Performance Indices | ||||||||
| R2 | Score | RMSE | Score | MAE | Score | VAF (%) | Score | |
| POA-RF | 0.8814 | 1 | 2.2052 | 1 | 0.8571 | 1 | 88.1907 | 1 |
| LHSPOA-RF | 0.9108 | 3 | 1.9128 | 3 | 0.7364 | 3 | 91.0880 | 3 |
| CMPOA-RF | 0.9062 | 2 | 1.9608 | 2 | 0.7732 | 2 | 90.6635 | 2 |
| Models | UCS Prediction | |||||||
| Performance Indices | ||||||||
| R2 | Score | RMSE | Score | MAE | Score | VAF (%) | Score | |
| POA-RF | 0.9663 | 1 | 0.8865 | 1 | 0.6060 | 1 | 96.6339 | 1 |
| LHSPOA-RF | 0.9857 | 3 | 0.5781 | 3 | 0.4233 | 3 | 98.5909 | 3 |
| CMPOA-RF | 0.9726 | 2 | 0.7995 | 2 | 0.5595 | 2 | 97.2639 | 2 |
| Models | ETR Prediction | |||||||
| Performance Indices | ||||||||
| R2 | Score | RMSE | Score | MAE | Score | VAF (%) | Score | |
| POA-RF | 0.8790 | 1 | 2.1400 | 1 | 1.2675 | 1 | 87.9153 | 1 |
| LHSPOA-RF | 0.9065 | 3 | 1.8814 | 3 | 0.9913 | 3 | 91.3652 | 3 |
| CMPOA-RF | 0.9047 | 2 | 1.8993 | 2 | 1.0537 | 2 | 90.5980 | 2 |
| Models | UCS Prediction | Hyperparameter | |||
| Performance Indices | |||||
| R2 | RMSE | MAE | VAF (%) | ||
| BPNN | 0.8782 | 1.6859 | 1.1049 | 88.1409 | Nh = 1; Ne = 8 |
| SVR | 0.9406 | 1.1779 | 0.8091 | 94.0956 | Pc = 64; k1 = 0.5 |
| ELM | 0.9334 | 1.2464 | 1.0643 | 93.6570 | Nn = 40 |
| KELM | 0.9356 | 1.2257 | 0.8654 | 93.5694 | Rc = 32; k2 = 0.5 |
| Models | ETR Prediction | Hyperparameter | |||
| Performance Indices | |||||
| R2 | RMSE | MAE | VAF (%) | ||
| BPNN | 0.7926 | 2.8016 | 1.5106 | 79.2861 | Nh = 1; Ne = 6 |
| SVR | 0.7838 | 2.8604 | 1.5438 | 78.4293 | Pc = 35; k1 = 0.25 |
| ELM | 0.6641 | 3.5650 | 2.7334 | 69.6411 | Nn = 60 |
| KELM | 0.8388 | 2.4700 | 1.3255 | 83.8904 | Rc = 55; k2 = 0.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, X.; Cui, Z.; Sheng, Q.; Zhou, J.; Li, C. Application of the Improved POA-RF Model in Predicting the Strength and Energy Absorption Property of a Novel Aseismic Rubber-Concrete Material. Materials 2023, 16, 1286. https://doi.org/10.3390/ma16031286
Mei X, Cui Z, Sheng Q, Zhou J, Li C. Application of the Improved POA-RF Model in Predicting the Strength and Energy Absorption Property of a Novel Aseismic Rubber-Concrete Material. Materials. 2023; 16(3):1286. https://doi.org/10.3390/ma16031286
Chicago/Turabian StyleMei, Xiancheng, Zhen Cui, Qian Sheng, Jian Zhou, and Chuanqi Li. 2023. "Application of the Improved POA-RF Model in Predicting the Strength and Energy Absorption Property of a Novel Aseismic Rubber-Concrete Material" Materials 16, no. 3: 1286. https://doi.org/10.3390/ma16031286
APA StyleMei, X., Cui, Z., Sheng, Q., Zhou, J., & Li, C. (2023). Application of the Improved POA-RF Model in Predicting the Strength and Energy Absorption Property of a Novel Aseismic Rubber-Concrete Material. Materials, 16(3), 1286. https://doi.org/10.3390/ma16031286








