The Influence of Fly Ash on the Tensile Creep Prediction of High-Strength Concrete at Early Ages
Abstract
:1. Introduction
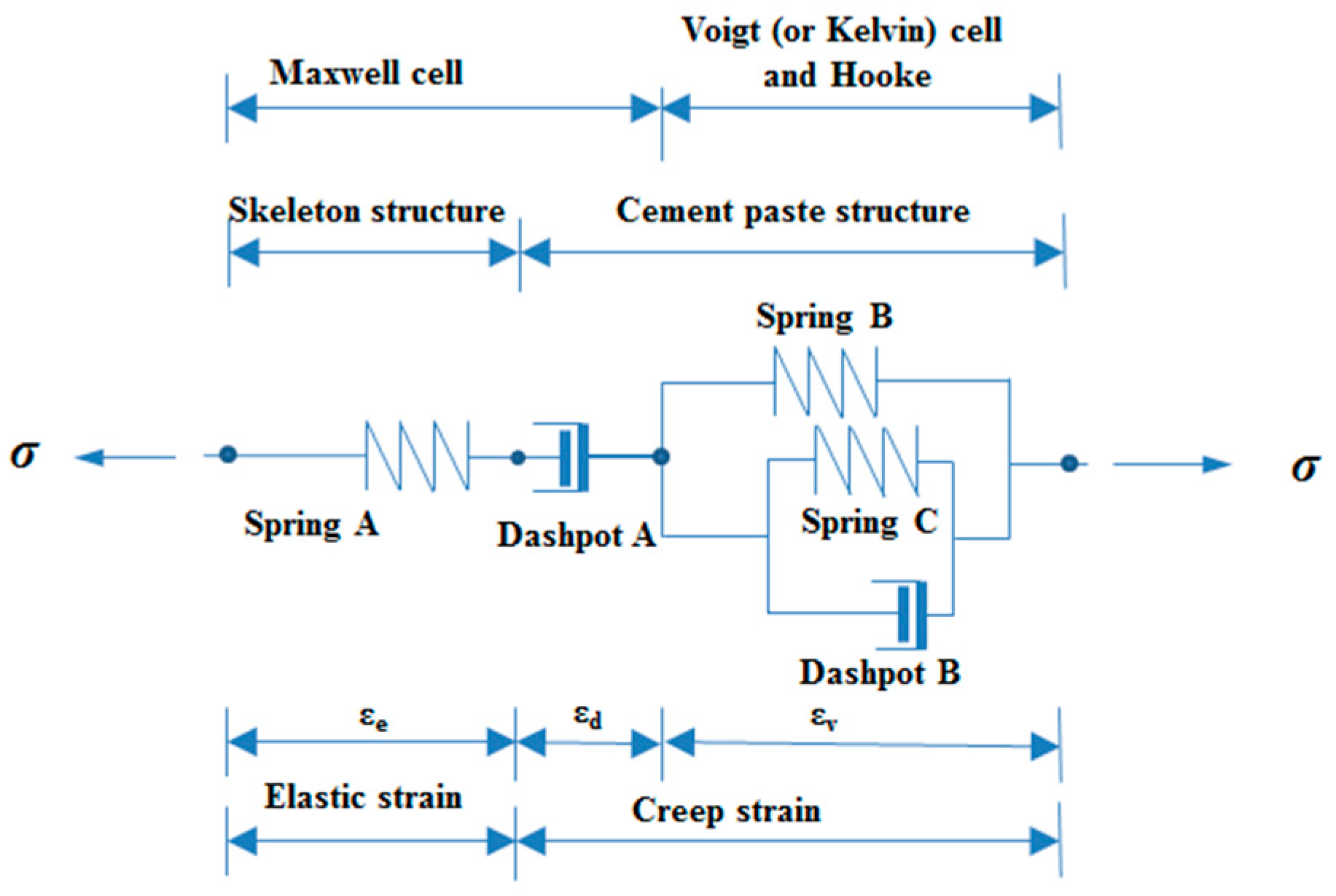
2. Prediction Models of Early-Age TC Considering the Paste Property
3. Raw Materials and Experimental Methods
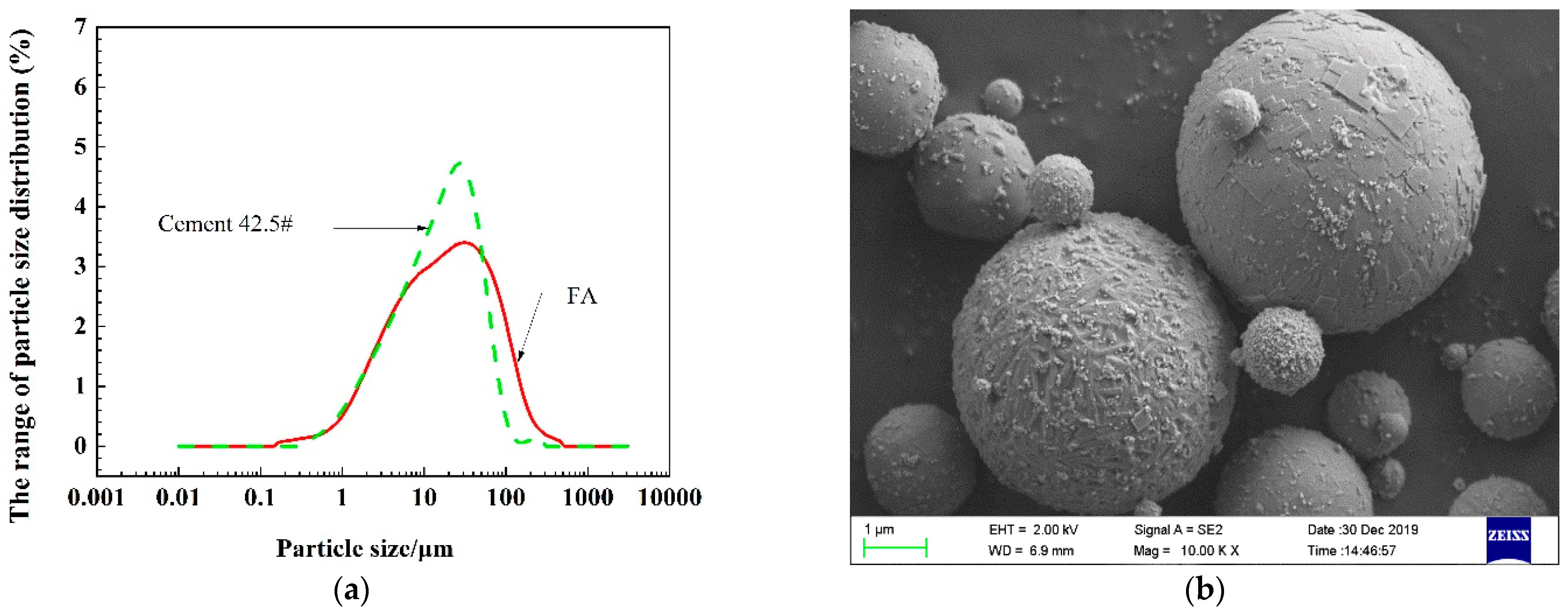
3.1. Raw Materials and Mix Proportion
3.2. Basic Experimental Parameters and Mechanical Property Index Stress Level Determination
3.2.1. Stress Level Determination
3.2.2. Loading Ages
3.3. Tensile Creep Test Method
3.3.1. Specimen Size
3.3.2. Curing Temperature Condition
3.3.3. Test Procedure
4. Applicability Analysis of Different Six Creep Models
4.1. Calculation Parameters of Six Creep Models
4.2. Calculation Parameters of Six Creep Models
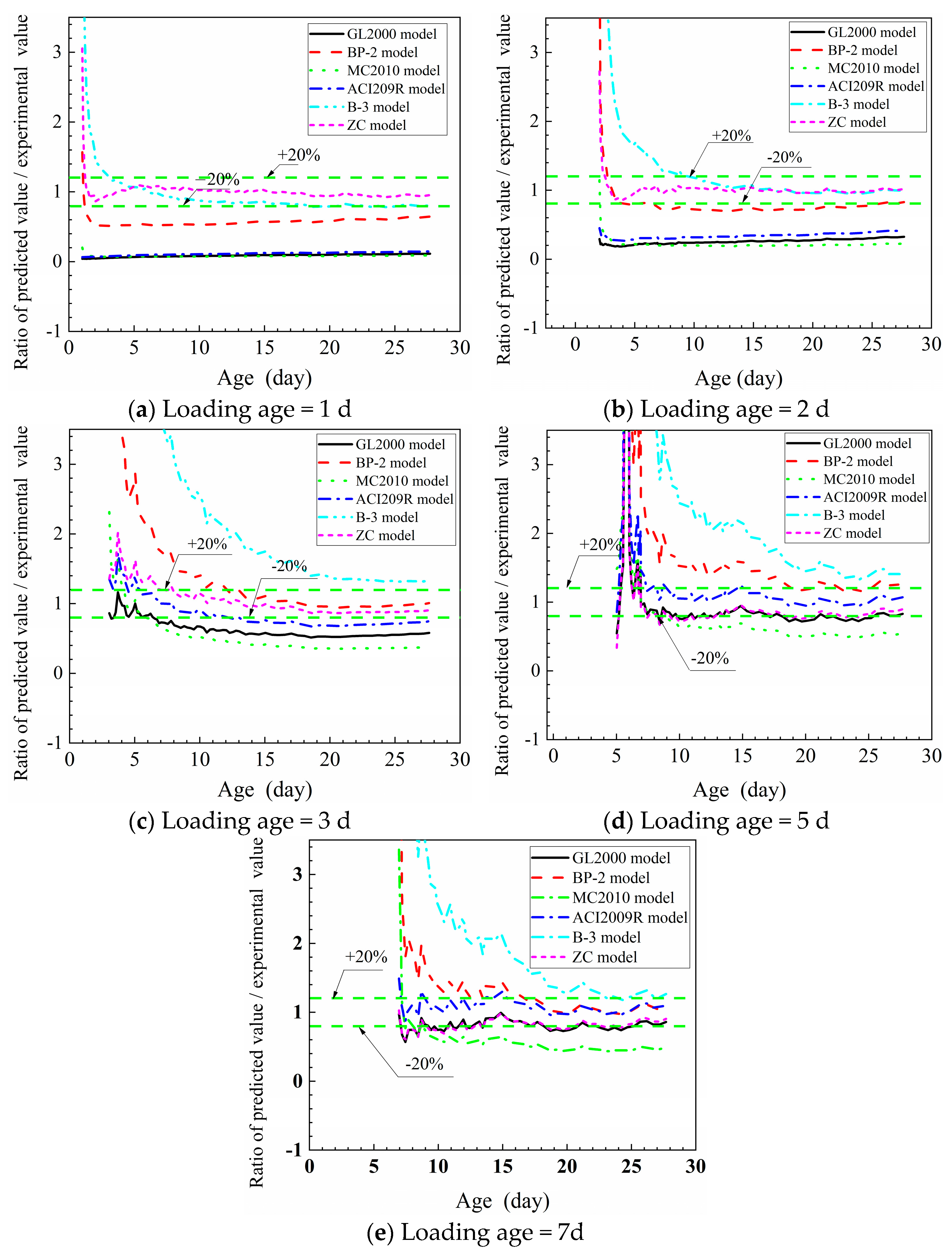
4.3. Prediction Accuracy Analysis of Six Creep Models
5. Discussion
6. Conclusions
- (1)
- The TC was significantly affected at early ages by the paste properties development and the FA. The rate of TC development was faster when the loading age was greater.
- (2)
- The comparison results between the tensile creep experimental values and the model predictions values of HSC with 30% FA of tensile creep and the model predictions showed that the errors of BP-2, B-3, MC2010, ACI 209R, and GL 2000 models were relatively larger than ZC model, especially when loading age was less than 3d.
- (3)
- The ZC model can be developed to consider the time-dependent property of a paste containing FA. The parameter q was introduced in order to reflect the influence of FA on paste, and it agreed well with the experimental values of early-age TC of HSC containing FA.
- (4)
- The effect of different types of SCMs on paste properties is different. The applicability of the TC prediction model to HSC containing other SCMs remains to be further investigated. A more comprehensive concrete creep prediction model could be useful for concrete production requirements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shen, D.; Liu, C.; Jiang, J.; Kang, J.; Li, M. Influence of super absorbent polymers on early-age behavior and tensile creep of internal curing high strength concrete. Constr. Build. Mater. 2020, 258, 120068. [Google Scholar] [CrossRef]
- Zhang, T.; Qin, W. Tensile creep due to restraining stresses in high-strength concrete at early ages. Cem. Concr. Res. 2006, 36, 584–591. [Google Scholar] [CrossRef]
- Shen, D.; Jiang, J.; Wang, W.; Shen, J.; Jiang, G. Tensile creep and cracking resistance of concrete with different water-to-cement ratios at early age. Constr. Build. Mater. 2017, 146, 410–418. [Google Scholar] [CrossRef]
- Fu, C.; Fang, D.; Ye, H.; Huang, L.; Wang, J. Bond degradation of non-uniformly corroded steel rebars in concrete. Eng. Struct. 2021, 226, 111392. [Google Scholar] [CrossRef]
- Ni, T.; Zhou, R.; Gu, C.; Yang, Y. Measurement of concrete crack feature with android smartphone APP based on digital image processing techniques. Measurement 2019, 150, 107093. [Google Scholar] [CrossRef]
- Neville, A.M.; Dilger, W.H.; Brooks, J.J. Creep of Plain and Structural Concrete; Construction Press: New York, NY, USA, 1983. [Google Scholar]
- Cheng, Z.; Zhao, R.; Yuan, Y.; Li, F.; Castel, A.; Xu, T. Ageing coefficient for early age tensile creep of blended slag and low calcium fly ash geopolymer concrete. Constr. Build. Mater. 2022, 262, 119855. [Google Scholar] [CrossRef]
- Gu, C.; Wang, Y.; Gao, F.; Yang, Y.; Ni, T.; Liu, J.; Lou, X.; Chen, J. Early age tensile creep of high performance concrete containing mineral admixtures: Experiments and modeling. Constr. Build. Mater. 2019, 197, 766–777. [Google Scholar] [CrossRef]
- Ni, T.; Yang, Y.; Gu, C.; Liu, J.; Chen, J.; Lou, X. Early-Age Tensile Basic Creep Behavioral Characteristics of High-Strength Concrete Containing Admixtures. Adv. Civ. Eng. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Klausen, A.E.; Kanstad, T.; Bjøntegaard, Ø.; Sellevold, E. Comparison of tensile and compressive creep of fly ash concretes in the hardening phase. Cem. Concr. Res. 2017, 95, 188–194. [Google Scholar] [CrossRef]
- Han, F.; He, X.; Zhang, Z.; Liu, J. Hydration heat of slag or fly ash in the composite binder at different temperatures. Thermochim. Acta. 2017, 655, 202–210. [Google Scholar] [CrossRef]
- Ji, G.M.; Kanstad, T.; Bjontegaard, O.; Sellevold, E.J. Tensile and compressive creep deformations of hardening concrete containing mineral additives. Mater. Struct. 2013, 46, 1167–1182. [Google Scholar] [CrossRef]
- Bažant, Z.P. Prediction of concrete creep and shrinkage: Past, present and future. NuEnD 2001, 203, 27–38. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Murphy, W.P. Creep and shrinkage prediction model for analysis and design of concrete structures: Model B3. Materiaux. Et. Constr. 1995, 28, 357–365. [Google Scholar]
- Bažant, Z.P.; Kim, J.-K. Improved prediction model for time-dependent deformations of concrete: Part 2—Basic creep. Mater. Struct. 1991, 24, 409. [Google Scholar] [CrossRef]
- Mehta, P.K. Concrete. Structure, Properties and Materials; China Electric Power Press: New York, NY, USA, 1986. [Google Scholar]
- Gamnitzer, P.; Brugger, A.; Drexel, M.; Hofstetter, G. Modelling of Coupled Shrinkage and Creep in Multiphase Formulations for Hardening Concrete. Materials 2019, 12, 1745. [Google Scholar] [CrossRef] [PubMed]
- Briffaut, M.; Benboudjema, F.; Torrenti, J.-M.; Nahas, G. Concrete early age basic creep: Experiments and test of rheological modelling approaches. Constr. Build. Mater. 2012, 36, 373–380. [Google Scholar] [CrossRef]
- Brown, L.; Allison, P.G.; Sanchez, F. Use of nanoindentation phase characterization and homogenization to estimate the elastic modulus of heterogeneously decalcified cement pastes. Mater. Design. 2018, 142, 308–318. [Google Scholar] [CrossRef]
- Gardner, N.J.; Lockman, M.J. Design provisions for drying shrinkage and creep of normal-strength concrete. ACI Mater. J. 2001, 98, 159–167. [Google Scholar]
- Giorla, A.B.; Dunant, C.F. Microstructural effects in the simulation of creep of concrete. Cem. Concr. Res. 2018, 105, 44–53. [Google Scholar] [CrossRef]
- Granger, L.P.; Bažant, Z.P. Effect of Composition on Basic Creep of Concrete and Cement Paste. J. Eng. Mech. 1995, 121, 1261–1270. [Google Scholar] [CrossRef]
- Chen, J.; Kuder, K.G.; Lehman, D.E.; Roeder, G.W.; Lowes, L.N. Creep modeling of concretes with high volumes of supplementary cementitious materials and its application to concrete-filled tubes. Mater. Struct. 2016, 50. Available online: https://10.1617/s11527-016-0955-9 (accessed on 22 September 2016). [CrossRef]
- Briffaut, M.; Benboudjema, F.; LaBorderie, C.; Torrenti, J.-M. Creep Consideration Effect on Meso-Scale Modeling of Concrete Hydration Process and Consequences on the Mechanical Behavior, J. Eng. Mech. 2013, 139, 1808–1817. [Google Scholar] [CrossRef]
- Lee, Y.; Yi, S.-T.; Kim, M.-S.; Kim, J.-K. Evaluation of a basic creep model with respect to autogenous shrinkage. Cem. Concr. Res. 2006, 36, 1268–1278. [Google Scholar] [CrossRef]
- Wei, Y.; Huang, J.; Liang, S. Measurement and modeling concrete creep considering relative humidity effect. MTDM 2020, 24, 161–177. [Google Scholar] [CrossRef]
- Forth, J.P. Predicting the tensile creep of concrete. Cem. Concr. Compos. 2015, 55, 70–80. [Google Scholar] [CrossRef]
- Atrushi, D. Tensile and Compressive Creep of Early Age Concrete: Testing and Modelling. Ph.D Theis, The Norwegian University of Science and Technology, Trondheim, Norway, 2003. [Google Scholar]
- Clark, L. CEB-FIP Model Code 1990; Thomas Telford Services Ltd., Thomas Telford House: Heron Quay, Switzerland, 2008. [Google Scholar]
- Lee, S.C. Re-evaluation of fibre-reinforced concrete tension model in CEB-FIP Model Code 2010. Mater. Res. Innov. 2015, 19 (Suppl. S8), S8-107-S8-110. [Google Scholar] [CrossRef]
- ACI Committee. Prediction of Creep, Shrinkage and Temperature Effects of Concrete Structures, Designing for Effect of Creep and Temperature; ACI. Committee: Detroit, MI, USA, 1982; pp. 51–139. [Google Scholar]
- Rhodes, J.A.; Geymayer, H.G.; Hope, B.B.; Lorman, W.R.; Means, J.A.; Ward, M.A.; Members, C.; Dougill, J.W.; Hilsdorf, H.K.; Carreira, D.J. Prediction of Creep, Shrinkage, and Temperature Effects in Concrete Structures; Reported by ACI Committee 209; ACI Committee: Detroit, MI, USA, 1997. [Google Scholar]
- Lou, X.T. Evaluation of Tensile Creep of High Strength Concrete Containing Mineral Admixtures at Early Ages Based on ZC Model. Master’s Thesis, Zhejiang University of Technology, Hangzhou, China, 2017. (In Chinese). [Google Scholar]
- Yang, Y.; Xu, S.; Ye, D.; Wang, Z. Tensile creep behavior of high strength concrete at early ages. J. Chin. Ceram. Soc. 2009, 37, 1124–1129. (In Chinese) [Google Scholar]
- Yang, Y.; Jiang, C.H.; Ye, D.Y.; Xu, S.F.; Kong, D.Y. Tensile creep prediction of HPC at early ages. J. Wuhan Univ. Technol. 2009, 31, 77–80. [Google Scholar] [CrossRef]
- Ni, T. Tensile Creep Characteristics and Its Evaluation of High Strength Concrete Containing Mineral Admixtures at Early Ages. Ph.D Thesis, Zhejiang University of Technology, Hangzhou, China, 2020. (In Chinese). [Google Scholar]
- NI, T.; Yang, Y.; Wu, Y.; Gu, C.; Liu, J. Experimental Study on Early-Age Tensile Creep of High Strength Concrete under Different Curing Temperatures. J. Build. Eng. 2018, 21, 732–738, 760. (In Chinese) [Google Scholar]
- Wei, Y.; Liang, S.; Guo, W. Decoupling of Autogenous Shrinkage and Tensile Creep Strain in High Strength Concrete at Early Ages. Exp Mech. 2017, 57, 475–485. [Google Scholar] [CrossRef]
- Shen, D.; Wen, C.; Zhu, P.; Wu, Y. Influence of Barchip fiber on early-age autogenous shrinkage of high-strength concrete internally cured with super absorbent polymers. Constr. Build. Mater. 2020, 264, 119983. [Google Scholar] [CrossRef]
- Shen, D.; Liu, C.; Kang, J.; Yang, Q.; Li, M.; Li, C.; Zeng, X. Early-age autogenous Shrinkage and tensile creep of hooked-end steel fiber reinforced concrete with different thermal treatment temperatures. Cem. Concr. Comp. 2022, 264, 104550. [Google Scholar] [CrossRef]
- Chen, H.; Sun, W.; Piet, S. Interfacial transition zone between aggregate and paste in cementitious composites (Ⅱ): Mechanism of formation and degradation of interfacial transition zone microstructure, and its influence factors. J. Chin. Ceram. Soc. 2004, 01, 70–79. (In chinese) [Google Scholar]
- Ni, T.; Ma, W.; Yang, Y.; Yu, J.; Liu, J.; Jiang, C.; Gu, C. Interface reinforcement and a new characterization method for pore structure of pervious concrete. Constr. Build. Mater. 2021, 267, 121052. [Google Scholar] [CrossRef]
- Königsberger, M.; Honório, T.; Sanahuja, J.; Delsaute, B.; Pichler, P.L.B. Homogenization of nonaging basic creep of cementitious materials: A multiscale modeling benchmark. Constr. Build. Mater. 2021, 290, 123144. [Google Scholar] [CrossRef]
- Vandamme, M.; Ulm, F.J. Nanogranular origin of concrete creep. Proc. Natl. Acad. Sci. USA 2009, 106, 10552–10557. [Google Scholar] [CrossRef] [PubMed]
- Müller, H.; Anders, D.I.; Breiner, D.I.; Vogel, D.I. Concrete: Treatment of types and properties in fib Model Code 2010. Struct. Concr. 2013, 14, 320–344. [Google Scholar] [CrossRef]
- Le Roy, R.; Le Maou, F.; Torrenti, J.M. Long term basic creep behavior of high performance concrete: Data and modelling. Mater. Struct. 2016, 50, 85. [Google Scholar] [CrossRef]


| Factors | Model | ||||||
|---|---|---|---|---|---|---|---|
| ZC | BP-2 | B-3 | MC2010 | ACI209R | GL2000 | ||
| Internal factors | Mass of aggregate | ● | ● | ||||
| Air content | ● | ● | |||||
| FA | ● | ||||||
| Cement type | ● | ● | ● | ● | ● | ● | |
| The specific gravity of the fine aggregate | ● | ● | |||||
| Slump | ● | ||||||
| Water-binder ratio | ● | ● | |||||
| External factors | Loading age | ● | ● | ● | ● | ● | ● |
| Calculating age | ● | ● | ● | ● | ● | ● | |
| Stress | ● | ● | ● | ● | ● | ● | |
| Cross-section shape | ● | ||||||
| 28d strength | ● | ● | ● | ● | ● | ● | |
| Cross section size | ● | ● | ● | ● | ● | ● | |
| 28d Elastic modulus | ● | ● | ● | ● | |||
| Ambient humidity | ● | ● | ● | ● | ● | ● | |
| Ambient temperature | ● | ● | |||||
| Drying age | ● |
| Materials | Index | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chemical Composition (%) | Physical Properties | |||||||||||
| SiO2 | Al2O3 | Cao | Fe2O3 | Na2O | MgO | SO3 | K2O | Specific Surface Area (m2/cm3) | Density (g/cm3) | Ignition Loss (%) | Average Grain Size (μm) | |
| Cement | 24.95 | 6.99 | 54.33 | 2.83 | 0.21 | 2.16 | 2.89 | 0.66 | 368 | 2.99 | 3.66 | 26.04 |
| FA | 46.6 | 41.4 | 3.18 | 3.90 | 0.00 | 0.22 | 0.61 | 0.72 | 337 | 2.03 | 4.79 | 62.12 |
| Cement | Fly Ash | Sand | Coarse Aggregate | Superplasticizer | Water |
|---|---|---|---|---|---|
| 391 | 167 | 687 | 988 | 11 | 167 |
| Loading Age (d) | Applied Load (kN) | Splitting Tensile Strength (MPa) | Compression Strength (Mpa) | Tensile Modulus of Elasticity (Gpa) |
|---|---|---|---|---|
| 1 | 5.99 | 1.27 | 9.81 | 21.67 |
| 2 | 12.77 | 2.71 | 27.55 | 29.02 |
| 3 | 15.03 | 3.19 | 31.50 | 33.11 |
| 5 | 17.52 | 3.72 | 42.67 | 37.10 |
| 7 | 18.36 | 3.90 | 51.91 | 40.09 |
| ZC model | |||||||
| 1 | 214.65 | 0.33 | 61.36 | 22.74 | 2.76 | ||
| 2 | 88.04 | 0.20 | 14.60 | 17.57 | 4.78 | ||
| 3 | 47.03 | 0.11 | 6.20 | 10.86 | 6.52 | ||
| 5 | 38.54 | 0.06 | 5.27 | 6.42 | 7.52 | ||
| 7 | 36.24 | 0.06 | 5.87 | 5.98 | 7.90 | ||
| BP-2 model | |||||||
| 1 | 1.49 | 0.29 | 0.28 | 21.31 | |||
| 2 | 1.49 | 0.29 | 0.28 | 39.13 | |||
| 3 | 1.49 | 0.29 | 0.28 | 50.58 | |||
| 5 | 1.49 | 0.29 | 0.28 | 50.81 | |||
| 7 | 1.49 | 0.29 | 0.28 | 56.88 | |||
| B-3 model | of Modified B-3 model | ||||||
| 1 | 9.70 | 0.77 | 566.75 | ||||
| 2 | 9.85 | 0.57 | 332.44 | ||||
| 3 | 9.94 | 0.48 | 292.18 | ||||
| 5 | 10.06 | 0.39 | 266.37 | ||||
| 7 | 10.15 | 0.33 | 256.65 | ||||
| 0.43 | 4.28 | 391.00 | 235.20 | 2.27 | 0.05 | ||
| MC2010 model | |||||||
| 1 | 0.91 | ||||||
| 2 | 0.80 | ||||||
| 3 | 0.74 | ||||||
| 5 | 0.68 | ||||||
| 7 | 0.64 | ||||||
| 1.98 | 0.60 | 0.87 | 0.70 | 1.35 | 294.43 | 44.07 | |
| ACI209R model | S/(S + G) | γφ | Slump (mm) | γs | |||
| 0.41 | 0.88 | 250 | 1.48 | ||||
| GL2000 model | v/s (mm) | h | |||||
| As others | 28.60 | 0.60 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, J.; Yao, S.; Huang, S.; Ni, T.; Jiang, C.; Yang, Y.; Kong, D. The Influence of Fly Ash on the Tensile Creep Prediction of High-Strength Concrete at Early Ages. Materials 2023, 16, 1337. https://doi.org/10.3390/ma16041337
Yao J, Yao S, Huang S, Ni T, Jiang C, Yang Y, Kong D. The Influence of Fly Ash on the Tensile Creep Prediction of High-Strength Concrete at Early Ages. Materials. 2023; 16(4):1337. https://doi.org/10.3390/ma16041337
Chicago/Turabian StyleYao, Jikai, Shuifeng Yao, Senle Huang, Tongyuan Ni, Chenhui Jiang, Yang Yang, and Deyu Kong. 2023. "The Influence of Fly Ash on the Tensile Creep Prediction of High-Strength Concrete at Early Ages" Materials 16, no. 4: 1337. https://doi.org/10.3390/ma16041337
APA StyleYao, J., Yao, S., Huang, S., Ni, T., Jiang, C., Yang, Y., & Kong, D. (2023). The Influence of Fly Ash on the Tensile Creep Prediction of High-Strength Concrete at Early Ages. Materials, 16(4), 1337. https://doi.org/10.3390/ma16041337







