Detection of Sleeve Grouting Compactness Based on Acoustic Emission Technology
Abstract
:1. Introduction
2. Experimental Test
2.1. Setting and Fabrication of Sleeve Grout Defects
2.2. Test Rigs and Methods
3. Basic Analysis Methods
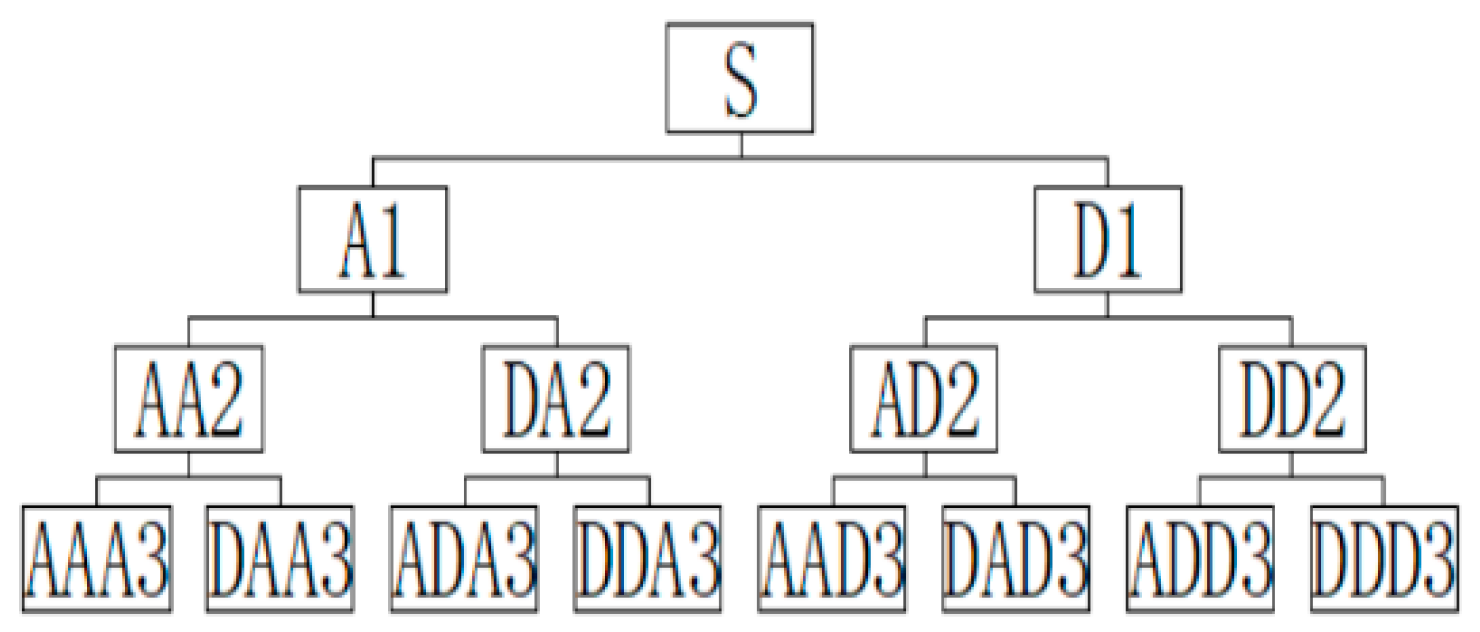
3.1. Wavelet Packet Analysis
3.2. Evaluation Index of Grout Saturation
- (1)
- After the acoustic emission signal S is decomposed by N-layer wavelet packet, the sub-signals in 2N frequency bands will be obtained at the N-layer, forming the signal set , in which one sub-signal is:In the formula: m—sampling length; j—frequency band serial number, .
- (2)
- Assuming that the energy of one of the sub-signals after decomposition of the response signal under i condition iswhere i—condition code.Then the wavelet packet energy of each frequency band formed by N-layer wavelet packet decomposition of response signal S under i condition can be expressed as
- (3)
- Let EPi be the sum of wavelet packet energies of each frequency band obtained by decomposition of response signalsThen, the proportion of wavelet packet energy in each frequency band iswhere
- (4)
- Assuming that the response signal decomposition wavelet packet energy ratio of 100%, sleeve grouting compactness iswhere h means healthy.
4. Test Results and Analysis
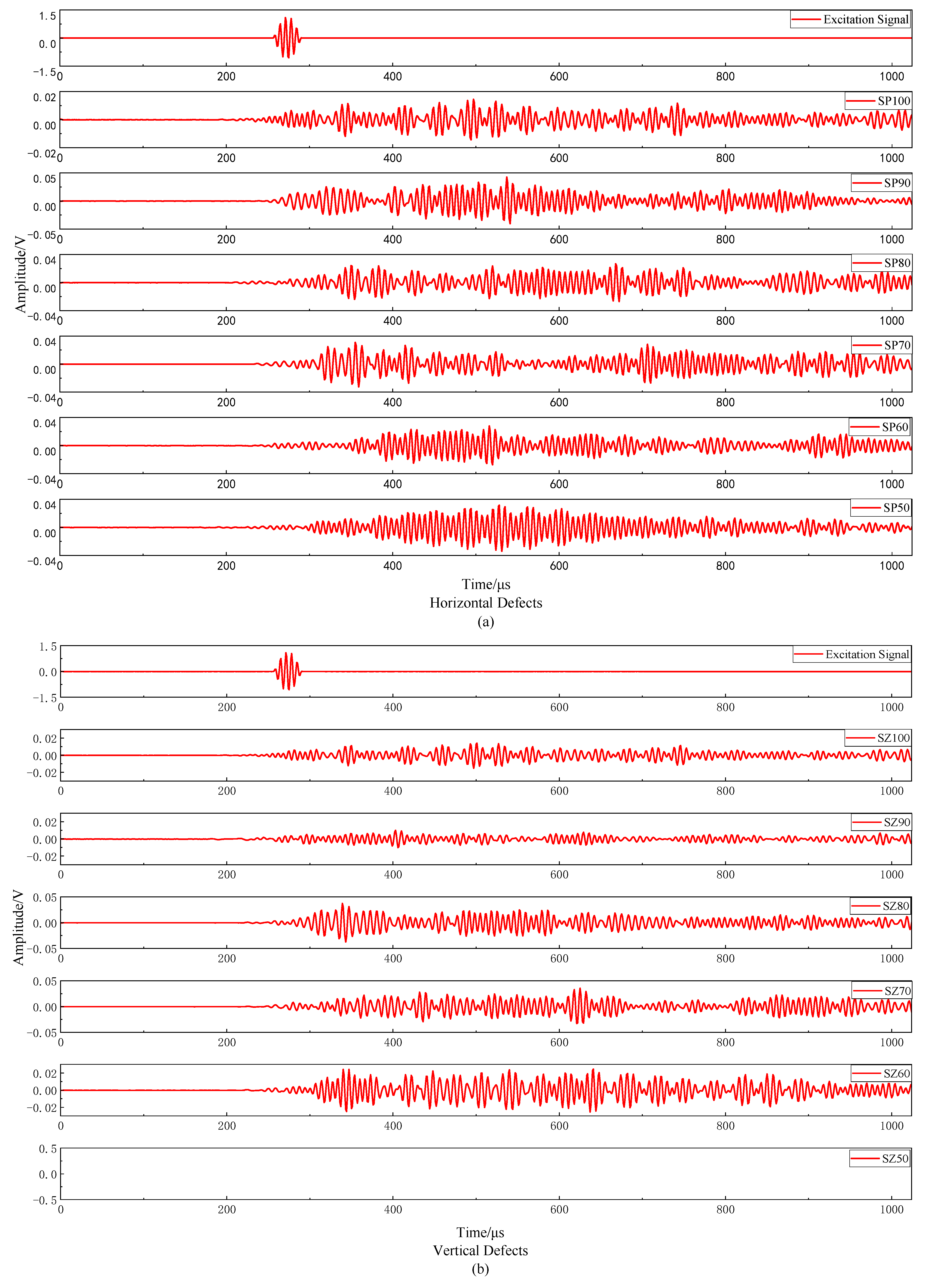
4.1. Characteristic Parameter Analysis of the Acoustic Emission Signal
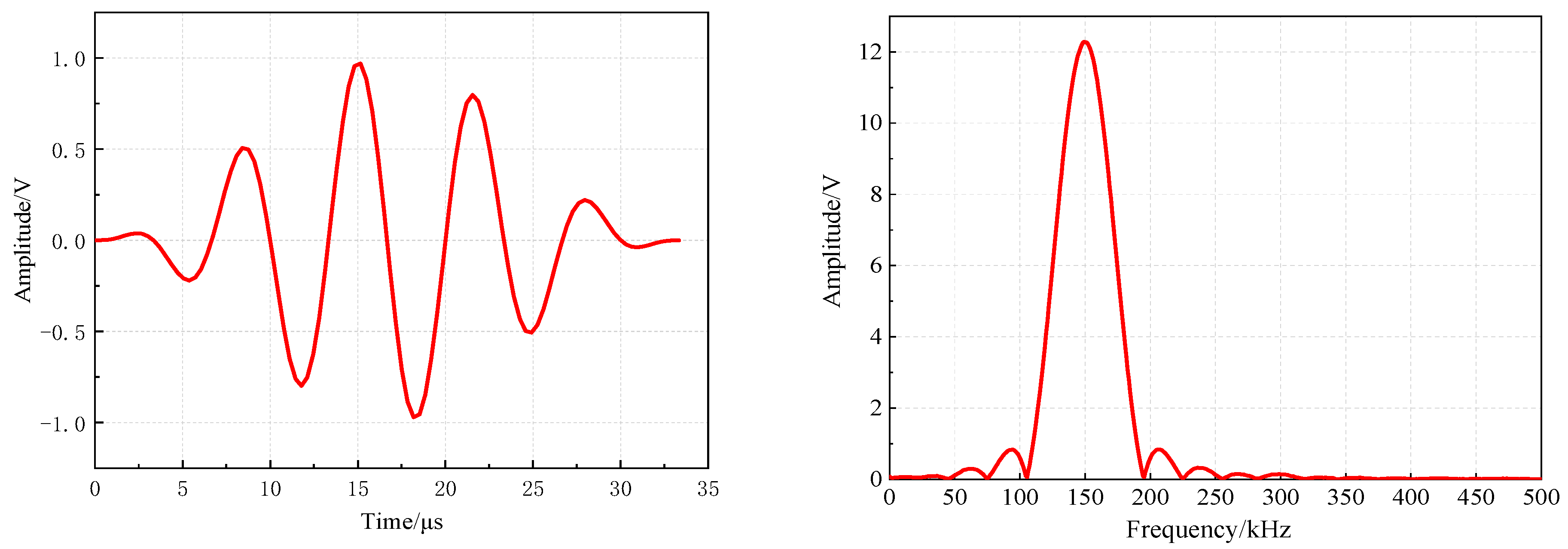
4.1.1. Acoustic Emission Signal Waveform Analysis
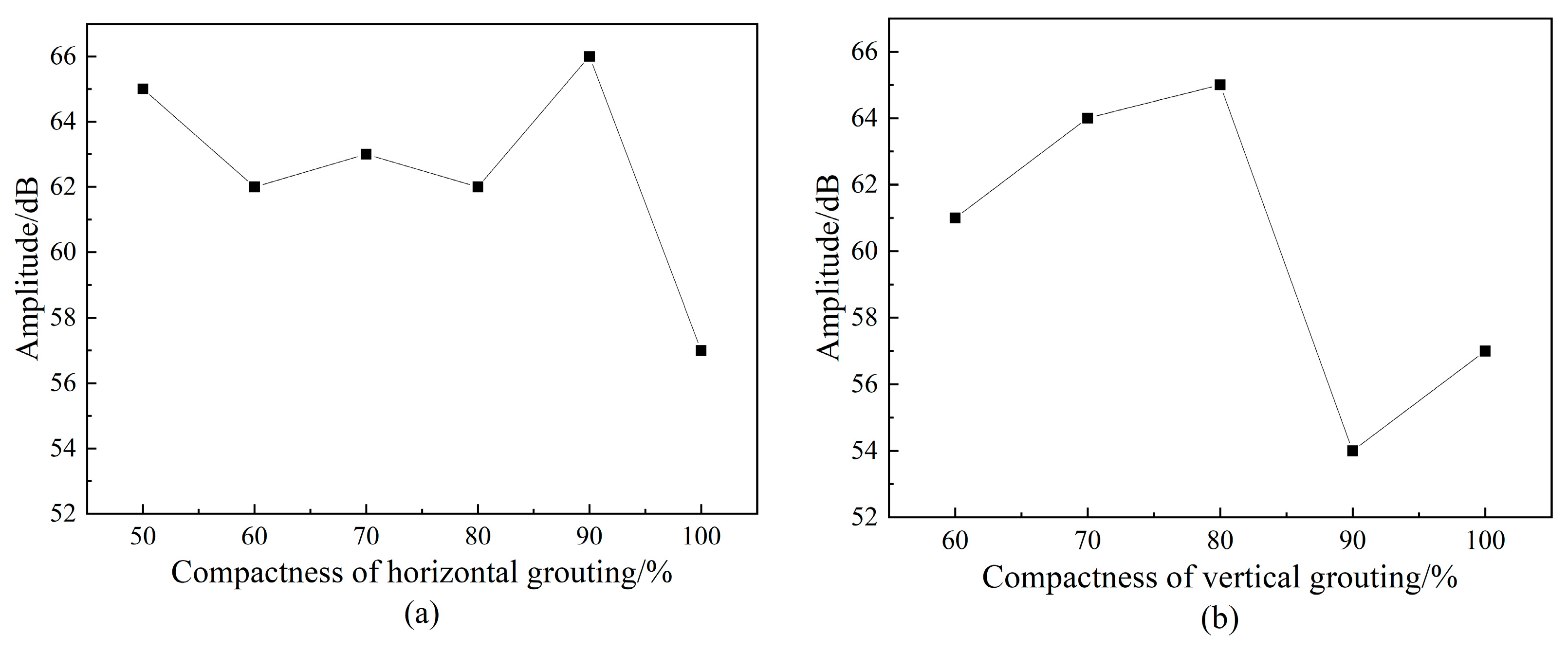
4.1.2. Amplitude Analysis of Acoustic Emission Signal
4.1.3. Acoustic Emission Signal Energy Analysis
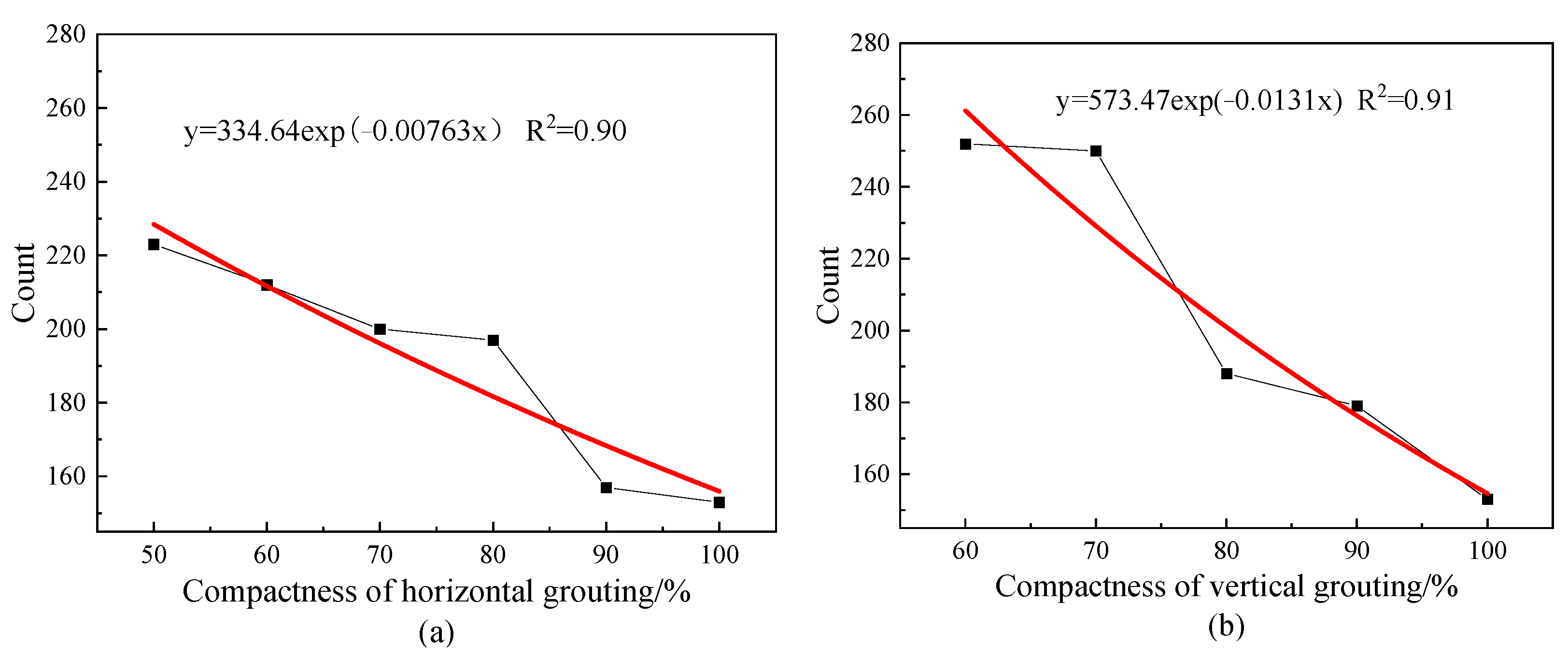
4.1.4. Analysis of the Count of the Acoustic Emission Signal
4.2. Acoustic Emission Signal Wavelet Analysis
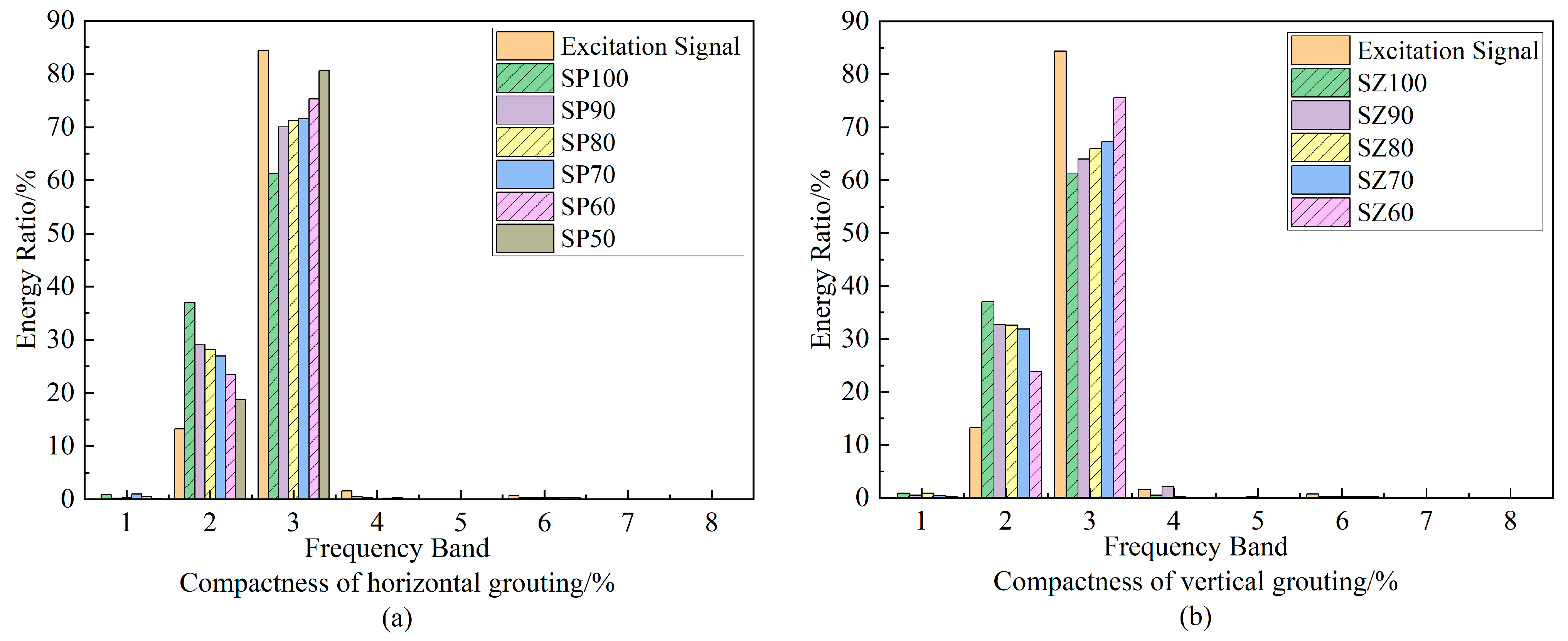
4.2.1. Wavelet Packet Energy Proportion Analysis
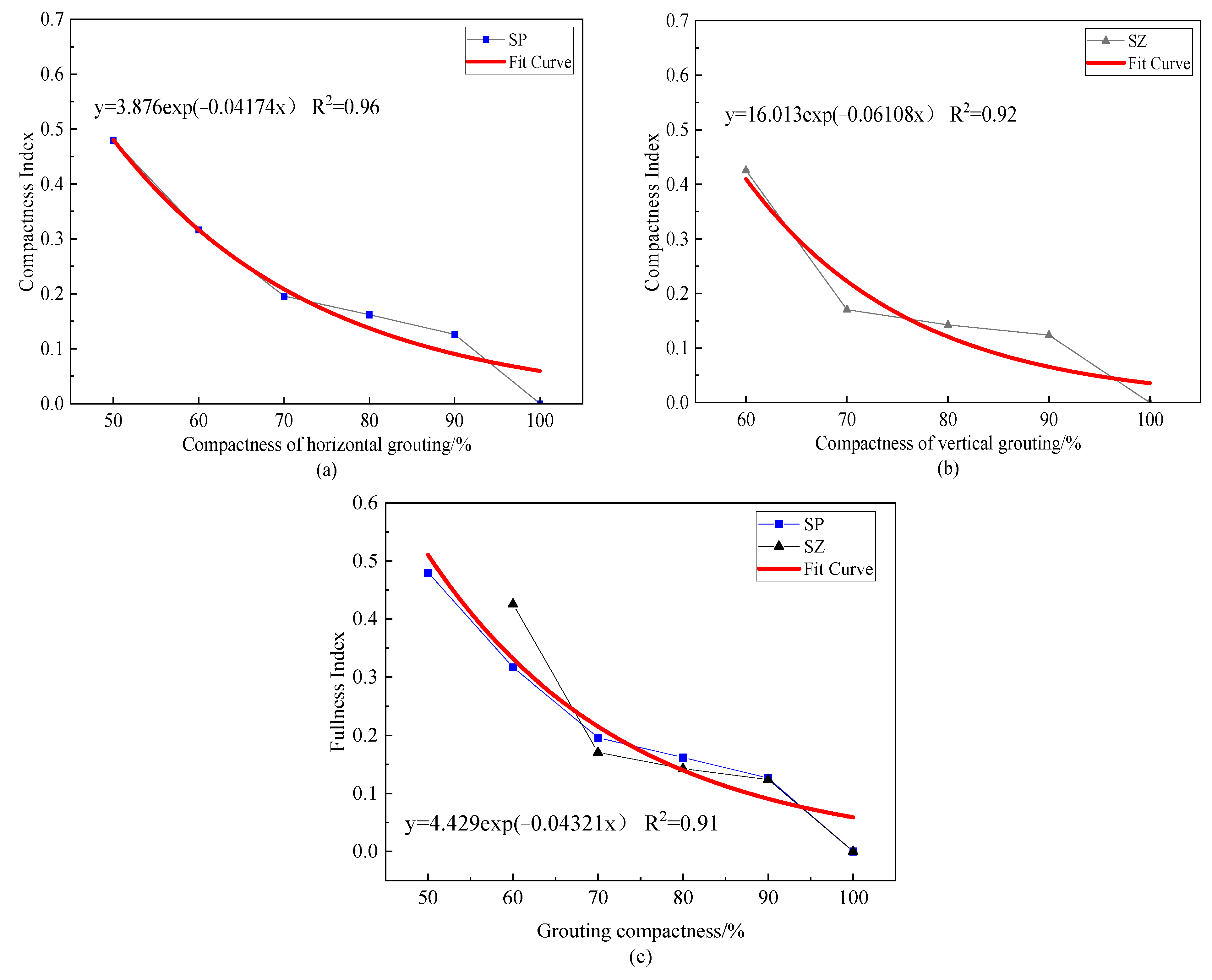
4.2.2. Analysis of Grouting Compactness Index
5. Conclusions
- When the sensors are arranged on both sides of the steel bar, the response signal cannot be received under the premise of ensuring that the instrument has no fault and the operation is correct, which indicates that the sleeve must have grout defects that seriously affect the connection performance of the steel bar.
- The amplitude and energy of AE signal characteristic parameters are susceptible to the interference of steel bars and grout materials due to the excitation signal, and their consistency with the change of grouting compactness is not obvious. The count can reflect the difference between different grouting compactness to a certain extent. With the increase of saturation, the count shows an exponential downward trend and the downward rate is affected by the shape of the grout material. The downward rate of vertical defects is slightly larger than that of horizontal defects.
- Whether the shape of the grout material is horizontal or vertical, the increase of grouting compactness will lead to a decrease of energy proportion in the range of approximately 125–187.5 kHz and an increase of energy proportion in the range of approximately 62.5–125 kHz, indicating that the increase of saturation will affect the transformation of high-frequency components in the signal to low-frequency components, but the vertical defect will accelerate the transformation of high-frequency components.
- Based on the energy proportion of wavelet packet decomposition, the evaluation index FI of grouting compactness is proposed to quantitatively evaluate the size of saturation. The results show that the FI value of the saturation index decreases significantly with the increase of saturation, and the decreasing trend is an exponential function, indicating that the specimen with defects can greatly reduce the attenuation of energy in the signal.
- The change in the FI value has a high consistency with the defect size and has little relationship with the distribution form of grout material in the sleeve. Therefore, the filling saturation index FI under the two distribution forms of grout material can be combined and fitted, and the general law of FI and grouting compactness can be further obtained.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Švajlenka, J.; Kozlovská, M.; Pošiváková, T. Analysis of Selected Building Constructions Used in Industrial Construction in Terms of Sustainability Benefits. Sustainability 2018, 10, 4394. [Google Scholar]
- Goh, E.; Loosemore, M. The impacts of industrialization on construction subcontractors: A resource-based view. Constr. Manag. Econ. 2017, 35, 288–304. [Google Scholar] [CrossRef]
- Ameli, M.; Brown, D.; Parks, J.; Pantelides, C. Seismic Column-to-Footing Connections Using Grouted Splice Sleeves. ACI Struct. J. 2016, 113, 1021. [Google Scholar] [CrossRef]
- Ferreira, M.; Bachega, L.; Catoia, B. Monolithic equivalent stiffness of precast columns with grouted splice sleeve connections. Rev. IBRACON Estrut. E Mater. 2021, 14, e14115. [Google Scholar] [CrossRef]
- Xu, C.; Liu, H.; Du, X. Experimental study on connection performance of grouted sleeve splicing for rebars under high stress repeated tension-compression loading. J. Build. Struct. 2018, 39, 178–184+193. (In Chinese) [Google Scholar]
- Tullini, N.; Minghini, F. Grouted sleeve connections used in precast reinforced concrete construction—Experimental investigation of a column-to-column joint. Eng. Struct. 2016, 127, 784–803. [Google Scholar]
- Yan, Q.; Chen, T.; Xie, Z. Seismic experimental study on a precast concrete beam-column connection with grout sleeves. Eng. Struct. 2018, 155, 330–344. [Google Scholar] [CrossRef]
- Wu, Y.; Gu, S.; Zhang, J.; Cao, K. Study on the influence of grouting plumpness on the mechanical properties of grouting joint of steel sleeve. Constr. Qual. 2020, 38, 76–80+89. (In Chinese) [Google Scholar]
- Xu, F.; Wang, K.; Wang, S.; Li, W.; Liu, W.; Du, D. Experimental bond behavior of deformed rebars in half-grouted sleeve connections with insufficient grouting defect. Constr. Build. Mater. 2018, 185, 264–274. [Google Scholar]
- Jiang, S.; Cai, W. Ultrasonic testing method of grouting sleeve compactness. J. Vib. Shock 2018, 37, 43–49. (In Chinese) [Google Scholar]
- Yan, H.; Song, B.; Wang, M. Ultrasonic Testing Signal of Grouting Defect in Prefabricated Building Sleeve. Ekoloji 2019, 28, 945–953. [Google Scholar]
- Liu, H.; Li, X.; Xu, Q. Test on detection of grouting compactness of grout sleeve by impact-echo method. Nondestruct. Test. 2017, 39, 12–16. (In Chinese) [Google Scholar]
- Liu, Y.L.; Shi, J.J.; Huang, J.; Wei, G.S.; Wu, Z.X. Grouting Defect Detection of Lapped Bar Connections Based on Impact-Echo Method. Shock Vib. 2019, 2019, 1934240. [Google Scholar] [CrossRef]
- Zhen, Z.; Xiao, Y.; Li, D.; Tian, Y.; Xie, X.; Zhang, T. Research on inspection method of sleeve grouting connector based on ct technology. Constr. Technol. 2018, 47, 69–74. (In Chinese) [Google Scholar]
- Guo, H.; Xu, F.; Dai, W.; Liu, Y.; Wang, S. Experimental study on the compactness detection of grouting of steel sleeve by X-ray method. Constr. Technol. 2018, 47, 40–43. (In Chinese) [Google Scholar]
- Gao, R.; Li, X.; Wang, Z.; Zhang, F.; Xu, Q. Research on testing technology of grouting fullness of sleeve based on embedded steel wire drawing method. Constr. Technol. 2017, 46, 1–5. (In Chinese) [Google Scholar]
- Cui, L.; Liu, W.; Zhang, X. Field test of grouting plumpness of prefabricated outer wall sleeve of a concrete structure. Archit. Technol. 2018, 49, 169–170. (In Chinese) [Google Scholar]
- Li, J.; He, S.; Chen, W.; Yan, W.; Sun, B. Identification and application of sleeve grouting plumpness based on piezoelectric impedance effect. China Civ. Eng. J. 2020, 53, 65–77+117. (In Chinese) [Google Scholar]
- Zhang, R.; Guo, L.; Li, W. Combining thermal loading system with acoustic emission technology to acquire the complete stress-deformation response of plain concrete in direct tension. Materials 2021, 14, 602. [Google Scholar]
- Van Hieu, B.; Choi, S.; Kim, Y.U.; Park, Y.; Jeong, T. Wireless transmission of acoustic emission signals for real-time monitoring of leakage in underground pipes. KSCE. J. Civ. Eng. 2011, 15, 805–812. [Google Scholar]
- Li, J.; Xu, F.; Wang, T.; Shi, S. Research on the evolution of shield segment cracks based on acoustic emission and cmod. Materials 2022, 15, 5829. [Google Scholar] [CrossRef]
- Hu, Y.; Li, S.; Li, D.; Vadim, S. Yield criteria and strength conditions considering comprehensive mechanical and acoustic emission characteristics of tension–torsion composite deformation of nylon materials. Compos. Struct. 2020, 243, 112278. [Google Scholar]
- Zhao, K.; Liu, Z.; Zeng, P.; Gong, C.; Li, Y. Fracture process analysis and acoustic emission response of cemented tailings backfill with different sizes under uniaxial compression. Materials 2022, 15, 8038. [Google Scholar] [CrossRef]
- Wu, Y.; Li, S.; Wang, D. Characteristic analysis of acoustic emission signals of masonry specimens under uniaxial compression test. Constr. Build. Mater. 2019, 196, 637–648. [Google Scholar]
- Abouhussien, A.A.; Hassan, A.A.A. The Use of Acoustic Emission Intensity Analysis for the Assessment of Cover Crack Growth in Corroded Concrete Structures. J. Nondestruct. Eval. 2016, 35, 52. [Google Scholar] [CrossRef]
- Wang, X.; Liu, D.; Zhang, Y.; Jiao, Y. Fracture characterization of ultra-high performance concrete notched beams under the influence of different material factors based on acoustic emission technique. Materials 2021, 14, 4608. [Google Scholar] [CrossRef]
- Yang, K.; Li, D.; He, Z.; Zhou, H.; Li, J. Study on acoustic emission characteristics of low-temperature asphalt concrete cracking damage. Materials 2021, 14, 881. [Google Scholar]
- Parks, J.E.; Papulak, T.; Pantelides, C.P. Acoustic emission monitoring of grouted splice sleeve connectors and reinforced precast concrete bridge assemblies. Constr. Build. Mater. 2016, 122, 537–547. [Google Scholar] [CrossRef]
- Han, R.; Li, S.; Sun, W. Effect of grouting material strength on bond strength of sleeve and acoustic emission characterization of bond failure damage process. Constr. Build. Mater. 2022, 324, 126503. [Google Scholar] [CrossRef]
- Ma, Y.; Li, S.; Wu, Y.; Wang, D.; Liu, M. Acoustic emission testing method for the sleeve grouting compactness of fabricated structure. Constr. Build. Mater. 2019, 221, 800–810. [Google Scholar] [CrossRef]
- Ma, Y. Acoustic Emission Testing Method for Grouting Compactness of Grouted Sleeve of Fabricated Shear Wall. Master’s Thesis, Zhengzhou University, Zhengzhou, China, 2020. (In Chinese). [Google Scholar]
- Li, S.; Liu, X.; Ma, Y.; Zhang, L.; Feng, H. Influence of grouted sleeve and concrete strength of fabricated shear wall on acoustic emission detection method for sleeve compactness. J. Build. Eng. 2021, 43, 102541. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, L.; Chen, C.; Long, Z.; Wang, Y. Ultrasonic Detection Method for Grouted Defects in Grouted Splice Sleeve Connector Based on Wavelet Pack Energy. Sensors 2019, 19, 1642. [Google Scholar]
- Li, D.; Liu, H. Detection of sleeve grouting connection defects in fabricated structural joints based on ultrasonic guided waves. Smart Mater. Struct. 2019, 28, 085033. [Google Scholar]
- Coifman, R.R.; Wickerhauser, M.V. Entropy-based algorithms for best basis selection. IEEE Trans. Inf. Theory 1992, 38, 713–718. [Google Scholar] [CrossRef]
- Zhu, H.; Sun, Y.; Dong, Z.; Chen, D.; Wu, G. Research on defect detection and stress propagation simulation of grout sleeve based on piezoelectric ceramics. J. Archit. Eng. 2022, 39, 117–126. (In Chinese) [Google Scholar]
- Zhang, X.; Zhou, D.; Tang, H.; Han, X. Experimental study of grout defect identification in precast column based on wavelet packet analysis. Int. J. Distrib. Sens. Netw. 2019, 15, 1550147719889590. [Google Scholar]
- Lv, S. Acoustic Emission Monitoring of High Strength Bolted Connections under Cyclic Loading. Master’s Thesis, Hefei University of Technology, Hefei, China, 2021. (In Chinese). [Google Scholar]
- Xu, B.; Fan, X.; Wang, H.; Zhou, S.; Wang, C.; Chen, H.; Ge, H. Experimental study on grout defects detection for grouted splice sleeve connectors using stress wave measurement. Constr. Build. Mater. 2021, 274, 121755. [Google Scholar] [CrossRef]
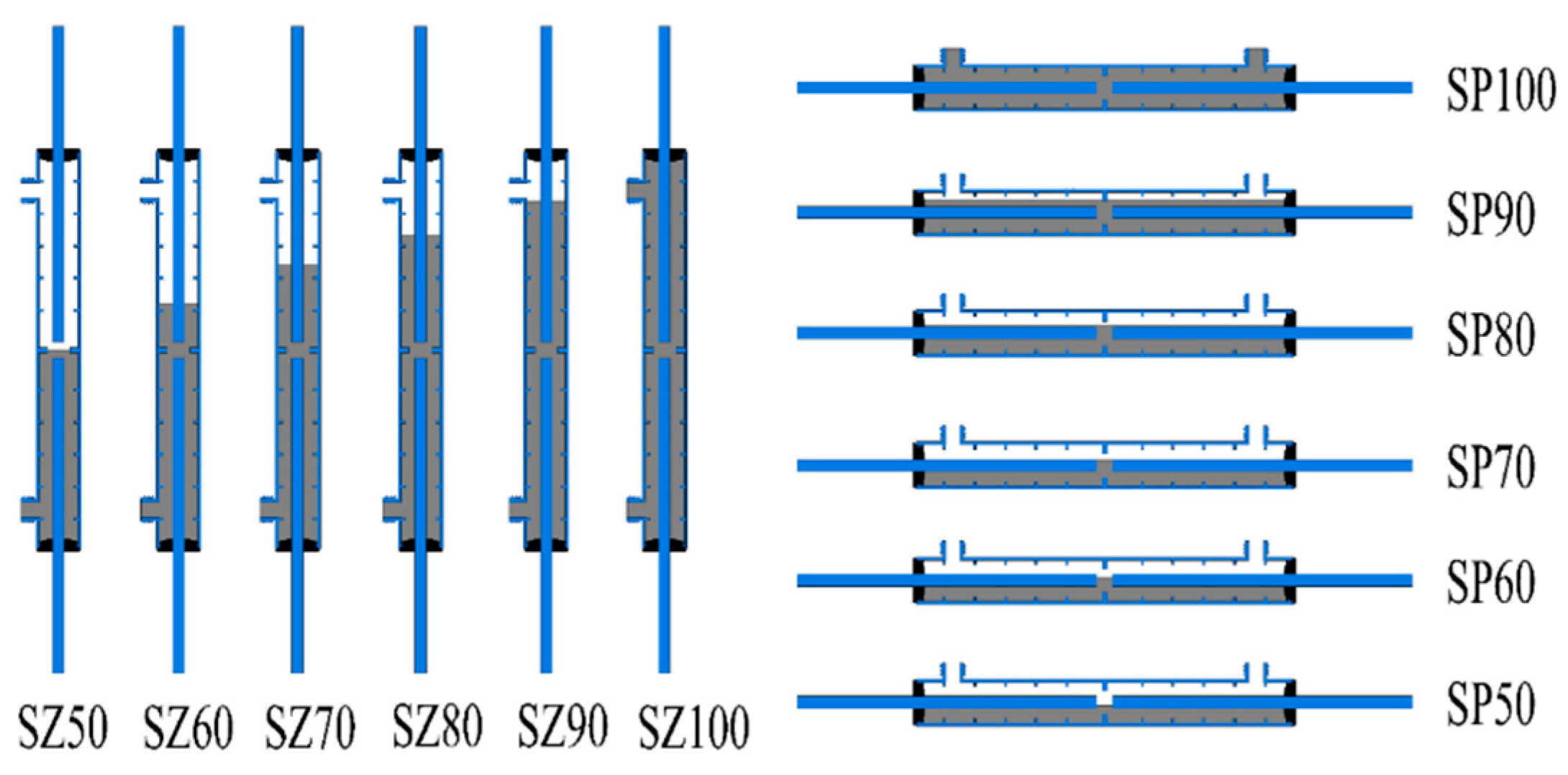


| Specimen Number | Defect Type | Saturation of Grout (%) | Sleeve Type | Steel Bar Diameter (mm) | Anchorage Length (mm) |
|---|---|---|---|---|---|
| SP100 | Horizontal defects | 100% | GTZQ4-20A | 20 | 160 |
| SP90 | 90% | ||||
| SP80 | 80% | ||||
| SP70 | 70% | ||||
| SP60 | 60% | ||||
| SP50 | 50% | ||||
| SZ100 | Vertical defects | 100% | GTZQ4-20A | 20 | 160 |
| SZ90 | 90% | ||||
| SZ80 | 80% | ||||
| SZ70 | 70% | ||||
| SZ60 | 60% | ||||
| SZ50 | 50% |
| Pre-Gain (dB) | Threshold (dB) | Sampling Rate (MSPS) | Sampling Length | Sampling Time (ms) | PDT (μs) | HDT (μs) | HLT (μs) |
|---|---|---|---|---|---|---|---|
| 26 | 35 | 1 | 1k | 1.024 | 100 | 200 | 300 |
| Frequency Band Number | Node Number | Frequency Range (kHz) |
|---|---|---|
| 1 | 7 | 0~62.5 |
| 2 | 8 | 62.5~125 |
| 3 | 10 | 125~187.5 |
| 4 | 9 | 187.5~250 |
| 5 | 13 | 250~312.5 |
| 6 | 14 | 312.5~375 |
| 7 | 12 | 375~437.5 |
| 8 | 11 | 437.5~500 |
| Saturation of Grout | Amplitude (dB) | Energy (mV × ms) | Count | |||
|---|---|---|---|---|---|---|
| Horizontal | Vertical | Horizontal | Vertical | Horizontal | Vertical | |
| 100% | 57 | 57 | 30 | 30 | 153 | 153 |
| 90% | 66 | 54 | 69 | 18 | 157 | 179 |
| 80% | 62 | 65 | 67 | 69 | 197 | 188 |
| 70% | 63 | 64 | 75 | 88 | 200 | 250 |
| 60% | 62 | 61 | 62 | 75 | 212 | 252 |
| 50% | 65 | - | 85 | - | 223 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, A.; Li, X.; Fu, F.; Chen, X.; Zhang, Y. Detection of Sleeve Grouting Compactness Based on Acoustic Emission Technology. Materials 2023, 16, 1455. https://doi.org/10.3390/ma16041455
Yu A, Li X, Fu F, Chen X, Zhang Y. Detection of Sleeve Grouting Compactness Based on Acoustic Emission Technology. Materials. 2023; 16(4):1455. https://doi.org/10.3390/ma16041455
Chicago/Turabian StyleYu, Aiping, Xianghao Li, Feng Fu, Xuandong Chen, and Yan Zhang. 2023. "Detection of Sleeve Grouting Compactness Based on Acoustic Emission Technology" Materials 16, no. 4: 1455. https://doi.org/10.3390/ma16041455
APA StyleYu, A., Li, X., Fu, F., Chen, X., & Zhang, Y. (2023). Detection of Sleeve Grouting Compactness Based on Acoustic Emission Technology. Materials, 16(4), 1455. https://doi.org/10.3390/ma16041455






