An Extended Hydro-Mechanical Coupling Model Based on Smoothed Particle Hydrodynamics for Simulating Crack Propagation in Rocks under Hydraulic and Compressive Loads
Abstract
:1. Introduction
2. Seepage Model of Fractured Rock Mass Based on SPH
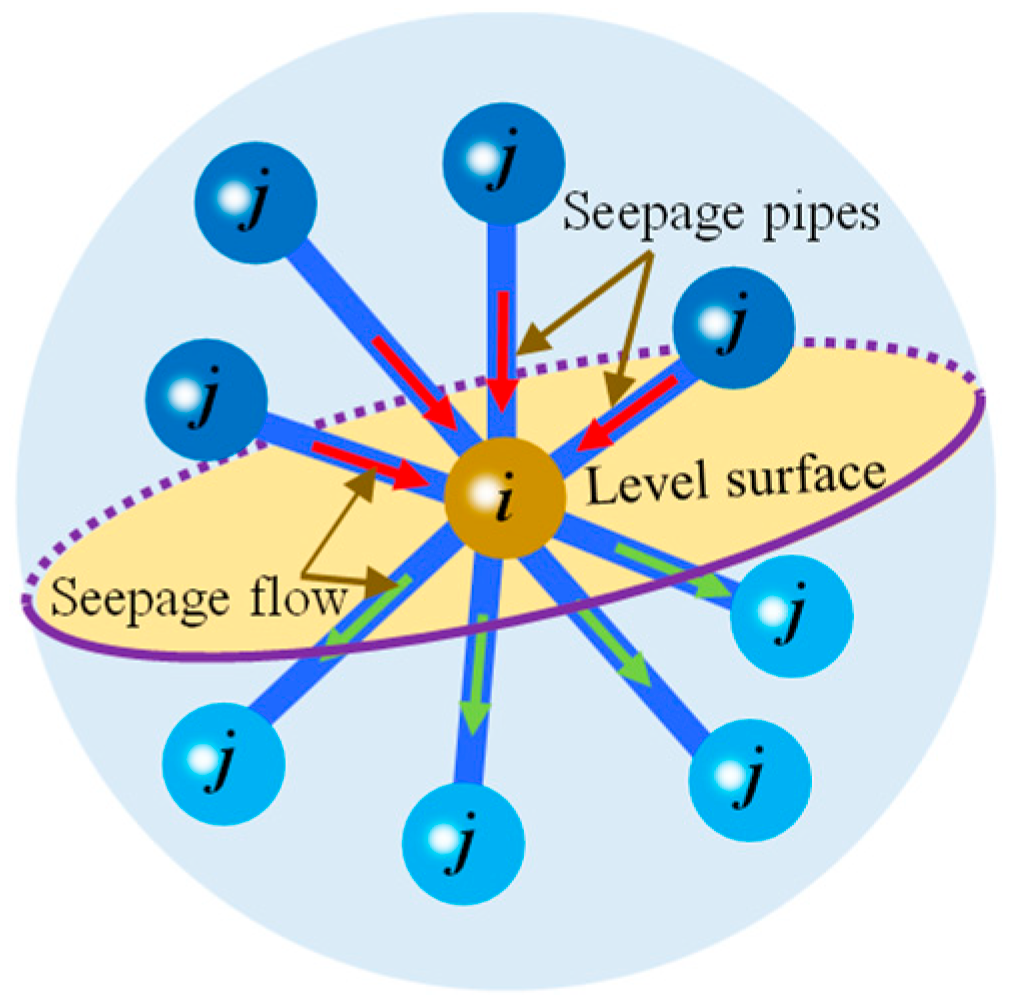
2.1. Seepage Control Equation of Fractured Rock Mass and Its Discretization
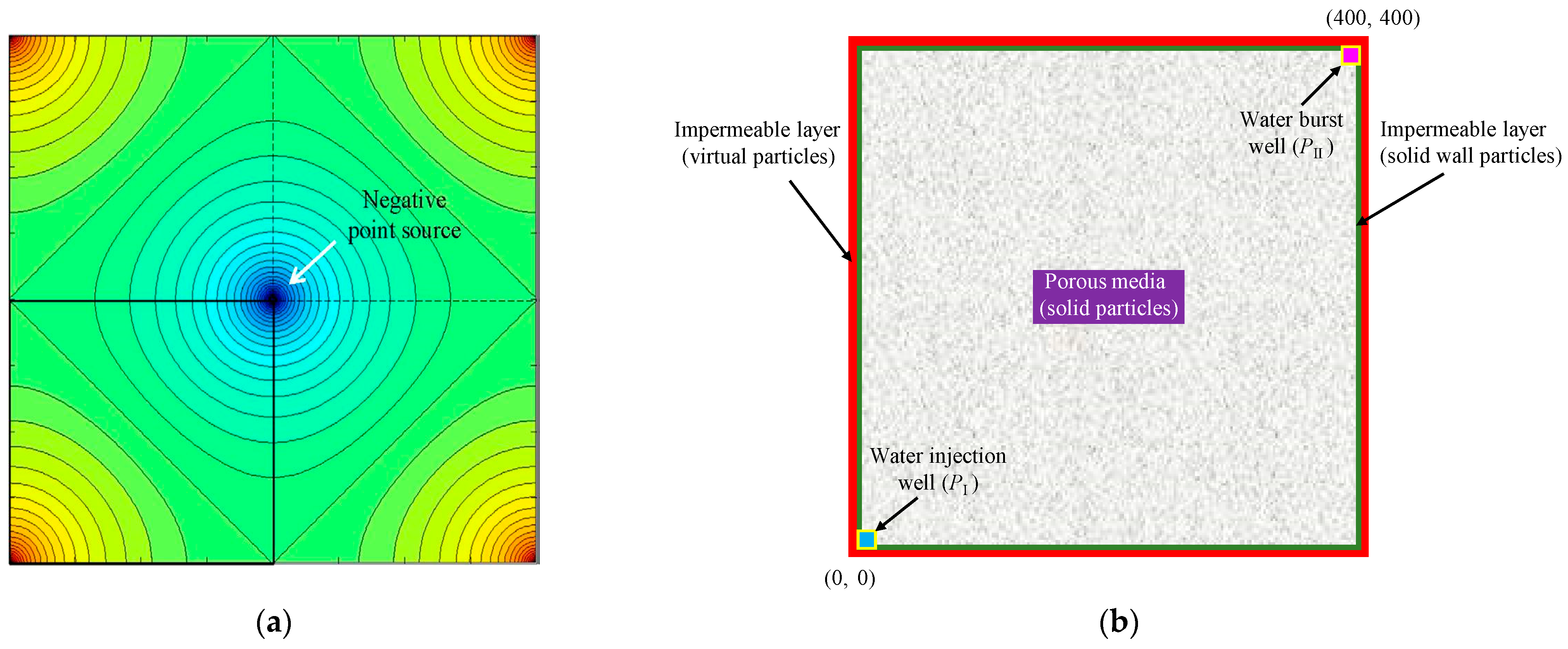
2.2. Benchmark Example—Two-Dimensional Seepage Simulation of Intact Rock Sample
2.3. Two-Dimensional Seepage Characteristics for a Rock Sample with a Prefabricated Horizontal Penetrating Flaw
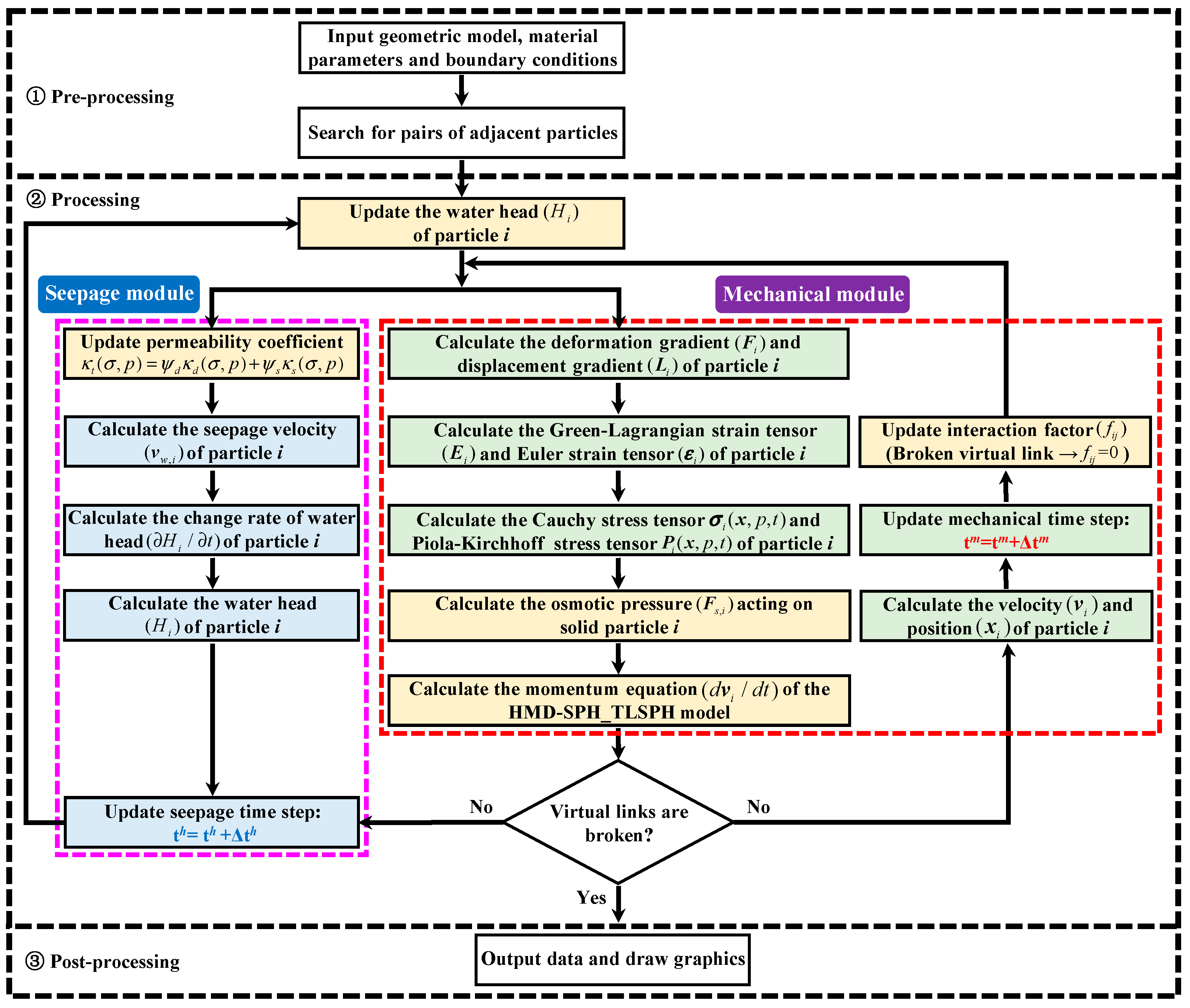
3. Extended Hydro-Mechanical Coupling Model Based on TLF-SPH
3.1. Hydro-Mechanical Coupling Constitutive Equation
3.2. Hydro-Mechanical Coupling Momentum Equation Considering the Osmotic Pressure Effect
3.3. Seepage Control Equation Considering Hydro-Mechanical Damage Coupling Effect
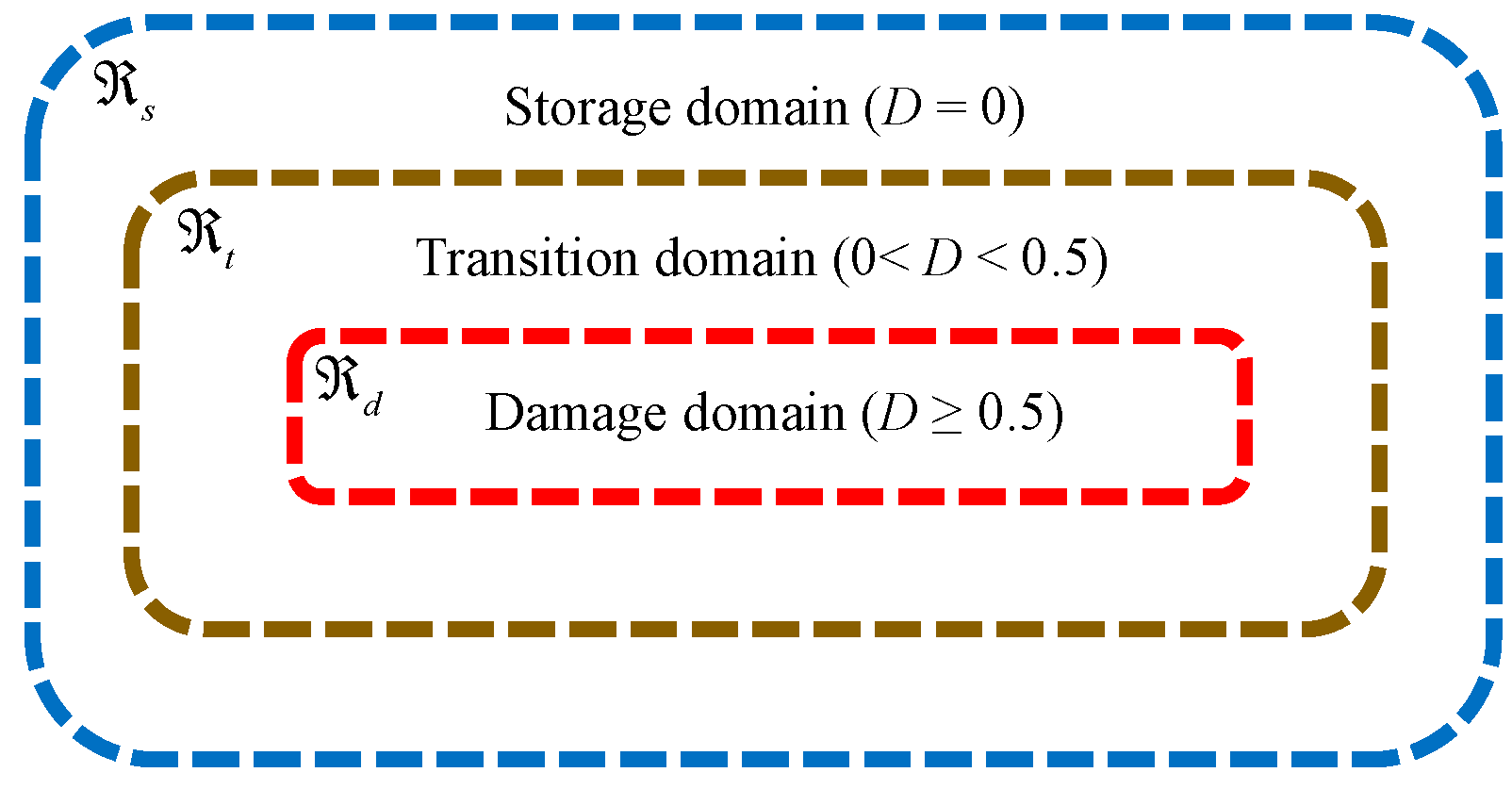
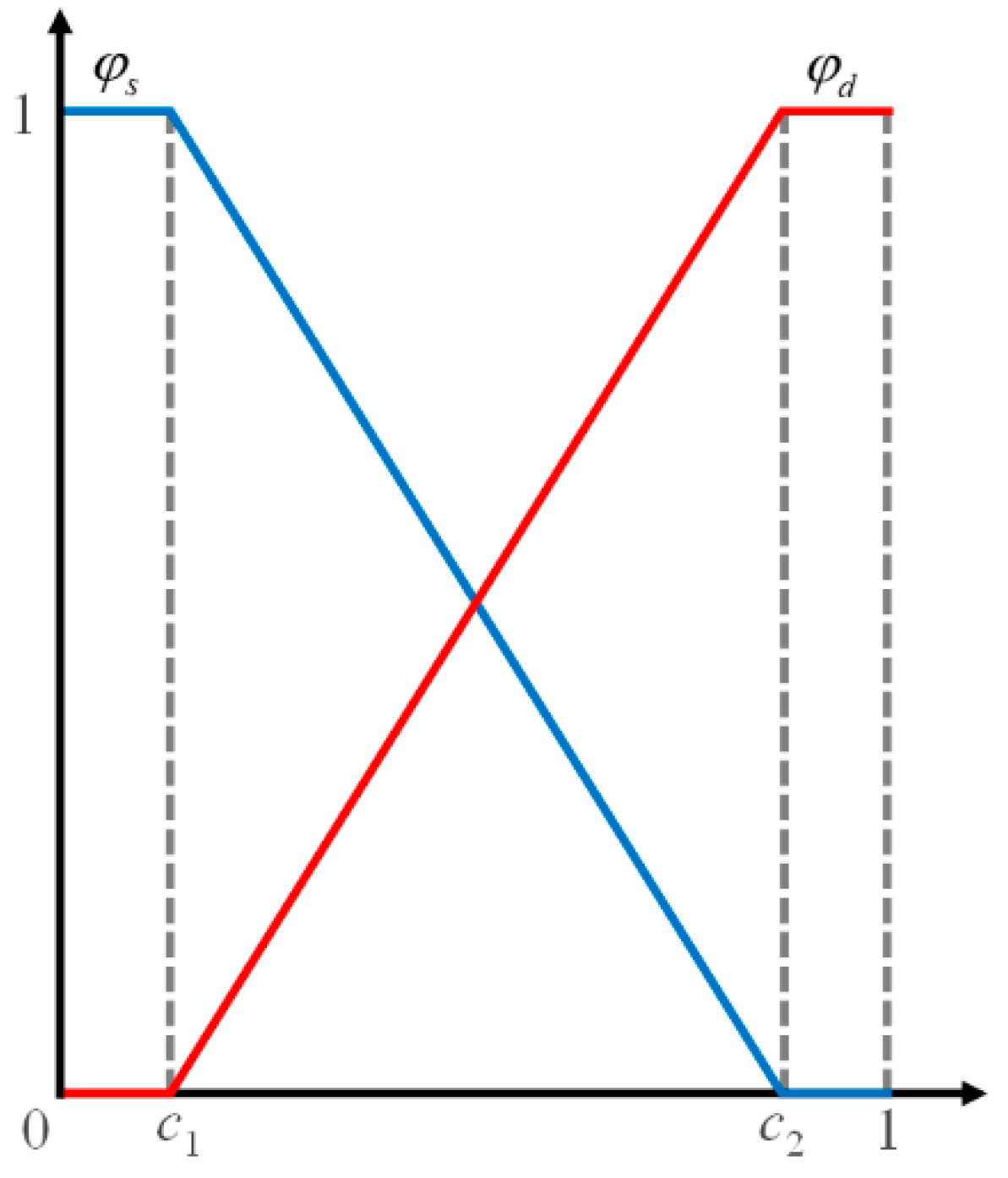
3.4. Failure Criteria and Damage Treatment
4. Simulation Results and Analysis
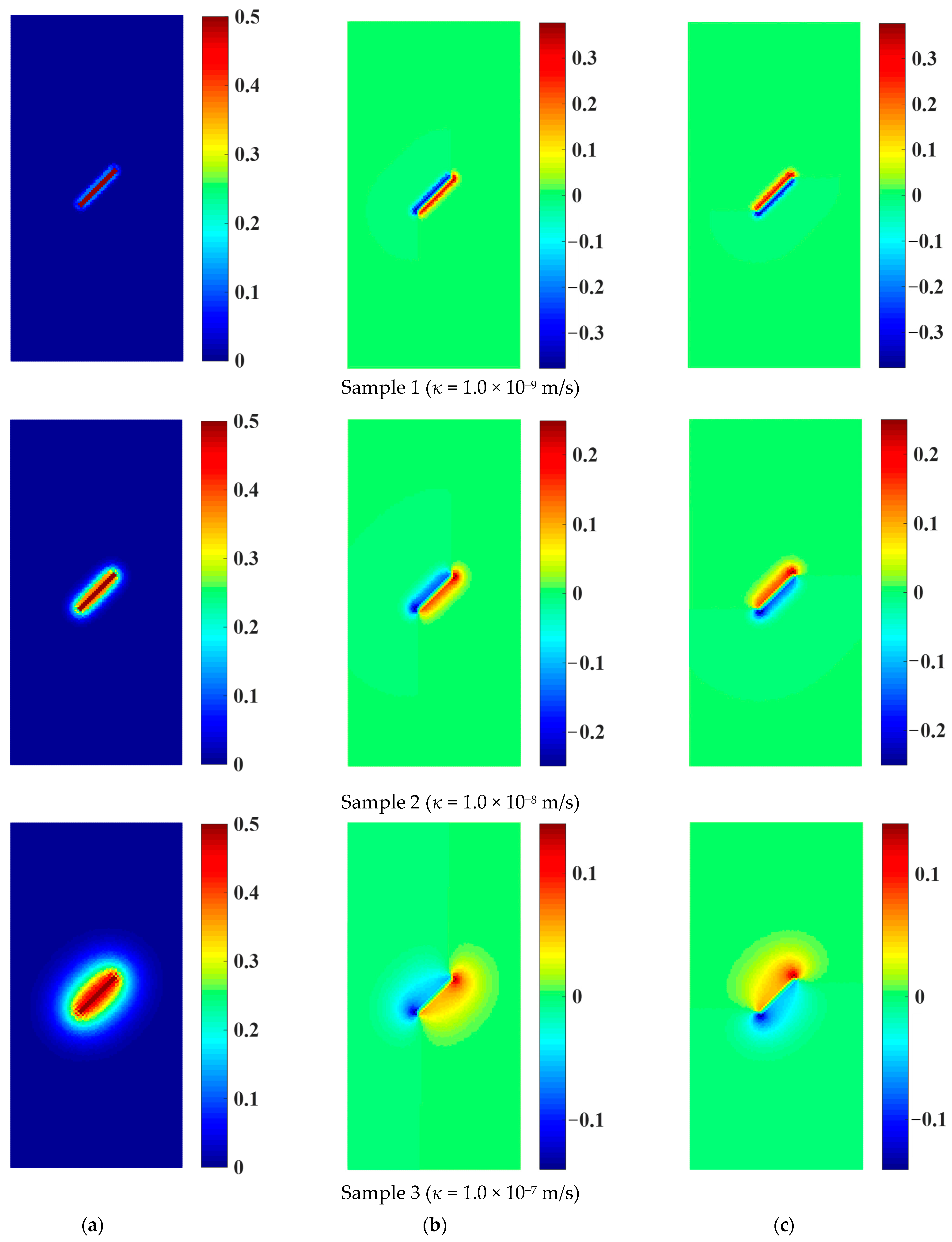
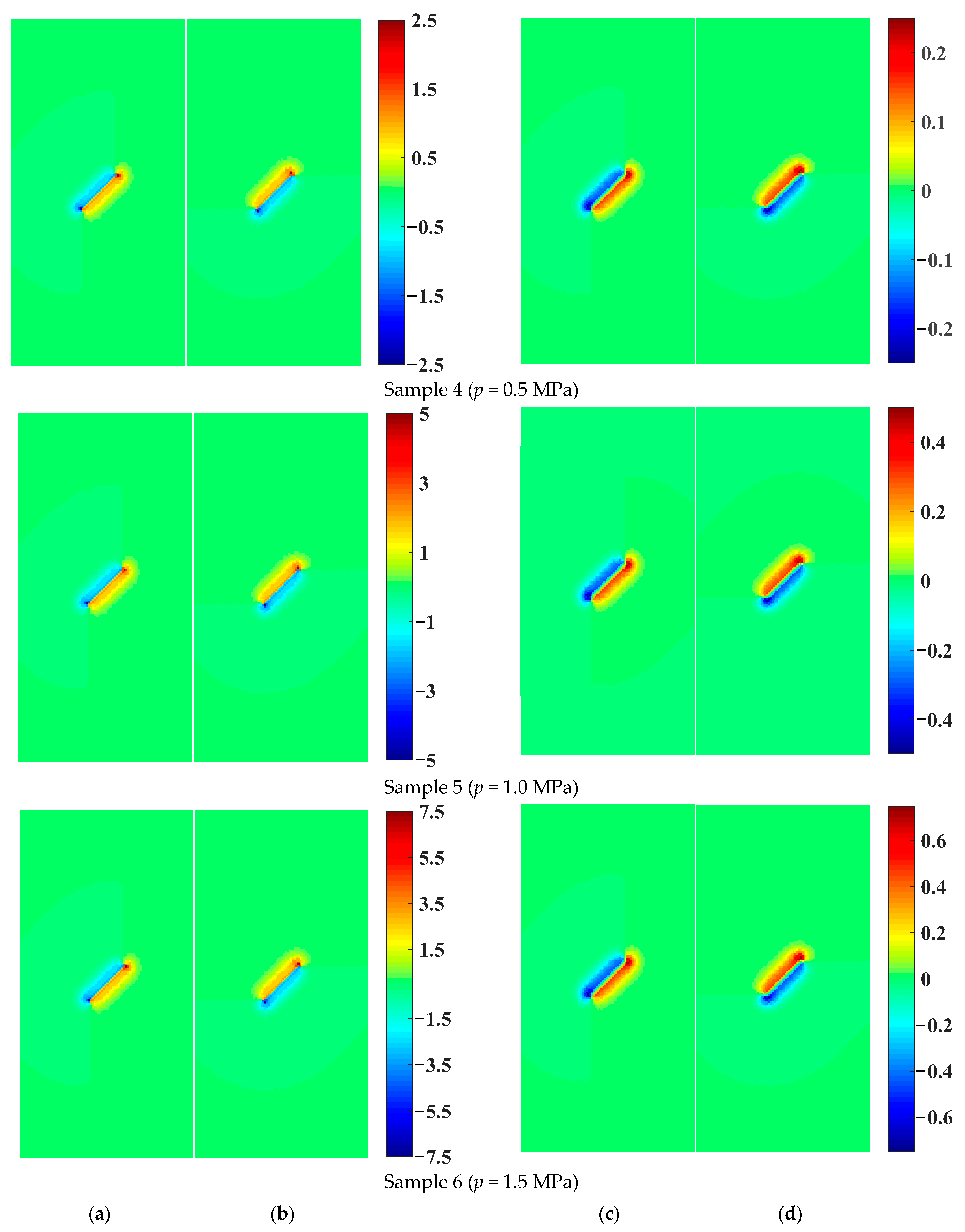
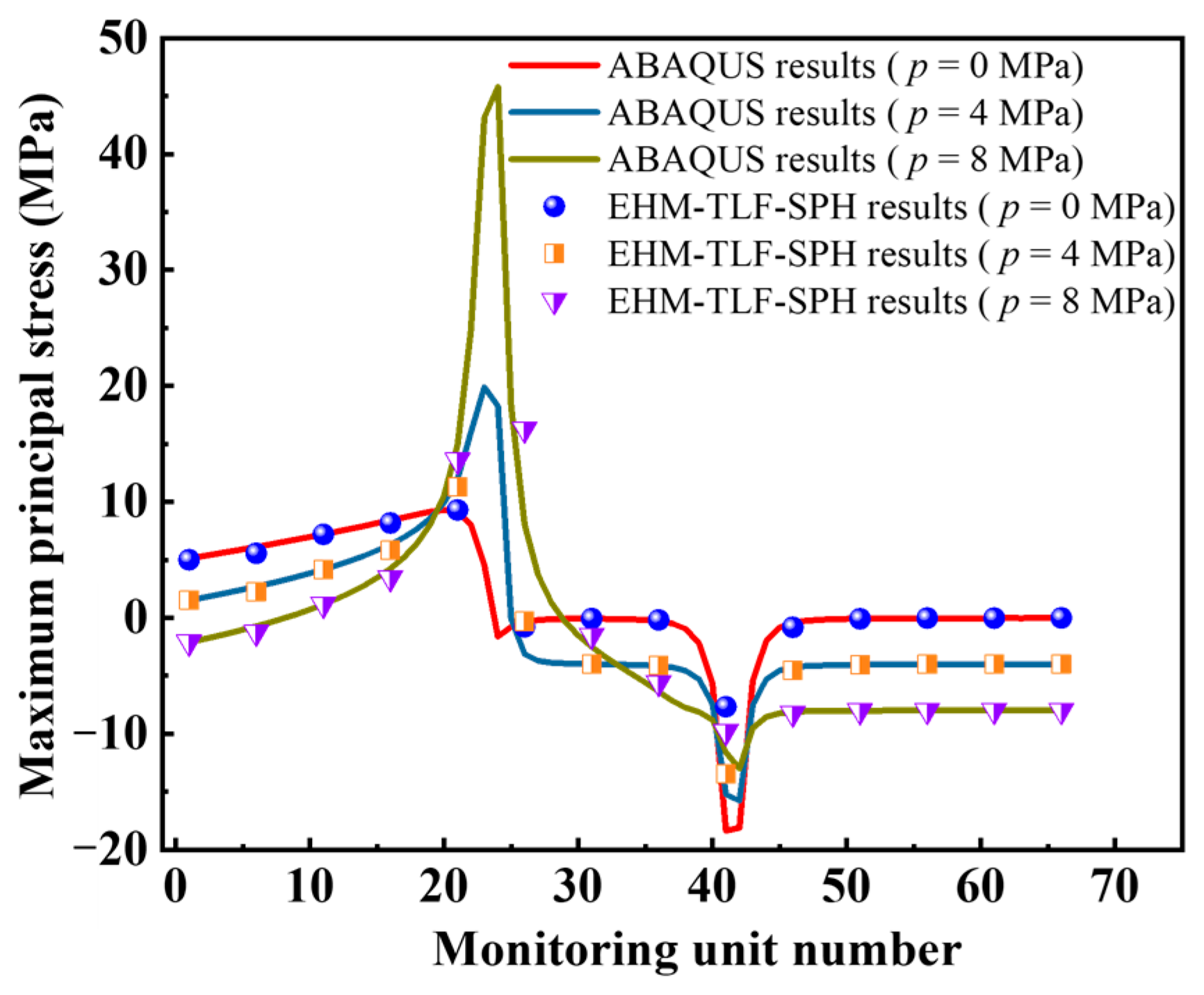
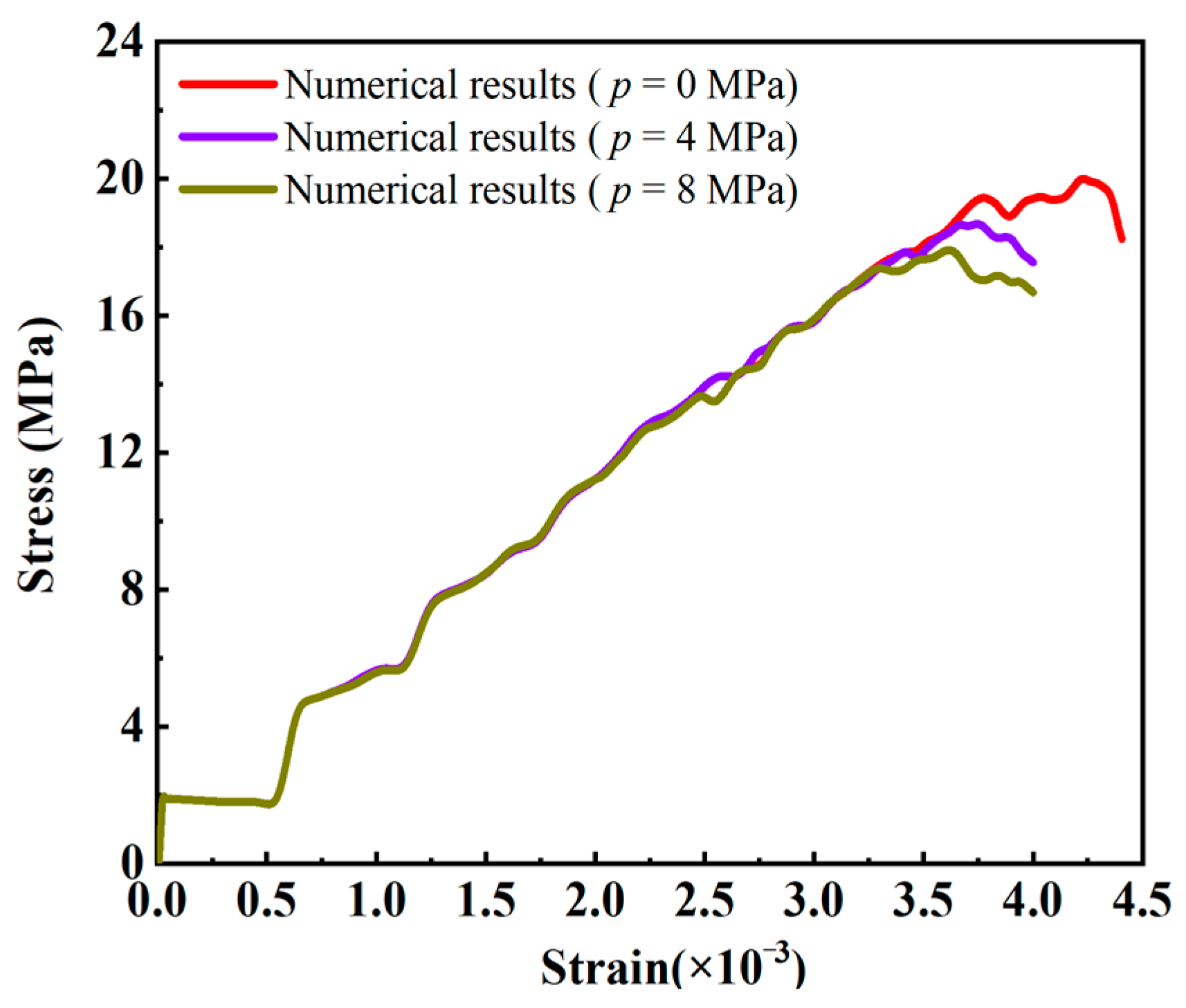
4.1. Influence of Permeability Coefficient and Flaw Water Pressure on Osmotic Pressure
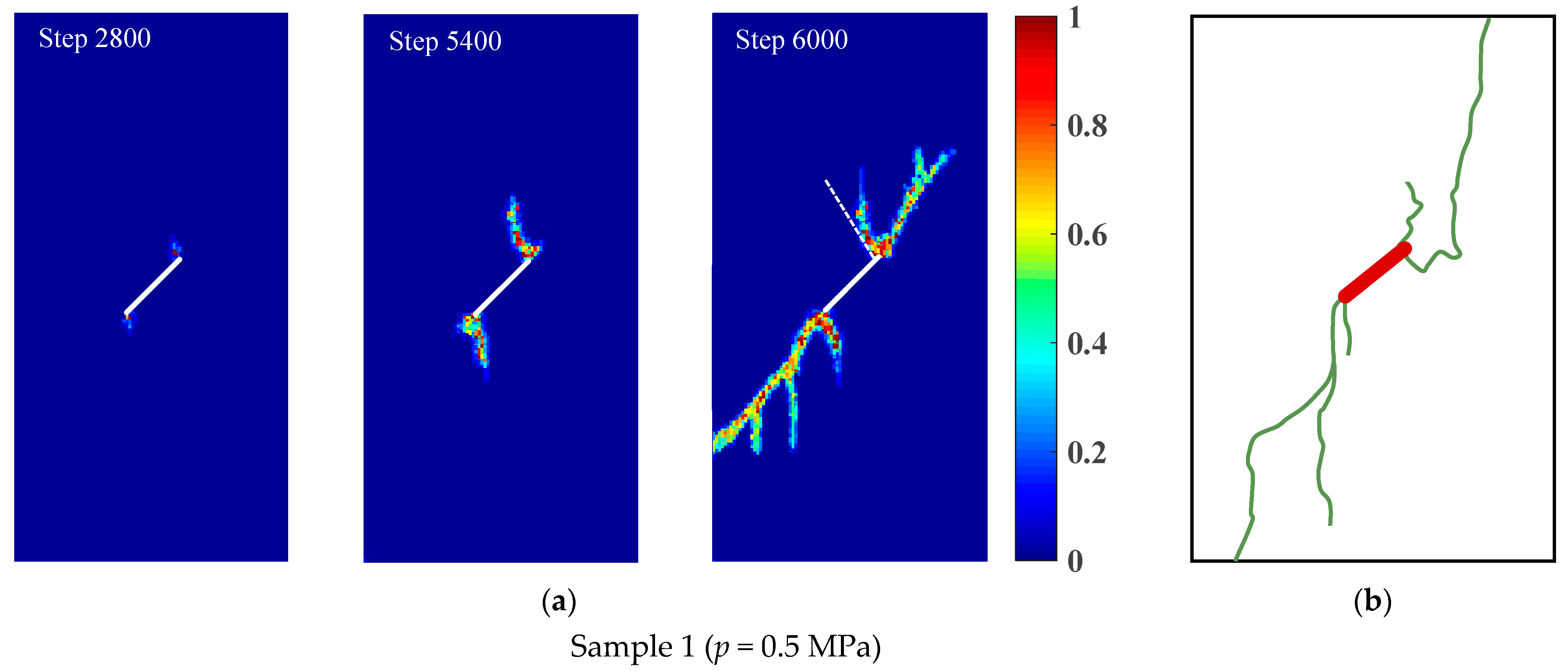
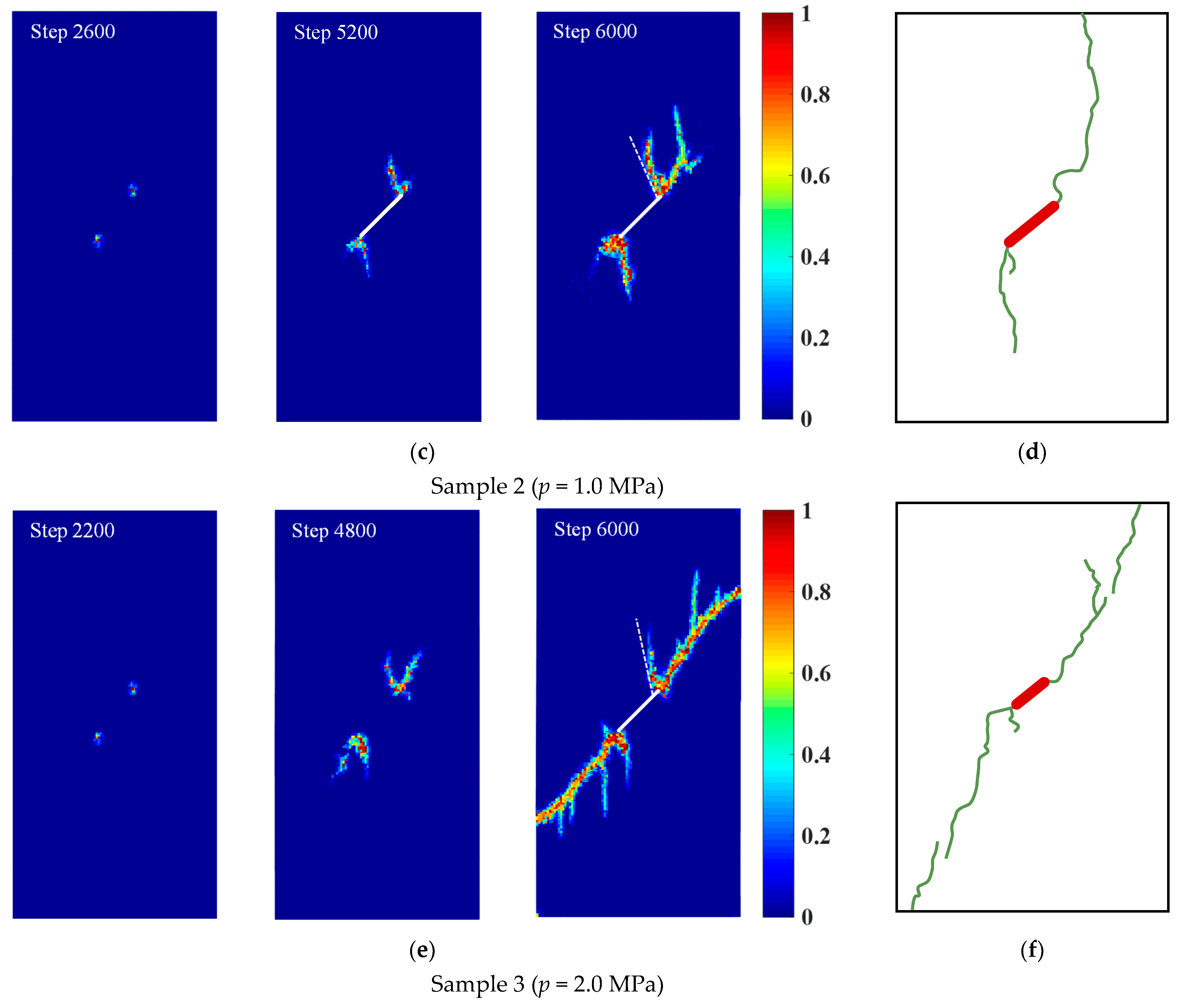
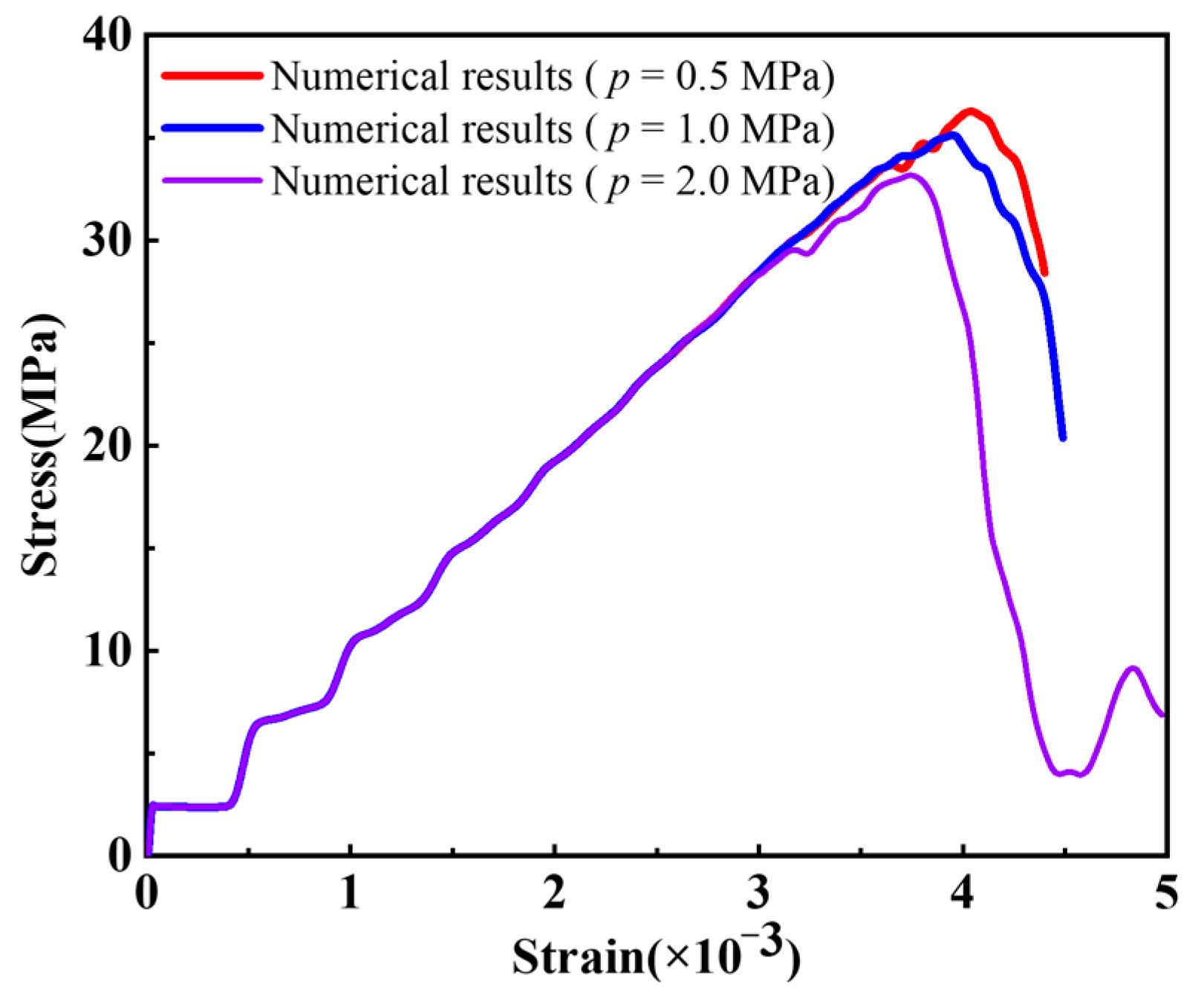
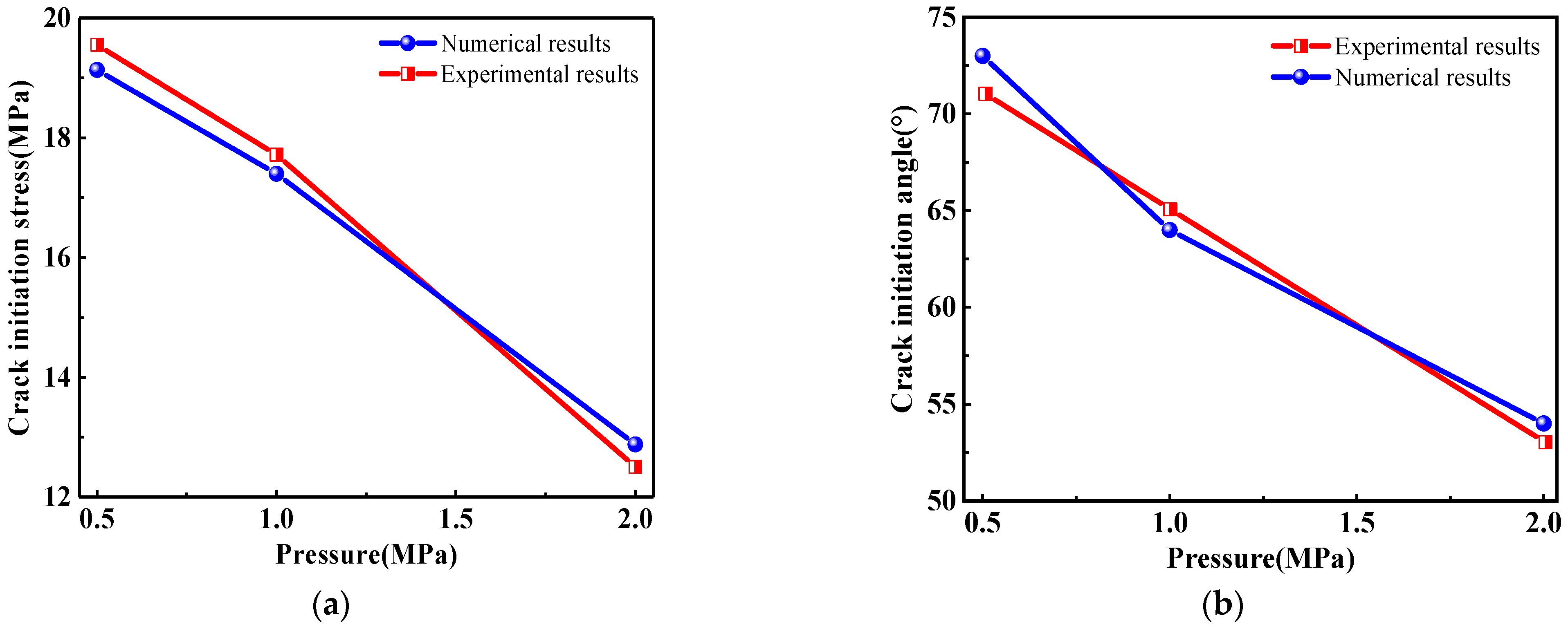
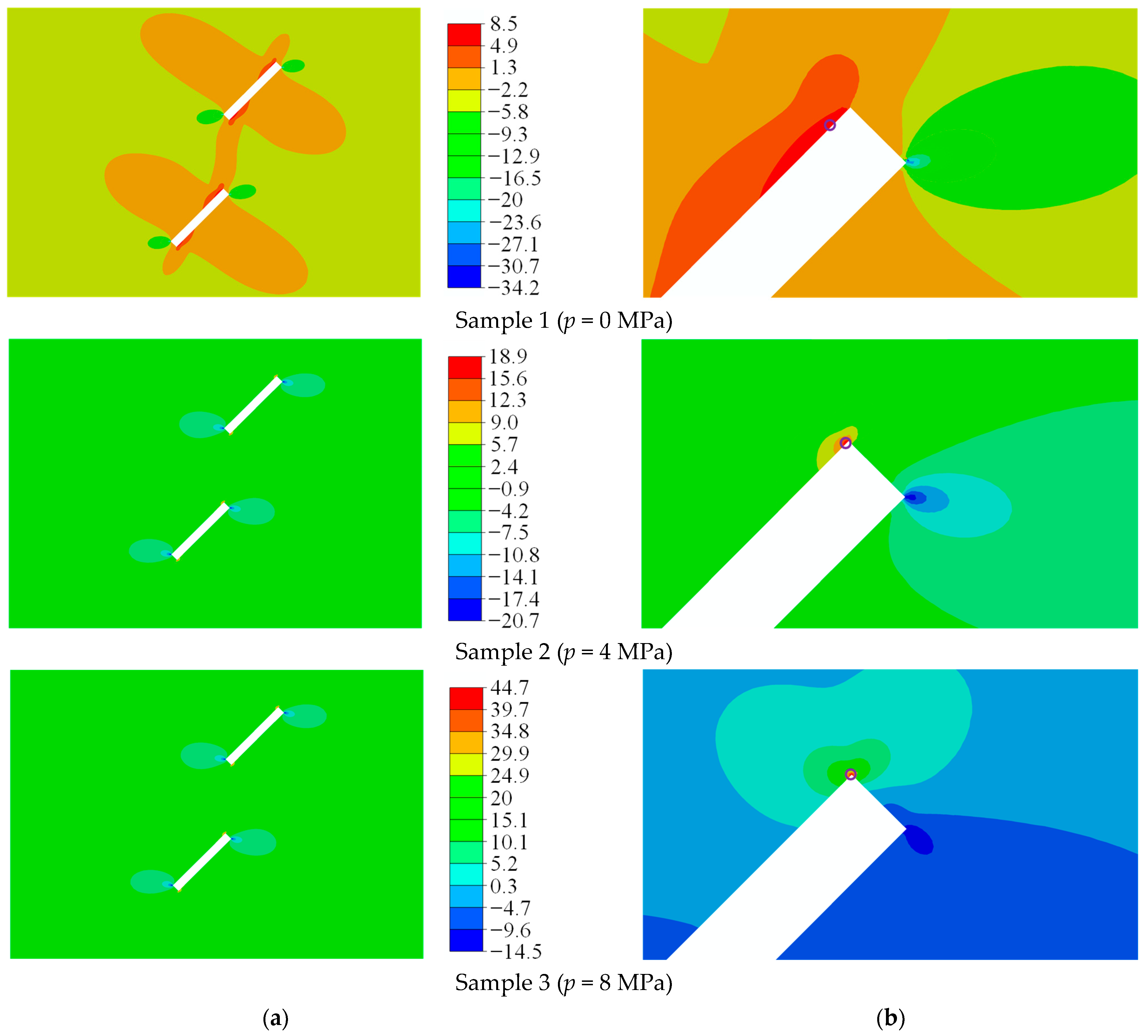
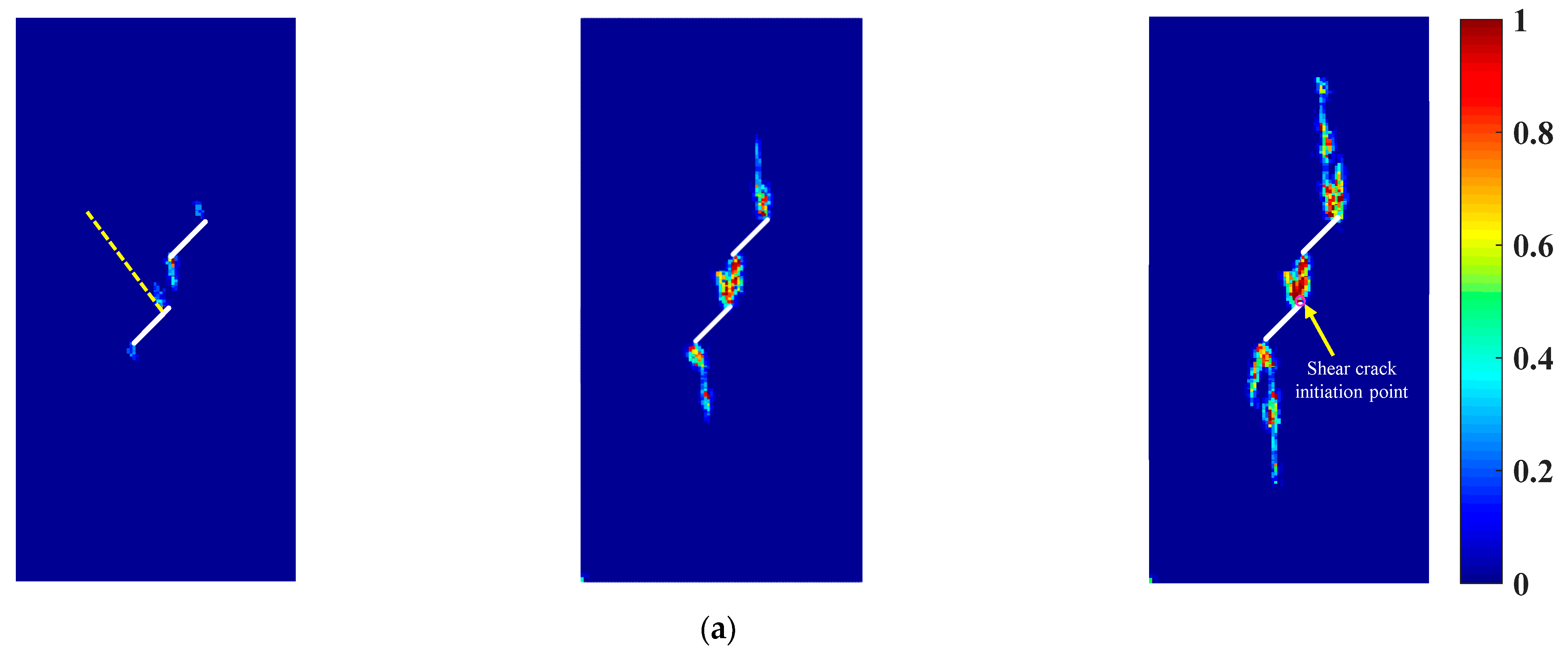
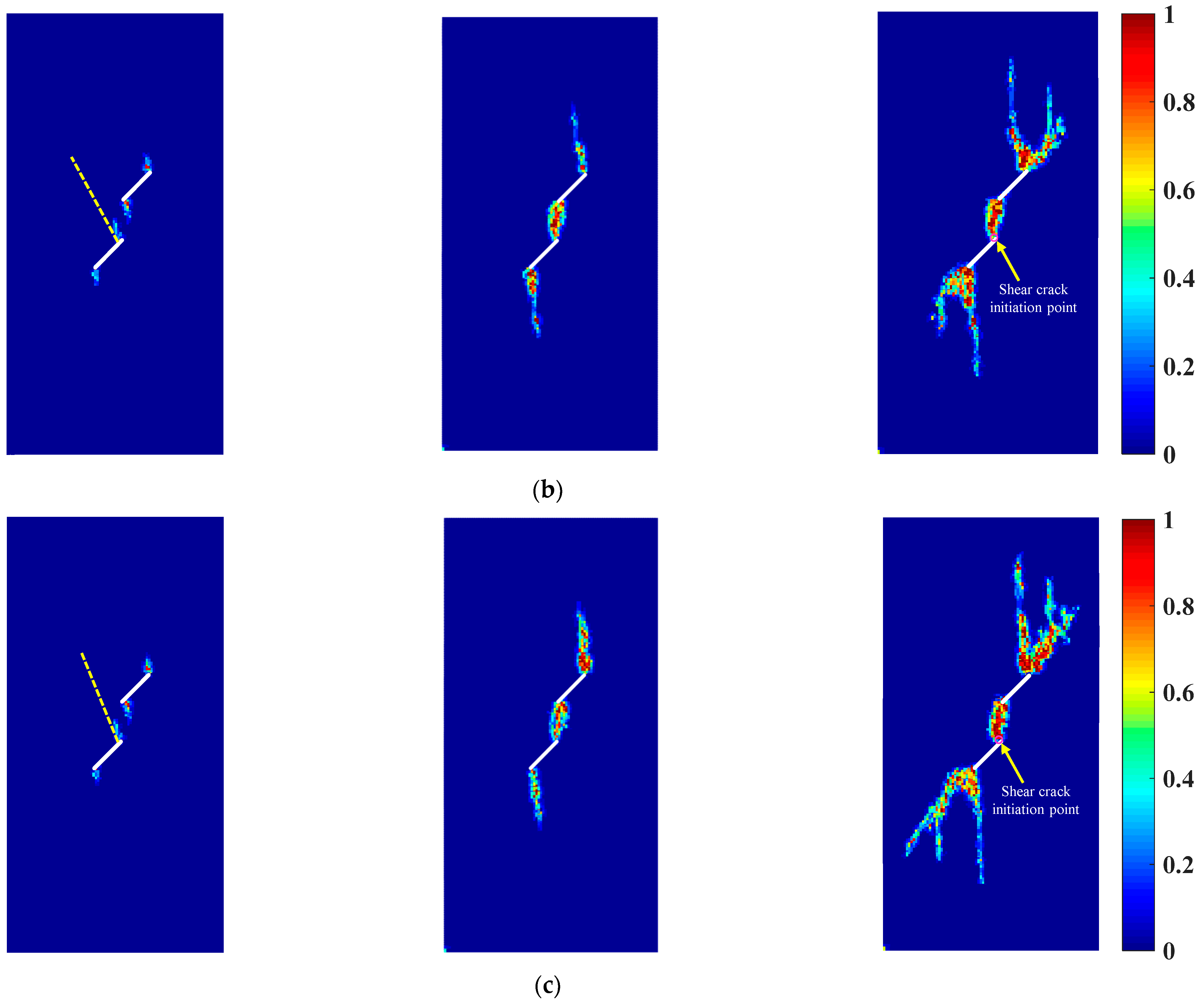
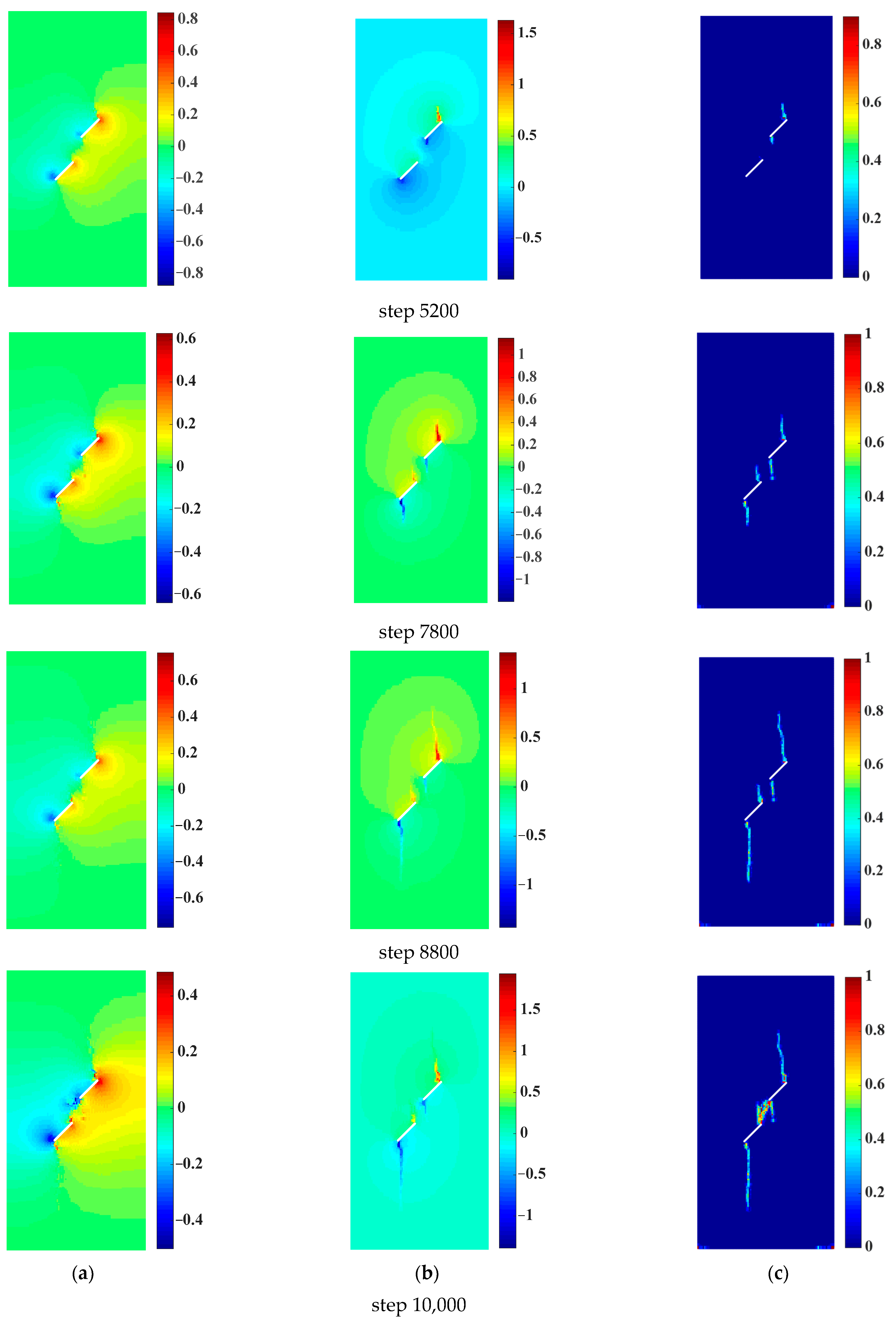
4.2. Crack Initiation and Propagation of Rock Samples with a Prefabricated Flaw under Uniaxial Compression and Flaw Water Pressure
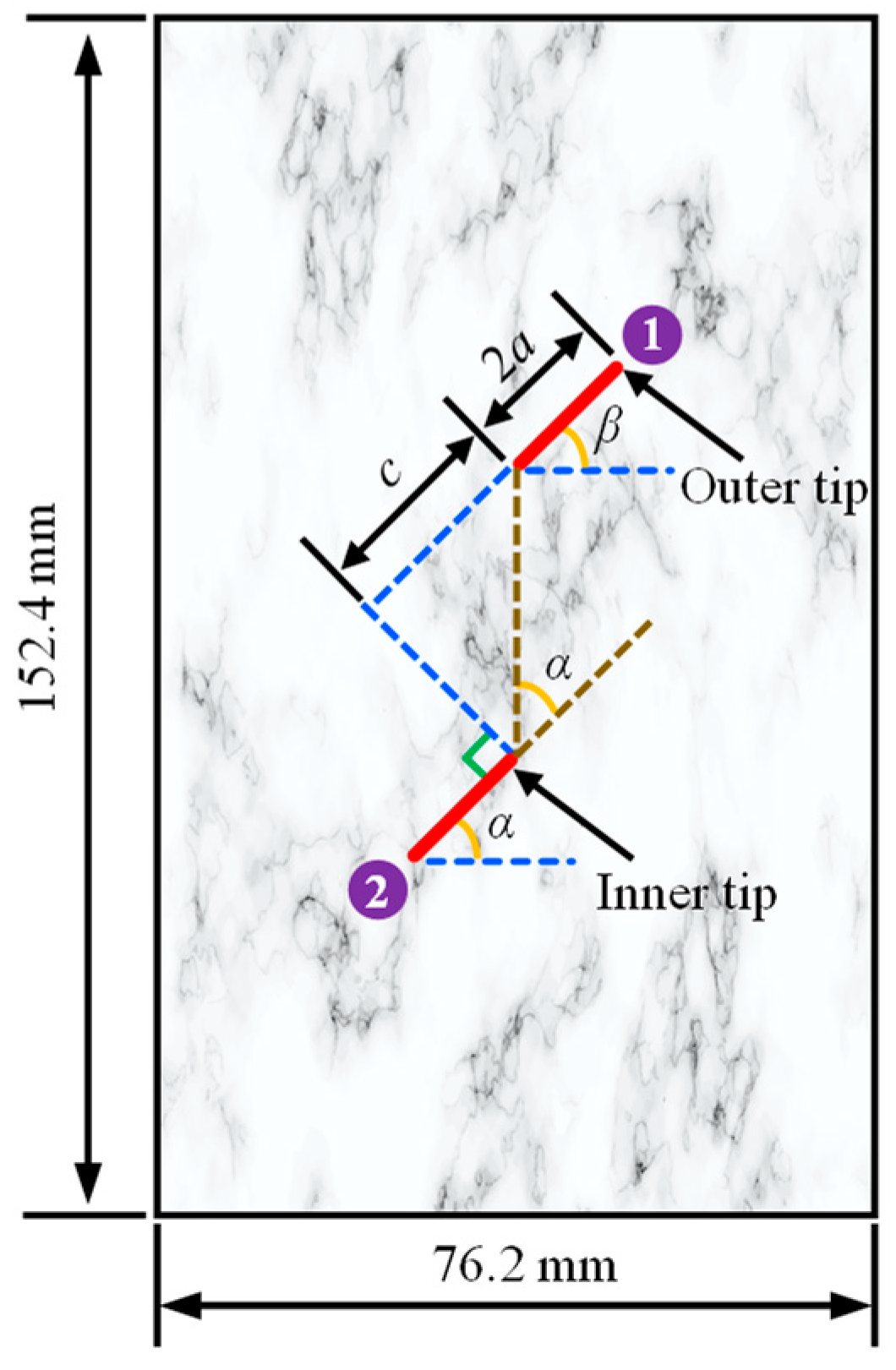
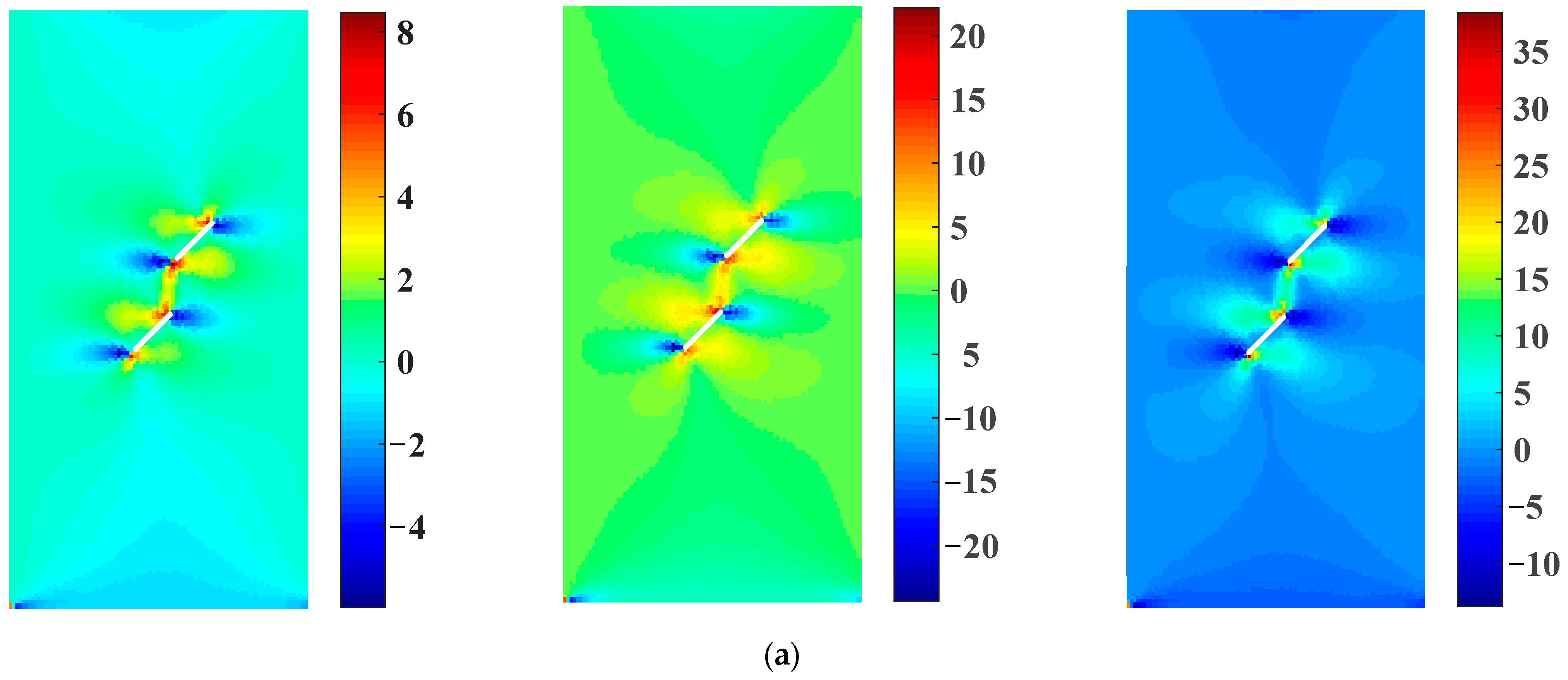
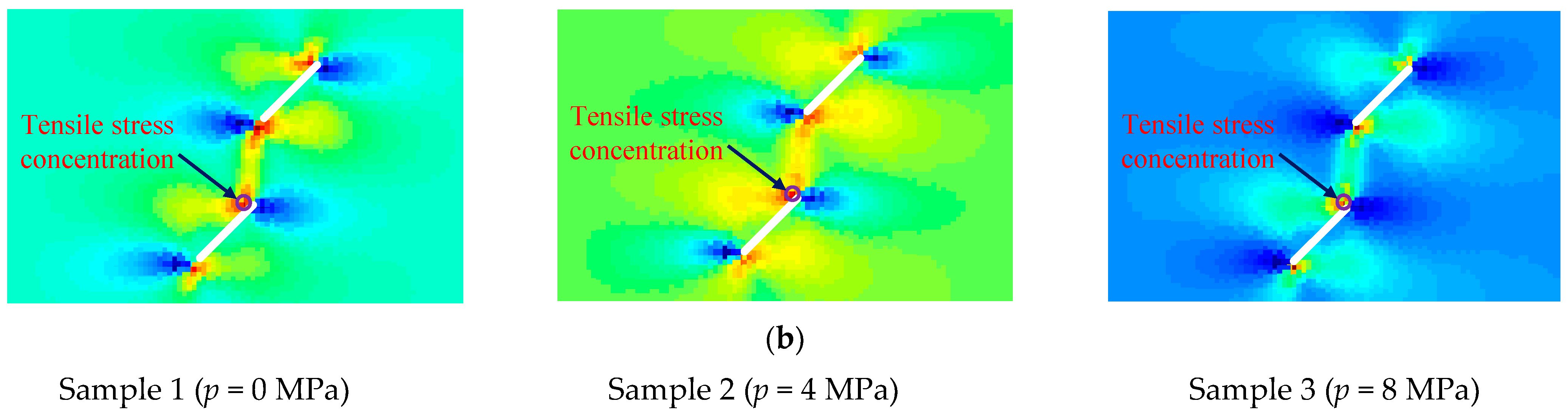
4.3. Crack Propagation and Coalescence of Rock Samples with Two Prefabricated Flaws under Uniaxial Compression and Flaw Water Pressure
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Q.S.; Gan, L.; Wu, Z.J.; Zhou, Y. Analysis of spatial distribution of cracks caused by hydraulic fracturing based on zero-thickness cohesive elements. J. China Coal Soc. 2018, 43, 393–402. (In Chinese) [Google Scholar]
- Silva, B.G.; Einstein, H.H. Finite Element study of fracture initiation in flaws subject to internal fluid pressure and vertical stress. Int. J. Solids Struct. 2014, 51, 4122–4136. [Google Scholar] [CrossRef]
- Robert, Y.J. Advanced Hydraulic Fracture Modeling: Peridynamics, Inelasticity, and Coupling to FEM. Ph.D. Thesis, University of Texas, Austin, TX, USA, 2018. [Google Scholar]
- Bi, J.; Zhou, X.P. A novel numerical algorithm for simulation of initiation, propagation and coalescence of flaws subject to internal fluid pressure and vertical stress in the framework of general particle dynamics. Rock Mech. Rock Eng. 2017, 50, 1833–1849. [Google Scholar] [CrossRef]
- Zheng, F.; Zhuang, X.Y.; Zheng, H.; Jiao, Y.-Y.; Rabczuk, T. Discontinuous deformation analysis with distributed bond for the modelling of rock deformation and failure. Comput. Geotech. 2021, 139, 104413. [Google Scholar] [CrossRef]
- Xu, X.Y.; Wu, Z.J.; Sun, H.; Weng, L.; Chu, Z.F.; Liu, Q.S. An extended numerical manifold method for simulation of grouting reinforcement in deep rock tunnels. Tunn. Undergr. Sp. Tech. 2021, 115, 104020. [Google Scholar] [CrossRef]
- Sun, H.; Wu, Z.J.; Zheng, L.G.; Yang, Y.T.; Huang, D. An extended numerical manifold method for unsaturated soil-water interaction analysis at micro-scale. Int. J. Numer. Anal. Met. 2021, 45, 1500–1525. [Google Scholar] [CrossRef]
- Wu, Z.J.; Sun, H.; Wong, L.N.Y. A cohesive element-based numerical manifold method for hydraulic fracturing modelling with Voronoi grains. Rock Mech. Rock Eng. 2019, 52, 2335–2359. [Google Scholar] [CrossRef]
- Zhang, H.H.; Li, L.X.; An, X.M.; Ma, G.W. Numerical analysis of 2-D crack propagation problems using the numerical manifold method. Eng. Anal. Bound. Elem. 2010, 34, 41–50. [Google Scholar] [CrossRef]
- Ajayi, K.; Shahbazi, K.; Tukkaraja, P.; Katzenstein, K. Numerical investigation of the effectiveness of radon control measures in cave mines. Int. J. Min. Sci. Technol. 2019, 29, 469–475. [Google Scholar] [CrossRef]
- Liu, Q.S.; Sun, L. Simulation of coupled hydro-mechanical interactions during grouting process in fractured media based on the combined finite-discrete element method. Tunn. Undergr. Sp. Tech. 2019, 84, 472–486. [Google Scholar] [CrossRef]
- Sun, L.; Grasselli, G.; Liu, Q.S.; Tang, X.H. Coupled hydro-mechanical analysis for grout penetration in fractured rocks using the finite-discrete element method. Int. J. Rock Mech. Min. 2019, 124, 104138. [Google Scholar] [CrossRef]
- Helmons, R.L.J.; Miedema, S.A.; van Rhee, C. Simulating hydro mechanical effects in rock deformation by combination of the discrete element method and the smoothed particle method. Int. J. Rock Mech. Min. Sci. 2016, 86, 224–234. [Google Scholar] [CrossRef]
- Li, X.F.; Wang, S.B.; Ge, S.R.; Malekian, R.; Li, Z.X.; Li, Y.F. A study on drum cutting properties with full-scale experiments and numerical simulations. Measurement 2018, 114, 25–36. [Google Scholar] [CrossRef]
- Zhou, J.; Lan, H.X.; Zhang, L.Q.; Yang, D.X. Novel grain-based model for simulation of brittle failure of Alxa porphyritic granite. Eng. Geol. 2019, 251, 100–114. [Google Scholar] [CrossRef]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Huang, D.; Cai, Z.; Xu, Y.P. An extended ordinary state-based peridynamic approach for modelling hydraulic fracturing. Eng. Fract. Mech. 2020, 234, 107086. [Google Scholar] [CrossRef]
- Zhou, X.P.; Wang, Y.T.; Shou, Y.D. Hydromechanical bond-based peridynamic model for pressurized and fluid-driven fracturing processes in fissured porous rocks. Int. J. Rock Mech. Min. 2020, 132, 104383. [Google Scholar] [CrossRef]
- Shou, Y.D. Peridynamic Numerical Simulation of Thermo-Hydromechanical Coupled Problems in Crack-Weakened Rock. Ph.D. Thesis, Chongqing University, Chongqing, China, 2017. [Google Scholar]
- Zhou, X.P.; Shou, Y.D. Numerical simulation of failure of rock-like material subjected to compressive loads using improved peridynamic method. Int. J. Geomech. 2017, 17, 04016086. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to testing the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Xu, X.Y.; Yu, P. A technique to remove the tensile instability in weakly compressible SPH. Comput. Mech. 2018, 62, 963–990. [Google Scholar] [CrossRef]
- Ren, M.K.; Gu, J.F.; Li, Z.; Ruan, S.L.; Shen, C.Y. Simulation of polymer melt injection molding filling flow based on an improved SPH method with modified low-dissipation Riemann solver. Macromol. Theory Simul. 2021, 31, 2100029. [Google Scholar] [CrossRef]
- Mu, D.R.; Li, Z.M.; Tang, A.P.; Liu, Q.; Huang, D.L. A coupled thermo-mechanical bond-based smoothed particle dynamics model for simulating thermal cracking in rocks. Eng. Fract. Mech. 2022, 265, 108364. [Google Scholar] [CrossRef]
- Yu, S.Y.; Ren, X.H.; Zhang, J.X.; Sun, Z.H. An improved form of SPH method for simulating the thermo-mechanical-damage coupling problems and its applications. Rock Mech. Rock Eng. 2021, 55, 1633–1648. [Google Scholar] [CrossRef]
- Zhou, X.P.; Bi, J. Numerical simulation of thermal cracking in rocks based on general particle dynamics. J. Eng. Mech. 2018, 144, 04017156. [Google Scholar] [CrossRef]
- Gharehdash, S.; Barzegar, M.; Palymskiy, I.B.; Fomin, P.A. Blast induced fracture modelling using smoothed particle hydrodynamics. Int. J. Impact Eng. 2020, 135, 103235. [Google Scholar] [CrossRef]
- Gharehdash, S.; Sainsbury, B.-A.L.; Barzegar, M.; Palymskiy, I.B.; Fomin, P.A. Field scale modelling of explosion-generated crack densities in granitic rocks using dual-support smoothed particle hydrodynamics (DS-SPH). Rock Mech. Rock Eng. 2021, 54, 4419–4454. [Google Scholar] [CrossRef]
- Gharehdash, S.; Shen, L.M.; Gan, Y.X. Numerical study on mechanical and hydraulic behaviour of blast-induced fractured rock. Eng. Comput. 2019, 36, 915–929. [Google Scholar] [CrossRef]
- Yu, S.Y.; Ren, X.H.; Wang, H.J.; Zhang, J.X.; Sun, Z.H. Numerical simulation on the interaction modes between hydraulic and natural fractures based on a new SPH method. Arab. J. Sci. Eng. 2021, 46, 11089–11100. [Google Scholar]
- Mu, D.R.; Tang, A.P.; Huang, D.L. A hydraulic-mechanical coupling model based on smoothed particle dynamics for simulating rock fracture. Arab. J. Geosci. 2022, 15, 485. [Google Scholar] [CrossRef]
- Bi, J.; Zhou, X.P. Numerical simulation of kinetic friction in the fracture process of rocks in the framework of General Particle Dynamics. Comput. Geotech. 2017, 83, 1–15. [Google Scholar] [CrossRef]
- Snow, D.T. Anisotropic permeability of fractured media. Water Resour. Res. 1969, 5, 1273–1289. [Google Scholar] [CrossRef]
- Lee, S.; Wheeler, M.F.; Wick, T. Pressure and fluid-driven fracture propagation in porous media using an adaptive finite element phase field model. Comput. Methods Appl. Mech. Eng. 2016, 305, 111–132. [Google Scholar] [CrossRef]
- Wang, Y.T. The Coupled Thermo-Hydro-Chemo-Mechanical Peridynamics for Rock Masses and Numerical Study. Ph.D. Thesis, Chongqing University, Chongqing, China, 2019. [Google Scholar]
- Shou, Y.D.; Zhou, X.P. A coupled hydro-mechanical non-ordinary state-based peridynamics for the fissured porous rocks. Eng. Anal. Bound. Elem. 2021, 123, 133–146. [Google Scholar] [CrossRef]
- Katiyar, A.; Foster, J.T.; Ouchi, H.; Sharma, M.M. A peridynamic formulation of pressure driven convective fluid transport in porous media. J. Comput. Phys. 2014, 261, 209–229. [Google Scholar] [CrossRef]
- Peng, S.J. Hydraulic Fracture Simulation Method in Complex Reservoir by Using Virtual Internal Bond. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2018. [Google Scholar]
- Mu, D.R.; Wen, A.H.; Zhu, D.Q.; Tang, A.P.; Nie, Z.; Wang, Z.Y. An improved smoothed particle hydrodynamics method for simulating crack propagation and coalescence in brittle fracture of rock materials. Theory Appl. Fract. Mech. 2022, 119, 103355. [Google Scholar] [CrossRef]
- Belytschko, T.; Guo, Y.; Kam Liu, W.; Ping Xiao, S. A unified stability analysis of meshless particle methods. Int. J. Numer. Methods Eng. 2000, 48, 1359–1400. [Google Scholar] [CrossRef]
- Sun, P.N. Study on SPH Method for the Simulation of Object-Free Surface Interactions. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2018. [Google Scholar]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, W.J.; Dai, Z.L.; Xu, Q. Numerical simulation of flow processes in liquefied soils using a soil-water-coupled smoothed particle hydrodynamics method. Nat. Hazards 2013, 69, 809–827. [Google Scholar] [CrossRef]
- Sun, C.Q. Numerical Simulation Study of Disaster Evolution and Water Inrush in Filling Type Structure of Tunnel. Ph.D. Thesis, Shandong University, Jinan, China, 2016. [Google Scholar]
- Monaghan, J.J.; Gingold, R.A. Shock simulation by the particle method SPH. J. Comput. Phys. 1983, 52, 374–389. [Google Scholar] [CrossRef]
- Yang, T.H. Study on Infiltrate Character and Coupling Analysis of Seepage and Stress in Rock Failure Process. Ph.D. Thesis, Northeastern University, Boston, MA, USA, 2001. [Google Scholar]
- Wang, Y.T.; Zhou, X.P.; Xu, X. Numerical simulation of propagation and coalescence of flaws in rock materials under compressive loads using the extended non-ordinary state-based peridynamics. Eng. Fract. Mech. 2016, 163, 248–273. [Google Scholar] [CrossRef]
- Chakraborty, S.; Shaw, A. A pseudo-spring based fracture model for SPH simulation of impact dynamics. Int. J. Impact Eng. 2013, 58, 84–95. [Google Scholar] [CrossRef]
- Islam, M.R.I.; Peng, C. A Total Lagrangian SPH method for modelling damage and failure in solids. Int. J. Mech. Sci. 2019, 157–158, 498–511. [Google Scholar] [CrossRef]
- Mu, D.R.; Tang, A.P.; Li, Z.M.; Qu, H.G.; Huang, D.L. A bond-based smoothed particle hydrodynamics considering frictional contact effect for simulating rock fracture. Acta Geotech. 2022, 25, 1–25. [Google Scholar] [CrossRef]
- Wei, C.; Zhu, W.S.; Li, Y.; Wang, S.G.; Dong, Z.X.; Cai, W.B. Experimental study and numerical simulation of inclined flaws and horizontal fissures propagation and coalescence process in rocks. Rock Soil Mech. 2019, 40, 4533–4542+4553. [Google Scholar]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Shen, B.; Stephansson, O.; Einstein, H.H.; Ghahreman, B. Coalescence of fractures under shear stresses experiments. J. Geophys. Res. 1995, 100, 5975–5990. [Google Scholar] [CrossRef]
- Wong, N.Y. Crack Coalescence in Molded Gypsum and Carrara Marble. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2008. [Google Scholar]
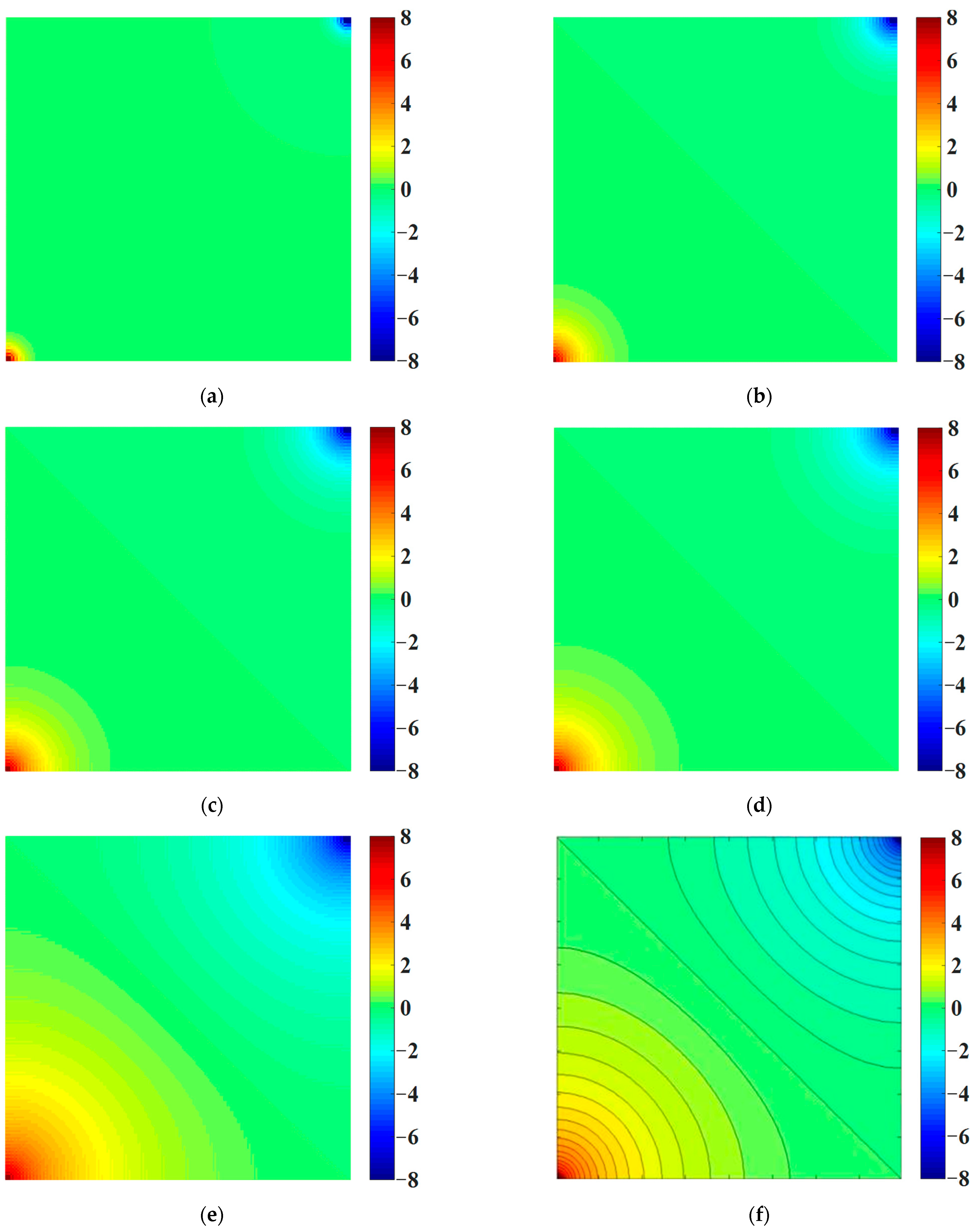
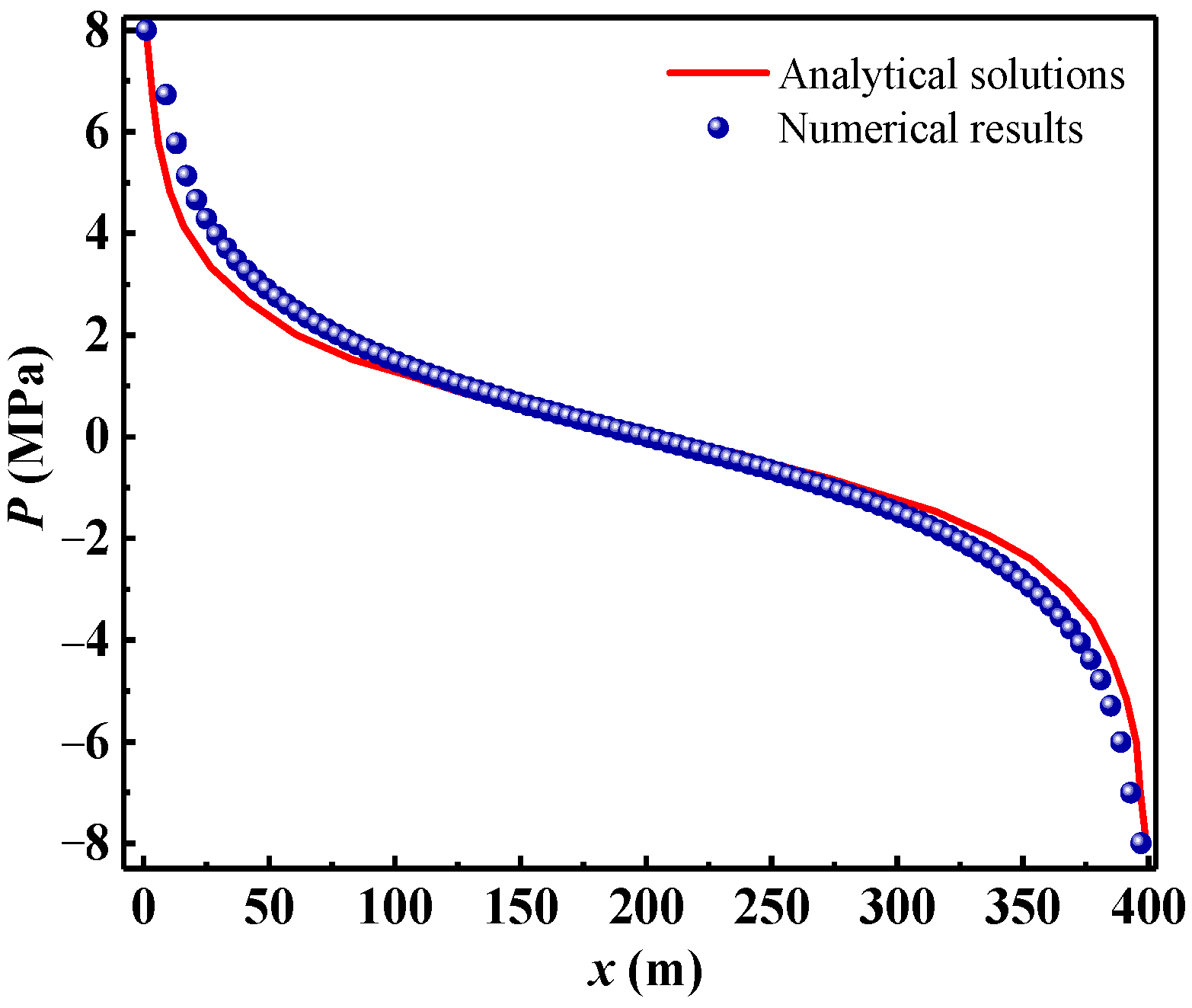
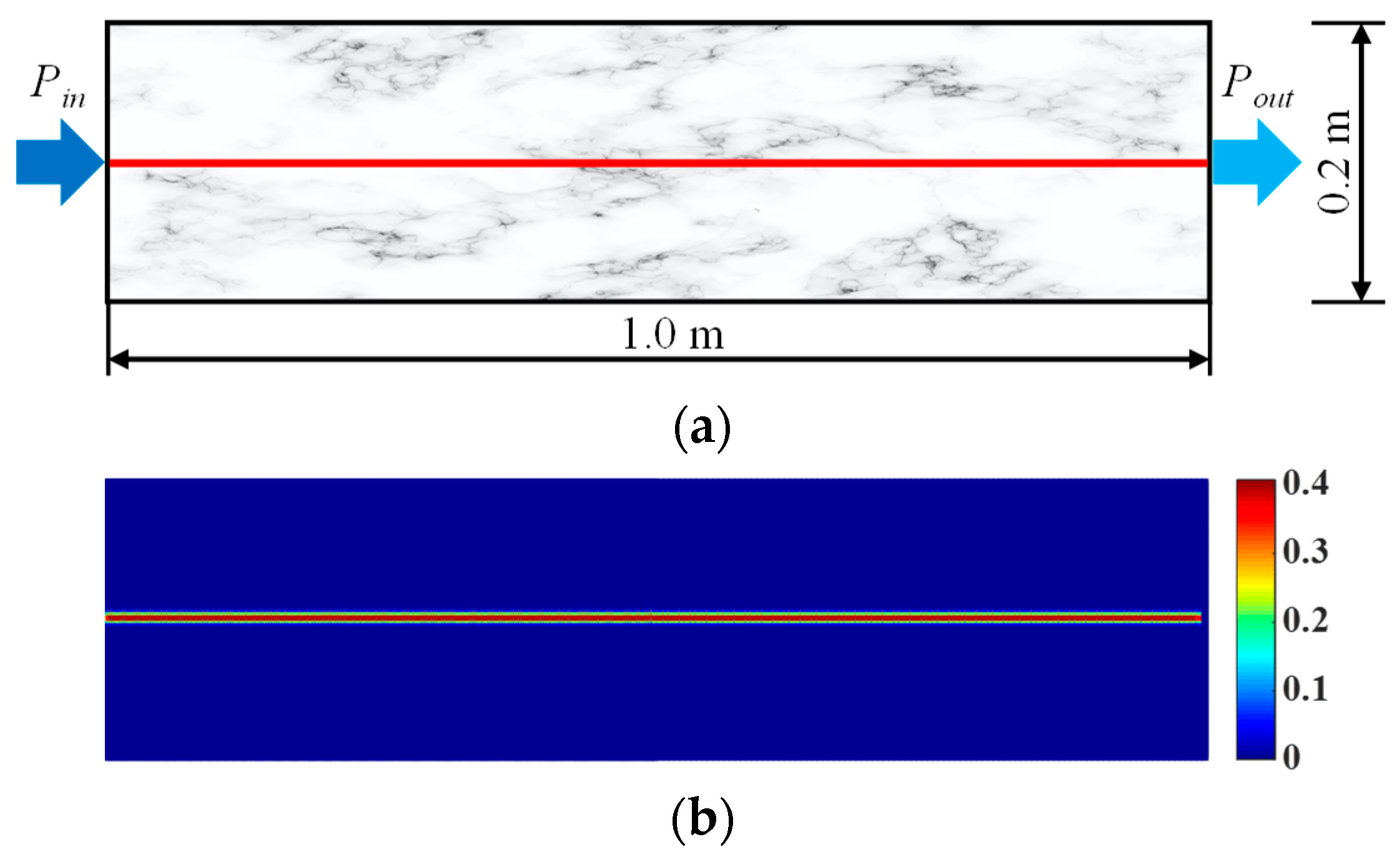
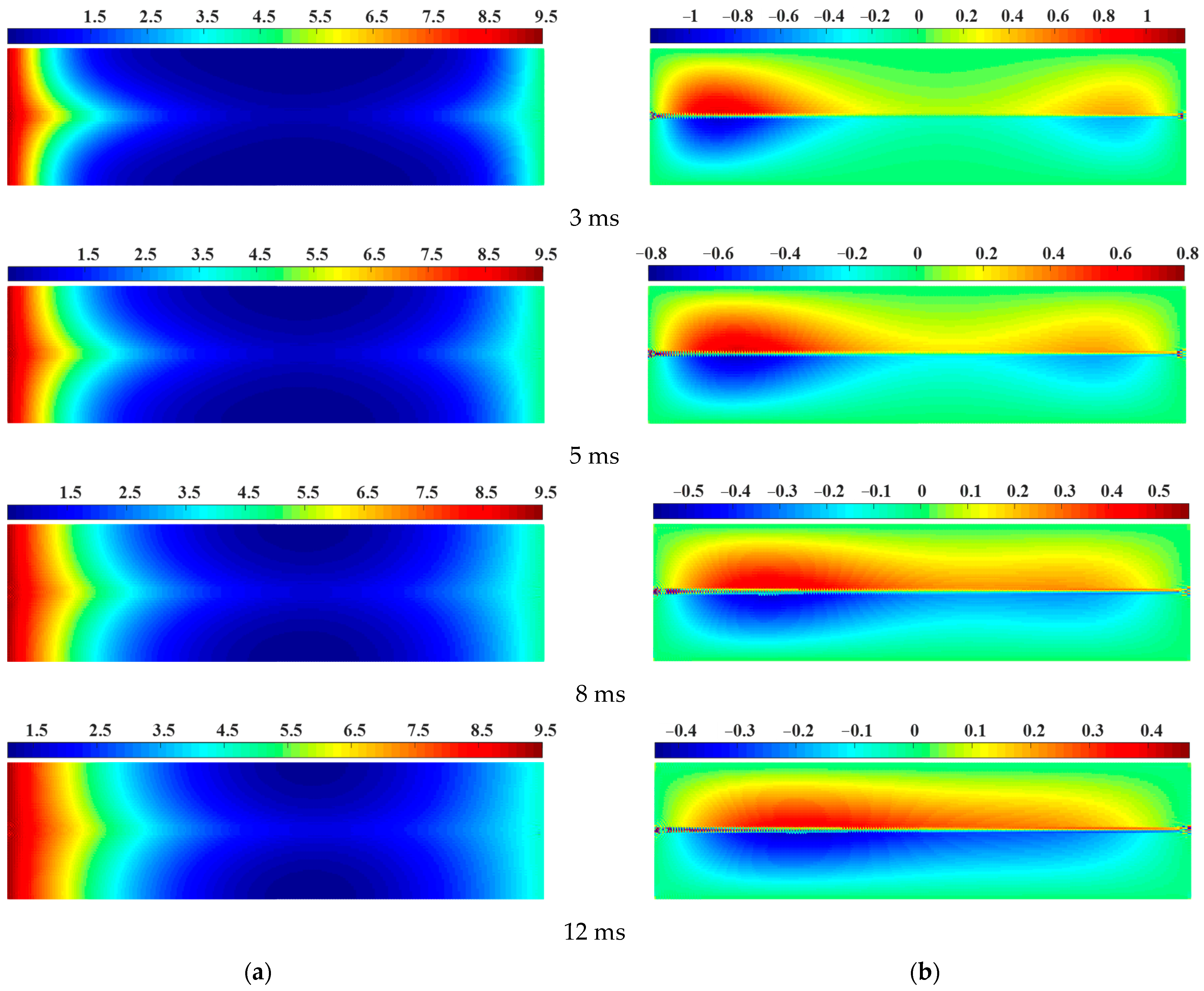
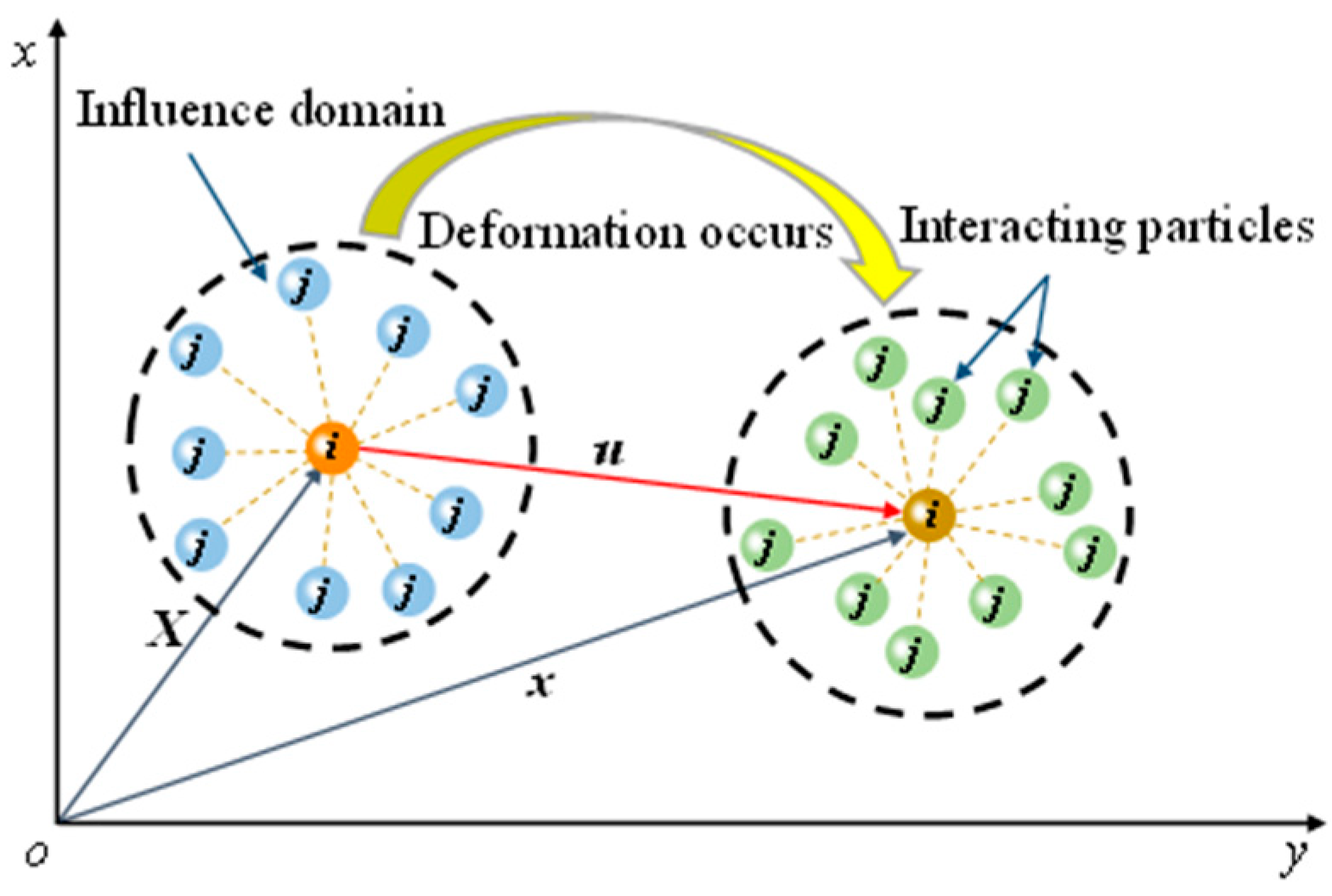
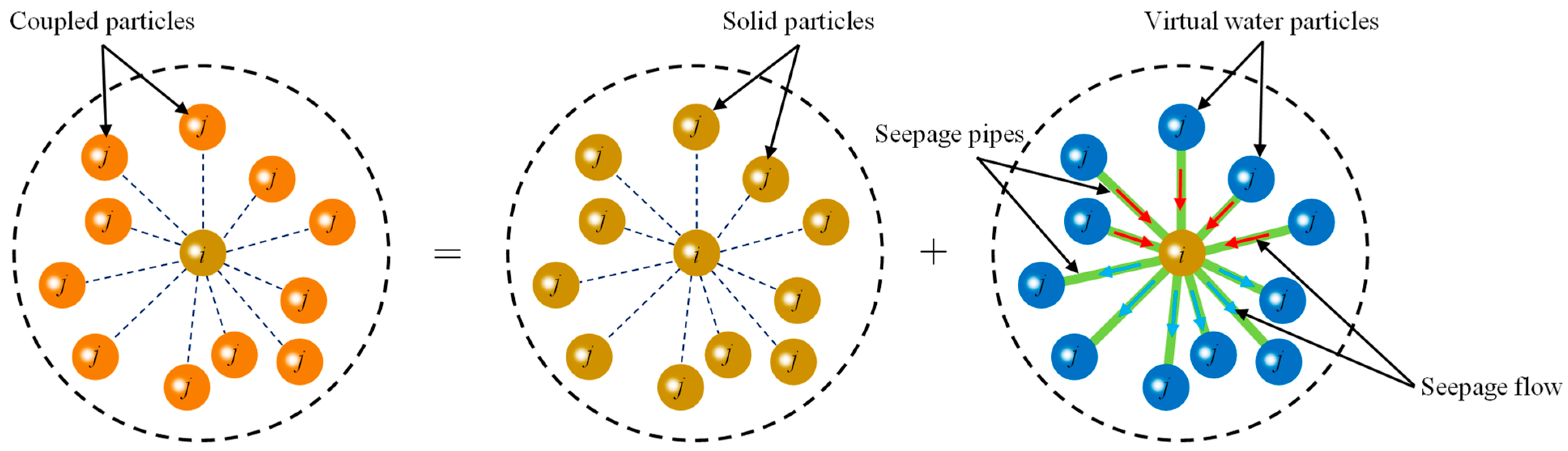
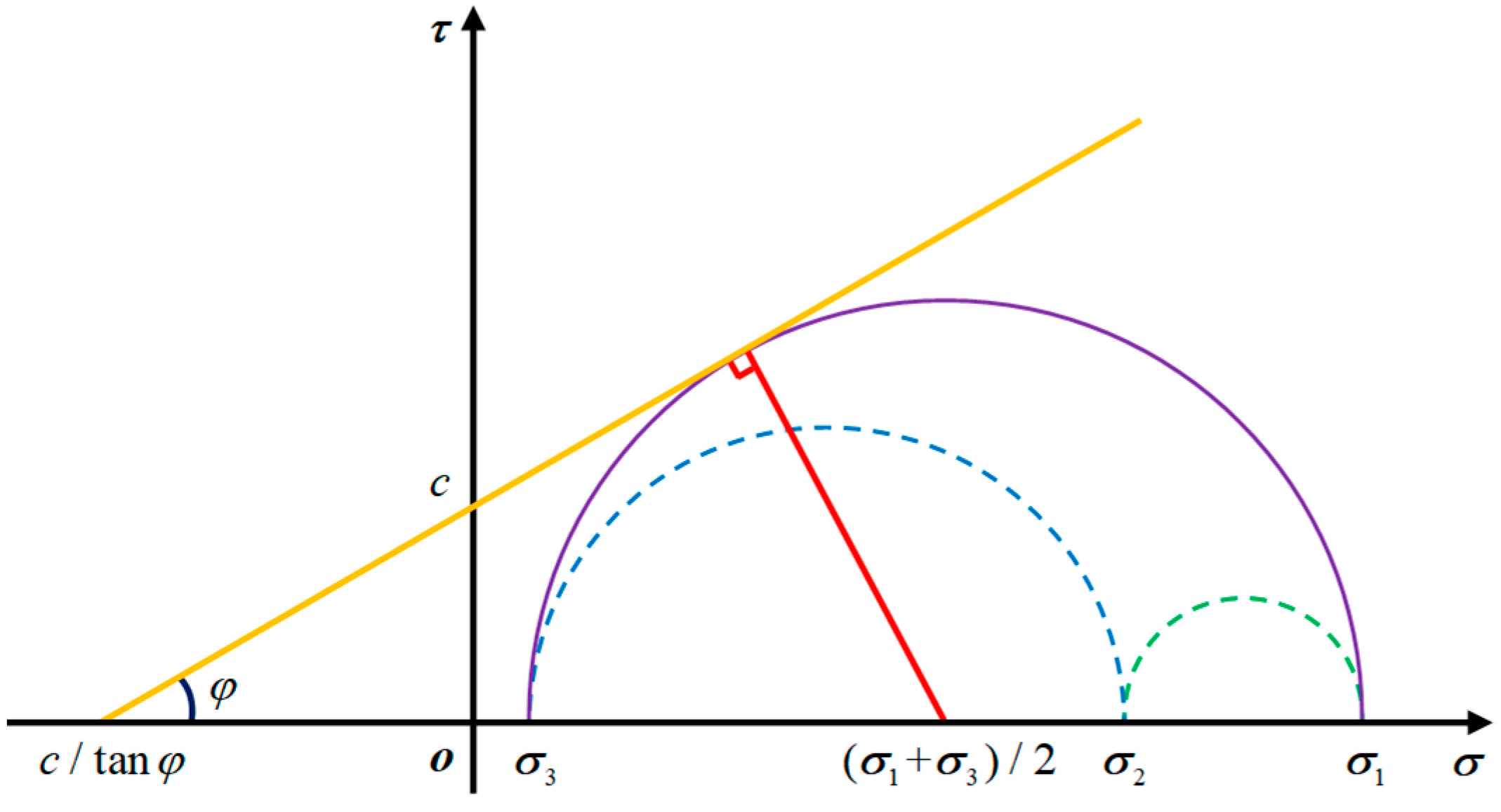
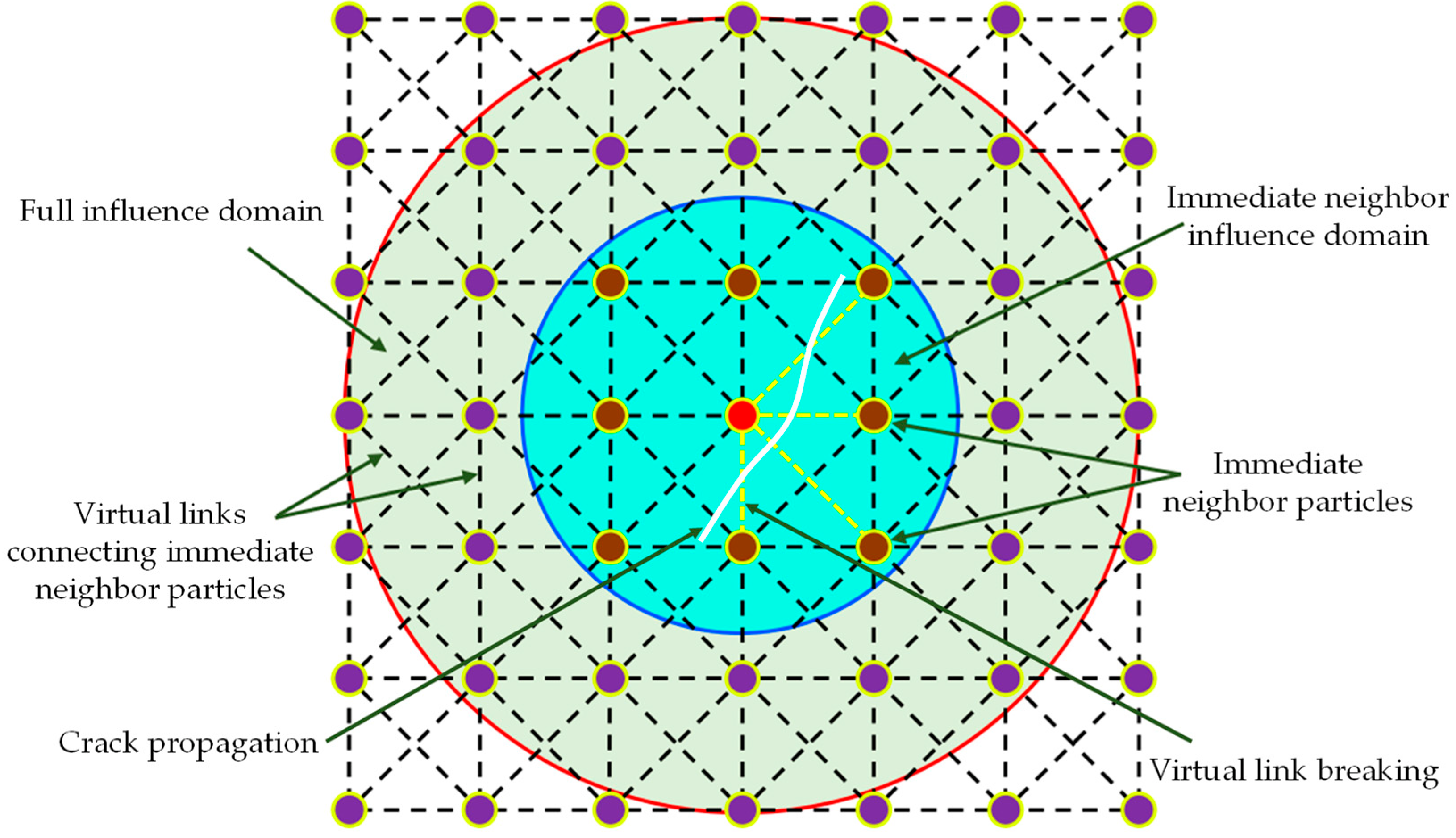


| Inflow Water Pressure, PI (MPa) | Outflow Water Pressure, PII (MPa) | Permeability Coefficient, κ(m/d) | Compressibility of Rock Mass, α (1/Pa) | Compressibility of Water, β (1/Pa) | Porosity |
|---|---|---|---|---|---|
| 8 | 8 | 0.0342 | 2.1 × 10−10 | 4.76 × 10−10 | 0.05 |
| Kinematic Viscosity of Water, u(Pa·s) | Specific Yield of Rock Mass, S(1/m) | Permeability Coefficient, κ(m/s) | Damage Threshold, c1 | Damage Threshold, c2 |
|---|---|---|---|---|
| 1.0 × 10−3 | 1.0 × 10−6 | 1.0 × 10−5 | 0 | 0.5 |
| Rock Density, ρ (kg/m3) | Elastic Modulus, E (GPa) | Poisson’s Ratio, v | Compressive Strength, σc | Cohesion, c (MPa) |
|---|---|---|---|---|
| 2260 | 10.2 | 0.14 | 40.26 | 23.6 |
| Rock Density, ρ (kg/m3) | Elastic Modulus, E (GPa) | Poisson’s Ratio, v | Tensile Strength, σt (MPa) | Cohesion, c (MPa) |
|---|---|---|---|---|
| 2650 | 6 | 0.28 | 23 | 33 |
| Rock Density, ρ (kg/m3) | Elastic Modulus, E (GPa) | Poisson’s Ratio, v | Tensile Strength, σt (MPa) |
|---|---|---|---|
| 2600 | 10 | 0.25 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, D.; Tang, A.; Qu, H.; Wang, J. An Extended Hydro-Mechanical Coupling Model Based on Smoothed Particle Hydrodynamics for Simulating Crack Propagation in Rocks under Hydraulic and Compressive Loads. Materials 2023, 16, 1572. https://doi.org/10.3390/ma16041572
Mu D, Tang A, Qu H, Wang J. An Extended Hydro-Mechanical Coupling Model Based on Smoothed Particle Hydrodynamics for Simulating Crack Propagation in Rocks under Hydraulic and Compressive Loads. Materials. 2023; 16(4):1572. https://doi.org/10.3390/ma16041572
Chicago/Turabian StyleMu, Dianrui, Aiping Tang, Haigang Qu, and Junjie Wang. 2023. "An Extended Hydro-Mechanical Coupling Model Based on Smoothed Particle Hydrodynamics for Simulating Crack Propagation in Rocks under Hydraulic and Compressive Loads" Materials 16, no. 4: 1572. https://doi.org/10.3390/ma16041572
APA StyleMu, D., Tang, A., Qu, H., & Wang, J. (2023). An Extended Hydro-Mechanical Coupling Model Based on Smoothed Particle Hydrodynamics for Simulating Crack Propagation in Rocks under Hydraulic and Compressive Loads. Materials, 16(4), 1572. https://doi.org/10.3390/ma16041572