Statistical Evaluation of CEB-FIP 2010 Model for Concrete Creep and Shrinkage
Abstract
:1. Introduction
2. CEB-FIP 2010 Model
2.1. Shrinkage
2.2. Creep
3. Creep and Shrinkage Test Data
3.1. The Shrinkage Experimental Database
3.2. The Creep Experimental Database
4. Model Evaluation Methods
5. Analysis Results
5.1. Evaluation of the Shrinkage Models
5.2. Evaluation of the Creep Models
5.3. Discussion
6. Conclusions
- (1)
- For the experimental shrinkage database used in this paper, 48 sets of test data were obtained in China, and the remaining 158 sets were from other countries. For the experimental creep database, 35 sets of test data were obtained in China, and the remaining 144 sets were from other countries. The distribution of the data over several influence parameters shows that the database constructed in this paper can well-represent the real engineering environment.
- (2)
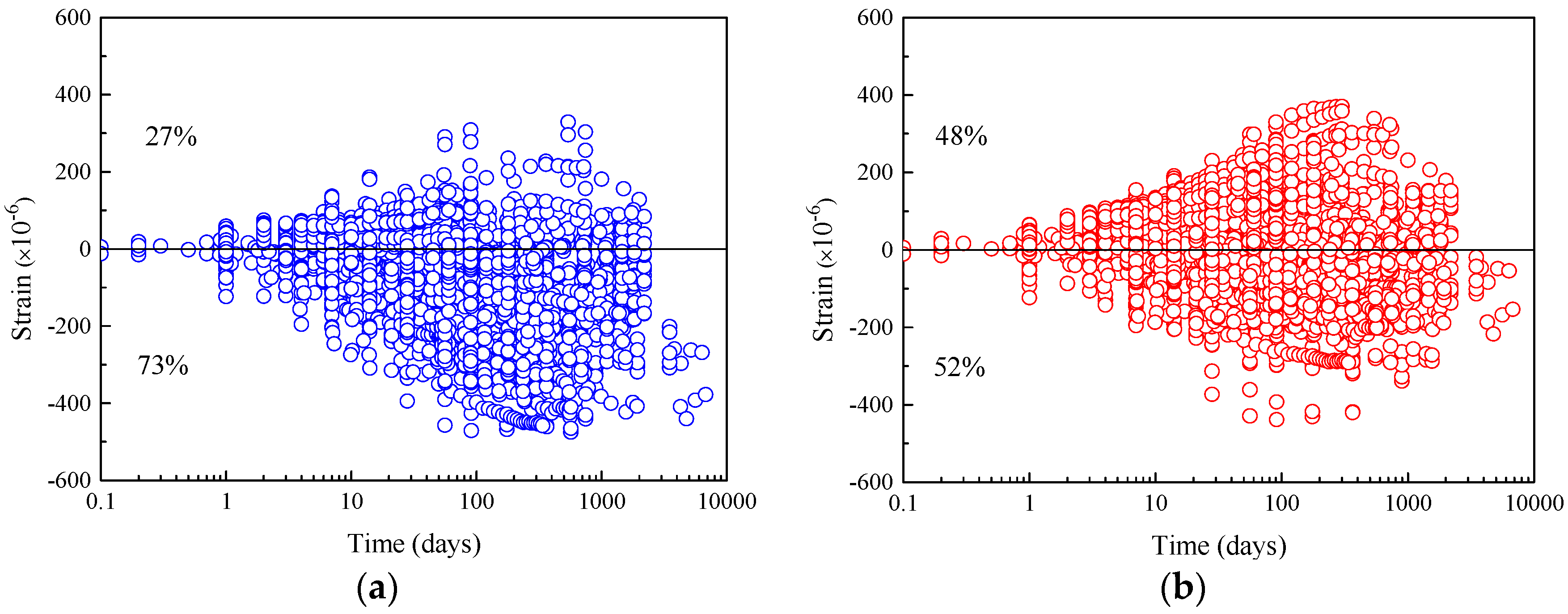
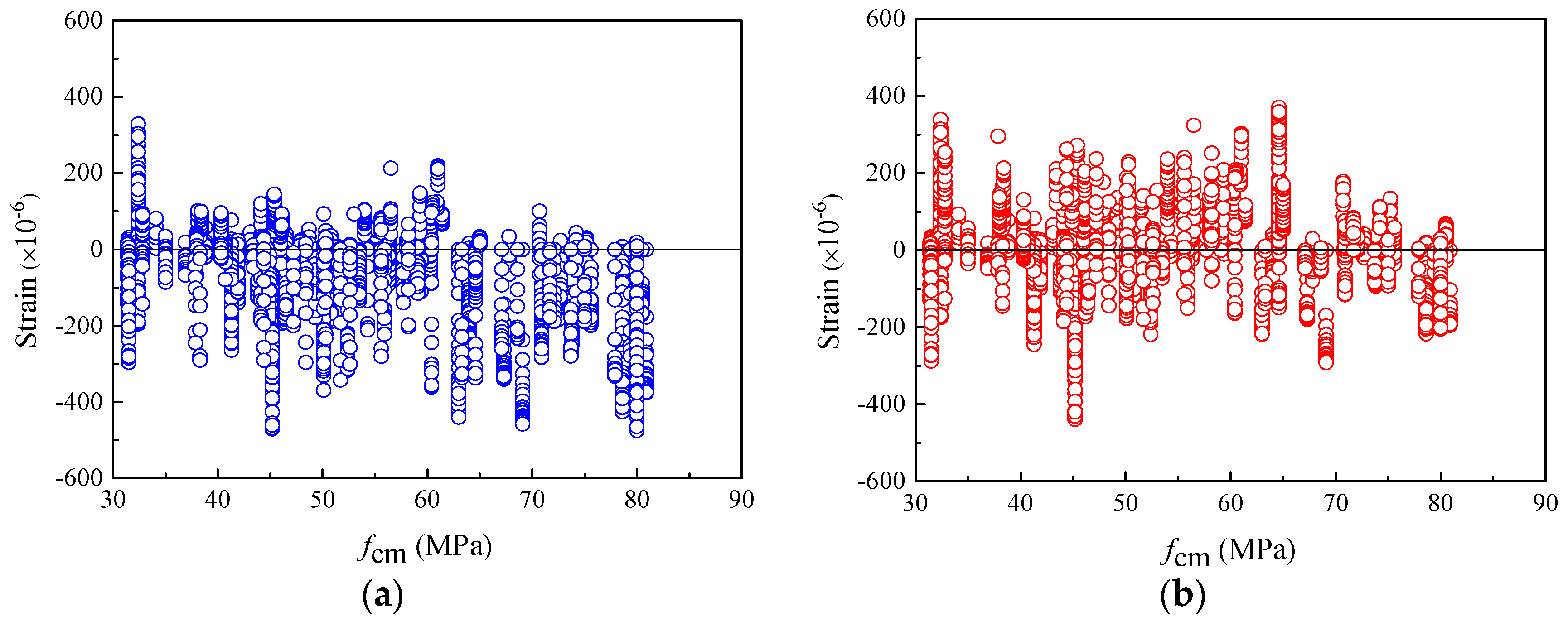
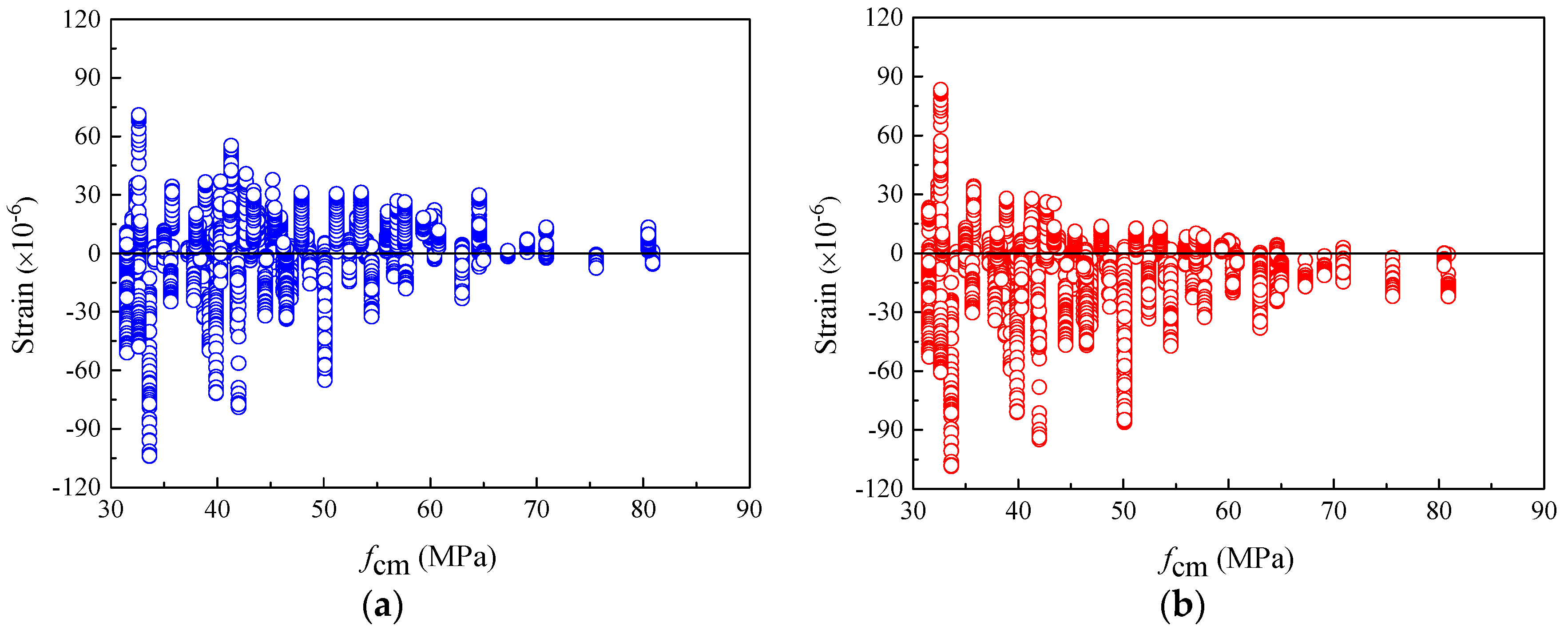
- The calculation results provided by the CEB-FIP 2010 model show that within the time interval of 0–9000 days, 52% and 48% of the shrinkage strain residuals of the total specimens are located in the negative and positive regions, respectively, while the positive and negative regions of the residuals of the 1990 model account for 73% and 27%. The residual distribution of shrinkage strain shows that the CEB-FIP 2010 shrinkage model has stable prediction performance, while the shrinkage strain of concrete is apparently underestimated by the previous 1990 model. In addition, the shrinkage strain residuals of concrete calculated by the CEB-FIP 2010 model are evenly distributed in the negative and positive regions under various compressive strengths fcm, even for concrete with compressive strengths above 40 MPa, which means that this model provides more accurate prediction of shrinkage strain in high-strength concrete.
- (3)
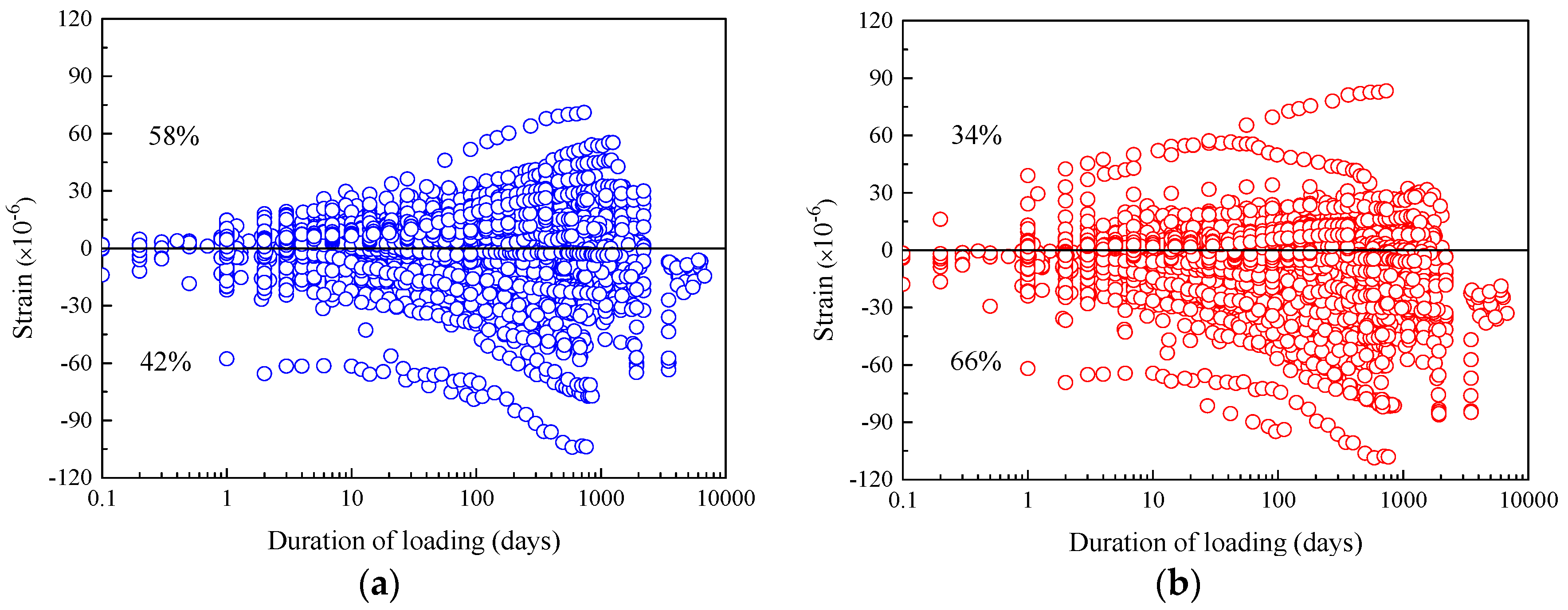
- For the residual value of creep compliance calculated by the CEB-FIP 2010 model, in the time interval of 0–9000 days, the residual values of creep compliance of 66% and 34% of the total specimens fall into the negative and positive regions, respectively, indicating that this model underestimates the creep compliance of concrete, which is similar to the evaluation results of the previous 1990 model. The CEB-FIP2010 creep model has no significant improvement in creep prediction. However, for the prediction of high-strength concrete creep compliance, the CEB-FIP 2010 model shows higher accuracy and better stability, which corrects the CEB-FIB 1990 model for overestimating the creep compliance of high-strength concrete.
- (4)
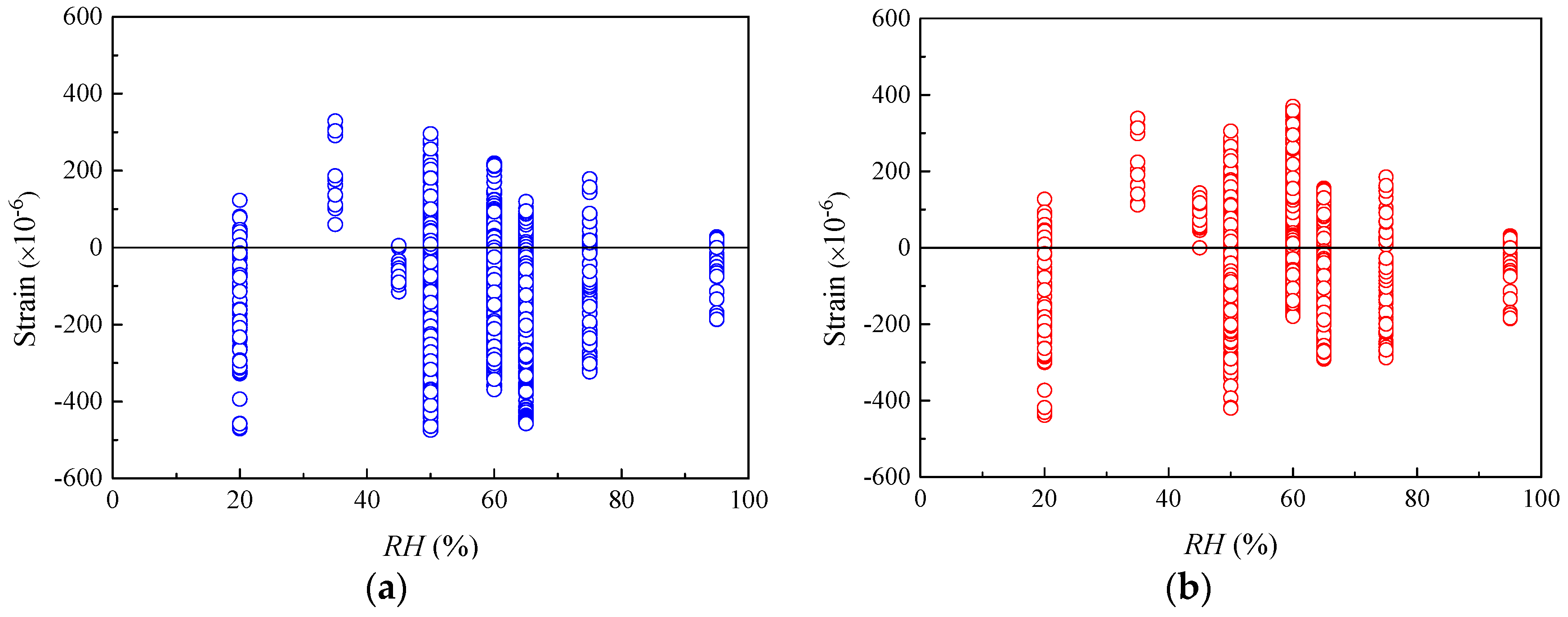
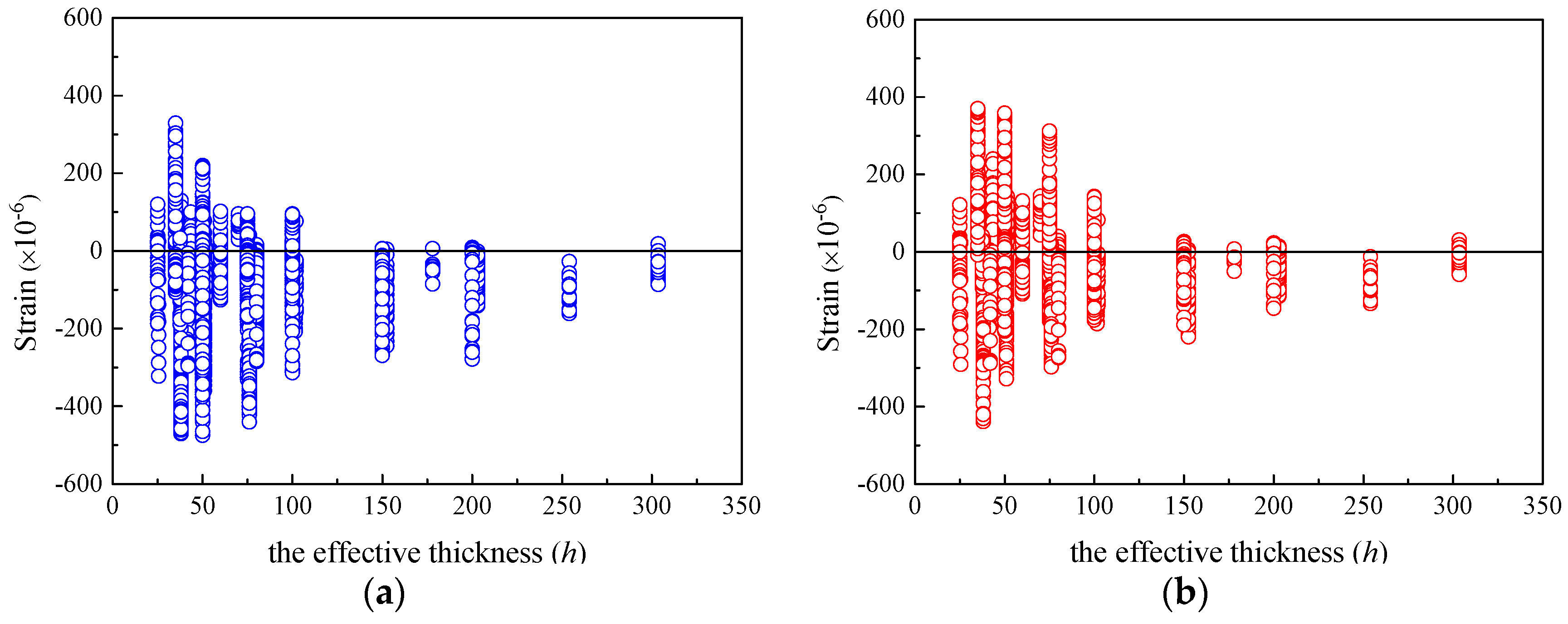
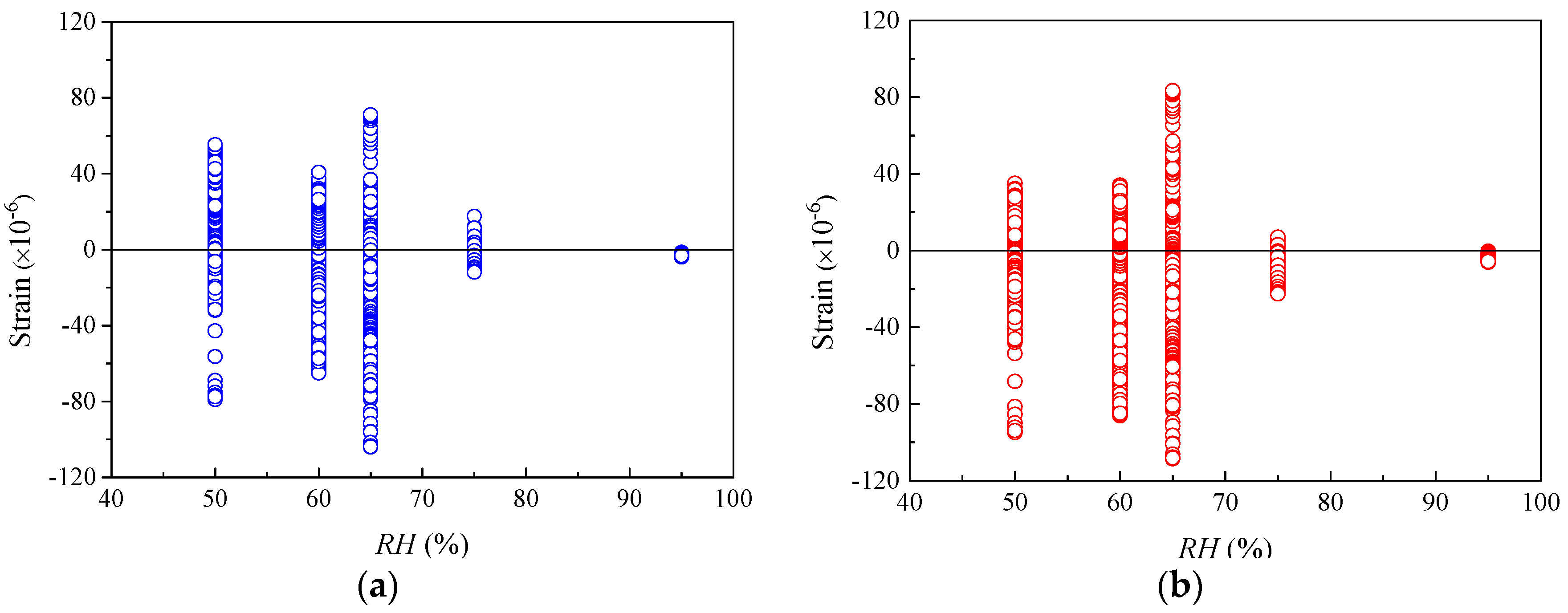
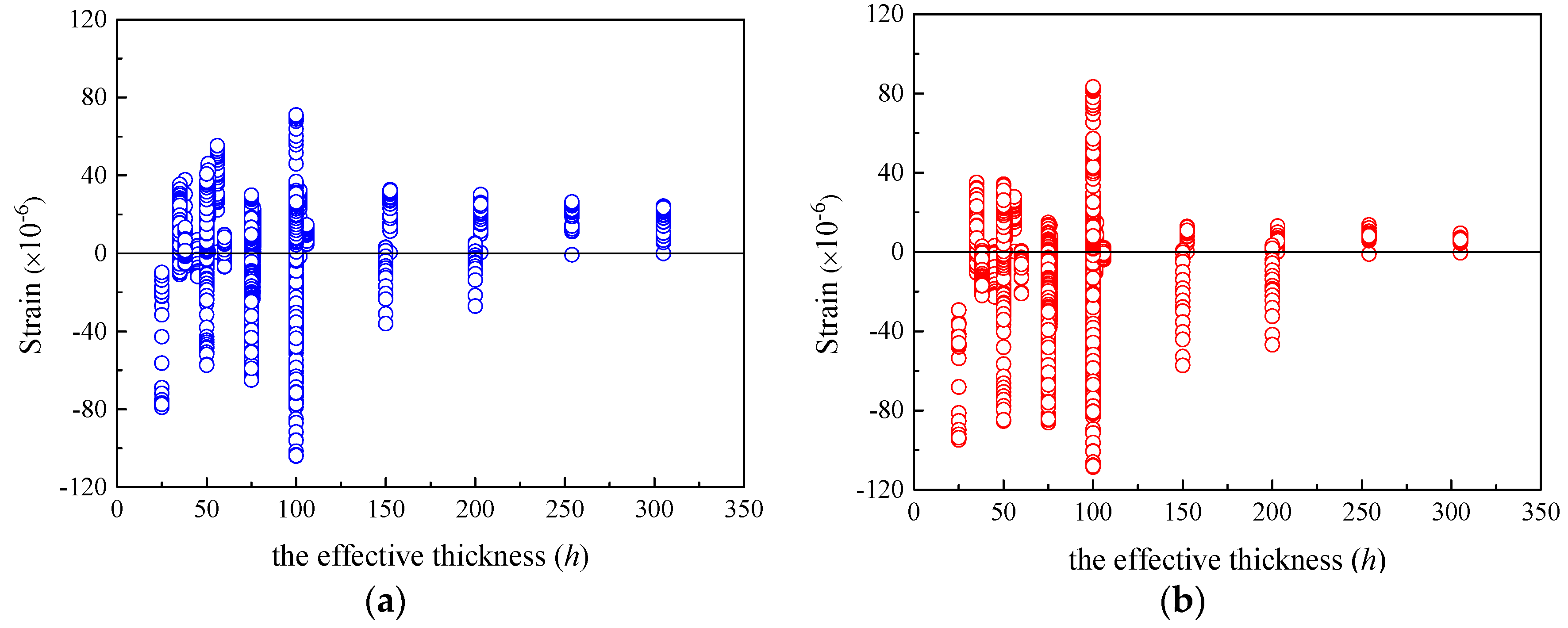
- For concrete specimens under the conditions of RH varying from 50% to 80%, the predicted results by both CEB-FIP models are favorable, which implies that the two models are applicable in practical environments with ordinary atmospheric humidity. Moreover, only for the specimens with h smaller than 100 mm, both CEB-FIP models exhibit satisfying predictive performance. Since the effective thicknesses of actual concrete members are usually larger than 100 mm, if the influence of member size effect is considered, the prediction results of these two CEB-FIP models are not reliable.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gailitis, R.; Figiela, B.; Abelkalns, K. Creep and shrinkage behaviour of disintegrated and non-disintegrated cement mortar. Materials 2021, 14, 7510. [Google Scholar] [CrossRef] [PubMed]
- Comité Euro-International Du Béton (CEB). CEB Design Manual on Structural Effects of Time-Dependent Behavior of Concrete; Chiorino, M.A., Ed.; Georgi Publishing Co.: Cicero, IN, USA, 1984. [Google Scholar]
- Chiorino, M.A.; Lacidogna, G. Structural effects of time-dependent behaviour of concrete in accordance with the CEB/FIP Model Code 1990. CEB Bull. Inf. 1993, 215. [Google Scholar]
- Chiorino, M.A.; Lacidogna, G. General Unified Approach for Creep Analysis of Concrete Structures. In Proceedings of the AC-RILEM Workshop on Creep and Shrinkage of Concrete, Paris, France, January 1999; Volume 3. [Google Scholar]
- Hojati, M.; Rajabipour, F.; Radlińska, A. Creep of alkali-activated cement mixtures. Case Stud. Constr. Mater. 2022, 16, e00954. [Google Scholar] [CrossRef]
- Dogan-Saglamtimur, N.; Bilgil, A. Reusability of ashes for the building sector to strengthen the sustainability of waste management. In Handbook of Research on Supply Chain Management for Sustainable Development; IGI Global: Hershey, PA, USA, 2018; pp. 265–281. [Google Scholar]
- Wassim, R.; Elise, Z.; Alaa, C. Experimental investigations and sensitivity analysis to explain the large creep of concrete deformations in the bridge of Cheviré. Case Stud. Constr. Mater. 2018, 9, 2–3. [Google Scholar]
- Zhou, Y.Q.; Du, H.; Liu, Y.H. An experimental study on mechanical, shrinkage and creep properties of early-age concrete affected by clay content on coarse aggregate. Case Stud. Constr. Mater. 2022, 16, 9–10. [Google Scholar] [CrossRef]
- ACI Committee 209. Prediction of Creep, Shrinkage, and Temperature Effects in Concrete Structures. In ACI Manual of Concrete Practice; American Concrete Institute: Detroit, MI, USA, 1999. [Google Scholar]
- American Association of State Highway and Transportation Officials (AASHTO). AASHTO LRFD Bridge Design Specifications, 4th ed.; American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2007. [Google Scholar]
- Comité Euro-International Du Béton (CEB). CEB-FIP Model Code 1990 for Concrete Structures; Comité Euro-International Du Béton (CEB): Lausanne, Switzerland, 1990. [Google Scholar]
- Gardner, N.J.; Zhao, J.W. Creep and shrinkage revisited. ACI Mater. J. 1993, 90, 236–246. [Google Scholar]
- Gardner, N.J.; Lockman, M.J. Design provisions for drying shrinkage and creep of normal-strength concrete. ACI Mater. J. 2001, 98, 159–167. [Google Scholar]
- Bazant, Z.P.; Baweja, S. Creep and shrinkage prediction model for analysis and design of concrete structures: Model B3. Mater. Struct. 1995, 28, 357–365. [Google Scholar]
- Wendner, R.; Hubler, M.H.; Bazant, Z.P. The B4 Model for Multi-decade Creep and Shrinkage Prediction. In Proceedings of the Ninth International Conference on Creep, Shrinkage, and Durability Mechanics, Cambridge, MA, USA, 22–25 September 2013. [Google Scholar]
- Zhu, Y.; Zhang, Y.; Hussein, H.H. Normal concrete and ultra-high-performance concrete shrinkage and creep models: Development and application. Adv. Struct. Eng. 2022, 25, 2400–2412. [Google Scholar] [CrossRef]
- Naser, A.F. A review study on theoretical comparison between time-dependent analysis models for prestressed concrete bridges. J. Kejuruter. 2022, 34, 375–385. [Google Scholar] [CrossRef]
- Dinkha, Y.Z.; Yousif, S.T. Time dependent properties of concrete: A state of the art review. J. Civ. Eng. Front. 2021, 2, 38–50. [Google Scholar] [CrossRef]
- Comité Euro-International Du Béton (CEB). CEB-FIP Model Code 2010 for Concrete Structures; Comité Euro-International Du Béton (CEB): Lausanne, Switzerland, 2010. [Google Scholar]
- Ministry of Transport of the People’s Republic of China. Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts; Ministry of Transport of the People’s Republic of China: Beijing, China, 2004. [Google Scholar]
- BS EN 1992-1-2; Eurocode 2: Design of Concrete Structures. British Standards Institution: London, UK, 2005.
- Pan, Z.F.; Li, B.; Lu, Z.T. Re-evaluation of CEB-FIP 1990 prediction models for creep and shrinkage with experimental database. Constr. Build. Mater. 2013, 38, 1022–1030. [Google Scholar] [CrossRef]
- Al-Manaseer, A.; Lam, J.P. Statistical evaluation of shrinkage and creep models. ACI Mater. J. 2005, 102, 170. [Google Scholar]
- Goel, R.; Kumar, R.; Paul, D.K. Comparative study of various creep and shrinkage prediction models for concrete. J. Mater. Civ. Eng. 2007, 19, 249–260. [Google Scholar] [CrossRef]
- Ojha, P.N.; Singh, B. Comparison of creep models and experimental verification of creep coefficients for normal and high strength concrete. J. Asian Concr. Fed. 2020, 6, 24–36. [Google Scholar] [CrossRef]
- Hwang, E.; Kim, G.; Koo, K. Compressive creep and shrinkage of high-strength concrete based on limestone coarse aggregate applied to high-rise buildings. Materials 2021, 14, 5026. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Baweja, S. Justification and refinements of model B3 for concrete creep and shrinkage 1. Statistics and sensitivity. Mater. Struct. 1995, 28, 415–430. [Google Scholar] [CrossRef]
- Muller, H.S.; Hilsdorf, H.K. Evaluation of the time-dependent behavior of concrete, summary report on the work of general task group 9. CEB Bull. Inf. 1990, 199. [Google Scholar]
- Bazant, Z.P.; Li, G.H. UNBIASED Statistical Comparison of Creep and Shrinkage Prediction Models; Structural Engineering Report No. 07-12/A210u; Department of Civil and Environmental Engineering, Northwestern University: Evanston, IL, USA, 2007. [Google Scholar]
- Bazant, Z.P.; Li, G.H. Comprehensive Database on Concrete Creep and Shrinkage; Structural Engineering Report No. 08-3/A210c; McCormick School of Engineering and Applied Science, Northwestern University: Evanston, IL, USA, 2008. [Google Scholar]
- Meng, S.; Guan, Y.; Zhou, X. Creep and Shrinkage Effects in the Continuous Rigid Frame of Sutong Bridge: Report No. 05Y02: Research Plan of Transportation Science in JiangSu Province; Southeast University: Nanjing, China, 2007. (In Chinese) [Google Scholar]
- Qin, H.; Pan, G. Study on deformation performance of high performance fly ash concrete used in Bridge Engineering. In Proceedings of the 11th National Conference on Concrete and Prestressed Concrete, Guiyang, China, 1–4 August 2001. (In Chinese). [Google Scholar]
- Mu, R. Experimental Study on Mix Design of High Strength High Performance Concrete Used in Sutong Bridge; Research Report; Jiangsu Research Institute of Building Science Co. Ltd.: Nanjing, China, 2005. (In Chinese) [Google Scholar]
- Ouyang, H.; Bai, Y.S. Test study of shrinkage and creep behavior of high performance concrete. Bridge Constr. 2006, 2, 4–6. (In Chinese) [Google Scholar]
- Zhou, J. Study and Application of C60 High Performance Concrete in Dubu No. 3 Bridge. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2009. (In Chinese). [Google Scholar]
- Wang, G. Experiment of Creep and Shrinkage of Concrete Used in Paksey Bridge Bengal; Research Report; China Railway Major Bridge Engineering Group Co. Ltd.: Wuhan, China, 2003. (In Chinese) [Google Scholar]
- Chen, C.; Huang, W. Creep of high performance concrete for bridges and its application. Hydro-Sci. Eng. 2007, 2, 1–9. (In Chinese) [Google Scholar]
- Li, J. Study on Impacts of Weight Fractions of Limestone Powder on Properties of Concrete. Master’s Thesis, Dalian University of Technology, Dalian, China, 2007. (In Chinese). [Google Scholar]
- Chen, L. Study on C60 Low Creep Concrete. Master’s Thesis, Central South University, Changsha, China, 2008. (In Chinese). [Google Scholar]
- Xie, C. Experimental study on creep deformation of long-span bridge with ballastless track. Sci. Technol. West China 2009, 8, 26–27. (In Chinese) [Google Scholar]
- Xu, J. Experimental and Theoretical Study on Creep and Shrinkage Effects in Continuous Concrete Bridges. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2008. (In Chinese). [Google Scholar]
| Strength (MPa) | 30–40 | 40–50 | 50–60 | 60–70 | 70–81 |
| Number of data sets | 34 (16.5%) | 79 (38.3%) | 39 (18.9%) | 32 (15.5%) | 22 (10.7%) |
| Relative humidity (%) | 20–40 | 40–60 | 60–80 | 80–95 | — |
| Number of data sets | 10 (4.9%) | 110 (53.4%) | 79 (38.3%) | 7 (3.4%) | — |
| Effective thickness (mm) | 25–45 | 45–70 | 70–100 | 100–305 | — |
| Number of data sets | 44 (21.4%) | 79 (38.3%) | 70 (34.0%) | 13 (6.3%) | — |
| Strength (MPa) | 30–40 | 40–50 | 50–60 | 60–70 | 70–81 |
| Number of data sets | 50 (27.9%) | 67 (37.4%) | 37 (20.7%) | 18 (10.1%) | 7 (3.9%) |
| Relative humidity (%) | 50 | 60 | 65 | 75–95 | — |
| Number of data sets | 35 (19.6%) | 64 (35.8%) | 74 (41.3%) | 6 (3.4%) | — |
| Effective thickness (mm) | 25–45 | 45–70 | 70–100 | 100–305 | — |
| Number of data sets | 22 (12.3%) | 46 (25.7%) | 100 (55.9%) | 11 (6.1%) | — |
| Age at loading (days) | 1–5 | 5–14 | 14–28 | ≥28 | — |
| Number of data sets | 17 (9.5%) | 49 (27.4%) | 75 (41.9%) | 38 (21.2%) | — |
| Period | 0–1000 Days | 1001–9000 Days | 0–9000 Days | ||||
|---|---|---|---|---|---|---|---|
| CEB 90 | CEB 10 | CEB 90 | CEB 10 | CEB 90 | CEB 10 | ||
| Residual a | Number of data points | 2660 (94%) | 178 (6%) | 2838 (100%) | |||
| RV > 0 | 728 (27%) | 1294 (49%) | 35 (20%) | 70 (39%) | 763 (27%) | 1364 (48%) | |
| RV < 0 | 1932 (73%) | 1366 (51%) | 143 (80%) | 108 (61%) | 2075 (73%) | 1474 (52%) | |
| |RV| < 100 με | 1553 (58%) | 1746 (66%) | 101 (57%) | 88 (49%) | 1654 (58%) | 1834 (65%) | |
| |RV| > 100 με | 1107 (42%) | 914 (34%) | 77 (43%) | 90 (51%) | 1184 (42%) | 1004 (35%) | |
| Period | 0–1000 Days | 1001–9000 Days | 0–9000 Days | ||||
|---|---|---|---|---|---|---|---|
| CEB 90 | CEB 10 | CEB 90 | CEB 10 | CEB 90 | CEB 10 | ||
| Residual | Number of data points | 3353 (93%) | 245 (7%) | 3598 (100%) | |||
| RV > 0 | 1960 (58%) | 1158 (35%) | 135 (55%) | 75 (31%) | 2095 (58%) | 1233 (34%) | |
| RV < 0 | 1393 (42%) | 2195 (65%) | 110 (45%) | 170 (69%) | 1503 (42%) | 2365 (66%) | |
| |RV| < 33 με/MPa | 3125 (93%) | 2984 (89%) | 220 (90%) | 197 (80%) | 3345 (93%) | 3181 (88%) | |
| |RV| > 33 με/MPa | 228 (7%) | 369 (11%) | 25 (10%) | 48 (20%) | 253 (7%) | 417 (12%) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Z.; Zhang, H.; Zeng, B.; Wang, Y. Statistical Evaluation of CEB-FIP 2010 Model for Concrete Creep and Shrinkage. Materials 2023, 16, 1576. https://doi.org/10.3390/ma16041576
Pan Z, Zhang H, Zeng B, Wang Y. Statistical Evaluation of CEB-FIP 2010 Model for Concrete Creep and Shrinkage. Materials. 2023; 16(4):1576. https://doi.org/10.3390/ma16041576
Chicago/Turabian StylePan, Zuanfeng, Haipeng Zhang, Bin Zeng, and Yuwei Wang. 2023. "Statistical Evaluation of CEB-FIP 2010 Model for Concrete Creep and Shrinkage" Materials 16, no. 4: 1576. https://doi.org/10.3390/ma16041576
APA StylePan, Z., Zhang, H., Zeng, B., & Wang, Y. (2023). Statistical Evaluation of CEB-FIP 2010 Model for Concrete Creep and Shrinkage. Materials, 16(4), 1576. https://doi.org/10.3390/ma16041576






