Parameter Optimization of RB-SiC Polishing by Femtosecond Laser
Abstract
:1. Introduction
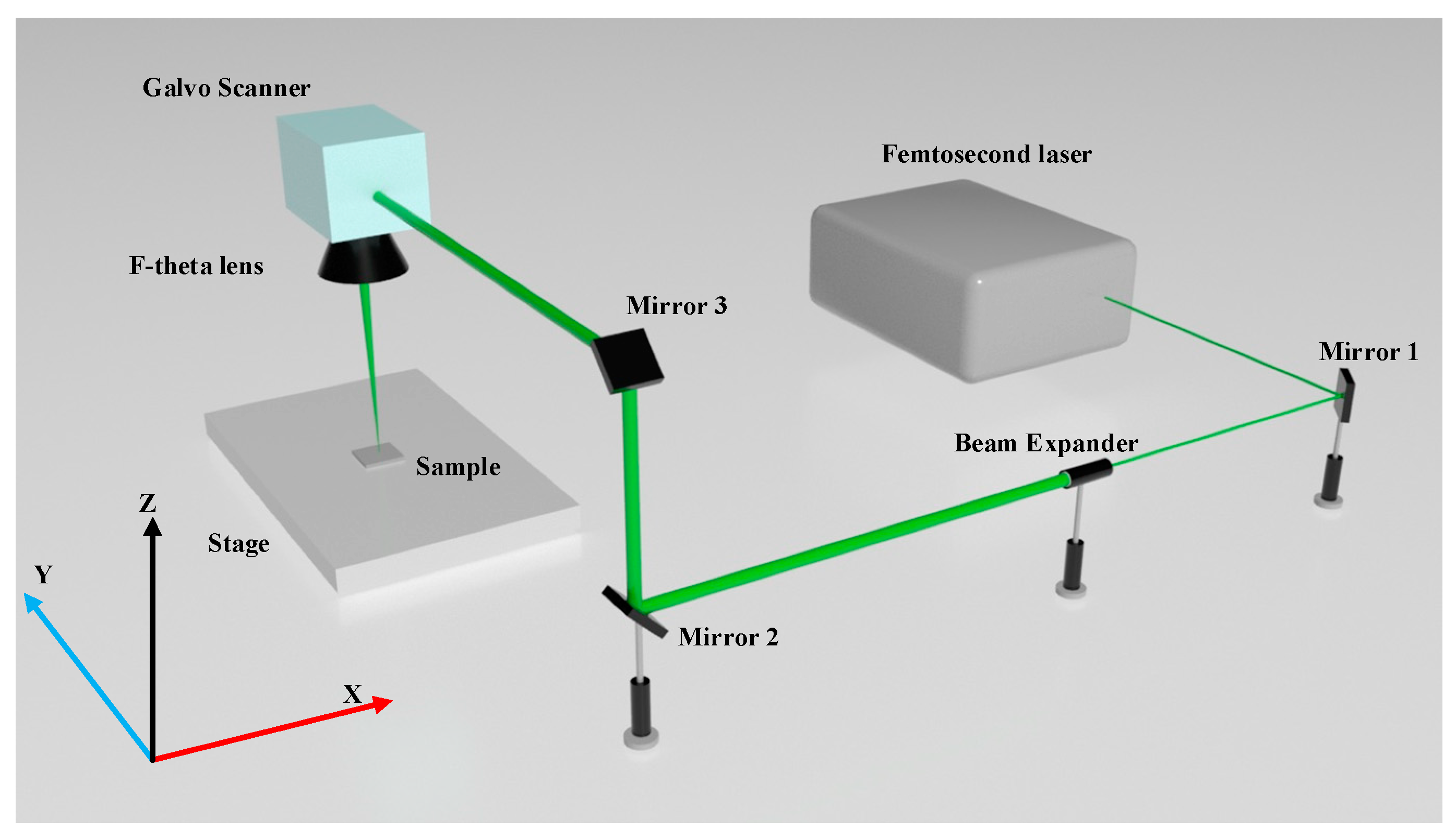
2. Experimental Details
2.1. Materials and Experimental Conditions
2.2. Two-Temperature Model
2.3. Scanning Strategy
3. Results
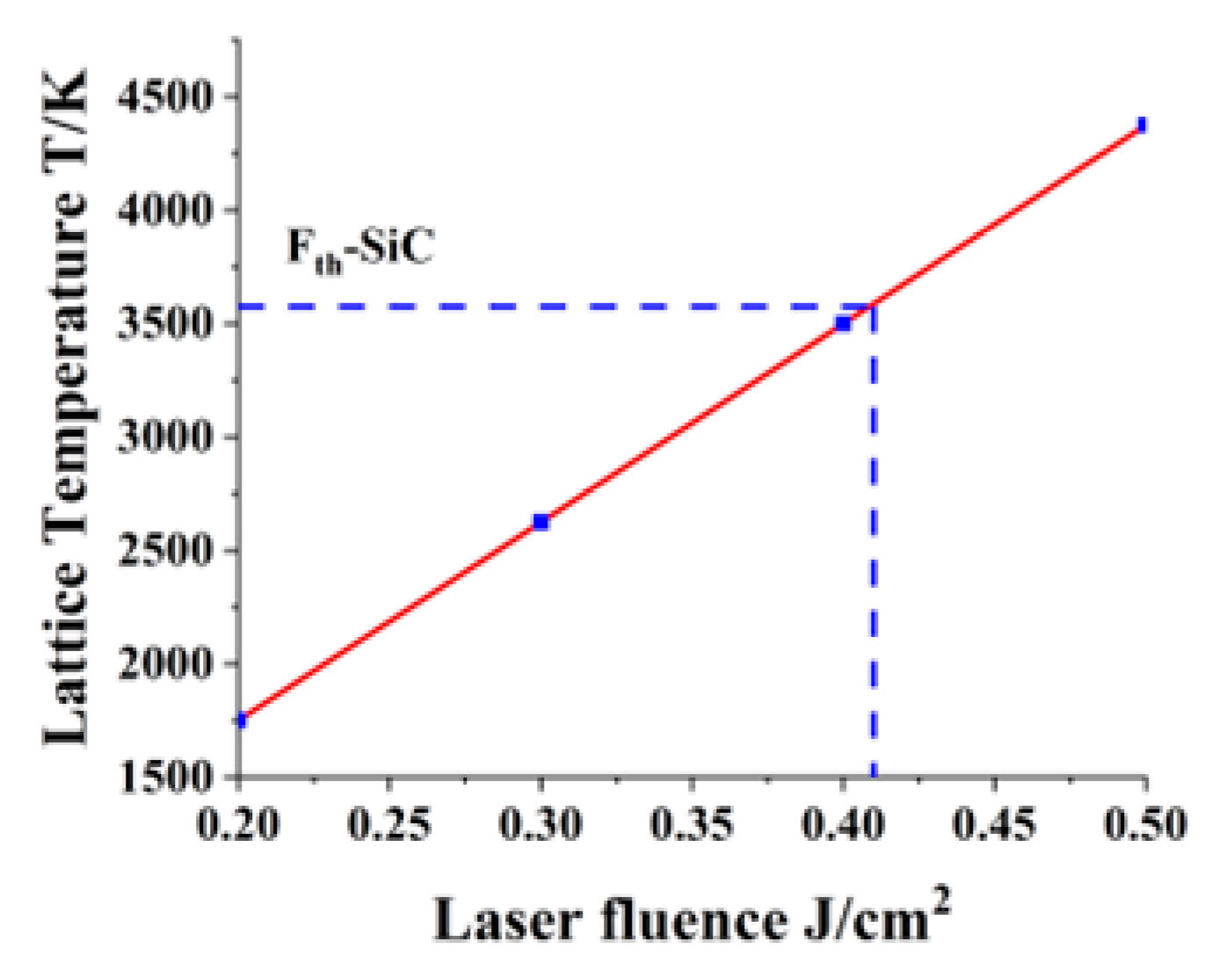
3.1. Ablation Threshold of Silicon Carbide
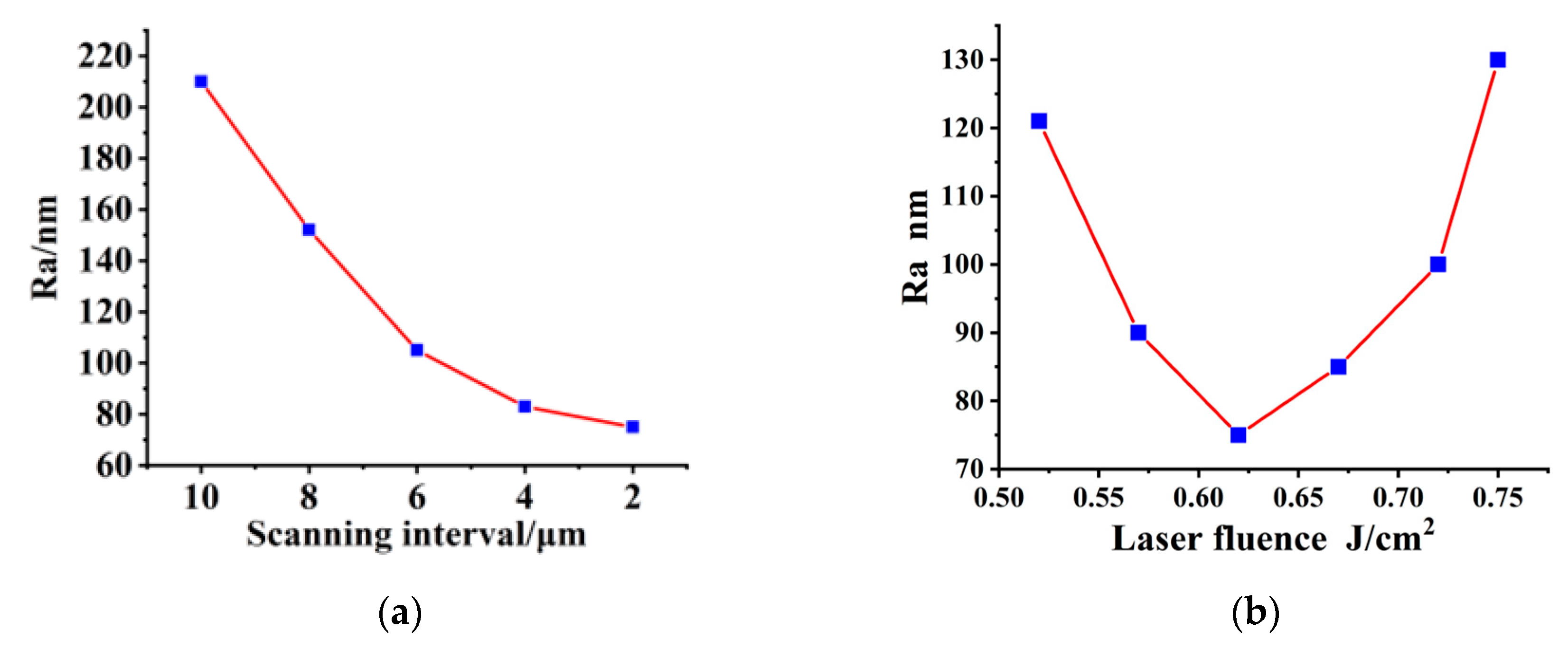
3.2. Influence of Laser Fluence and Scanning Pitch on Polishing
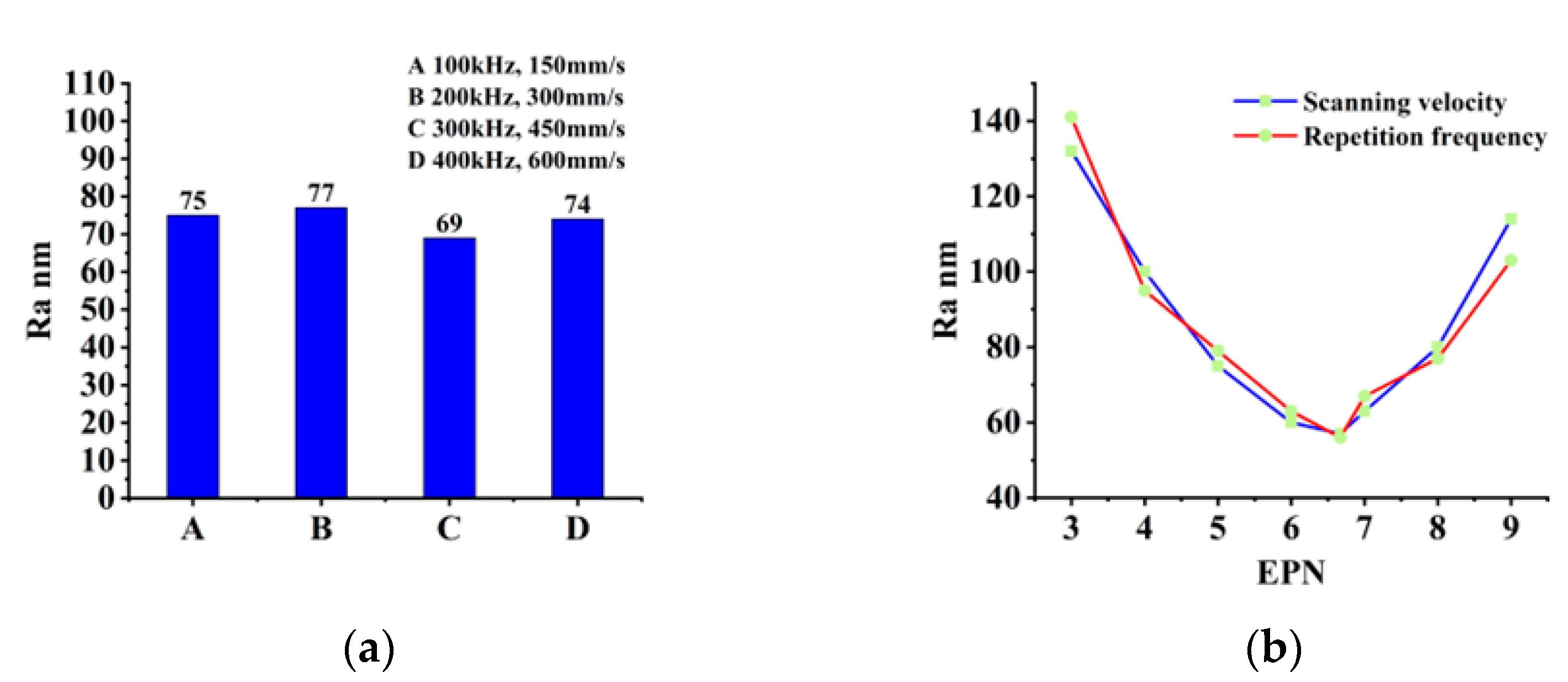
3.3. Influence of Equivalent Pulse Numbers on Polishing
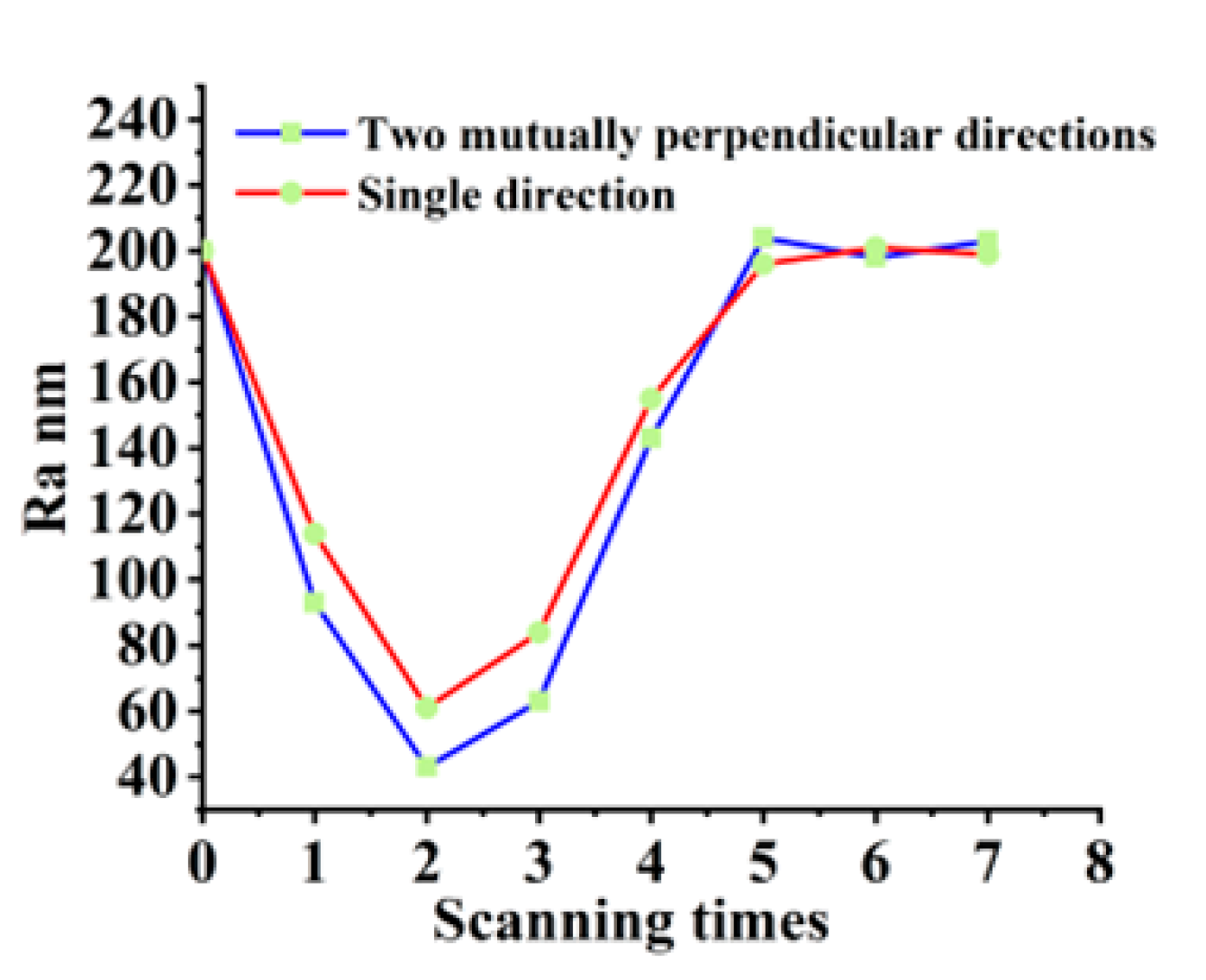
3.4. Influence of Scanning Model and Times on Polishing
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Redding, D.; Feinberg, L.; Postman, M.; Stahl, H.P.; Stahle, C.; Thronson, H. Beyond JWST: Performance Requirements for a Future Large UVOIR Space Telescope; SPIE: Bellingham, DC, USA, 2014; Volume 9143. [Google Scholar]
- Nguyen, T.; Liu, D.; Thongkaew, K.; Li, H.; Qi, H.; Wang, J. The wear mechanisms of reaction bonded silicon carbide under abrasive polishing and slurry jet impact conditions. Wear 2018, 410, 156–164. [Google Scholar] [CrossRef]
- Rajak, D.K.; Wagh, P.H.; Linul, E. A review on synthetic fibers for polymer matrix composites: Performance, failure modes and applications. Materials 2022, 15, 4790. [Google Scholar] [CrossRef] [PubMed]
- Brinksmeier, E.; Riemer, O.; Gessenharter, A. Finishing of structured surfaces by abrasive polishing. Precis. Eng. 2006, 30, 325–336. [Google Scholar] [CrossRef]
- Hashmi, A.W.; Mali, H.S.; Meena, A.; Saxena, K.K.; Puerta, A.P.V.; Prakash, C.; Buddhi, D.; Davim, J.; Abdul-Zahra, D.S. Understanding the mechanism of abrasive-based finishing processes using mathematical modeling and numerical simulation. Metals 2022, 12, 1328. [Google Scholar] [CrossRef]
- Vora, H.; Orent, T.W.; Stokes, R.I. Mechanochemical Polishing of Silicon Nitride. J. Am. Ceram. Soc. 1982, 65, c140–c141. [Google Scholar] [CrossRef]
- Nowak, K.M.; Baker, H.J.; Hall, D.R. Efficient laser polishing of silica micro-optic components. Applied Optics 2006, 45, 162–171. [Google Scholar] [CrossRef]
- Mi, S.; Toros, A.; Graziosi, T.; Quack, N. Non-contact polishing of single crystal diamond by ion beam etching. Diam. Relat. Mater. 2019, 92, 248–252. [Google Scholar] [CrossRef]
- Cheng, H.; Feng, Z.; Wang, Y.; Lei, S. Magnetorheological Finishing of SiC Aspheric Mirrors. Mater. Manuf. Process. 2005, 20, 917–931. [Google Scholar] [CrossRef]
- Yuan, Z.; He, Y.; Sun, X.; Wen, Q.J.M. UV-TiO2 photocatalysis-assisted chemical mechanical polishing 4H-SiC wafer. Mater. Manuf. Process. 2018, 33, 1214–1222. [Google Scholar] [CrossRef]
- Kubota, A.; Nagae, S.; Motoyama, S. High-precision mechanical polishing method for diamond substrate using micron-sized diamond abrasive grains. Diam. Relat. Mater. 2020, 101, 107644. [Google Scholar] [CrossRef]
- Tam, H.Y.; Cheng, H.B.; Wang, Y.W. Removal rate and surface roughness in the lapping and polishing of RB-SiC optical components. J. Mater. Process. Technol. 2007, 192–193, 276–280. [Google Scholar] [CrossRef]
- Zhao, J.; Zhan, J.; Jin, R.; Tao, M. An oblique ultrasonic polishing method by robot for free-form surfaces. Int. J. Mach. Tools Manuf. 2000, 40, 795–808. [Google Scholar] [CrossRef]
- Temmler, A.; Willenborg, E.; Wissenbach, K. Laser Polishing; SPIE: Bellingham, DC, USA, 2012; Volume 8243. [Google Scholar]
- Shao, Y.; Sun, S.-F.; Liu, G.-L.; Wang, P.-P.; Shao, J.; Zhang, F.-Y.; Wang, X. Laser-assisted thermochemical ultrahigh-precision polishing of titanium in phosphoric acid solution. Int. J. Adv. Manuf. Technol. 2021, 115, 1201–1210. [Google Scholar] [CrossRef]
- Weingarten, C.; Heidrich, S.; Wu, Y.; Willenborg, E. Laser Polishing of Glass; SPIE: Bellingham, DC, USA, 2015; Volume 9633. [Google Scholar]
- Sassmannshausen, A.; Brenner, A.; Finger, J. Ultrashort pulse laser polishing by continuous surface melting. J. Mater. Process. Technol. 2021, 293, 117058. [Google Scholar] [CrossRef]
- Temmler, A.; Liu, D.; Luo, J.; Poprawe, R. Influence of pulse duration and pulse frequency on micro-roughness for laser micro polishing (LµP) of stainless steel AISI 410. Appl. Surf. Sci. 2020, 510, 145272. [Google Scholar] [CrossRef]
- Zhang, R.; Huang, C.; Wang, J.; Chu, D.; Liu, D.; Feng, S. Experimental investigation and optimization of femtosecond laser processing parameters of silicon carbide–based on response surface methodology. Ceram. Int. 2022, 48, 14507–14517. [Google Scholar] [CrossRef]
- Qu, Y.; Choi, H.; Perry, T.; Jeon, Y.; Pfefferkorn, F.; Li, X.; Duffie, N. Numerical and Experimental Investigation of Micromelting for Laser Micro Polishing of Meso/Micro Metallic Components. In Proceedings of the ASME 2006 International Manufacturing Science and Engineering Conference, Ypsilanti, MI, USA, 8–11 October 2006; pp. 1063–1070. [Google Scholar]
- Chen, H.; Wei, C.; Cao, Z.; Peng, X.; Jiang, Z.; Shao, J.J.O.M.E. Femtosecond laser-selective polishing of RB-SiC at a fluence between its two-phase threshold. Opt. Mater. Express 2022, 12, 1491–1501. [Google Scholar] [CrossRef]
- Gamaly, E.G.; Luther-Davies, B.; Kolev, V.Z.; Madsen, N.R.; Duering, M.; Rode, A.V. Ablation of metals with picosecond laser pulses: Evidence of long-lived non-equilibrium surface states. Laser Part. Beams 2005, 23, 167–176. [Google Scholar] [CrossRef]
- Bulgakova, N.M.; Stoian, R.; Rosenfeld, A.; Hertel, I.V.; Marine, W.; Campbell, E.E.B. A general continuum approach to describe fast electronic transport in pulsed laser irradiated materials: The problem of Coulomb explosion. Appl. Phys. A 2005, 81, 345–356. [Google Scholar] [CrossRef]
- Anisimov, S.; Kapeliovich, B.; Perelman, T. Electron emission from metal surfaces exposed to ultrashort laser pulses. Zh. Eksp. Teor. Fiz. 1974, 66, 375–377. [Google Scholar]
- Christensen, B.H.; Vestentoft, K.; Balling, P. Short-pulse ablation rates and the two-temperature model. Appl. Surf. Sci. 2007, 253, 6347–6352. [Google Scholar] [CrossRef]
- Bussière, B.; Sanner, N.; Sentis, M.; Utéza, O. Importance of surface topography on pulsed laser-induced damage threshold of Sapphire crystals. Sci. Rep. 2017, 7, 1249. [Google Scholar] [CrossRef]
- Zheng, Q.; Fan, Z.; Jiang, G.; Pan, A.; Yan, Z.; Lin, Q.; Cui, J.; Wang, W.; Mei, X. Mechanism and morphology control of underwater femtosecond laser microgrooving of silicon carbide ceramics. Opt. Express 2019, 27, 26264–26280. [Google Scholar] [CrossRef] [PubMed]
- Mizoshiri, M.; Yoshidomi, K. Cu Patterning Using Femtosecond Laser Reductive Sintering of CuO Nanoparticles under Inert Gas Injection. Materials 2021, 14, 3285. [Google Scholar] [CrossRef]
- Richerzhagen, B.; Kutsuna, M.; Okada, H.; Ikeda, T. Water-Jet-Guided Laser Processing; SPIE: Bellingham, DC, USA, 2003; Volume 4830. [Google Scholar]
- Peng, A.; Peng, Y.; Zhang, Y.; Li, K.; Chen, J. Absorption coefficient and damage threshold in single-crystalline silicon with femtosecond laser. J. Henan Norm. Univ. (Nat. Sci.) 2006, 34, 42–45. [Google Scholar]
- Zhang, H.Z.; Wang, H.Y.; Liu, F.F.; Wang, L. Investigation on femtosecond laser ablative processing of SiCp/AA2024 composites. J. Manuf. Process. 2020, 49, 227–233. [Google Scholar] [CrossRef]
- Kelly, R.; Miotello, A. Comments on explosive mechanisms of laser sputtering. Appl. Surf. Sci. 1996, 96–98, 205–215. [Google Scholar] [CrossRef]
- Dong, Y.; Molian, P. Femtosecond pulsed laser ablation of 3CSiC thin film on silicon. Appl. Phys. A 2003, 77, 839–846. [Google Scholar] [CrossRef]
- Luo, J.; Zhou, K.; Ma, Y.; Lei, Y.; Liu, H.; Tong, H.; Xiao, R.; Wang, Y.; Chen, Y.; Chen, Z.; et al. Femtosecond laser welding for robust and low loss optical fiber bonding. Opt. Express 2022, 30, 41092–41100. [Google Scholar] [CrossRef]
- Kang, N.; Li, S.; Zheng, Z.; Dai, Y. Experimental study on super smooth polishing of typical SIC optical materials. China Mech. Eng. 2008, 261, 2528–2531. [Google Scholar]






| Parameters | Value |
|---|---|
| Wavelength | 515 nm |
| Beam polarization | Linear |
| Pulse energy | 0~100 μJ |
| The full width at half maximum (FWHM) pulse duration | 282 fs |
| Laser beam diameter | 10 μm |
| Frequency | 60~1000 kHz |
| Maximum scanning velocity | 7000 mm/s |
| Focal length of the F-theta-lens | 100 mm |
| Parameters | Symbol | SiC [31] |
|---|---|---|
| Electron-phonon coupling strength | 1.12 × 1017 | |
| Heat capacity of electron | 78.3 | |
| Thermal conductivity of electron | 27.3 | |
| Heat capacity of lattice | 1.659 × 105 | |
| Thermal conductivity of lattice | 324 | |
| Reflectivity [1] | 0.8 | |
| Thermodynamic equilibrium critical temperature | 3973 | |
| Depth of scanning trajectory | 1.37 × 10−9 |
| Step | Abrasive Grain Size | Surface Roughness (Rq) | Time |
|---|---|---|---|
| 1 | W20 | 162.2 nm | 0.5 h |
| 2 | W7 | 162.2–56.1 nm | 0.5 h |
| 3 | W7 | 56.1–41.306 nm | 8 h |
| 4 | W0.5 | 41.036–18.753 nm | 4 h |
| 5 | W0.5 | 18.753–1.525 nm | 10 h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Liu, C.; Chen, T.; Shao, M.; Jiang, C.; Lu, C.; Song, S. Parameter Optimization of RB-SiC Polishing by Femtosecond Laser. Materials 2023, 16, 1582. https://doi.org/10.3390/ma16041582
Yang T, Liu C, Chen T, Shao M, Jiang C, Lu C, Song S. Parameter Optimization of RB-SiC Polishing by Femtosecond Laser. Materials. 2023; 16(4):1582. https://doi.org/10.3390/ma16041582
Chicago/Turabian StyleYang, Tingkai, Changhua Liu, Tao Chen, Meng Shao, Chun Jiang, Changzheng Lu, and Shijun Song. 2023. "Parameter Optimization of RB-SiC Polishing by Femtosecond Laser" Materials 16, no. 4: 1582. https://doi.org/10.3390/ma16041582
APA StyleYang, T., Liu, C., Chen, T., Shao, M., Jiang, C., Lu, C., & Song, S. (2023). Parameter Optimization of RB-SiC Polishing by Femtosecond Laser. Materials, 16(4), 1582. https://doi.org/10.3390/ma16041582





