Critical Roles of Impurities and Imperfections in Various Phases of Materials
Abstract
1. Introduction
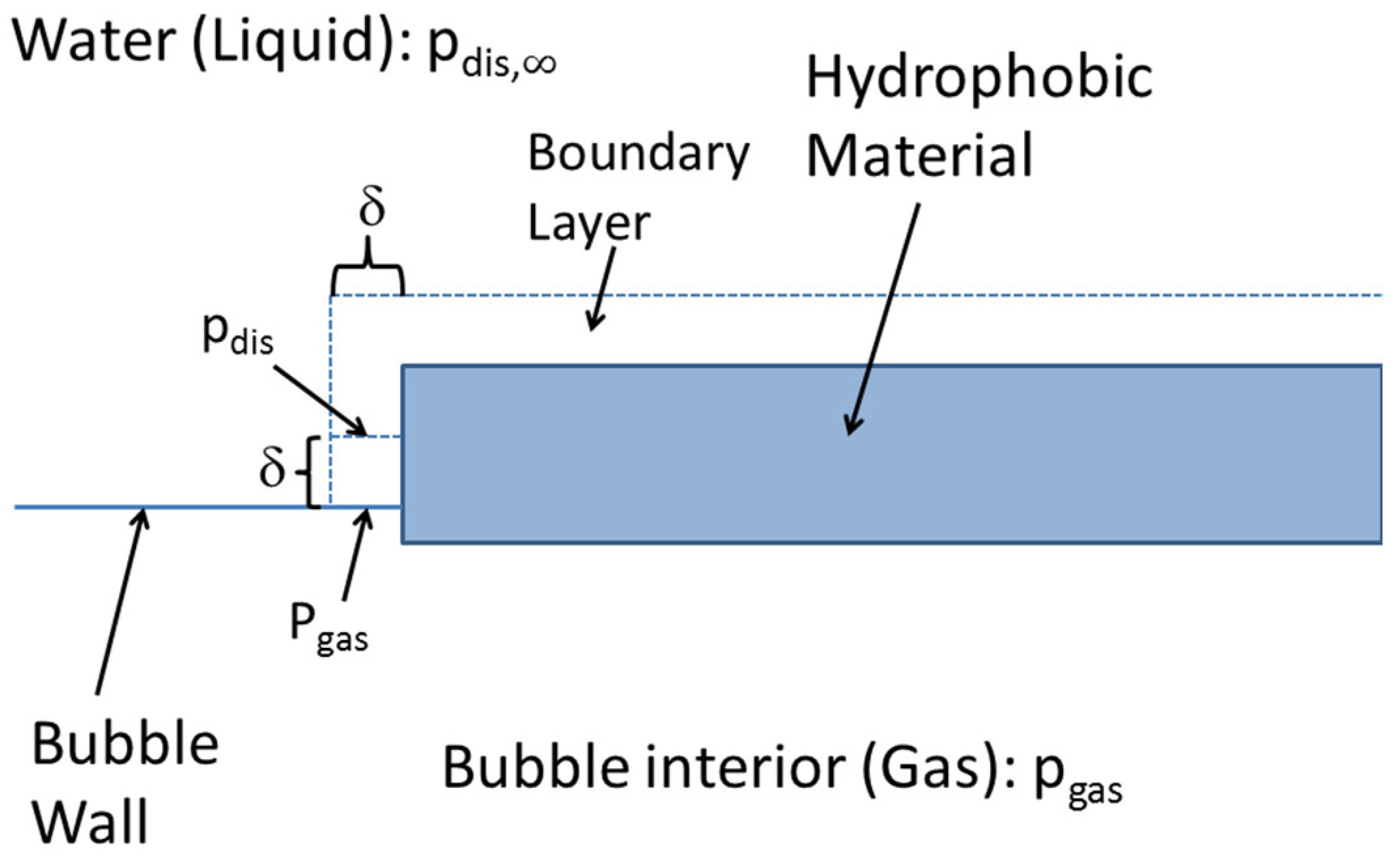
2. Bulk Nanobubbles (Ultrafine Bubbles)
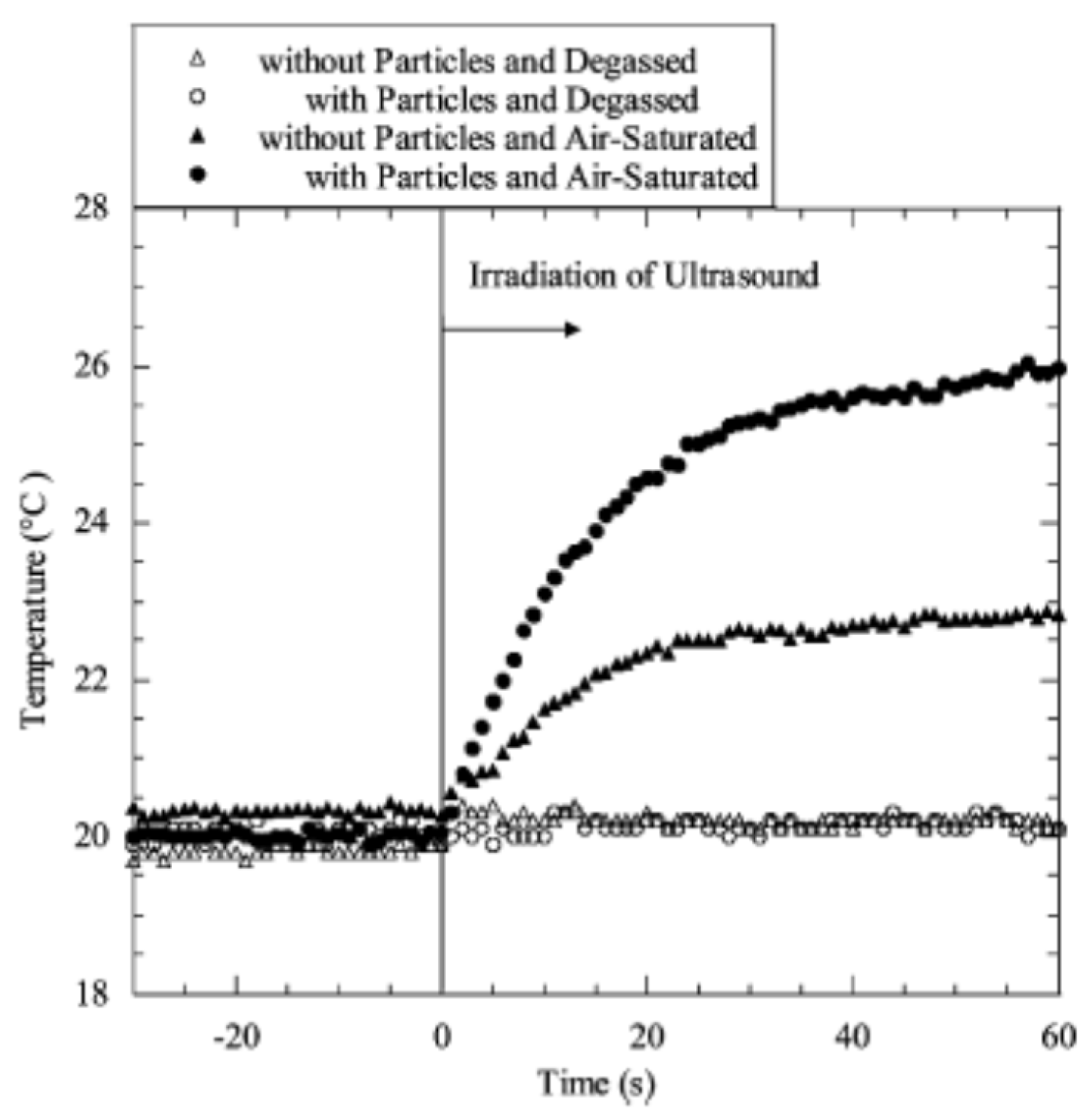
3. Acoustic Cavitation Threshold
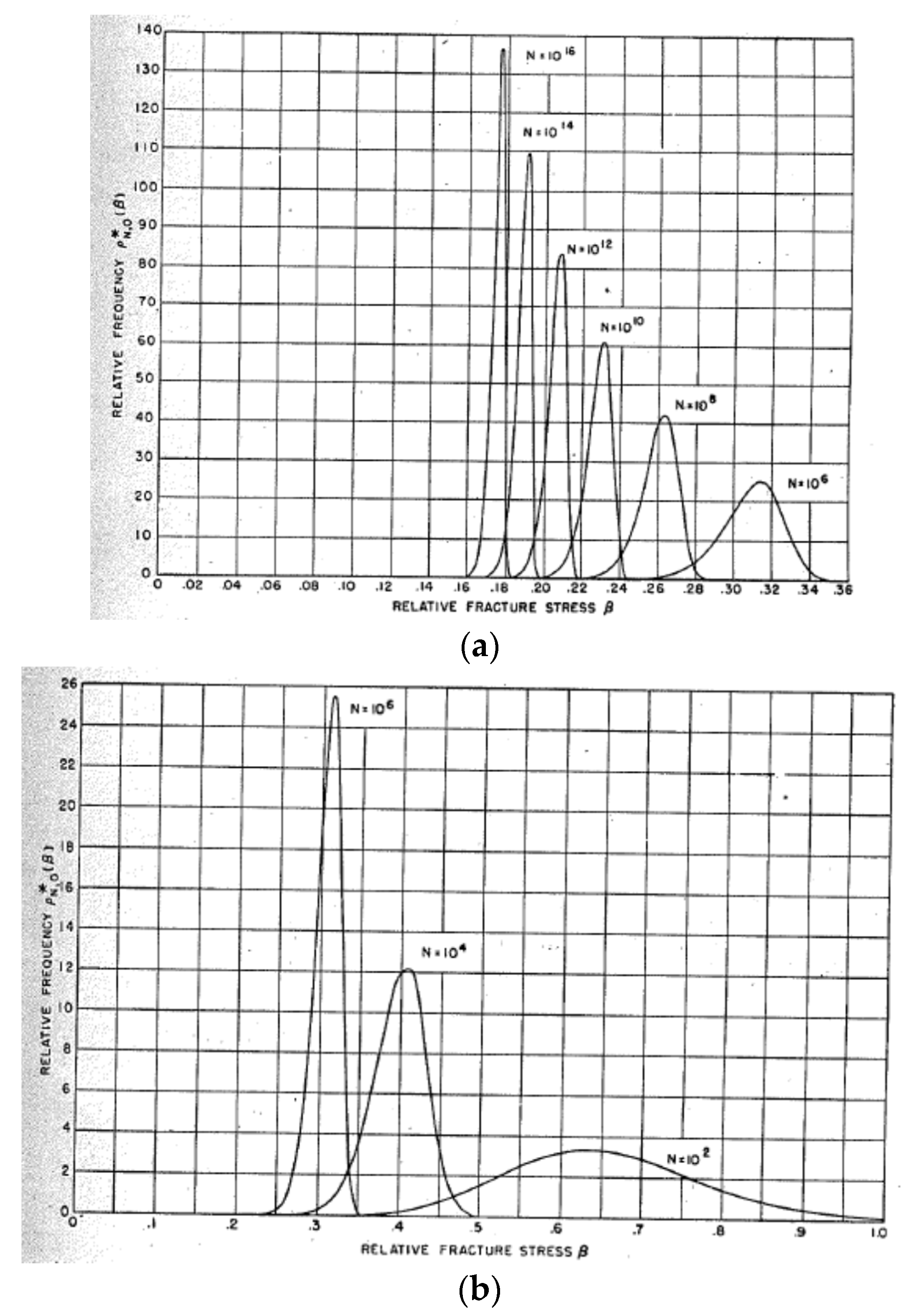
4. Strength of Brittle Ceramics
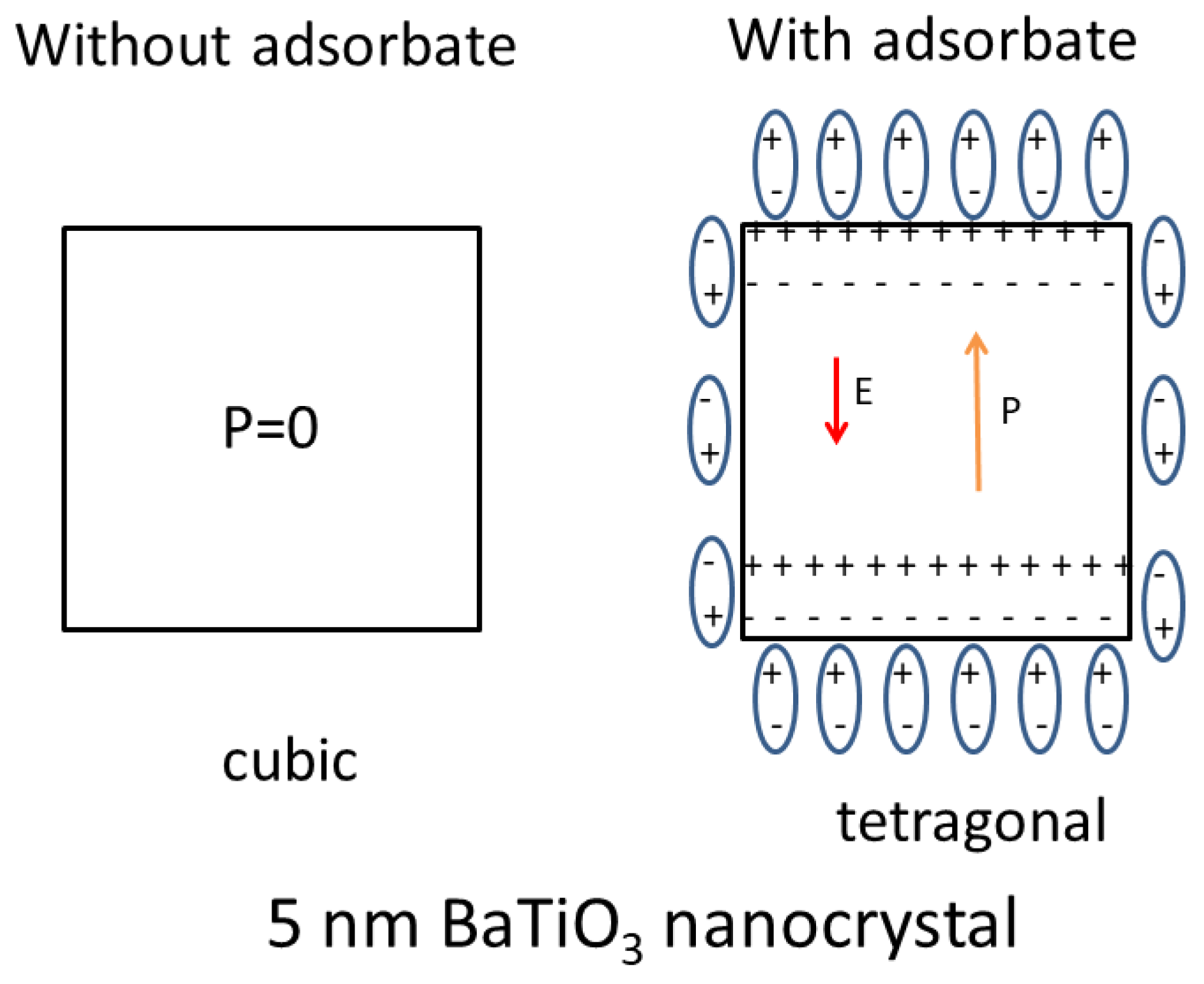
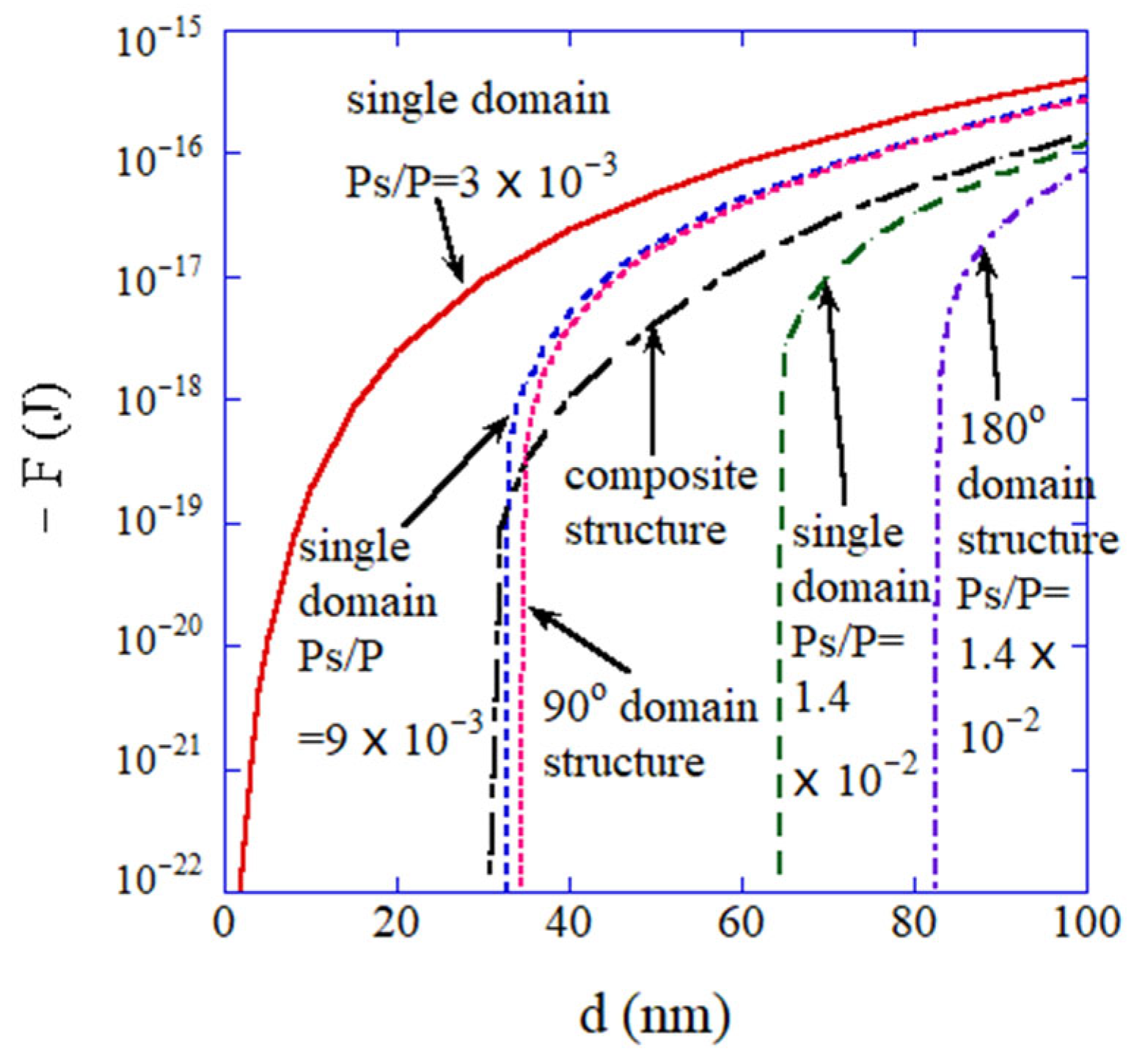
5. Size Effect of a BaTiO3 Nanocrystal
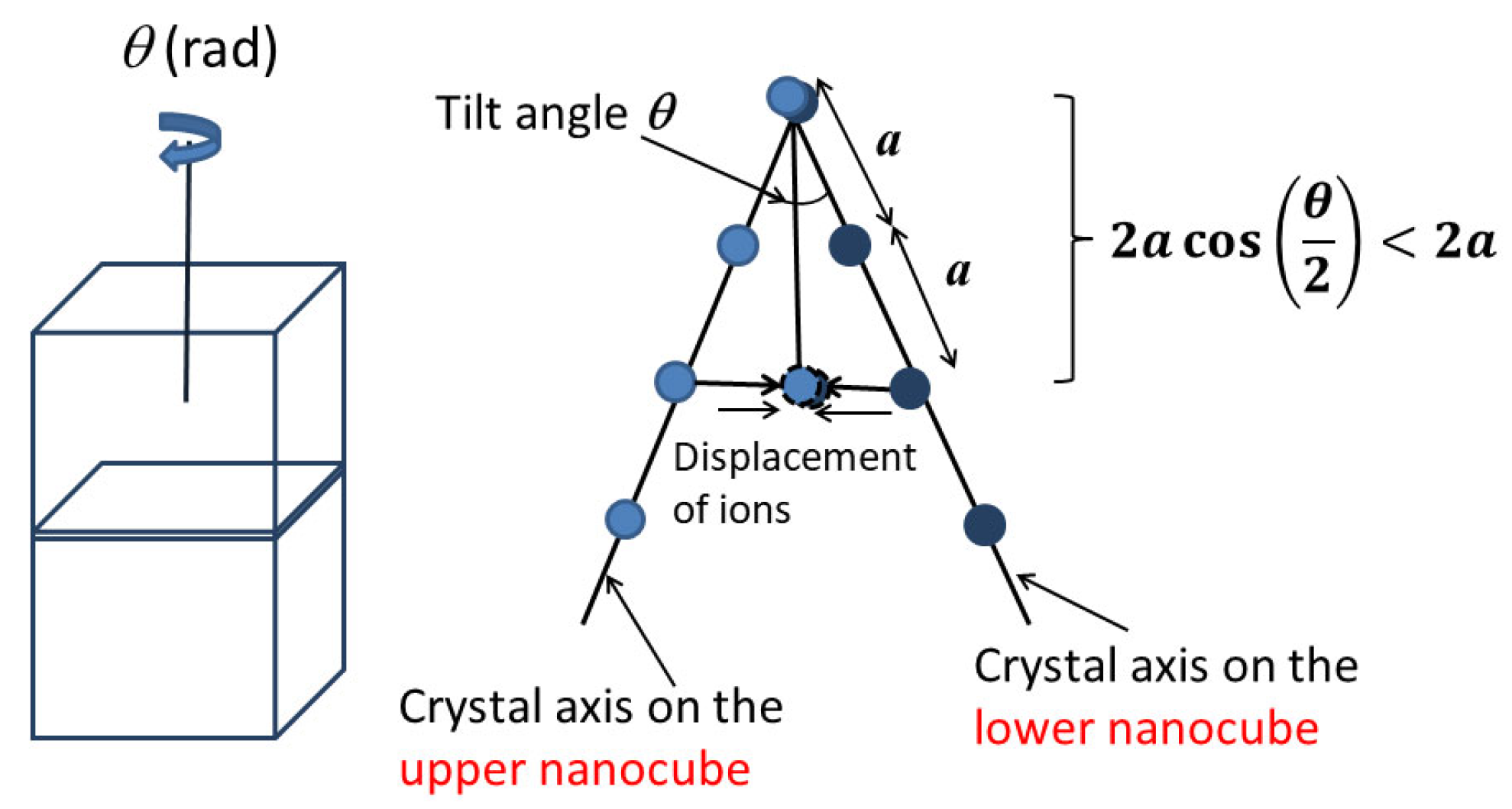
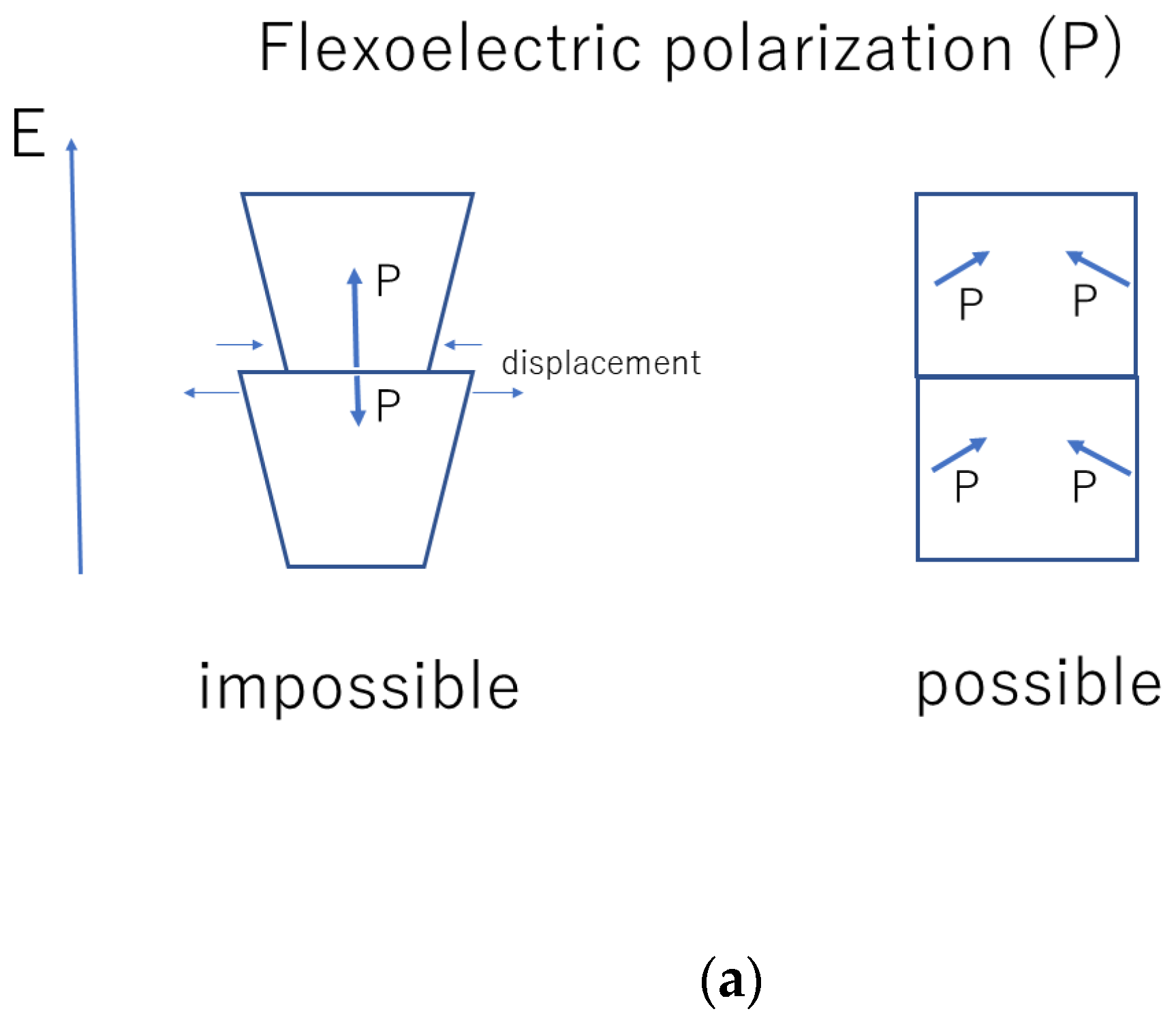
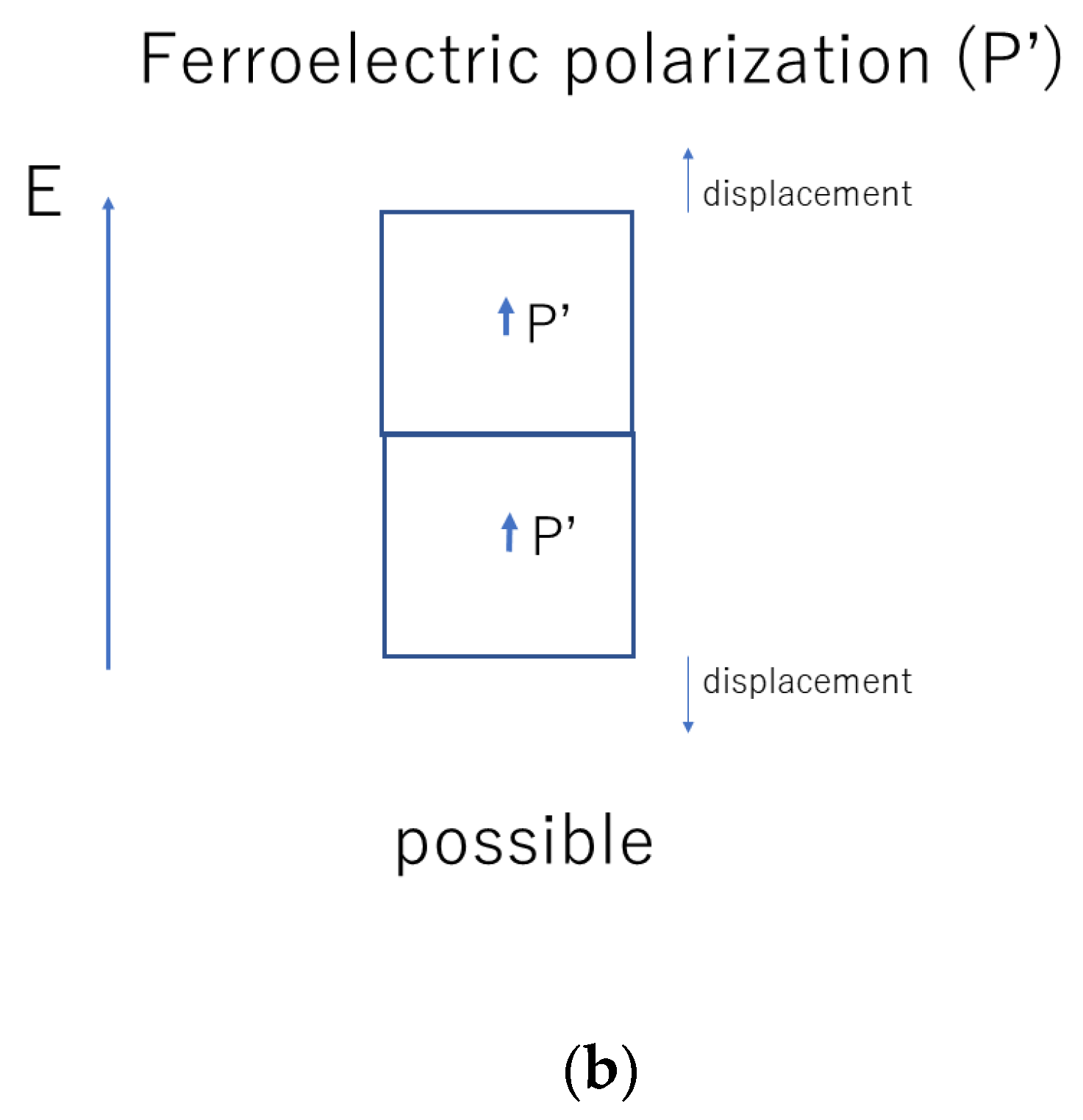
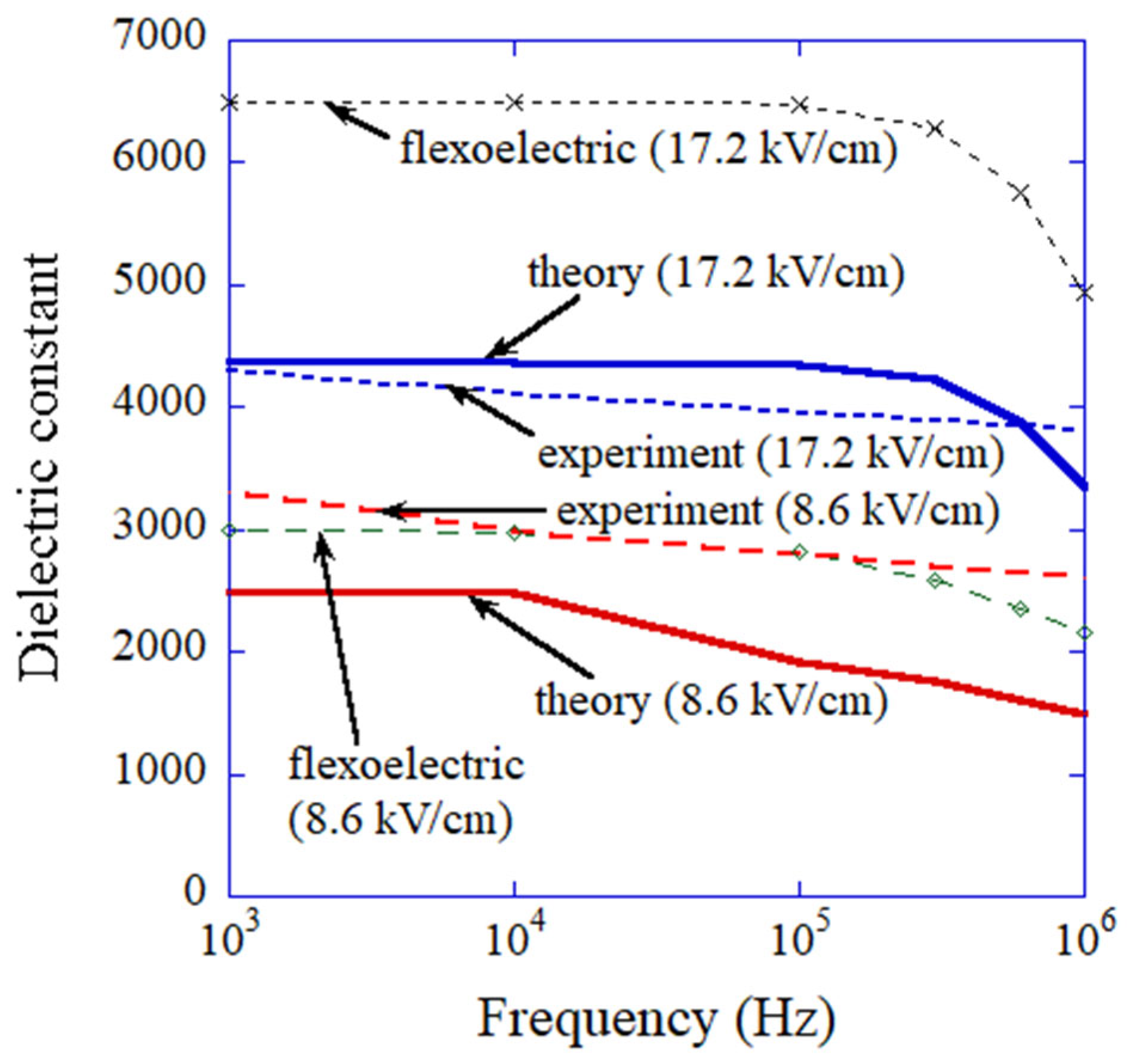
6. Dielectric Constant of an Assembly of BaTiO3 Nanocubes
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stoffel, R.P.; Wessel, C.; Lumey, M.-W.; Dronskowski, R. Ab initio thermochemistry of solid-state materials. Angew. Chem. Int. Ed. 2010, 49, 5242–5266. [Google Scholar] [CrossRef] [PubMed]
- Pedone, A.; Biczysko, M.; Barone, V. Environmental effects in computational spectroscopy: Accuracy and interpretation. ChemPhysChem 2010, 11, 1812–1832. [Google Scholar] [CrossRef] [PubMed]
- Kotliar, G.; Savrasov, S.Y.; Haule, K.; Oudovenko, V.S.; Parcollet, O.; Marianetti, C.A. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 2006, 78, 865–951. [Google Scholar] [CrossRef]
- Pulci, O.; Marsili, M.; Luppi, E.; Hogan, C.; Garbuio, V.; Sottile, F.; Magri, R.; Del Sole, R. Electronic excitations in solids: Density functional and Green’s function theory. Phys. Stat. Sol. 2005, 242, 2737–2750. [Google Scholar] [CrossRef]
- Chandra, Y.; Adhikari, S.; Saavedra Flores, E.I.; Figiel, L. Advances in finite element modelling of graphene and associated nanostructures. Mater. Sci. Eng. R 2020, 140, 100544. [Google Scholar] [CrossRef]
- Tankut, N.; Tankut, A.N.; Zor, M. Finite element analysis of wood materials. Drv. Ind. 2014, 65, 159–171. [Google Scholar] [CrossRef]
- Kaltenbach, C.; Laurien, E. CFD simulation of spray cooling in the model containment THAI. Nucl. Eng. Des. 2018, 328, 359–371. [Google Scholar] [CrossRef]
- Wang, W.; Lu, B.; Zhang, N.; Shi, Z.; Li, J. A review of multiscale CFD for gas-solid CFB modeling. Int. J. Multiph. Flow 2010, 36, 109–118. [Google Scholar] [CrossRef]
- Van Gunsteren, W.F.; Daura, X.; Hansen, N.; Mark, A.E.; Oostenbrink, C.; Riniker, S.; Smith, L.J. Validation of molecular simulation: An overview of issues. Angew. Chem. Int. Ed. 2018, 57, 884–902. [Google Scholar] [CrossRef] [PubMed]
- Venable, R.M.; Kramer, A.; Pastor, R.W. Molecular dynamics simulations of membrane permeability. Chem. Rev. 2019, 119, 5954–5997. [Google Scholar] [CrossRef] [PubMed]
- Pedone, A. Recent advances in solid-state NMR computational spectroscopy: The case of alumino-silicate glasses. Int. J. Quant. Chem. 2016, 116, 1520–1531. [Google Scholar] [CrossRef]
- Li, R.; Xie, L.; Wang, W.Y.; Liaw, P.K.; Zhang, Y. High-throughput calculations for high-entropy alloys: A brief review. Front. Mater. 2020, 7, 290. [Google Scholar] [CrossRef]
- Ikeda, Y.; Grabowski, B.; Kormann, F. Ab initio phase stabilities and mechanical properties of multicomponent alloys: A comprehensive review for high entropy alloys and compositionally complex alloys. Mater. Charact. 2019, 147, 464–511. [Google Scholar] [CrossRef]
- Cai, W.; Nix, W.D. Imperfections in Crystalline Solids; Cambridge Univ. Press: Cambridge, UK, 2016. [Google Scholar]
- Kofstad, P. Nonstoichiometry, Diffusion, and Electrical Conductivity in Binary Metal Oxides; Wiley-Interscience: New York, NY, USA, 1972. [Google Scholar]
- German, R.M. Sintering: From Empirical Observations to Scientific Principles; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Yasui, K.; Hamamoto, K. Comparison between cold sintering and dry pressing of CaCO3 at room temperature by numerical simulations. AIP Adv. 2022, 12, 045304. [Google Scholar] [CrossRef]
- Yasui, K.; Hamamoto, K. Importance of dislocations in ultrasound-assisted sintering of silver nanoparticles. J. Appl. Phys. 2021, 130, 194901. [Google Scholar] [CrossRef]
- Greenwood, N.N. Ionic Crystals, Lattice Defects and Nonstoichiometry; Butterworth: London, UK, 1968. [Google Scholar]
- Buckley, H.E. Crystal Growth; John Wiley & Sons: New York, NY, USA, 1951. [Google Scholar]
- Yabe, A. History of ultrafine bubbles. In Ultrafine Bubbles; Terasaka, K., Yasui, K., Kanematsu, W., Aya, N., Eds.; Jenny Stanford Pub.: Singapore, 2022; pp. 1–16. [Google Scholar]
- Alheshibri, M.; Qian, J.; Jehannin, M.; Craig, V.S.J. A history of nanobubbles. Langmuir 2016, 32, 11086–11100. [Google Scholar] [CrossRef]
- Bunkin, N.F.; Shkirin, A.V. Nanobubble clusters of dissolved gas in aqueous solutions of electrolyte. II. Theoretical interpretation. J. Chem. Phys. 2012, 137, 054707. [Google Scholar] [CrossRef]
- Nirmalkar, N.; Pacek, A.W.; Barigou, M. Interpreting the interfacial and colloidal stability of bulk nanobubbles. Soft Matter 2018, 14, 9643–9656. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, Z.; Zhang, X. Surface enrichment of ions leads to the stability of bulk nanobubbles. Soft Matter 2020, 16, 5470–5477. [Google Scholar] [CrossRef]
- Satpute, P.A.; Earthman, J.C. Hydroxyl ion stabilization of bulk nanobubbles resulting from microbubble shrinkage. J. Colloid Interface Sci. 2021, 584, 449–455. [Google Scholar] [CrossRef]
- Li, M.; Ma, X.; Eisener, J.; Pfeiffer, P.; Ohl, C.-D.; Sun, C. How bulk nanobubbles are stable over a wide range of temperatures. J. Colloid Interface Sci. 2021, 596, 184–198. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Li, M.; Pfeiffer, P.; Eisener, J.; Ohl, C.-D.; Sun, C. Ion adsorption stabilizes bulk nanobubbles. J. Colloid Interface Sci. 2022, 606, 1380–1394. [Google Scholar] [CrossRef]
- Koshoridze, S.I.; Levin, Y.K. Comment on “Can bulk nanobubbles be stabilized by electrostatic interaction?” by S. Wang, L. Zhou and Y. Gao, Phys. Chem. Chem. Phys., 2021, 23, 16501. Phys. Chem. Chem. Phys. 2022, 24, 10622–10625. [Google Scholar] [CrossRef] [PubMed]
- Sugano, K.; Miyoshi, Y.; Inazato, S. Study of ultrafine bubble stabilization by organic material adhesion. Jpn. J. Multiphase Flow 2017, 31, 299–306. [Google Scholar] [CrossRef]
- Lohse, D.; Zhang, X. Surface nanobubbles and nanodroplets. Rev. Mod. Phys. 2015, 87, 981–1035. [Google Scholar] [CrossRef]
- Yasui, K.; Tuziuti, T.; Kanematsu, W. Interaction of bulk nanobubbles (ultrafine bubbles) with a solid surface. Langmuir 2021, 37, 1674–1681. [Google Scholar] [CrossRef]
- Yasui, K.; Tuziuti, T.; Kanematsu, W.; Kato, K. Advanced dynamic-equilibrium model for a nanobubble and a micropancake on a hydrophobic or hydrophilic surface. Phys. Rev. E 2015, 91, 033008. [Google Scholar] [CrossRef]
- ISO 20480-1:2017; Fine Bubble Technology-General Principles for Usage and Measurement of Fine Bubbles-Part 1: Terminology. International Organization for Standardization: Geneva, Switzerland, 2017.
- Terasaka, K. Introduction to experiments. In Ultrafine Bubbles; Terasaka, K., Yasui, K., Kanematsu, W., Aya, N., Eds.; Jenny Stanford Pub.: Singapore, 2022; pp. 17–72. [Google Scholar]
- Wang, W.; Fan, W.; Huo, M.; Zhao, H.; Lu, Y. Hydroxyl radical generation and contaminant removal from water by the collapse of microbubbles under different hydrochemical conditions. Water Air Soil Pollut. 2018, 229, 86. [Google Scholar] [CrossRef]
- Takahashi, M.; Chiba, K.; Li, P. Free-radical generation from collapsing microbubbles in the absence of a dynamic stimulus. J. Phys. Chem. B 2007, 111, 1343–1347. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, M. Nanobubbles: An introduction. In Micro- and Nanobubbles; Tsuge, H., Ed.; Pan Stanford: Singapore, 2014; pp. 307–315. [Google Scholar]
- Sonoda, A. Real UFB sample measurements: A few cases. In Ultrafine Bubbles; Terasaka, K., Yasui, K., Kanematsu, W., Aya, N., Eds.; Jenny Stanford Pub.: Singapore, 2022; pp. 87–108. [Google Scholar]
- Kanematsu, W.; Tuziuti, T.; Yasui, K. The influence of storage conditions and container materials on the long term stability of bulk nanobubbles—Consideration from a perspective of interactions between bubbles and surroundings. Chem. Eng. Sci. 2020, 219, 115594. [Google Scholar] [CrossRef]
- Yasui, K. Theory of ultrafine bubbles. In Ultrafine Bubbles; Terasaka, K., Yasui, K., Kanematsu, W., Aya, N., Eds.; Jenny Stanford Pub.: Singapore, 2022; pp. 109–153. [Google Scholar]
- Yasui, K. Dynamics of acoustic bubbles. In Sonochemistry and the Acoustic Bubble; Grieser, F., Choi, P., Enomoto, N., Harada, H., Okitsu, K., Yasui, K., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 41–83. [Google Scholar]
- Yasui, K.; Tuziuti, T.; Kanematsu, W. High temperature and pressure inside a dissolving oxygen nanobubble. Ultrason. Sonochem. 2019, 55, 308–312. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K.; Tuzitui, T.; Kanematsu, W. Extreme conditions in a dissolving air nanobubble. Phys. Rev. E 2016, 94, 013106. [Google Scholar] [CrossRef] [PubMed]
- Alheshibri, M.; Craig, V.S.J. Differentiating between nanoparticles and nanobubbles by evaluation of the compressibility and density of nanoparticles. J. Phys. Chem. C 2018, 122, 21998–22007. [Google Scholar] [CrossRef]
- Eklund, F.; Alheshibri, M.; Swenson, J. Differentiating bulk nanobubbles from nanodroplets and nanoparticles. Curr. Opin. Colloid Interface Sci. 2021, 53, 101427. [Google Scholar] [CrossRef]
- Nirmalkar, N.; Pacek, A.W.; Barigou, M. On the existence and stability of bulk nanobubbles. Langmuir 2018, 34, 10964–10973. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.; Feng, Z.; Yang, F.; Gu, N. Bulk nanobubbles fabricated by repeated compression of microbubbles. Langmuir 2019, 35, 4238–4245. [Google Scholar] [CrossRef]
- Yasui, K. On some aspects of nanobubble-containing systems. Nanomaterials 2022, 12, 2175. [Google Scholar] [CrossRef]
- Tuziuti, T.; Yasui, K.; Kanematsu, W. Variations in the size distribution of bulk nanobubbles in response to static pressure increases. Jpn. J. Appl. Phys. 2020, 59, SKKD03. [Google Scholar] [CrossRef]
- Xiao, W.; Wang, X.; Zhou, L.; Zhou, W.; Wang, J.; Qin, W.; Qiu, G.; Hu, J.; Zhang, L. Influence of mixing and nanosolids on the formation of nanobubbles. J. Phys. Chem. B 2019, 123, 317–323. [Google Scholar] [CrossRef]
- Ke, S.; Xiao, W.; Quan, N.; Dong, Y.; Zhang, L.; Hu, J. Formation and stability of bulk nanobubbles in different solutions. Langmuir 2019, 35, 5250–5256. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, H.; Maeda, S.; Kashiwa, M.; Fujita, T. Measurement and identification of ultrafine bubbles by resonant mass measurement method. Proc. SPIE 2014, 9232, 92320S. [Google Scholar] [CrossRef]
- Tan, B.H.; An, H.; Ohl, C.-D. Stability of surface and bulk nanobubbles. Curr. Opin. Colloid Interface Sci. 2021, 53, 101428. [Google Scholar] [CrossRef]
- Yasui, K.; Tuziuti, T.; Kanematsu, W. Mysteries of bulk nanobubbles (ultrafine bubbles); stability and radical formation. Ultrason. Sonochem. 2018, 48, 259–266. [Google Scholar] [CrossRef]
- Yasui, K.; Tuziuti, T.; Kanematsu, W.; Kato, K. Dynamic equilibrium model for a bulk nanobubble and a microbubble partly covered with hydrophobic material. Langmuir 2016, 32, 11101–11110. [Google Scholar] [CrossRef] [PubMed]
- Sugano, K.; Miyoshi, Y.; Inazato, S. Study of ultrafine bubble stabilization by organic material adhesion. In Ultrafine Bubbles; Terasaka, K., Yasui, K., Kanematsu, W., Aya, N., Eds.; Jenny Stanford: Singapore, 2022; pp. 155–177. [Google Scholar]
- Yasui, K.; Tuziuti, T.; Izu, N.; Kanematsu, W. Is surface tension reduced by nanobubbles (ultrafine bubbles) generated by cavitation? Ultrason. Sonochem. 2019, 52, 13–18. [Google Scholar] [CrossRef] [PubMed]
- Ushida, A.; Hasegawa, T.; Takahashi, N.; Nakajima, T.; Murao, S.; Narumi, T.; Uchiyama, H. Effect of mixed nanobubble and microbubble liquids on the washing rate of cloth in an alternating flow. J. Surfact. Deterg. 2012, 15, 695–702. [Google Scholar] [CrossRef]
- Bu, X.; Zhou, S.; Tian, X.; Ni, C.; Nazari, S.; Alheshibri, M. Effect of aging time, airflow rate, and nonionic surfactants on the surface tension of bulk nanobubbles water. J. Mol. Liq. 2022, 359, 119274. [Google Scholar] [CrossRef]
- Zhou, S.; Nazari, S.; Hassanzadeh, A.; Bu, X.; Ni, C.; Peng, Y.; Xie, G.; He, Y. The effect of preparation time and aeration rate on the properties of bulk micro-nanobubble water using hydrodynamic cavitation. Ultrason. Sonochem. 2022, 84, 105965. [Google Scholar] [CrossRef]
- Mezger, M.; Schoder, S.; Reichert, H.; Schroder, H.; Okasinski, J.; Honkimaki, V.; Ralston, J.; Bilgram, J.; Roth, R.; Dosch, H. Water and ice in contact with octadecyl-trichlorosilane functionalized surfaces: A high resolution x-ray reflectivity study. J. Chem. Phys. 2008, 128, 244705. [Google Scholar] [CrossRef] [PubMed]
- Steitz, R.; Gutberlet, T.; Hauss, T.; Klosgen, B.; Krastev, R.; Schemmel, S.; Simonsen, A.C.; Findenegg, G.H. Nanobubbles and their precursor layer at the interface of water against a hydrophobic substrate. Langmuir 2003, 19, 2409–2418. [Google Scholar] [CrossRef]
- Peng, H.; Birkett, G.R.; Nguyen, A.V. Origin of interfacial nanoscopic gaseous domains and formation of dense gas layer at hydrophobic solid-water interface. Langmuir 2013, 29, 15266–15274. [Google Scholar] [CrossRef]
- Peng, H.; Hampton, M.A.; Nguyen, A.V. Nanobubbles do not sit alone at the solid-liquid interface. Langmuir 2013, 29, 6123–6130. [Google Scholar] [CrossRef]
- Lu, Y.-H.; Yang, C.-W.; Hwang, I.-S. Molecular layer of gaslike domains at a hydrophobic-water interface observed by frequency-modulation atomic force microscopy. Langmuir 2012, 28, 12691–12695. [Google Scholar] [CrossRef]
- Azadi, M.; Nguyen, A.V.; Yakubov, G.E. Attractive forces between hydrophobic solid surfaces measured by AFM on the first approach in salt solutions and in the presence of dissolved gases. Langmuir 2015, 31, 1941–1949. [Google Scholar] [CrossRef]
- Dammer, S.M.; Lohse, D. Gas enrichment at liquid-wall interfaces. Phys. Rev. Lett. 2006, 96, 206101. [Google Scholar] [CrossRef] [PubMed]
- Petsev, N.D.; Shell, M.S.; Leal, L.G. Dynamic equilibrium explanation for nanobubbles’ unusual temperature and saturation dependence. Phys. Rev. E 2013, 88, 010402. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2011; pp. 161–163. [Google Scholar]
- Yasui, K. Acoustic Cavitation and Bubble Dynamics; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Leighton, T.G. The Acoustic Bubble; Academic Press: London, UK, 1994. [Google Scholar]
- Young, F.R. Cavitation; Imperial College: London, UK, 1999. [Google Scholar]
- Gallego-Juarez, J.A.; Graff, K.F. (Eds.) Power Ultrasonics; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1982. [Google Scholar]
- Didenko, Y.T.; McNamara, W.B., III; Suslick, K.S. Temperature of multibubble sonoluminescence in water. J. Phys. Chem. A 1999, 103, 10783–10788. [Google Scholar] [CrossRef]
- McNamara, W.B., III; Didenko, Y.T.; Suslick, K.S. Pressure during sonoluminescence. J. Phys. Chem. B 2003, 107, 7303–7306. [Google Scholar] [CrossRef]
- Yasui, K. Production of O radicals from cavitation bubbles under ultrasound. Molecules 2022, 27, 4788. [Google Scholar] [CrossRef]
- Henglein, A. Contributions to various aspects of cavitation chemistry. In Advances in Sonochemistry; Mason, T.J., Ed.; JAI Press: London, UK, 1993; Volume 3, pp. 17–83. [Google Scholar]
- Yasui, K. Multibubble sonoluminescence from a theoretical perspective. Molecules 2021, 26, 4624. [Google Scholar] [CrossRef] [PubMed]
- Young, F.R. Sonoluminescence; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Yasui, K.; Tuziuti, T.; Sivakumar, M.; Iida, Y. Sonoluminescence. Appl. Spectrosc. Rev. 2004, 39, 399–436. [Google Scholar] [CrossRef]
- Brenner, M.P.; Hilgenfeldt, S.; Lohse, D. Single-bubble sonoluminescence. Rev. Mod. Phys. 2002, 74, 425–484. [Google Scholar] [CrossRef]
- Hata, T.; Yamawaki, N.; Nishiuchi, Y.; Okumura, H.; Akamatsu, S. Discrimination of ultra-fine bubbles and solid nanoparticles using the sonoluminescence effect. Bunseki Kagaku 2019, 68, 847–852. [Google Scholar] [CrossRef]
- Tuziuti, T.; Yasui, K.; Kanematsu, W. Influence of bulk nanobubble concentration on the intensity of sonoluminescence. Ultrason. Sonochem. 2021, 76, 105646. [Google Scholar] [CrossRef]
- Fisher, J.C. The fracture of liquids. J. Appl. Phys. 1948, 19, 1062–1067. [Google Scholar] [CrossRef]
- Temperley, H.N.V. The behavior of water under hydrostatic tension.III. Proc. Phys. Soc. Lond. 1947, 59, 199–208. [Google Scholar] [CrossRef]
- Galloway, W.J. An experimental study of acoustically induced cavitation in liquids. J. Acoust. Soc. Am. 1954, 26, 849–857. [Google Scholar] [CrossRef]
- Apfel, R.E. The role of impurities in cavitation-threshold determination. J. Acoust. Soc. Am. 1970, 48, 1179–1186. [Google Scholar] [CrossRef]
- Crum, L.A. Tensile-strength of water. Nature 1979, 278, 148–149. [Google Scholar] [CrossRef]
- Strasberg, M. Onset of ultrasonic cavitation in tap water. J. Acoust. Soc. Am. 1959, 31, 163–176. [Google Scholar] [CrossRef]
- Fox, F.E.; Herzfeld, K.F. Gas bubbles with organic skin as cavitation nuclei. J. Acoust. Soc. Am. 1954, 26, 984–989. [Google Scholar] [CrossRef]
- Yount, D.E.; Gillary, E.W.; Hoffman, D.C. A microscopic investigation of bubble formation nuclei. J. Acoust. Soc. Am. 1984, 76, 1511–1521. [Google Scholar] [CrossRef]
- Yount, D.E. Skins of varying permeability: A stabilization mechanism for gas cavitation nuclei. J. Acoust. Soc. Am. 1979, 65, 1429–1439. [Google Scholar] [CrossRef]
- Atchley, A.A.; Prosperetti, A. The crevice model of bubble nucleation. J. Acoust. Soc. Am. 1989, 86, 1065–1084. [Google Scholar] [CrossRef]
- Tuziuti, T.; Yasui, K.; Sivakumar, M.; Iida, Y.; Miyoshi, N. Correlation between acoustic cavitation noise and yield enhancement of sonochemical reaction by particle addition. J. Phys. Chem. A 2005, 109, 4869–4872. [Google Scholar] [CrossRef]
- Dehane, A.; Merouani, S.; Chibani, A.; Hamdaoui, O.; Yasui, K.; Ashokkumar, M. Estimation of the number density of active cavitation bubbles in a sono-irradiated aqueous solution using a thermodynamic approach. Ultrasonics 2022, 126, 106824. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Chang, J.; Bussonniere, A.; Xie, G.; Liu, Q. Evaluation of wettability of mineral particles via cavitation thresholds. Powder Technol. 2020, 362, 334–340. [Google Scholar] [CrossRef]
- Bussonniere, A.; Liu, Q.; Tsai, P.A. Cavitation nuclei regeneration in a water-particle suspension. Phys. Rev. Lett. 2020, 124, 034501. [Google Scholar] [CrossRef] [PubMed]
- Su, K.; Wu, J.; Xia, D.; Zhang, X. Clarification of regimes determining sonochemical reactions in solid particle suspensions. Ultrason. Sonochem. 2022, 82, 105910. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics, 4th ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Griffith, A.A. The phenomena of rupture and flow in solids. Phil. Trans. Ser. A 1920, 221, 163–198. [Google Scholar]
- Reichel, F.; Jeurgens, L.P.H.; Mittemeijer, E.J. The thermodynamic stability of amorphous oxide overgrowths on metals. Acta Mater. 2008, 56, 659–674. [Google Scholar] [CrossRef]
- Canepa, P.; Dawson, J.A.; Gautam, G.S.; Statham, J.M.; Parker, S.C.; Islam, M.S. Particle morphology and lithium segregation to surfaces of the Li7La3Zr2O12 solid electrolyte. Chem. Mater. 2018, 30, 3019–3027. [Google Scholar] [CrossRef]
- Munz, D.; Fett, T. Ceramics: Mechanical Properties, Failure Behaviour, Materials Selection; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Chiang, Y.M.; Birnie, D.P., III; Kingery, W.D. Physical Ceramics; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Kim, B.-N.; Wakayama, S. Simulation of microfracture process of brittle polycrystals: Microcracking and crack propagation. Comput. Mater. Sci. 1997, 8, 327–334. [Google Scholar] [CrossRef]
- Smith, R.W.; Srolovitz, D.J. Simulation of dynamic fracture of an impact-loaded brittle solid: Microcracked and polycrystalline solids. Model. Simul. Mater. Sci. Eng. 1995, 3, 665–688. [Google Scholar] [CrossRef]
- Shih, C.J.; Meyers, M.A.; Nesterenko, V.F.; Chen, S.J. Damage evolution in dynamic deformation of silicon carbide. Acta Mater. 2000, 48, 2399–2420. [Google Scholar] [CrossRef]
- Dai, J.; Su, H.; Wang, Z.; Xu, J.; Fu, Y.; Chen, J. Damage formation mechanisms of sintered silicon carbide during single-diamond grinding. Ceram. Int. 2021, 47, 28419–28428. [Google Scholar] [CrossRef]
- Argon, A.S.; Orowan, E. Crack nucleation in MgO single crystal. Philos. Mag. 1964, 9, 1023–1039. [Google Scholar] [CrossRef]
- Stokes, R.J.; Johnston, T.L.; Li, C.H. The relationship between plastic flow and the fracture mechanism in magnesium oxide single crystal. Philos. Mag. 1959, 4, 920–932. [Google Scholar] [CrossRef]
- Stokes, R.J.; Johnston, T.L.; Li, C.H. Crack formation in magnesium oxide single crystals. Philos. Mag. 1958, 3, 718–725. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Z.; Zhang, P.; Li, C.; Zhang, Z. Dislocation arrangements with slip bands during fatigue cracking. Mater. Charact. 2018, 145, 96–100. [Google Scholar] [CrossRef]
- Hunsche, A.; Neumann, P. Quantitative measurement of persistent slip band profiles and crack initiation. Acta Metall. 1986, 34, 207–217. [Google Scholar] [CrossRef]
- Woods, P.J. Low-amplitude fatigue of copper and copper-5 at. % aluminium single crystals. Philos. Mag. 1973, 28, 155–191. [Google Scholar] [CrossRef]
- Cai, M. Practical estimates of tensile strength and Hoek-Brown strength parameter of brittle rocks. Rock Mech. Rock Eng. 2010, 43, 167–184. [Google Scholar] [CrossRef]
- Sheorey, P.R. Empirical Rock Failure Criteria; A. A. Balkema: Rotterdam, The Netherlands, 1997. [Google Scholar]
- Fisher, J.C.; Hollomon, J.H. A statistical theory of fracture. Trans. Am. Inst. Min. Metall. Eng. 1947, 171, 546–561. [Google Scholar]
- Guo, N.; Shen, H.-Z.; Shen, P. One-step synthesis and densification of BaTiO3 by reactive cold sintering. Scr. Mater. 2022, 213, 114628. [Google Scholar] [CrossRef]
- Tsuji, K.; Ndayishimiye, A.; Lowum, S.; Floyd, R.; Wang, K.; Wetherington, M.; Maria, J.-P.; Randall, C.A. Single step densification of high permittivity BaTiO3 ceramics at 300 °C. J. Eur. Ceram. Soc. 2020, 40, 1280–1284. [Google Scholar] [CrossRef]
- Jona, F.; Shirane, G. Ferroelectric Crystals; Dover: New York, NY, USA, 1993. [Google Scholar]
- Akdogan, E.K.; Leonard, M.R.; Safari, A. Size effects in ferroelectric ceramics. In Handbook of Low and High Dielectric Constant Materials and Their Applications: Phenomena, Properties, and Applications; Nalwa, H.S., Ed.; Academic Press: San Diego, CA, USA, 1999; Volume 2, pp. 61–112. [Google Scholar]
- Uchino, K.; Sadanaga, E.; Hirose, T. Dependence of the crystal-structure on particle-size in barium-titanate. J. Am. Ceram. Soc. 1989, 72, 1555–1558. [Google Scholar] [CrossRef]
- Begg, B.D.; Vance, E.R.; Nowotny, J. Effect of particle-size on the room-temperature crystal-structure of barium-titanate. J. Am. Ceram. Soc. 1994, 77, 3186–3192. [Google Scholar] [CrossRef]
- Li, X.; Shih, W.-H. Size effects in barium titanate particles and clusters. J. Am. Ceram. Soc. 1997, 80, 2844–2852. [Google Scholar] [CrossRef]
- Yamamoto, T.; Niori, H.; Moriwake, H. Particle-size dependence of crystal structure of BaTiO3 powder. Jpn. J. Appl. Phys. 2000, 39, 5683–5686. [Google Scholar] [CrossRef]
- Wada, S.; Yasuno, H.; Hoshina, T.; Nam, S.-M.; Kakemoto, H.; Tsurumi, T. Preparation of nm-sized barium titanate fine particles and their powder dielectric properties. Jpn. J. Appl. Phys. 2003, 42, 6188–6195. [Google Scholar] [CrossRef]
- Hoshina, T.; Kakemoto, H.; Tsurumi, T.; Wada, S.; Yashima, M. Size and temperature induced phase transition behaviors of barium titanate nanoparticles. J. Appl. Phys. 2006, 99, 054311. [Google Scholar] [CrossRef]
- Polking, M.J.; Han, M.-G.; Yourdkhani, A.; Petkov, V.; Kisielowski, C.F.; Volkov, V.V.; Zhu, Y.; Caruntu, G.; Alivisatos, A.P.; Ramesh, R. Ferroelectric order in individual nanometre-scale crystals. Nat. Mater. 2012, 11, 700–709. [Google Scholar] [CrossRef]
- Yasui, K.; Kato, K. Influence of adsorbate-induced charge screening, depolarization factor, mobile carrier concentration, and defect-induced microstrain on the size effect of a BaTiO3 nanoparticle. J. Phys. Chem. C 2013, 117, 19632–19644. [Google Scholar] [CrossRef]
- Chandra, P.; Littlewood, P.B. A Landau primer for ferroelectrics. In Physics of Ferroelectrics; Rabe, K.M., Ahn, C.H., Triscone, J.-M., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Topics Appl. Physics Volume 105, pp. 69–116. [Google Scholar]
- Fatuzzo, E.; Merz, W.J. Ferroelectricity; North-Holland Pub.: Amsterdam, The Netherlands, 1967. [Google Scholar]
- Lines, M.E.; Glass, A.M. Principles and Applications of Ferroelectrics and Related Materials; Oxford Univ. Press: Oxford, UK, 1977. [Google Scholar]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons: New York, NY, USA, 2005; pp. 458–459. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Shih, W.Y.; Shih, W.-H.; Aksay, I.A. Size dependence of the ferroelectric transition of small BaTiO3 particles: Effect of depolarization. Phys. Rev. B 1994, 50, 15575–15585. [Google Scholar] [CrossRef]
- He, D.Y.; Qiao, L.J.; Volinsky, A.A.; Bai, Y.; Wu, M.; Chu, W.Y. Humidity effects on (001) BaTiO3 single crystal surface water adsorption. Appl. Phys. Lett. 2011, 98, 062905. [Google Scholar] [CrossRef]
- Jiang, B.; Bai, Y.; Chu, W.Y.; Shi, S.Q.; Qiao, L.J.; Su, Y.J. Effect of humidity on domain switching behaviors of BaTiO3 single crystal under sustained load. Appl. Surf. Sci. 2008, 254, 5594–5598. [Google Scholar] [CrossRef]
- Spanier, J.E.; Kolpak, A.M.; Urban, J.J.; Grinberg, I.; Ouyang, L.; Yun, W.S.; Rappe, A.M.; Park, H. Ferroelectric phase transition in individual single-crystalline BaTiO3 nanowires. Nano Lett. 2006, 6, 735–739. [Google Scholar] [CrossRef]
- Akbarian, D.; Yilmaz, D.E.; Cao, Y.; Ganesh, P.; Dabo, I.; Munro, J.; Ginhoven, R.V.; van Duin, A.C.T. Understanding the influence of defects and surface chemistry on ferroelectric switching: A ReaxFF investigation of BaTiO3. Phys. Chem. Chem. Phys. 2019, 21, 18240–18249. [Google Scholar] [CrossRef]
- Li, D.; Zhao, M.H.; Garra, J.; Kolpak, A.M.; Rappe, A.M.; Bonnell, D.A.; Vohs, J.M. Direct in situ determination of the polarization dependence of physisorption on ferroelectric surfaces. Nat. Mater. 2008, 7, 473–477. [Google Scholar] [CrossRef] [PubMed]
- Kalinin, S.V.; Bonnell, D.A. Local potential and polarization screening on ferroelectric surfaces. Phys. Rev. B 2001, 63, 125411. [Google Scholar] [CrossRef]
- Jiang, B.; Bai, Y.; Cao, J.-L.; Su, Y.; Shi, S.-Q.; Chu, W.; Qiao, L. Delayed crack propagation in barium titanate single crystals in humid air. J. Appl. Phys. 2008, 103, 116102. [Google Scholar] [CrossRef]
- Shin, J.; Nascimento, V.B.; Geneste, G.; Rundgren, J.; Plummer, E.W.; Dkhil, B.; Kalinin, S.V.; Baddorf, A.P. Atomistic screening mechanism of ferroelectric surfaces: An in situ study of the polar phase in ultrathin BaTiO3 films exposed to H2O. Nano Lett. 2009, 9, 3720–3725. [Google Scholar] [CrossRef] [PubMed]
- Peter, F.; Szot, K.; Waser, R.; Reichenberg, B.; Tiedke, S.; Szade, J. Piezoresponse in the light of surface adsorbates: Relevance of defined surface conditions for perovskite materials. Appl. Phys. Lett. 2004, 85, 2896–2898. [Google Scholar] [CrossRef]
- Aoyagi, S.; Kuroiwa, Y.; Sawada, A.; Yamashita, I.; Atake, T. Composite structure of BaTiO3 nanoparticle investigated by SR X-ray diffraction. J. Phys. Soc. Jpn. 2002, 71, 1218–1221. [Google Scholar] [CrossRef]
- Hoshina, T.; Wada, S.; Kuroiwa, Y.; Tsurumi, T. Composite structure and size effect of barium titanate nanoparticles. Appl. Phys. Lett. 2008, 93, 192914. [Google Scholar] [CrossRef]
- Wada, S.; Yazawa, A.; Hoshina, T.; Kameshima, Y.; Kakemoto, H.; Tsurumi, T.; Kuroiwa, Y. Preparation of barium titanate nanoparticle sphere arrays and their dielectric properties. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 1895–1899. [Google Scholar] [CrossRef] [PubMed]
- Tsurumi, T.; Hoshina, T.; Takeda, H.; Mizuno, Y.; Chazono, H. Size effect of barium titanate and computer-aided design of multilayered ceramic capacitors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 1513–1522. [Google Scholar] [CrossRef] [PubMed]
- Kato, K.; Mimura, K.; Dang, F.; Imai, H.; Wada, S.; Osada, M.; Haneda, H.; Kuwabara, M. BaTiO3 nanocube and assembly to ferroelectric supracrystals. J. Mater. Res. 2013, 28, 2932–2945. [Google Scholar] [CrossRef]
- Kato, K.; Dang, F.; Mimura, K.; Kinemuchi, Y.; Imai, H.; Wada, S.; Osada, M.; Haneda, H.; Kuwabara, M. Nano-sized cube-shaped single crystalline oxides and their potentials; composition, assembly and functions. Adv. Powder Technol. 2014, 25, 1401–1414. [Google Scholar] [CrossRef]
- Mimura, K.; Kato, K. Dielectric properties of micropatterns consisting of barium titanate single-crystalline nanocubes. Jpn. J. Appl. Phys. 2015, 54, 10NA11. [Google Scholar] [CrossRef]
- Kishi, H.; Mizuno, Y.; Chazono, H. Base-metal electrode-multilayer ceramic capacitors: Past, present and future perspectives. Jpn. J. Appl. Phys. 2003, 42, 1–15. [Google Scholar] [CrossRef]
- Mimura, K.; Kato, K. Enhanced dielectric properties of BaTiO3 nanocube assembled film in metal-insulator-metal capacitor structure. Appl. Phys. Express 2014, 7, 061501. [Google Scholar] [CrossRef]
- Mimura, K.; Kato, K. Dielectric properties of barium titanate nanocube ordered assembly sintered at various temperatures. Jpn. J. Appl. Phys. 2014, 53, 09PA03. [Google Scholar] [CrossRef]
- Yasui, K.; Kato, K. Oriented attachment of cubic or spherical BaTiO3 nanocrystals by van der Waals torque. J. Phys. Chem. C 2015, 119, 24597–24605. [Google Scholar] [CrossRef]
- Ma, Q.; Kato, K. Crystallographic fusion behavior and interface evolution of mono-layer BaTiO3 nanocube arrangement. CrystEngComm 2016, 18, 1543–1549. [Google Scholar] [CrossRef]
- Tsurumi, T.; Li, J.; Hoshina, T.; Kakemoto, H.; Nakada, M.; Akedo, J. Ultrawide range dielectric spectroscopy of BaTiO3-based perovskite dielectrics. Appl. Phys. Lett. 2007, 91, 182905. [Google Scholar] [CrossRef]
- Teranishi, T.; Hoshina, T.; Tsurumi, T. Wide range dielectric spectroscopy on perovskite dielectrics. Mater. Sci. Eng. B 2009, 161, 55–60. [Google Scholar] [CrossRef]
- Kamalasanan, M.N.; Kumar, N.D.; Chandra, S. Dielectric and ferroelectric properties of BaTiO3 thin films grown by the sol-gel process. J. Appl. Phys. 1993, 74, 5679–5686. [Google Scholar] [CrossRef]
- Cho, C.R.; Kwun, S.I.; Noh, T.W.; Jang, M.S. Electrical properties of sol-gel deposited BaTiO3 thin films on Si(100) substrate. Jpn. J. Appl. Phys. 1997, 36, 2196–2199. [Google Scholar] [CrossRef]
- Kato, K.; Tanaka, K.; Suzuki, K.; Kayukawa, S. Phase transition in bottom-up BaTiO3 films on Si. Appl. Phys. Lett. 2007, 91, 172907. [Google Scholar] [CrossRef]
- Tanaka, K.; Suzuki, K.; Kato, K. Fabrication of BaTiO3 thin films using modified chemical solutions and sintering method. Jpn. J. Appl. Phys. 2008, 47, 7480–7485. [Google Scholar] [CrossRef]
- Nakasone, F.; Kobayashi, K.; Suzuki, T.; Mizuno, Y.; Chazono, H.; Imai, H. Nanoparticle-sintered BaTiO3 thin films and its orientation control by solid phase epitaxy. Jpn. J. Appl. Phys. 2008, 47, 8518–8524. [Google Scholar] [CrossRef]
- Yasui, K.; Itasaka, H.; Mimura, K.; Kato, K. Dynamic dielectric-response model of flexoelectric polarization from kHz to MHz range in an ordered assembly of BaTiO3 nanocubes. J. Phys. Condens. Matter 2020, 32, 495301. [Google Scholar] [CrossRef]
- Yasui, K.; Itasaka, H.; Mimura, K.; Kato, K. Coexistence of flexo- and ferro-electric effects in an ordered assembly of BaTiO3 nanocubes. Nanomaterials 2022, 12, 188. [Google Scholar] [CrossRef]
- Jiang, X.; Huang, W.; Zhang, S. Flexoelectric nano-generator: Materials, structures and devices. Nano Energy 2013, 2, 1079–1092. [Google Scholar] [CrossRef]
- Yudin, P.V.; Tagantsev, A.K. Fundamentals of flexoelectricity in solids. Nanotechnology 2013, 24, 432001. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Gu, Y.; Zhang, S.; Chen, L.-Q. Flexoelectricity in solids: Progress, challenges, and perspectives. Prog. Mater. Sci. 2019, 106, 100570. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Flexoelectricity of barium titanate. Appl. Phys. Lett. 2006, 88, 232902. [Google Scholar] [CrossRef]
- Zhuang, X.; Nguyen, B.H.; Nanthakumar, S.S.; Tran, T.Q.; Alajlan, N.; Rabczuk, T. Computational modeling of flexoelectricity—A review. Energies 2020, 13, 1326. [Google Scholar] [CrossRef]
- Lee, D.; Yoon, A.; Jang, S.Y.; Yoon, J.-G.; Chung, J.-S.; Kim, M.; Scott, F.; Noh, T.W. Giant flexoelectric effect in ferroelectric epitaxial thin films. Phys. Rev. Lett. 2011, 107, 057602. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Noh, T.W. Giant flexoelectric effect through interfacial strain relaxation. Phil. Trans. R. Soc. A 2012, 370, 4944–4957. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K.; Mimura, K.; Izu, N.; Kato, K. Numerical calculations of temperature dependence of dielectric constant for an ordered assembly of BaTiO3 nanocubes with small tilt angles. Jpn. J. Appl. Phys. 2018, 57, 031501. [Google Scholar] [CrossRef]
- Yasui, K. Merits and demerits of ODE modeling of physicochemical systems for numerical simulations. Molecules 2022, 27, 5860. [Google Scholar] [CrossRef]
- Tsurumi, T.; Adachi, H.; Kakemoto, H.; Wada, S.; Mizuno, Y.; Chazono, H.; Kishi, H. Dielectric properties of BaTiO3-based ceramics under high electric field. Jpn. J. Appl. Phys. 2002, 41, 6929–6933. [Google Scholar] [CrossRef]
- Mimura, K.; Kato, K. Dielectric properties of barium zirconate titanate nanocube 3D-ordered assemblies. J. Ceram. Soc. Jpn. 2018, 126, 321–325. [Google Scholar] [CrossRef]
- Tsurumi, T.; Yamamoto, Y.; Kakemoto, H.; Wada, S.; Chazono, H.; Kishi, H. Dielectric properties of BaTiO3-BaZrO3 ceramics under a high electric field. J. Mater. Res. 2002, 17, 755–759. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, G.; Fu, C.; Cai, W.; Gao, R.; Wang, F. Effects of sintering temperature and holding time on the microstructure and electric properties of Ba(Zr0.3Ti0.7)O3 ceramics. Process. Appl. Ceram. 2018, 12, 45–55. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasui, K. Critical Roles of Impurities and Imperfections in Various Phases of Materials. Materials 2023, 16, 1612. https://doi.org/10.3390/ma16041612
Yasui K. Critical Roles of Impurities and Imperfections in Various Phases of Materials. Materials. 2023; 16(4):1612. https://doi.org/10.3390/ma16041612
Chicago/Turabian StyleYasui, Kyuichi. 2023. "Critical Roles of Impurities and Imperfections in Various Phases of Materials" Materials 16, no. 4: 1612. https://doi.org/10.3390/ma16041612
APA StyleYasui, K. (2023). Critical Roles of Impurities and Imperfections in Various Phases of Materials. Materials, 16(4), 1612. https://doi.org/10.3390/ma16041612





