Static Analysis of Wooden Beams Strengthened with FRCM-PBO Composite in Bending
Abstract
1. Introduction
2. Description of the Research
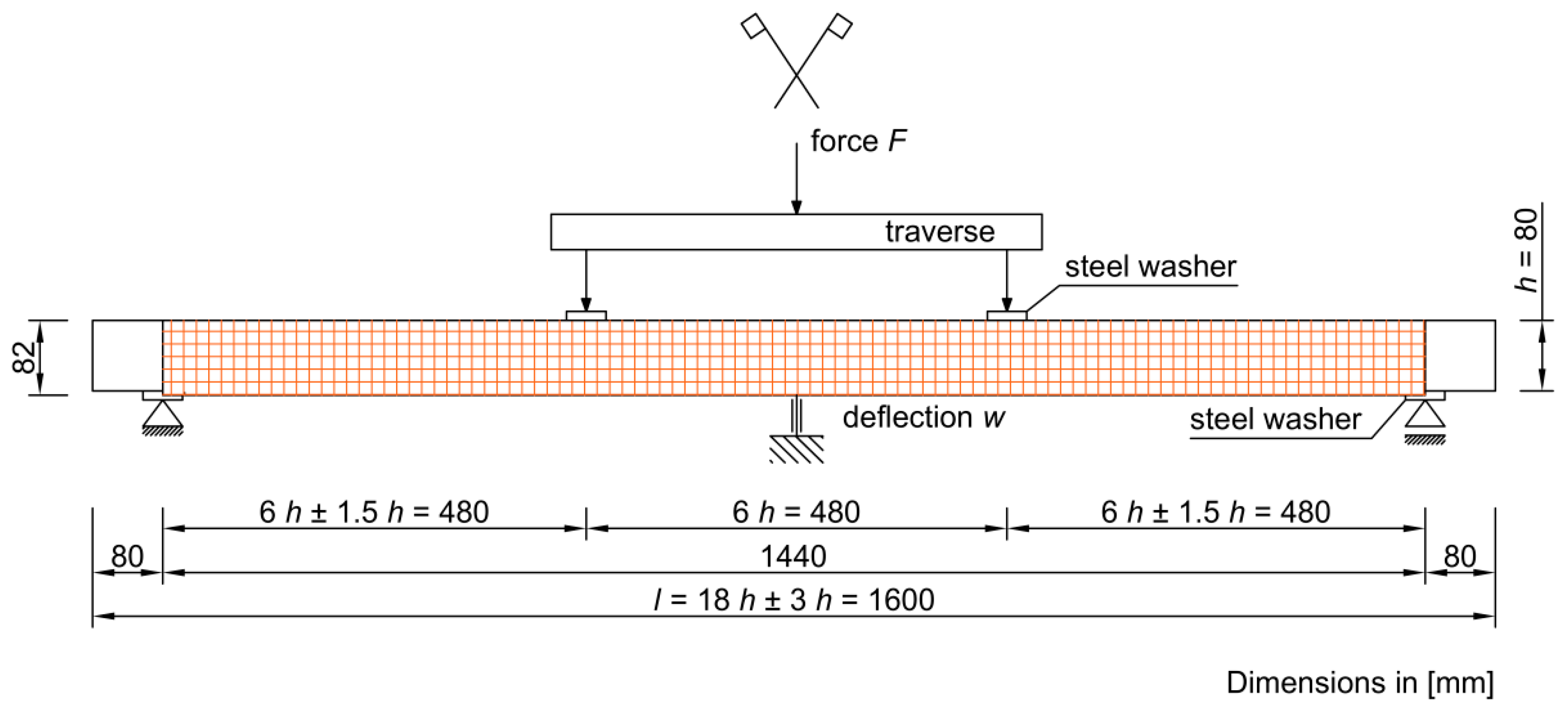
2.1. Methodology: Assumptions Adopted in the Research
- h—height of the test sample [mm].
- One level of load velocity v = 0.3 mm/s was assumed—for beams of the A and F series.
- Em,g—modulus of elasticity [GPa];
- B—width of the cross-section [mm];
- H—height of the cross-section [mm];
- L—span of the tested element in the axes of supports [mm];
- F2 − F1—load increase in the linear range [N];
- w2 − w1—deflection increase corresponding to the load increase [mm];
- a—distance from the point of application of the concentrated force to the nearest support according to Figure 1 [mm].
- σm—maximum bending stress [MPa];
- Fmax—maximum destructive force [N];
- a—distance from the point of application of the concentrated force to the nearest support [mm];W—bending section modulus;
- W—bending section modulus [mm];
- b—sample width [mm];
- h—sample height [mm];
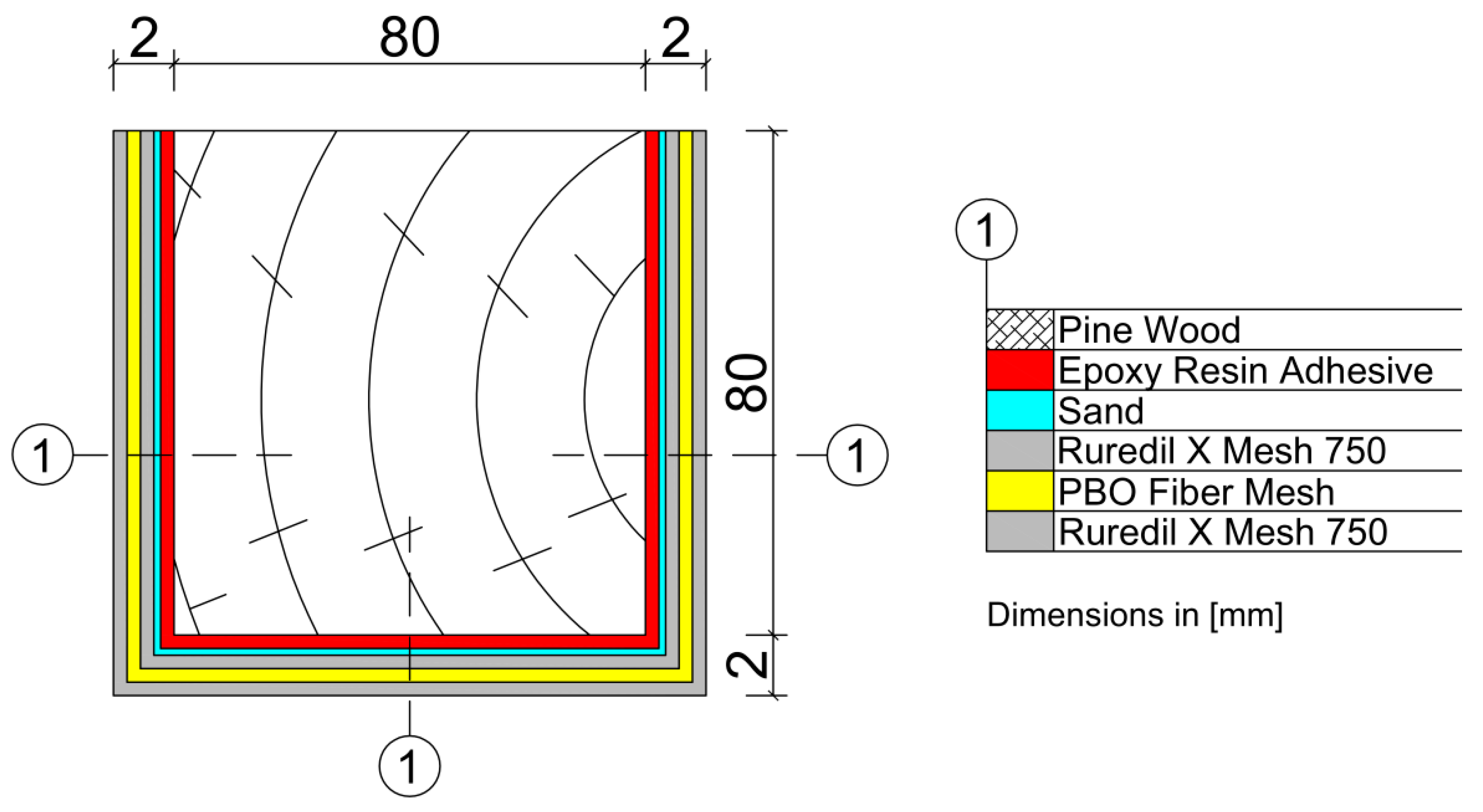
2.2. Material
3. Results and Discussion
4. Conclusions
- −
- destructive force by 141.46%;
- −
- maximum bending stress by 118.9%;
- −
- modulus of elasticity by 18.32%;
- −
- time needed to destroy the sample by 106.56%;
- −
- deflections by 115.58%.
- −
- no influence of the load speed on the change of strength parameters;
- −
- slip-effect characteristic of the FRCM–PBO composite occurring between the mortar and the fibers, manifested by premature detachment of the fibers from the matrix.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kossakowski, P. Load-bearing capacity of wooden beams reinforced with composite sheets. Struct. Environ. 2011, 3, 14–22. [Google Scholar]
- Morales-Conde, M.J.; Rodríguez-Liñán, C.; Rubio-de Hita, P. Bending and shear reinforcements for timber beams using GFRP plates. Constr. Build. Mater. 2015, 96, 461–472. [Google Scholar] [CrossRef]
- Sedivka, P.; Bomba, J.; Bohm, M.; Zeidler, A. Determination of strength characteristics of construction timber strengthened with carbon and glass fibre composite using a destructive method. BioResources 2015, 10, 4674–4685. [Google Scholar] [CrossRef]
- Sena-Cruz, J.; Branco, J.; Jorge, M.; Barros, J.; Silva, C.; Cunha, V.M.C.F. Bond behavior between glulam and GFRP’s by pullout tests. Compos. Part B Eng. 2012, 43, 1045–1055. [Google Scholar] [CrossRef]
- Valipour, H.R.; Crews, K. Efficient finite element modelling of timber beams strengthened with bonded fibre reinforced polymers. Constr. Build. Mater. 2011, 25, 3291–3300. [Google Scholar] [CrossRef]
- Ashari, B.; Guan, Z.W.; Kitamori, A.; Jung, K.; Komatsu, K. Structural behaviour of glued laminated timber beams pre-stressed by compressed wood. Constr. Build. Mater. 2012, 29, 24–32. [Google Scholar] [CrossRef]
- Brol, J.; Markowska, M. Estimation of the load carrying capacity of the timber beams strengthened with FRP strips. Ann. Wars. Univ. Life Sci.—SGGW For. Wood Technol. 2014, 88, 33–37. [Google Scholar]
- Sokołowski, P.; Kossakowski, P.G. Estimation of the moduls fir wood reinforced with PBO fiber mesh. Arch. Civ. Eng. 2018, 64, 105–121. [Google Scholar] [CrossRef]
- Thorhallsson, E.R.; Hinriksson, G.I.; Snæbjorns, J.T. Strength and stiffness of glulam beams reinforced with glass and basalt fibres. Compos. Part B 2017, 15, 300–307. [Google Scholar] [CrossRef]
- Yusof, A.; Saleh, A.L. Flexural strengthening of timber beams using glass fibre reinforced polymer. Electron. J. Struct. Eng. 2010, 10, 48–56. [Google Scholar] [CrossRef]
- Adam, M.; Luhring, A.; Popp, M.; Fecht, S.; Vallee, T. Pre-applicable structural adhesives for timber engineering: Glued-in G-FRP rods. Int. J. Adhes. Adhes. 2016, 67, 121–127. [Google Scholar] [CrossRef]
- Stanila, O.; Isopescu, D.; Raluca, H. Timber Elements: Traditional and Modern Strengthening Techniques. Bull. Polytech. Inst. Jassy. Constr. Archit. Sect. LVI 2010, 56, 75–86. [Google Scholar]
- Borri, A.; Corradi, M. Strengthening of timber beams with high strength steel cords. Compos. Part B 2011, 42, 1480–1491. [Google Scholar] [CrossRef]
- Brückner, A.; Ortlepp, R.; Curbach, M. Anchoring of shear strengthening for T-beams made of textile reinforced concrete (TRC). Mater. Struct. 2008, 41, 407–418. [Google Scholar] [CrossRef]
- Baggio, D.; Soudki, K.; Noël, M. Strengthening of shear critical RC beams with various FRP systems. Constr. Build. Mater. 2014, 66, 634–644. [Google Scholar] [CrossRef]
- Nowak, T. Analiza pracy statycznej zginanych belek drewnianych wzmacnianych przy użyciu CFRP. Ph.D. Thesis, Wroclaw University of Technology, Wrocław, Poland, 2009. [Google Scholar]
- Ruredil, X. Mesh Gold Data Sheet; Ruredil SPA: Milan, Italy, 2009. [Google Scholar]
- Urbańska, D.; Trapko, T. Wzmocnienie Kompozytowe PBO-FRCM cz 1. Build. 92 Sierpień 2017, 21, 92–94. [Google Scholar]
- Urbańska, D.; Musiał, M. Wzmocnienie Kompozytowe PBO-FRCM cz 2. Build. 64 Wrzesień 2017, 21, 64–66. [Google Scholar]
- Tzoura, E.; Triantafillou, T.C. Shear strengthening of reinforced concrete T-beams under cyclic loading with TRM or FRP jackets. Mater. Struct. 2016, 49, 17–28. [Google Scholar] [CrossRef]
- Trapko, T.; Urbańska, D.; Kamiński, M. Shear strengthening of reinforced concrete beams with PBO-FRCM composites. Compos. Part B Eng. 2015, 80, 63–72. [Google Scholar] [CrossRef]
- Stefańczyk, B. Budownictwo ogólne. Materiały i Wyroby Budowlane. Tom 1; Arkady: Warszawa, Poland, 2005. [Google Scholar]
- Rudziński L Konstrukcje drewniane. Naprawy. Wzmocnienia. Przykłady Obliczeń; Wydawnictwo Politechniki Świętokrzyskiej: Kielce, Poland, 2010. [Google Scholar]
- PN 408: 2010+A1; Timber Structures-Structural Timber and Glued Laminated Timber—Determination of Some Physical and Mechanical Properties. Polish Committee for Standardization: Warsaw, Poland, 2012.
- PN-EN 384:2004; Drewno konstrukcyjne. Oznaczanie Wartości Charakterystycznych Właściwości Mechanicznych i Gęstości. Polish Committee for Standardization: Warsaw, Poland, 2016.
- Sokołowski, P.; Bąk-Patyna, P.; Bysiec, D.; Maleska, T. Experimental Test of Reinforced Timber of FRCM-PBO with Pull-Off Adhesion Method. Materials 2022, 15, 7702. [Google Scholar] [CrossRef] [PubMed]
- Sokołowski, P. Static analysis of beams strengthened in bending with PBO fiber mesh. Ph.D. Thesis, Kielce University of Technology, Wrocław, Poland, 2021. [Google Scholar]


| Beam Number | Dimensions (mm) | Density (g/mm3) | Humidity (%) | Beam Weight without Reinforcement (g) | Mass of Finishing Layers and Reinforcements (g) | Total Mass of the Beam (g) |
|---|---|---|---|---|---|---|
| A-1 | 80 × 80 × 1600 | 0.000467 | 13.97 | 4777 | - | 4777 |
| A-2 | 80 × 80 × 1600 | 0.000465 | 13.60 | 4762 | - | 4762 |
| A-3 | 80 × 80 × 1600 | 0.000465 | 13.35 | 4766 | - | 4766 |
| A-4 | 80 × 80 × 1600 | 0.000468 | 14.25 | 4788 | - | 4788 |
| A-5 | 80 × 80 × 1600 | 0.000468 | 13.62 | 4793 | - | 4793 |
| Beam Number | Dimensions (mm) | Density (g/mm3) | Humidity (%) | Beam Weight without Reinforcement (g) | Mass of Finishing Layers and Reinforcements (g) | Total Mass of the Beam (g) |
|---|---|---|---|---|---|---|
| F-1 | 84 × 82 × 1600 | 0.000603 | 14.25 | 4795 | 1848 | 6643 |
| F-2 | 84 × 82 × 1600 | 0.000600 | 13.30 | 4789 | 1820 | 6609 |
| F-3 | 84 × 82 × 1600 | 0.000609 | 13.57 | 4785 | 1925 | 6710 |
| F-4 | 84 × 82 × 1600 | 0.000613 | 13.32 | 4791 | 1967 | 6758 |
| F-5 | 84 × 82 × 1600 | 0.000605 | 13.95 | 4786 | 1881 | 6667 |
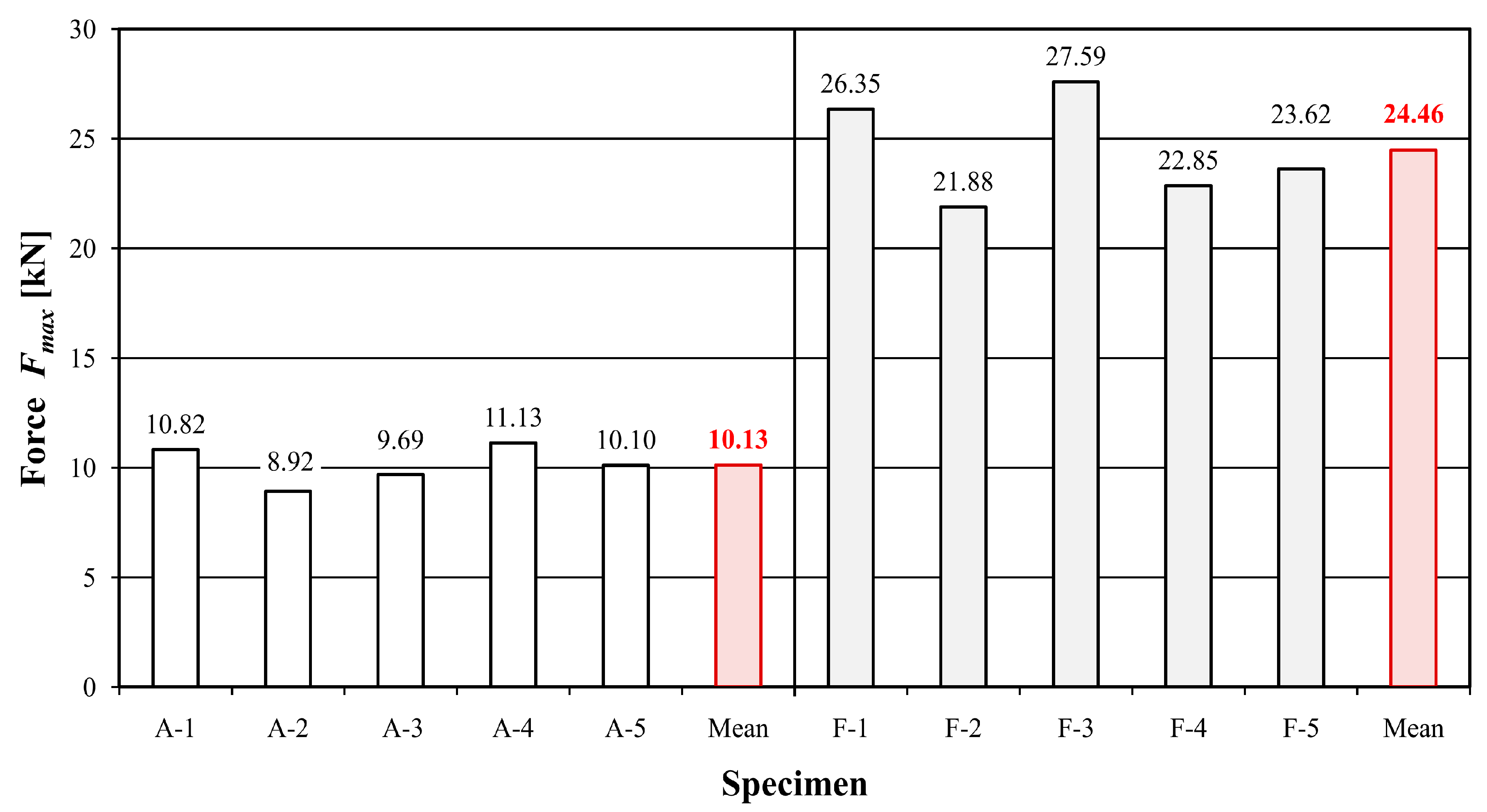
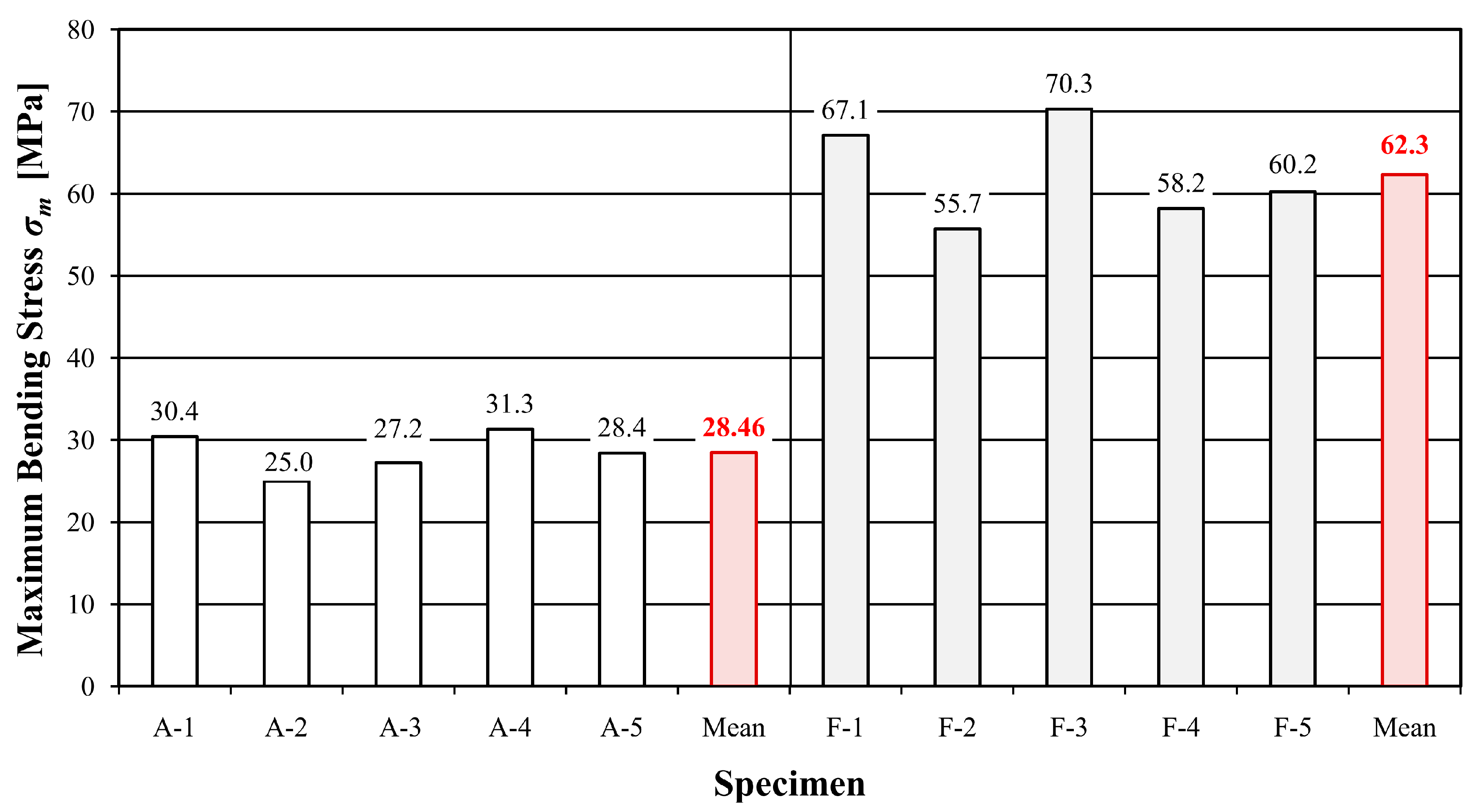
| Beam Number | Time t (sek) | Deflection w (mm) | Destructive Force Fmax (kN) | Modulus of Elasticity Em,g (GPa) | Maximum Bending Stress σm (MPa) |
|---|---|---|---|---|---|
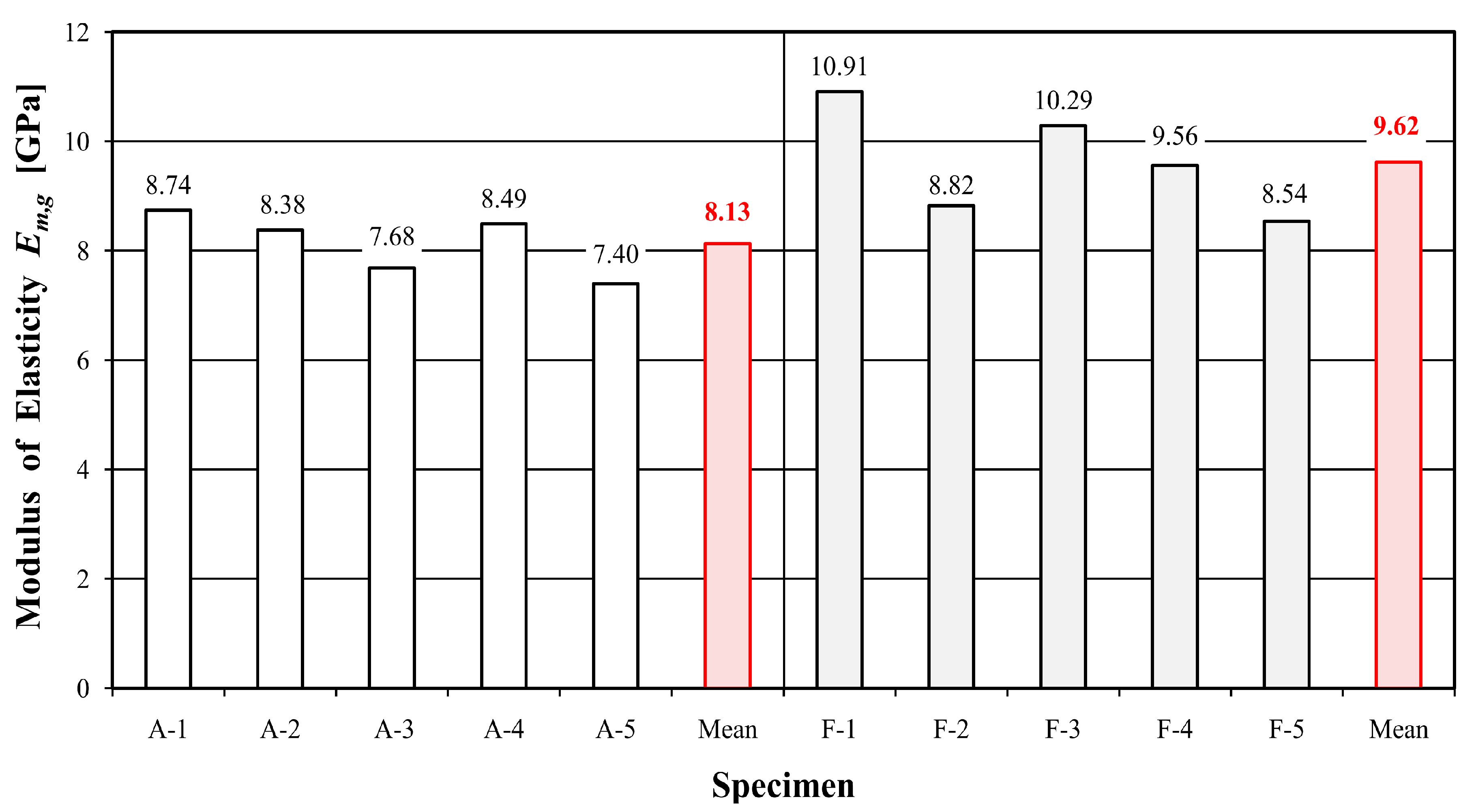
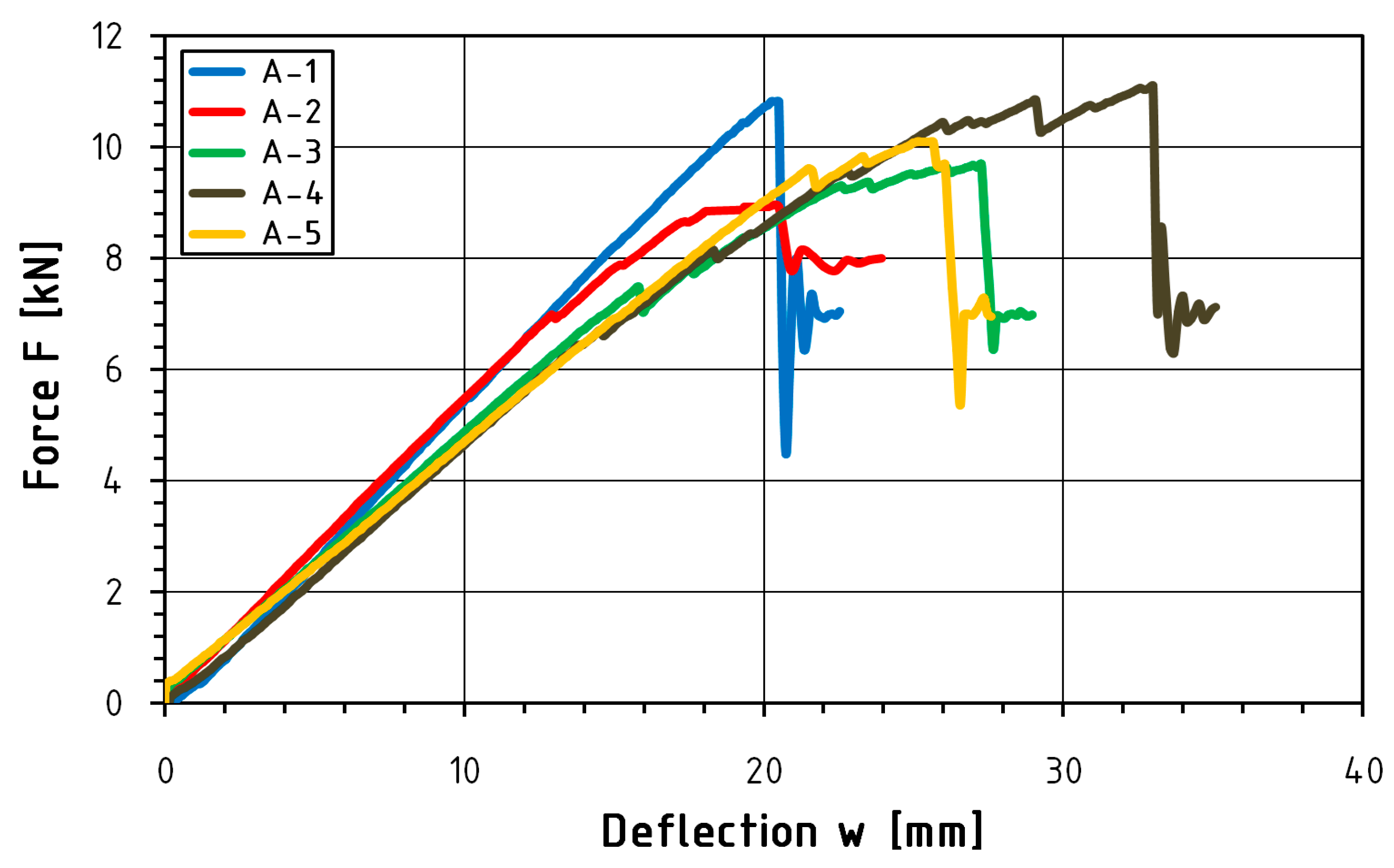
| A-1 | 159.2 | 20.43 | 10.82 | 8.74 | 30.4 |
| A-2 | 149.0 | 19.50 | 8.92 | 8.38 | 25.0 |
| A-3 | 205.0 | 27.09 | 9.69 | 7.68 | 27.2 |
| A-4 | 232.2 | 33.02 | 11.13 | 8.49 | 31.3 |
| A-5 | 191.8 | 25.43 | 10.10 | 7.40 | 28.4 |
| Beam Number | Time t (sek) | Deflection w (mm) | Destructive Force Fmax (kN) | Modulus of Elasticity Em,g (GPa) | Maximum Bending Stress σm (MPa) |
|---|---|---|---|---|---|
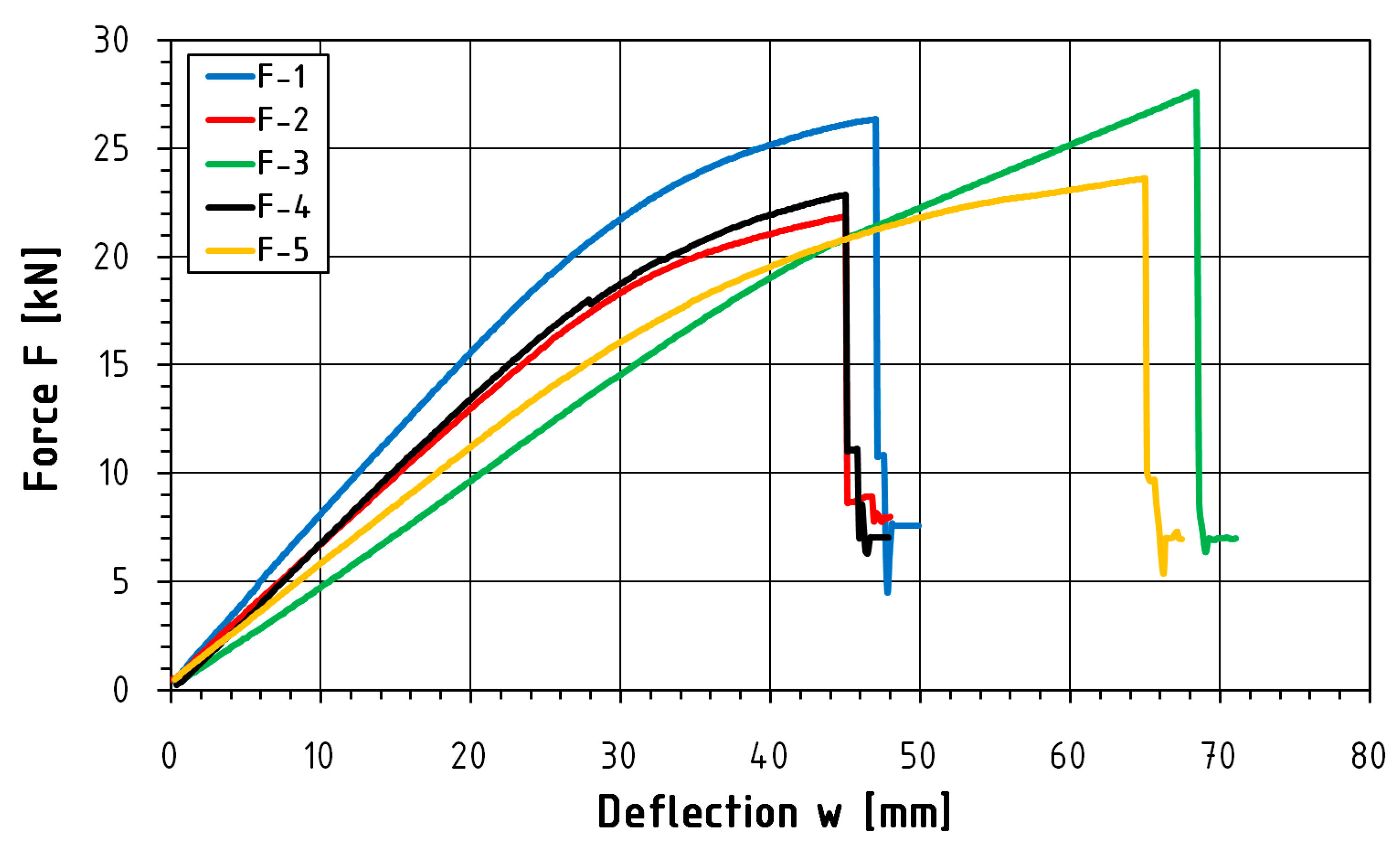
| F-1 | 342.8 | 46.66 | 26.35 | 10.91 | 67.1 |
| F-2 | 329.4 | 44.87 | 21.88 | 8.82 | 55.7 |
| F-3 | 507.2 | 68.77 | 27.59 | 10.29 | 70.3 |
| F-4 | 329.8 | 44.92 | 22.85 | 9.56 | 58.2 |
| F-5 | 426.2 | 65.23 | 23.62 | 8.54 | 60.2 |
| Time t (sek) | Deflection w (mm) | Destructive Force Fmax (kN) | Modulus of Elasticity Em,g (GPa) | Maximum Bending Stresses σm (MPa) | |
|---|---|---|---|---|---|
| Arithmetic average | 187.4 | 25.09 | 10.13 | 8.13 | 28.46 |
| Standard deviation | 33.9 | 5.47 | 0.88 | 0.56 | 2.51 |
| Coefficient of variation | 0.18 | 0.21 | 0.08 | 0.07 | 0.08 |
| Time t (sek) | Deflection w (mm) | Destructive Force Fmax (kN) | Modulus of Elasticity Em,g (GPa) | Maximum Bending Stresses σm (MPa) | |
|---|---|---|---|---|---|
| Arithmetic average | 387.1 | 54.09 | 24.46 | 9.62 | 62.3 |
| Standard deviation | 78.30 | 11.87 | 2.41 | 0.99 | 6.16 |
| Coefficient of variation | 0.20 | 0.21 | 0.09 | 0.1 | 0.09 |
| Parameter | Series A | Series F | Increase (%) |
|---|---|---|---|
| Destructive force (kN) | 10.13 | 24.46 | 141.46 |
| Modulus of elasticity (GPa) | 8.13 | 9.62 | 18.32 |
| Maximum bending stresses (MPa) | 28.46 | 62.30 | 118.9 |
| Time (sek) | 187.40 | 387.10 | 106.56 |
| Deflection (mm) | 25.09 | 54.09 | 115.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sokołowski, P.K.; Kossakowski, P.G. Static Analysis of Wooden Beams Strengthened with FRCM-PBO Composite in Bending. Materials 2023, 16, 1870. https://doi.org/10.3390/ma16051870
Sokołowski PK, Kossakowski PG. Static Analysis of Wooden Beams Strengthened with FRCM-PBO Composite in Bending. Materials. 2023; 16(5):1870. https://doi.org/10.3390/ma16051870
Chicago/Turabian StyleSokołowski, Piotr Kazimierz, and Paweł Grzegorz Kossakowski. 2023. "Static Analysis of Wooden Beams Strengthened with FRCM-PBO Composite in Bending" Materials 16, no. 5: 1870. https://doi.org/10.3390/ma16051870
APA StyleSokołowski, P. K., & Kossakowski, P. G. (2023). Static Analysis of Wooden Beams Strengthened with FRCM-PBO Composite in Bending. Materials, 16(5), 1870. https://doi.org/10.3390/ma16051870







