Macro–Mesoscale Modeling of the Evolution of the Surface Roughness of the Al Metallization Layer of an IGBT Module during Power Cycling
Abstract
:1. Introduction
2. Experimental Process
2.1. Experimental Sample of an IGBT Module
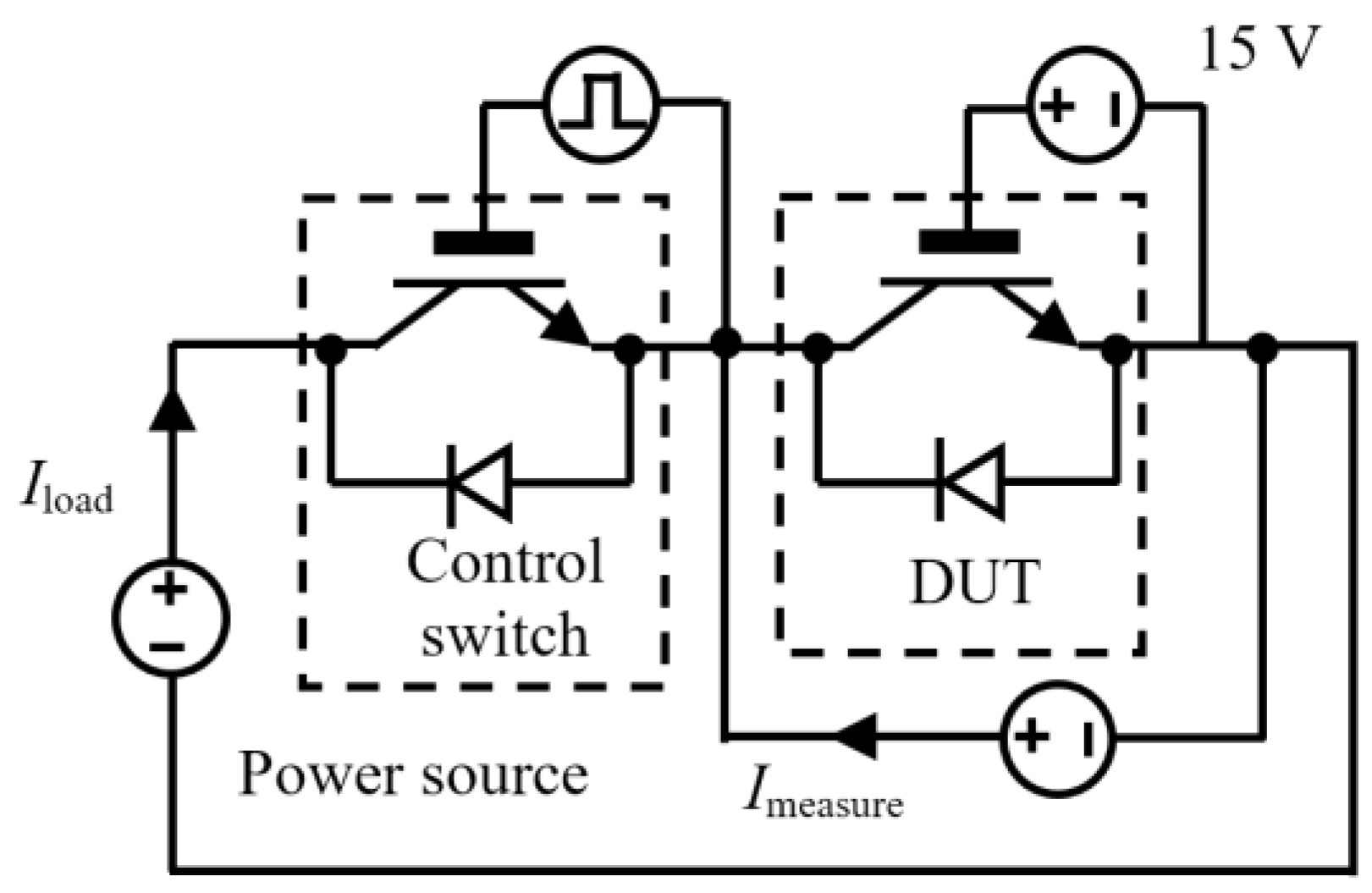
2.2. Power Cycling Test
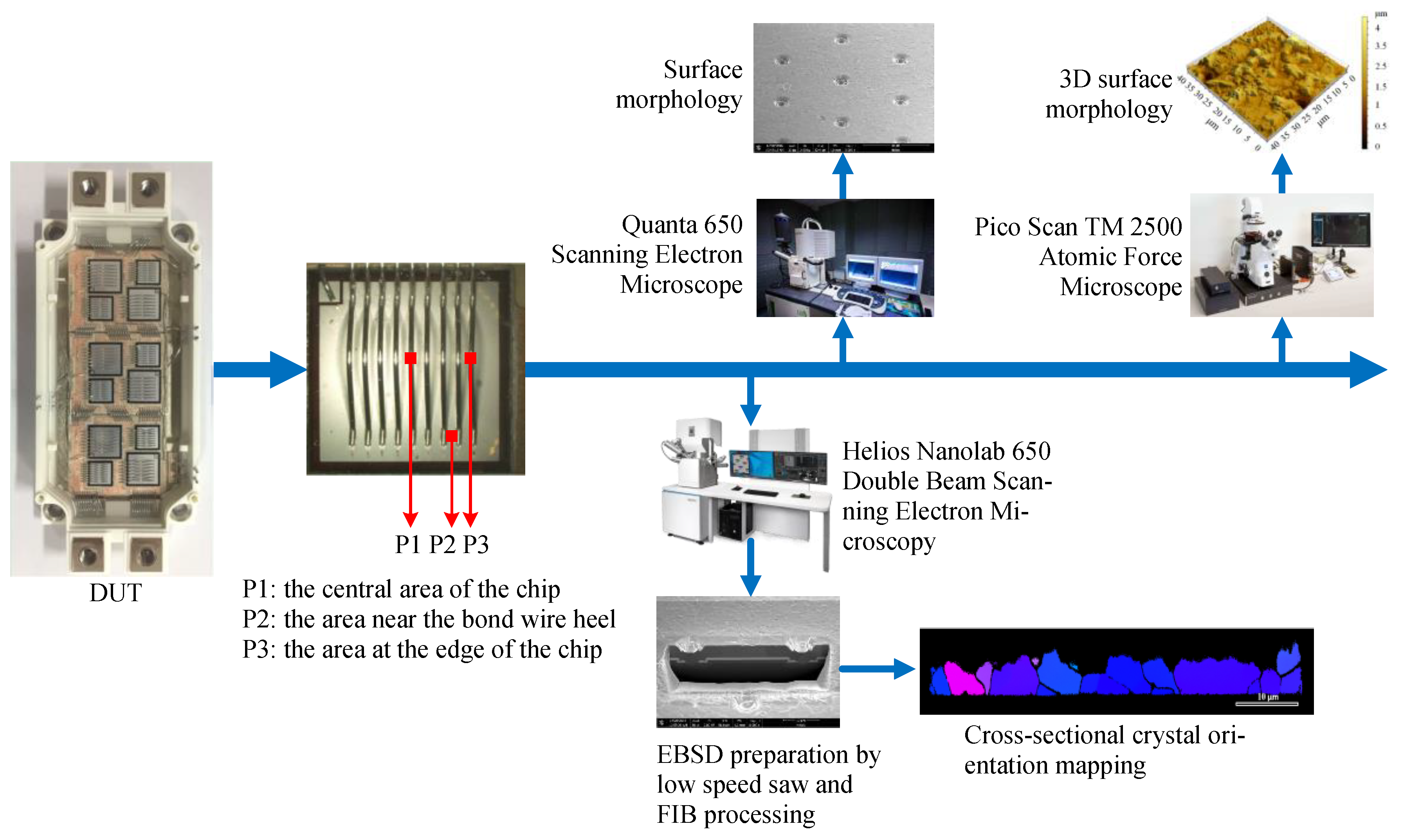
2.3. Experimental Observation of the Evolution of the Microstructure of the Al Metallization Layer
3. Numerical Analysis of the Surface Roughness of the Al Metallization Layer of the IGBT Module
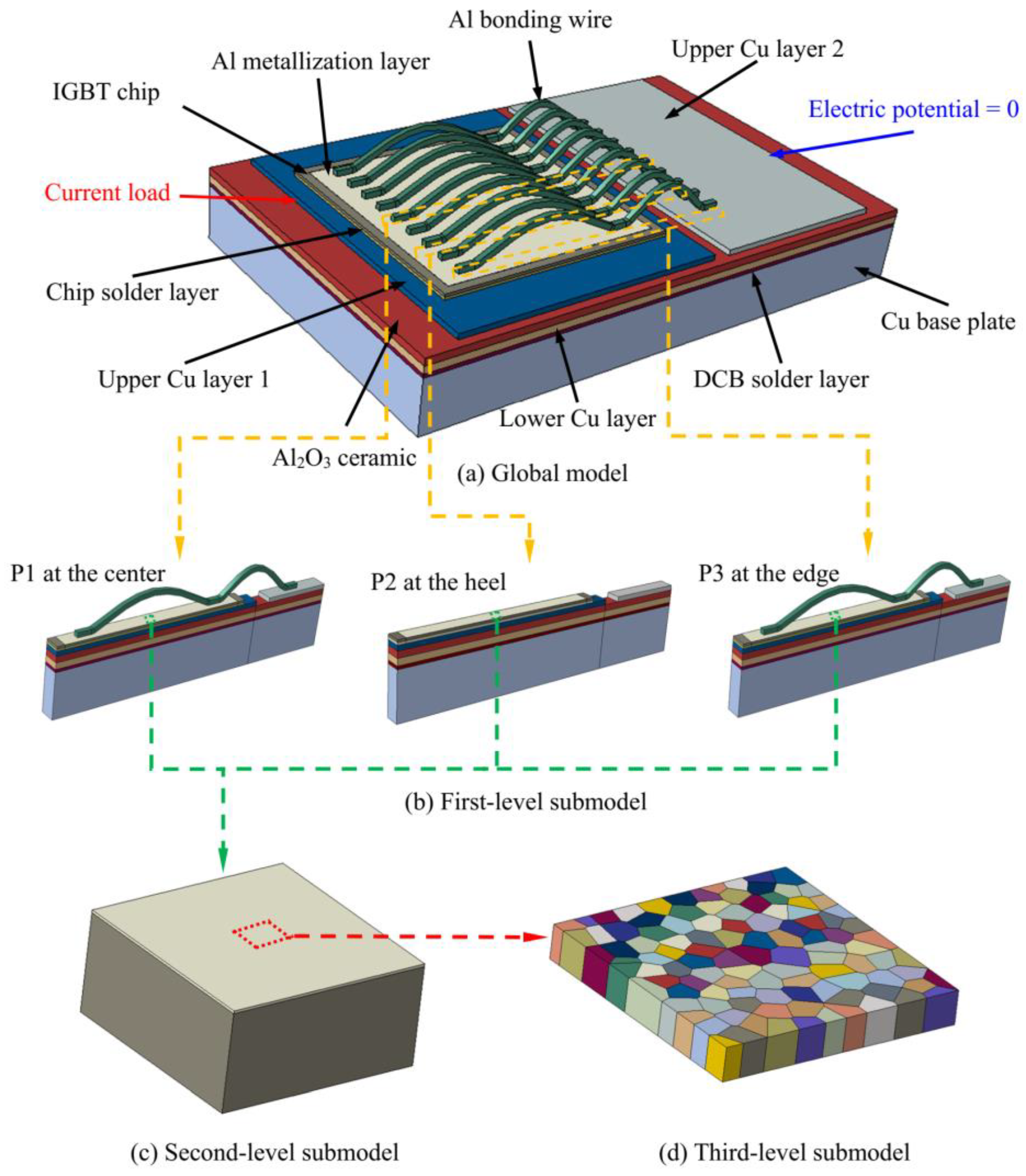
3.1. Submodel for the IGBT Module
3.2. Crystal Thermo–Elasto–Plasticity Constitutive Equation
3.2.1. Kinematics
3.2.2. Rate-Dependent Hardening Model
3.3. Thermal–Electrical–Structural FE Analysis of the Global Model and Submodel
4. Results and Discussion
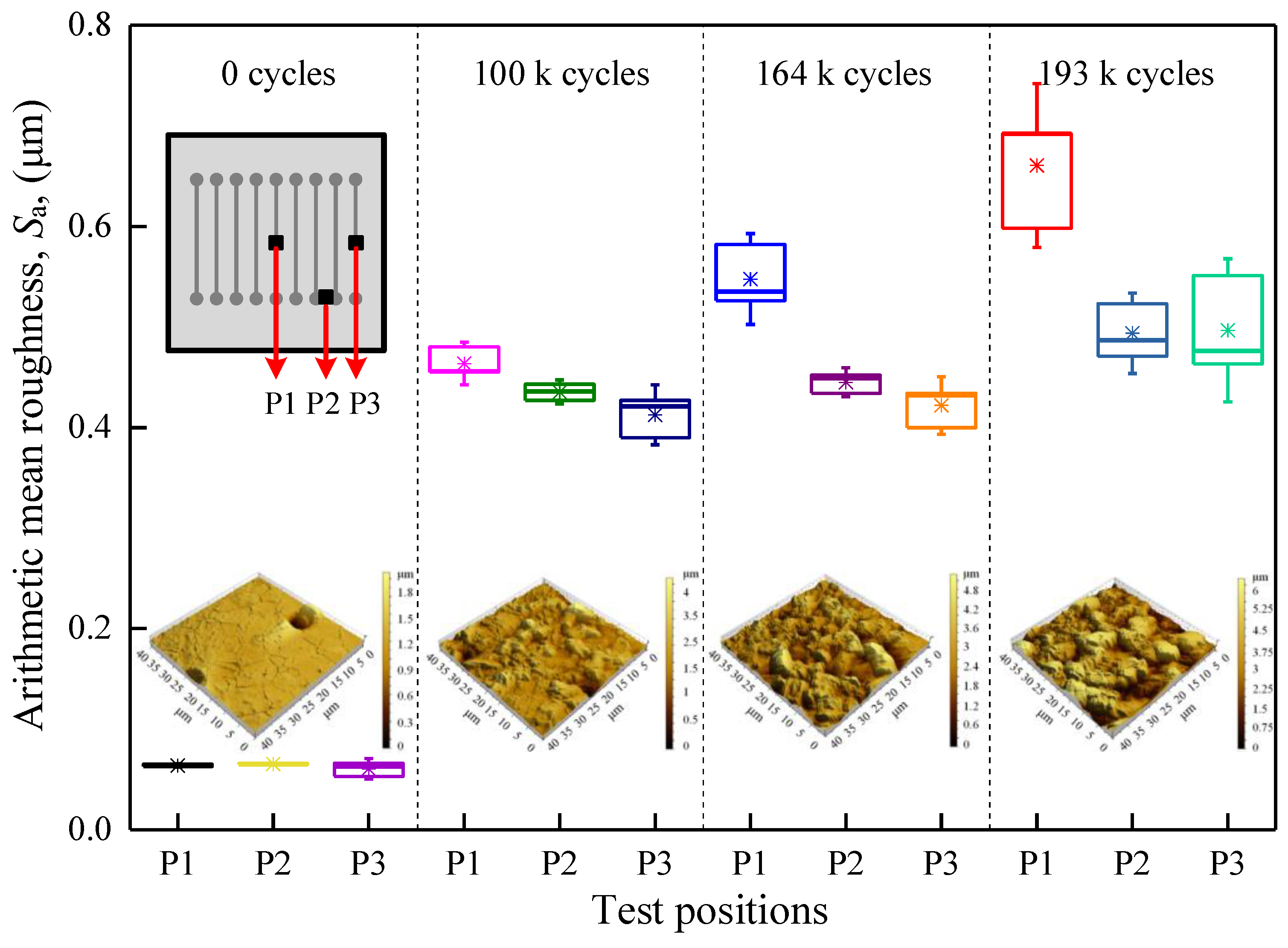
4.1. Experimental Observation of the Evolution of the Surface Morphology of the Al Metallization Layer during Power Cycling
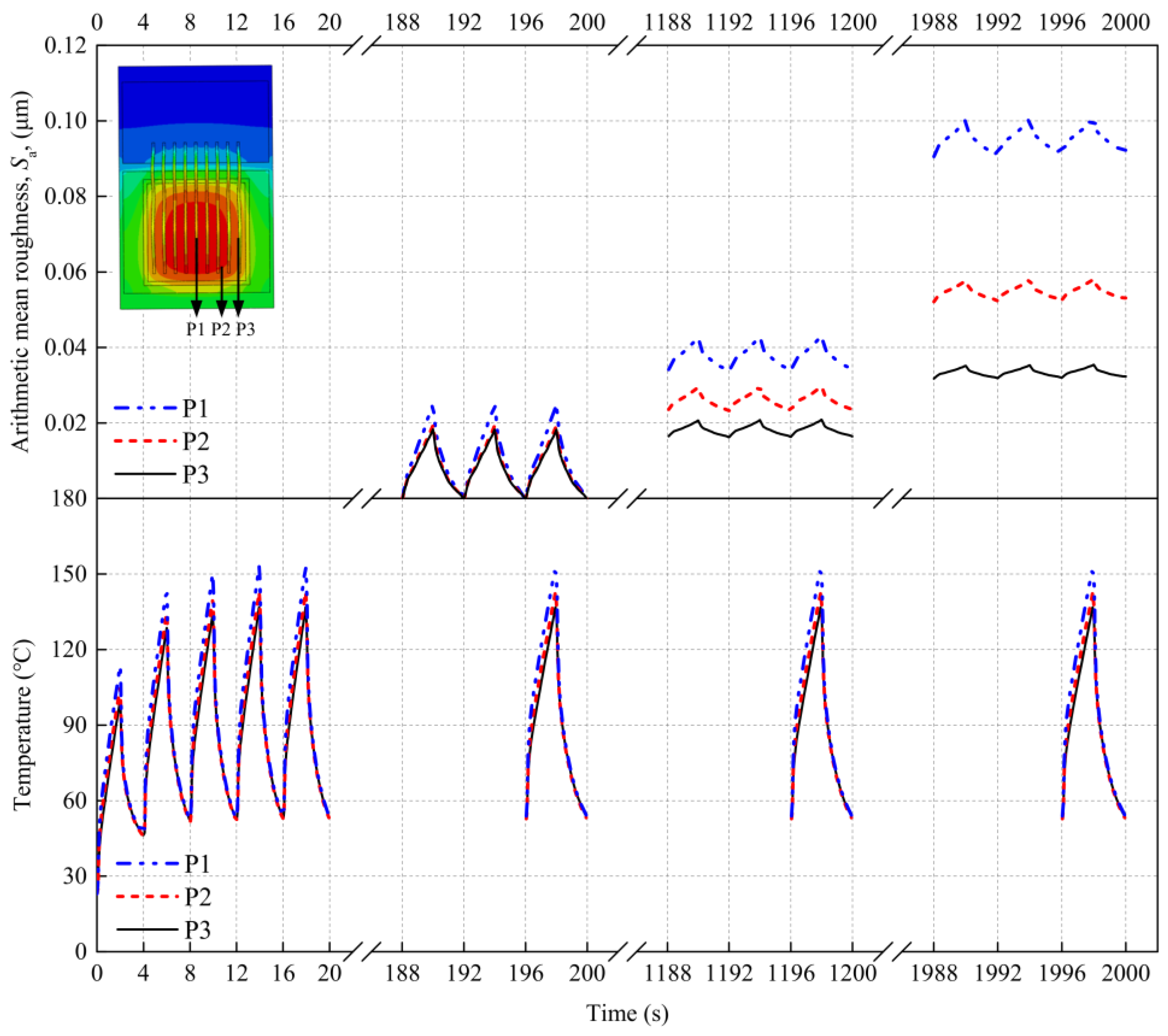
4.2. External Factor Affecting the Surface Roughness of the Al Metallization Layer—Temperature
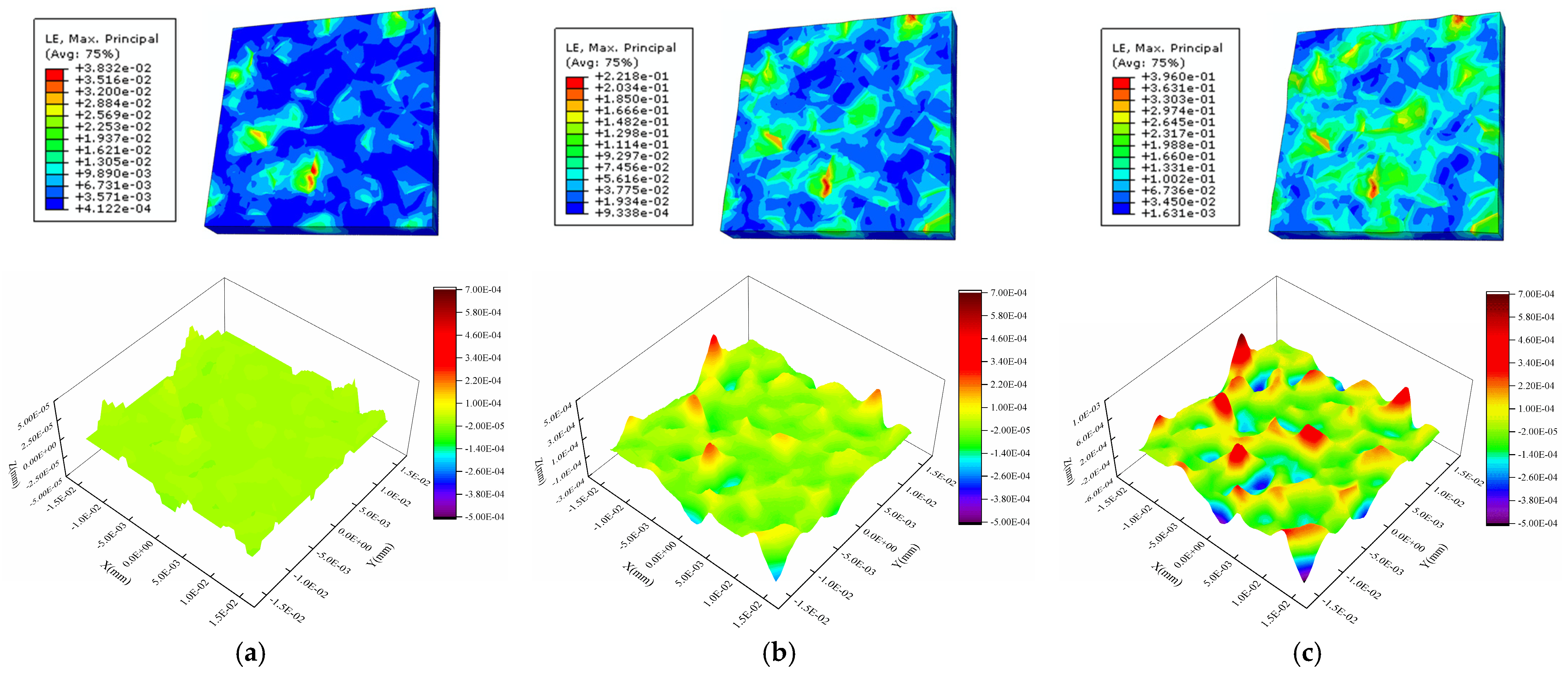
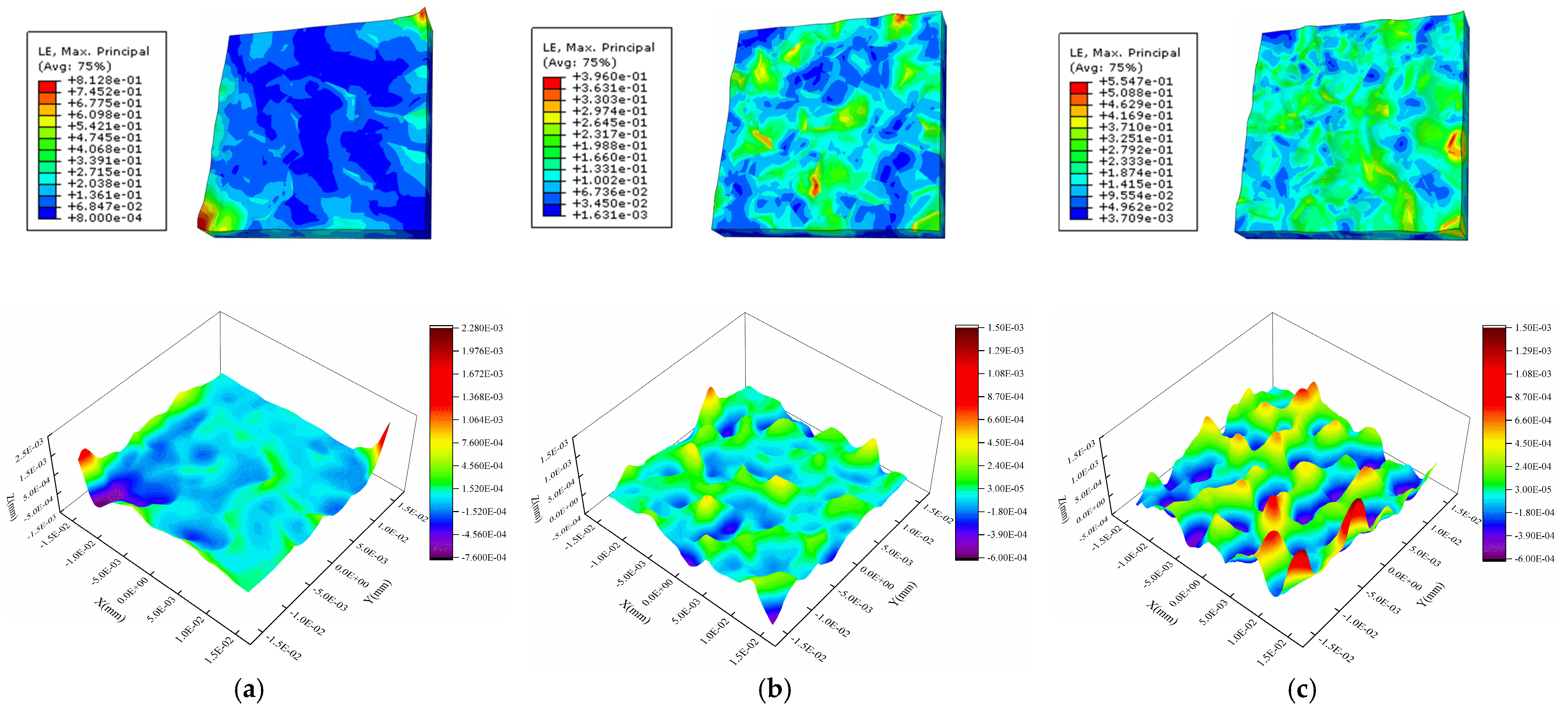
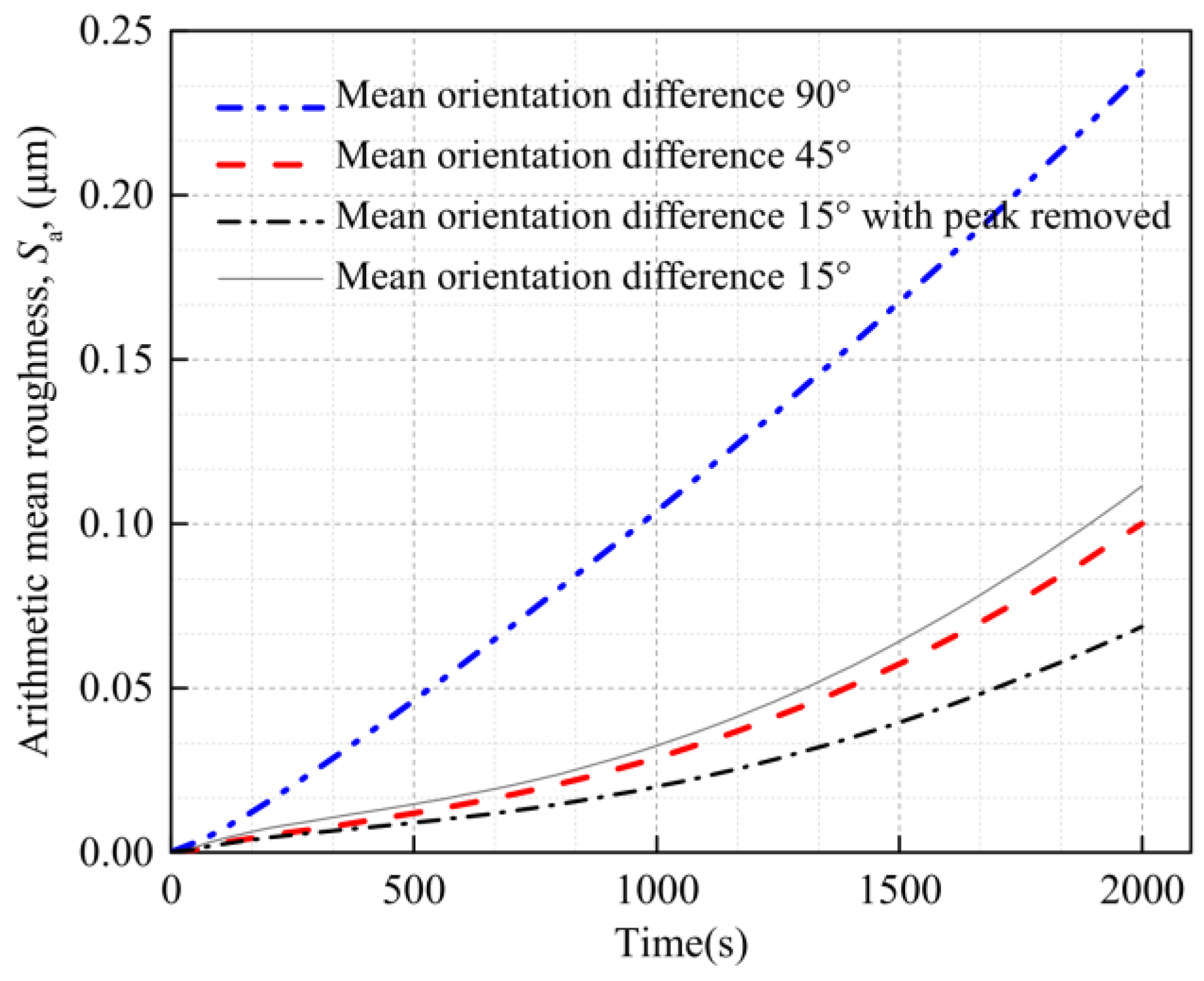
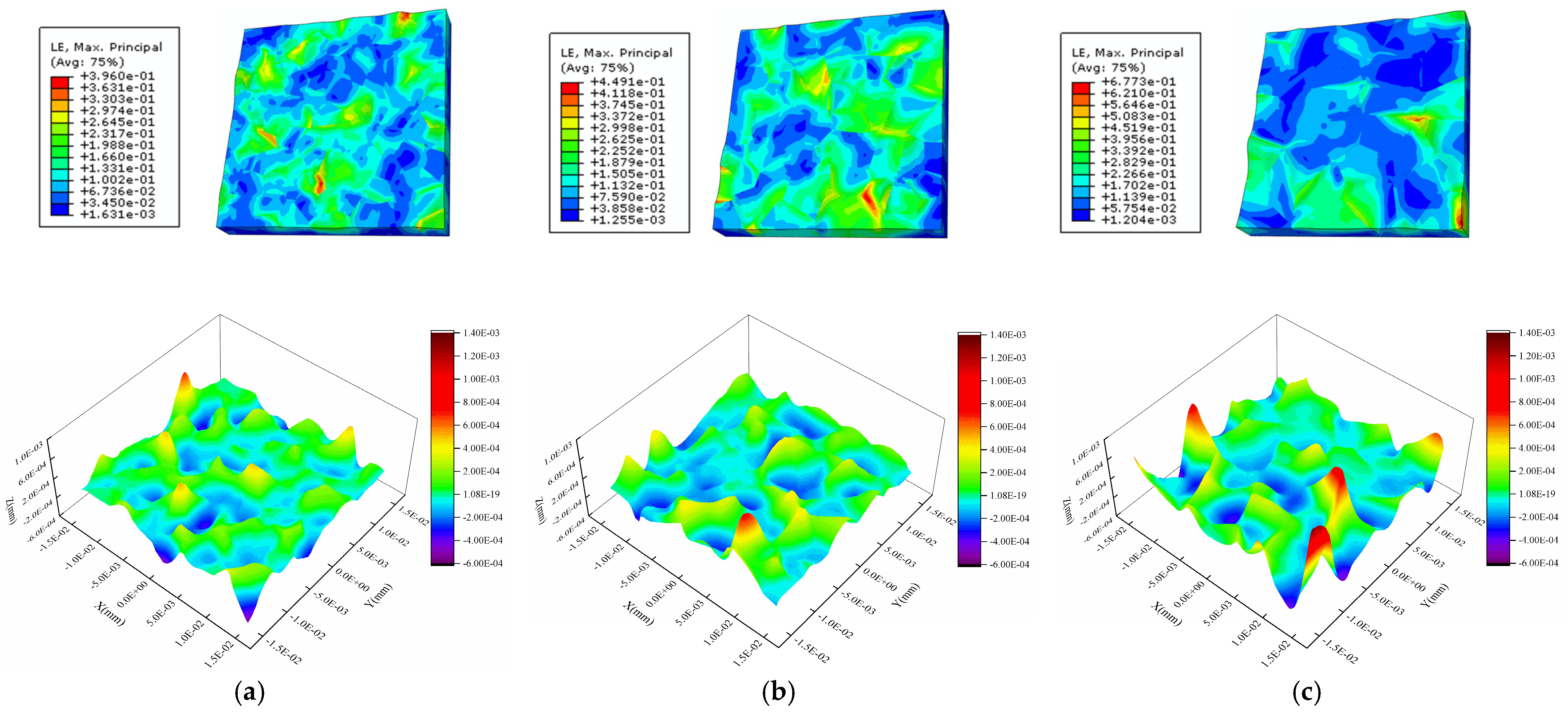
4.3. Internal Factor Affecting the Surface Roughness of the Al Metallization Layer—Grain Orientation
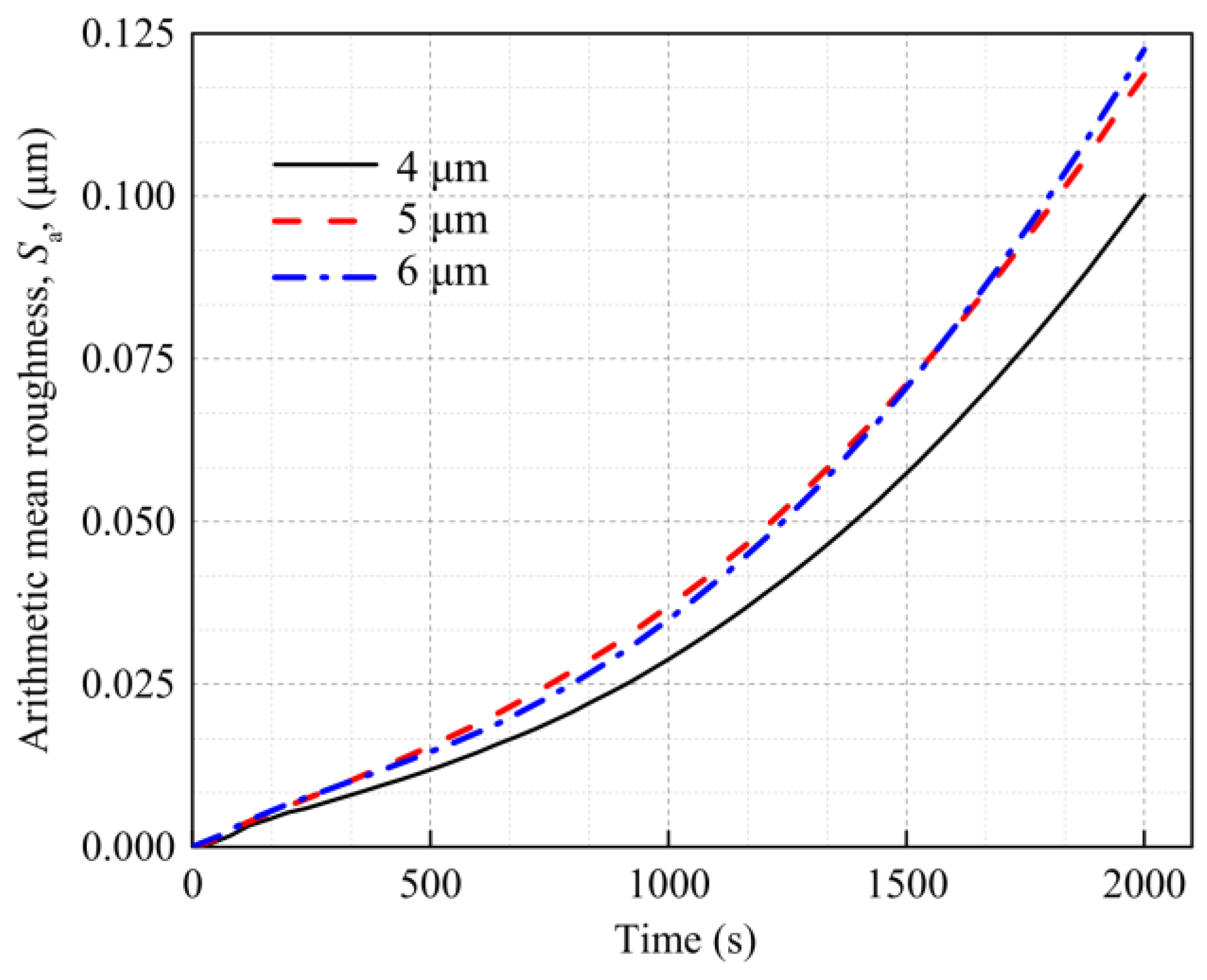
4.4. Internal Factor Affecting the Surface Roughness of the Al Metallization Layer—Grain Size
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ciappa, M.; Malberti, P. Plastic-strain of aluminum interconnections during pulsed operation of IGBT multichip modules. Qual. Reliab. Eng. Int. 1996, 12, 297–303. [Google Scholar] [CrossRef]
- Zhao, J.Y.; An, T.; Fang, C.; Bie, X.; Qin, F.; Chen, P.; Dai, Y. A study on the effect of microstructure evolution of the aluminum metallization layer on its electrical performance during power cycling. IEEE Trans. Power Electron. 2019, 34, 11036–11045. [Google Scholar] [CrossRef]
- Ciappa, M. Selected failure mechanisms of modern power modules. Microelectron. Reliab. 2002, 42, 653–667. [Google Scholar] [CrossRef]
- Durand, C.; Klingler, M.; Coutellier, D.; Naceur, H. Study of fatigue failure in Al-chip-metallization during power cycling. Eng. Fract. Mech. 2015, 138, 127–145. [Google Scholar] [CrossRef]
- Baker, N.; Liserre, M.; Dupont, L.; Avenas, Y. Improved reliability of power modules: A review of online junction temperature measurement methods. IEEE Ind. Electron. Mag. 2014, 8, 17–27. [Google Scholar] [CrossRef] [Green Version]
- Yousef, V.Y.; Nima, A.; Ebrahim, A. A thermal-calorimetric gas flow meter with improved isolating feature. Microsyst. Technol. 2017, 23, 1927–1936. [Google Scholar]
- Magnani, A.; Napoli, F.; Riccio, M. Thermal feedback blocks for fast and reliable electrothermal circuit simulation of power circuits at module level. In Proceedings of the 28th International Symposium on Power Semiconductor Devices and ICs (ISPSD), Prague, Czech Republic, 12–16 July 2016; pp. 187–190. [Google Scholar]
- Napoli, F.; Magnani, A.; Coppola, M. Real-time temperature cycling estimation of lGBT power modules with power in-line measurements and compact thermal modeling. In Proceedings of the 5th IET International Conference on Renewable Power Generation (RPG), London, UK, 21–23 September 2016; pp. 1–6. [Google Scholar]
- Ruffilli, R.; Berkani, M.; Dupuy, P.; Lefebvre, S.; Weber, Y.; Legros, M. Mechanisms of power module source metal degradation during electro-thermal aging. Microelectron. Reliab. 2017, 76, 507–511. [Google Scholar] [CrossRef] [Green Version]
- Heinz, W.; Pippan, R.; Dehm, G. Investigation of the fatigue behavior of Al thin films with different microstructure. Mater. Sci. Eng. A 2010, 527, 7757–7763. [Google Scholar] [CrossRef]
- Martineau, D.; Levade, C.; Legros, M.; Dupuy, P.; Mazeaud, T. Universal mechanisms of al metallization ageing in power MOSFET devices. Microelectron. Reliab. 2014, 54, 2432–2439. [Google Scholar] [CrossRef]
- Pietranico, S.; Lefebvre, S.; Pommier, S.; Bouaroudj, M.B.; Bontemps, S. A study of the effect of degradation of the aluminium metallization layer in the case of power semiconductor devices. Microelectron. Reliab. 2011, 51, 1824–1829. [Google Scholar] [CrossRef]
- Smet, V.; Forest, F.; Huselstein, J.J.; Richardeau, F.; Khatir, Z.; Lefebvre, S.; Berkani, M. Ageing and failure modes of IGBT modules in high-temperature power cycling. IEEE Trans. Ind. Electron. 2012, 58, 4931–4941. [Google Scholar] [CrossRef]
- Raabe, D.; Ma, D.; Roters, F. Effects of Initial orientation, sample geometry single crystal microcompression: A crystal plasticity finite element study. Acta Met. 2007, 12, 4567–4583. [Google Scholar] [CrossRef]
- Liu, C.S.; Xu, W.J.; Niu, T.H.; Chen, Y. Roughness evolution of constrained surface based on crystal plasticity finite element model and coupled Eulerian-Lagrangian method. Comput. Mater. Sci. 2022, 201, 110900. [Google Scholar] [CrossRef]
- Feng, Z.Y.; Li, H.; Yang, J.C.; Huang, H.; Li, G.; Huang, D. Macro-meso scale modeling and simulation of surface roughening: Aluminum alloy tube bending. Int. J. Mech. Sci. 2018, 144, 696–707. [Google Scholar] [CrossRef]
- Pedersen, K.B.; Kristensen, P.K.; Popok, V.; Pedersen, K. Micro-sectioning approach for quality and reliability assessment of wire bonding interfaces in IGBT modules. Microelectron. Reliab. 2013, 53, 1422–1426. [Google Scholar] [CrossRef]
- Raabe, D. Computational Material Science: The Simulation of Materials Microstructures and Properties; Wiley-VCH: Weinheim, Germany, 1998. [Google Scholar]
- Torquato, S. Random Heterogeneous Materials: Microstructure and Macroscopic Properties; Springer: New York, NY, USA, 2002. [Google Scholar]
- Asaro, R.J.; Rice, J.R. Strain localization in ductile single crystals. J. Mech. Phys. Solids 1977, 25, 309–338. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Tang, Q.H.; Wang, T. A new thermo-elasto-plasticity constitutive theory for polycrystalline metals. Acta Mech. Sin. 2015, 31, 338–348. [Google Scholar] [CrossRef] [Green Version]
- Valery, B.; Mikhail, I.M.; Alexander, H.K.; LeSar, R. Effects of Schmid factor and slip nucleation on deformation mechanism in columnar-grained nanotwinned Ag and Cu. J. Appl. Phys. 2015, 117, 285–302. [Google Scholar]
- Ganapathy, S.; Zabaras, N. A continuum sensitivity method for finite thermo-inelastic deformations with applications to the design of hot forming processes. Int. J. Numer. Methods Eng. 2002, 55, 1391–1437. [Google Scholar]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.; Bieler, T.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Hutchinson, J.; Neale, K. Influence of strain-rate sensitivity on necking under uniaxial tension. Acta Metall. 1977, 25, 839–846. [Google Scholar] [CrossRef]
- Alexandrov, S. A property of equations of rigid plastic material obeying a voce-type hardening law. Meccanica 1999, 34, 349–356. [Google Scholar] [CrossRef]
- Huang, Y.G. A User-Material Subroutine Incorporating Single Crystal Plasticity in the ABAQUS Finite Element Program; Harvard University: Cambridge, UK, 1991. [Google Scholar]
- Roters, F.; Wang, Y.; Kuo, J.C.; Raabe, D. Comparison of single crystal simple shear deformation experiments with crystal plasticity finite element simulations. Adv. Eng. Mater. 2004, 6, 653. [Google Scholar] [CrossRef]
- Kang, G.; Dong, C.; Guo, S. Finite element analysis for uniaxial time-dependent ratcheting of SiCP/6061A1 composites at room and high temperatures. Mater. Sci. Eng. A 2007, 458, 170–183. [Google Scholar] [CrossRef]
- Hung, T.; Chiang, S.; Huang, C.; Lee, C.; Chiang, K. Thermal-mechanical behavior of the bonding wire for a power module subjected to the power cycling test. Microelectron. Reliab. 2011, 51, 1819–1823. [Google Scholar] [CrossRef]
- Xu, L.; Liu, Y.; Liu, S. Modeling and simulation of power electronic modules with microchannel coolers for thermo-mechanical performance. Microelectron. Reliab. 2014, 54, 2824–2835. [Google Scholar] [CrossRef]
- Tseng, H.; Wu, M. Electro-thermal-mechanical modeling of wire bonding failures in IGBT. In Proceedings of the IMPACT, Taipei, Taiwan, 22–25 October 2013; pp. 152–157. [Google Scholar]
- Wu, Y.; Zhou, M.; Qin, H. A comparative investigation of the electromigration behavior between wedge-type and line-type Cu/Sn3.0Ag0.5Cu/Cu interconnects. In Proceedings of the ICEPT-HDP, Shanghai, China, 8–11 August 2011; pp. 971–975. [Google Scholar]
- ABAQUS Version 6.14 Documentation; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2014.










| IGBT Layer, Measure | Length (mm) | Width (mm) | Thickness (mm) |
|---|---|---|---|
| IGBT chip | 13 | 13 | 0.15 |
| IGBT chip solder | 13 | 13 | 0.15 |
| Upper copper layer 1 | 15 | 18 | 0.30 |
| Upper copper layer 2 | 10 | 18 | 0.30 |
| Ceramic substrate | 19 | 30 | 0.40 |
| Lower copper layer | 19 | 30 | 0.40 |
| Base solder | 98 | 44 | 0.20 |
| Copper base plate | 120 | 60 | 3.00 |
| Material Parameters | Symbol | Value | Unit | |
|---|---|---|---|---|
| Elastic parameters | Elastic constants | C11 | 108,000 | MPa |
| C12 | 62,000 | MPa | ||
| C44 | 28,300 | MPa | ||
| Plastic parameters | Rate-dependent sensitivity exponent | n | 10 | - |
| Reference shear strain rate | 0.001 | s−1 | ||
| Initial hardening modulus | h0 | 60 | - | |
| Saturation stress | τs | 61 | MPa | |
| Initial critical resolved shear stress | τ0 | 21.17 | MPa | |
| Ratio of latent hardening to self-hardening | q | 1.4 | - | |
| Volume thermal expansion coefficient | A | 24 | ppm/°C | |
| Materials | Young’s Modulus (GPa) | Poisson’s Ratio | Coefficient of Thermal Expansion (ppm/°C) | Thermal Conduction (W/m·K) | Electrical Conductivity (1/mΩ·mm) | Density (kg/m3) | Specific Heat (J/kg·K) |
|---|---|---|---|---|---|---|---|
| Cu [32] | 128 | 0.36 | 16.4 | 400 | 59.523 | 8920 | 380 |
| Ceramic [32] | 345 | 0.25 | 7.2 | 20 | 1 × 10−18 | 3960 | 753 |
| Al [32] | 70.6 | 0.34 | 24 | 237 | 37.735 | 2700 | 900 |
| Si [32] | 130 | 0.22 | 2.5 | 148 | Temperature-dependent | 2330 | 700 |
| Sn3.0Ag0.5Cu solder [33] | 10.6 | 0.35 | 25 | 57 | 9.615 | 7300 | 230 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, T.; Zheng, X.; Qin, F.; Dai, Y.; Gong, Y.; Chen, P. Macro–Mesoscale Modeling of the Evolution of the Surface Roughness of the Al Metallization Layer of an IGBT Module during Power Cycling. Materials 2023, 16, 1936. https://doi.org/10.3390/ma16051936
An T, Zheng X, Qin F, Dai Y, Gong Y, Chen P. Macro–Mesoscale Modeling of the Evolution of the Surface Roughness of the Al Metallization Layer of an IGBT Module during Power Cycling. Materials. 2023; 16(5):1936. https://doi.org/10.3390/ma16051936
Chicago/Turabian StyleAn, Tong, Xueheng Zheng, Fei Qin, Yanwei Dai, Yanpeng Gong, and Pei Chen. 2023. "Macro–Mesoscale Modeling of the Evolution of the Surface Roughness of the Al Metallization Layer of an IGBT Module during Power Cycling" Materials 16, no. 5: 1936. https://doi.org/10.3390/ma16051936
APA StyleAn, T., Zheng, X., Qin, F., Dai, Y., Gong, Y., & Chen, P. (2023). Macro–Mesoscale Modeling of the Evolution of the Surface Roughness of the Al Metallization Layer of an IGBT Module during Power Cycling. Materials, 16(5), 1936. https://doi.org/10.3390/ma16051936









