Fatigue Life Prediction of Notched Details Using SWT Model and LEFM-Based Approach
Abstract
1. Introduction
2. Numerical Implementation of Fatigue in Abaqus
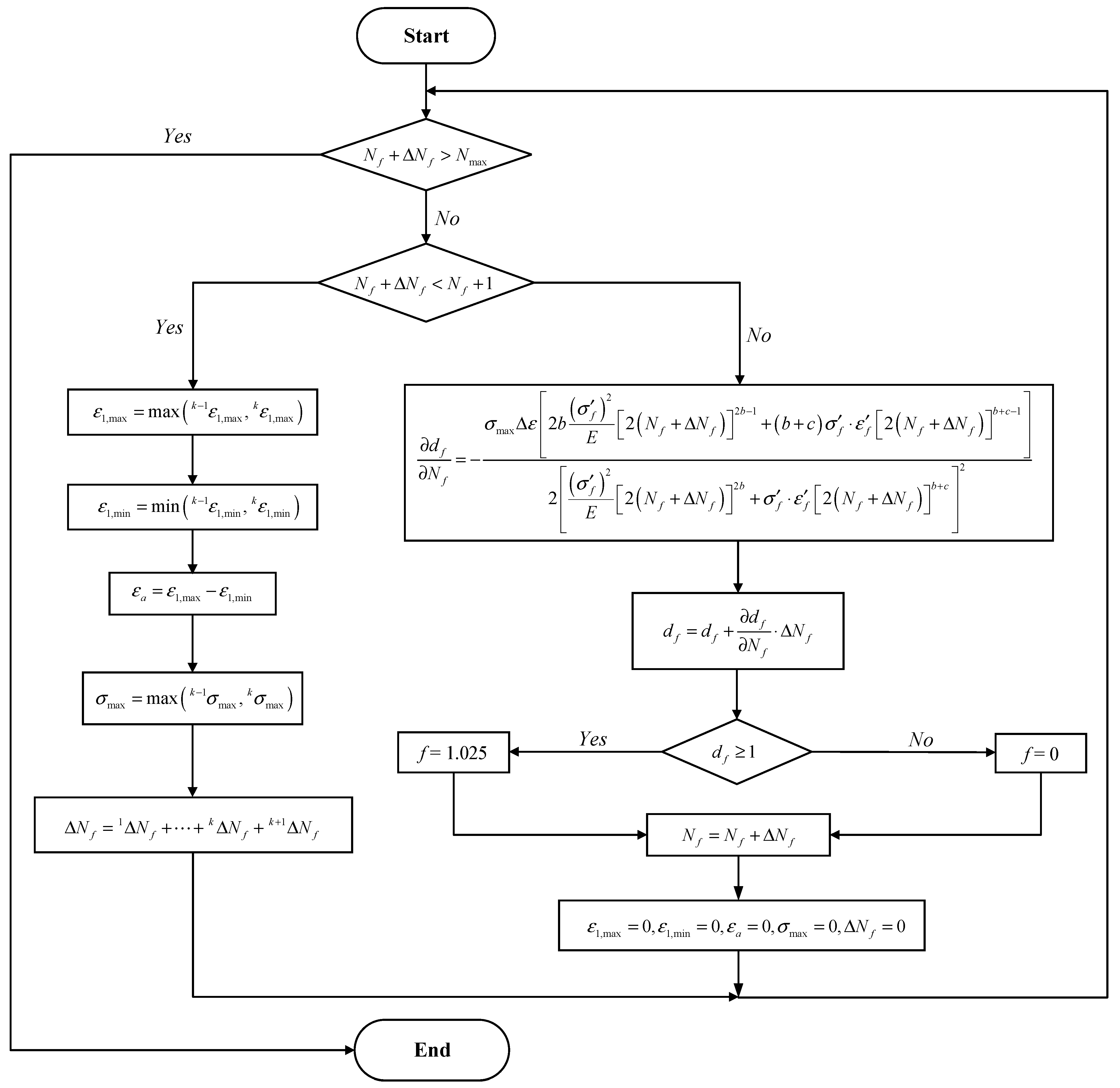
2.1. Algorithm for the UDMGINI Subroutine
| N | is the number of nodal points in a finite element; |
| Ni (x) | is the standard shape function; |
| ui | is the standard nodal displacement related to the standard shape function; |
| M | is the number of enriched nodes in a finite element; |
| Nj (x) | is the shape function of the enriched part; |
| aj | is the nodal DOF corresponding to the enrichment function; |
| H (x) | is the Heaviside enrichment function, defined as Equation (6). |
| φ (x) | is the signed distance function; |
| x* | is the closest point projection of x onto the crack surface Γd; |
| nΓd | is the normal vector to the crack surface at point x*. |
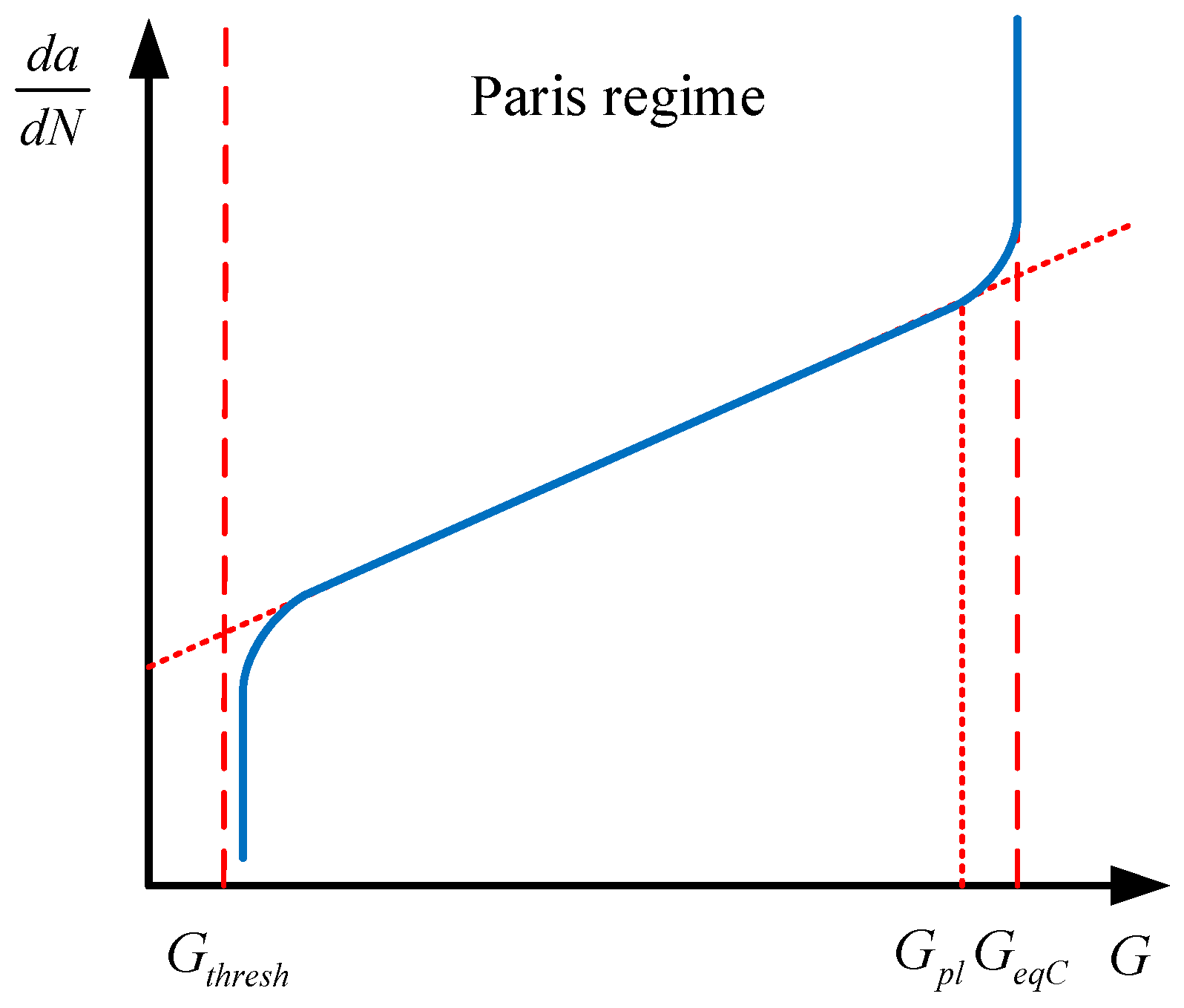
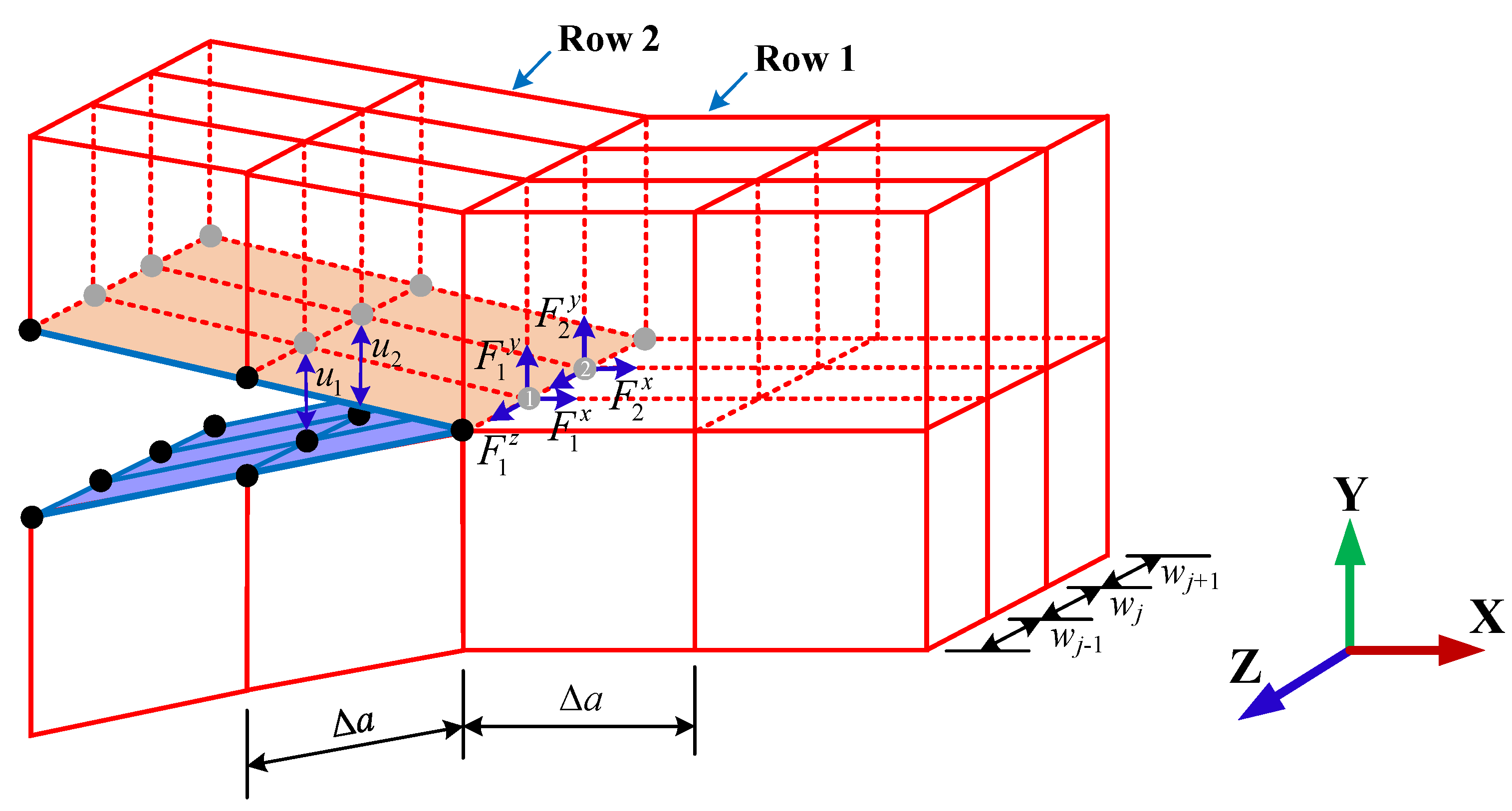
2.2. LEFM-Based Fatigue Crack Propagation Analysis
3. Fatigue Test and Numerical Model
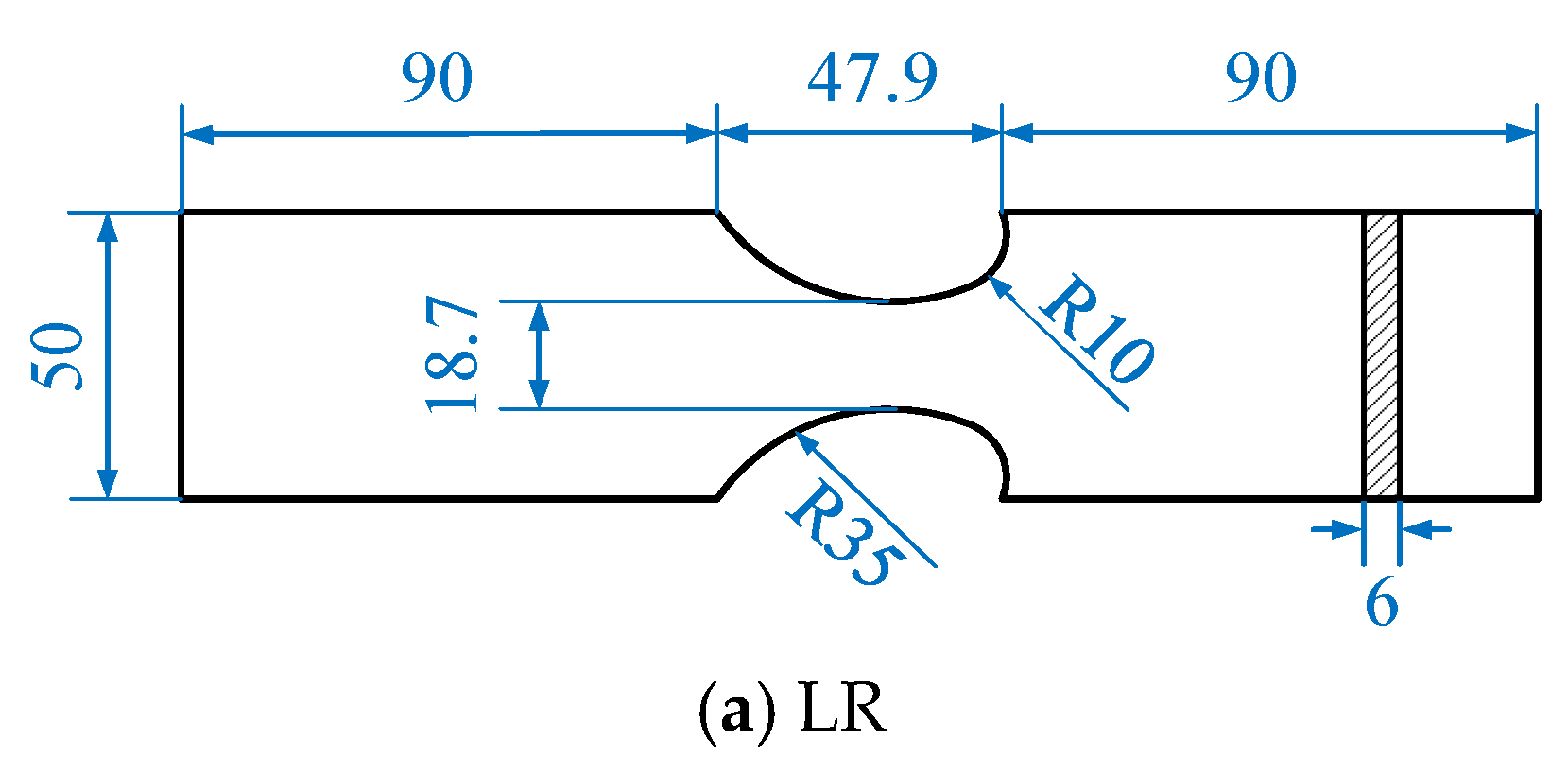
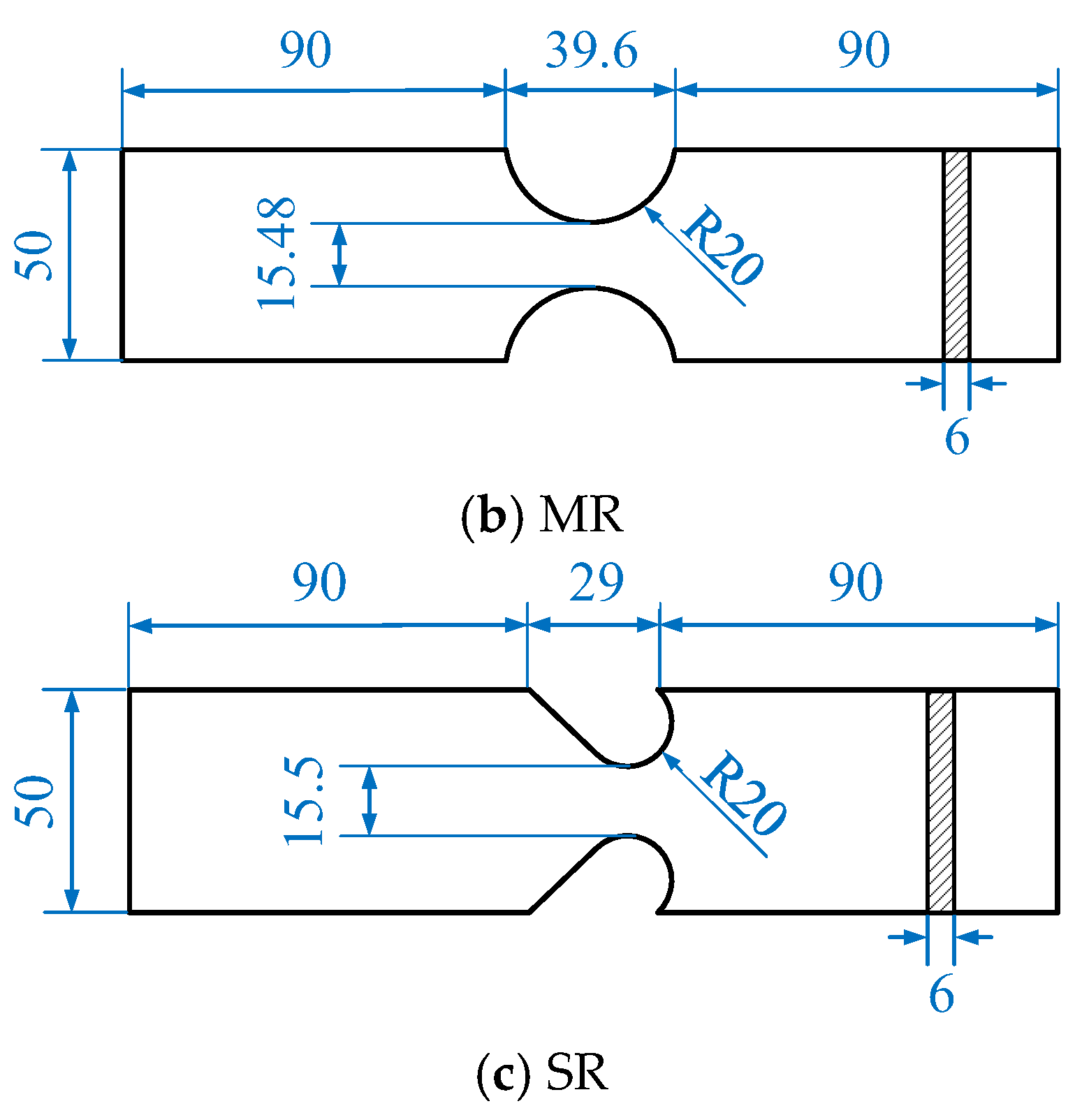
3.1. Description of the Fatigue Test
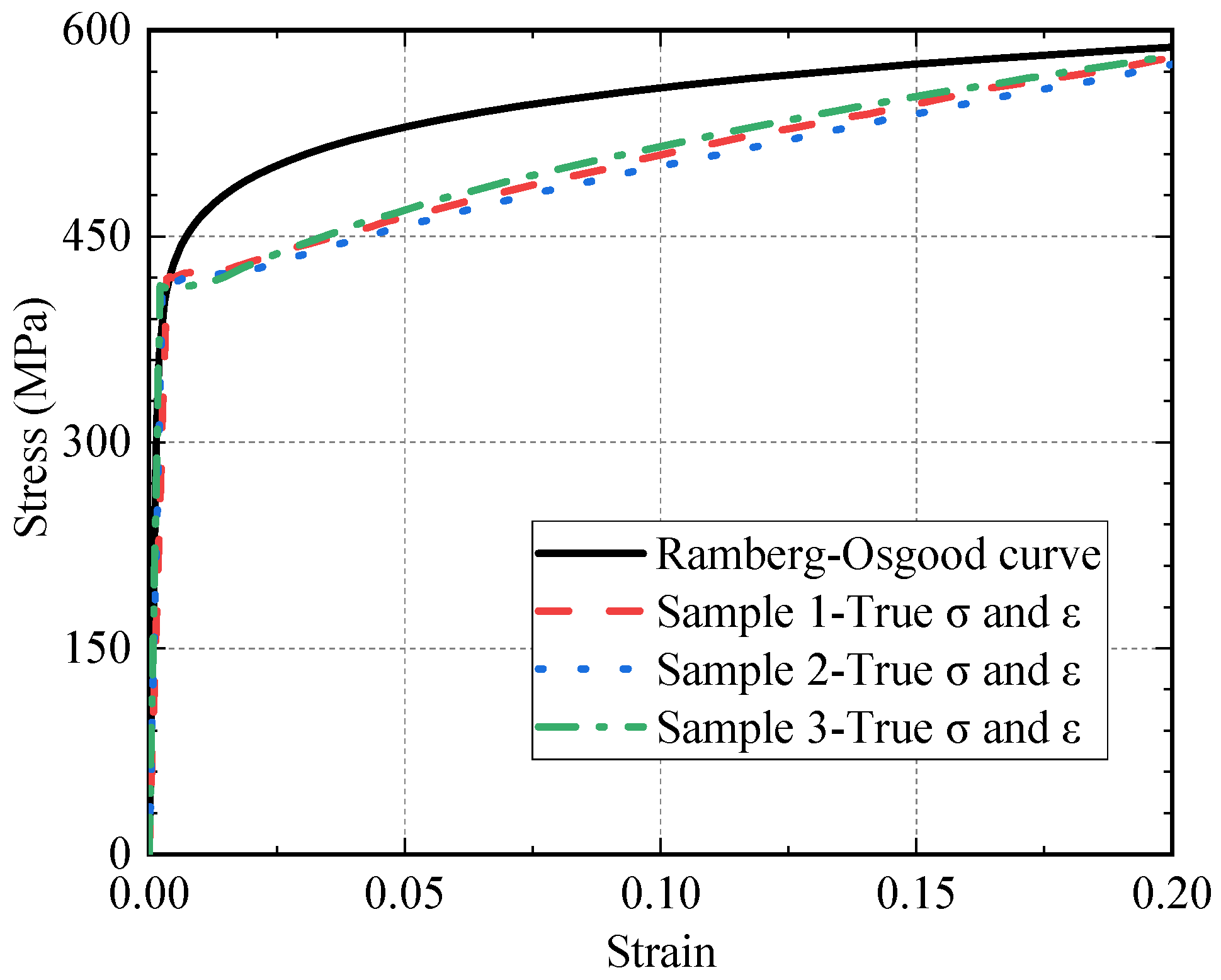
3.2. Constitutive Model of Steel Plate
3.3. Element and Load/Boundary Conditions
4. Results and Discussion
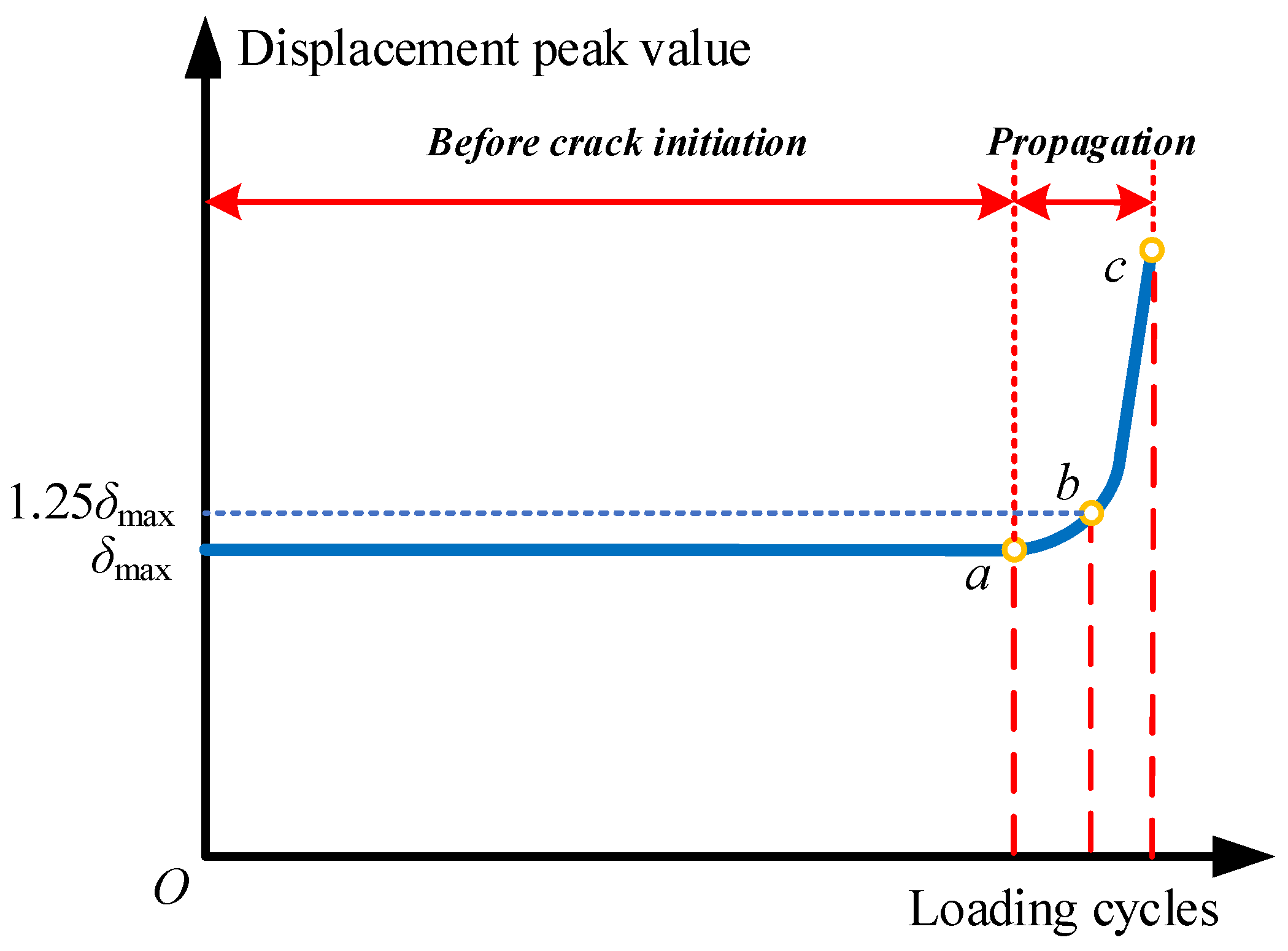
4.1. Fatigue Life
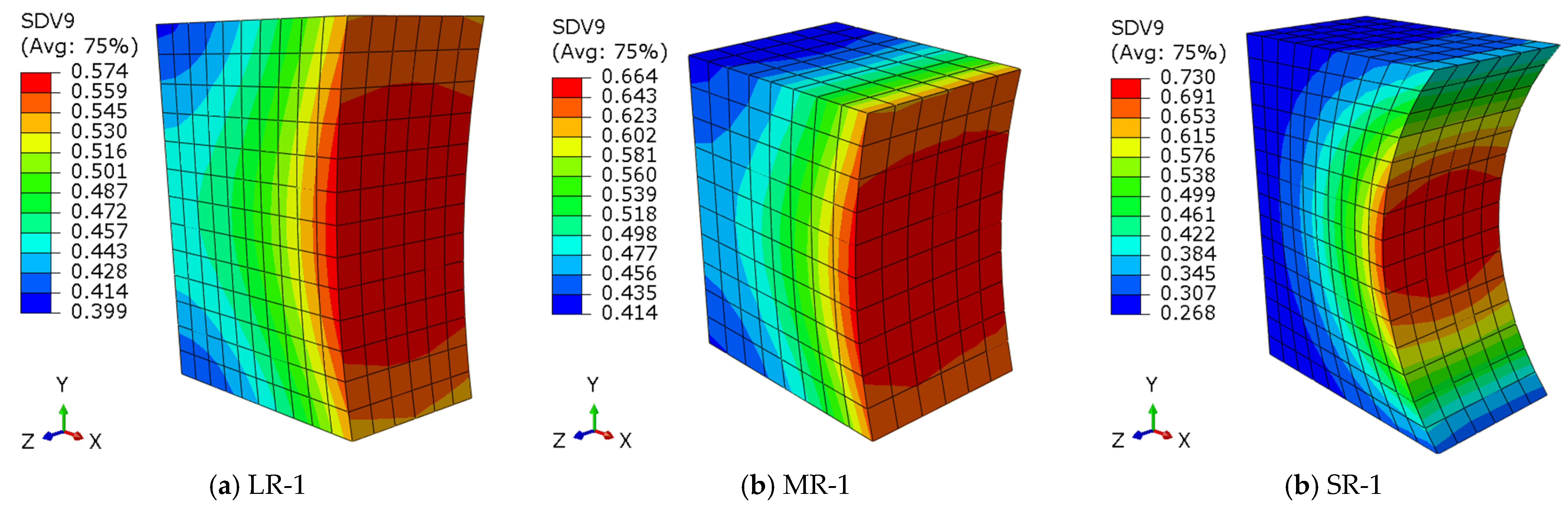
4.2. Strain Evolutions
5. Conclusions
- (1)
- A new SWT-model-based algorithm for the fatigue crack initiation life prediction of notched details in the HCF regime is proposed by considering the cycle-by-cycle fatigue damage accumulation, and the damage model is implemented by employing the UDMGINI subroutine written with Fortran code. A good agreement between the predicted fatigue initiation life and experimental results is confirmed.
- (2)
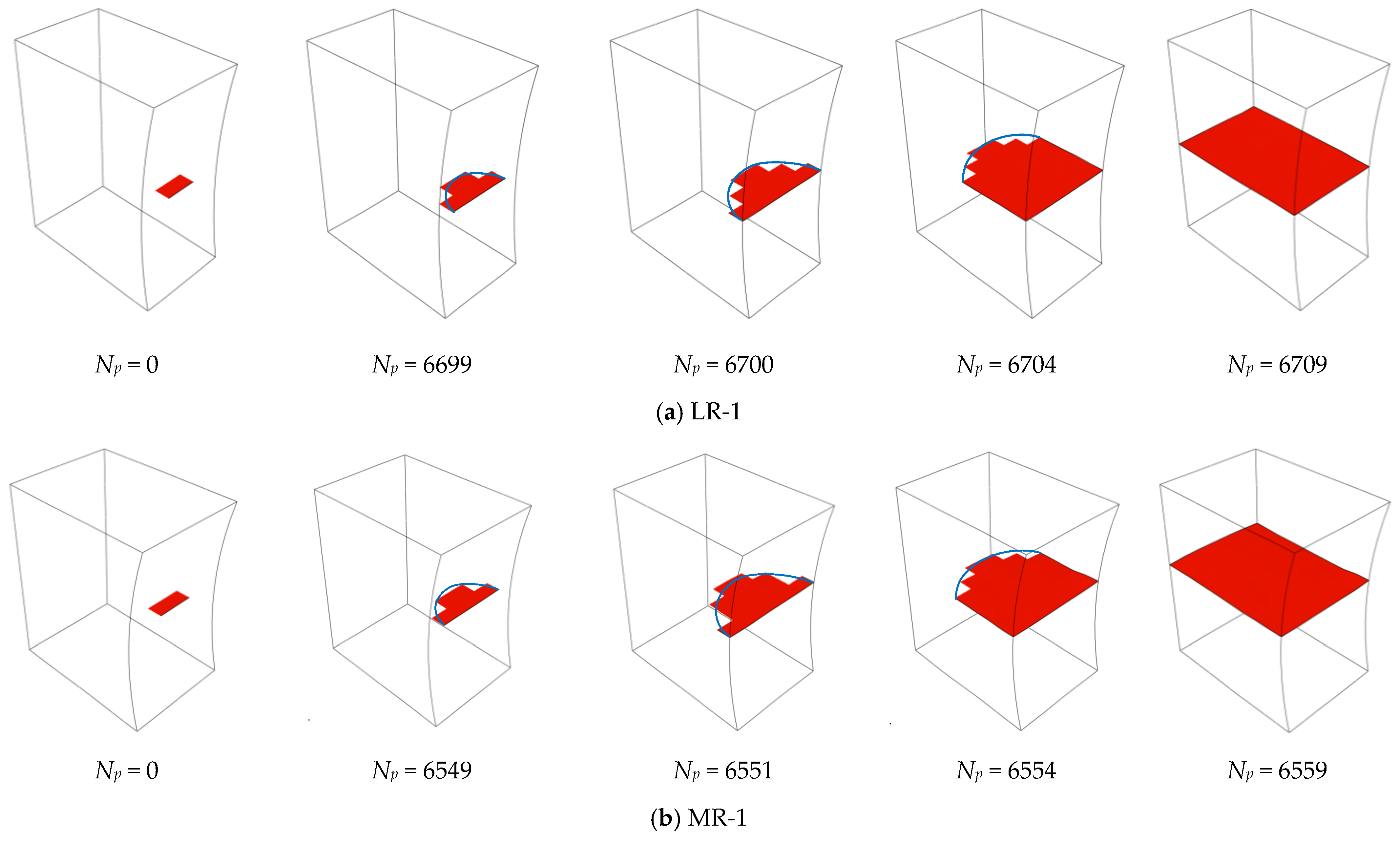
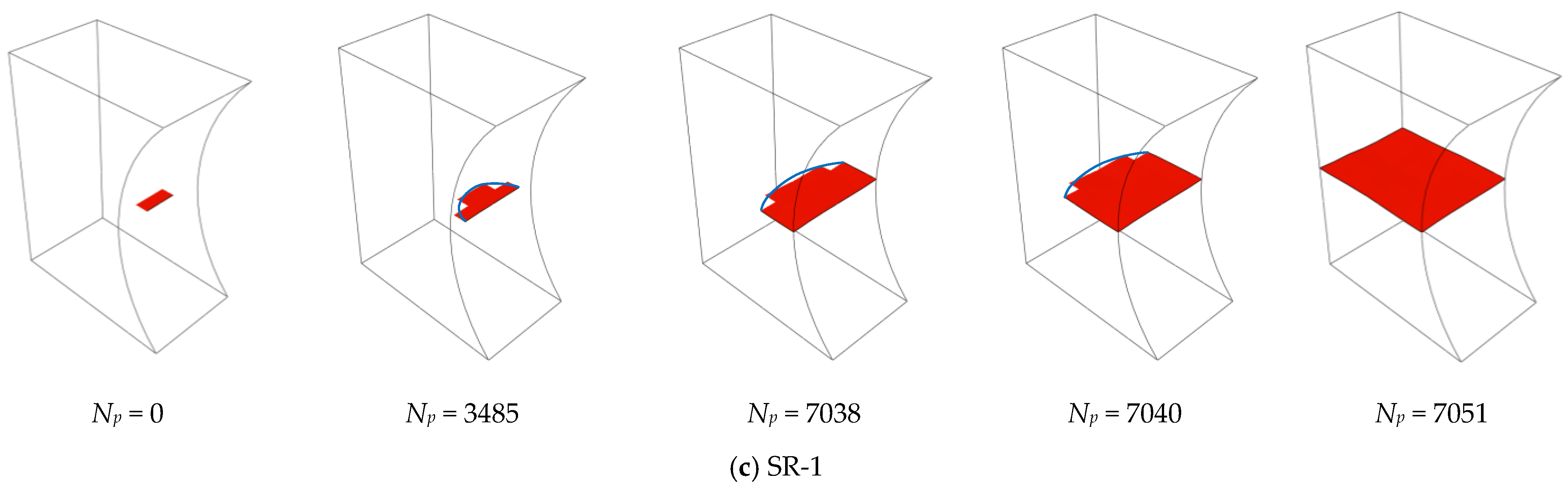
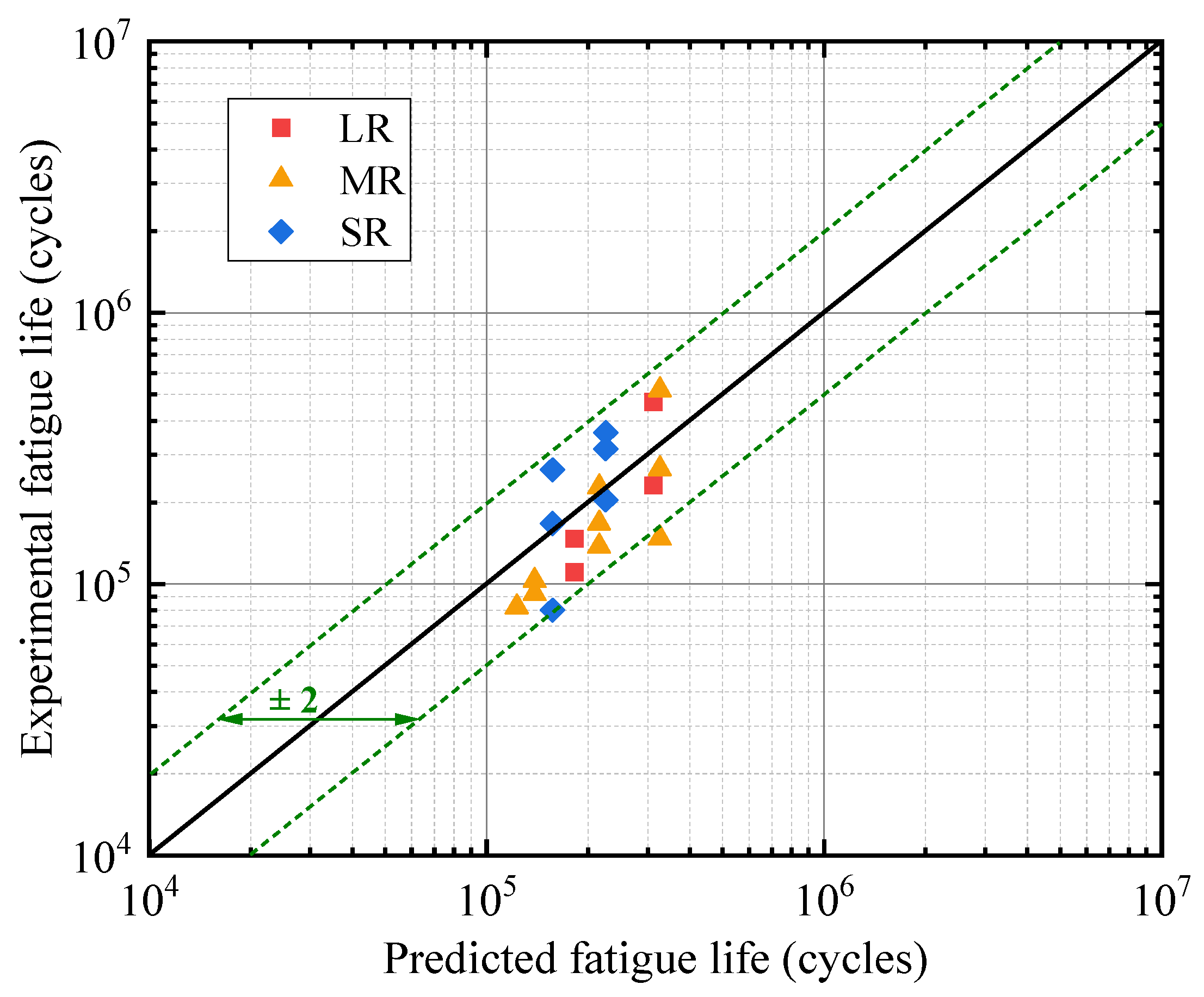
- The established numerical models based on UDMGINI and VCCT are validated and agree well with the tests, and the prediction of the total fatigue life falls within a scatter factor of 2. The failure modes predicated by the simulation are the same with the tests.
- (3)
- Notch details with different root radii were investigated, and it was found that, as the notch root radius decreases, the high-damage-factor zone of fatigue damage becomes more concentrated, making it vulnerable to fatigue damage.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fricke, W. Fatigue analysis of welded joints: State of development. Mar. Struct. 2003, 16, 185–200. [Google Scholar] [CrossRef]
- Chen, Z.; Li, C.; He, J.; Xin, H. Retrofit Fatigue Cracked Diaphragm Cutouts Using Improved Geometry in Orthotropic Steel Decks. Appl. Sci. 2020, 10, 3983. [Google Scholar] [CrossRef]
- Ke, L.; Li, C.; He, J.; Lu, Y.; Jiao, Y.; Liu, Y. Fatigue evaluation and CFRP strengthening of diaphragm cutouts in orthotropic steel decks. Steel Compos. Struct. 2021, 39, 453–469. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, J.; Huang, Y.; Carpinteri, A. Hot-spot stress models of cutout detail on orthotropic steel bridge decks. J. Constr. Steel Res. 2021, 183, 106762. [Google Scholar] [CrossRef]
- Liao, D.; Zhu, S.; Correia, J.; Jesus, A.M.D.; Berto, F. Recent advances on notch effect in metal fatigue: A review. Fatigue Fract. Engng. Mater. Struct. 2020, 43, 637–659. [Google Scholar] [CrossRef]
- Liao, D.; Zhu, S. Energy field intensity approach for notch fatigue analysis. Int. J. Fatigue 2019, 127, 190–202. [Google Scholar] [CrossRef]
- He, J.; Zhu, S.; Taddesse, A.T.; Niu, X. Evaluation of critical distance, highly stressed volume, and weakest-link methods in notch fatigue analysis. Int. J. Fatigue 2022, 162, 106950. [Google Scholar] [CrossRef]
- Navathe, P.R. Evaluation of Local Stress-Strain Methods; University of Regina: Regina, SK, Canada, 1997. [Google Scholar]
- Neuber, H. Theory of Notch Stresses: Principles for Exact Calculation of Strength with Reference to Structural Form and Material; USAEC Office of Technical Information: Germantown, MD, USA, 1958. [Google Scholar]
- Susmel, L.; Taylor, D. A novel formulation of the theory of critical distances to estimate lifetime of notched components in the medium-cycle fatigue regime. Fatigue Fract. Engng. Mater. Struct. 2007, 30, 567–581. [Google Scholar] [CrossRef]
- Yao, W. Stress field intensity approach for predicting fatigue life. Int. J. Fatigue 1993, 15, 243–246. [Google Scholar] [CrossRef]
- Branco, R.; Prates, P.A.; Costa, J.D.; Borrego, L.P.; Berto, F.; Kotousov, A.; Antunes, F.V. Rapid assessment of multiaxial fatigue lifetime in notched components using an averaged strain energy density approach. Int. J. Fatigue 2019, 124, 89–98. [Google Scholar] [CrossRef]
- Kallmeyer, A.R.; Krgo, A.; Kurath, P. Evaluation of Multiaxial Fatigue Life Prediction Methodologies for Ti-6Al-4V. ASME J. Eng. Mater. Technol. 2002, 124, 229–237. [Google Scholar] [CrossRef]
- EN 1993-1-9; Eurocode 3: Design of steel structures—Part 1–9: Fatigue. European Committee for Standardization: Brussels, Belgium, 2005.
- Firdaus, S.M.; Arifin, A.; Abdullah, S.; Singh, S.S.K.; Nor, N.M. Fatigue Life Assessment of API Steel Grade X65 Pipeline Using a Modified Basquin Parameter of the Magnetic Flux Leakage Signal. Materials 2023, 16, 464. [Google Scholar] [CrossRef]
- Shigley, J.E.; Mischke, C.R. Mechanical Engineering Design; McGraw-Hill: New York, NY, USA, 1989. [Google Scholar]
- Filippinia, M.; Folettia, S.; Pasquerob, G. Assessment of Multiaxial Fatigue Life Prediction Methodologies for Inconel 718. Procedia Eng. 2010, 2, 2347–2356. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, H.; Zhang, S.; He, T.; Liu, X.; Chang, X. An Experimental Study on Low-Cycle Fatigue Crack Initiation Life Prediction of Powder Superalloy FGH96 Based on the Manson-Coffin and Damage Mechanics Methods. Metals 2021, 11, 489. [Google Scholar] [CrossRef]
- Morrow, J. Cyclic plastic strain energy and fatigue of metals. In Internal Friction, Damping, and Cyclic Plasticity; American Society for Testing and Materials STP-378; ASTM International: West Conshohocken, PA, USA, 1965; pp. 45–87. [Google Scholar]
- Smith, K.N.; Watson, P.; Topper, T.H. A Stress-strain Function for the Fatigue of Metals. J. Mater. 1970, 5, 767–778. [Google Scholar]
- Xin, H.; Veljkovic, M. Fatigue Crack Initiation Prediction Using Phantom Nodes-Based Extended Finite Element Method for S355 and S690 Steel Grades. Eng. Fract. Mech. 2019, 214, 164–176. [Google Scholar] [CrossRef]
- Fatemi, A.; Kurath, P. Multiaxial Fatigue Life Predictions Under the Influence of Mean Stresses. J. Eng. Mater. Technol. 1988, 110, 380–388. [Google Scholar] [CrossRef]
- Glinka, G.; Wang, G.; Plumtree, A. Mean Stress Effects in Multiaxial Fatigue. Fatigue Fract. Engng. Mater. Struct. 1995, 18, 755–764. [Google Scholar] [CrossRef]
- Liu, K.C. A Method Based on Virtual Strain-Energy Parameters for Multiaxial Fatigue Life Prediction; Advances in Multiaxial Fatigue, ASTM STP 1191; McDowell, D.L., Ellis, R., Eds.; American Society for Testing and Materials: Philadelphia, PA, USA, 1993; pp. 67–84. [Google Scholar]
- Chu, C.C.; Conle, F.A.; Bonnen, J.J.F. Multiaxial Stress-Strain Modeling and Fatigue Life Prediction of SAE Axle Shafts; Advances in Multiaxial Fatigue, ASTM STP 1191; McDowell, D.L., Ellis, R., Eds.; American Society for Testing and Materials: Philadelphia, PA, USA, 1993; pp. 37–54. [Google Scholar]
- Socie, D.F.; Marquis, G.R. Multiaxial Fatigue; SAE International: Warrendale, PA, USA, 1999. [Google Scholar]
- SIMULIA. User Assistance 2022; Dassault Syst Simulia Corp: Johnston, RI, USA, 2022. [Google Scholar]
- Khoei, A.R. Extended Finite Element Method: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Cruces, A.S.; Lopez-Crespo, P.; Moreno, B.; Antunes, F.V. Multiaxial Fatigue Life Prediction on S355 Structural and Offshore Steel Using the SKS Critical Plane Model. Metals 2018, 8, 1060. [Google Scholar] [CrossRef]
- Gupta, R.S. Prediction of Fatigue Crack Propagation in Orthotropic Steel Decks Using XFEM Based on LEFM and VCCT; Delft University of Technology: Delft, The Netherlands, 2019. [Google Scholar]
- Zhao, X.; Mo, Z.; Guo, Z.; Li, J. A modified three-dimensional virtual crack closure technique for calculating stress intensity factors with arbitrarily shaped finite element mesh arrangements across the crack front. Theor. Appl. Fract. Mech. 2020, 109, 102695. [Google Scholar] [CrossRef]
- Hao, R.; Lehto, P.; Lin, W. Critical Distance-based Fatigue Life Evaluation of Blunt Notch Details in Steel Bridges. J. Constr. Steel Res. 2023, 201, 107738. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; National Advisory Committee for Aeronautics: WA, USA, 1943. [Google Scholar]
- Yang, X.; Wang, J.; Liu, J. High temperature LCF life prediction of notched DS Ni-based superalloy using critical distance concept. Int. J. Fatigue 2011, 33, 1470–1476. [Google Scholar] [CrossRef]





| σ’f (MPa) | ε’f | b | c | |
|---|---|---|---|---|
| Cruces [29] | 564.4 | 0.1554 | −0.0576 | −0.4658 |
| Material | c3 | c4 | GIC (N/mm) | GIIC (N/mm) | GIIIC (N/mm) | am | an | am |
|---|---|---|---|---|---|---|---|---|
| S355 | 1.4 × 10−5 | 1.8121 | 6.5 | 6.5 | 6.5 | 1 | 1 | 1 |
| Sample | Nominal Yield Stress (MPa) | Nominal Tensile Strength (MPa) | Elastic Modulus (GPa) | Elongation (%) |
|---|---|---|---|---|
| S355-1 | 413 | 476.6 | 208.1 | 45.6 |
| S355-2 | 410 | 475.2 | 212.5 | 30.9 |
| S355-3 | 414 | 475.7 | 212.2 | 51.6 |
| Mean | 412.3 | 475.8 | 210.9 | 42.7 |
| Series | Δσnom (MPa) | Crack Initiation Life (Including Propagation Life Until Point b) | ||||||
|---|---|---|---|---|---|---|---|---|
| Sample 1 | Sample 2 | Sample 3 | Average | Standard Deviation | XFEM | XFEM/Average | ||
| LR | 360.96 | 110,894 | 147,454 | -- | 129,174 | 18,280 | 175,077 | 1.355 |
| 352.94 | 231,352 | 470,240 | -- | 350,796 | 119,444 | 303,472 | 0.865 | |
| MR | 377.91 | 82,440 | -- | -- | 82,440 | -- | 116,326 | 1.411 |
| 370.16 | 92,200 | 103,035 | -- | 97,618 | 5418 | 130,848 | 1.340 | |
| 360.47 | 228,083 | 137,804 | 167,747 | 177,878 | 37,546 | 202,484 | 1.138 | |
| 350.78 | 265,791 | 147,792 | 519,846 | 311,143 | 155,239 | 311,628 | 1.002 | |
| SR | 344.52 | 167,454 | 80,273 | 263,909 | 170,545 | 75,000 | 149,489 | 0.877 |
| 332.90 | 315,173 | 204,465 | 362,291 | 294,043 | 66,153 | 213,190 | 0.725 | |
| Series | Δσnom (MPa) | Crack propagation | |||||
|---|---|---|---|---|---|---|---|
| Sample 1 | Sample 2 | Sample 3 | Average | XFEM | XFEM/Average | ||
| LR | 360.96 | 8902 | 9333 | -- | 9118 | 6709 | 0.736 |
| 352.94 | 10,548 | 9534 | -- | 10,041 | 8042 | 0.801 | |
| MR | 377.91 | 6042 | -- | -- | 6042 | 6559 | 1.086 |
| 370.16 | 7788 | 7560 | -- | 7674 | 7785 | 1.014 | |
| 360.47 | 8241 | 6661 | 8248 | 7717 | 13,158 | 1.705 | |
| 350.78 | 9823 | 8799 | 2140 | 6921 | 14,291 | 2.065 | |
| SR | 344.52 | 4945 | 7103 | 5852 | 5967 | 7051 | 1.182 |
| 332.90 | 4112 | 8097 | 5873 | 6027 | 12,046 | 1.999 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, R.; Wen, Z.; Xin, H.; Lin, W. Fatigue Life Prediction of Notched Details Using SWT Model and LEFM-Based Approach. Materials 2023, 16, 1942. https://doi.org/10.3390/ma16051942
Hao R, Wen Z, Xin H, Lin W. Fatigue Life Prediction of Notched Details Using SWT Model and LEFM-Based Approach. Materials. 2023; 16(5):1942. https://doi.org/10.3390/ma16051942
Chicago/Turabian StyleHao, Rui, Zongyi Wen, Haohui Xin, and Weiwei Lin. 2023. "Fatigue Life Prediction of Notched Details Using SWT Model and LEFM-Based Approach" Materials 16, no. 5: 1942. https://doi.org/10.3390/ma16051942
APA StyleHao, R., Wen, Z., Xin, H., & Lin, W. (2023). Fatigue Life Prediction of Notched Details Using SWT Model and LEFM-Based Approach. Materials, 16(5), 1942. https://doi.org/10.3390/ma16051942








