Different Conical Angle Connection of Implant and Abutment Behavior: A Static and Dynamic Load Test and Finite Element Analysis Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Instruments
2.2. Static Load Test Protocol
2.3. Dynamic Load Test Protocol
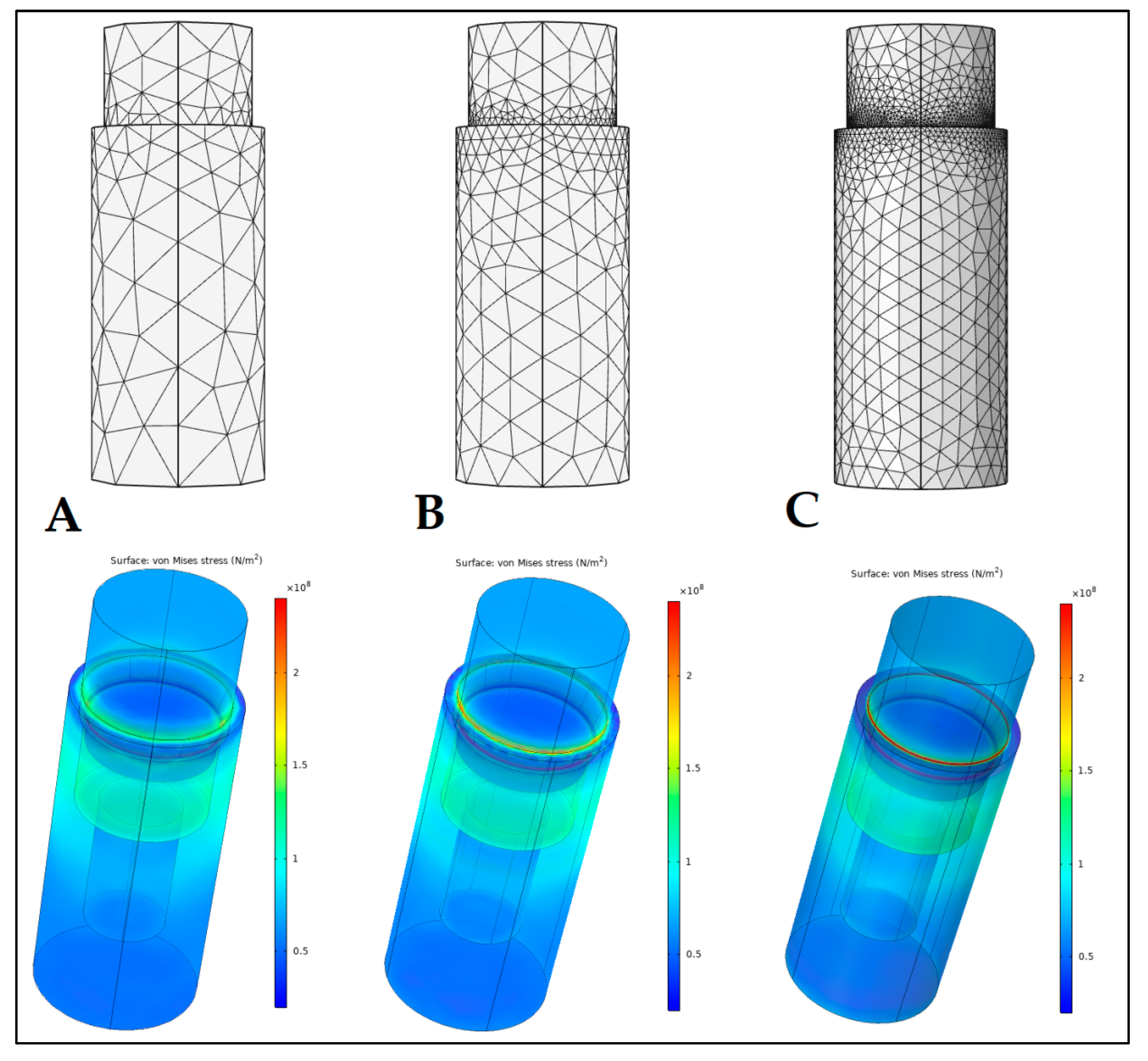
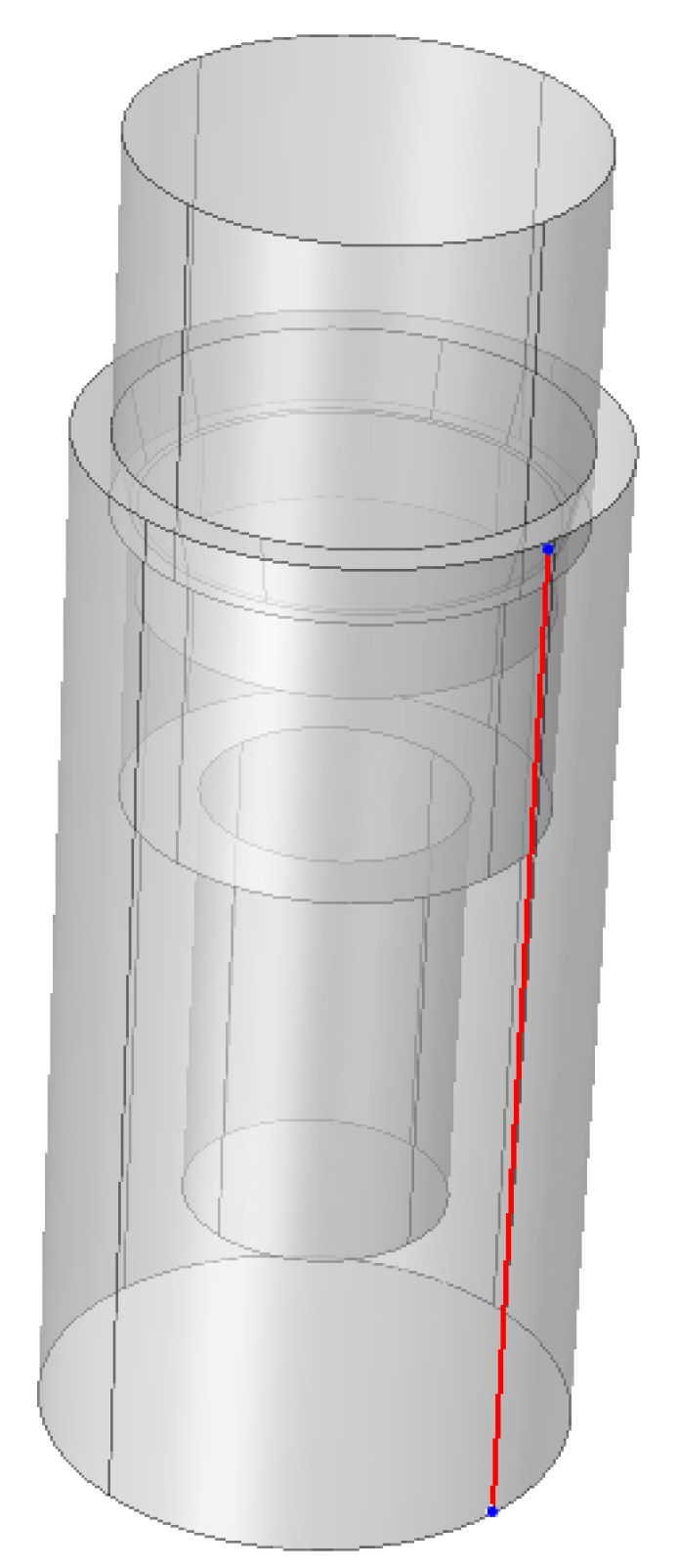
2.4. Finite Element Analysis (FEA)
2.5. Statistical Analysis
3. Results
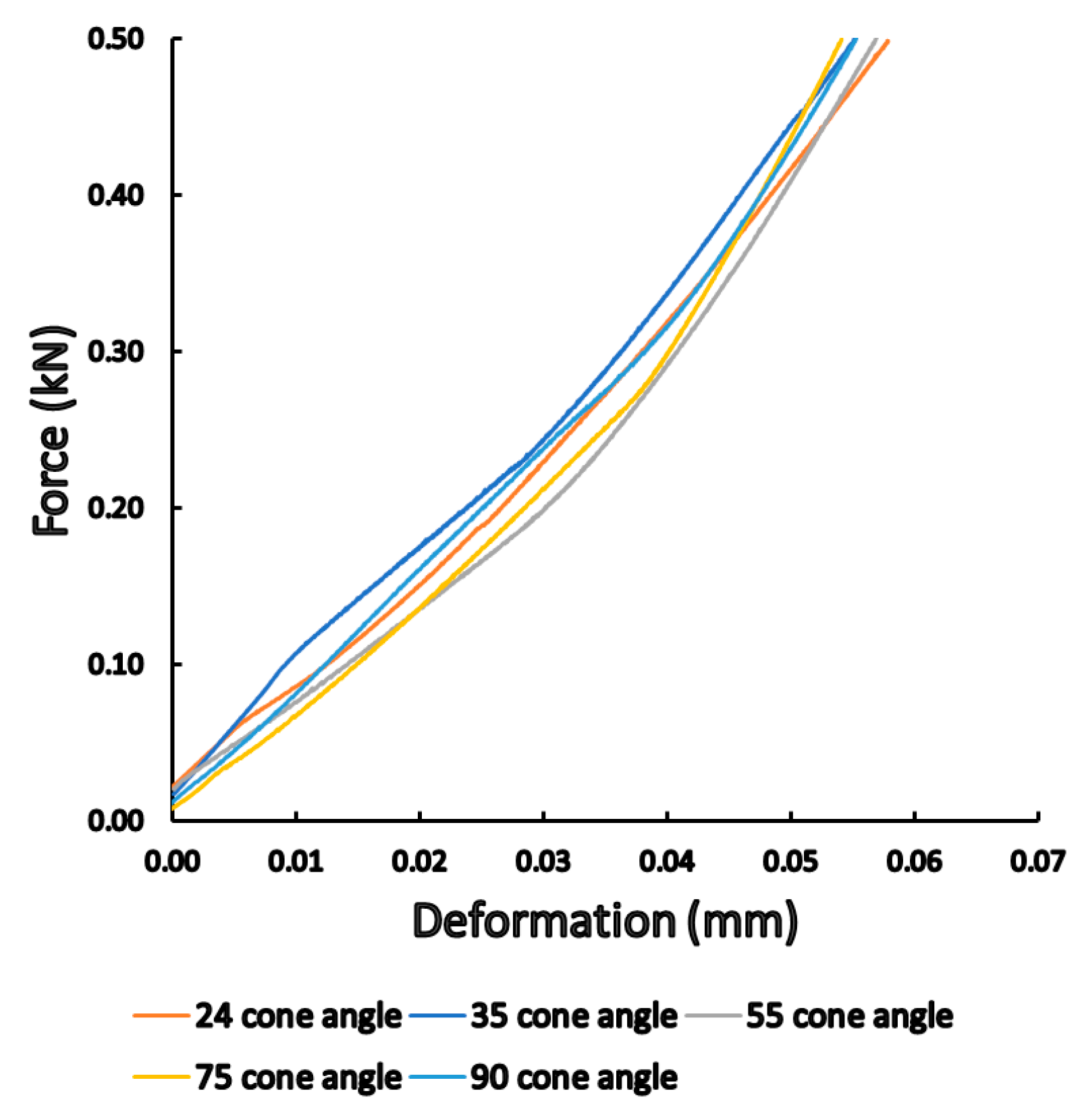
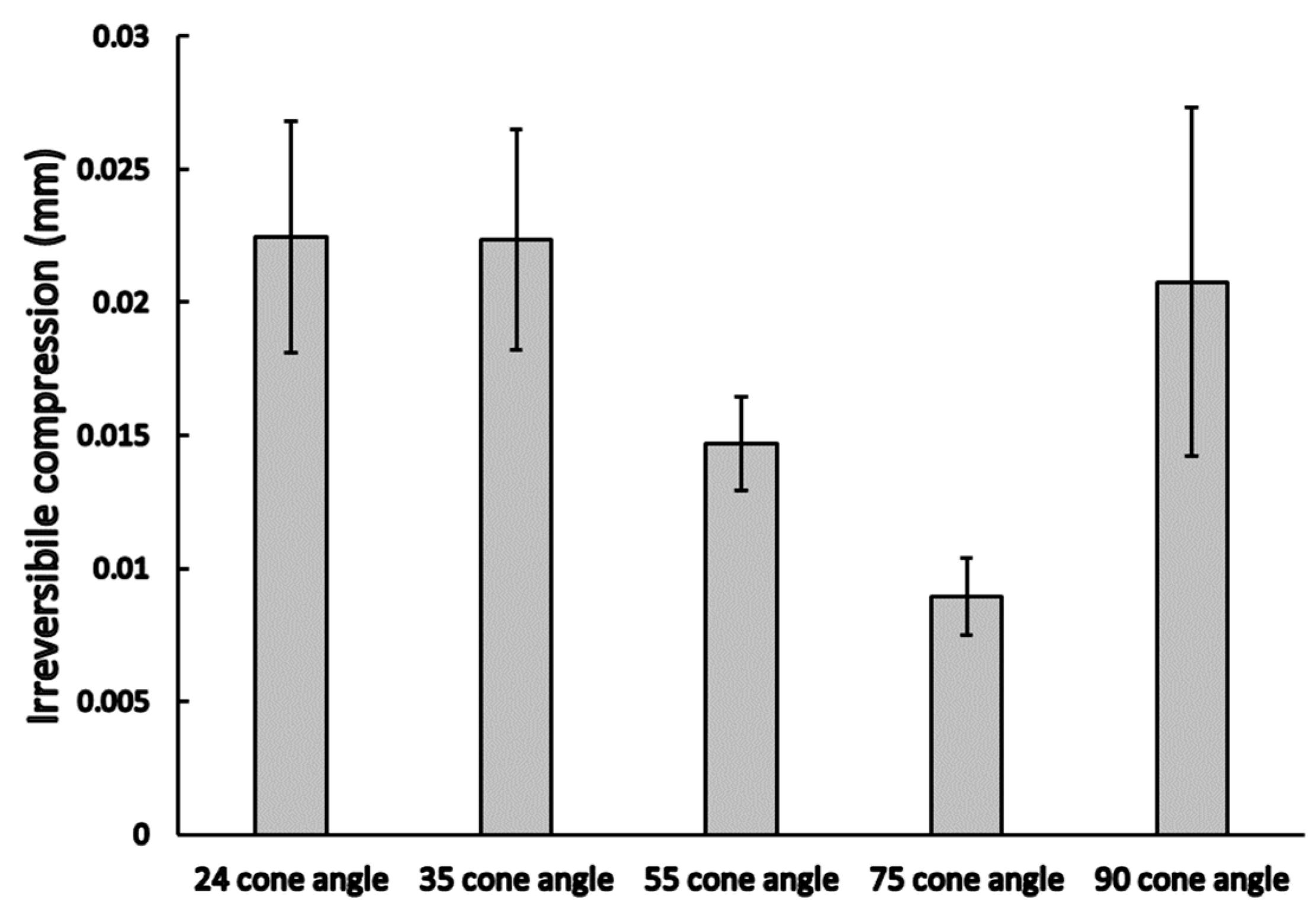
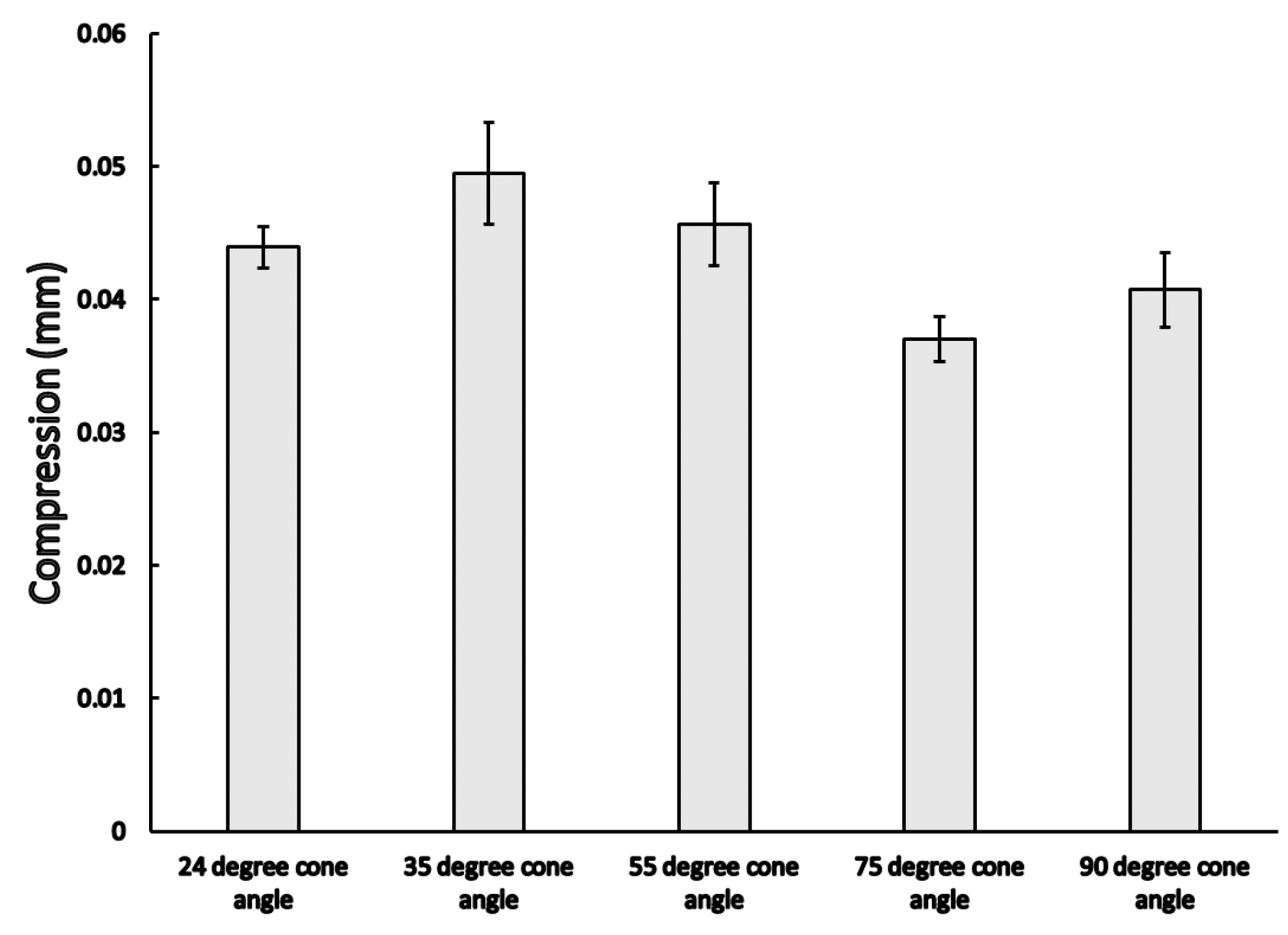
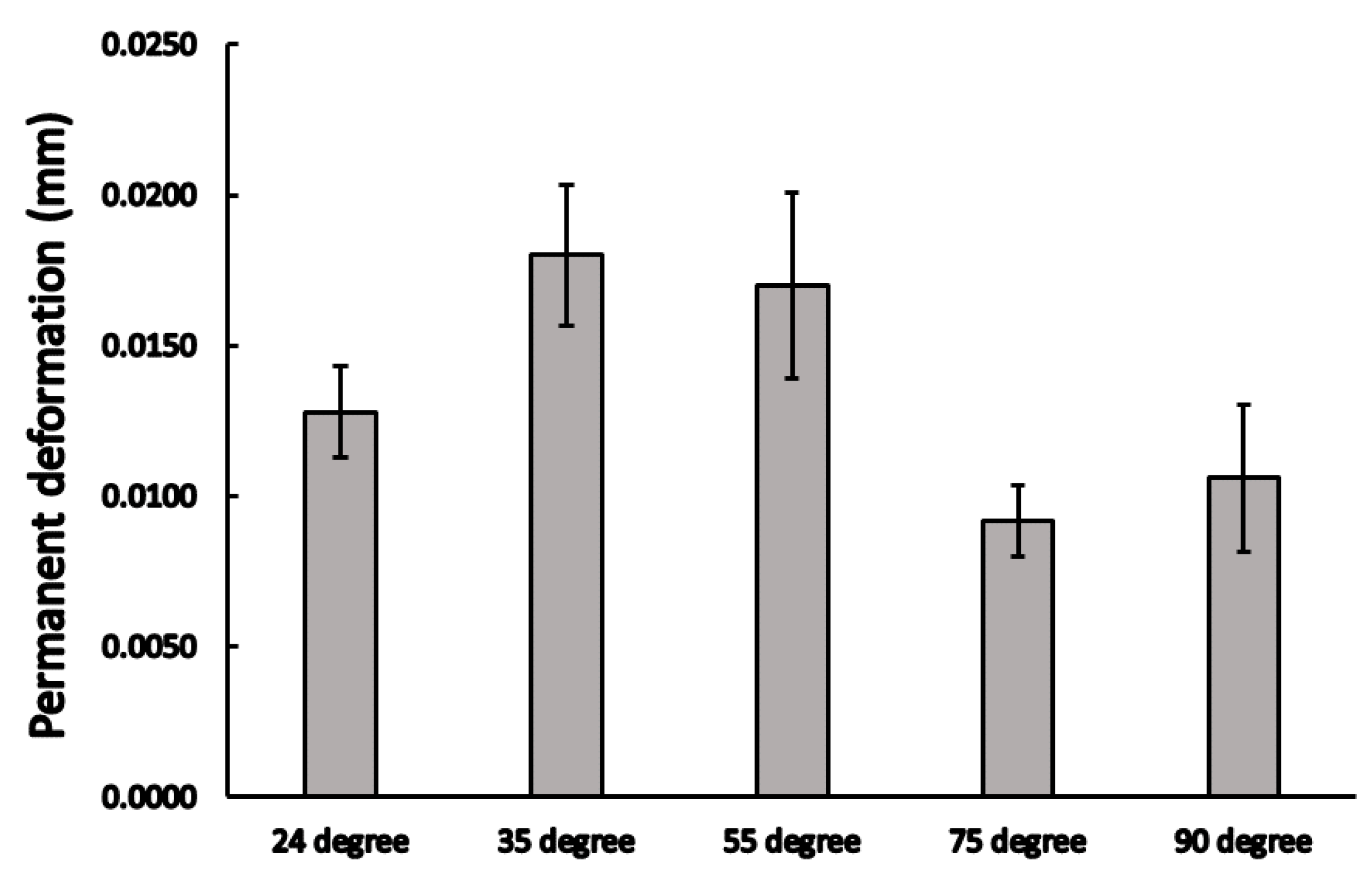
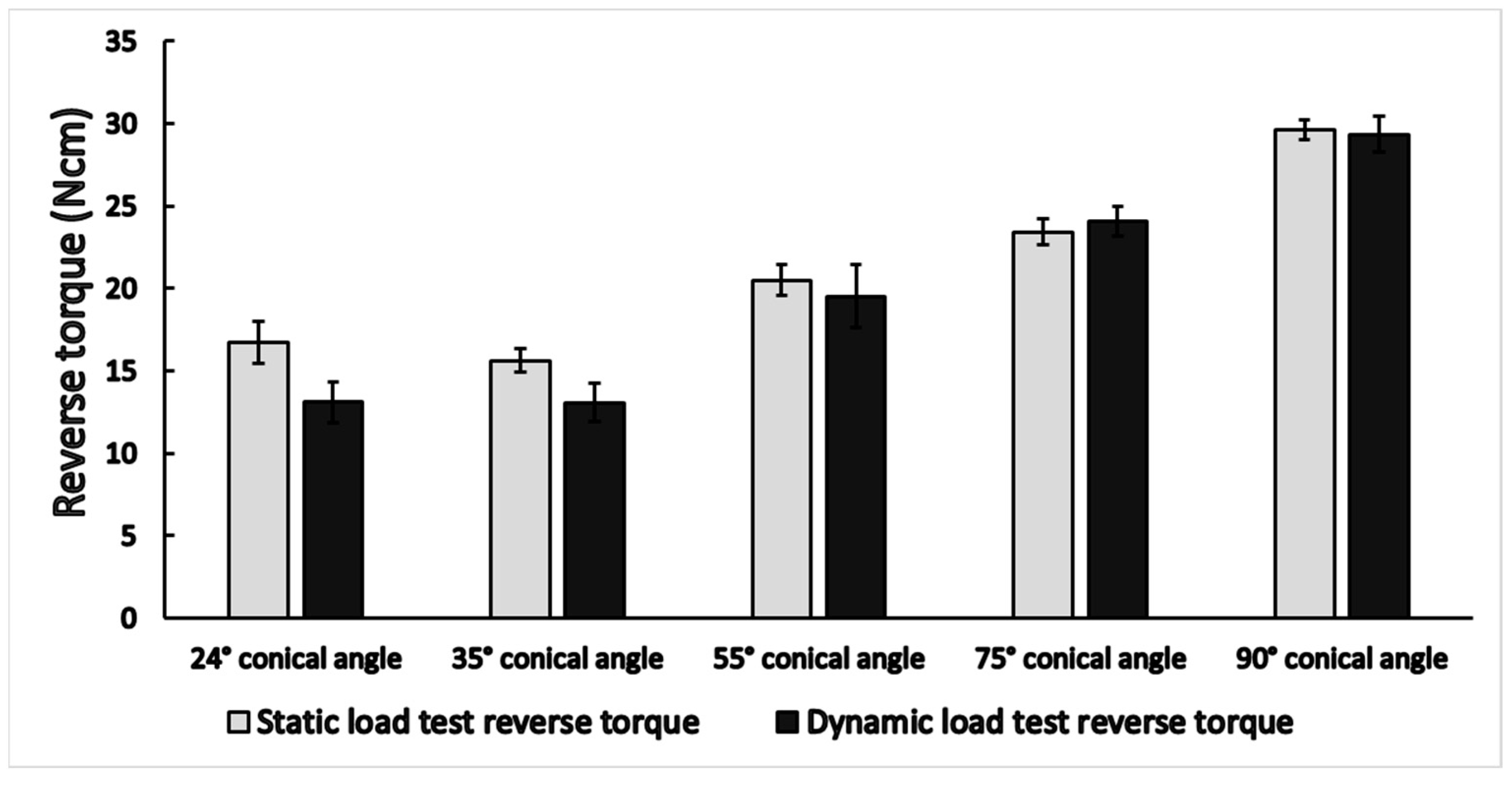
3.1. Static Load Results
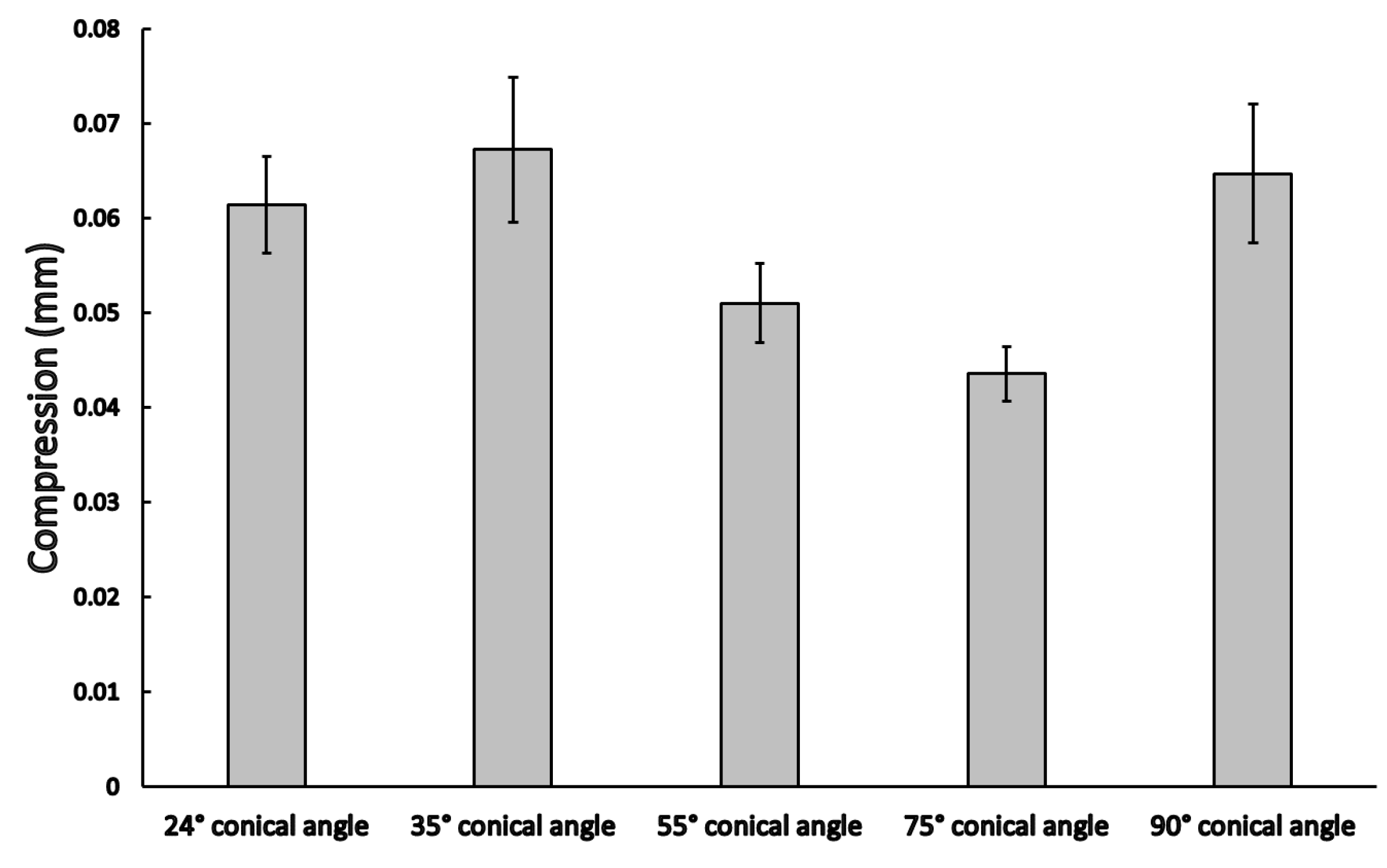
3.2. Dynamic Load Results
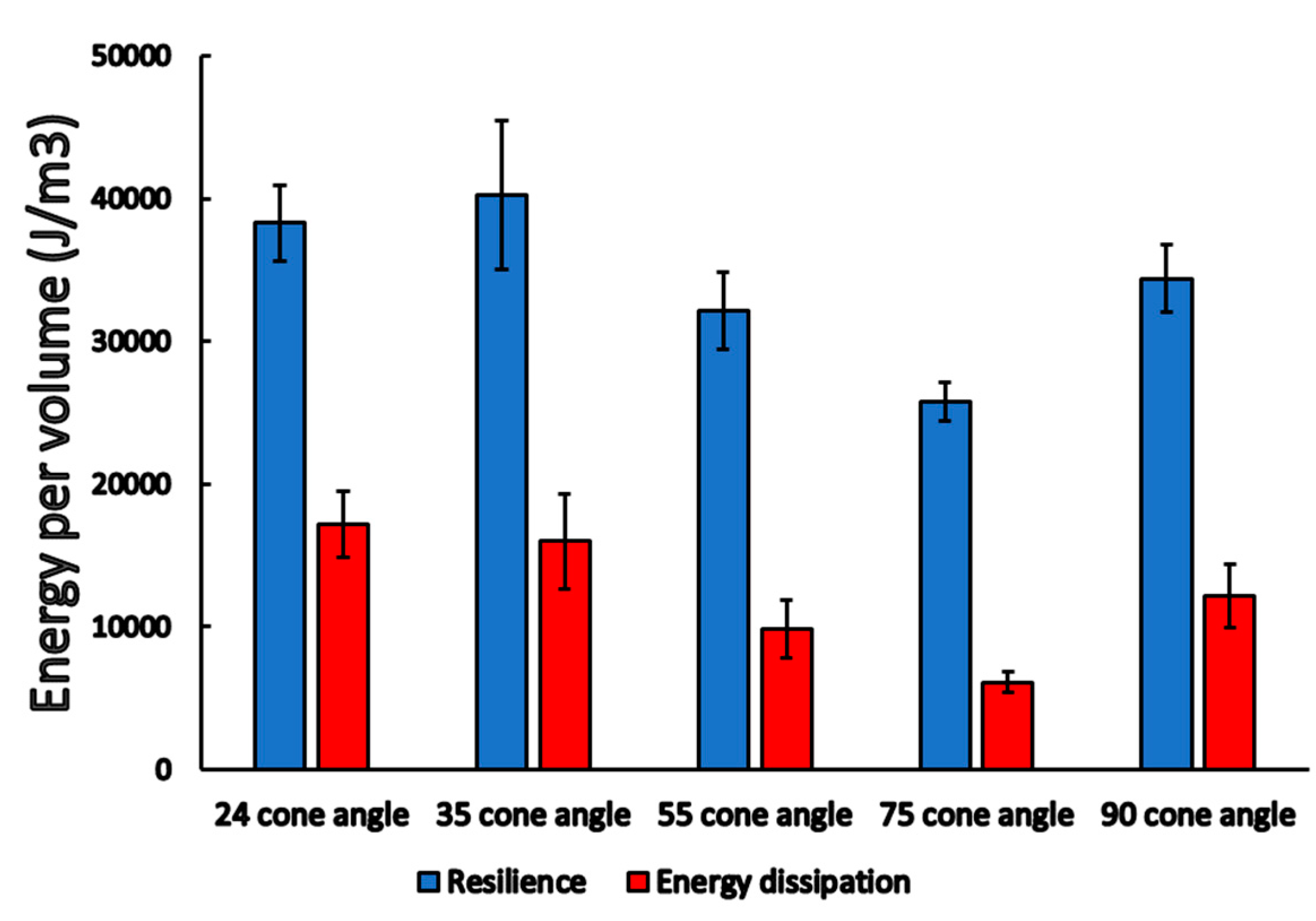
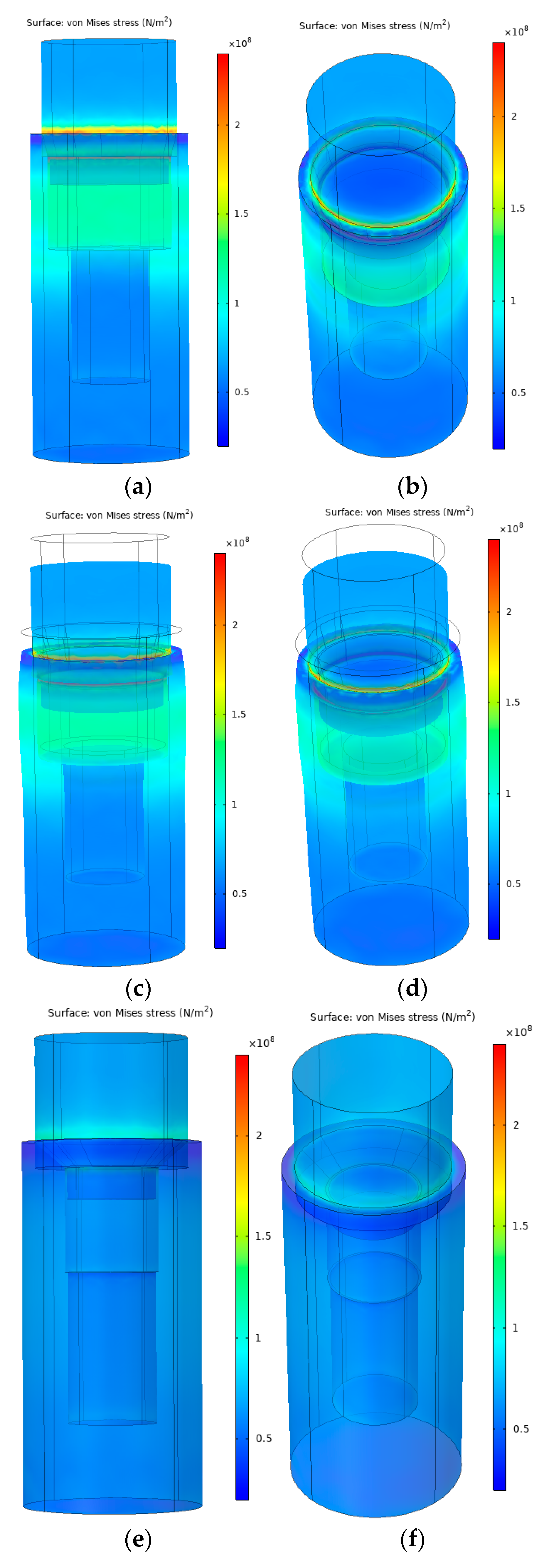
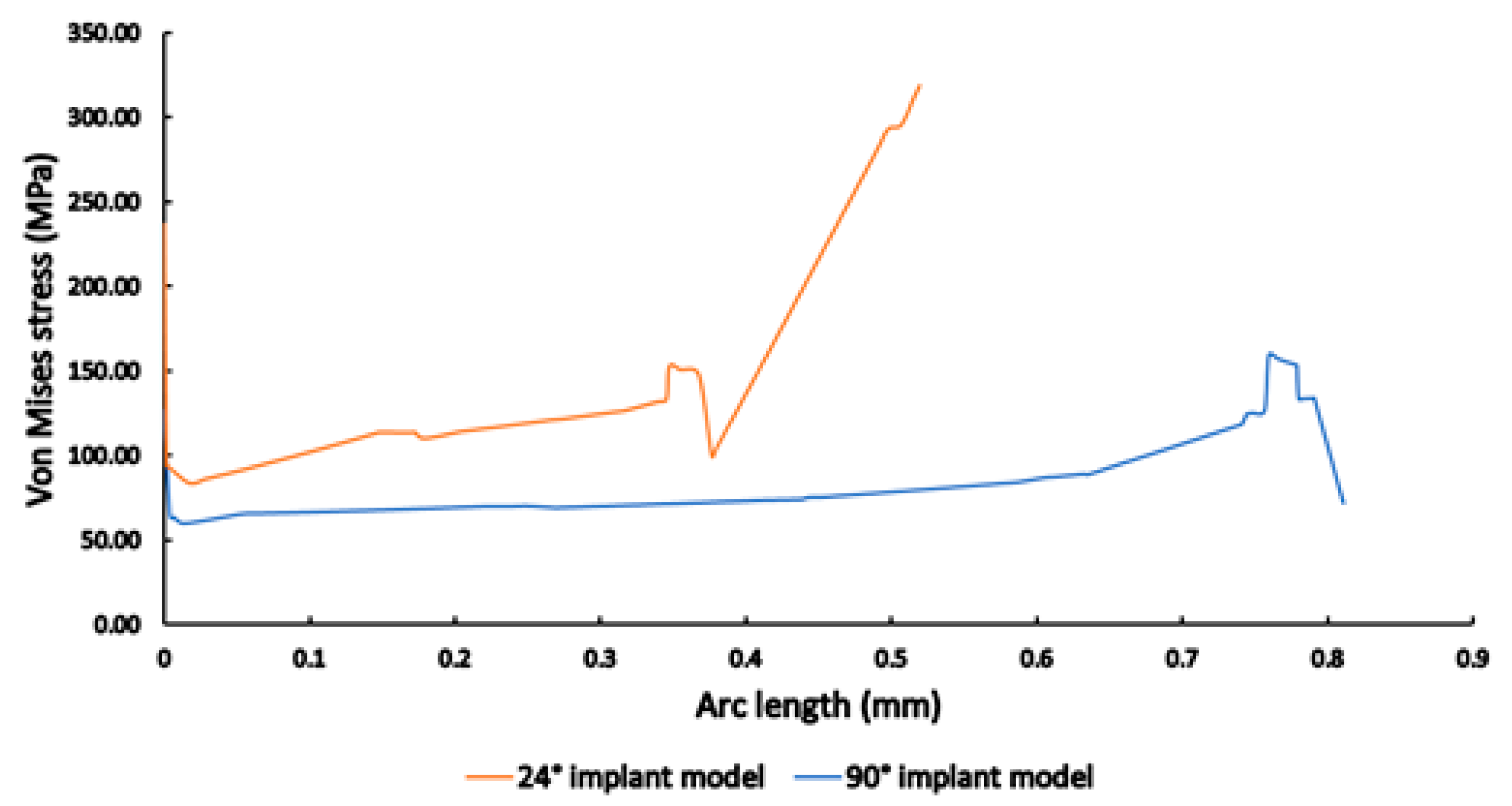
3.3. Finite Element Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haugen, H.J.; Chen, H. Is There a Better Biomaterial for Dental Implants than Titanium?—A Review and Meta-Study Analysis. J. Funct. Biomater. 2022, 13, e46. [Google Scholar] [CrossRef] [PubMed]
- Pandey, C.; Rokaya, D.; Bhattarai, B.P. Contemporary Concepts in Osseointegration of Dental Implants: A Review. BioMed Res. Int. 2022, 2022, e6170452. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Gupta, H.; Tandan, A. Technical complications of implant-causes and management: A comprehensive review. Natl. J. Maxillofac. Surg. 2015, 6, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Velasco-Ortega, E.; Flichy-Fernández, A.; Punset, M.; Jiménez-Guerra, A.; Manero, J.M.; Gil, J. Fracture and Fatigue of Titanium Narrow Dental Implants: New Trends in Order to Improve the Mechanical Response. Materials 2019, 12, e3728. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zarb, G.A.; Schmitt, A. The longitudinal clinical effectiveness of osseointegrated dental implants: The Toronto study. Part III. Problems and complication encountered. J. Prosthet. Dent. 1990, 64, 185–194. [Google Scholar] [CrossRef] [PubMed]
- Vigolo, P.; Fonzi, F.; Majzoub, Z.; Cordioli, G. An in vitro evaluation of titanium, zirconia, and alumina procera abutments with hexagonal connection. Int. J. Oral. Maxillofac. Implant. 2006, 21, 575–580. [Google Scholar]
- Khraisat, A.; Stegaroiu, R.; Nomura, S.; Miyakawa, O. Fatigue resistance of two implant/abutment joint designs. J. Prosthet. Dent. 2002, 88, 604–610. [Google Scholar] [CrossRef] [PubMed]
- Leutert, C.R.; Stawarczyk, B.; Truninger, T.C.; Hämmerle, C.H.; Sailer, I. Bending moments and types of failure of zirconia and titanium abutments with internal implant-abutment connections: A laboratory study. Int. J. Oral Maxillofac. Implant. 2012, 27, 505–512. [Google Scholar]
- Binon, P.P. Implants and components: Entering the new millennium. Int. J. Oral Maxillofac. Implant. 2000, 15, 76–94. [Google Scholar]
- Gracis, S.; Michalakis, K.; Vigolo, P.; von Steyern, V.P.; Zwahlen, M.; Sailer, I. Internal vs. external connections for abutments/reconstructions: A systematic review. Clin. Oral Implant. Res. 2012, 23, 202–216. [Google Scholar] [CrossRef]
- de Moraes, D.S.L.; Verri, F.R.; Santiago, J.J.F.; Almeida, D.A.F.; Lemos, C.A.A.; Gomes, J.M.L.; Pellizzer, E.P. Three-Dimensional Finite Element Analysis of Varying Diameter and Connection Type in Implants with High Crown-Implant Ratio. Braz. Dent. J. 2018, 29, 36–42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Merz, B.R.; Hunenbart, S.; Belser, U.C. Mechanics of the implant-abutment connection: An 8-degree taper compared to a butt joint connection. Int. J. Oral Maxillofac. Implant. 2000, 15, 19–26. [Google Scholar]
- Kuang-Ta, Y.; Kao, H.; Cheng, C.K.; Fang, H.W.; Hsu, M.L. Mechanical performance of conical implant-abutment connections under different cyclic loading conditions. J. Mech. Behav. Biomed. Mater. 2019, 90, 426–432. [Google Scholar]
- Hsien-Ching, H.; Chiung-Shing, H.; Yu-Hwa, P. The compressive strength of implant-abutment complex with different connection designs. J. Dent. Sci. 2019, 14, 318–324. [Google Scholar]
- Alikhasi, M.; Monzavi, A.; Bassir, S.H.; Naini, R.B.; Khosronedjad, N.; Keshavarz, S. A comparison of precision of fit, rotational freedom, and torque loss with copy-milled zirconia and pre- fabricated titanium abutments. Int. J. Oral Maxillofac. Implant. 2013, 28, 996–1002. [Google Scholar] [CrossRef]
- Vinhas, A.S.; Aroso, C.; Salazar, F.; López-Jarana, P.; Ríos-Santos, J.V.; Herrero-Climent, M. Review of the Mechanical Behavior of Different Implant-Abutment Connections. Int. J. Environ. Res. Public Health 2020, 17, 8685. [Google Scholar] [CrossRef]
- Ricomini, F.A.P.; Fernandes, F.S.F.; Straioto, F.G.; da Siva, J.W.; Cury, D.A.A. Preload Loss and Bacterial Penetration on Different Implant-Abutment Connection Systems. Braz. Dent. J. 2010, 21, 123–129. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Wang, J. Mechanism of and factors associated with the loosening of the implant abutment screw: A review. J. Esthet. Restor. Dent. 2019, 31, 338–345. [Google Scholar] [CrossRef] [PubMed]
- Alsubaiy, E.F. Abutment screw loosening in implants: A literature review. J. Family Med. Prim. Care 2020, 9, 5490–5494. [Google Scholar] [CrossRef] [PubMed]
- Hyon-Woo, S.; Seong-Joo, H.; Jai-Young, K.; Seong-Kyun, K.; Shin-Koo, K. Axial Displacement of External and Internal Implant-Abutment Connection Evaluated by Linear Mixed Model Analysis. Int. J. Oral Maxillofac. Implant. 2015, 30, 1387–1399. [Google Scholar]
- Germán, R.S.; Ortiz, M.M.; Sánchez, P.R.; Zavala, N.A.; Romo, G.F.R. Analysis of the Mechanical Behavior and Effect of Cyclic Fatigue on the Implant-Abutment Interface. Odovtos Int. J. Dent. Sci. 2021, 23, 104–114. [Google Scholar]
- Chu, C.M.; Huang, H.L.; Hsu, J.T.; Fuh, L.J. Influences of internal tapered abutment designs on bone stresses around a dental implant: Three-dimensional finite element method with statistical evaluation. J. Periodontol. 2012, 83, 111–118. [Google Scholar] [CrossRef]
- Caricasulo, R.; Malchiodi, L.; Ghensi, P.; Fantozzi, G.; Cucchi, A. The influence of implant-abutment connection to peri-implant bone loss: A systematic review and meta-analysis. Clin. Implant Dent. Relat. Res. 2018, 20, 653–664. [Google Scholar] [CrossRef] [PubMed]
- Chrcanovic, B.R.; Albrektsson, T.; Wennerberg, A. Platform switch and dental implants: A meta-analysis. J. Dent. 2015, 43, 629–646. [Google Scholar] [CrossRef] [PubMed]
- Schiegnitz, E.; Al-Nawas, B. Narrow-diameter implants: A systematic review and meta-analysis. Clin. Oral Impl. Res. 2018, 29, 21–40. [Google Scholar] [CrossRef] [Green Version]
- Sasada, Y.; Cochran, D.L. Implant-Abutment Connections. A Review of Biologic Consequences and Peri-implantitis Implications. Int. J. Oral Maxillofac. Implant. 2017, 32, 1296–1307. [Google Scholar] [CrossRef] [Green Version]
- Al-Nsour, M.M.; Hsun-Liang, C.; Hom-Lay, W. Effect of the Platform-Switching Technique on Preservation of Peri-implant Marginal Bone: A Systematic Review. Int. J. Oral Maxillofac. Implant. 2012, 27, 138–145. [Google Scholar]
- Cumbo, C.; Marigo, L.; Somma, F.; La Torre, G.; Minciacchi, I.; D’Addona, A. Implant platform switching concept: A literature review. Eur. Rev. Med. Pharmacol. Sci. 2013, 17, 392–397. [Google Scholar]
- Lazzara, R.J.; Porter, S.S. Platform switching: A new concept in implant dentistry for controlling postrestorative crestal bone levels. Int. J. Periodontics Restor. Dent. 2006, 26, 9–17. [Google Scholar]
- Moon, I.S.; Berglundh, T.; Abrahamsson, I.; Linder, E.; Lindhe, J. The barrier between the keratinized mucosa and the dental implant. An experimental study in the dog. J. Clin. Periodontol. 1999, 26, 658–663. [Google Scholar] [CrossRef]
- Elleuch, S.; Jrad, H.; Kessentini, A.; Wali, M.; Dammak, F. Design optimization of implant geometrical characteristics enhancing primary stability using FEA of stress distribution around dental prosthesis. Comp. Methods Biomech. Biomed. Eng. 2021, 24, 1035–1051. [Google Scholar] [CrossRef] [PubMed]
- Camps-Font, O.; Rubianes-Porta, L.; Valmaseda-Castellón, E.; Jung, R.E.; Gay-Escoda, C.; Figueiredo, R. Comparison of external, internal flat-to-flat, and conical implant abutment connections for implant-supported prostheses: A systematic review and network meta-analysis of randomized clinical trials. J. Prosthet. Dent. 2021. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, V.V.M.; Faé, D.S.; Rosa, C.D.D.R.D.; Bento, V.A.A.; Lacerda, M.F.L.S.; Pellizzer, E.P.; Lemos, C.A.A. Is the clinical performance of internal conical connection better than internal non-conical connection for implant-supported restorations? A systematic review with meta-analysis of randomized controlled trials. J. Prosthodont. 2023. [Google Scholar] [CrossRef] [PubMed]
- Santonocito, D.; Nicita, F.; Risitano, G. A Parametric Study on a Dental Implant Geometry Influence on Bone Remodelling through a Numerical Algorithm. Prothesis 2021, 3, 157–172. [Google Scholar] [CrossRef]
- Tu, M.G.; Hsu, J.T.; Fuh, L.J.; Lin, D.J.; Huang, H.L. Effects of cortical bone thickness and implant length on bone strain and interfacial micromotion in an immediately loaded implant. Int. J. Oral. Maxillofac. Implant. 2010, 25, 706–714. [Google Scholar]
- Beviacqua, M.; Tealdo, T.; Menini, M.; Mossolov, A.; Drago, C.; Pera, P. The influence of cantilever length and implant inclination on stress distribution in maxillary implant-supported fixed dentures. J. Prosthetic. Dent. 2011, 105, 5–13. [Google Scholar] [CrossRef]
- Xia, D.; Lin, H.; Yuan, S.; Bai, W.; Zheng, G. Dynamic Fatigue Performance of Implant-abutment Assemblies with Different Tightening Torque Values. Biomed. Mater. Eng. 2014, 24, 2143–2146. [Google Scholar] [CrossRef] [Green Version]
- Han, J.; Ma, Q. Finite Element Analysis of Geotechnical Excavation Based on COMSOL Multiphysics. IOP Conf. Ser. Mater. Sci. Eng. 2019, 592, e012060. [Google Scholar] [CrossRef] [Green Version]
- Dawit-Bogale, A.; Jeng, Y.R. Three-dimensional finite element investigation into effects of implant thread design and loading rate on stress distribution in dental implants and anisotropic bone. Materials 2021, 14, 6974. [Google Scholar]
- da Rocha, S.S.; Adabo, G.L.; Henriques, G.E.P.; Nóbilo, M.A.A. Vickers Hardness of Cast Commercially Pure Titanium and Ti-6Al-4V Alloy Submitted to Heat Treatments. Braz. Dent. J. 2006, 17, 126–129. [Google Scholar] [CrossRef]
- González-Carrasco, J.L. Metals as bone repair materials. In Bone Repair Biomaterials: Regeneration and Clinical Applications, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 154–193. [Google Scholar]
- Di Fiore, A.; Montagner, M.; Sivolella, S.; Stellini, E.; Yilmaz, B.; Brunello, G. Peri-Implant Bone Loss and Overload: A Systematic Review Focusing on Occlusal Analysis through Digital and Analogic Methods. J. Clin. Med. 2022, 11, 4812. [Google Scholar] [CrossRef] [PubMed]
- Karl, M.; Taylor, T.D. Parameters determining micromotion at the implant-abutment interface. Int. J. Oral Maxillofac. Implant. 2014, 29, 1338–1347. [Google Scholar] [CrossRef] [Green Version]
- Boyer, R.; Welsch, G.; Collings, E.W. (Eds.) Materials Properties Handbook: Titanium Alloys; ASM International: Novelty, OH, USA, 1998. [Google Scholar]
- Zhao, W.; Xie, Z.; Li, X.; Yue, X.; Sun, J. Compression after impact behavior of titanium honeycomb sandwich structures. J. Sandw. Struct. Mat. 2017, 20, e1099636217707150. [Google Scholar] [CrossRef]
- Bertolini, M.M.; Cury, B.A.A.; Pizzoloto, L.; Acapa, I.R.H.; Shibli, J.A.; Bordin, D. Does traumatic occlusal forces lead to peri-implant bone loss? A systematic review. Braz. Oral Res. 2019, 33, e069. [Google Scholar] [CrossRef] [Green Version]
- Mihalko, W.M.; May, T.C.; Kay, J.F.; Krause, W.R. Finite element analysis of interface geometry effects on the crestal bone surrounding a dental implant. Implant Dent. 1992, 1, 212–217. [Google Scholar] [CrossRef] [PubMed]
- Chamay, A.; Tschantz, P. Mechanical influences in bone remodeling. Experimental research on Wolff’s law. J. Biomech. 1972, 5, 173–180. [Google Scholar] [CrossRef] [PubMed]
- Fung, Y.C. Biomechanics, Mechanical Properties of Living Tissues; Springer: New York, NY, USA, 1981; pp. 383–415. [Google Scholar]
- Nagy, Á.L.; Tóth, Z.; Tarjányi, T.; Práger, N.T.; Baráth, Z.L. Biomechanical properties of the bone during implant placement. BMC Oral Health 2021, 21, e86. [Google Scholar] [CrossRef]
- Tyagi, R.; Kumar, S.; Aggarwal, R.; Choudhary, S.; Malethia, A.; Saini, N. A 3-D Finite Element Analysis of Stress Distribution on Implant-supported Fixed Prosthesis with Four Different Commercially Available Implant Systems. J. Contemp. Dent. Pract. 2020, 21, 835–840. [Google Scholar]
- Dinc, M.M.; Turkoglu, P.; Selvi, F. Biomechanical evaluation of stress distributions at the implant-abutment complex and peri-implant bone around mandibular dental implants with different neck geometries and inclinations. Proc. Inst. Mech. Eng. H 2021, 235, 1035–1045. [Google Scholar] [CrossRef]
- Baggi, L.; Cappelloni, I.; Di Girolamo, M.; Maceri, F.; Vairo, G. The influence of implant diameter and length on stress distribution of osseointegrated implants related to crestal bone geometry: A three-dimensional finite element analysis. J. Prosthet. Dent. 2008, 100, 422–431. [Google Scholar] [CrossRef] [Green Version]
- Paepoemsin, T.; Reichart, P.A.; Chaijareenont, P.; Strietzel, F.P.; Khongkhunthian, P. Removal torque evaluation of three different abutment screws for single implant restorations after mechanical cyclic loading. Oral Implantol. 2016, 9, 213–221. [Google Scholar]
- Benjaboonyazit, K.; Chaijareenont, P.; Khongkhunthian, P. Removal torque pattern of a combined cone and octalobule index implant-abutment connection at different cyclic loading: An in-vitro experimental study. Int. J. Implant. Dent. 2019, 5, 1. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Cha, H.S. Screw loosening and changes in removal torque relative to abutment screw length in a dental implant with external abutment connection after oblique cyclic loading. J. Adv. Prosthodont. 2018, 10, 415–421. [Google Scholar] [CrossRef] [Green Version]
- Nugala, B.; Kumar, B.B.S.; Sahitya, S.; Krishna, P.M. Biologic width and its importance in periodontal and restorative dentistry. J. Conserv. Dent. 2012, 15, 12–17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hang, J.T.; Kang, Y.; Xu, G.K.; Gao, H. A hierarchical cellular structural model to unravel the universal power-law rheological behavior of living cells. Nat. Commun. 2021, 12, e6067. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Hang, J.T.; Chang, Z.; Xu, G.K. Static and dynamic mechanics of cell monolayers: A multi-scale structural model. Acta Mech. Sin. 2022, 38, e222006. [Google Scholar] [CrossRef]






| 24° | 35° | 55° | 75° | 90° | |
|---|---|---|---|---|---|
| 24° | - | 0.721 | 0.030 | 0.002 | 0.145 |
| 35° | 0.666 | - | 0.065 | 0.004 | 0.260 |
| 55° | 0.174 | 0.077 | - | 0.250 | 0.493 |
| 75° | 0.008 | 0.003 | 0.159 | - | 0.079 |
| 90° | 0.404 | 0.215 | 0.626 | 0.070 | - |
| 24° | 35° | 55° | 75° | 90° | |
|---|---|---|---|---|---|
| 24° | - | ||||
| 35° | 0.234 | - | |||
| 55° | 0.204 | 0.932 | - | ||
| 75° | 0.141 | 0.011 | 0.009 | - | |
| 90° | 0.490 | 0.065 | 0.055 | 0.422 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Körtvélyessy, G.; Szabó, Á.L.; Pelsőczi-Kovács, I.; Tarjányi, T.; Tóth, Z.; Kárpáti, K.; Matusovits, D.; Hangyási, B.D.; Baráth, Z. Different Conical Angle Connection of Implant and Abutment Behavior: A Static and Dynamic Load Test and Finite Element Analysis Study. Materials 2023, 16, 1988. https://doi.org/10.3390/ma16051988
Körtvélyessy G, Szabó ÁL, Pelsőczi-Kovács I, Tarjányi T, Tóth Z, Kárpáti K, Matusovits D, Hangyási BD, Baráth Z. Different Conical Angle Connection of Implant and Abutment Behavior: A Static and Dynamic Load Test and Finite Element Analysis Study. Materials. 2023; 16(5):1988. https://doi.org/10.3390/ma16051988
Chicago/Turabian StyleKörtvélyessy, Győző, Árpád László Szabó, István Pelsőczi-Kovács, Tamás Tarjányi, Zsolt Tóth, Krisztina Kárpáti, Danica Matusovits, Botond Dávid Hangyási, and Zoltán Baráth. 2023. "Different Conical Angle Connection of Implant and Abutment Behavior: A Static and Dynamic Load Test and Finite Element Analysis Study" Materials 16, no. 5: 1988. https://doi.org/10.3390/ma16051988
APA StyleKörtvélyessy, G., Szabó, Á. L., Pelsőczi-Kovács, I., Tarjányi, T., Tóth, Z., Kárpáti, K., Matusovits, D., Hangyási, B. D., & Baráth, Z. (2023). Different Conical Angle Connection of Implant and Abutment Behavior: A Static and Dynamic Load Test and Finite Element Analysis Study. Materials, 16(5), 1988. https://doi.org/10.3390/ma16051988







