A Fast Design Method of Anisotropic Dielectric Lens for Vortex Electromagnetic Wave Based on Deep Learning
Abstract
1. Introduction
2. Deep Learning Neural Network Establishment and Training
3. Reverse Design
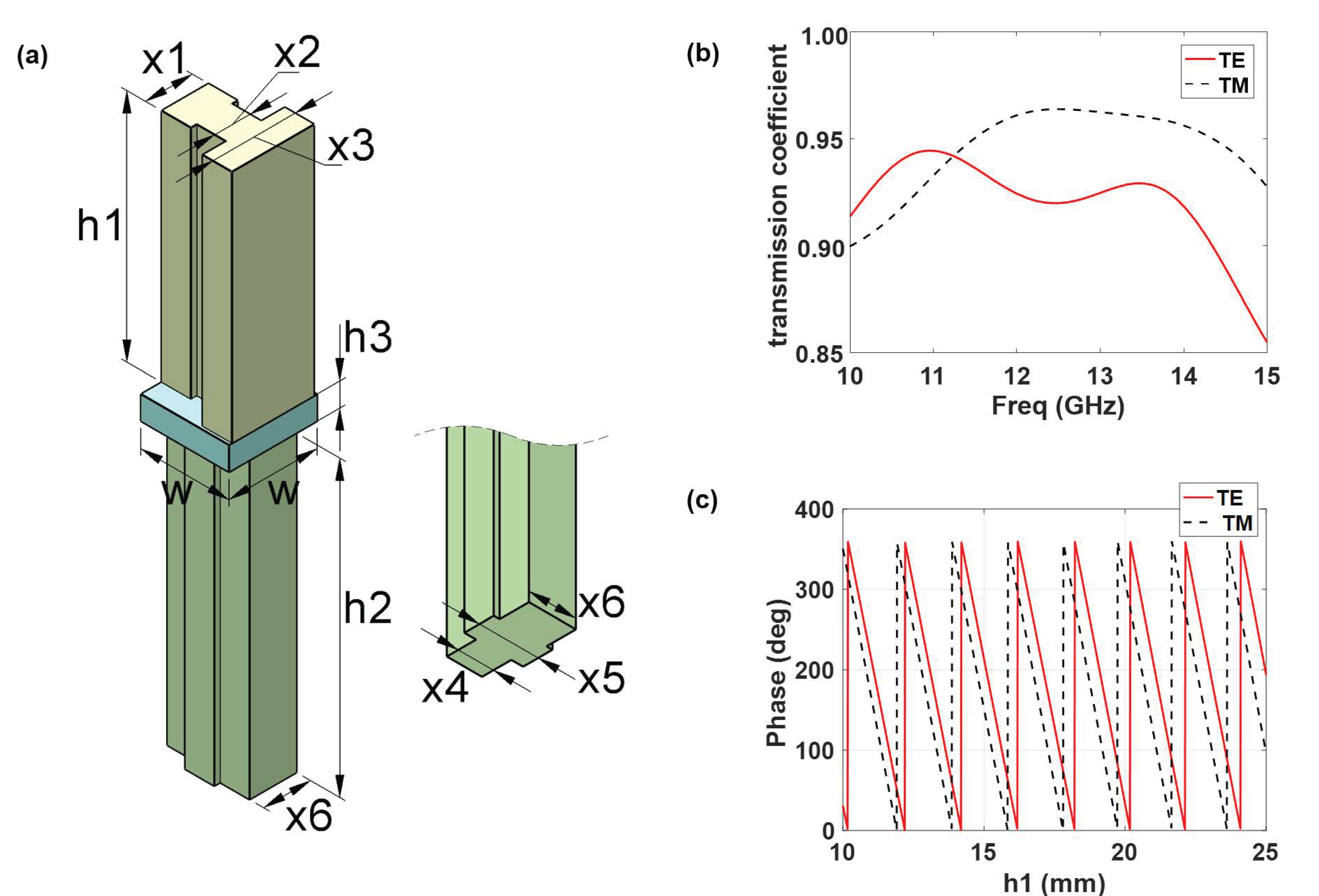
3.1. Design Method
3.2. Model 1
3.3. Model 2
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thidé, B.; Then, H.; Sjöholm, J.; Palmer, K.; Bergman, J.; Carozzi, T.; Istomin, Y.N.; Ibragimov, N.; Khamitova, R. Utilization of photon orbital angular momentum in the low-frequency radio domain. Phys. Rev. Lett. 2007, 99, 087701. [Google Scholar] [CrossRef] [PubMed]
- Padgett, M.J. Orbital angular momentum 25 years on. Opt. Express 2017, 25, 11265–11274. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, S.M.; Daldorff, L.K.; Bergman, J.E.; Karlsson, R.L.; Thidé, B.; Forozesh, K.; Carozzi, T.D.; Isham, B. Orbital angular momentum in radio—A system study. IEEE Trans. Antennas Propag. 2009, 58, 565–572. [Google Scholar] [CrossRef]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef]
- O’neil, A.; MacVicar, I.; Allen, L.; Padgett, M. Intrinsic and extrinsic nature of the orbital angular momentum of a light beam. Phys. Rev. Lett. 2002, 88, 053601. [Google Scholar] [CrossRef]
- Chen, R.; Zhou, H.; Moretti, M.; Wang, X.; Li, J. Orbital angular momentum waves: Generation, detection, and emerging applications. IEEE Commun. Surv. Tutor. 2019, 22, 840–868. [Google Scholar] [CrossRef]
- Li, L.; Li, F. Beating the Rayleigh limit: Orbital-angular-momentum-based super-resolution diffraction tomography. Phys. Rev. E 2013, 88, 033205. [Google Scholar] [CrossRef]
- Liu, H.; Cheng, Y.; Qin, Y.; Yuan, T.; Liu, K. Electromagnetic vortex carrying orbital angular momentum in radar imaging. In Proceedings of the Eighth International Conference on Digital Image Processing (ICDIP 2016), Chengdou, China, 20–22 May 2016; International Society for Optics and Photonics: Bellingham, WA, USA; p. 100333L. [Google Scholar]
- Liang, B.; Shen, F.; Wang, S.M.; Zhou, Y.; Yang, Y.; Cheng, K.; Zhang, G.; Zheng, Y.; Liu, Q.H.; Gong, Y. Reconstruction of three-dimensional objects in layered composite structures from multimode orbital angular momentum. Phys. Rev. E 2022, 105, 025302. [Google Scholar] [CrossRef]
- Mahmouli, F.E.; Walker, S. Orbital angular momentum generation in a 60GHz wireless radio channel. In Proceedings of the 20th Telecommunications Forum (TELFOR), Belgrade, Serbia, 22 November 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 315–318. [Google Scholar]
- Wang, J.; Yang, J.-Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Zhu, L.; Wei, X.; Wang, J.; Zhang, Z.; Li, Z.; Zhang, H.; Li, S.; Wang, K.; Liu, J. Experimental demonstration of basic functionalities for 0.1-THz orbital angular momentum (OAM) communications. In Proceedings of the OFC 2014, San Francisco, CA, USA, 9–13 March 2014; IEEE: Piscataway, NJ, USA; pp. 1–3. [Google Scholar]
- Yan, Y.; Xie, G.; Lavery, M.P.; Huang, H.; Ahmed, N.; Bao, C.; Ren, Y.; Cao, Y.; Li, L.; Zhao, Z. High-capacity millimetre-wave communications with orbital angular momentum multiplexing. Nat. Commun. 2014, 5, 4876. [Google Scholar] [CrossRef]
- Mari, E.; Spinello, F.; Oldoni, M.; Ravanelli, R.A.; Romanato, F.; Parisi, G. Near-field experimental verification of separation of OAM channels. IEEE Antennas Wirel. Propag. Lett. 2014, 14, 556–558. [Google Scholar] [CrossRef]
- Tamburini, F.; Mari, E.; Sponselli, A.; Thidé, B.; Bianchini, A.; Romanato, F. Encoding many channels on the same frequency through radio vorticity: First experimental test. New J. Phys. 2012, 14, 033001. [Google Scholar] [CrossRef]
- Lin, M.; Gao, Y.; Liu, P.; Liu, J. Theoretical analyses and design of circular array to generate orbital angular momentum. IEEE Trans. Antennas Propag. 2017, 65, 3510–3519. [Google Scholar] [CrossRef]
- Stegenburgs, E.; Bertoncini, A.; Trichili, A.; Alias, M.S.; Ng, T.K.; Alouini, M.-S.; Liberale, C.; Ooi, B.S. Near-infrared OAM communication using 3D-printed microscale spiral phase plates. IEEE Commun. Mag. 2019, 57, 65–69. [Google Scholar] [CrossRef]
- Isakov, D.; Wu, Y.; Allen, B.; Grant, P.; Stevens, C.; Gibbons, G. Evaluation of the Laguerre–Gaussian mode purity produced by three-dimensional-printed microwave spiral phase plates. R. Soc. Open Sci. 2020, 7, 200493. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.L.; Jiang, L.J.; Sha, W.E. Artificial perfect electric conductor-perfect magnetic conductor anisotropic metasurface for generating orbital angular momentum of microwave with nearly perfect conversion efficiency. J. Appl. Phys. 2016, 119, 064506. [Google Scholar] [CrossRef]
- Chen, M.L.; Jiang, L.J.; Sha, W.E. Orbital angular momentum generation and detection by geometric-phase based metasurfaces. Appl. Sci. 2018, 8, 362. [Google Scholar] [CrossRef]
- Niederriter, R.D.; Siemens, M.E.; Gopinath, J.T. Simultaneous control of orbital angular momentum and beam profile in two-mode polarization-maintaining fiber. Opt. Lett. 2016, 41, 5736–5739. [Google Scholar] [CrossRef]
- Singh, S.; Bisharat, D.A.; Sievenpiper, D. Topological antennas: Aperture radiators, leaky-wave surfaces, and orbital angular momentum beam generation. J. Appl. Phys. 2021, 130, 023101. [Google Scholar] [CrossRef]
- Mudanyali, O.; Yildiz, S.; Semerci, O.; Yapar, A.; Akduman, I. A microwave tomographic approach for nondestructive testing of dielectric coated metallic surfaces. IEEE Geosci. Remote. Sens. Lett. 2008, 5, 180–184. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, Y.; McGloin, D.; Unnithan, R.R.; Li, S.; Liao, S.; Xue, Q. 3-D printed planar dielectric linear-to-circular polarization conversion and beam-shaping lenses using coding polarizer. IEEE Trans. Antennas Propag. 2020, 68, 4332–4343. [Google Scholar] [CrossRef]
- Wu, G.-B.; Chan, K.F.; Qu, S.-W.; Tong, K.F.; Chan, C.H. Orbital angular momentum (OAM) mode-reconfigurable discrete dielectric lens operating at 300 GHz. IEEE Trans. Terahertz Sci. Technol. 2020, 10, 480–489. [Google Scholar] [CrossRef]
- Qin, F.; Wan, L.; Li, L.; Zhang, H.; Wei, G.; Gao, S. A transmission metasurface for generating OAM beams. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1793–1796. [Google Scholar] [CrossRef]
- Guo, K.; Zheng, Q.; Yin, Z.; Guo, Z. Generation of mode-reconfigurable and frequency-adjustable OAM beams using dynamic reflective metasurface. IEEE Access 2020, 8, 75523–75529. [Google Scholar] [CrossRef]
- Yang, L.-J.; Sun, S.; Wei, E. Ultrawideband reflection-type metasurface for generating integer and fractional orbital angular momentum. IEEE Trans. Antennas Propag. 2019, 68, 2166–2175. [Google Scholar] [CrossRef]
- Lin, Z.; Ba, Z.; Wang, X. Broadband high-efficiency electromagnetic orbital angular momentum beam generation based on a dielectric metasurface. IEEE Photonics J. 2020, 12, 4600611. [Google Scholar] [CrossRef]
- Yoo, H.-J. Deep convolution neural networks in computer vision: A review. IEIE Trans. Smart Process. Comput. 2015, 4, 35–43. [Google Scholar] [CrossRef]
- Buhrmester, V.; Münch, D.; Arens, M. Analysis of explainers of black box deep neural networks for computer vision: A survey. Mach. Learn. Knowl. Extr. 2021, 3, 966–989. [Google Scholar] [CrossRef]
- Young, T.; Hazarika, D.; Poria, S.; Cambria, E. Recent trends in deep learning based natural language processing. IEEE Comput. Intell. Mag. 2018, 13, 55–75. [Google Scholar] [CrossRef]
- Otter, D.W.; Medina, J.R.; Kalita, J.K. A survey of the usages of deep learning for natural language processing. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 604–624. [Google Scholar] [CrossRef]
- Deng, L.; Hinton, G.; Kingsbury, B. New types of deep neural network learning for speech recognition and related applications: An overview. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 4–10 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 8599–8603. [Google Scholar]
- Zhang, Z.; Geiger, J.; Pohjalainen, J.; Mousa, A.E.-D.; Jin, W.; Schuller, B. Deep learning for environmentally robust speech recognition: An overview of recent developments. ACM Trans. Intell. Syst. Technol. (TIST) 2018, 9, 1–28. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, Y.; Wang, X.; Tang, X. Deep learning face representation by joint identification-verification. In Proceedings of the Advances in Neural Information Processing Systems 27, Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Alghaili, M.; Li, Z.; Ali, H.A. Facefilter: Face identification with deep learning and filter algorithm. Sci. Program. 2020, 2020, 7846264. [Google Scholar] [CrossRef]
- Shan, T.; Pan, X.; Li, M.; Xu, S.; Yang, F. Coding programmable metasurfaces based on deep learning techniques. IEEE J. Emerg. Sel. Top. Circuits Syst. 2020, 10, 114–125. [Google Scholar] [CrossRef]
- An, S.; Zheng, B.; Tang, H.; Shalaginov, M.Y.; Zhou, L.; Li, H.; Kang, M.; Richardson, K.A.; Gu, T.; Hu, J. Multifunctional metasurface design with a generative adversarial network. Adv. Opt. Mater. 2021, 9, 2001433. [Google Scholar] [CrossRef]
- An, S.; Zheng, B.; Shalaginov, M.Y.; Tang, H.; Li, H.; Zhou, L.; Ding, J.; Agarwal, A.M.; Rivero-Baleine, C.; Kang, M. A freeform dielectric metasurface modeling approach based on deep neural networks. arXiv 2020, arXiv:2001.00121. [Google Scholar]
- Zhang, Q.; Liu, C.; Wan, X.; Zhang, L.; Liu, S.; Yang, Y.; Cui, T.J. Machine-learning designs of anisotropic digital coding metasurfaces. Adv. Theory Simul. 2019, 2, 1800132. [Google Scholar] [CrossRef]
- Roberts, N.B.; Keshavarz Hedayati, M. A deep learning approach to the forward prediction and inverse design of plasmonic metasurface structural color. Appl. Phys. Lett. 2021, 119, 061101. [Google Scholar] [CrossRef]
- Jiang, L.; Li, X.; Wu, Q.; Wang, L.; Gao, L. Neural network enabled metasurface design for phase manipulation. Opt. Express 2021, 29, 2521–2528. [Google Scholar] [CrossRef]
- Ghorbani, F.; Beyraghi, S.; Shabanpour, J.; Oraizi, H.; Soleimani, H.; Soleimani, M. Deep neural network-based automatic metasurface design with a wide frequency range. Sci. Rep. 2021, 11, 7102. [Google Scholar] [CrossRef]
- Shi, X.; Qiu, T.; Wang, J.; Zhao, X.; Qu, S. Metasurface inverse design using machine learning approaches. J. Phys. Appl. Phys. 2020, 53, 275105. [Google Scholar] [CrossRef]
- Ho, Y.; Wookey, S. The real-world-weight cross-entropy loss function: Modeling the costs of mislabeling. IEEE Access 2019, 8, 4806–4813. [Google Scholar] [CrossRef]
- Nwankpa, C.; Ijomah, W.; Gachagan, A.; Marshall, S. Activation functions: Comparison of trends in practice and research for deep learning. arXiv 2018, arXiv:1811.03378. [Google Scholar]
- Xu, J.; Li, Z.; Du, B.; Zhang, M.; Liu, J. Reluplex made more practical: Leaky ReLU. In Proceedings of the 2020 IEEE Symposium on Computers and communications (ISCC), Rennes, France, 7–10 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–7. [Google Scholar]
- Wu, G.-B.; Chan, K.F.; Chan, C.H. 3-D printed terahertz lens to generate higher order Bessel beams carrying OAM. IEEE Trans. Antennas Propag. 2020, 69, 3399–3408. [Google Scholar] [CrossRef]
- Ran, Y.; Liang, J.; Cai, T.; Ji, W.; Wang, G. High-performance broadband vortex beam generator based on double-layered reflective metasurface. Aip Adv. 2018, 8, 095201. [Google Scholar] [CrossRef]
- Guan, L.; He, Z.; Ding, D.; Yu, Y.; Zhang, W.; Chen, R. Polarization-controlled shared-aperture metasurface for generating a vortex beam with different modes. IEEE Trans. Antennas Propag. 2018, 66, 7455–7459. [Google Scholar] [CrossRef]
- Kumar, A.; Pant, S.; Ram, M. System reliability optimization using gray wolf optimizer algorithm. Qual. Reliab. Eng. Int. 2017, 33, 1327–1335. [Google Scholar] [CrossRef]
- Purushothaman, R.; Rajagopalan, S.; Dhandapani, G. Hybridizing Gray Wolf Optimization (GWO) with Grasshopper Optimization Algorithm (GOA) for text feature selection and clustering. Appl. Soft Comput. 2020, 96, 106651. [Google Scholar] [CrossRef]






| Layer | Neurons | Activation Function |
|---|---|---|
| Input | 10 | – |
| Hidden layer 1 | 110 | Tanh |
| Hidden layer 2 | 100 | LeakyReLU |
| Hidden layer 3 | 90 | LeakyReLU |
| Hidden layer 4 | 80 | LeakyReLU |
| Hidden layer 5 | 70 | LeakyReLU |
| Hidden layer 6 | 60 | LeakyReLU |
| Hidden layer 7 | 50 | LeakyReLU |
| Hidden layer 8 | 40 | LeakyReLU |
| Hidden layer 9 | 360 | LeakyReLU |
| output | 360 | Tanh |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, B.; Zhang, Y.; Zhou, Y.; Liu, W.; Ni, T.; Wang, A.; Fan, Y. A Fast Design Method of Anisotropic Dielectric Lens for Vortex Electromagnetic Wave Based on Deep Learning. Materials 2023, 16, 2254. https://doi.org/10.3390/ma16062254
Liang B, Zhang Y, Zhou Y, Liu W, Ni T, Wang A, Fan Y. A Fast Design Method of Anisotropic Dielectric Lens for Vortex Electromagnetic Wave Based on Deep Learning. Materials. 2023; 16(6):2254. https://doi.org/10.3390/ma16062254
Chicago/Turabian StyleLiang, Bingyang, Yonghua Zhang, Yuanguo Zhou, Weiqiang Liu, Tao Ni, Anyi Wang, and Yanan Fan. 2023. "A Fast Design Method of Anisotropic Dielectric Lens for Vortex Electromagnetic Wave Based on Deep Learning" Materials 16, no. 6: 2254. https://doi.org/10.3390/ma16062254
APA StyleLiang, B., Zhang, Y., Zhou, Y., Liu, W., Ni, T., Wang, A., & Fan, Y. (2023). A Fast Design Method of Anisotropic Dielectric Lens for Vortex Electromagnetic Wave Based on Deep Learning. Materials, 16(6), 2254. https://doi.org/10.3390/ma16062254






