Vibration Analysis of Locally Resonant Beams with L-Joint Using an Exact Wave-Based Vibration Approach
Abstract
1. Introduction
Notation
2. Wave-Based Analysis Methodology
2.1. Overview
2.2. Propagation Matrix

2.3. Reflection at a Free Boundary
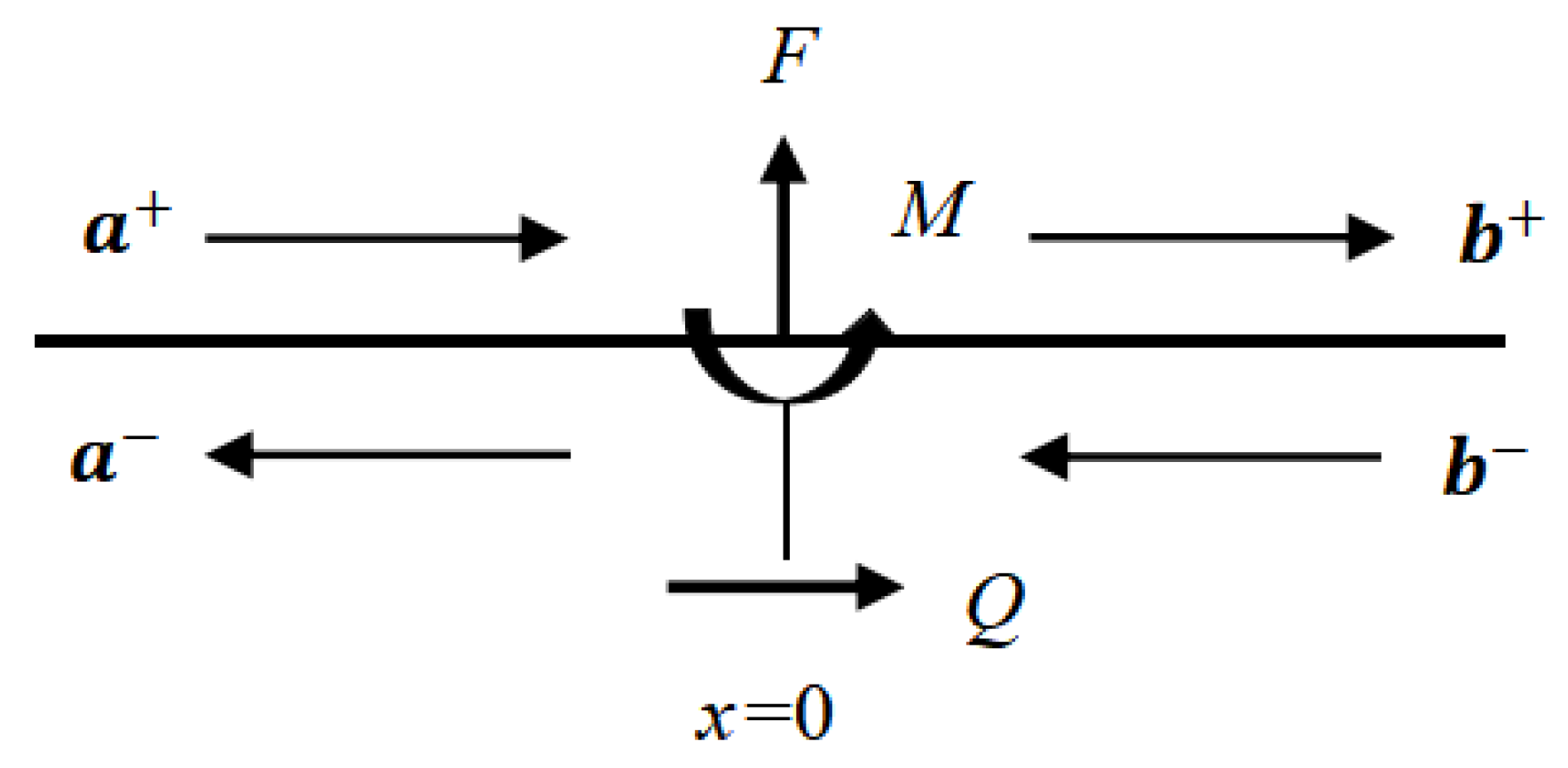
2.4. Applied Forces and Moments
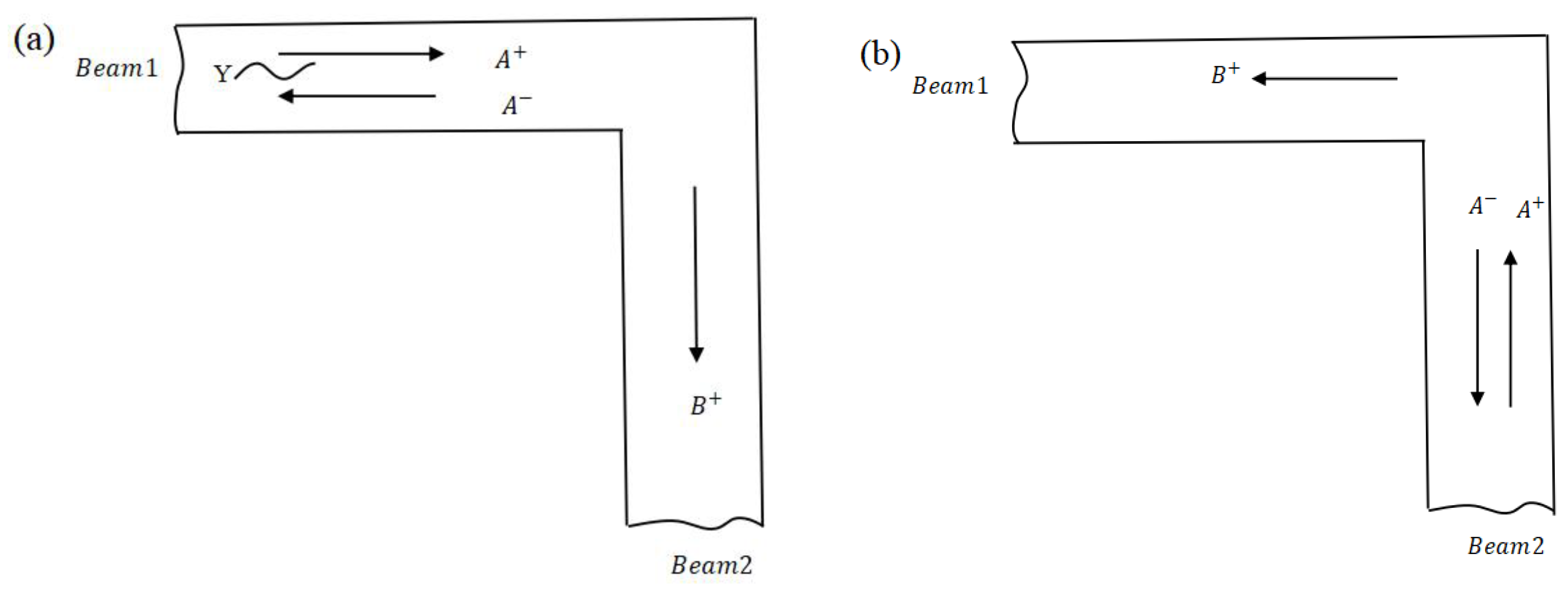
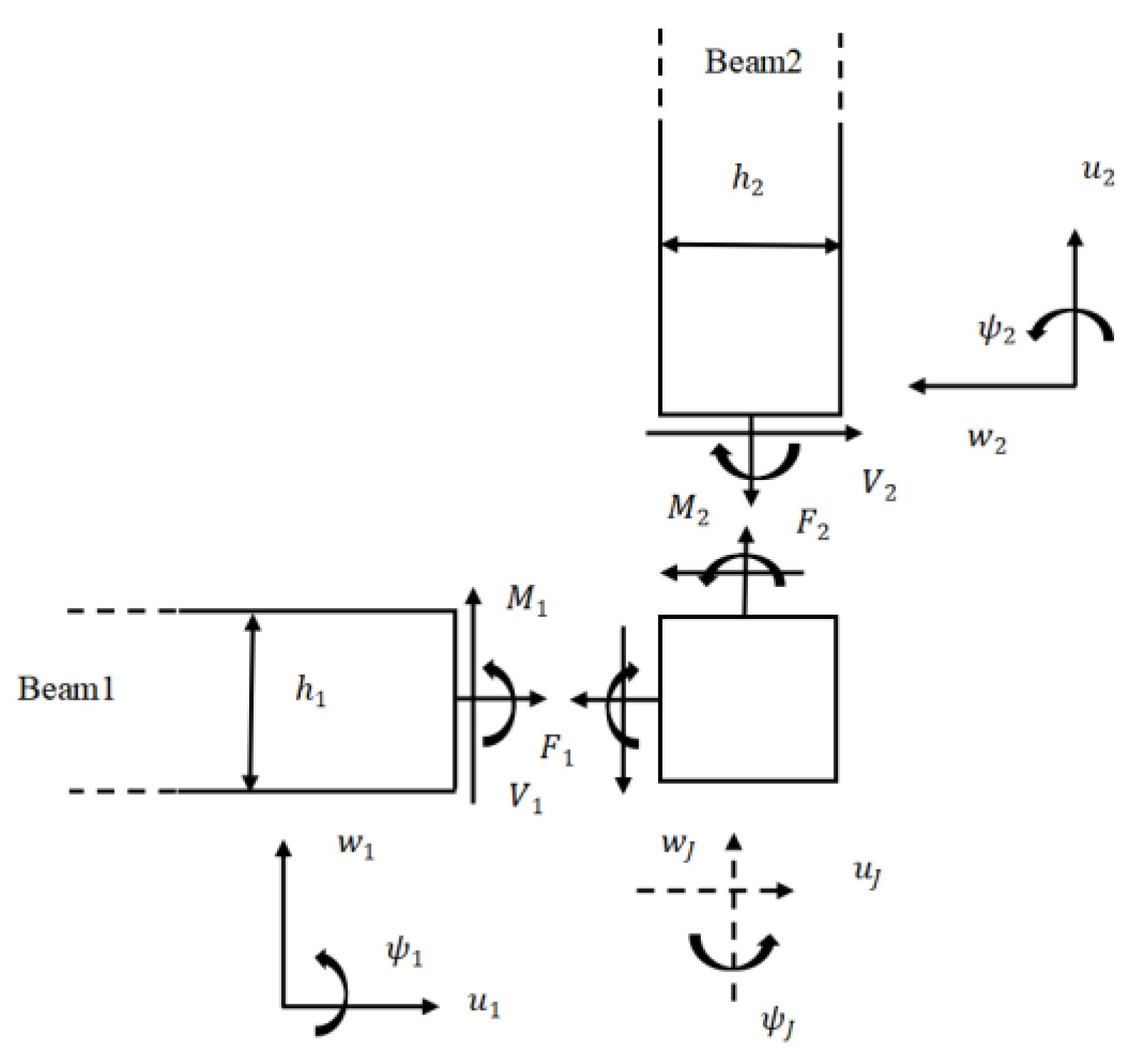
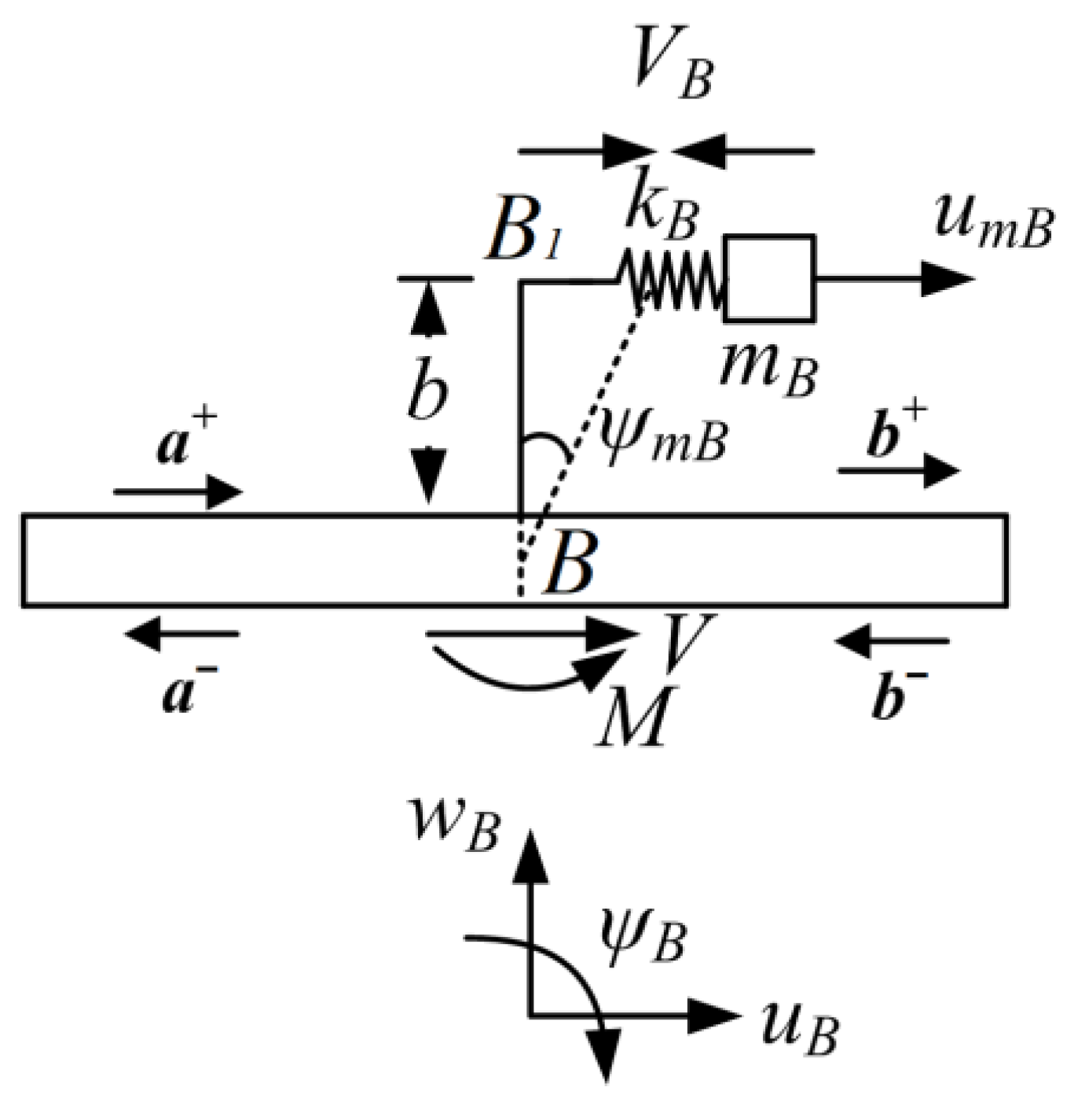
2.5. Transmission and Reflection at L-Joint
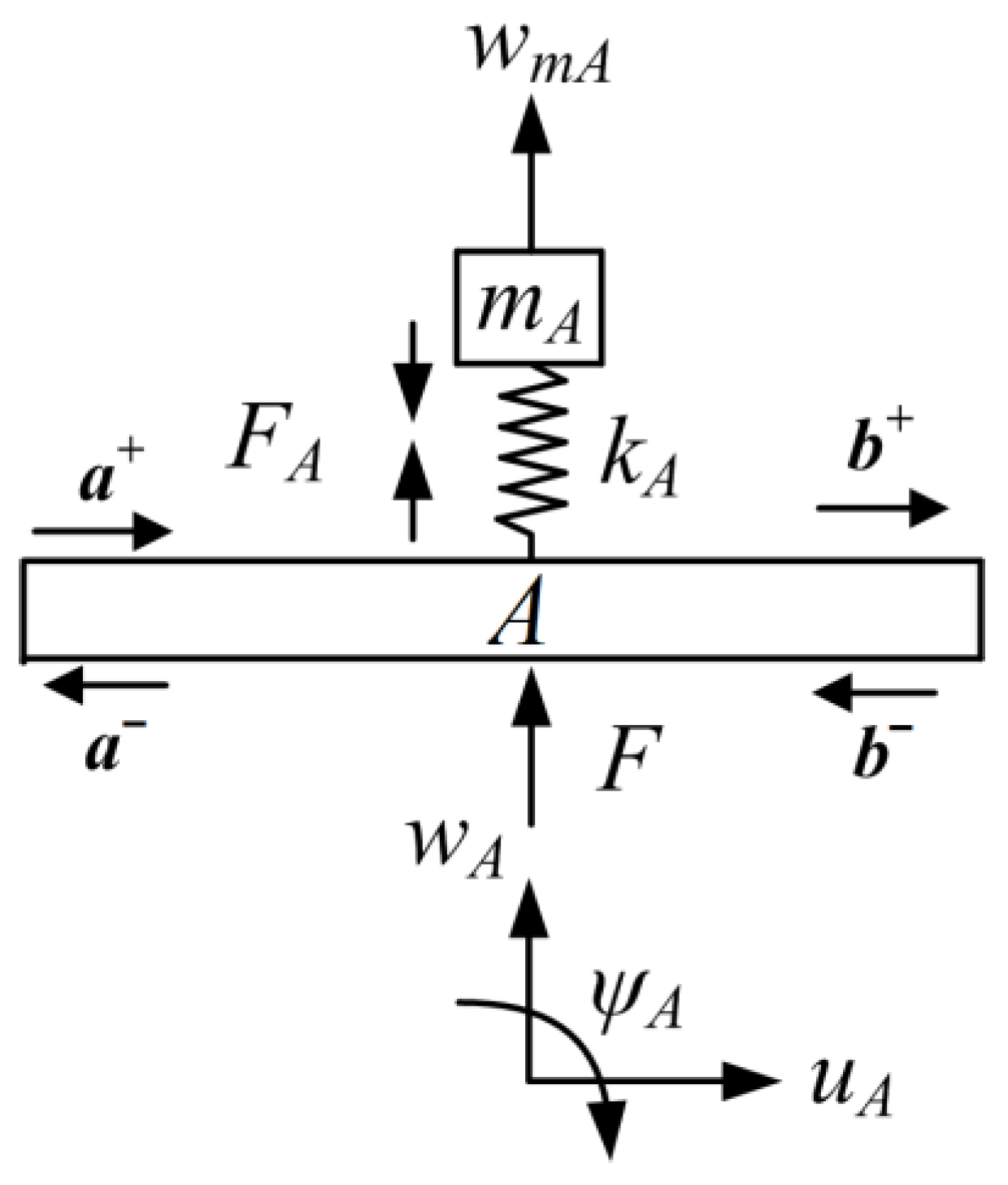
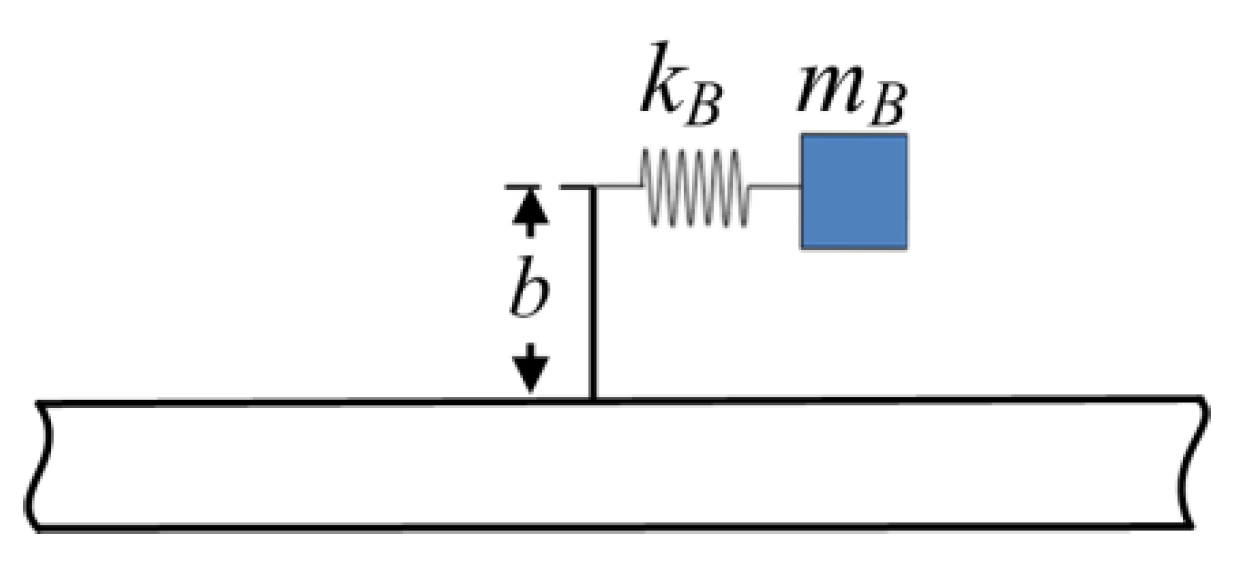
2.6. Transmission and Reflection at the Transverse-Force Type Resonator Attached Point
2.7. Transmission and Reflection at the Longitudinal Force-Moment Type Resonator Attached Point
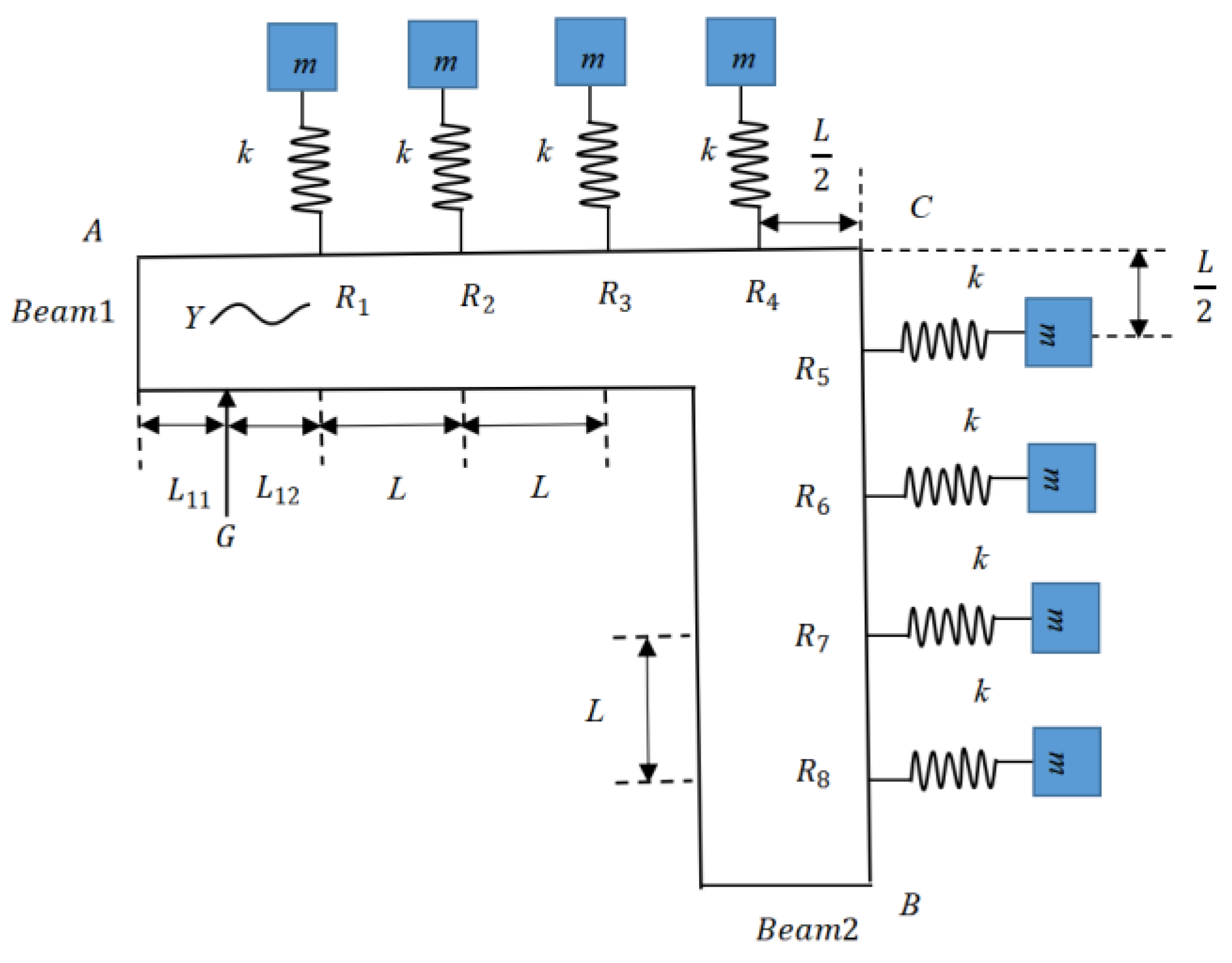
3. Vibration Analysis with Wave-based Approach
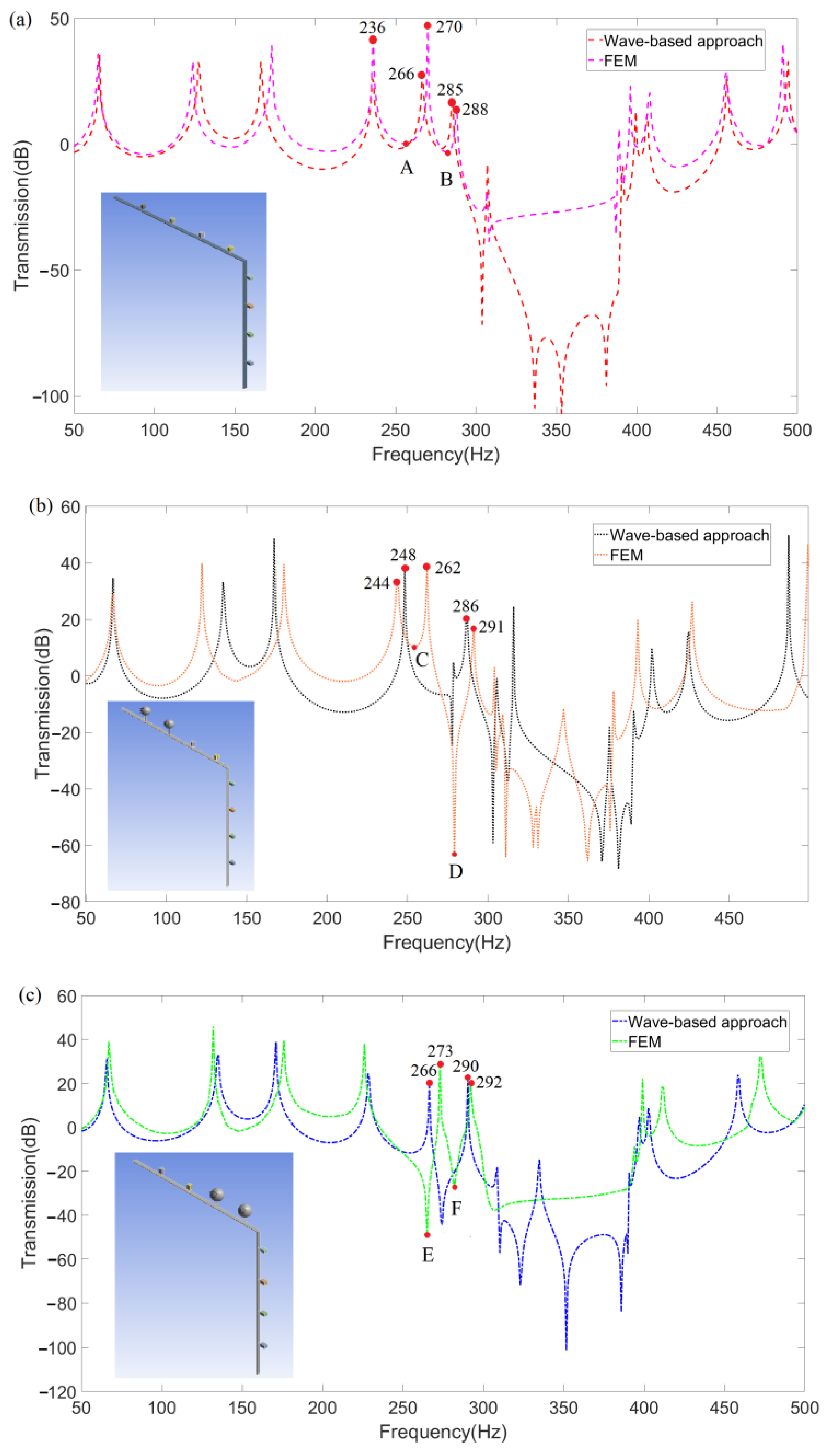
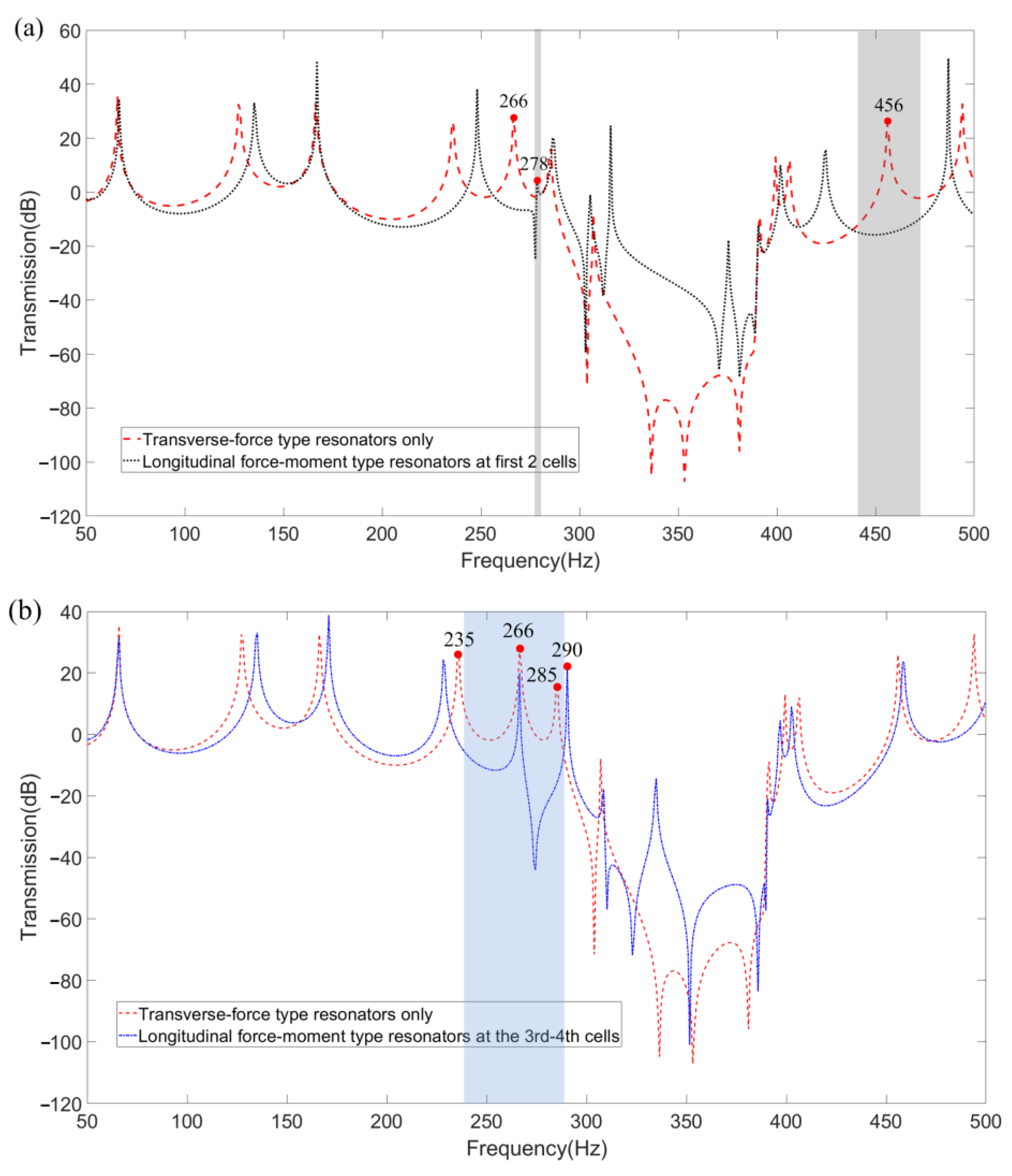
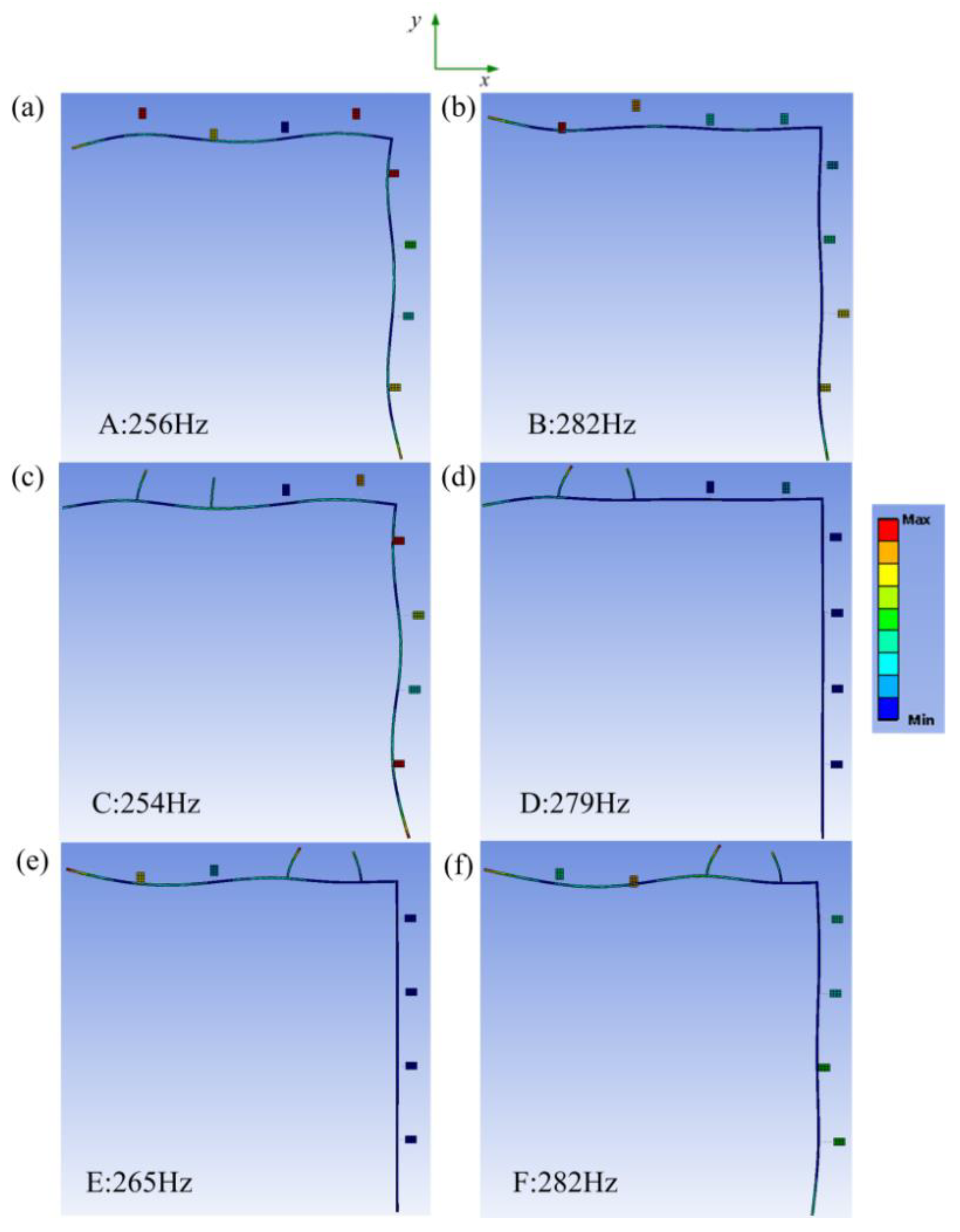
4. Numerical Results and Discussion
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mei, C.; Li, L.; Tang, H.; Han, X.; Wang, X.; Hu, Y. Broadening band gaps of shear horizontal waves of metamaterials via graded hierarchical architectures. Compos. Struct. 2021, 271, 114118. [Google Scholar] [CrossRef]
- Stein, A.; Nouh, M.; Singh, T. Widening, transition and coalescence of local resonance band gaps in multi-resonator acoustic metamaterials: From unit cells to finite chains. J. Sound Vib. 2022, 523, 116716. [Google Scholar] [CrossRef]
- Chen, A.; Wang, Y.; Wang, Y.; Zhou, H.; Yuan, S. Design of Acoustic/Elastic Phase Gradient Metasurfaces: Principles, Functional Elements, Tunability, and Coding. ASME Appl. Mech. Rev. 2022, 74, 020801. [Google Scholar] [CrossRef]
- Zhang, G.; Gao, Y. Topological design and magnetic tunability of a novel cross-like holes phononic crystal with low frequency. Mech. Adv. Mater. Struct. 2021, 29, 6144–6153. [Google Scholar] [CrossRef]
- Cui, J.; Yang, T.; Niu, M.; Chen, L. Tunable Roton-Like Dispersion Relation With Parametric Excitations. ASME J. Appl. Mech. 2022, 89, 111005. [Google Scholar] [CrossRef]
- Chronopoulos, D.; Antoniadis, I.; Collet, M.; Ichchou, M. Enhancement of wave damping within metamaterials having embedded negative stiffness inclusions. Wave Motion 2015, 58, 165–179. [Google Scholar] [CrossRef]
- Chronopoulos, D.; Antoniadis, I.; Ampatzidis, T. Enhanced acoustic insulation properties of composite metamaterials having embedded negative stiffness inclusions. Extrem. Mech. Lett. 2017, 12, 48–54. [Google Scholar] [CrossRef]
- Aghighi, F.; Morris, J.; Amirkhizi, A.V. Low-frequency micro-structured mechanical metamaterials. Mech. Mater. 2019, 130, 65–75. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Chen, Z.; Gong, X.; Du, H.; Zhang, S.; Sun, S. Investigation of a novel MRE metamaterial sandwich beam with real-time tunable band gap characteristics. J. Sound Vib. 2022, 527, 116870. [Google Scholar] [CrossRef]
- Zhao, P.; Zhang, K.; Deng, Z. Size effects on the band gap of flexural wave propagation in one-dimensional periodic micro-beams. Compos. Struct. 2021, 271, 114162. [Google Scholar] [CrossRef]
- Zuo, S.; Ni, T.; Wu, X.; Fan, J. Studies of band gaps in flexural vibrations of a locally resonant beam with novel multi-oscillator configuration. J. Vib. Control. 2017, 23, 1663–1674. [Google Scholar] [CrossRef]
- Goldsberry, B.M.; Haberman, M.R. Negative stiffness honeycombs as tunable elastic metamaterials. J. Appl. Phys. 2018, 123, 091711. [Google Scholar] [CrossRef]
- Giri, T.R.; Mailen, R. Controlled snapping sequence and energy absorption in multistable mechanical metamaterial cylinders. Int. J. Mech. Sci. 2021, 204, 106541. [Google Scholar] [CrossRef]
- Guo, P.; Zhou, Q.Z. An Analytical, Numerical, and Experimental Investigation on Transverse Vibrations of a Finite Locally Resonant Beam. Shock. Vib. 2022, 2022, 6875718. [Google Scholar] [CrossRef]
- Wang, T.; Sheng, M.; Qin, Q. Multi-flexural band gaps in an Euler–Bernoulli beam with lateral local resonators. Phys. Lett. A 2016, 380, 525–529. [Google Scholar] [CrossRef]
- Leong, E.C.; Cheng, Z.Y. Timoshenko beam effect in flexural resonant column tests. Soils Found. 2019, 59, 234–239. [Google Scholar] [CrossRef]
- Kamotski, I.V.; Smyshlyaev, V.P. Bandgaps in two-dimensional high-contrast periodic elastic beam lattice materials. J. Mech. Phys. Solids 2019, 123, 292–304. [Google Scholar] [CrossRef]
- Burlon, A.; Failla, G. Flexural wave propagation in locally-resonant beams with uncoupled/coupled bending-torsion beam-like resonators. Int. J. Mech. Sci. 2022, 215, 106925. [Google Scholar] [CrossRef]
- Kim, T.; Lee, U. Temporal and spatial-domain DFT-based spectral element model for the dynamic analysis of a rectangular Mindlin plate. J. Sound Vib. 2021, 509, 116220. [Google Scholar] [CrossRef]
- Fortunato, D.; Hale, N.; Townsend, A. The ultraspherical spectral element method. J. Comput. Phys. 2021, 436, 110087. [Google Scholar] [CrossRef]
- Rui, X.; Bestle, D.; Wang, G.; Zhang, J.; Rui, X.; He, B. A new version of the Riccati transfer matrix method for multibody systems consisting of chain and branch bodies. Multibody Syst. Dyn. 2020, 49, 337–354. [Google Scholar] [CrossRef]
- Rui, X.; Wang, G.; He, B. Differential quadrature discrete time transfer matrix method for vibration mechanics. Adv. Mech. Eng. 2019, 11, 1–14. [Google Scholar] [CrossRef]
- Lu, H.; Rui, X.; Zhang, X. A computationally efficient modeling method for the vibration analyses of two-dimensional system structures using reduced transfer matrix method for multibody system. J. Sound Vib. 2021, 502, 116096. [Google Scholar] [CrossRef]
- Feyzollahzadeh, M.; Bamdad, M. A modified transfer matrix method to reduce the calculation time: A case study on beam vibration. Math. Comput. 2020, 378, 125238. [Google Scholar] [CrossRef]
- Bakhtiari-Nejad, F.; Saffari, R. Modified finite elements method to investigate vibrations of the main cables in suspended bridges. Eng. Struct. 2020, 216, 110701. [Google Scholar] [CrossRef]
- Sun, S.; Zhou, M.; Lu, W.; Davarpanah, A. Application of symmetry law in numerical modeling of hydraulic fracturing by finite element method. Symmetry 2020, 12, 1122. [Google Scholar] [CrossRef]
- Marin, M.; Hobiny, A.; Abbas, I. The effects of fractional time derivatives in porothermoelastic materials using finite element method. Mathematics 2021, 9, 1606. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Zhu, J.; Zhu, L.; Liu, C. Vibration Estimation in Power Transformers Based on Dynamic Magnetostriction Model and Finite-Element Analysis. IEEE Trans. Appl. Supercond. 2021, 31, 5500904. [Google Scholar] [CrossRef]
- Mei, C. In-plane vibrations of classical planar frame structures—An exact wave-based analytical solution. J. Vib. Control. 2010, 16, 1265–1285. [Google Scholar] [CrossRef]
- Mei, C. Wave Analysis of In-Plane Vibrations of H- and T-shaped Planar Frame Structures. ASME J. Vib. Acoust. 2008, 130, 061004. [Google Scholar] [CrossRef]
- Mei, C. Wave Analysis of In-Plane Vibrations of L-Shaped and Portal Planar Frame Structures. ASME J. Vib. Acoust. 2012, 134, 021011. [Google Scholar] [CrossRef]
- Mei, C.; Sha, H. An Exact Analytical Approach for Free Vibration Analysis of Built-Up Space Frames. ASME J. Vib. Acoust. 2015, 137, 031005. [Google Scholar] [CrossRef]
- Mei, C. A Wave-Based Analytical Solution to Free Vibrations in a Combined Euler–Bernoulli Beam/Frame and a Two-Degree-of-Freedom Spring–Mass System. ASME J. Vib. Acoust. 2018, 140, 061001. [Google Scholar] [CrossRef]
- Lv, H.; Zhang, Y. A wave-based vibration analysis of a finite Timoshenko locally resonant beam suspended with periodic uncoupled force-moment type resonators. Crystals 2020, 10, 1132. [Google Scholar] [CrossRef]
- Lv, H.; Zhang, Y. Wide Band-gaps in Finite Timoshenko Locally Resonant Beams Carrying Periodic Separated Force and Moment Resonators: Forced Vibration Analysis Based on an Exact Wave-Based Approach. J. Vib. Eng. Technol. 2021, 9, 1109–1121. [Google Scholar] [CrossRef]
- Lv, H.; Li, S.; Huang, X.; Yu, Z. Band-Gap Properties of Finite Locally Resonant Beam Suspended Periodically with Two-Degree-of-Freedom Force Type Resonators. Crystals 2021, 11, 716. [Google Scholar] [CrossRef]
- Lv, H.; Li, S.; Huang, X.; Yu, Z. Vibration Analysis of a Finite Lightweight Locally Resonant Beam Suspended with Periodic Force-Moment-Type Resonators inside Using an Exact Wave-Based Approach. Symmetry 2022, 14, 1542. [Google Scholar] [CrossRef]
- Balaji, N.N.; Brake, M.R.W.; Leamy, M.J. Wave-based analysis of jointed elastic bars: Nonlinear periodic response. Nonlinear Dyn. 2022, 110, 2005–2031. [Google Scholar] [CrossRef]
- Ghannadi, P.; Kourehli, S.S.; Mirjalili, S. A review of the application of the simulated annealing algorithm in structural health monitoring (1995–2021). Frat. Ed. Integrità Strutt. 2023, 64, 51–76. [Google Scholar] [CrossRef]
- Gharehbaghi, V.R.; Noroozinejad Farsangi, E.; Noori, M.; Yang, T.Y.; Li, S.; Nguyen, A.; Málaga-Chuquitaype, C.; Gardoni, P.; Mirjalili, S. A Critical Review on Structural Health Monitoring: Definitions, Methods, and Perspectives. Arch. Comput. Methods Eng. 2022, 29, 2209–2235. [Google Scholar] [CrossRef]
- Ghannadi, P.; Kourehli, S.S.; Mirjalili, S. The Application of PSO in Structural Damage Detection: An Analysis of the Previously Released Publications (2005–2020). Frat. Ed Integrità Strutt. 2022, 16, 460–489. [Google Scholar] [CrossRef]
- Leamy, M.J. Exact wave-based Bloch analysis procedure for investigating wave propagation in two-dimensional periodic lattices. J. Sound Vib. 2012, 331, 1580–1596. [Google Scholar] [CrossRef]
- Graff, K.F. Wave Motion in Elastic Solids; Ohio State University Press: Columbus, OH, USA, 1975. [Google Scholar]
- Yu, D.; Liu, Y.; Wang, G.; Zhao, H.; Qiu, J. Flexural vibration band gaps in Timoshenko beams with locally resonant structures. J. Appl. Phys. 2006, 100, 124901. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Young’s modulus | |
| Poisson’s ratio | |
| Shear modulus | |
| Mass density | |
| A | Area of the cross section |
| Shear coefficient | |
| Spring stiffness | |
| L | Lattice constant |
| Frequency | |
| m | Resonator mass |
| Rotation angle | |
| Area moment of inertia | |
| Transverse deflection | |
| Longitudinal deflection |
| Parameter | Value |
|---|---|
| LR | Locally resonant |
| AMs | Acoustics metamaterials |
| EMs | Elastic metamaterials |
| PCs | Phononic crystals |
| SEM | Spectral element method |
| TMM | Transfer matrix method |
| FEM | Finite element method |
| FRF | Frequency response function |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, H.; Zhang, R.; Chen, C.; Ma, H.; Huang, X.; Yu, Z. Vibration Analysis of Locally Resonant Beams with L-Joint Using an Exact Wave-Based Vibration Approach. Materials 2023, 16, 2276. https://doi.org/10.3390/ma16062276
Lv H, Zhang R, Chen C, Ma H, Huang X, Yu Z. Vibration Analysis of Locally Resonant Beams with L-Joint Using an Exact Wave-Based Vibration Approach. Materials. 2023; 16(6):2276. https://doi.org/10.3390/ma16062276
Chicago/Turabian StyleLv, Hangyuan, Rong Zhang, Changji Chen, Hui Ma, Xianzhen Huang, and Zhongliang Yu. 2023. "Vibration Analysis of Locally Resonant Beams with L-Joint Using an Exact Wave-Based Vibration Approach" Materials 16, no. 6: 2276. https://doi.org/10.3390/ma16062276
APA StyleLv, H., Zhang, R., Chen, C., Ma, H., Huang, X., & Yu, Z. (2023). Vibration Analysis of Locally Resonant Beams with L-Joint Using an Exact Wave-Based Vibration Approach. Materials, 16(6), 2276. https://doi.org/10.3390/ma16062276







