Mechanisms of Hydride Nucleation, Growth, Reorientation, and Embrittlement in Zirconium: A Review
Abstract
:1. Introduction
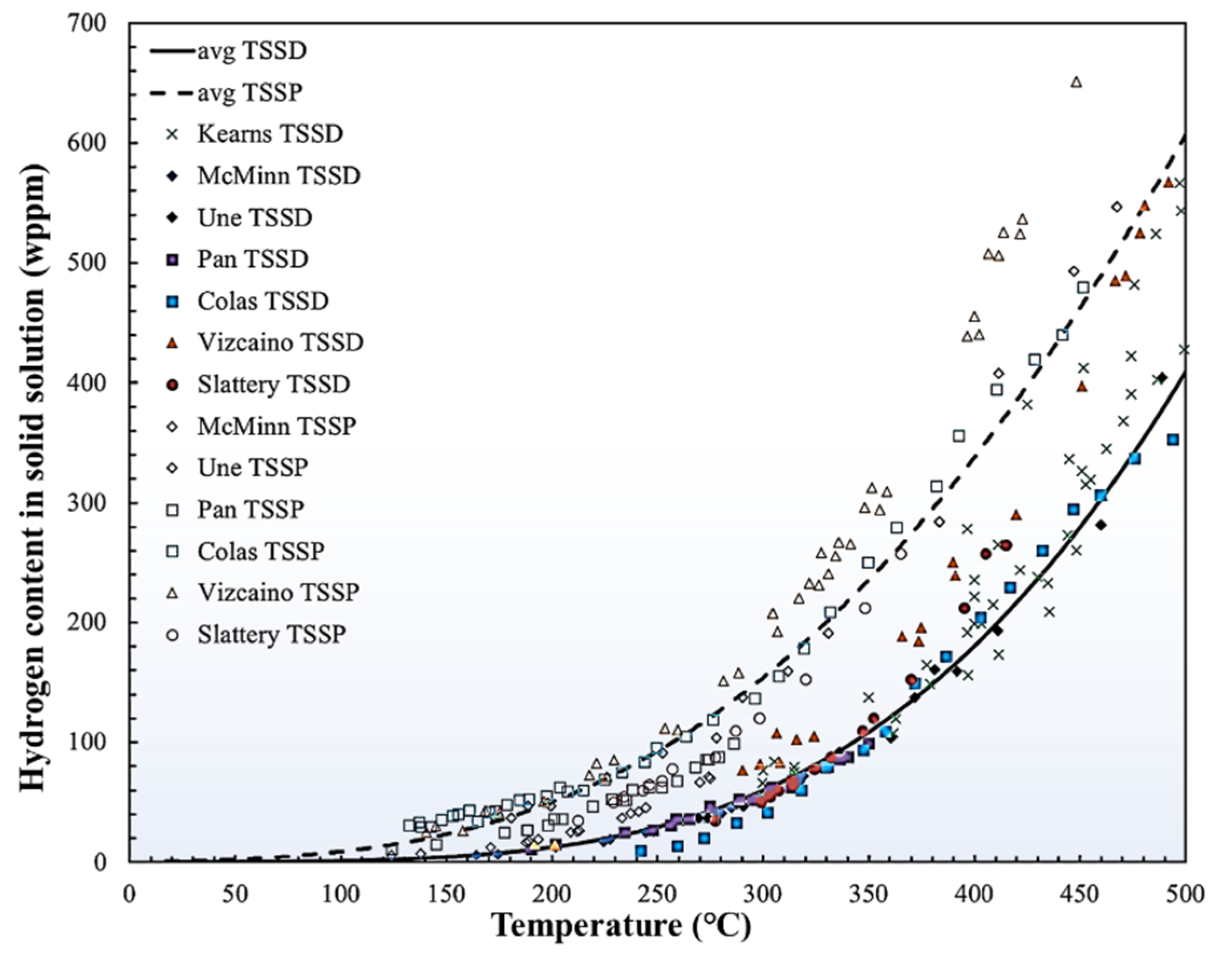
2. Hydride Nucleation and Growth Behaviors
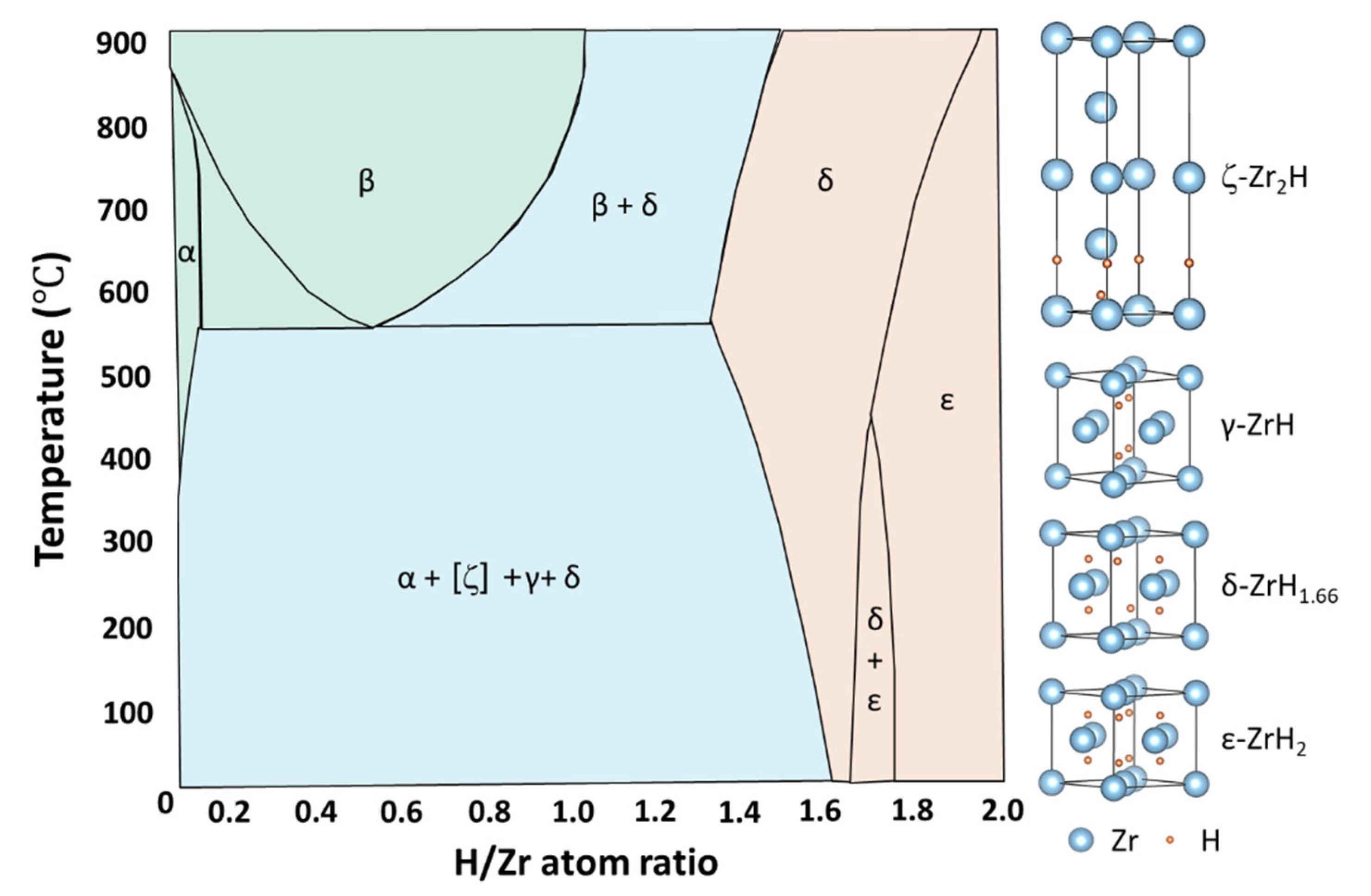
2.1. Hydride Phases and Their Transition
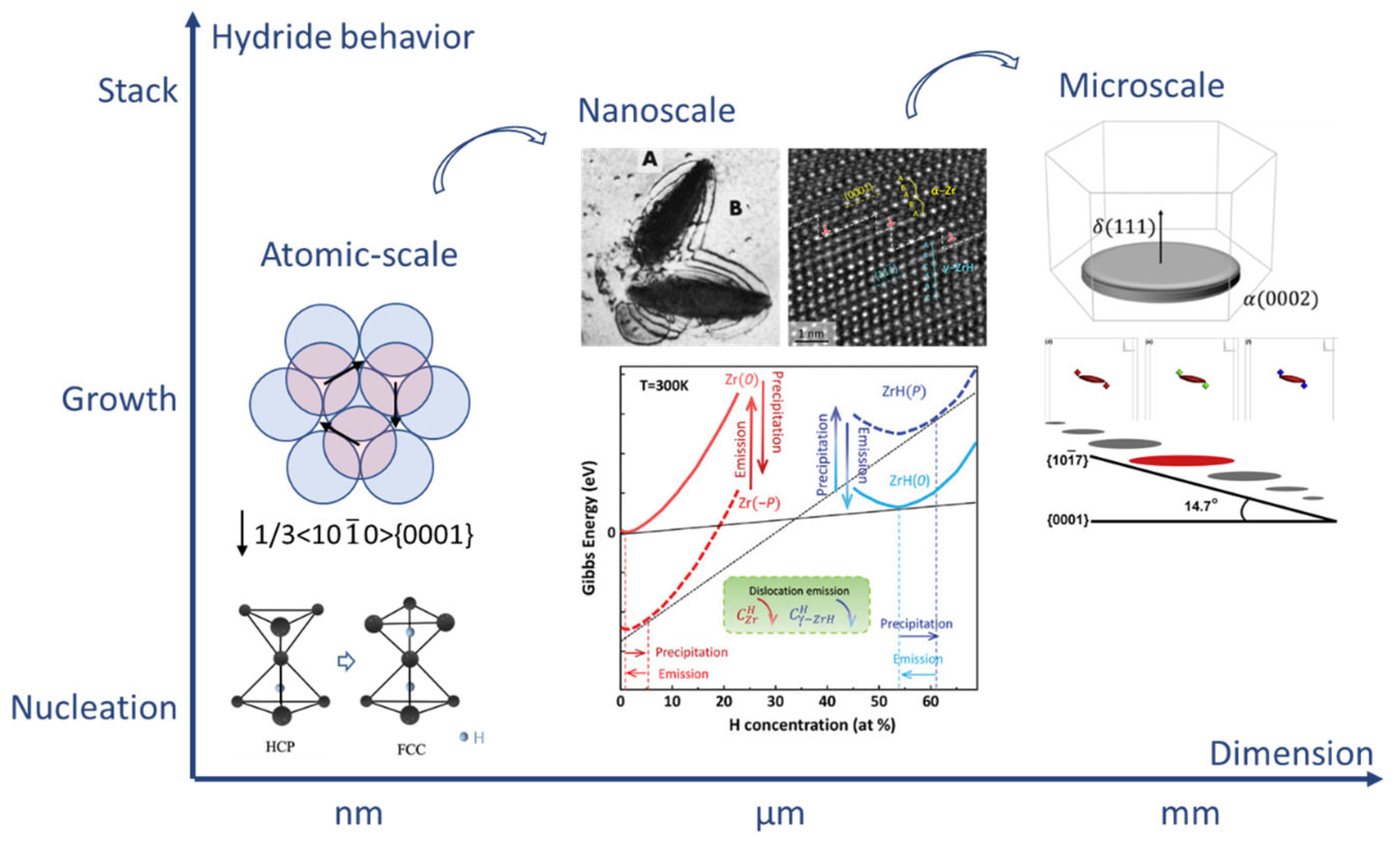
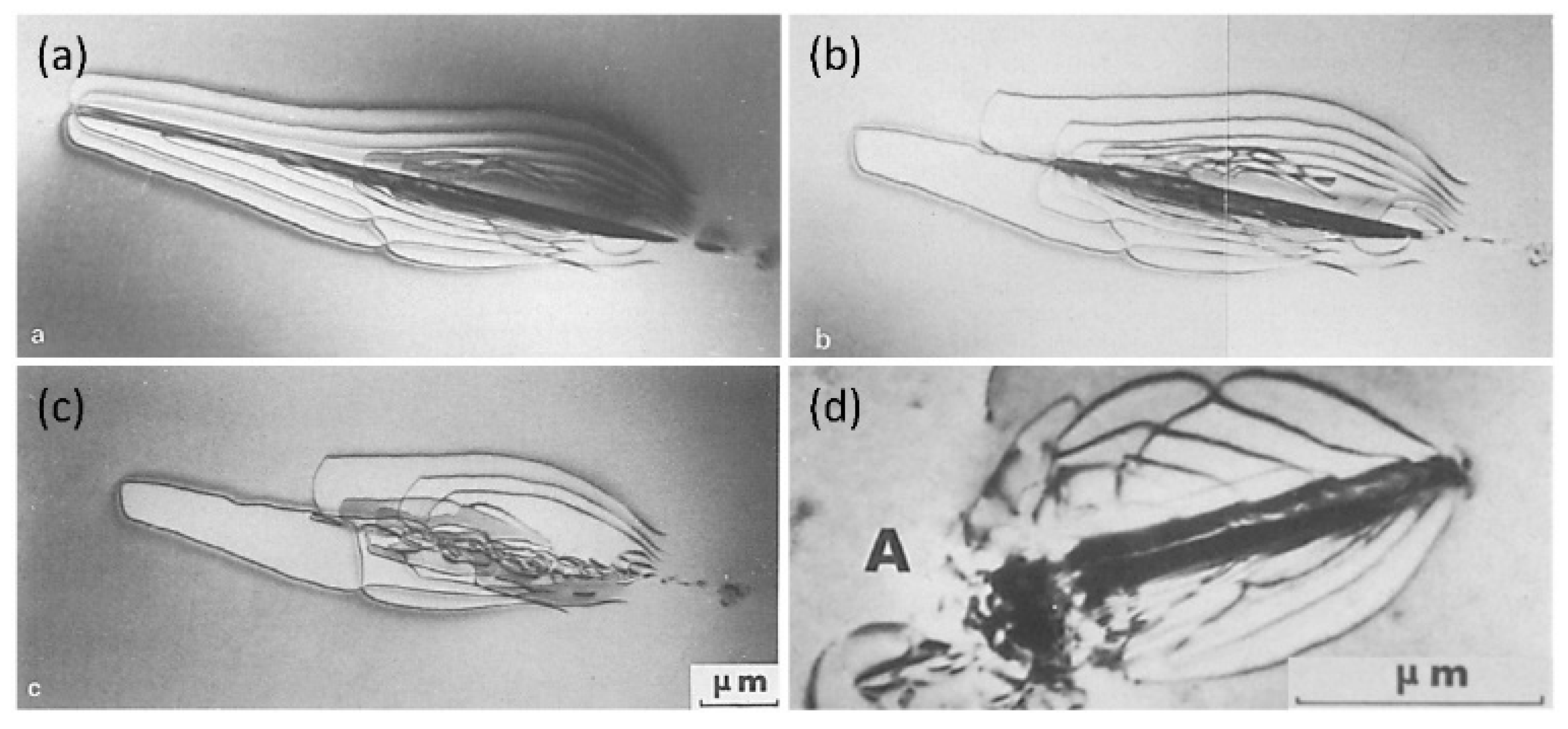
2.2. Mechanism of Hydride Nucleation and Growth
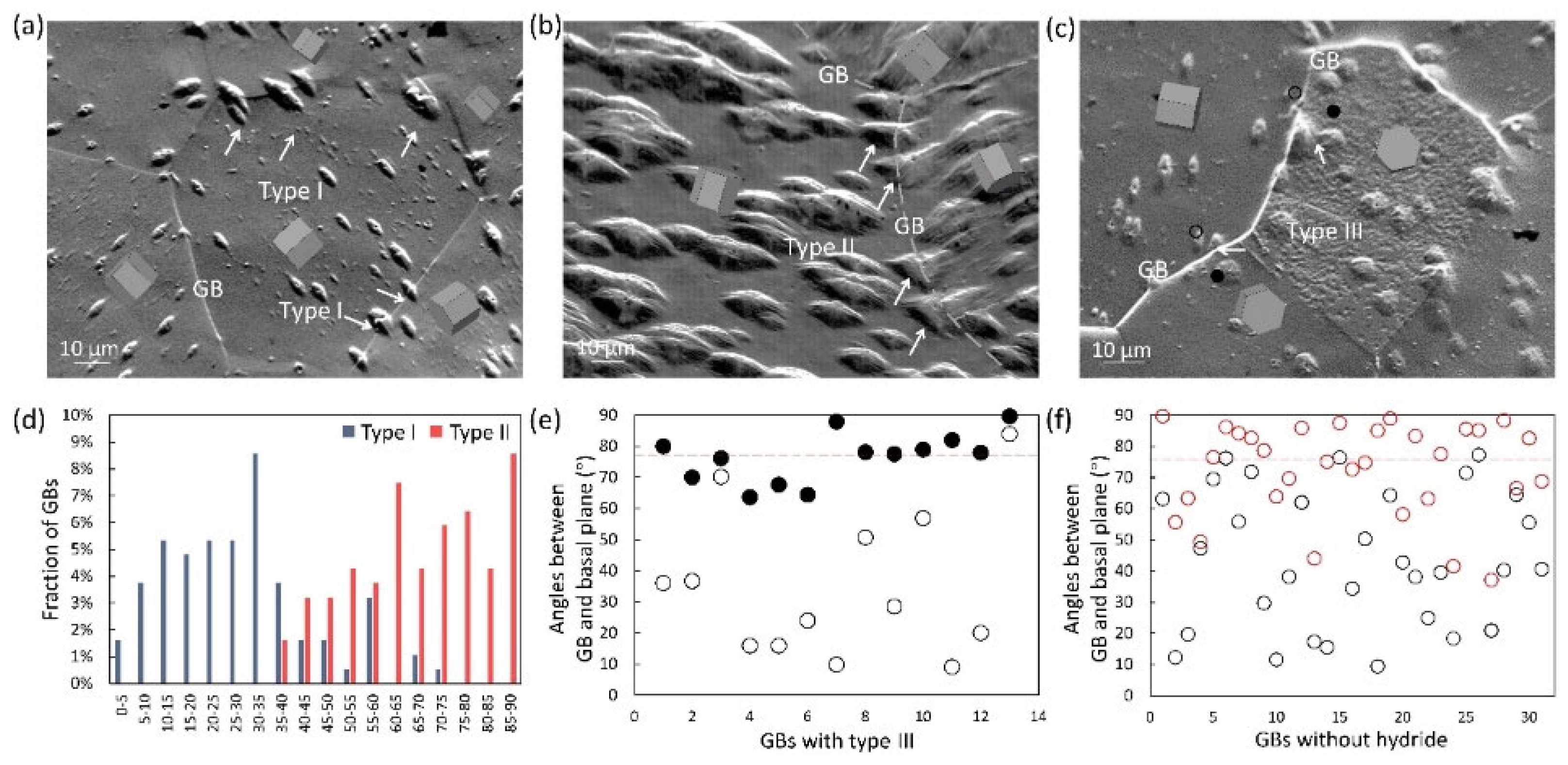
2.3. Effects of Interface on Hydrides
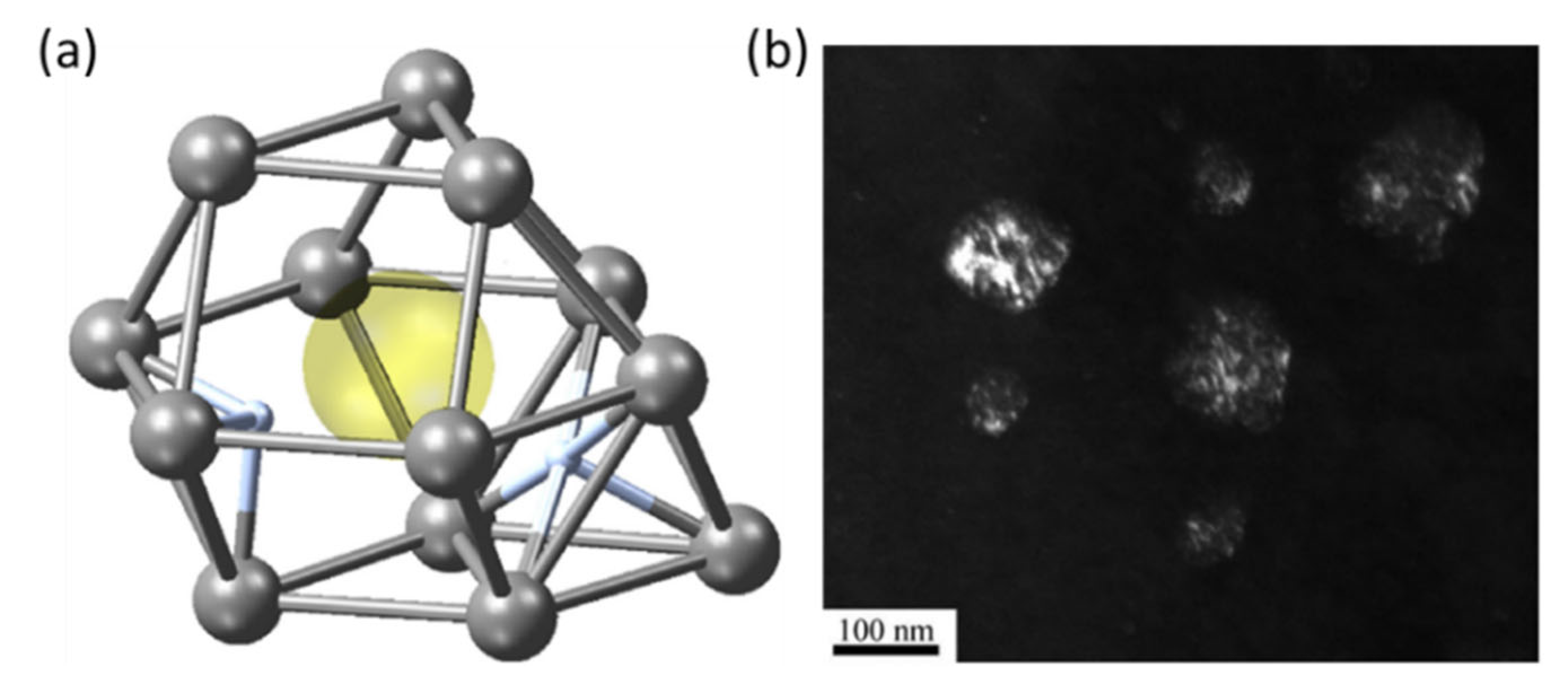
2.4. Effect of Irradiation Defect on Hydride Formation
3. Hydride Reorientation under External Stress
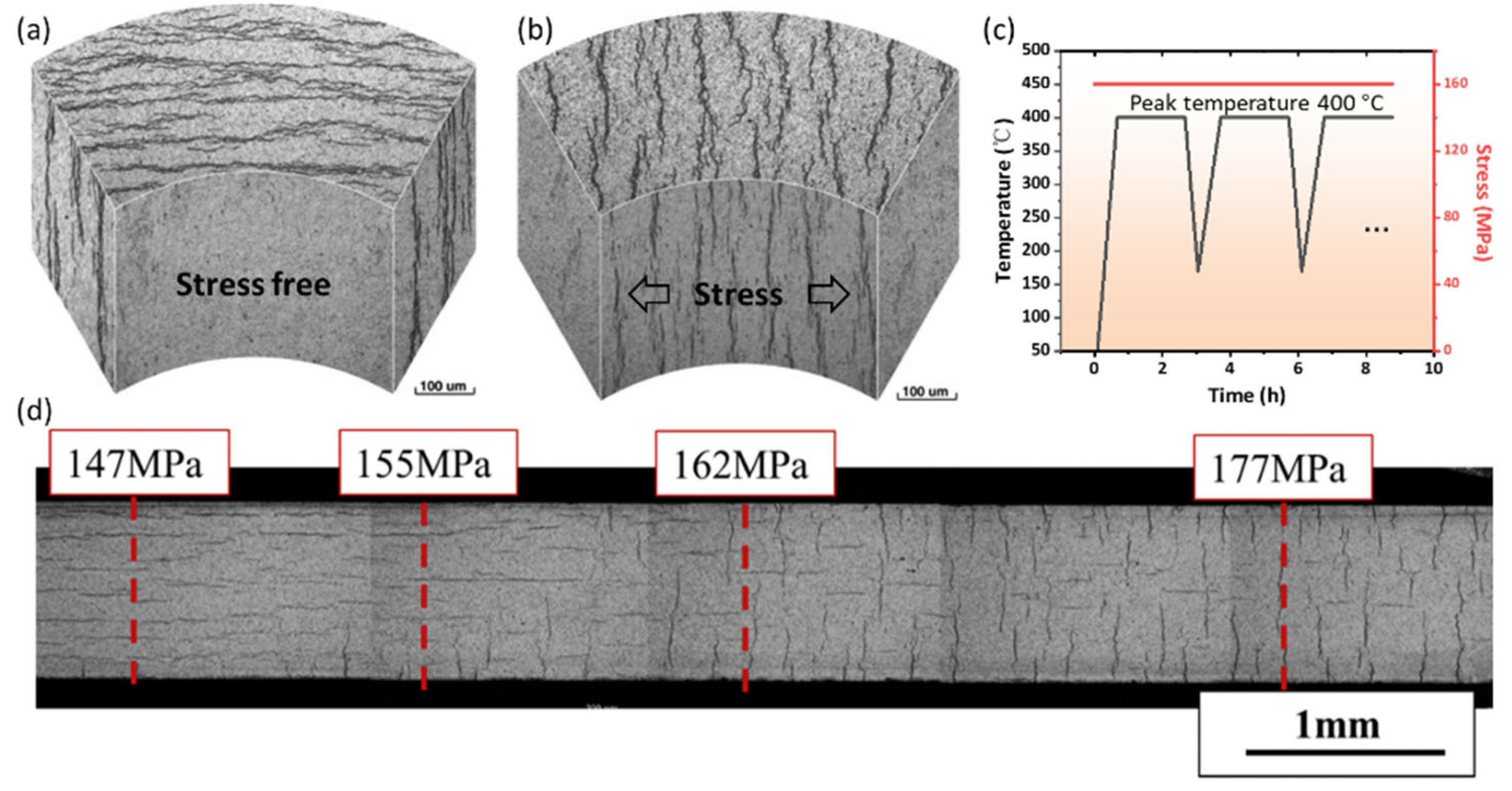
3.1. Threshold Stress for Hydride Reorientation
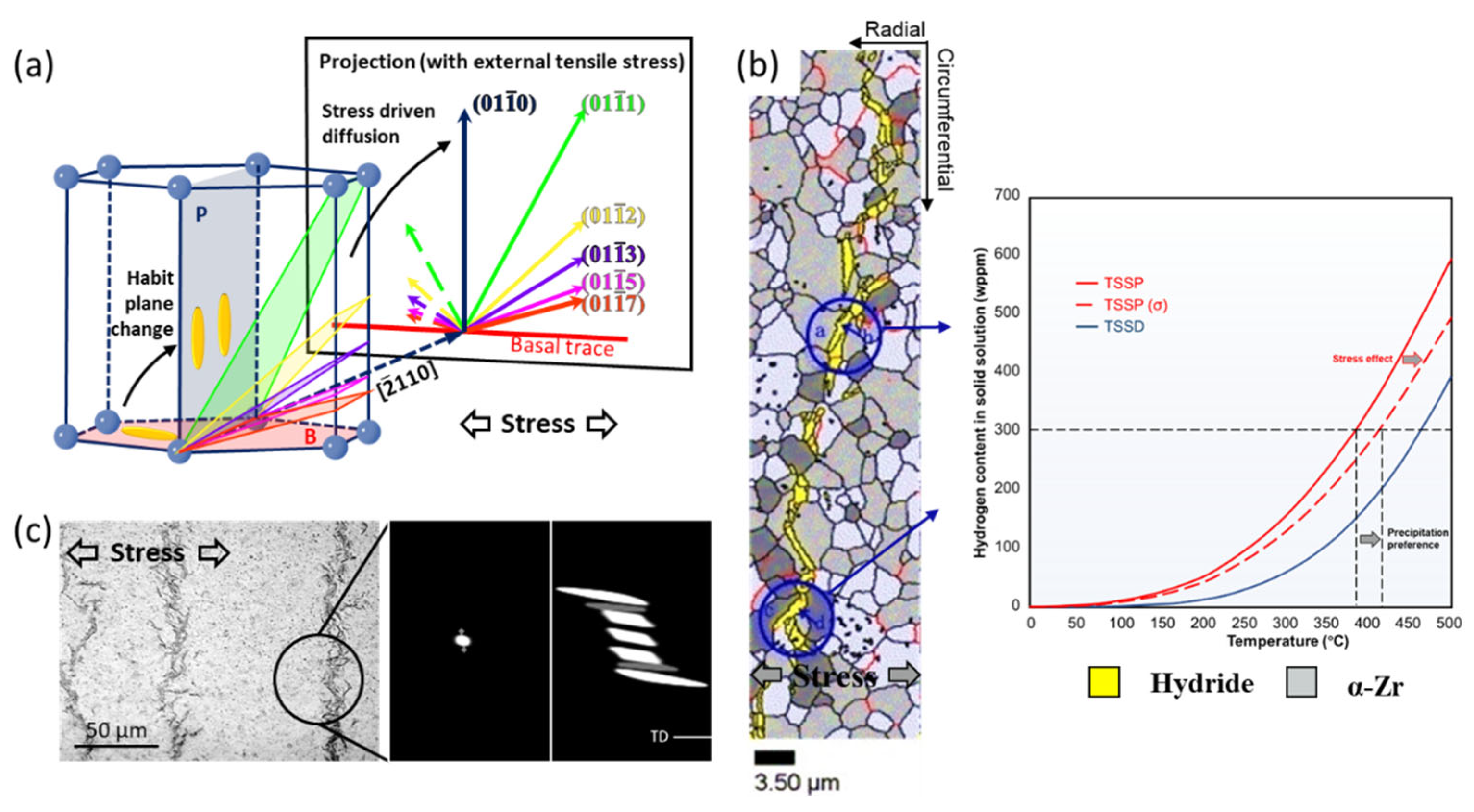
3.2. Mechanism of Hydride Reorientation
4. Hydride-Induced Embrittlement
4.1. Mechanical Properties of Hydrides
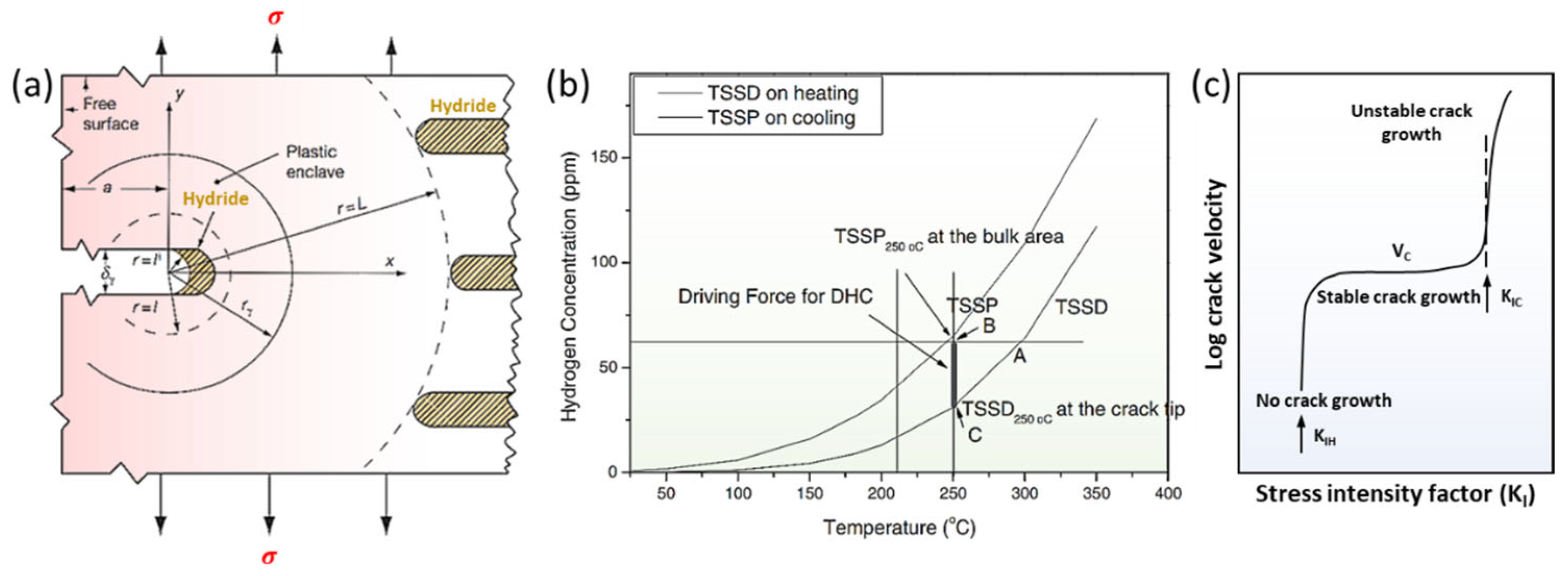
4.2. Delayed Hydride Cracking
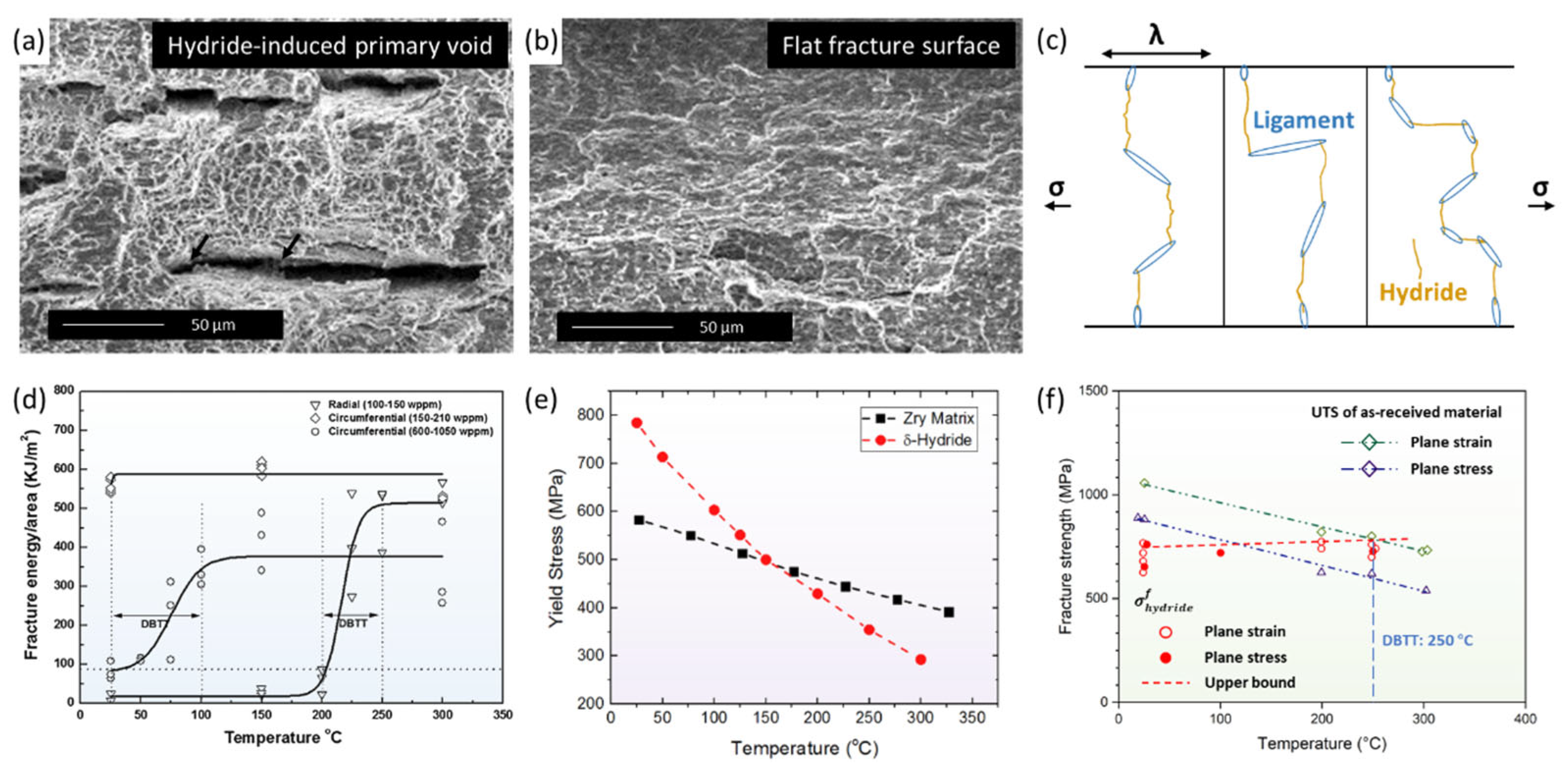
4.3. Local Hydride Embrittlement
4.4. Hydride Reorientation Embrittlement
5. Conclusions and Prospects
- (1)
- Clarifying the mechanism of hydride reorientation
- (2)
- Revealing the effect of reoriented hydrides on DBTs in Zr
- (3)
- Discovering the effect of alloying elements on Zr hydride
- (4)
- Strengthening the atomic-scale simulations of Zr hydride
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cox, B. Some thoughts on the mechanisms of in-reactor corrosion of zirconium alloys. J. Nucl. Mater. 2005, 336, 331–368. [Google Scholar] [CrossRef]
- Suman, S.; Khan, M.K.; Pathak, M.; Singh, R.N. Hydrogen in Zircaloy: Mechanism and its impacts. Int. J. Hydrogen Energy 2015, 40, 5976–5994. [Google Scholar] [CrossRef]
- Northwood, D.O.; Kosasih, U. Hydrides and delayed hydrogen cracking in zirconium and its alloys. Int. Mater. Rev. 1983, 28, 92–121. [Google Scholar] [CrossRef]
- Holt, R.A. In-reactor deformation of cold-worked Zr–2.5Nb pressure tubes. J. Nucl. Mater. 2008, 372, 182–214. [Google Scholar] [CrossRef]
- Jang, K.N.; Kim, K.T. The effect of neutron irradiation on hydride reorientation and mechanical property degradation of zirconium alloy cladding. Nucl. Eng. Technol. 2017, 49, 1472–1482. [Google Scholar] [CrossRef]
- Motta, A.T.; Capolungo, L.; Chen, L.Q.; Cinbiz, M.N.; Daymond, M.R.; Koss, D.A.; Lacroix, E.; Pastore, G.; Simon, P.C.A.; Tonks, M.R.; et al. Hydrogen in zirconium alloys: A review. J. Nucl. Mater. 2019, 518, 440–460. [Google Scholar] [CrossRef] [Green Version]
- Nilsson, K.F.; Negyesi, M.; Szaraz, Z.; Simonovski, I. An evaluation of the segmented expanding cone-mandrel test to assess hydride re-orientation and ductility reduction for Zircaloy-2 cladding tubes. J. Nucl. Mater. 2015, 466, 220–233. [Google Scholar] [CrossRef]
- Kook, D.; Choi, J.; Kim, J.; Kim, Y. Review of spent fuel integrity evaluation for dry storage. Nucl. Eng. Technol. 2013, 45, 115–124. [Google Scholar] [CrossRef] [Green Version]
- Singh, R.N.; Mukherjee, S.; Gupta, A.; Banerjee, S. Terminal solid solubility of hydrogen in Zr-alloy pressure tube materials. J. Alloys Compd. 2005, 389, 102–112. [Google Scholar] [CrossRef]
- Pan, Z.L.; Ritchie, I.G.; Puls, M.P. The terminal solid solubility of hydrogen and deuterium in Zr-2.5Nb alloys. J. Nucl. Mater. 1996, 228, 227–237. [Google Scholar] [CrossRef]
- Une, K.; Ishimoto, S. Dissolution and precipitation behavior of hydrides in Zircaloy-2 and high Fe Zircaloy. J. Nucl. Mater. 2003, 322, 66–72. [Google Scholar] [CrossRef]
- Zanellato, O.; Preuss, M.; Buffiere, J.Y.; Ribeiro, F.; Steuwer, A.; Desquines, J.; Andrieux, J.; Krebs, B. Synchrotron diffraction study of dissolution and precipitation kinetics of hydrides in Zircaloy-4. J. Nucl. Mater. 2012, 420, 537–547. [Google Scholar] [CrossRef]
- Carpenter, G.J.C. The dilatational misfit of zirconium hydrides precipitated in zirconium. J. Nucl. Mater. 1973, 48, 264–266. [Google Scholar] [CrossRef]
- Carpenter, G.J.C.; Watters, J.F.; Gilbert, R.W. Dislocations generated by zirconium hydride precipitates in zirconium and some of its alloys. J. Nucl. Mater. 1973, 48, 267–276. [Google Scholar] [CrossRef]
- Kolesnik, M.; Aliev, T.; Likhanskii, V. The modeling of the hydrogen solid solubility hysteresis in zirconium alloys. Acta Mater. 2019, 177, 131–140. [Google Scholar] [CrossRef]
- Lu, K.; Kontis, P.; Wang, S.; Birch, R.; Wenman, M.; Gault, B.; Britton, T.B. Nanoscale characterization of hydrides and secondary phase particles in Zircaloy-4. arXiv 2021, arXiv:2109.10955. [Google Scholar]
- Lumley, S.C.; Grimes, R.W.; Murphy, S.T.; Burr, P.A.; Chroneos, A.; Tuckey, P.R.C.; Wenman, M.R. The thermodynamics of hydride precipitation: The importance of entropy, enthalpy and disorder. Acta Mater. 2014, 79, 351–362. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Morniroli, J.P.; Legris, A.; Ambard, A.; Khin, Y.; Legras, L.; Yrieix, M.B. Identification and characterization of a new zirconium hydride. J. Microsc. 2008, 232, 410–421. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, R.; Shu, G.; Wu, P.; Xiao, H. First-principles study of different polymorphs of crystalline zirconium hydride. J. Phys. Chem. C 2010, 114, 22361–22368. [Google Scholar] [CrossRef]
- Njifon, I.C.; Torres, E. A first principles investigation of the hydrogen-strain synergy on the formation and phase transition of hydrides in zirconium. Acta Mater. 2021, 202, 222–231. [Google Scholar] [CrossRef]
- Wimmer, E.; Christensen, M.; Wolf, W.; Howland, W.H.; Kammenzind, B. Hydrogen in zirconium: Atomistic simulations of diffusion and interaction with defects using a new embedded atom method potential. J. Nucl. Mater. 2020, 532, 152055. [Google Scholar] [CrossRef]
- Domain, C.; Besson, R.; Legris, A. Atomic-scale ab-initio study of the Zr-H system: I. Bulk properties. Acta Mater. 2002, 50, 3513–3526. [Google Scholar] [CrossRef]
- Bradbrook, J.S.; Lorimer, G.W.; Ridley, N. The precipitation of zirconium hydride in zirconium and zircaloy-2. J. Nucl. Mater. 1972, 42, 142–160. [Google Scholar] [CrossRef]
- Nath, B.; Lorimer, G.W.; Ridley, N. The relationship between gamma and delta hydrides in zirconium-hydrogen alloys of low hydrogen concentration. J. Nucl. Mater. 1974, 49, 262–280. [Google Scholar] [CrossRef]
- Mishr, S.; Sivaramakrihnan, K.S.; Asundi, M.K. Formation of the gamma phase by a peritectoid reaction in the zirconium-hydrogen system. J. Nucl. Mater. 1972, 45, 235–244. [Google Scholar] [CrossRef]
- Kim, S.D.; Kim, J.S.; Yoon, J. Phase analysis of hydride blister in zirconium alloy. J. Alloys Compd. 2018, 735, 2007–2011. [Google Scholar] [CrossRef]
- Root, J.H.; Small, W.M.; Khatamian, D.; Woo, O.T. Kinetics of the δ to γ zirconium hydride transformation in Zr-2.5Nb. Acta Mater. 2003, 51, 2041–2053. [Google Scholar] [CrossRef]
- Maimaitiyili, T.; Steuwer, A.; Bjerken, C.; Blomqvist, J.; Hoelzel, M.; Ion, J.C. The preparation of Zr-deuteride and phase stability studies of the Zr-D system. J. Nucl. Mater. 2017, 485, 243–252. [Google Scholar] [CrossRef] [Green Version]
- Jia, Y.J.; Beyerlein, I.J.; Han, W.Z. Precipitation characteristics and distributions of subsurface hydrides in zirconium. Acta Mater. 2021, 216, 117146. [Google Scholar] [CrossRef]
- Tulk, E.; Kerr, M.; Daymond, M.R. Study on the effects of matrix yield strength on hydride phase stability in Zircaloy-2 and Zr 2.5 wt% Nb. J. Nucl. Mater. 2012, 425, 93–104. [Google Scholar] [CrossRef]
- Lanzani, L.; Ruch, M. Comments on the stability of zirconium hydride phases in Zircaloy. J. Nucl. Mater. 2004, 324, 165–176. [Google Scholar] [CrossRef]
- Sidhu, S.S.; Murthy, N.S.S.; Campos, F.P.; Zauberis, D.D. Neutron and X-ray diffraction studies of nonstoichiometric metal hydrides. Adv. Chem. 1963, 39, 87–98. [Google Scholar]
- Buongiorno, J.; Sterbentz, J.W.; MacDonald, P.E. Study of solid moderators for the thermal-spectrum supercritical water-cooled reactor. Nucl. Technol. 2006, 153, 282–303. [Google Scholar] [CrossRef]
- Bair, J.; Zaeem, M.A.; Schwen, D. Formation path of δ hydrides in zirconium by multiphase field modeling. Acta Mater. 2017, 123, 235–244. [Google Scholar] [CrossRef]
- Thuinet, L.; Besson, R. Ab initio study of competitive hydride formation in zirconium alloys. Intermetallics 2012, 20, 24–32. [Google Scholar] [CrossRef]
- Zhang, Y.; Bai, X.M.; Yu, J.; Tonks, M.R.; Noordhoek, M.J.; Phillpot, S.R. Homogeneous hydride formation path in α-Zr: Molecular dynamics simulations with the charge-optimized many-body potential. Acta Mater. 2016, 111, 357–365. [Google Scholar] [CrossRef] [Green Version]
- Udagawa, Y.; Yamaguchi, M.; Abe, H.; Sekimura, N.; Fuketa, T. Ab initio study on plane defects in zirconium–hydrogen solid solution and zirconium hydride. Acta Mater. 2010, 58, 3927–3938. [Google Scholar] [CrossRef]
- Carpenter, G.J.C. The precipitation of γ-zirconium hydride in zirconium. Acta Metall. 1978, 26, 1225–1235. [Google Scholar] [CrossRef]
- Li, S.; Wang, Y.; Che, Z.; Liu, G.; Ren, Y.; Wang, Y. Investigations of deformation-induced δ → ζ phase transformation in zirconium hydride by in situ high-energy X-ray diffraction. Acta Mater. 2017, 140, 168–175. [Google Scholar] [CrossRef]
- Steuwer, A.; Santisteban, J.R.; Preuss, M.; Peel, M.J.; Buslaps, T.; Harada, M. Evidence of stress-induced hydrogen ordering in zirconium hydrides. Acta Mater. 2009, 57, 145–152. [Google Scholar] [CrossRef]
- Barrow, A.T.W.; Korinek, A.; Daymond, M.R. Evaluating zirconium–zirconium hydride interfacial strains by nano-beam electron diffraction. J. Nucl. Mater. 2013, 432, 366–370. [Google Scholar] [CrossRef]
- Hanlon, S.M.; Persaud, S.Y.; Daymond, M.R. Advanced characterization of hydrides in zirconium alloys. In Proceedings of the 18th International Conference on Environmental Degradation of Materials in Nuclear Power Systems—Water Reactors, Portland, OR, USA, 13–17 August 2017; Jackson, J.H., Paraventi, D., Wright, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1793–1813. [Google Scholar]
- Cassidy, M.P.; Wayman, C.M. The crystallography of hydride formation in zirconium: II. the δ → ε transformation. Metall. Mater. Trans. A 1980, 11, 57–67. [Google Scholar] [CrossRef]
- Maimaitiyili, T.; Steuwer, A.; Blomqvist, J.; Bjerken, C.; Blackmur, M.S.; Zanellato, O.; Andrieux, J.; Ribeiro, F. Observation of the δ to ε Zr-hydride transition by in-situ synchrotron X-ray diffraction. Cryst. Res. Technol. 2016, 51, 663–670. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Yang, Y.; Zhang, Y.; Liu, J.; You, L.; Song, X. Study of the microstructure evolution of zirconium alloy during deuterium absorption at high temperature. J. Nucl. Mater. 2017, 493, 448–459. [Google Scholar] [CrossRef]
- Barraclough, K.G.; Beevers, C.J. Some observations on the phase transformations in zirconium hydrides. J. Nucl. Mater. 1970, 34, 125–134. [Google Scholar] [CrossRef]
- Zhu, X.; Lin, D.Y.; Fang, J.; Gao, X.Y.; Zhao, Y.F.; Song, H.F. Structure and thermodynamic properties of zirconium hydrides by structure search method and first principles calculations. Comput. Mater. Sci. 2018, 150, 77–85. [Google Scholar] [CrossRef] [Green Version]
- Chung, H.M.; Daum, R.S.; Hiller, J.M. Characteristics of hydride precipitation and reorientation in spent-fuel cladding. In Proceedings of the Zirconium in the Nuclear Industry: Thirteenth International Symposium, Annecy, France, 10–14 June 2002; Moan, G.D., Rudling, P., Eds.; ASTM: West Conshohocken, PA, USA, 2002; pp. 561–566. [Google Scholar]
- Simon, P.C.A.; Frank, C.; Chen, L.Q.; Daymond, M.R.; Tonks, M.R.; Motta, A.T. Quantifying the effect of hydride microstructure on zirconium alloys embrittlement using image analysis. J. Nucl. Mater. 2021, 547, 152817. [Google Scholar] [CrossRef]
- Domain, C.; Legris, A. Investigation of glide properties in hexagonal titanium and zirconium: An ab initio atomic scale study. In Proceedings of the lUTAM Symposium on Mesoscopic Dynamics of Fracture Process and Materials Strength, Solid Mechanics and its Applications, Osaka, Japan, 6–11 July 2003; Kitagawa, H., Shibutani, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 411–420. [Google Scholar]
- Shinohara, Y.; Abe, H.; Iwai, T.; Sekimura, N.; Kido, T.; Yamamoto, H.; Taguchi, T. In situ TEM observation of growth process of zirconium hydride in Zircaloy-4 during hydrogen ion implantation. J. Nucl. Sci. Technol. 2009, 46, 564–571. [Google Scholar] [CrossRef]
- Han, G.M.; Zhao, Y.F.; Zhou, C.B.; Lin, D.Y.; Zhu, X.Y.; Zhang, J.; Hu, S.Y.; Song, H.F. Phase-field modeling of stacking structure formation and transition of δ-hydride precipitates in zirconium. Acta Mater. 2019, 165, 528–546. [Google Scholar] [CrossRef]
- Wang, S.; Giuliani, F.; Britton, T.B. Microstructure and formation mechanisms of δ-hydrides in variable grain size Zircaloy-4 studied by electron backscatter diffraction. Acta Mater. 2019, 169, 76–87. [Google Scholar] [CrossRef]
- Bailey, J.E. Electron microscope observations on the precipitation of zirconium hydride in zirconium. Acta Metall. 1963, 11, 267–280. [Google Scholar] [CrossRef]
- Reali, L.; Balint, D.S.; Wenman, M.R. Dislocation modelling of the plastic relaxation and thermal ratchetting induced by zirconium hydride precipitation. J. Mech. Phys. Solids 2022, 167, 104988. [Google Scholar] [CrossRef]
- Liu, S.M.; Ishii, A.; Mi, S.B.; Ogata, S.; Li, J.; Han, W.Z. Dislocation-mediated hydride precipitation in zirconium. Small 2021, 18, 2105881. [Google Scholar] [CrossRef]
- Conforto, E.; Cohendoz, S.; Girault, P.; Berziou, C.; Feaugas, X. Hydride precipitates in zirconium alloys: Evolution of dissolution and precipitation temperatures during thermal cycling correlated to microstructure features. In Proceedings of the TMS 2017 146th Annual Meeting & Exhibition Supplemental Proceedings, Pittsburgh, PA, USA, February 2017; The Minerals, Metals & Materials Society TMS, Ed.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 771–782. [Google Scholar]
- Cameron, D.J.; Duncan, R.G. On the existence of a memory effect in hydride precipitation in cold-worked Zr-2.5% Nb. J. Nucl. Mater. 1977, 68, 340–344. [Google Scholar] [CrossRef]
- Carpenter, G.J.C.; Watters, J.F. An in-situ study of the dissolution of γ-zirconium hydride in zirconium. J. Nucl. Mater. 1978, 73, 190–197. [Google Scholar] [CrossRef]
- Li, W.; Hanlon, S.; Bickel, G.; Buyers, A.; Walters, L.; Long, F. Microstructure and hydrides in the near rolled-joint regions of ex-service CANDU pressure Microstructure and hydrides in the near rolled-joint regions of ex-service CANDU pressure tube tube. J. Nucl. Mater. 2020, 539, 152316. [Google Scholar] [CrossRef]
- Long, F.; Hanlon, S.; Daymond, M.R. Transformation behavior of hydrides precipitated with or without stress in Zr-2.5Nb investigated by in-situ S/TEM thermal cycling. J. Nucl. Mater. 2022, 559, 153428. [Google Scholar] [CrossRef]
- Long, F.; Goldthorpe, S.; Daymond, M.R. Effect of metallurgical variables on hydride precipitation behavior in Zr-2.5Nb micro pressure tubes. J. Nucl. Mater. 2022, 571, 153987. [Google Scholar] [CrossRef]
- Weatherly, G.C. The precipitation of γ-hydride plates in zirconium. Acta Metall. 1981, 29, 501–512. [Google Scholar] [CrossRef]
- Zhao, H.; Hu, X.; Song, M.; Ni, S. Mechanisms for deformation induced hexagonal close-packed structure to face-centered cubic structure transformation in zirconium. Scr. Mater. 2017, 132, 63–67. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Sui, M. Formation mechanism of hydride precipitation in commercially pure titanium. J. Mater. Sci. Technol. 2021, 81, 108–116. [Google Scholar] [CrossRef]
- Jia, Y.J.; Han, W.Z. Effect of external stress on hydride reorientation in zirconium. Acta Mater. 2022, 235, 118100. [Google Scholar] [CrossRef]
- Shukla, S.; Singh, P.; Roy, T.; Kashyap, Y.S.; Shukla, M.; Singh, R.N. Investigation of hydrogen diffusivity in Zr-2.5%Nb alloy pressure tube material using Metallography and Neutron Radiography. J. Nucl. Mater. 2021, 544, 152679. [Google Scholar] [CrossRef]
- Khatamian, D. Solubility and partitioning of hydrogen in metastable Zr-based alloys used in the nuclear industry. J. Alloys Compd. 1999, 293–295, 893–899. [Google Scholar] [CrossRef]
- Khatamian, D.; Ling, V.C. Hydrogen solubility limits in α- and β-zirconium. J. Alloys Compd. 1997, 253–254, 162–166. [Google Scholar] [CrossRef]
- Pittinato, G.F.; Hanna, W.D. Hydrogen in β transformed Ti-6Al-4V. Metall. Mater. Trans. B 1972, 3, 2905–2909. [Google Scholar] [CrossRef]
- Simpson, L.A.; Cann, C.D. The effect of microstructure on rates of delayed hydride cracking in Zr-2.5%Nb alloy. J. Nucl. Mater. 1984, 126, 70–73. [Google Scholar] [CrossRef]
- Krishna, K.V.M.; Srivastava, D.; Dey, G.K.; Hiwarkar, V.; Samajdar, I.; Banerjee, S. Role of grain/phase boundary nature on the formation of hydrides in Zr–2.5%Nb alloy. J. Nucl. Mater. 2011, 414, 270–275. [Google Scholar] [CrossRef]
- Perovic, V.; Weatherly, G.C.; Simpson, C.J. Hydride precipitation in α/β zirconium alloys. Acta Metall. 1983, 31, 1381–1391. [Google Scholar] [CrossRef]
- Kim, J.; Plancher, E.; Tasan, C.C. Hydrogenation-induced lattice expansion and its effects on hydrogen diffusion and damage in Ti–6Al–4V. Acta Mater. 2020, 188, 686–696. [Google Scholar] [CrossRef]
- Kim, J.; Tasan, C.C. Microstructural and micro-mechanical characterization during hydrogen charging: An in situ scanning electron microscopy study. Int. J. Hydrogen Energy 2019, 44, 6333–6343. [Google Scholar] [CrossRef]
- Perovic, V.; Weatherly, G.C.; MacEwen, S.R.; Leger, M. The influence of prior deformation on hydride precipitation in zircaloy. Acta Metall. 1992, 40, 363–372. [Google Scholar] [CrossRef]
- Chai, L.; Luan, B.; Murty, K.L.; Liu, Q. Twinning during recrystallization cooling in α-Zr alloy. Mater. Sci. Eng. A 2013, 576, 320–325. [Google Scholar] [CrossRef]
- Qin, W.; Kumar, N.A.P.K.; Szpunar, J.A.; Kozinski, J. Intergranular δ-hydride nucleation and orientation in zirconium alloys. Acta Mater. 2011, 59, 7010–7021. [Google Scholar] [CrossRef]
- Ambler, J.F.R. Grain boundary hydride habit in Zircaloy-2. J. Nucl. Mater. 1968, 28, 237–245. [Google Scholar] [CrossRef]
- Kumar, N.A.P.K.; Szpunar, J.A.; He, Z. Preferential precipitation of hydrides in textured zircaloy-4 sheets. J. Nucl. Mater. 2010, 403, 101–107. [Google Scholar] [CrossRef]
- Arunachalam, V.S.; Lehtinen, B.; Ostberg, G. The orientation of zirconium hydride on grain boundaries in zircaloy-2. J. Nucl. Mater. 1967, 21, 241–248. [Google Scholar] [CrossRef]
- Kim, J.S.; Kim, S.D.; Yoon, J. Hydride formation on deformation twin in zirconium alloy. J. Nucl. Mater. 2016, 482, 88–92. [Google Scholar] [CrossRef]
- Yan, C.; Wang, R.; Wang, Y.; Wang, X.; Bai, G. Effects of ion irradiation on microstructure and properties of zirconium alloys—A review. Nucl. Eng. Technol. 2015, 47, 323–331. [Google Scholar] [CrossRef] [Green Version]
- Vizcaino, P.; Banchik, A.D.; Abriata, J.P. Hydrogen in Zircaloy-4: Effects of the neutron irradiation on the hydride formation. J. Mater. Sci. 2007, 42, 6633–6637. [Google Scholar] [CrossRef]
- Christensen, M.; Wolf, W.; Freeman, C.; Wimmer, E.; Adamson, R.B.; Hallstadius, L.; Cantonwine, P.E.; Mader, E.V. H in α-Zr and in zirconium hydrides: Solubility, effect on dimensional changes, and the role of defects. J. Phys. Condens. Matter. 2014, 27, 025402. [Google Scholar] [CrossRef] [Green Version]
- Vizcaino, P.; Banchik, A.D.; Abriata, J.P. Solubility of hydrogen in Zircaloy-4: Irradiation induced increase and thermal recovery. J. Nucl. Mater. 2002, 304, 96–106. [Google Scholar] [CrossRef]
- Liu, S.M.; Beyerlein, I.J.; Han, W.Z. Two-dimensional vacancy platelets as precursors for basal dislocation loops in hexagonal zirconium. Nat. Commun. 2020, 11, 5766. [Google Scholar] [CrossRef] [PubMed]
- Tournadre, L.; Onimus, F.; Bechade, J.L. Toward a better understanding of the hydrogen impact on the radiation induced growth of zirconium alloys. J. Nucl. Mater. 2013, 441, 222–231. [Google Scholar] [CrossRef]
- Li, F.; Li, S.; Liu, G.; Chen, X.; Wang, Y. Formation and characterization of circular δ-hydride in Zircaloy-4 under ion irradiation. J. Nucl. Mater. 2019, 513, 1–7. [Google Scholar] [CrossRef]
- Oono, N.; Kasada, R.; Higuchi, T.; Sakamoto, K.; Nakatsuka, M.; Hasegawa, A.; Kondo, S.; Iwata, N.Y.; Matsui, H.; Kimura, A. Comparison of irradiation hardening and microstructure evolution in ion-irradiated delta and epsilon hydrides. J. Nucl. Mater. 2013, 442, S826–S829. [Google Scholar] [CrossRef]
- Chu, H.C.; Wu, S.K.; Kuo, R.C. Hydride reorientation in Zircaloy-4 cladding. J. Nucl. Mater. 2008, 373, 319–327. [Google Scholar] [CrossRef]
- Kim, Y.J.; Kook, D.H.; Kim, T.H.; Kim, J.S. Stress and temperature-dependent hydride reorientation of Zircaloy-4 cladding and its effect on the ductility degradation. J. Nucl. Sci. Technol. 2014, 52, 717–727. [Google Scholar] [CrossRef]
- Cinbiz, M.N.; Koss, D.A.; Motta, A.T. The influence of stress state on the reorientation of hydrides in a zirconium alloy. J. Nucl. Mater. 2016, 477, 157–164. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.I.; Lee, K.W. Stress-induced reorientation of hydrides and mechanical properties of Zircaloy-4 cladding tubes. J. Nucl. Mater. 2005, 340, 203–208. [Google Scholar] [CrossRef]
- Kim, J.S.; Kim, Y.J.; Kook, D.H.; Kim, Y.S. A study on hydride reorientation of Zircaloy-4 cladding tube under stress. J. Nucl. Mater. 2015, 456, 246–252. [Google Scholar] [CrossRef]
- Lee, J.M.; Kim, H.A.; Kook, D.H.; Kim, Y.S. A study on the effects of hydrogen content and peak temperature on threshold stress for hydride reorientation in Zircaloy-4 cladding. J. Nucl. Mater. 2018, 509, 285–294. [Google Scholar] [CrossRef]
- Cha, H.; Won, J.J.; Jang, K.N.; An, J.H.; Kim, K.T. Tensile hoop stress-, hydrogen content- and cooling rate-dependent hydride reorientation behaviors of Zr alloy cladding tubes. J. Nucl. Mater. 2015, 464, 53–60. [Google Scholar] [CrossRef]
- Singh, R.N.; Mikin, L.; Dey, G.K.; Sah, D.N.; Batra, I.S.; Stahle, P. Influence of temperature on threshold stress for reorientation of hydrides and residual stress variation across thickness of Zr–2.5Nb alloy pressure tube. J. Nucl. Mater. 2006, 359, 208–219. [Google Scholar] [CrossRef]
- Marshall, R.P. Control of hydride orientation in zircaloy by fabrication practice. J. Nucl. Mater. 1967, 24, 49–59. [Google Scholar] [CrossRef]
- Marshall, R.P. Influence of fabrication history on stress-oriented hydrides in zircaloy tubing. J. Nucl. Mater. 1967, 24, 34–48. [Google Scholar] [CrossRef]
- Sakamoto, K.; Nakatsuka, M. Stress reorientation of hydrides in recrystallized Zircaloy-2 sheet. J. Nucl. Sci. Technol. 2006, 43, 1136–1141. [Google Scholar] [CrossRef]
- Billone, M.C.; Burtseva, T.A.; Einziger, R.E. Ductile-to-brittle transition temperature for high-burnup cladding alloys exposed to simulated drying-storage conditions. J. Nucl. Mater. 2013, 433, 431–448. [Google Scholar] [CrossRef]
- Hardie, D.; Shanahan, M.W. Stress reorientation of hydrides in zirconium−2.5% niobium. J. Nucl. Mater. 1975, 55, 1–13. [Google Scholar] [CrossRef]
- Min, S.J.; Kim, M.S.; Kim, K.T. Cooling rate- and hydrogen content-dependent hydride reorientation and mechanical property degradation of Zr–Nb alloy claddings. J. Nucl. Mater. 2013, 441, 306–314. [Google Scholar] [CrossRef]
- Singh, R.N.; Kishore, R.; Singh, S.S.; Sinha, T.K.; Kashyap, B.P. Stress-reorientation of hydrides and hydride embrittlement of Zr–2.5 wt% Nb pressure tube alloy. J. Nucl. Mater. 2004, 325, 26–33. [Google Scholar] [CrossRef]
- Desquines, J.; Drouan, D.; Billone, M.; Puls, M.P.; March, P.; Fourgeaud, S.; Getrey, C.; Elbaz, V. Influence of temperature and hydrogen content on stress-induced radial hydride precipitation in Zircaloy-4 cladding. J. Nucl. Mater. 2014, 453, 131–150. [Google Scholar] [CrossRef]
- Colas, K.B.; Motta, A.T.; Almer, J.D.; Daymond, M.R.; Kerr, M.; Banchik, A.D.; Vizcaino, P.; Santisteban, J.R. In situ study of hydride precipitation kinetics and re-orientation in Zircaloy using synchrotron radiation. Acta Mater. 2010, 58, 6575–6583. [Google Scholar] [CrossRef]
- Colas, K.B.; Motta, A.T.; Daymond, M.R.; Almer, J.D. Effect of thermos-mechanical cycling on zirconium hydride reorientation studied in situ with synchrotron X-ray diffraction. J. Nucl. Mater. 2013, 440, 586–595. [Google Scholar] [CrossRef]
- Kim, S.; Kang, J.H.; Lee, Y. Hydride embrittlement resistance of Zircaloy-4 and Zr-Nb alloy cladding tubes and its implications on spent fuel management. J. Nucl. Mater. 2022, 599, 153393. [Google Scholar] [CrossRef]
- Qin, W.; Szpunar, J.A.; Kumar, N.A.P.K.; Kozinski, J. Microstructural criteria for abrupt ductile-to-brittle transition induced by δ-hydrides in zirconium alloys. Acta Mater. 2014, 81, 219–229. [Google Scholar] [CrossRef]
- Thuinet, L.; Legris, A.; Zhang, L.; Ambard, A. Mesoscale modeling of coherent zirconium hydride precipitation under an applied stress. J. Nucl. Mater. 2013, 438, 32–40. [Google Scholar] [CrossRef]
- Simon, P.C.A.; Aagesen, L.K.; Jokisaari, A.M.; Chen, L.Q.; Daymond, M.R.; Motta, A.T.; Tonks, M.R. Investigation of δ zirconium hydride morphology in a single crystal using quantitative phase field simulations supported by experiments. J. Nucl. Mater. 2021, 557, 153303. [Google Scholar] [CrossRef]
- Cann, C.D.; Sexton, E.E. An electron optical study of hydride precipitation and growth at crack tips in zirconium. Acta Metall. 1980, 28, 1215–1221. [Google Scholar] [CrossRef]
- Une, K.; Nogita, K.; Ishimoto, S.; Ogata, K. Crystallography of zirconium hydrides in recrystallized zircaloy-2 fuel cladding by electron backscatter diffraction. J. Nucl. Sci. Technol. 2004, 41, 731–740. [Google Scholar] [CrossRef]
- Une, K.; Ishimoto, S. EBSP measurements of hydrogenated Zircaloy-2 claddings with stress-relieved and recrystallized annealing conditions. J. Nucl. Mater. 2006, 357, 147–155. [Google Scholar] [CrossRef]
- Alvarez, M.A.V.; Santisteban, J.R.; Vizcaino, P.; Flores, A.V.; Banchik, A.D. Hydride reorientation in Zr2.5Nb studied by synchrotron X-ray diffraction. Acta Mater. 2012, 60, 6892–6906. [Google Scholar] [CrossRef]
- Toghraee, A.; Bair, J.; Zaeem, M.A. Effects of applied load on formation and reorientation of zirconium hydrides: A multiphase field modeling study. Comput. Mater. Sci. 2021, 192, 110367. [Google Scholar] [CrossRef]
- Puls, M.P.; Shi, S.Q.; Rabier, J. Experimental studies of mechanical properties of solid zirconium hydrides. J. Nucl. Mater. 2005, 336, 73–80. [Google Scholar] [CrossRef]
- Xu, J.; Shi, S.Q. Investigation of mechanical properties of ε-zirconium hydride using micro- and nano-indentation techniques. J. Nucl. Mater. 2004, 327, 165–170. [Google Scholar] [CrossRef]
- Wang, Z.; Garbe, U.; Li, H.; Studer, A.J.; Harrison, R.P.; Callaghan, M.D.; Wang, Y.; Liao, X. Hydrogen-induced microstructure, texture and mechanical property evolutions in a high-pressure torsion processed zirconium alloy. Scr. Mater. 2012, 67, 752–755. [Google Scholar] [CrossRef] [Green Version]
- Simpson, L.A.; Cann, C.D. Fracture toughness of zirconium hydride and its influence on the crack resistance of zirconium alloys. J. Nucl. Mater. 1979, 87, 303–316. [Google Scholar] [CrossRef]
- Sarkar, A.; Boopathy, K.; Eapen, J.; Murty, K.L. Creep behavior of hydrogenated zirconium alloys. J. Mater. Eng. Perform. 2014, 23, 3649–3656. [Google Scholar] [CrossRef]
- Suman, S.; Khan, M.K.; Pathak, M.; Singh, R.N. Effects of hydrogen on thermal creep behaviour of Zircaloy fuel cladding. J. Nucl. Mater. 2018, 498, 20–32. [Google Scholar] [CrossRef]
- Wang, S.; Giuliani, F.; Britton, T.B. Slip–hydride interactions in Zircaloy-4: Multiscale mechanical testing and characterization. Acta Mater. 2020, 200, 537–550. [Google Scholar] [CrossRef]
- Dutton, R.; Nuttall, K.; Puls, M.P.; Simpson, L.A. Mechanisms of hydrogen induced delayed cracking in hydride forming materials. Metall. Trans. 1977, 8, 1553–1562. [Google Scholar] [CrossRef]
- Puls, M.P. Review of the thermodynamic basis for models of delayed hydride cracking rate in zirconium alloys. J. Nucl. Mater. 2009, 393, 350–367. [Google Scholar] [CrossRef]
- Kim, Y.S.; Park, S.S. Stage I and II behaviors of delayed hydride cracking velocity in zirconium alloys. J. Alloys Compd. 2008, 453, 210–214. [Google Scholar] [CrossRef]
- Kim, Y.S. Driving force for delayed hydride cracking of zirconium alloys. Met. Mater. Int. 2005, 11, 29–38. [Google Scholar] [CrossRef]
- Kim, Y.S. Comment on ‘The first step for delayed hydride cracking in zirconium alloys’ by G.A. McRae et al., J. Nucl. Mater. 396 (2010) 130–143. J. Nucl. Mater. 2010, 396, 144–148. [Google Scholar] [CrossRef]
- Kim, Y.S.; Ahn, S.B.; Cheong, Y.M. Precipitation of crack tip hydrides in zirconium alloys. J. Alloys Compd. 2007, 429, 221–226. [Google Scholar] [CrossRef]
- McRae, G.A.; Coleman, C.E.; Leitch, B.W. The first step for delayed hydride cracking in zirconium alloys. J. Nucl. Mater. 2010, 396, 130–143. [Google Scholar] [CrossRef]
- Puls, M.P. Comments on author’s reply to “Review of the thermodynamic basis for models of delayed hydride cracking rate in zirconium alloys”, M.P. Puls in J. Nucl. Mater. 393 (2009) 350–367. J. Nucl. Mater. 2010, 399, 248–258. [Google Scholar] [CrossRef]
- Ponzoni, L.M.E.; Mieza, J.I.; Heras, E.D.L.; Domizzi, G. Comparison of delayed hydride cracking behavior of two zirconium alloys. J. Nucl. Mater. 2013, 439, 238–242. [Google Scholar] [CrossRef]
- Shi, S.Q.; Shek, G.K.; Puls, M.P. Hydrogen concentration limit and critical temperatures for delayed hydride cracking in zirconium alloys. J. Nucl. Mater. 1995, 218, 189–201. [Google Scholar] [CrossRef]
- Singh, R.N.; Roychowdhury, S.; Sinha, V.P.; Sinha, T.K.; De, P.K.; Banerjee, S. Delayed hydride cracking in Zr–2.5Nb pressure tube material: Influence of fabrication routes. Mater. Sci. Eng. A 2004, 374, 342–350. [Google Scholar] [CrossRef]
- Sunil, S.; Bind, A.K.; Khandelwal, H.K.; Singh, R.N.; Chakravartty, J.K. Delayed hydride cracking behavior of Zr-2.5Nb alloy pressure tubes for PHWR700. J. Nucl. Mater. 2015, 466, 208–219. [Google Scholar] [CrossRef]
- Shimada, S.; Etoh, E.; Hayashi, H.; Tukuta, Y. A metallographic and fractographic study of outside-in cracking caused by power ramp tests. J. Nucl. Mater. 2004, 327, 97–113. [Google Scholar] [CrossRef]
- Kubo, T.; Kobayashi, Y.; Uchikoshi, H. Measurements of delayed hydride cracking propagation rate in the radial direction of Zircaloy-2 cladding tubes. J. Nucl. Mater. 2012, 427, 18–29. [Google Scholar] [CrossRef]
- Holston, A.M.A.; Stjarnsater, J. On the effect of temperature on the threshold stress intensity factor of delayed hydride cracking in light water reactor fuel cladding. Nucl. Eng. Technol. 2017, 49, 663–667. [Google Scholar] [CrossRef]
- Menibus, A.H.; Auzoux, Q.; Dieye, O.; Berger, P.; Bosonnet, S.; Foy, E.; Macdonald, V.; Besson, J.; Crepin, J. Formation and characterization of hydride blisters in Zircaloy-4 cladding tubes. J. Nucl. Mater. 2014, 449, 132–147. [Google Scholar] [CrossRef] [Green Version]
- Nagase, F. Hydride behavior in Zircaloy cladding tube during high-temperature transients. J. Nucl. Mater. 2011, 415, 117–122. [Google Scholar] [CrossRef]
- Singh, R.N.; Kishore, R.; Sinha, T.K.; Kashyap, B.P. Hydride blister formation in Zr–2.5wt%Nb pressure tube alloy. J. Nucl. Mater. 2002, 301, 153–164. [Google Scholar] [CrossRef]
- Alvarez, M.A.V.; Santisteban, J.R.; Domizzi, G.; Almer, A. Phase and texture analysis of a hydride blister in a Zr–2.5%Nb tube by synchrotron X-ray diffraction. Acta Mater. 2011, 59, 2210–2220. [Google Scholar] [CrossRef]
- Kerr, D.; Long, F.; Domizzi, G.; Daymond, M.R. Orientation relationships between α-zirconium and δ-hydride within a hydride blister. J. Appl. Crystallogr. 2017, 50, 349–356. [Google Scholar] [CrossRef]
- Santisteban, J.R.; Steuwer, A.; Domizzi, G.; Pell, M.J. Determination of residual stresses around blisters in Zr-2.5%Nb pressure tubes. Powder Diffr. 2009, 24, S72–S76. [Google Scholar] [CrossRef] [Green Version]
- Domizzi, G.; Vigna, G.; Bermudez, S.; Garcia, J.O. Hydride distribution around a blister in Zr–2.5Nb pressure tubes. J. Nucl. Mater. 1999, 275, 255–267. [Google Scholar] [CrossRef]
- Field, G.J.; Dunn, J.T.; Cheadle, B.A. Analysis of the pressure tube failure at pickering NGS “A” Unit 2 nuclear systems department. Can. Metall. Q 1985, 24, 181–188. [Google Scholar] [CrossRef]
- Menibus, A.H.; Auzoux, Q.; Mongabure, P.; Macdonald, V.; Jolu, T.L.; Besson, J.; Crepin, J. Fracture of Zircaloy-4 cladding tubes with or without hydride blisters in uniaxial to plane strain conditions with standard and optimized expansion due to compression tests. Mater. Sci. Eng. A 2014, 604, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Pierron, O.N.; Koss, D.A.; Motta, A.T.; Chan, K.S. The influence of hydride blisters on the fracture of Zircaloy-4. J. Nucl. Mater. 2003, 322, 21–35. [Google Scholar] [CrossRef]
- Kuroda, M.; Yoshioka, K.; Yamanaka, S.; Anada, H.; Nagase, F.; Uetsuka, H. Influence of precipitated hydride on the fracture behavior of zircaloy fuel cladding tube. J. Nucl. Sci. Technol. 2000, 37, 670–675. [Google Scholar] [CrossRef]
- Nagase, F.; Fuketa, T. Investigation of hydride rim effect on failure of Zircaloy-4 cladding with tube burst test. J. Nucl. Sci. Technol. 2005, 42, 58–65. [Google Scholar] [CrossRef]
- Kim, J.S.; Kim, H.A.; Kang, S.Y.; Kim, Y.S. Effects of hydride rim on the ductility of Zircaloy-4 cladding. J. Nucl. Mater. 2019, 523, 383–390. [Google Scholar] [CrossRef]
- Puls, M.P. Determination of fracture initiation in hydride blisters using acoustic emission. Metall. Trans. A 1988, 19, 2247–2257. [Google Scholar] [CrossRef]
- Plyasov, A.A.; Novikov, V.V.; Devyatko, Y.N. A review of hydride reorientation in zirconium alloys for water-cooled reactors. Phys. At. Nucl. 2020, 83, 1407–1424. [Google Scholar] [CrossRef]
- Raynaud, P.A.; Koss, D.A.; Motta, A.T. Crack growth in the through-thickness direction of hydrided thin-wall Zircaloy sheet. J. Nucl. Mater. 2012, 420, 69–82. [Google Scholar] [CrossRef]
- Chu, H.C.; Wu, S.K.; Chien, K.F.; Kuo, R.C. Effect of radial hydrides on the axial and hoop mechanical properties of Zircaloy-4 cladding. J. Nucl. Mater. 2007, 362, 93–103. [Google Scholar] [CrossRef]
- Kim, J.S.; Kim, T.H.; Kook, D.H.; Kim, Y.S. Effects of hydride morphology on the embrittlement of Zircaloy-4 cladding. J. Nucl. Mater. 2015, 456, 235–245. [Google Scholar] [CrossRef]
- Sharma, R.K.; Bind, A.K.; Avinash, G.; Singh, R.N.; Tewari, A.; Kashyap, B.P. Effect of radial hydride fraction on fracture toughness of CWSR Zr-2.5%Nb pressure tube material between ambient and 300 °C temperatures. J. Nucl. Mater. 2018, 508, 546–555. [Google Scholar] [CrossRef]
- Min, S.J.; Won, J.J.; Kim, K.T. Terminal cool-down temperature-dependent hydride reorientations in Zr–Nb Alloy claddings under dry storage conditions. J. Nucl. Mater. 2014, 448, 172–183. [Google Scholar] [CrossRef]
- Sharma, R.K.; Sunil, S.; Kumawat, B.K.; Singh, R.N.; Tewari, A.; Kashyap, B.P. Influence of hydride orientation on fracture toughness of CWSR Zr-2.5%Nb pressure tube material between RT and 300 °C. J. Nucl. Mater. 2017, 488, 231–244. [Google Scholar] [CrossRef]
- Chan, K.S. A fracture model for hydride-induced embrittlement. Acta Metall. 1995, 43, 4325–4335. [Google Scholar] [CrossRef]
- Qin, W.; Szpunar, J.A.; Kozinski, J. Hydride-induced degradation of hoop ductility in textured zirconium-alloy tubes: A theoretical analysis. Acta Mater. 2012, 60, 4845–4855. [Google Scholar] [CrossRef]
- Daum, R.S.; Majumdar, S.; Liu, Y.; Billone, M.C. Radial-hydride embrittlement of high-burnup Zircaloy-4 fuel cladding. J. Nucl. Sci. Technol. 2006, 43, 1054–1067. [Google Scholar] [CrossRef]
- Li, J.; Li, M.; Guan, B.; Xin, Y.; Wu, Y.; Liu, X.; Chen, G. Uncovering the hydride orientation-mediated hoop fatigue mechanism in a zirconium alloy cladding tube. Int. J. Plast. 2022, 159, 103440. [Google Scholar] [CrossRef]
- Wang, H.; Thomas, J.; Okuniewski, M.A.; Tomar, V. Constitutive modeling of δ-phase zircaloy hydride based on strain rate dependent nanoindentation and nano-scale impact dataset. Int. J. Plast. 2020, 133, 102787. [Google Scholar] [CrossRef]
- Kubo, T.; Kobayashi, Y.; Uchikoshi, H. Determination of fracture strength of δ-zirconium hydrides embedded in zirconium matrix at high temperatures. J. Nucl. Mater. 2013, 435, 222–230. [Google Scholar] [CrossRef]
- Choubey, R.; Puls, M.P. Crack initiation at long radial hydrides in Zr-2.5nb pressure tube material at elevated temperatures. Metall. Mater. Trans. A 1994, 25, 993–1004. [Google Scholar] [CrossRef]
- Tondro, A.; Abdolvand, H. Quantifying hydrogen concentration in the vicinity of zirconium hydrides and deformation twins. J. Mech. Phys. Solids 2021, 148, 104287. [Google Scholar] [CrossRef]
- Courty, O.; Motta, A.T.; Hales, J.D. Modeling and simulation of hydrogen behavior in Zircaloy-4 fuel cladding. J. Nucl. Mater. 2014, 452, 311–320. [Google Scholar] [CrossRef]
- Tummala, H.; Capolungo, L.; Tome, C.N. Quantifying the stress state in the vicinity of a δ-hydride in α-zirconium. J. Nucl. Mater. 2018, 511, 406–416. [Google Scholar] [CrossRef]
- Abdolvand, H. Progressive modelling and experimentation of hydrogen diffusion and precipitation in anisotropic polycrystals. Int. J. Plast. 2019, 116, 39–61. [Google Scholar] [CrossRef]
- Noordhoek, M.J.; Liang, T.; Chiang, T.W.; Sinnott, S.B.; Phillpot, S.R. Mechanisms of Zr surface corrosion determined via molecular dynamics simulations with charge-optimized many-body (COMB) potentials. J. Nucl. Mater. 2014, 452, 285–295. [Google Scholar] [CrossRef]
- Phillpot, S.R.; Antony, A.C.; Shi, L.; Fullarton, M.L.; Liang, T.; Sinnott, S.B.; Zhang, Y.; Biner, S.B. Charge Optimized Many Body (COMB) potentials for simulation of nuclear fuel and clad. Comput. Mater. Sci. 2018, 148, 231–241. [Google Scholar] [CrossRef]


| OR | [uvtw]α | [uvw]hydride | Misfit between γ and α (%) | Misfit between δ and α (%) |
|---|---|---|---|---|
| {0001}//{111} <110>//<110> | [0001] | [111] | 5.69 | 7.25 |
| [110] | [110] | 0.54 | 4.60 | |
| [100] | [112] | 5.64 | 4.58 | |
| {0001}//{001} <110>//<110> | [0001] | [001] | −3.48 | −7.09 |
| [110] | [110] | 0.54 | 4.60 | |
| [100] | [110] | 16.14 | 20.82 |
| Parameter | Definition | Calculation Formula | Variable |
|---|---|---|---|
| Fn(40) | Fraction of the number of radial hydrides | ||
| N Number of all hydrides | |||
| F1(45) | Fraction of the length of radial hydrides | 𝐿45Length of hydrides in the radial direction ±45° | |
| L Length of all hydrides | |||
| RHF | Radial-hydride fraction | Weighting factor; value for hydride in the radial direction between 0–35 is 1, value for the direction between 35 and 50 is 0.5, and value for the direction between 50–90 is 0. | |
| RHCF | Radial-hydride continuity factor | 𝐿𝑅Maximum length of the continuous radial hydride | |
| Cladding-wall thickness |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Y.-J.; Han, W.-Z. Mechanisms of Hydride Nucleation, Growth, Reorientation, and Embrittlement in Zirconium: A Review. Materials 2023, 16, 2419. https://doi.org/10.3390/ma16062419
Jia Y-J, Han W-Z. Mechanisms of Hydride Nucleation, Growth, Reorientation, and Embrittlement in Zirconium: A Review. Materials. 2023; 16(6):2419. https://doi.org/10.3390/ma16062419
Chicago/Turabian StyleJia, Yu-Jie, and Wei-Zhong Han. 2023. "Mechanisms of Hydride Nucleation, Growth, Reorientation, and Embrittlement in Zirconium: A Review" Materials 16, no. 6: 2419. https://doi.org/10.3390/ma16062419
APA StyleJia, Y.-J., & Han, W.-Z. (2023). Mechanisms of Hydride Nucleation, Growth, Reorientation, and Embrittlement in Zirconium: A Review. Materials, 16(6), 2419. https://doi.org/10.3390/ma16062419