Evolution of the Strengthening Effects of In Situ TiB Fibers in a Ti Composite with Various Levels of Thermal Processing
Abstract
1. Introduction
2. Experimental Procedures
2.1. Preparation of the Composite
2.2. Thermal Deformation
2.3. Characterization of Microstructure and Mechanical Properties
3. Results and Discussion
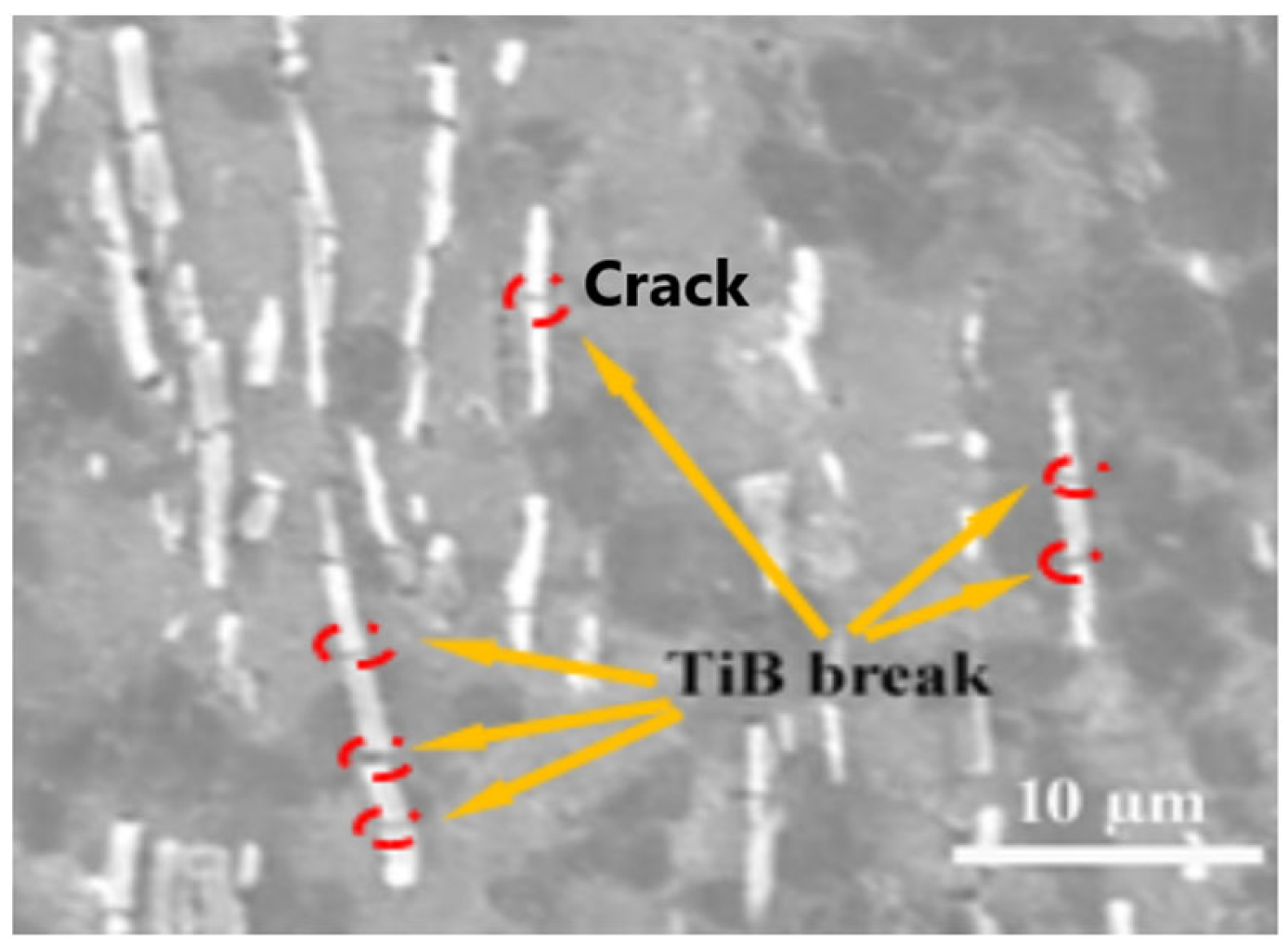
3.1. The Morphology and Formation Mechanism of TiB Fibers
3.2. Changes in Microstructure during Thermal Deformation
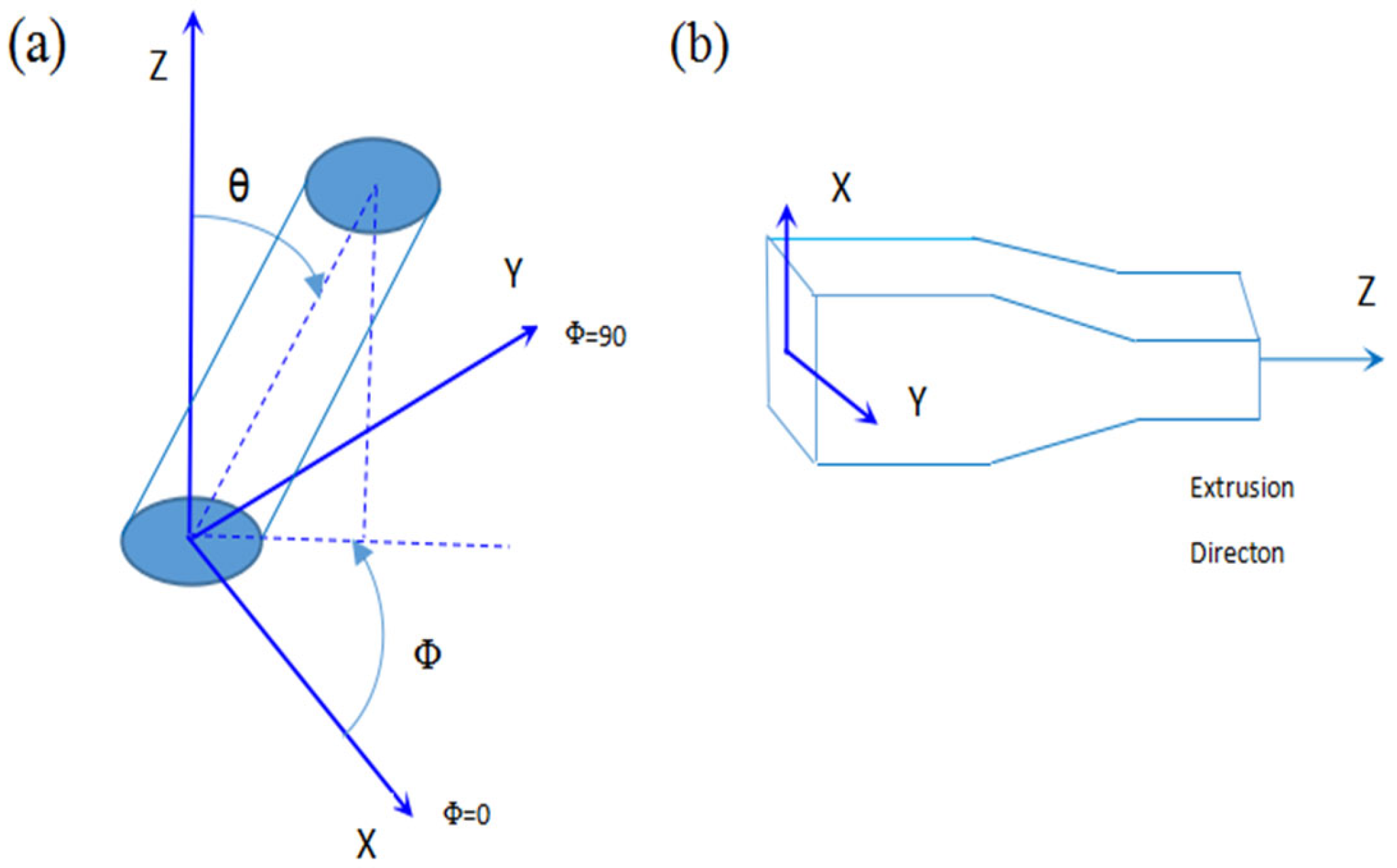
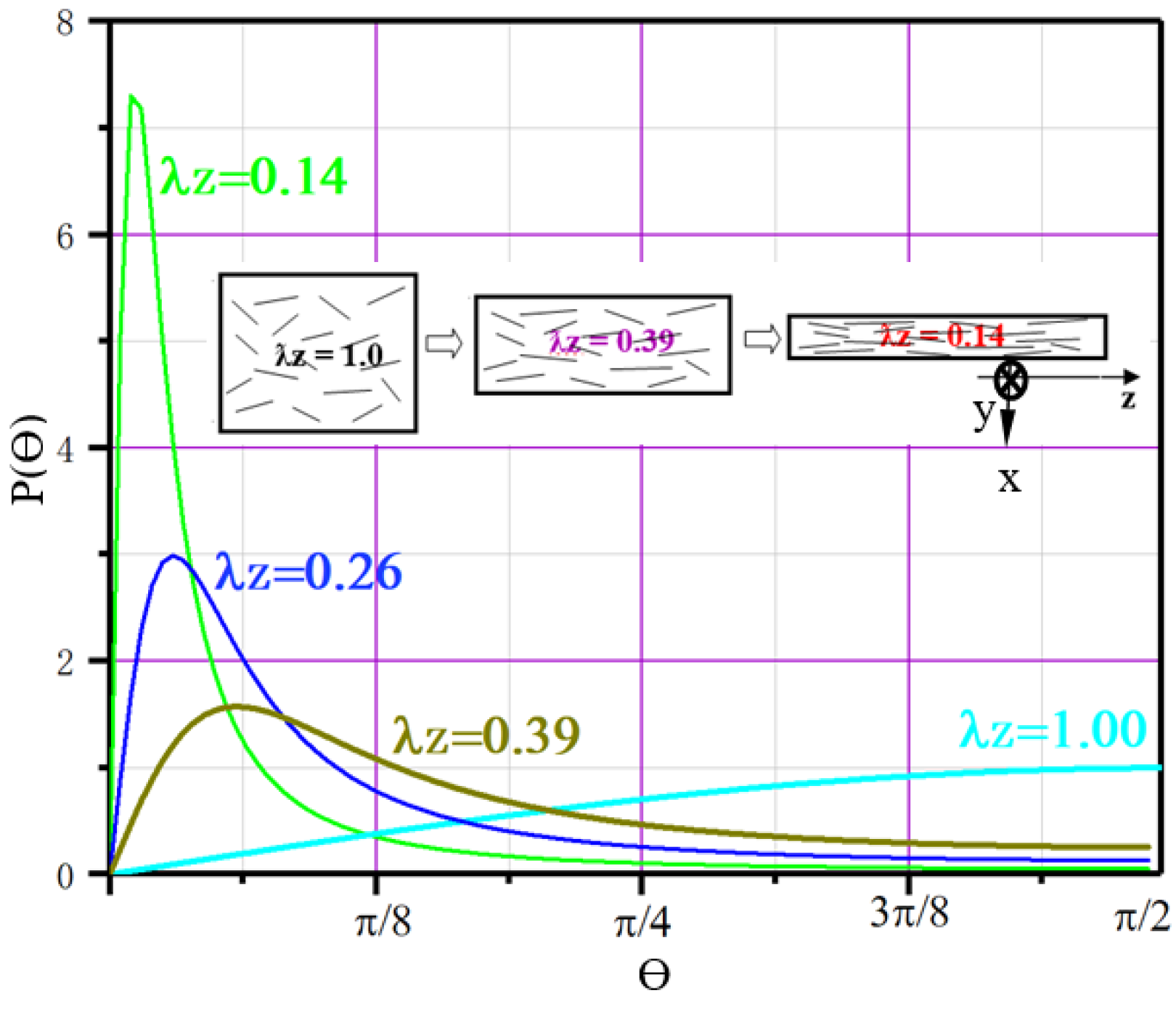
3.2.1. Changes in the Orientation of TiB Fibers
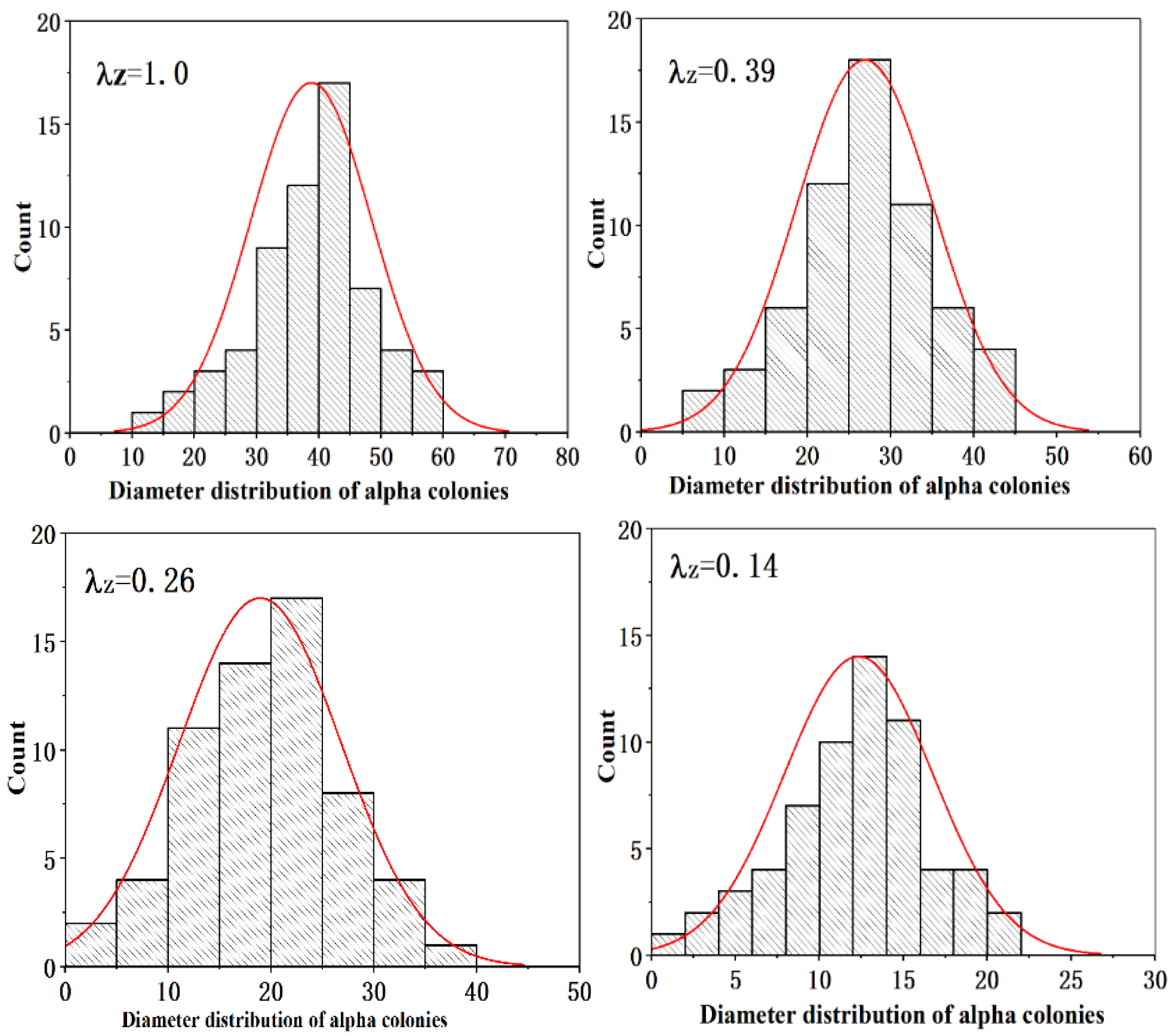
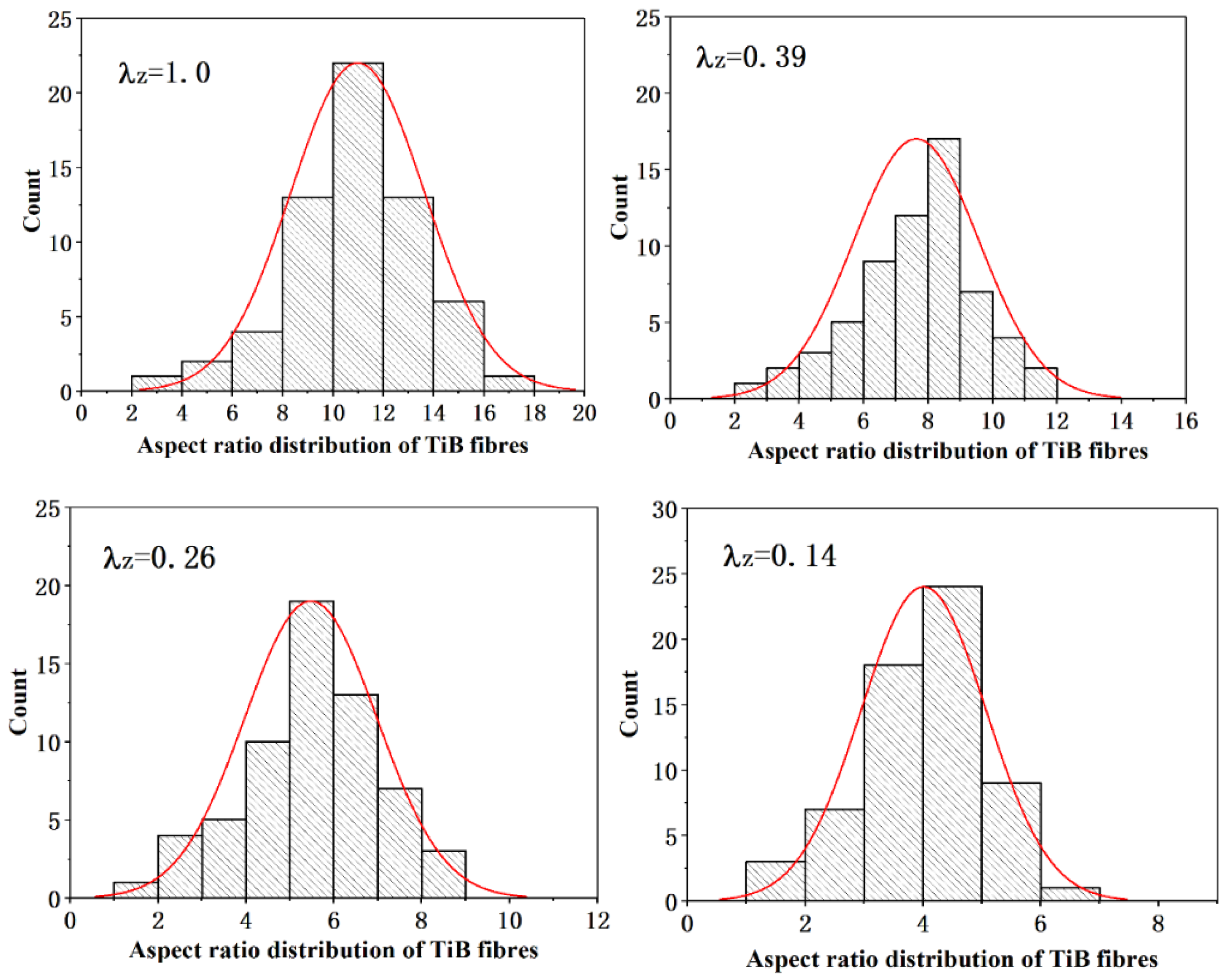
3.2.2. Changes in the Size of the Alpha Colonies and the Aspect Ratio of TiB Fibers
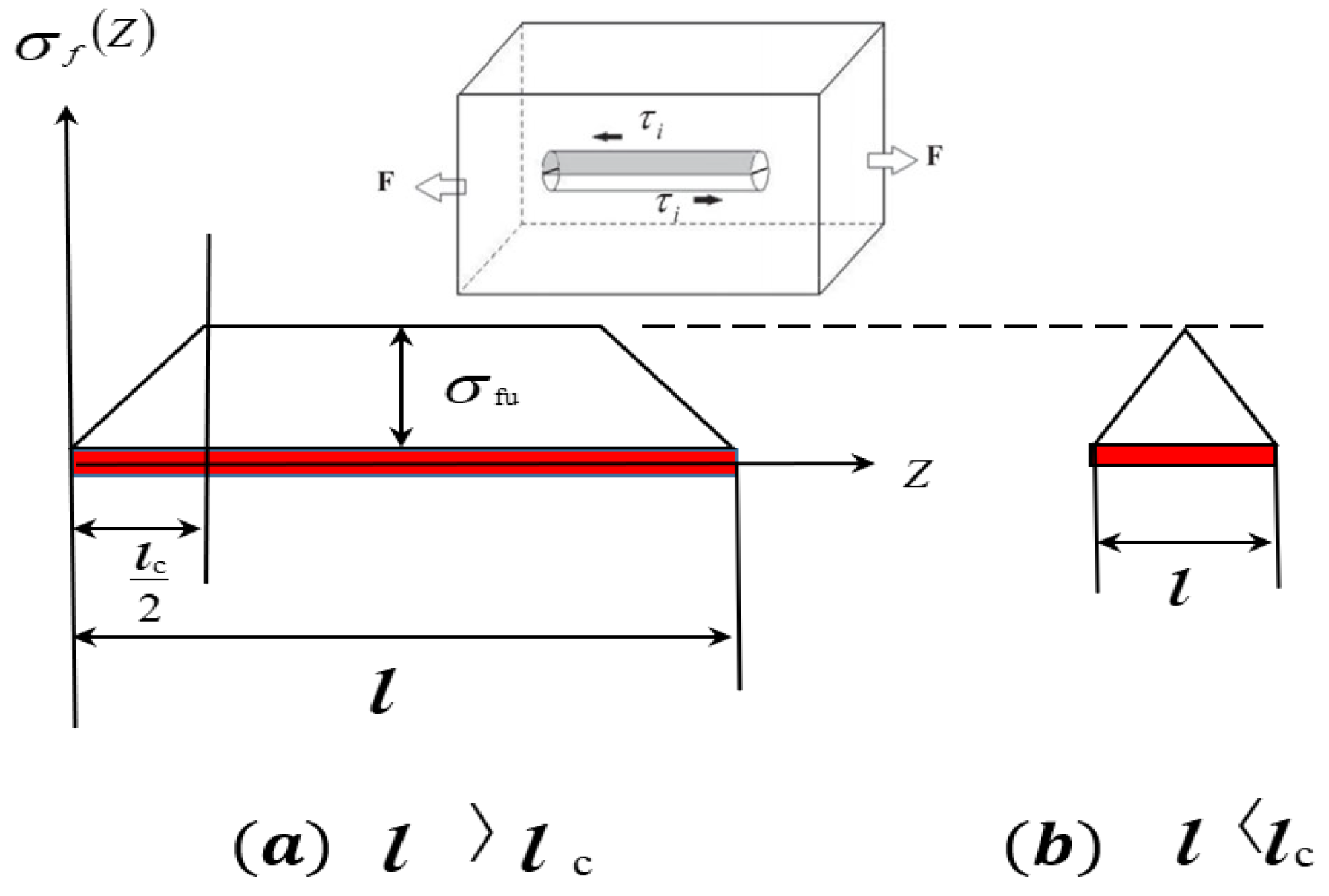
3.3. Model of the Strengthening Effect of the Short In Situ TiB Fibers
3.4. Strengthening through Microstructural Refinement
4. Conclusions
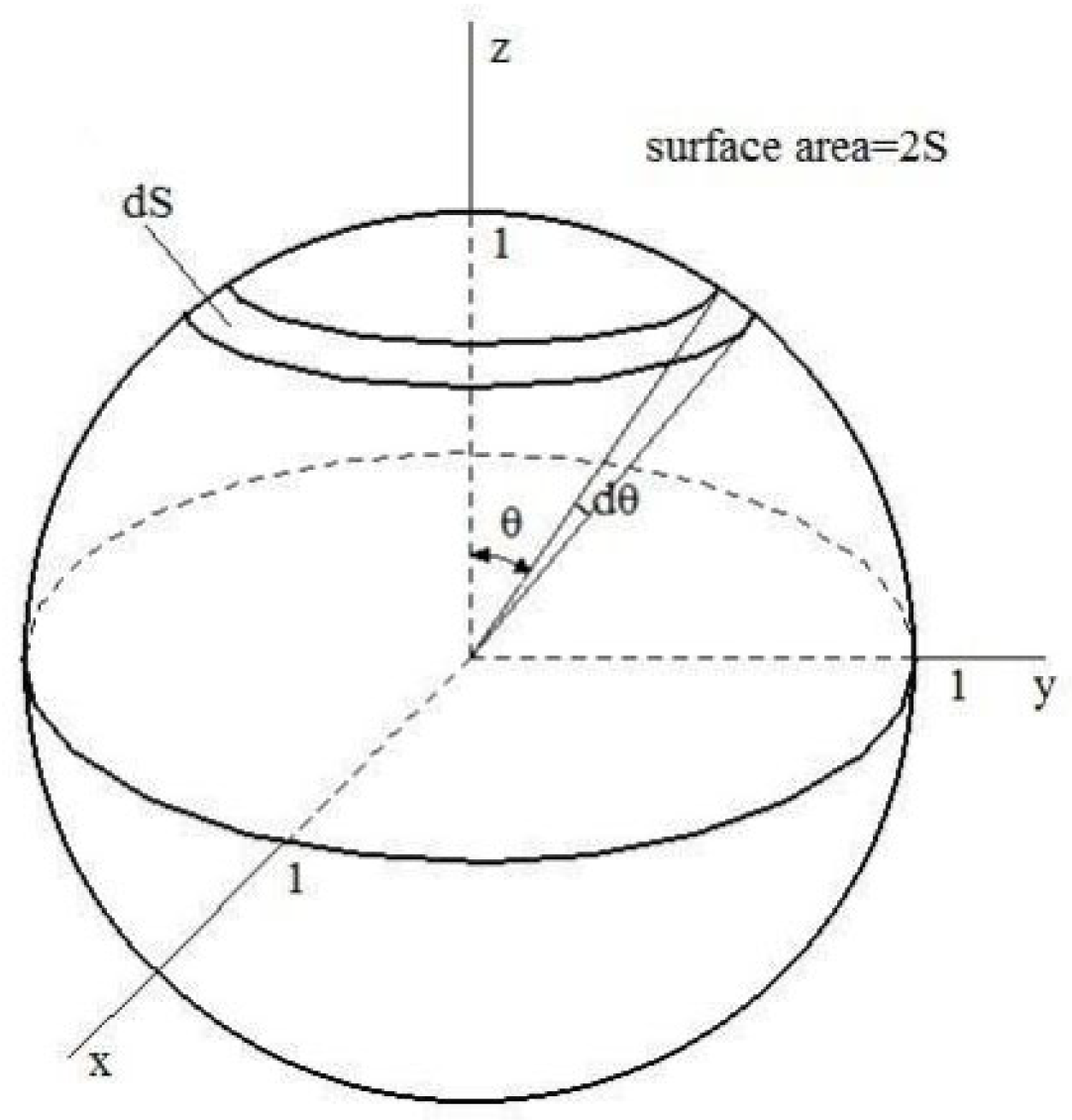
- The orientation of the TiB fibers was totally random in the as-cast composite, and the probability density distribution function of the TiB fibers’ orientation (P(θ)) with respect to the direction of elongation can be described as . Based on a shear-lag model of stress transfer, the equation of the strengthening factor (C0) of in situ TiB fibers was simplified. In this equation, C0 can be calculated with the distribution density function of the TiB fibers’ orientation (P(θ)), and C0 was calculated to be just 0.125 for the as-cast composite because of the random distribution of the TiB fibers’ orientation.
- The distribution of the aspect ratio of the TiB fibers was changed by thermal processing because the TiB fibers broke. The aspect ratio of the fibers decreased with the deformation ratio, which could be interpreted by the shear-lag model. According to this model, TiB fibers tend to break if their length/aspect ratio is larger than the critical length/aspect ratio. Furthermore, the alpha colonies in the composite were refined significantly by thermal deformation.
- With the pseudo-affine deformation scheme, the evolution of the TiB fibers’ orientation and their probability density distribution function during compression deformation was deduced and modeled. With this model, the strengthening factor (C0) was calculated to be 0.520, 0.688 and 0.858 for λZ = 0.39, 0.26 and 0.14, respectively. Compared with the as-cast composite, C0 was improved significantly by thermal processing with different deformation ratios. The modeled C0 of the TiB fibers agreed well with the measured C0 of the as-cast composite. However, the modeled values deviated gradually upward from the measured ones when the deformation ratio increased. This deviation in C0 may be attributed to the TiB fibers breaking during thermomechanical processing, which decreased the stress in the TiB fibers transferred from the matrix described by the shear-lag model.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huang, L.J.; Geng, L.; Peng, H.X. Microstructurally inhomogeneous composites: Is a homogeneous reinforcement distribution optimal? Prog. Mater. Sci. 2015, 71, 93–168. [Google Scholar] [CrossRef]
- Tjong, S.C.; Ma, Z.Y. Microstructural and mechanical characteristics of in situ metal matrix composites. Mater. Sci. Eng. 2000, R 29, 49–113. [Google Scholar] [CrossRef]
- Vedani, M.; D’Errico, F.; Gariboldi, E. Mechanical and fracture behaviour of aluminium-based discontinuously reinforced composites at hot working temperatures. Compos. Sci. Technol. 2006, 66, 343–349. [Google Scholar] [CrossRef]
- Cao, H.J.; Tan, Z.Q.; Fan, G.L.; Guo, Q.; Su, Y.S.; Li, Z.Q.; Xiong, D.B. Wide and fine alignment control and interface modification for high-performance thermally conductive graphite/copper composite. Compos. Part B Eng. 2020, 191, 107965. [Google Scholar] [CrossRef]
- Tan, Z.; Ji, G.; Addad, A.; Li, Z.; Silvain, J.F.; Zhang, D. Tailoring interfacial bonding states of highly thermal performance diamond/Al composites: Spark plasma sintering vs. vacuum hot pressing. Compos. Part A Appl. Sci. Manuf. 2016, 91, 9–19. [Google Scholar] [CrossRef]
- Xu, R.; Tan, Z.; Xiong, D.; Fan, G.; Guo, Q.; Zhang, J.; Su, Y.; Li, Z.; Zhang, D. Balanced strength and ductility in CNT/Al composites achieved by flake powder metallurgy via shift-speed ball milling. Compos. Part A Appl. Sci. Manuf. 2017, 96, 57–66. [Google Scholar] [CrossRef]
- Liu, Q.; Fan, G.; Tan, Z.; Guo, Q.; Xiong, D.; Su, Y.; Li, Z.; Zhang, D. Reinforcement with intragranular dispersion of carbon nanotubes in aluminum matrix composites. Compos. Part B Eng. 2021, 217, 108915. [Google Scholar] [CrossRef]
- Khoddam, S.; Estrin, Y.; Kim, H.S.; Bouaziz, O. Torsional and compressive behaviours of a hybrid material: Spiral fiber reinforced metal matrix composite. Mater. Des. 2015, 85, 404–411. [Google Scholar] [CrossRef]
- Dong, Z.; Sun, C. Testing and modeling of yarn pull-out in plain woven Kevlar fabrics. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1863–1869. [Google Scholar] [CrossRef]
- Xu, R.; Tan, Z.; Fan, G.; Ji, G.; Xiong, D.B.; Guo, Q.; Su, Y.; Li, Z.; Zhang, D. High-strength CNT/Al-Zn-Mg-Cu composites with improved ductility achieved by flake powder metallurgy via elemental alloying. Compos. Part A Appl. Sci. Manuf. 2018, 111, 1–11. [Google Scholar] [CrossRef]
- Zhu, D.; Mobasher, B.; Vaidya, A.; Rajan, S.D. Mechanical behaviors of Kevlar 49 fabric subjected to uniaxial, biaxial tension and in-plane large shear deformation. Compos. Sci. Technol. 2013, 74, 121–130. [Google Scholar] [CrossRef]
- Ma, F.; Shi, Z.; Liu, P.; Li, W.; Liu, X.; Chen, X.; He, D.; Zhang, K.; Pan, D.; Zhang, D. Strengthening effect of in situ TiC particles in Ti matrix composite at temperature range for hot working. Mater. Charact. 2016, 120, 304–310. [Google Scholar] [CrossRef]
- Ma, F.; Lu, S.; Liu, P.; Li, W.; Liu, X.; Chen, X.; Zhang, K.; Pan, D.; Lu, W.; Zhang, D. Microstructure and mechanical properties variation of TiB/Ti matrix composite by thermo-mechanical processing in beta phase field. J. Alloys Compd. 2017, 695, 1515–1522. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, X.; Chen, J.; Dong, H.; Song, Y. Strength model of the matrix element in SiC/SiC composites. Mater. Des. 2016, 101, 66–71. [Google Scholar] [CrossRef]
- Miranda, A.T.; Bolzoni, L.; Barekar, N.; Huang, Y.; Shin, J.; Ko, S.H.; McKay, B.J. Processing, structure and thermal conductivity correlation in carbon fiber reinforced aluminium metal matrix composites. Mater. Des. 2018, 156, 329–339. [Google Scholar] [CrossRef]
- Ma, F.; Wang, C.; Liu, P.; Li, W.; Liu, X.; Chen, X.; Zhang, K.; Han, Q. Microstructure and mechanical properties of Ti matrix composite reinforced with 5 vol.% TiC after various thermo-mechanical treatments. J. Alloys Compd. 2018, 758, 78–84. [Google Scholar] [CrossRef]
- Liu, Y.J.; Li, S.J.; Wang, H.L.; Hou, W.T.; Hao, Y.L.; Yang, R.; Sercombe, T.B.; Zhang, L.C. Microstructure, defects and mechanical behavior of beta-type titanium porous structures manufactured by electron beam melting and selective laser melting. Acta Mater. 2016, 113, 56–67. [Google Scholar] [CrossRef]
- Attar, H.; Prashanth, K.G.; Zhang, L.C.; Calin, M.; Okulov, I.V.; Scudino, S.; Yang, C.; Eckert, J. Effect of powder particle shape on the properties of in situ Ti–TiB composite materials produced by selective laser melting. J. Mater. Sci. Technol. 2015, 31, 1001–1005. [Google Scholar] [CrossRef]
- Han, S.; Yang, L.W.; Liu, H.T.; Sun, X.; Jiang, R.; Mao, W.G.; Chen, Z.H. Micro-mechanical properties and interfacial engineering of SiC fiber reinforced sol-gel fabricated mullite matrix composites. Mater. Des. 2017, 131, 265–272. [Google Scholar] [CrossRef]
- Zhu, D.; Soranakom, C.; Mobasher, B.; Rajan, S.D. Experimental study and modeling of single yarn pull-out behavior of Kevlar 49 fabric. Compos. Part A Appl. Sci. Manuf. 2011, 42, 868–879. [Google Scholar] [CrossRef]
- Frazer, D.; Abad, M.D.; Krumwiede, D.; Back, C.A.; Khalifa, H.E.; Deck, C.P.; Hosemann, P. Localized mechanical property assessment of SiC/SiC composite materials. Compos. Part A Appl. Sci. Manuf. 2015, 70, 93–101. [Google Scholar] [CrossRef]
- Ma, F.; Zhou, J.; Liu, L.; Li, W.; Liu, X.; Pan, D.; Lu, W.; Zhang, D. Strengthening effects of TiC particles and microstructure refinement in in situ TiC-reinforced Ti matrix composites. Mater. Charact. 2017, 127, 27–34. [Google Scholar] [CrossRef]
- Gorsse, S.; Miracle, D.B. Mechanical properties of Ti-6Al-4V/TiB composites with randomly oriented and aligned TiB reinforcements. Acta Mater. 2003, 51, 2427–2442. [Google Scholar] [CrossRef]
- Zhang, Z.; Fan, G.; Tan, Z.; Zhao, H.; Xu, Y.; Xiong, D.; Li, Z. Bioinspired multiscale Al2O3-rGO/Al laminated composites with superior mechanical properties. Compos. Part B Eng. 2021, 217, 108916. [Google Scholar] [CrossRef]
- Mutel, A.T.; Kamal, M.R. Rheological behaviour of fiber orientation in slit flow of fiber reinforced thermoplastics. Polym. Compos. 1991, 12, 137–145. [Google Scholar] [CrossRef]
- Ausias, G.; Jarrin, J.; Vincent, M. Optimisation of the tube-extrusion die for short-fiber-filled polymers. Compos. Sci. Technol. 1996, 56, 719–724. [Google Scholar] [CrossRef]
- Guell, D.C.; Graham, A.L. Improved mechanical properties in hydrodynamically aligned short fiber composite materials. J. Compos. Mater. 1996, 30, 2–12. [Google Scholar] [CrossRef]
- Jiang, Y.; Tan, Z.; Xu, R.; Fan, G.; Xiong, D.B.; Guo, Q.; Su, Y.; Li, Z.; Zhang, D. Tailoring the structure and mechanical properties of graphene nanosheet/aluminum composites by flake powder metallurgy via shift-speed ball milling. Compos. Part A Appl. Sci. Manuf. 2018, 111, 73–82. [Google Scholar] [CrossRef]
- Guo, X.; Wang, L.; Wang, M.; Qin, J.; Zhang, D.; Lu, W. Effects of degree of deformation on the microstructure, mechanical properties and texture of hybrid-reinforced titanium matrix composites. Acta Mater. 2012, 60, 2656–2667. [Google Scholar] [CrossRef]
- Ma, F.; Liu, P.; Li, W.; Liu, X.; Chen, X.; Zhang, K.; Pan, D.; Lu, W. The mechanical behavior dependence on the TiB whisker realignment during hot-working in titanium matrix composites. Sci. Rep. 2016, 6, 36126. [Google Scholar] [CrossRef]
- Ma, F.; Zheng, B.; Liu, P.; Li, W.; Liu, X.; Chen, X.; Zhang, K.; Pan, D.; Lu, W. Modeling of effects of thermomechanical processing on elevated-temperature mechanical properties of in situ (TiB+ TiC)/Ti-1100 composite. J. Mater. Sci. 2016, 51, 7502–7511. [Google Scholar] [CrossRef]
- Ma, F.; Lu, S.; Liu, P.; Li, W.; Liu, X.; Chen, X.; Zhang, K.; Pan, D. Evolution of strength and fibers orientation of a short-fibers reinforced Ti matrix composite after extrusion. Mater. Des. 2017, 126, 297–304. [Google Scholar] [CrossRef]
- Ma, F.; Wang, T.; Liu, P.; Li, W.; Liu, X.; Chen, X.; Pan, D.; Lu, W. Mechanical properties and strengthening effects of in situ (TiB+TiC)/Ti-1100 composite at elevated temperatures. Mater. Sci. Eng. A 2016, 654, 352–358. [Google Scholar] [CrossRef]
- Li, D.X.; Ping, D.H.; Lu, Y.X.; Ye, H.Q. Characterization of the microstructure in TiB-whisker reinforced Ti alloy matrix composite. Mater. Lett. 1993, 16, 322–326. [Google Scholar] [CrossRef]
- Lundstrom, T. Boron and Refractory Borides; Matkovich, V.I., Ed.; Springer: Berlin/Heidelberg, Germany, 1977; pp. 351–376. [Google Scholar]
- Lu, W.J.; Zhang, D.; Zhang, X.N.; Wu, R.J.; Sakata, T.; Mori, H. Microstructure and tensile properties of in situ (TiB+ TiC)/Ti6264 (TiB:TiC=1:1) composites prepared by common casting technique. Mater. Sci. Eng. A 2001, 311, 142–150. [Google Scholar] [CrossRef]
- Hine, P.J.; Tsui, S.W.; Coates, P.D.; Ward, I.M.; Duckett, R.A. Measuring the development of fiber orientation during the melt extrusion of short glass fiber reinforced polypropylene. Compos. A Appl. Sci. Manuf. 1997, 28, 949–958. [Google Scholar] [CrossRef]
- Dinh, S.M.; Armstrong, R.C. A rheological equation of state for semiconcentrated fiber suspensions. J. Rheol. 1984, 28, 207–227. [Google Scholar] [CrossRef]
- Hine, P.J.; Davidson, N.; Duckett, R.A.; Ward, I.M. Modelling the elastic properties of fiber reinforced composites. I: Orientation measurement. Compos. Sci. Technol. 1993, 47, 65–73. [Google Scholar] [CrossRef]
- Huang, G.; Guo, X.; Han, Y.; Wang, L.; Lu, W.; Zhang, D. Effect of extrusion dies angle on the microstructure and properties of (TiB+TiC)/Ti6Al4V in situ titanium matrix composite. Mater. Sci. Eng. A 2016, 667, 317–325. [Google Scholar] [CrossRef]
- Cox, H. The elasticity and strength of paper and other fibrous materials. J. Appl. Phys. 1952, 3, 72–79. [Google Scholar] [CrossRef]
- Friend, C.M. The effect of matrix properties on reinforcement in short alumina fiber-aluminium metal matrix composites. J. Mater. Sci. 1987, 22, 3005–3010. [Google Scholar] [CrossRef]
- Fukuda, H.; Chou, T.W. Probabilistic theory of the strength of short-fiber composites with variable fiber length and orientation. J. Mater. Sci. 1982, 17, 1003–1007. [Google Scholar] [CrossRef]
- Thostenson, E.T.; Li, C.; Chou, T.W. Nanocomposites in context. Compos. Sci. Technol. 2005, 65, 491–516. [Google Scholar] [CrossRef]
- Xiao, L.; Lu, W.J.; Qin, J.N.; Chen, Y.F.; Zhang, D.; Wang, M.M.; Zhu, F.; Ji, B. Steady state creep of in situ TiB plus La2O3 reinforced high temperature titanium matrix composite. Mater. Sci. Eng. A 2009, 499, 500–503. [Google Scholar] [CrossRef]
- Hall, E.O. The deformation and aging of mild steel. Proc. Phys. Soc. Lond. B 1951, 64, 747–752. [Google Scholar] [CrossRef]
- Boricova, E.A.; Chen, S.Q. (Eds.) Titanium Alloy Metallography; National Defence Industry Press: Beijing, China, 1986. [Google Scholar]




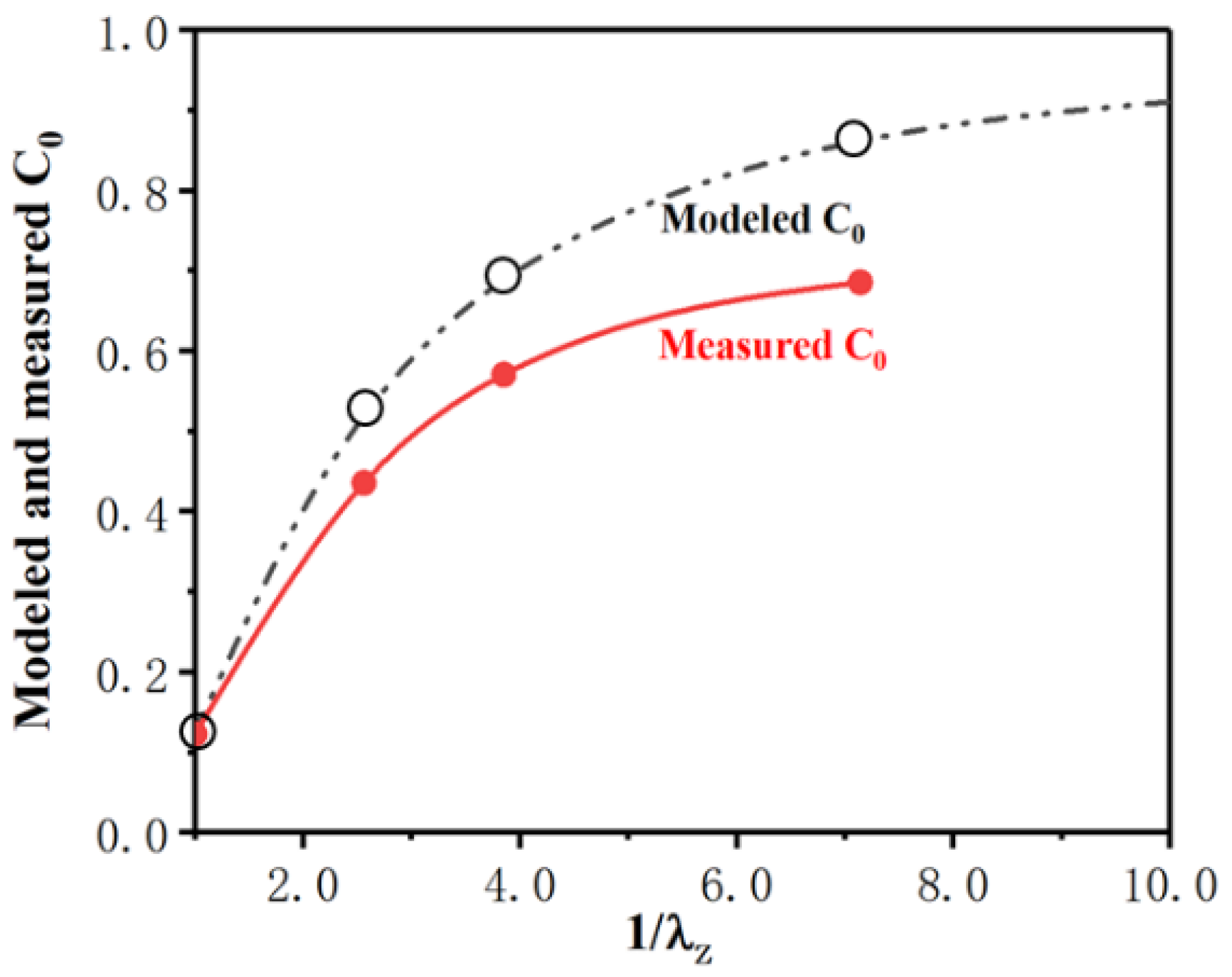
| Deformation Ratio (λ) | UTS (MPa) 823 K | δ (%) 823 K | UTS (MPa) 923 K | δ (%) 923 K | Modeled C0 | Measured C0 | Relative Error of C0 (%) | |
|---|---|---|---|---|---|---|---|---|
| λx, λy | λz | |||||||
| 1.00 | 1.00 | 620.2 ± 41 | 7.3 ± 0.4 | 582.3 ± 33 | 7.9 ± 0.7 | 0.125 | 0.123 | −1.626 |
| 1.56 | 0.39 | 713.8 ± 46 | 10.6 ± 0.8 | 657.5 ± 41 | 11.7 ± 0.9 | 0.520 | 0.488 | −6.557 |
| 1.96 | 0.26 | 789.6 ± 56 | 14.5 ± 0.8 | 719.3 ± 45 | 16.3 ± 1.1 | 0.688 | 0.623 | −10.433 |
| 2.67 | 0.14 | 819.3 ± 62 | 15.3 ± 1.0 | 742.7 ± 53 | 18.1 ± 1.2 | 0.858 | 0.729 | −17.695 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, P.; Ma, F.; Liu, P.; Li, W.; Liu, X.; Chen, X.; Zhang, K. Evolution of the Strengthening Effects of In Situ TiB Fibers in a Ti Composite with Various Levels of Thermal Processing. Materials 2023, 16, 2472. https://doi.org/10.3390/ma16062472
Zhao P, Ma F, Liu P, Li W, Liu X, Chen X, Zhang K. Evolution of the Strengthening Effects of In Situ TiB Fibers in a Ti Composite with Various Levels of Thermal Processing. Materials. 2023; 16(6):2472. https://doi.org/10.3390/ma16062472
Chicago/Turabian StyleZhao, Peifeng, Fengcang Ma, Ping Liu, Wei Li, Xinkuan Liu, Xiaohong Chen, and Ke Zhang. 2023. "Evolution of the Strengthening Effects of In Situ TiB Fibers in a Ti Composite with Various Levels of Thermal Processing" Materials 16, no. 6: 2472. https://doi.org/10.3390/ma16062472
APA StyleZhao, P., Ma, F., Liu, P., Li, W., Liu, X., Chen, X., & Zhang, K. (2023). Evolution of the Strengthening Effects of In Situ TiB Fibers in a Ti Composite with Various Levels of Thermal Processing. Materials, 16(6), 2472. https://doi.org/10.3390/ma16062472









