Toward Elucidating the Influence of Hydrostatic Pressure Dependent Swelling Behavior in the CERCER Composite
Abstract
:1. Introduction
2. Materials and Method
2.1. Swelling Model with Recrystallization, Resolution and Hydrostatic Pressure
2.2. Three-Dimensional Stress Update Algorithm
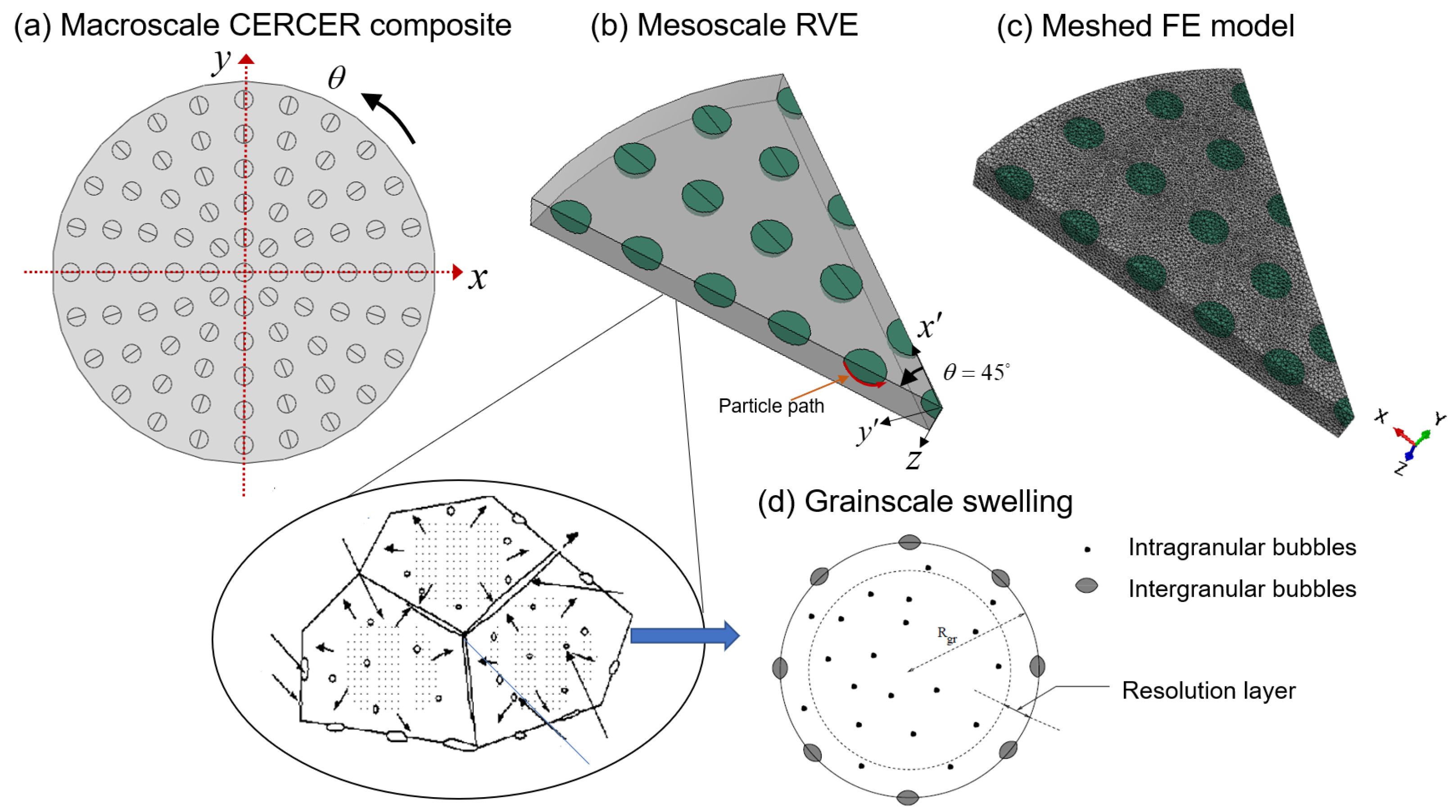
2.3. Finite Element Model
2.4. Simulations and Data Analyses
3. Results
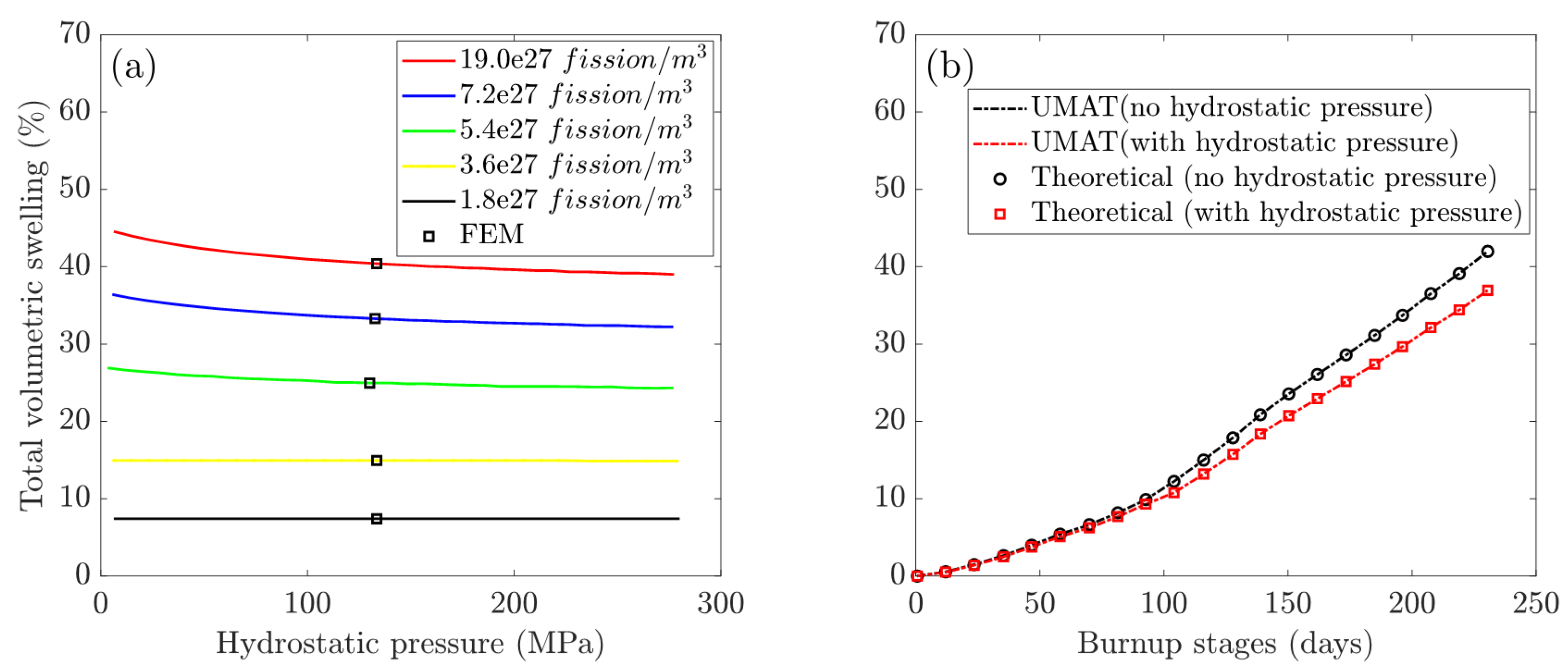
3.1. Model Verification
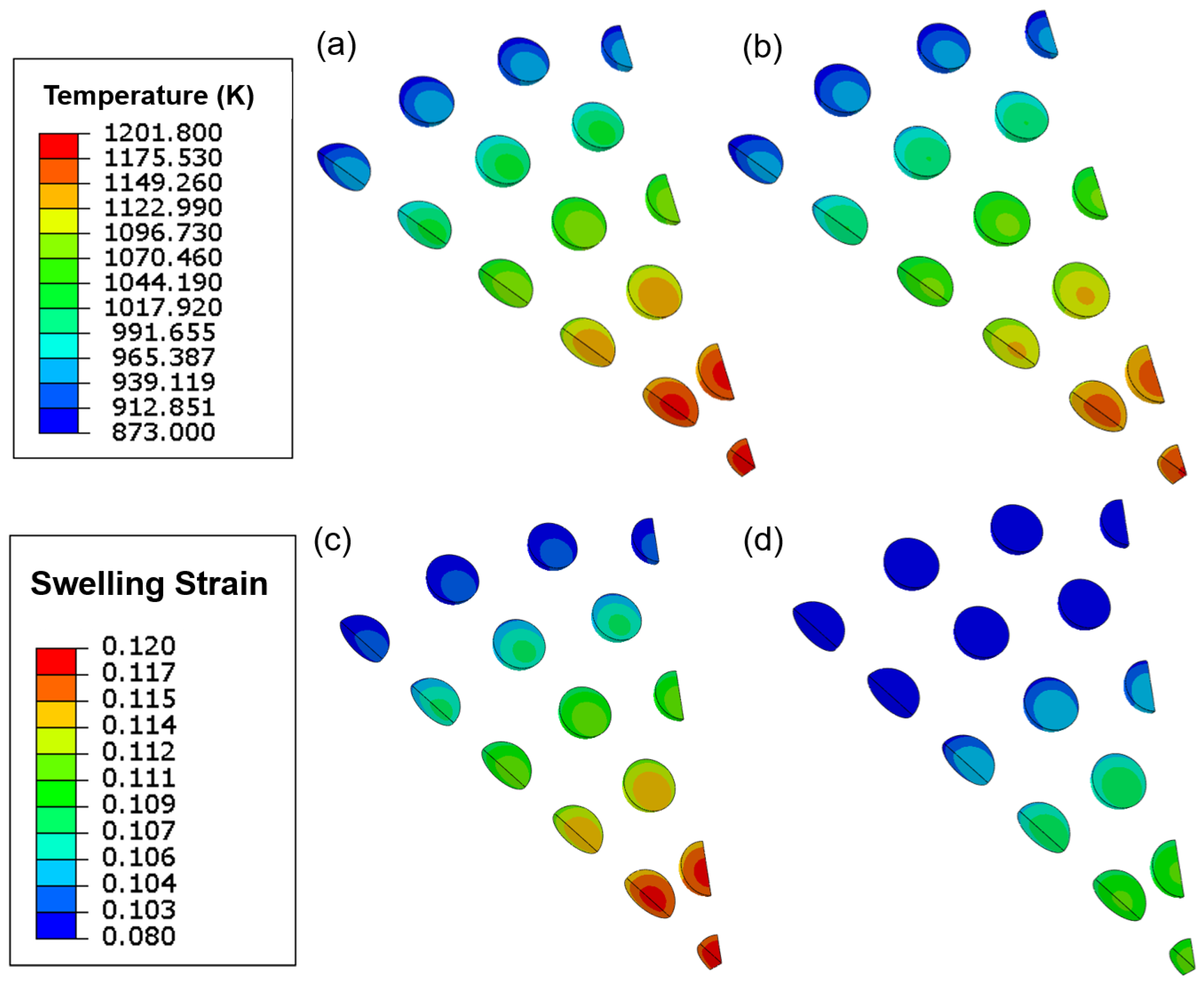
3.2. The Swelling Behavior of Fission within the CERCER
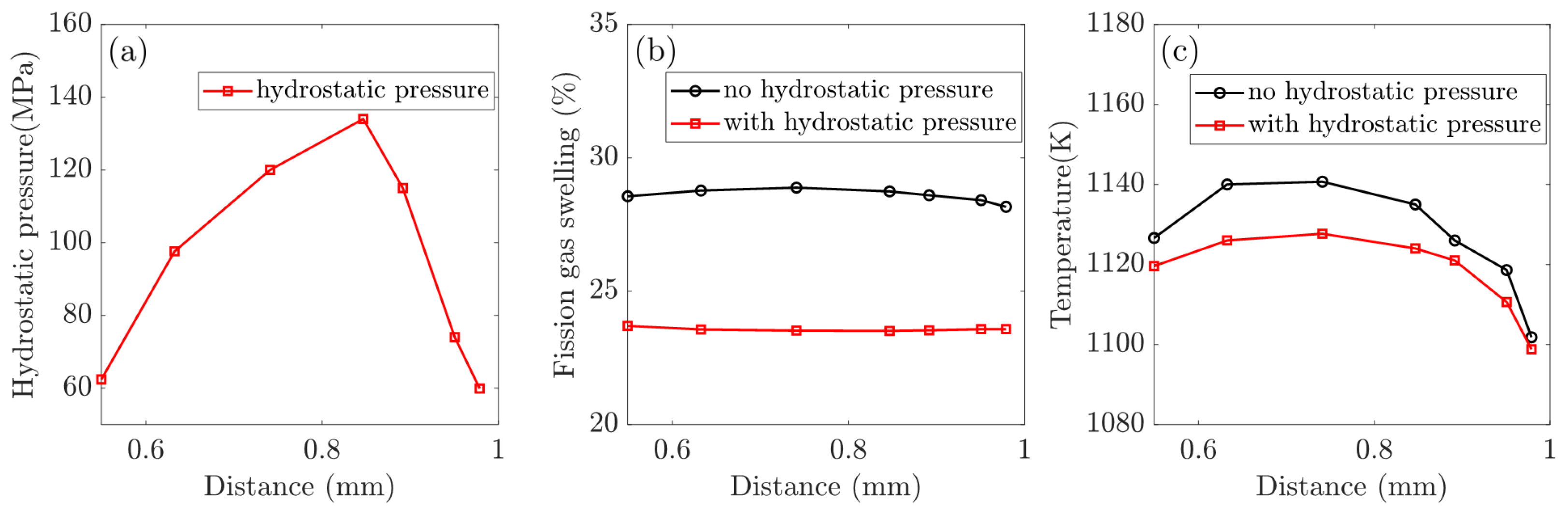
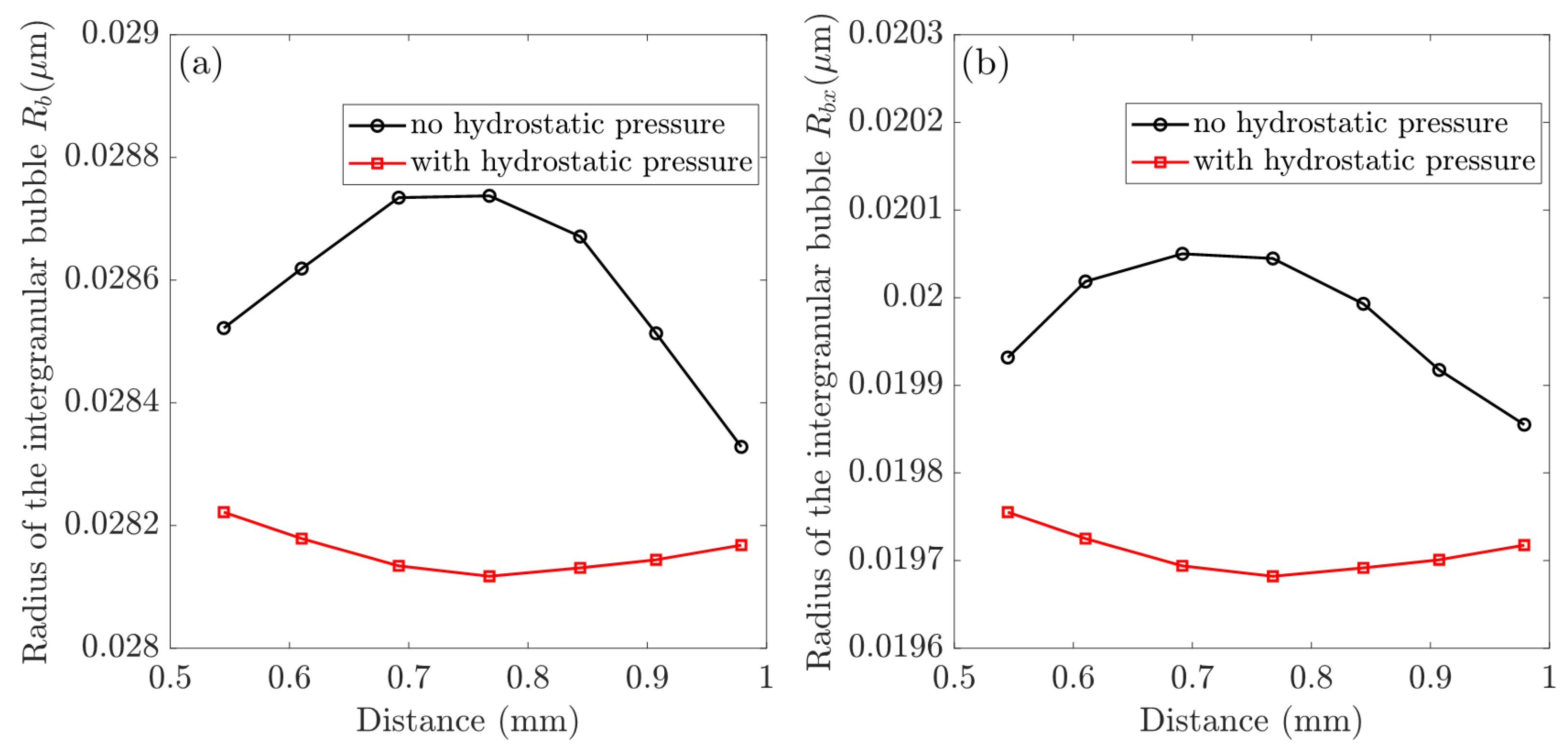
3.3. The Effects of Hydrostatic Pressure on the In-Pile Behavior of CERCER Composites
4. Discussion and Outlook
4.1. The Swelling Behavior of Fission with the CERCER Composite
4.2. Hydrostatic Pressure Effects on the In-Pile Behavior of the CERCER Composite
4.3. Limitations and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Description of the Gas Swelling Model for Fuels
Appendix A.1. Governing Equations for Gas Diffusion
Appendix A.2. Calculation of Swelling for Fuels
| Parameter | Value | Unit |
|---|---|---|
| Y | 0.25 | - |
| z | 4 | - |
| a | - | |
| m | ||
| 1 | N/m | |
| m | ||
| m | ||
| m/atom | ||
| 0.6 | - | |
| m | ||
| m | ||
| m | ||
| m/N |
Appendix B. Irradiation-Induced Creep in MgO Matrix
References
- Gohar, Y.; Cao, Y.; Kraus, A.R. ADS design concept for disposing of the US spent nuclear fuel inventory. Ann. Nucl. Energy 2021, 160, 108385. [Google Scholar] [CrossRef]
- Abderrahim, H.A.; Giot, M. The Accelerator Driven Systems, a 21st Century Option for Closing Nuclear Fuel Cycles and Transmuting Minor Actinides. Sustainability 2021, 13, 12643. [Google Scholar] [CrossRef]
- Chen, X.N.; Rineiski, A.; Maschek, W.; Liu, P.; Boccaccini, C.M.; Sobolev, V.; Delage, F.; Rimpault, G. Comparative studies of CERCER and CERMET fuels for EFIT from the viewpoint of core performance and safety. Prog. Nucl. Energy 2011, 53, 855–861. [Google Scholar] [CrossRef]
- Neeft, E.; Bakker, K.; Schram, R.; Conrad, R.; Konings, R. The EFTTRA-T3 irradiation experiment on inert matrix fuels. J. Nucl. Mater. 2003, 320, 106–116. [Google Scholar] [CrossRef]
- Sobolev, V.; Uyttenhove, W.; Thetford, R.; Maschek, W. Prognosis and comparison of performances of composite CERCER and CERMET fuels dedicated to transmutation of TRU in an EFIT ADS. J. Nucl. Mater. 2011, 414, 257–264. [Google Scholar] [CrossRef]
- Kotomin, E.; Kuzovkov, V.; Popov, A.I.; Maier, J.; Vila, R. Anomalous kinetics of diffusion-controlled defect annealing in irradiated ionic solids. J. Phys. Chem. A 2018, 122, 28–32. [Google Scholar] [CrossRef]
- Neeft, E.; Bakker, K.; Belvroy, R.; Tams, W.; Schram, R.; Conrad, R.; van Veen, A. Mechanical behaviour of macro-dispersed inert matrix fuels. J. Nucl. Mater. 2003, 317, 217–225. [Google Scholar] [CrossRef]
- Georgenthum, V.; Brillaud, J.; Chauvin, N.; Pelletier, M.; Noirot, J.; Placq, D. Experimental study and modelling of the thermoelastic behaviour of composite fuel in reactors-emphasis on spinel based composites. Prog. Nucl. Energy 2001, 38, 317–320. [Google Scholar] [CrossRef]
- Vu, T.M.; Hartanto, D.; Ha, P.N.V. Neutronics study on small power ADS loaded with recycled inert matrix fuel for transuranic elements transmutation using Serpent code. Nucl. Eng. Technol. 2021, 53, 2095–2103. [Google Scholar] [CrossRef]
- Wallenius, J.; Pillon, S.; Zaboudko, L. Fuels for accelerator-driven systems. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2006, 562, 625–629. [Google Scholar] [CrossRef]
- Rest, J. A model for the effect of the progression of irradiation-induced recrystallization from initiation to completion on swelling of UO2 and U–10Mo nuclear fuels. J. Nucl. Mater. 2005, 346, 226–232. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, J.; Ding, S. A new method for solving the fission gas diffusion equations with time-varying diffusion coefficient and source term considering recrystallization of fuel grains. Nucl. Mater. Energy 2019, 20, 100686. [Google Scholar] [CrossRef]
- Tonks, M.; Andersson, D.; Devanathan, R.; Dubourg, R.; El-Azab, A.; Freyss, M.; Iglesias, F.; Kulacsy, K.; Pastore, G.; Phillpot, S.R.; et al. Unit mechanisms of fission gas release: Current understanding and future needs. J. Nucl. Mater. 2018, 504, 300–317. [Google Scholar] [CrossRef] [Green Version]
- Booth, A. A Method of Calculating Gas Diffusion from UO2 Fuel and Its Application to the X-2-F Test; AECL 496 CRDC-721; Atomic Energy of Canada Ltd.: Chalk River, ON, Canada, 1957; Available online: https://www.osti.gov/biblio/4331839 (accessed on 14 February 2023).
- Rest, J. Modeling of Fission-Gas Induced Swelling of Nuclear Fuels. 2016. Available online: https://www.researchgate.net/publication/283763006_Modeling_of_Fission-Gas-Induced_Swelling_of_Nuclear_Fuels (accessed on 16 February 2022).
- Cui, Y.; Ding, S.; Huo, Y.; Wang, C.; Yang, L. An efficient numerical method for intergranular fission gas evolution under transient with piecewise boundary resolution. J. Nucl. Mater. 2013, 443, 570–578. [Google Scholar] [CrossRef]
- Gong, X.; Zhao, Y.; Ding, S. A new method to simulate the micro-thermo-mechanical behaviors evolution in dispersion nuclear fuel elements. Mech. Mater. 2014, 77, 14–27. [Google Scholar] [CrossRef]
- Yang, G.; Liao, H.; Ding, T.; Chen, H. Preliminary study on the thermal-mechanical performance of the U3Si2/Al dispersion fuel plate under normal conditions. Nucl. Eng. Technol. 2021, 53, 3723–3740. [Google Scholar] [CrossRef]
- Zhao, Y.; Ding, S.; Zhang, X.; Wang, C.; Yang, L. Effects of fuel particle size and fission-fragment-enhanced irradiation creep on the in-pile behavior in CERCER composite pellets. J. Nucl. Mater. 2016, 482, 278–293. [Google Scholar] [CrossRef]
- Kong, X.; Tian, X.; Yan, F.; Ding, S.; Hu, S.; Burkes, D.E. Thermo-mechanical behavior simulation coupled with the hydrostatic-pressure-dependent grain-scale fission gas swelling calculation for a monolithic UMo fuel plate under heterogeneous neutron irradiation. Open Eng. 2018, 8, 243–260. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Wei, H.; Zhang, J.; Tang, C.; Lu, C.; Huang, C.; Ding, S.; Li, Y. Modelling of effective irradiation swelling for inert matrix fuels. Nucl. Eng. Technol. 2021, 53, 2616–2628. [Google Scholar] [CrossRef]
- Ding, S.; Zhao, Y.; Wan, J.; Gong, X.; Wang, C.; Yang, L.; Huo, Y. Simulation of the irradiation-induced micro-thermo-mechanical behaviors evolution in ADS nuclear fuel pellets. J. Nucl. Mater. 2013, 442, 90–99. [Google Scholar] [CrossRef]
- Zhao, Y.; Ding, S.; Huo, Y.; Wang, C.; Yang, L. Irradiation-induced thermomechanical behavior in ads composite fuel pellets: Mechanism and main influencing factors. J. Therm. Stresses 2016, 39, 630–657. [Google Scholar] [CrossRef]
- Spino, J.; Rest, J.; Goll, W.; Walker, C. Matrix swelling rate and cavity volume balance of UO2 fuels at high burn-up. J. Nucl. Mater. 2005, 346, 131–144. [Google Scholar] [CrossRef]
- Suzuki, M. Light Water Reactor Fuel Analysis Code FEMAXI-V (Ver. 1); Technical Report; Japan Atomic Energy Research Institute: Ibaraki, Japan, 2000. [Google Scholar]
- Speight, M. A calculation on the migration of fission gas in material exhibiting precipitation and re-solution of gas atoms under irradiation. Nucl. Sci. Eng. 1969, 37, 180–185. [Google Scholar] [CrossRef]
- Baubekova, G.; Akilbekov, A.; Feldbach, E.; Grants, R.; Manika, I.; Popov, A.I.; Schwartz, K.; Vasil’chenko, E.; Zdorovets, M.; Lushchik, A. Accumulation of radiation defects and modification of micromechanical properties under MgO crystal irradiation with swift 132Xe ions. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2020, 463, 50–54. [Google Scholar] [CrossRef]
- El-Azab, A.; Ghoniem, N. Viscoelastic analysis of mismatch stresses in ceramic matrix composites under high-temperature neutron irradiation. Mech. Mater. 1995, 20, 291–303. [Google Scholar] [CrossRef]

| Fission Rate | Fast Neutron Flux | Heat Generation Rate |
|---|---|---|
| (fission/m s) | (n/cm s) | (W/mm) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Chen, Z.; Zhao, Y. Toward Elucidating the Influence of Hydrostatic Pressure Dependent Swelling Behavior in the CERCER Composite. Materials 2023, 16, 2644. https://doi.org/10.3390/ma16072644
Zhao J, Chen Z, Zhao Y. Toward Elucidating the Influence of Hydrostatic Pressure Dependent Swelling Behavior in the CERCER Composite. Materials. 2023; 16(7):2644. https://doi.org/10.3390/ma16072644
Chicago/Turabian StyleZhao, Jian, Zhenyue Chen, and Yunmei Zhao. 2023. "Toward Elucidating the Influence of Hydrostatic Pressure Dependent Swelling Behavior in the CERCER Composite" Materials 16, no. 7: 2644. https://doi.org/10.3390/ma16072644
APA StyleZhao, J., Chen, Z., & Zhao, Y. (2023). Toward Elucidating the Influence of Hydrostatic Pressure Dependent Swelling Behavior in the CERCER Composite. Materials, 16(7), 2644. https://doi.org/10.3390/ma16072644







