Characterization of the 1-(5-(4,5-Dimethyl-1,3,2-dioxoborolan-2-yl)thiophen-2-yl)ethanone Using NMR 13C, 1H and 11B through the Density Functional Theory
Abstract
1. Introduction
2. Theoretical Background
2.1. Nuclear Magnetic Resonance
2.2. Pseudopotentials in a Magnetic Field
3. Methodology
3.1. Analysis and Optimization
3.2. Optimization of the and Molecules, and the Unitary Cell of the Structure
3.3. NMR of the and Molecules, and the Unitary Cell of the Structure
3.4. Software
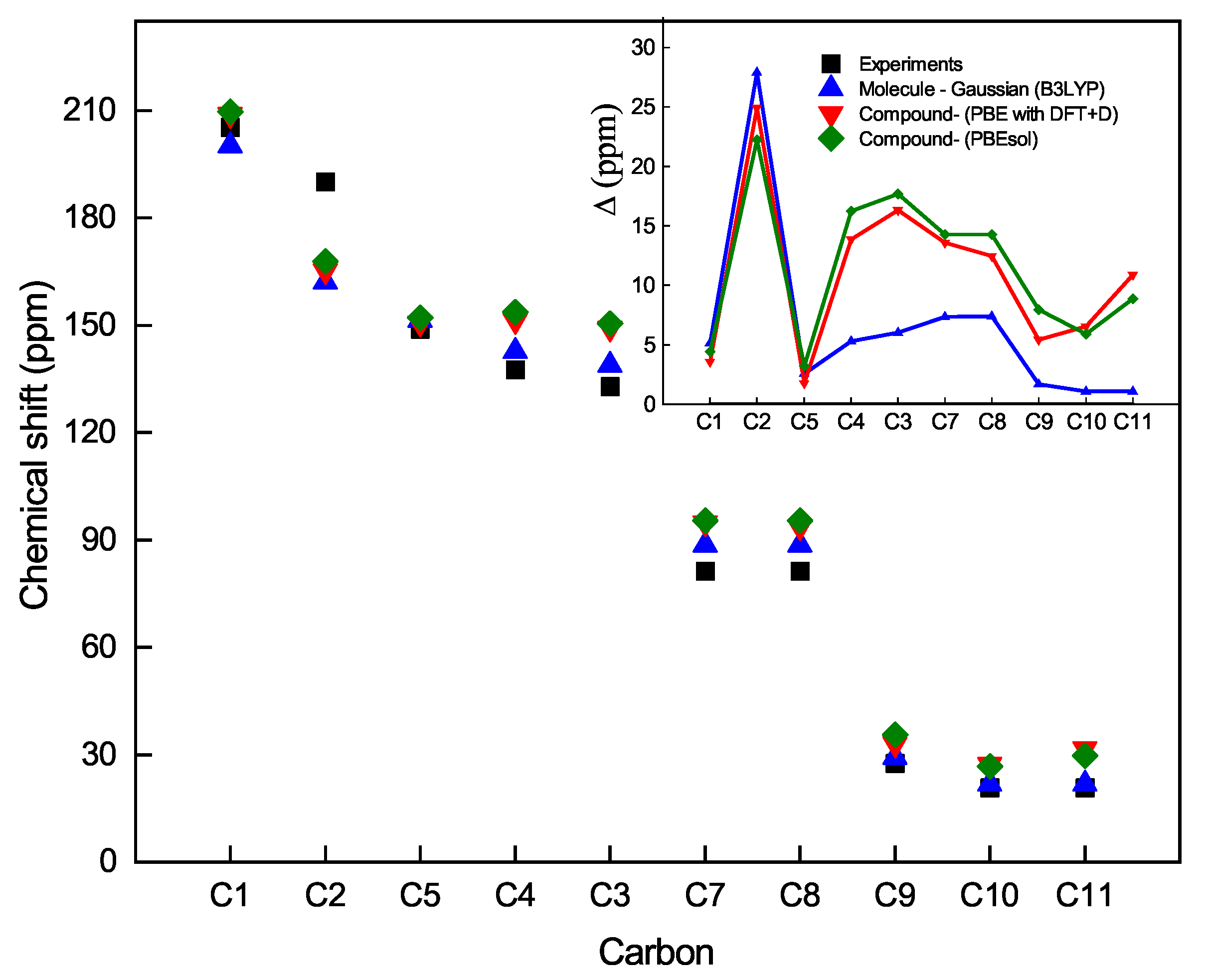
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Band Structure and Density of the State
| Real Space Vectors | High Symmetry Points of the Reciprocal Space |
|---|---|
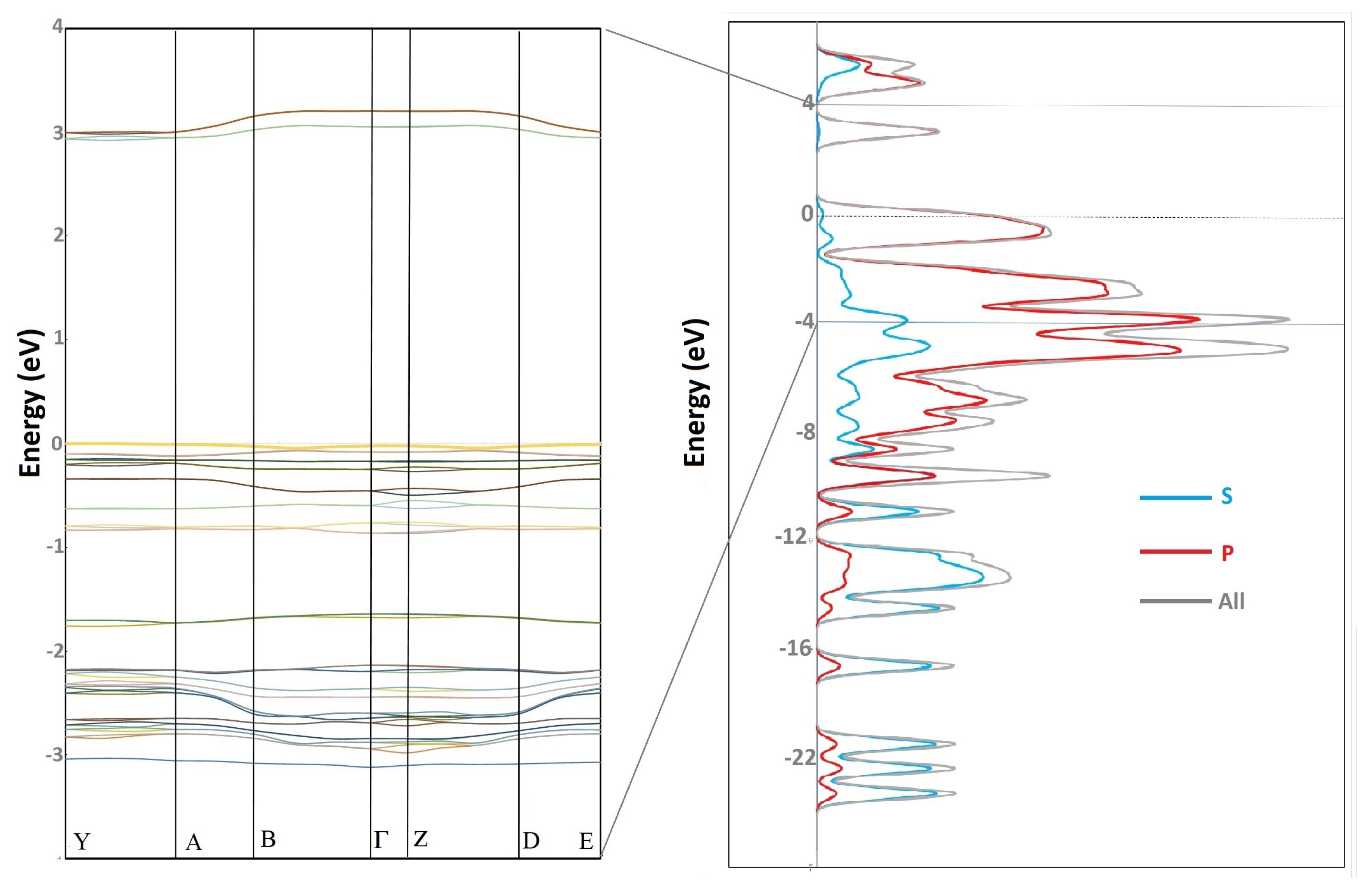
References
- Atieh, Z.; Allouche, A.-R.; Graveron-Demilly, D.; Aubert-Frécon, M. Density functional theory (DFT) calculations of the proton nuclear magnetic resonance (NMR) spin-Hamiltonian parameters for serine. Meas. Sci. Technol. 2011, 22, 114015. [Google Scholar] [CrossRef]
- Pierens, G.K.; Venkatachalam, T.; Reutens, D.C. NMR and DFT investigations of structure of colchicine in various solvents including density functional theory calculations. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Unzueta, P.A.; Greenwell, C.S.; Beran, G.J. Predicting density functional theory-quality nuclear magnetic resonance chemical shifts via δ-machine learning. J. Chem. Theory Comput. 2021, 17, 826–840. [Google Scholar] [CrossRef] [PubMed]
- Scholz, S.; Kidd, J.B.; Capaldo, L.; Flikweert, N.E.; Littlefield, R.M.; Yoon, T.P. Construction of Complex Cyclobutane Building Blocks by Photosensitized [2 + 2] Cycloaddition of Vinyl Boronate Esters. Org. Lett. 2021, 23, 3496–3501. [Google Scholar] [CrossRef]
- Sharma, H.A.; Essman, J.Z.; Jacobsen, E.N. Enantioselective catalytic 1, 2-boronate rearrangements. Science 2021, 374, 752–757. [Google Scholar] [CrossRef]
- Guevara, U.; López, R.; Blanco, J.; Núñez, J. Theoretical study of electronic properties and spin density in Pt-Co alloys. Mater. Res. Express. 2019, 6, 096514. [Google Scholar] [CrossRef]
- Blanco, J.; Guevara, U.; Lozada, R.; Castro, O. Electronic and structural properties in nanocluster Aln-xNix. J. Phys. Conf. Ser. 2021, 1938, 012002. [Google Scholar] [CrossRef]
- Silverstein, R.M.; Webster, F.X.; Kiemle, D.J.; Bryce, D.L. Spectrometric Identification of Organic Compounds, 8th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2005. [Google Scholar]
- Pretsch, E.; Bühlmann, P.; Badertscher, M. Structure Determination of Organic Compound, 4th ed.; Springer: Berlin, Germany, 2020. [Google Scholar] [CrossRef]
- Henning, A. Proton and multinuclear magnetic resonance spectroscopy in the human brain at ultra-high field strength: A review. Neuroimage 2018, 168, 181–198. [Google Scholar] [CrossRef]
- Debiais, M.; Vasseur, J.-J.; Smietana, M. Applications of the Reversible Boronic Acids/Boronate Switch to Nucleic Acids. Chem. Rec. 2022, 22, e202200085. [Google Scholar] [CrossRef]
- D’Alterio, M.C.; Casals-Cruañas, E.; Tzouras, N.V.; Talarico, G.; Nolan, S.P.; Poater, A. Mechanistic Aspects of the Palladium-Catalyzed Suzuki-Miyaura Cross-Coupling Reaction. Chem. Eur. J. 2021, 27, 13481–13493. [Google Scholar] [CrossRef]
- Hoffmann, C.; Jourdain, M.; Grandjean, A.; Titz, A.; Jung, G. β -Boronic Acid-Substituted Bopidy Dyes for Fluorescence Anisotropy Analysis of Carbohidrate Binding. Anal. Chem. 2022, 94, 6112–6119. [Google Scholar] [CrossRef]
- Schnürch, M.; Holzweber, M.; Mihovilovic, M.; Stanetty, P. A facile and green synthetic route to boronic acid esters utilizing mechanochemistry. Green Chem. 2007, 9, 139–145. [Google Scholar] [CrossRef]
- Das, B.C.; Nandwana, N.K.; Das, S.; Nandwana, V.; Shareef, M.A.; Das, Y.; Saito, M.; Weiss, L.M.; Almaguel, F.; Hosmane, N.S.; et al. Boron Chemicals in Drug Discovery and Development: Synthesis and Medicinal Perspective. Molecules 2022, 27, 2615. [Google Scholar] [CrossRef]
- Urdaneta, N.; Nuñez, J.; González, T.; Briceño, A. 1-[5-(4, 5-Dimethyl-1, 3, 2-dioxaborolan-2-yl) thiophen-2-yl] ethanone and 4-(4, 4, 5, 5-tetramethyl-1, 3, 2-dioxaborolan-2-yl) benzaldehyde. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 2012, 68, o213–o215. [Google Scholar] [CrossRef]
- Hore, P.J. Nuclear Magnetic Resonance; Oxford University Press Inc.: New York, NY, USA, 2015. [Google Scholar]
- Kumar, A.; Gadre, S.R. Molecular Electrostatic Potential-Based Atoms in Molecules: Shielding Effects and Reactivity Patterns. Aust. J. Chem. 2016, 69, 975–982. [Google Scholar] [CrossRef]
- Herring, C. A New Method for Calculating Wave Functions in Crystals. Phys. Rev. 1940, 57, 1169–1177. [Google Scholar] [CrossRef]
- Phillips, J.C.; Kleinman, L. New Method for Calculating Wave Functions in Crystals and Molecules. Phys. Rev. 1959, 116, 287–294. [Google Scholar] [CrossRef]
- Hopfield, J.J. Kinetic proofreading: A new mechanism for reducing errors in biosynthetic processes requiring high specificity. Proc. Natl. Acad. Sci. 1974, 71, 4135–4139. [Google Scholar] [CrossRef]
- Starkloff, T.; Joannopoulos, J.D. Local pseudopotential theory for transition metals. Phys. Rev. B. 1977, 16, 5212–5215. [Google Scholar] [CrossRef]
- Hamann, D.; Schlüter, M.; Chiang, C. Norm-conserving pseudopotentials. Phys. Rev. Lett. 1979, 43, 1494. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Pickard, C.J.; Mauri, F. All-electron magnetic response with pseudopotentials: NMR chemical shifts. Phys. Rev. B 2001, 63, 245101. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2016; Available online: https://Gaussian.com/ (accessed on 18 November 2022).
- Boys, S.F. Electronic wave functions-I. A general method of calculation for the stationary states of any molecular system. Proc. R. Soc. A 1950, 200, 542–554. [Google Scholar] [CrossRef]
- Davidson, E.R.; Feller, D. Basis set selection for molecular calculations. Chem. Rev. 1986, 86, 681–696. [Google Scholar] [CrossRef]
- Cao, Y.; Romero, J.; Olson, J.P.; Degroote, M.; Johnson, P.D.; Kieferová, M.; Kivlichan, I.D.; Menke, T.; Peropadre, B.; Sawaya, N.P.D.; et al. Quantum Chemistry in the Age of Quantum Computing. Chem. Rev. 2019, 119, 10856–10915. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Li, X.; Frisch, M.J. Energy-Represented Direct Inversion in the Iterative Subspace within a Hybrid Geometry Optimization Method. J. Chem. Theory Comput. 2006, 2, 835–839. [Google Scholar] [CrossRef]
- Urdaneta, N.; Núñez, J.; González, T.; Briceño, A. 1-[5-(4,5-Dimethyl-1,3,2-dioxaborolan- 2-yl)thiophen-2-yl]ethanone and 4-(4,4,5,5-tetramethyl-1,3,2-dioxaborolan- 2-yl)benzaldehyde. Acta Crystallogr. Sect. C 2012, 44, 213–215. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Fuer Krist. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Yates, J.R.; Pickard, C.J.; Mauri, F. Calculation of NMR chemical shifts for extended systems using ultrasoft pseudopotentials. Phys. Rev. B 2007, 76, 024401. [Google Scholar] [CrossRef]
- Andreev, V.P.; Tafeenko, V.A.; Ivashevskaya, S.N. Molecular complexes of heteroaromatic N-oxides with boron trifluoride. Russ. J. Gen. Chem. 2014, 84, 255–258. [Google Scholar] [CrossRef]
- Cortés, F.; Cuevas, G.; Tenorio, J.; Rochín, A. Asignación inequívoca de las señales del espectro de resonancia magnética nuclear de 1H y 13C de monoterpenos empleando métodos computacionales. Soc. Quim. Mex. 2000, 44, 7–10. [Google Scholar]
- Pesyan, N.; Sadeghali, B.; Enayati, M.; Hoseinpour, S.; Ostadhosseini, N. X-Ray, IR, NMR, UV-visible spectra and DFT analysis of 5-aryloxy-(1H)-tetrazoles, structure, conformation and tautomerism. Curr. Chem. Lett. 2014, 3, 85–96. [Google Scholar] [CrossRef]
- Carey, F.; Sundberg, R. Advanced Organic Chemistry, Part A: Structure and Mechanisms, 5th ed.; Springer Science+Business Media, LLC: New York, NY, USA, 2007. [Google Scholar] [CrossRef]


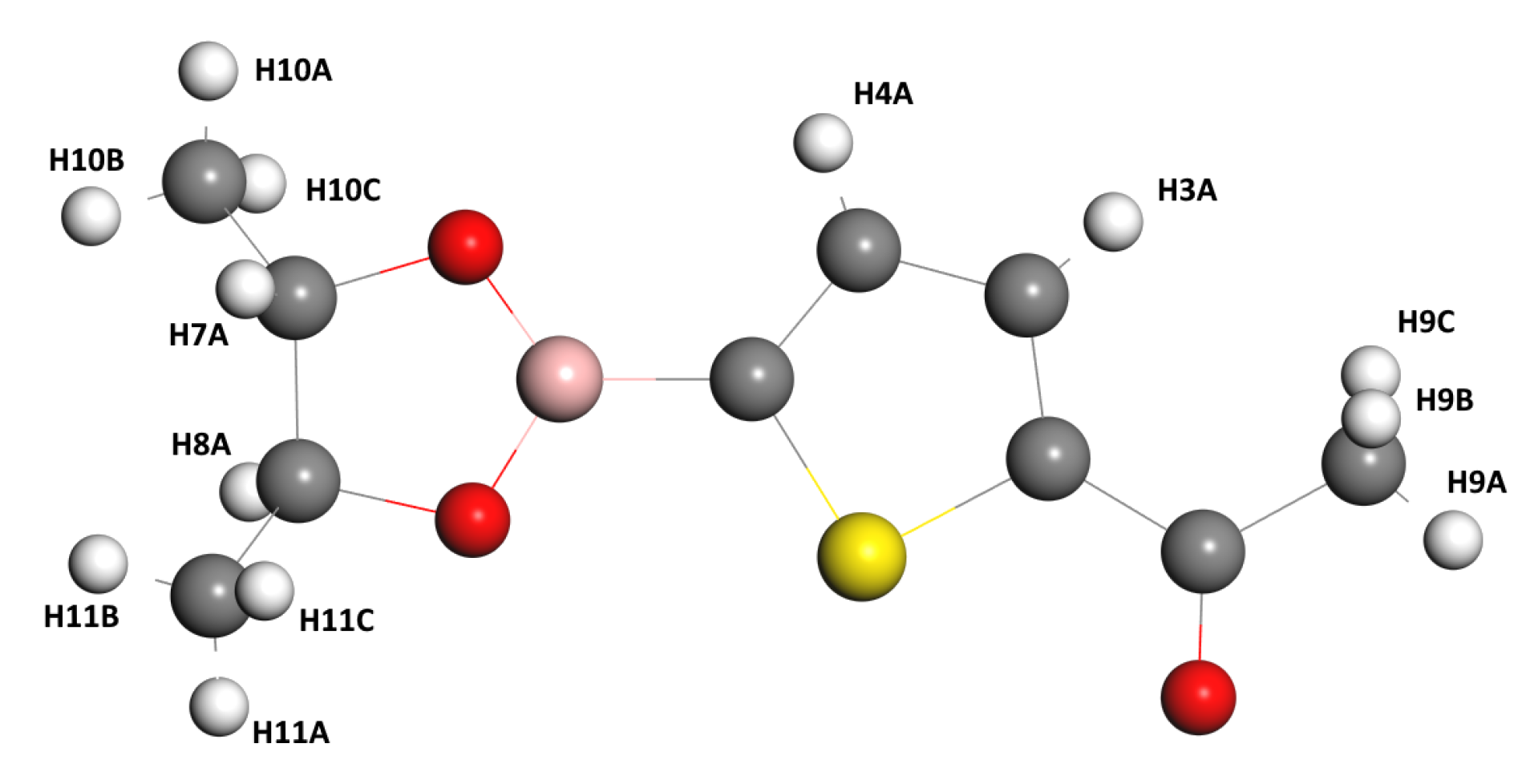
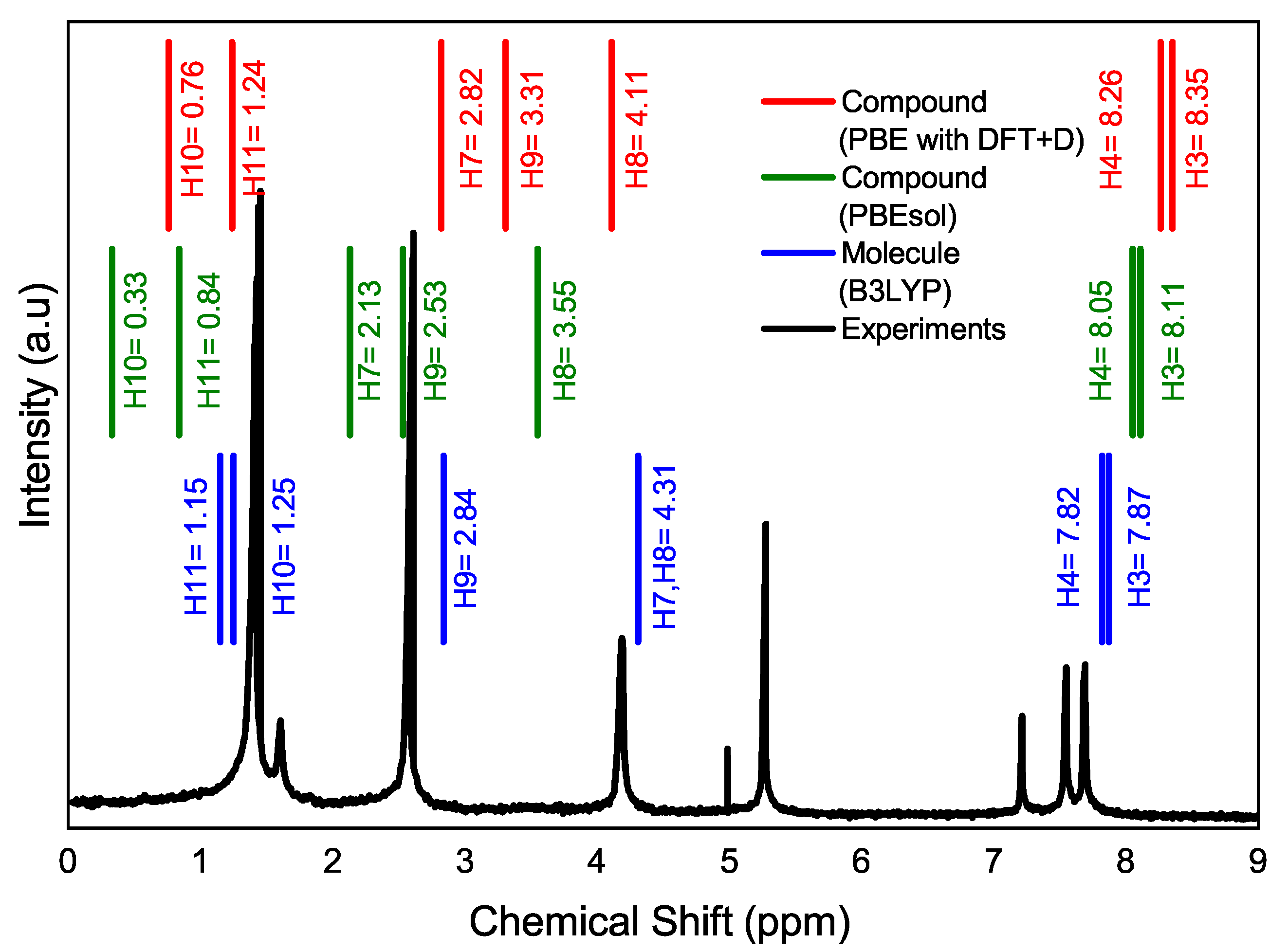
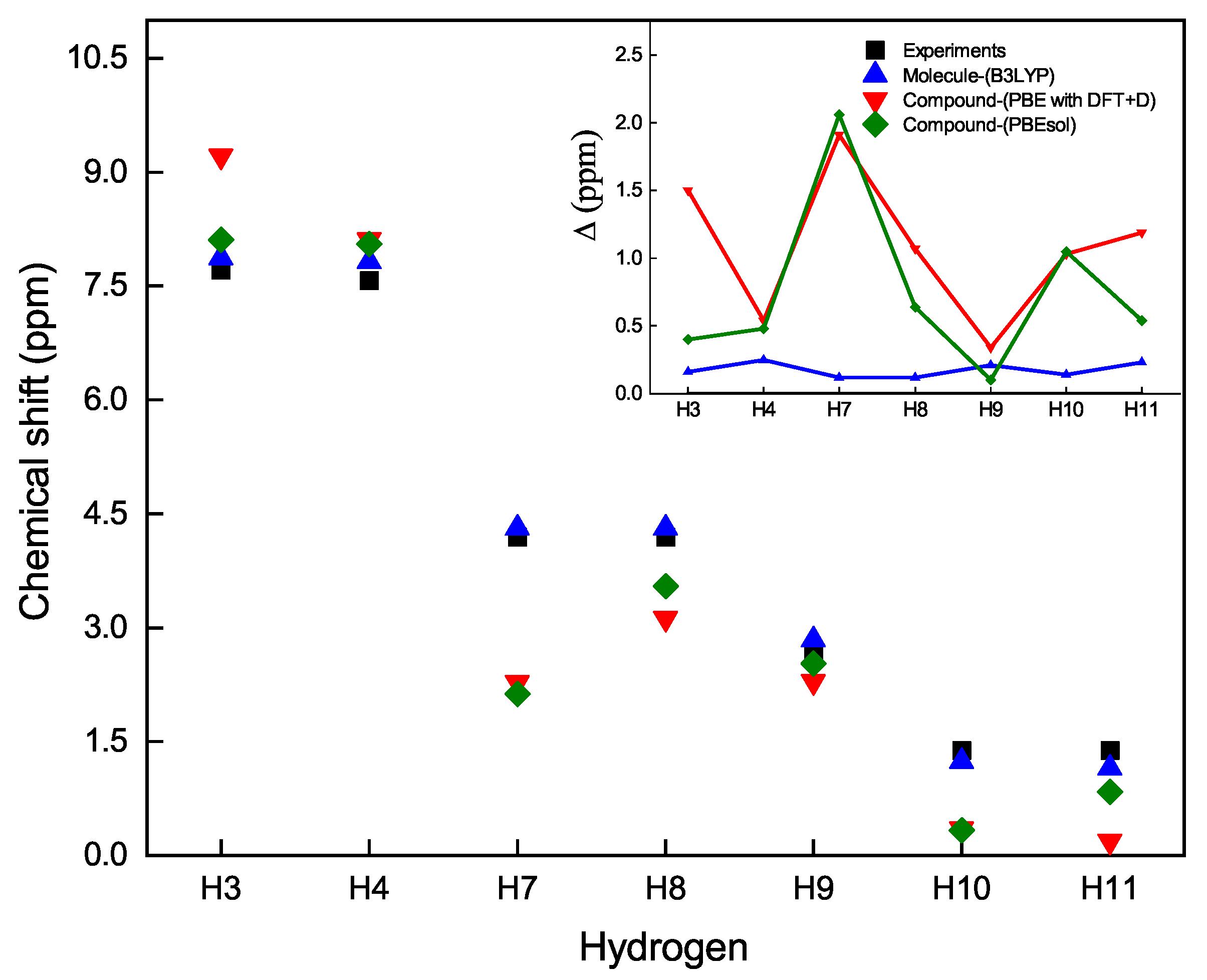
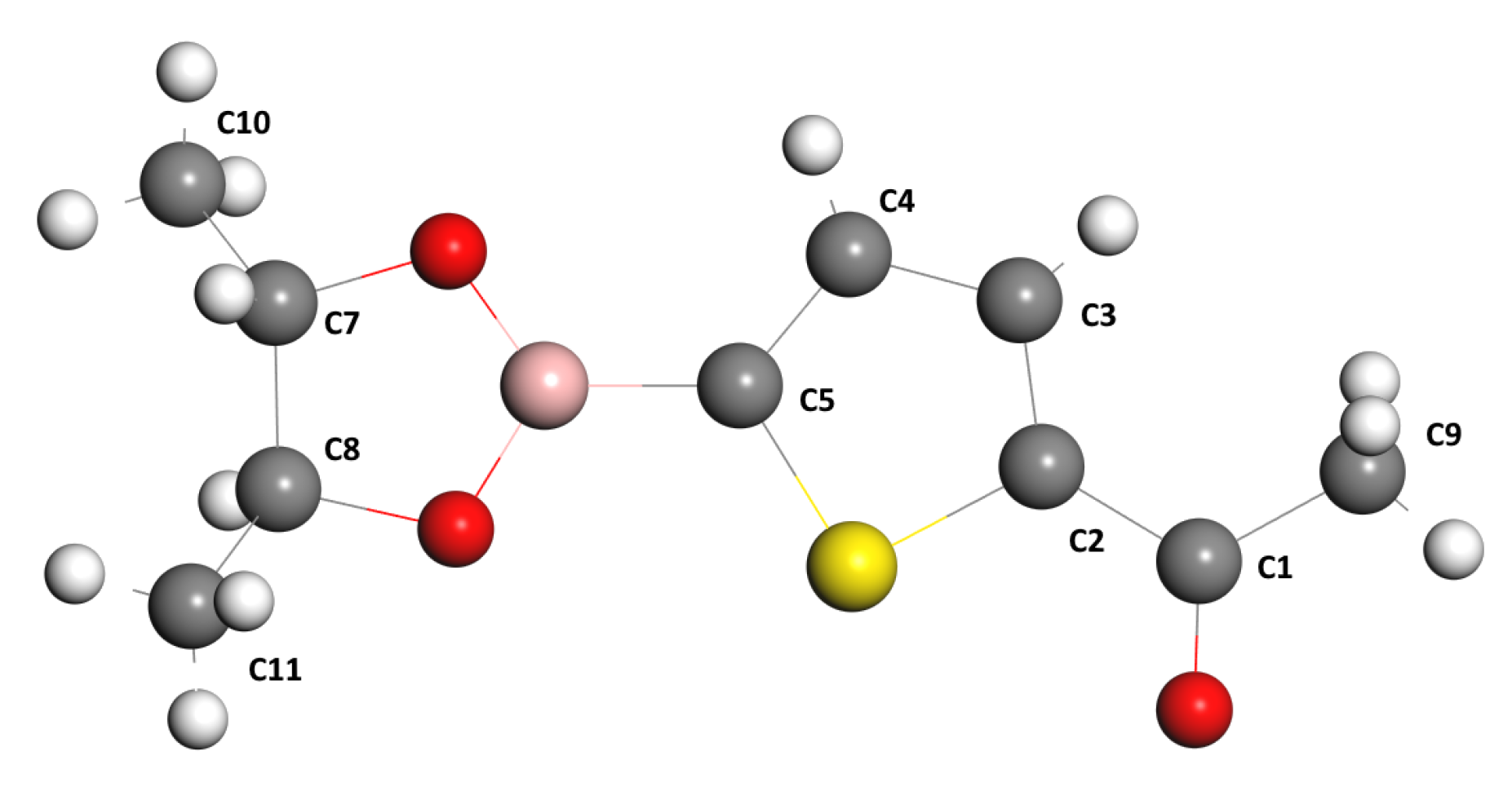
| Characteristic | Experimental [35] | Optimized Lattice Structure | |
|---|---|---|---|
| Empiric formula | - | - | |
| Spacial group | (monoclinic) | PBE-GGA | PBEsol-GGA |
| Lattice parameters | Å | Å | Å |
| Å | Å | Å | |
| Å | Å | Å | |
| Lattice angles | |||
| Bonds (All Lengths in Å) | Experimental Bond Lengths [35] | Optimization (CASTEP-PBE) | Optimization (CASTEP-PBEsol) | Optimization (Gaussian-B3LYP) |
|---|---|---|---|---|
| C3–H3A | ||||
| C4–H4A | ||||
| C7–H7A | ||||
| C8–H8A | ||||
| C9–H9 | ||||
| C10–H10 | ||||
| C11–H11 |
| Bonds (All Lengths in Å) | Experimental Bond Lengths [35] | Optimization (CASTEP-PBE) | Optimization (CASTEP-PBEsol) | Optimization (Gaussian-B3LYP) |
|---|---|---|---|---|
| C1–C2 | ||||
| C2–C3 | ||||
| C3–C4 | ||||
| C4–C5 | ||||
| C1–C9 | ||||
| C7–C8 | ||||
| C8–C11 | ||||
| C7–C10 |
| Bonds (All Lengths in Å) | Experimental Bond Lengths [35] | Optimization (CASTEP-PBE) | Optimization (CASTEP-PBEsol) | Optimization (Gaussian-B3LYP) |
|---|---|---|---|---|
| C–H | ||||
| C–Si |
| Bonds (All Lengths in Å) | Experimental Bond Lengths [38] | Optimization (CASTEP-PBE) | Optimization (CASTEP-PBEsol) | Optimization (Gaussian-B3LYP) |
|---|---|---|---|---|
| C–H | ||||
| O–B | ||||
| F–B |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guevara, U.J.; Núñez R., J.B.; Lozada-Yavina, R.; Tiutiunnyk, A.; Pérez, L.M.; Díaz, P.; Urdaneta, N.; Laroze, D. Characterization of the 1-(5-(4,5-Dimethyl-1,3,2-dioxoborolan-2-yl)thiophen-2-yl)ethanone Using NMR 13C, 1H and 11B through the Density Functional Theory. Materials 2023, 16, 3037. https://doi.org/10.3390/ma16083037
Guevara UJ, Núñez R. JB, Lozada-Yavina R, Tiutiunnyk A, Pérez LM, Díaz P, Urdaneta N, Laroze D. Characterization of the 1-(5-(4,5-Dimethyl-1,3,2-dioxoborolan-2-yl)thiophen-2-yl)ethanone Using NMR 13C, 1H and 11B through the Density Functional Theory. Materials. 2023; 16(8):3037. https://doi.org/10.3390/ma16083037
Chicago/Turabian StyleGuevara, Ulises J., Jesús B. Núñez R., Rafael Lozada-Yavina, Anton Tiutiunnyk, Laura M. Pérez, Pablo Díaz, Neudo Urdaneta, and David Laroze. 2023. "Characterization of the 1-(5-(4,5-Dimethyl-1,3,2-dioxoborolan-2-yl)thiophen-2-yl)ethanone Using NMR 13C, 1H and 11B through the Density Functional Theory" Materials 16, no. 8: 3037. https://doi.org/10.3390/ma16083037
APA StyleGuevara, U. J., Núñez R., J. B., Lozada-Yavina, R., Tiutiunnyk, A., Pérez, L. M., Díaz, P., Urdaneta, N., & Laroze, D. (2023). Characterization of the 1-(5-(4,5-Dimethyl-1,3,2-dioxoborolan-2-yl)thiophen-2-yl)ethanone Using NMR 13C, 1H and 11B through the Density Functional Theory. Materials, 16(8), 3037. https://doi.org/10.3390/ma16083037







