Evaluation of Piezoresistive and Electrical Properties of Conductive Nanocomposite Based on Castor-Oil Polyurethane Filled with MWCNT and Carbon Black
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
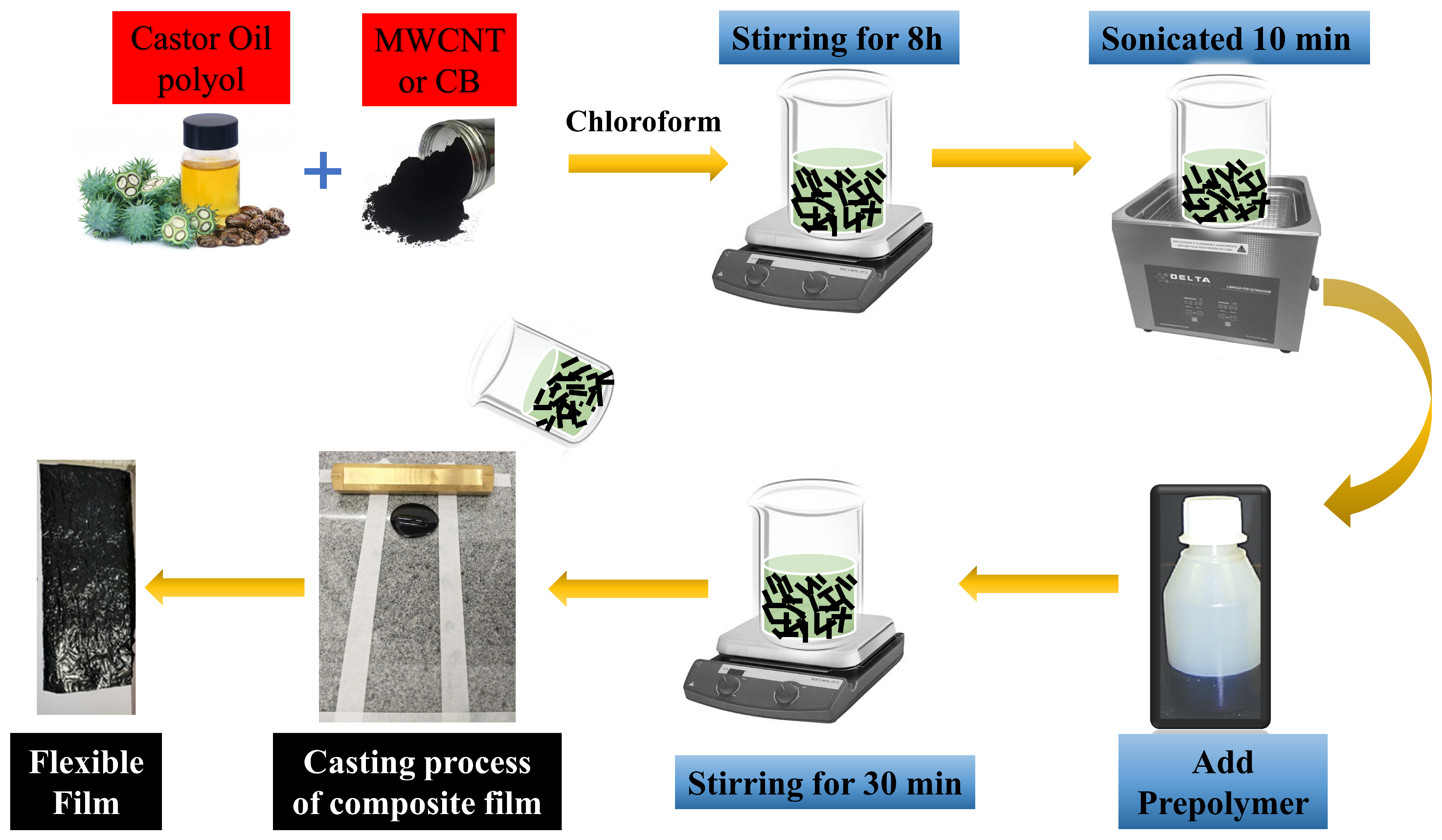
2.2. Conducting Nanocomposite Preparation
2.3. Characterization
3. Results and Discussion
3.1. Morphological Analysis
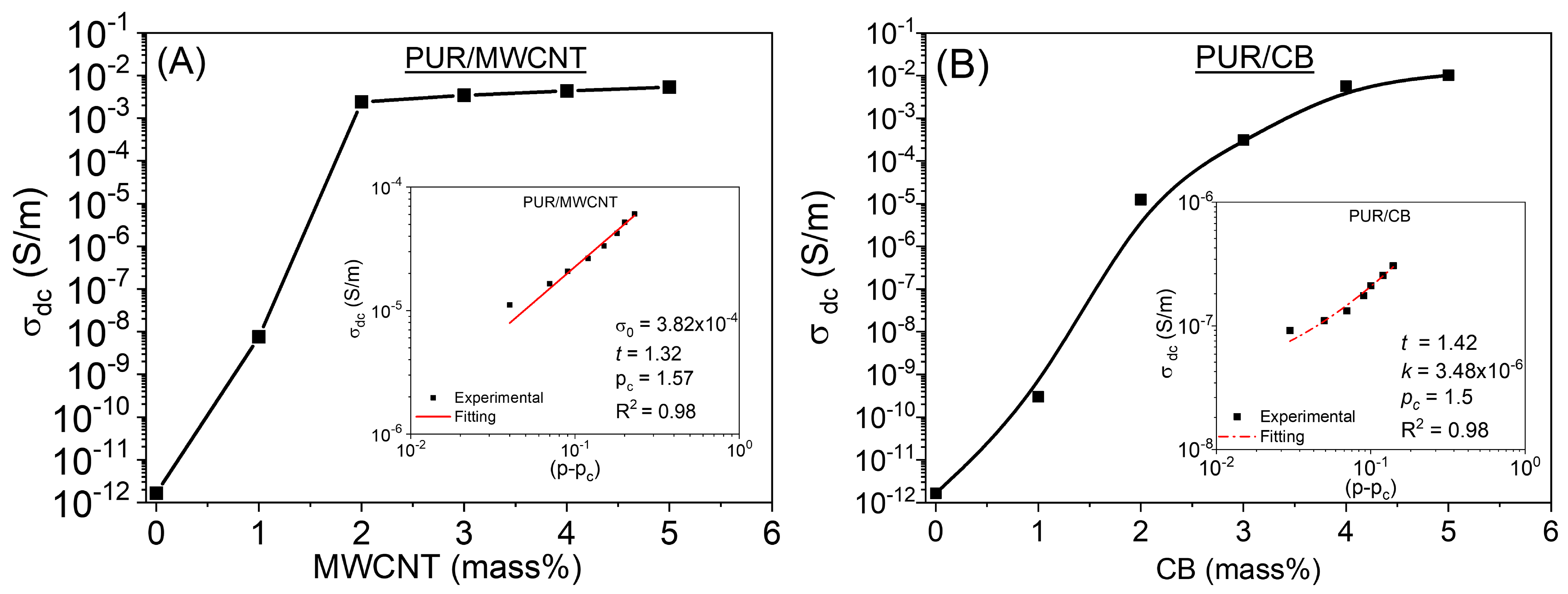
3.2. DC Electrical Conductivity
3.3. Impedance Spectroscopy (IS)
3.4. Piezoresistivity Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Silva, M.J.; Sanches, A.O.; Cena, C.R.; Nagashima, H.N.; Medeiros, E.S.; Malmonge, J.A. Study of the Electrical Conduction Process in Natural Rubber-based Conductive Nanocomposites Filled with Cellulose Nanowhiskers Coated by Polyaniline. Polym. Compos. 2021, 42, 1519–1529. [Google Scholar] [CrossRef]
- Kalia, S.; Dufresne, A.; Cherian, B.M.; Kaith, B.S.; Avérous, L.; Njuguna, J.; Nassiopoulos, E. Cellulose-Based Bio- and Nanocomposites: A Review. Int. J. Polym. Sci. 2011, 2011, 837875. [Google Scholar] [CrossRef]
- Siracusa, V.; Blanco, I. Bio-Polyethylene (Bio-PE), Bio-Polypropylene (Bio-PP) and Bio-Poly(Ethylene Terephthalate) (Bio-PET): Recent Developments in Bio-Based Polymers Analogous to Petroleum-Derived Ones for Packaging and Engineering Applications. Polymers 2020, 12, 1641. [Google Scholar] [CrossRef]
- Costa, J.G.L.; Rodrigues, P.H.F.; Paim, L.L.; Sanches, A.O.; Malmonge, J.A.; da Silva, M.J. 1-3 Castor Oil-Based Polyurethane/PZT Piezoelectric Composite as a Possible Candidate for Structural Health Monitoring. Mater. Res. 2020, 23, 1–9. [Google Scholar] [CrossRef]
- Kaikade, D.S.; Sabnis, A.S. Polyurethane Foams from Vegetable Oil-Based Polyols: A Review. Polym. Bull. 2022, 80, 2239–2261. [Google Scholar] [CrossRef]
- Alves, F.C.; dos Santos, V.F.; Monticeli, F.M.; Ornaghi, H.; da Sliva Barud, H.; Mulinari, D.R. Efficiency of Castor Oil–Based Polyurethane Foams for Oil Sorption S10 and S500: Influence of Porous Size and Statistical Analysis. Polym. Polym. Compos. 2021, 29, S1063–S1074. [Google Scholar] [CrossRef]
- Saha, P.; Khomlaem, C.; Aloui, H.; Kim, B.S. Biodegradable Polyurethanes Based on Castor Oil and Poly (3-Hydroxybutyrate). Polymers 2021, 13, 1387. [Google Scholar] [CrossRef]
- Sardari, A.; Sabbagh Alvani, A.A.; Ghaffarian, S.R. Castor Oil-Derived Water-Based Polyurethane Coatings: Structure Manipulation for Property Enhancement. Prog. Org. Coat. 2019, 133, 198–205. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Tai, W. Castor Oil-Based Polyurethane Resin for Low-Density Composites with Bamboo Charcoal. Polymers 2018, 10, 1100. [Google Scholar] [CrossRef]
- Gama, N.; Ferreira, A.; Barros-Timmons, A. Cure and Performance of Castor Oil Polyurethane Adhesive. Int. J. Adhes. Adhes. 2019, 95, 102413. [Google Scholar] [CrossRef]
- Panda, S.S.; Panda, B.P.; Nayak, S.K.; Mohanty, S. A Review on Waterborne Thermosetting Polyurethane Coatings Based on Castor Oil: Synthesis, Characterization, and Application. Polym. Plast. Technol. Eng. 2018, 57, 500–522. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Y.; Liang, H.; Liang, D.; Cao, H.; Liu, C.; Qian, Y.; Lu, Q.; Zhang, C. High Bio-Content Castor Oil Based Waterborne Polyurethane/Sodium Lignosulfonate Composites for Environmental Friendly UV Absorption Application. Ind. Crops Prod. 2019, 142, 111836. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, Y.; Tao, Y.; Wang, B.; Cheng, W.; Jie, G.; Song, L.; Hu, Y. Self-Healable Castor Oil-Based Waterborne Polyurethane/MXene Film with Outstanding Electromagnetic Interference Shielding Effectiveness and Excellent Shape Memory Performance. J. Colloid. Interface Sci. 2021, 588, 164–174. [Google Scholar] [CrossRef] [PubMed]
- Vieira Amorim, F.; José Ribeiro Padilha, R.; Maria Vinhas, G.; Ramos Luiz, M.; Costa de Souza, N.; Medeiros Bastos de Almeida, Y. Development of Hydrophobic Polyurethane/Castor Oil Biocomposites with Agroindustrial Residues for Sorption of Oils and Organic Solvents. J. Colloid. Interface Sci. 2021, 581, 442–454. [Google Scholar] [CrossRef] [PubMed]
- Rebeque, P.V.; Silva, M.J.; Cena, C.R.; Nagashima, H.N.; Malmonge, J.A.; Kanda, D.H.F. Analysis of the Electrical Conduction in Percolative Nanocomposites Based on Castor-Oil Polyurethane with Carbon Black and Activated Carbon Nanopowder. Polym. Compos. 2019, 40, 7–15. [Google Scholar] [CrossRef]
- Merlini, C.; Pegoretti, A.; Vargas, P.C.; da Cunha, T.F.; Ramôa, S.D.A.S.; Soares, B.G.; Barra, G.M.O. Electromagnetic Interference Shielding Effectiveness of Composites Based on Polyurethane Derived from Castor Oil and Nanostructured Carbon Fillers. Polym. Compos. 2019, 40, E78–E87. [Google Scholar] [CrossRef]
- Wang, M.; Tang, X.-H.; Cai, J.-H.; Wu, H.; Shen, J.-B.; Guo, S.-Y. Construction, Mechanism and Prospective of Conductive Polymer Composites with Multiple Interfaces for Electromagnetic Interference Shielding: A Review. Carbon. N. Y. 2021, 177, 377–402. [Google Scholar] [CrossRef]
- Bakkali, H.; Dominguez, M.; Batlle, X.; Labarta, A. Universality of the Electrical Transport in Granular Metals. Sci. Rep. 2016, 6, 29676. [Google Scholar] [CrossRef]
- Deniz, W.D.S.; Lima, T.H.C.; Arlindo, E.P.S.; Junior, G.C.F. Prevulcanized Natural Rubber and Carbon Black: High-Deformation Piezoresistive Composites. Mater. Lett. 2019, 253, 427–429. [Google Scholar] [CrossRef]
- Bunde, A.; Dieterich, W. Percolation in Composites. J. Electroceram 2000, 5, 81–92. [Google Scholar] [CrossRef]
- Folorunso, O.; Hamam, Y.; Sadiku, R.; Ray, S.S.; Joseph, A.G. Parametric Analysis of Electrical Conductivity of Polymer-Composites. Polymers 2019, 11, 1250. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.Q.; Liang, J.Z. A Percolation Model for Insulator-Metal Transition in Polymer-Conductor Composites. Appl. Phys. Lett. 2008, 93, 131918. [Google Scholar] [CrossRef]
- Sen, A.K.; Bhattacharya, S. Variable Range Hopping Conduction in Complex Systems and a Percolation Model with Tunneling. In Continuum Models and Discrete Systems; Springer: Dordrecht, The Netherlands, 2004; pp. 367–373. [Google Scholar]
- Psarras, G.C. Hopping Conductivity in Polymer Matrix–Metal Particles Composites. Compos. Part A Appl. Sci. Manuf. 2006, 37, 1545–1553. [Google Scholar] [CrossRef]
- Huang, J.C. Carbon Black Filled Conducting Polymers and Polymer Blends. Adv. Polym. Technol. 2002, 21, 299–313. [Google Scholar] [CrossRef]
- Gupta, A.; Goyal, R.K. Electrical Properties of Polycarbonate/Expanded Graphite Nanocomposites. J. Appl. Polym. Sci. 2019, 13, 47274. [Google Scholar] [CrossRef]
- Mogha, A.; Kaushik, A. Functionalized Multiwall Carbon Nanotubes to Enhance Dispersion in Castor Oil-Based Polyurethane Nanocomposites. Fuller. Nanotub. Carbon. Nanostruct. 2021, 29, 907–914. [Google Scholar] [CrossRef]
- Dai, Z.; Jiang, P.; Zhang, P.; Wai, P.T.; Bao, Y.; Gao, X.; Xia, J.; Haryono, A. Multiwalled Carbon Nanotubes/Castor-oil–Based Waterborne Polyurethane Nanocomposite Prepared Using a Solvent-free Method. Polym. Adv. Technol. 2021, 32, 1038–1048. [Google Scholar] [CrossRef]
- Acuña, P.; Zhang, J.; Yin, G.-Z.; Liu, X.-Q.; Wang, D.-Y. Bio-Based Rigid Polyurethane Foam from Castor Oil with Excellent Flame Retardancy and High Insulation Capacity via Cooperation with Carbon-Based Materials. J. Mater. Sci. 2021, 56, 2684–2701. [Google Scholar] [CrossRef]
- Sinh, L.H.; Luong, N.D.; Seppälä, J. Enhanced Mechanical and Thermal Properties of Polyurethane/Functionalised Graphene Oxide Composites by in Situ Polymerisation. Plast. Rubber Compos. 2019, 48, 466–476. [Google Scholar] [CrossRef]
- Mohammadi, A.; Hosseinipour, M.; Abdolvand, H.; Najafabadi, S.A.A.; Sahraneshin Samani, F. Improvement in Bioavailability of Curcumin within the Castor-oil Based Polyurethane Nanocomposite through Its Conjugation on the Surface of Graphene Oxide Nanosheets. Polym. Adv. Technol. 2022, 33, 1126–1136. [Google Scholar] [CrossRef]
- Li, J.-W.; Tsen, W.-C.; Tsou, C.-H.; Suen, M.-C.; Chiu, C.-W. Synthetic Environmentally Friendly Castor Oil Based-Polyurethane with Carbon Black as a Microphase Separation Promoter. Polymers 2019, 11, 1333. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Tewatia, P.; Samota, S.; Rattan, G.; Kaushik, A. Ameliorating Properties of Castor Oil Based Polyurethane Hybrid Nanocomposites via Synergistic Addition of Graphene and Cellulose Nanofibers. J. Ind. Eng. Chem. 2022, 109, 492–509. [Google Scholar] [CrossRef]
- Min, Y.K.; Eom, T.; Kim, H.; Kang, D.; Lee, S.-E. Independent Heating Performances in the Sub-Zero Environment of MWCNT/PDMS Composite with Low Electron-Tunneling Energy. Polymers 2023, 15, 1171. [Google Scholar] [CrossRef] [PubMed]
- Kamedulski, P.; Lukaszewicz, J.P.; Witczak, L.; Szroeder, P.; Ziolkowski, P. The Importance of Structural Factors for the Electrochemical Performance of Graphene/Carbon Nanotube/Melamine Powders towards the Catalytic Activity of Oxygen Reduction Reaction. Materials 2021, 14, 2448. [Google Scholar] [CrossRef] [PubMed]
- Rozhin, P.; Kralj, S.; Soula, B.; Marchesan, S.; Flahaut, E. Hydrogels from a Self-Assembling Tripeptide and Carbon Nanotubes (CNTs): Comparison between Single-Walled and Double-Walled CNTs. Nanomaterials 2023, 13, 847. [Google Scholar] [CrossRef] [PubMed]
- Chung, D.D.L. A Critical Review of Piezoresistivity and Its Application in Electrical-Resistance-Based Strain Sensing. J. Mater. Sci. 2020, 55, 15367–15396. [Google Scholar] [CrossRef]
- Nayak, L.; Rahaman, M.; Aldalbahi, A.; Kumar Chaki, T.; Khastgir, D. Polyimide-Carbon Nanotubes Nanocomposites: Electrical Conduction Behavior under Cryogenic Condition. Polym. Eng. Sci. 2017, 57, 291–298. [Google Scholar] [CrossRef]
- Spahr, M.E.; Gilardi, R.; Bonacchi, D. Carbon Black for Electrically Conductive Polymer Applications. In Fillers for Polymer Applications; Springer: Cham, Switzerland, 2017; pp. 375–400. [Google Scholar]
- Zhang, Q.; Wang, J.; Zhang, B.-Y.; Guo, B.-H.; Yu, J.; Guo, Z.-X. Improved Electrical Conductivity of Polymer/Carbon Black Composites by Simultaneous Dispersion and Interaction-Induced Network Assembly. Compos. Sci. Technol. 2019, 179, 106–114. [Google Scholar] [CrossRef]
- Silva, M.J.D.; Kanda, D.H.F.; Nagashima, H.N. Mechanism of Charge Transport in Castor Oil-Based Polyurethane/Carbon Black Composite (PU/CB). J. Non Cryst. Solids 2012, 358, 270–275. [Google Scholar] [CrossRef]
- Kirkpatrick, S. Percolation and Conduction. Rev. Mod. Phys. 1973, 45.4, 574–588. [Google Scholar] [CrossRef]
- Shao, W.Z.; Xie, N.; Zhen, L.; Feng, L.C. Conductivity Critical Exponents Lower than the Universal Value in Continuum Percolation Systems. J. Phys. Condens. Matter 2008, 20, 395235. [Google Scholar] [CrossRef]
- Panda, M.; Srinivas, V.; Thakur, A.K. Non-Universal Scaling Behavior of Polymer-Metal Composites across the Percolation Threshold. Results Phys. 2015, 5, 136–141. [Google Scholar] [CrossRef]
- Marsden, A.J.; Papageorgiou, D.G.; Vallés, C.; Liscio, A.; Palermo, V.; Bissett, M.A.; Young, R.J.; Kinloch, I.A. Electrical Percolation in Graphene–Polymer Composites. 2d Mater. 2018, 5, 032003. [Google Scholar] [CrossRef]
- Shi, Y.D.; Li, J.; Tan, Y.J.; Chen, Y.F.; Wang, M. Percolation Behavior of Electromagnetic Interference Shielding in Polymer/Multi-Walled Carbon Nanotube Nanocomposites. Compos. Sci. Technol. 2019, 170, 70–76. [Google Scholar] [CrossRef]
- Mazaheri, M.; Payandehpeyman, J.; Jamasb, S. Modeling of Effective Electrical Conductivity and Percolation Behavior in Conductive-Polymer Nanocomposites Reinforced with Spherical Carbon Black. Appl. Compos. Mater. 2022, 29, 695–710. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. Tuning of a Mechanics Model for the Electrical Conductivity of CNT-Filled Samples Assuming Extended CNT. Eur. Phys. J. Plus 2021, 137, 24. [Google Scholar] [CrossRef]
- Macdonald, J.R. Impedance Spectroscopy: Models, Data Fitting, and Analysis. Solid State Ion. 2005, 176, 1961–1969. [Google Scholar] [CrossRef]
- Dyre, J.C.; Schrøder, T.B. Universality of Ac Conduction in Disordered Solids. Rev. Mod. Phys. 2000, 72, 873–892. [Google Scholar] [CrossRef]
- Bianchi, R.F.; Leal Ferreira, G.F.; Lepienski, C.M.; Faria, R.M. Alternating Electrical Conductivity of Polyaniline. J. Chem. Phys. 1999, 110, 4602–4607. [Google Scholar] [CrossRef]
- Dyre, J.C. The Random Free-Energy Barrier Model for Ac Conduction in Disordered Solids. J. Appl. Phys. 1988, 64, 2456–2468. [Google Scholar] [CrossRef]
- Kilbride, B.E.; Coleman, J.N.; Fraysse, J.; Fournet, P.; Cadek, M.; Drury, A.; Hutzler, S.; Roth, S.; Blau, W.J. Experimental Observation of Scaling Laws for Alternating Current and Direct Current Conductivity in Polymer-Carbon Nanotube Composite Thin Films. J. Appl. Phys. 2002, 92, 4024–4030. [Google Scholar] [CrossRef]
- Ma, B.; Wang, Y.; Wang, K.; Li, X.; Liu, J.; An, L. Frequency-Dependent Conductive Behavior of Polymer-Derived Amorphous Silicon Carbonitride. Acta Mater. 2015, 89, 215–224. [Google Scholar] [CrossRef]
- Alptekin, S.; Tataroğlu, A.; Altındal, Ş. Dielectric, Modulus and Conductivity Studies of Au/PVP/n-Si (MPS) Structure in the Wide Range of Frequency and Voltage at Room Temperature. J. Mater. Sci. Mater. Electron. 2019, 30, 6853–6859. [Google Scholar] [CrossRef]
- Dhahri, A.; Dhahri, E.; Hlil, E.K. Electrical Conductivity and Dielectric Behaviour of Nanocrystalline La0.6 Gd0.1 Sr0.3 Mn0.75 Si0.25 O3. RSC Adv. 2018, 8, 9103–9111. [Google Scholar] [CrossRef] [PubMed]
- Jouni, M.; Faure-Vincent, J.; Fedorko, P.; Djurado, D.; Boiteux, G.; Massardier, V. Charge Carrier Transport and Low Electrical Percolation Threshold in Multiwalled Carbon Nanotube Polymer Nanocomposites. Carbon. N. Y. 2014, 76, 10–18. [Google Scholar] [CrossRef]
- Freire Filho, F.C.M.; Santos, J.A.; Sanches, A.O.; Medeiros, E.S.; Malmonge, J.A.; Silva, M.J. Dielectric, Electric, and Piezoelectric Properties of Three-phase Piezoelectric Composite Based on Castor-oil Polyurethane, Lead Zirconate Titanate Particles and Multiwall Carbon Nanotubes. J. Appl. Polym. Sci. 2023, 140, e53572. [Google Scholar] [CrossRef]
- Li, B.; Randall, C.A.; Manias, E. Polarization Mechanism Underlying Strongly Enhanced Dielectric Permittivity in Polymer Composites with Conductive Fillers. J. Phys. Chem. C 2022, 126, 7596–7604. [Google Scholar] [CrossRef]
- Sanches, A.O.; Kanda, D.H.F.; Malmonge, L.F.; da Silva, M.J.; Sakamoto, W.K.; Malmonge, J.A. Synergistic Effects on Polyurethane/Lead Zirconate Titanate/Carbon Black Three-Phase Composites. Polym. Test. 2017, 60, 253–259. [Google Scholar] [CrossRef]
- Amoozegar, V.; Sherafat, Z.; Bagherzadeh, E. Enhanced Dielectric and Piezoelectric Properties in Potassium Sodium Niobate/Polyvinylidene Fluoride Composites Using Nano-Silicon Carbide as an Additive. Ceram. Int. 2021, 47, 28260–28267. [Google Scholar] [CrossRef]
- Achour, M.E.; Brosseau, C.; Carmona, F. Dielectric Relaxation in Carbon Black-Epoxy Composite Materials. J. Appl. Phys. 2008, 103, 094103. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, X.; Zhang, H. Influence of the Relaxation of Maxwell-Wagner-Sillars Polarization and Dc Conductivity on the Dielectric Behaviors of Nylon 1010. J. Appl. Phys. 2006, 100, 054104. [Google Scholar] [CrossRef]
- Asandulesa, M.; Kostromin, S.; Tameev, A.; Aleksandrov, A.; Bronnikov, S. Molecular Dynamics and Conductivity of a PTB7:PC71BM Photovoltaic Polymer Blend: A Dielectric Spectroscopy Study. ACS Appl. Polym. Mater. 2021, 3, 4869–4878. [Google Scholar] [CrossRef]
- Asandulesa, M.; Kostromin, S.; Podshivalov, A.; Tameev, A.; Bronnikov, S. Relaxation Processes in a Polymer Composite for Bulk Heterojunction: A Dielectric Spectroscopy Study. Polymer 2020, 203, 122785. [Google Scholar] [CrossRef]
- Sousa, E.A.; Lima, T.H.C.; Arlindo, E.P.S.; Sanches, A.O.; Sakamoto, W.K.; Fuzari-Junior, G. de C. Multicomponent Polyurethane–Carbon Black Composite as Piezoresistive Sensor. Polym. Bull. 2020, 77, 3017–3031. [Google Scholar] [CrossRef]
- Costa, P.; Oliveira, J.; Horta-Romarís, L.; Abad, M.-J.; Moreira, J.A.; Zapiráin, I.; Aguado, M.; Galván, S.; Lanceros-Mendez, S. Piezoresistive Polymer Blends for Electromechanical Sensor Applications. Compos. Sci. Technol. 2018, 168, 353–362. [Google Scholar] [CrossRef]
- Gonçalves, B.F.; Costa, P.; Oliveira, J.; Ribeiro, S.; Correia, V.; Botelho, G.; Lanceros-Mendez, S. Green Solvent Approach for Printable Large Deformation Thermoplastic Elastomer Based Piezoresistive Sensors and Their Suitability for Biomedical Applications. J. Polym. Sci. B. Polym. Phys. 2016, 54, 2092–2103. [Google Scholar] [CrossRef]





| Samples | MWCNT (g) | CB (g) |
|---|---|---|
| PUR/MWCNT1 | 0.030 | 0 |
| PUR/MWCNT2 | 0.061 | 0 |
| PUR/MWCNT3 | 0.093 | 0 |
| PUR/MWCNT4 | 0.125 | 0 |
| PUR/MWCNT5 | 0.158 | 0 |
| PUR/CB1 | 0 | 0.030 |
| PUR/CB2 | 0 | 0.061 |
| PUR/CB3 | 0 | 0.093 |
| PUR/CB4 | 0 | 0.125 |
| PUR/CB5 | 0 | 0.158 |
| Samples | σdc (S/m) | A | n | R2 |
|---|---|---|---|---|
| Neat PUR | 1.72 × 10−11 | 3.27 × 10−11 | 1.15 | 0.95 |
| PUR/CB (99/1) | 4.65 × 10−10 | 3.52 × 10−11 | 0.92 | 0.97 |
| PUR/CB (98/2) | 1.73 × 10−7 | 8.49 × 10−10 | 0.80 | 0.99 |
| PUR/CB (97/3) | 1.66 × 10−6 | 1.88 × 10−9 | 0.76 | 0.97 |
| PUR/CB (96/4) | 1.15 × 10−4 | 1.40 × 10−8 | 0.72 | 0.99 |
| PUR/CB (95/5) | 1.15 × 10−3 | 3.41 × 10−7 | 0.70 | 0.80 |
| PUR/MWCNT (99/1) | 7.01 × 10−9 | 5.38 × 10−9 | 0.86 | 0.96 |
| PUR/MWCNT (98/2) | 6.17 × 10−4 | 1.39 × 10−8 | 0.83 | 0.97 |
| PUR/MWCNT (97/3) | 6.65 × 10−3 | 4.06 × 10−8 | 0.79 | 0.95 |
| PUR/MWCNT (96/4) | 1.44 × 10−2 | 2.05 × 10−8 | 0.75 | 0.92 |
| PUR/MWCNT (95/5) | 1.21 × 10−2 | 1.08 × 10−8 | 077 | 0.90 |
| Samples | ε’ (1 kHz) | ε’ (1 MHz) | ε” (1 kHz) | ε” (1 MHz) |
|---|---|---|---|---|
| PUR | 3.52 | 6.23 | 0.82 | 39.2 |
| PUR/MWCNT1 | 2.87 | 2.16 | 0.32 | 0.26 |
| PUR/MWCNT2 | 4.72 | 2.21 | 1.15 | 0.41 |
| PUR/MWCNT3 | 3.45 | 2.11 | 0.36 | 0.27 |
| PUR/MWCNT4 | 11.01 | 5.30 | 1.88 | 0.86 |
| PUR/MWCNT5 | 29.44 | 8.94 | 21.95 | 2.01 |
| PUR/CB1 | 2.56 | 1.88 | 0.27 | 0.24 |
| PUR/CB2 | 17.80 | 5.04 | 10.66 | 1.08 |
| PUR/CB3 | 24.31 | 5.19 | 41.01 | 1.17 |
| PUR/CB4 | 65.21 | 10.16 | 2801.92 | 8.64 |
| PUR/CB5 | 70.14 | 20.12 | 20,515.62 | 31.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melo, D.S.; Reis, I.C.; Queiroz, J.C.; Cena, C.R.; Nahime, B.O.; Malmonge, J.A.; Silva, M.J. Evaluation of Piezoresistive and Electrical Properties of Conductive Nanocomposite Based on Castor-Oil Polyurethane Filled with MWCNT and Carbon Black. Materials 2023, 16, 3223. https://doi.org/10.3390/ma16083223
Melo DS, Reis IC, Queiroz JC, Cena CR, Nahime BO, Malmonge JA, Silva MJ. Evaluation of Piezoresistive and Electrical Properties of Conductive Nanocomposite Based on Castor-Oil Polyurethane Filled with MWCNT and Carbon Black. Materials. 2023; 16(8):3223. https://doi.org/10.3390/ma16083223
Chicago/Turabian StyleMelo, Diego S., Idalci C. Reis, Júlio C. Queiroz, Cicero R. Cena, Bacus O. Nahime, José A. Malmonge, and Michael J. Silva. 2023. "Evaluation of Piezoresistive and Electrical Properties of Conductive Nanocomposite Based on Castor-Oil Polyurethane Filled with MWCNT and Carbon Black" Materials 16, no. 8: 3223. https://doi.org/10.3390/ma16083223






