Modeling and Testing of a Composite Steel–Concrete Joint for Hybrid Girder Bridges
Abstract
:1. Introduction
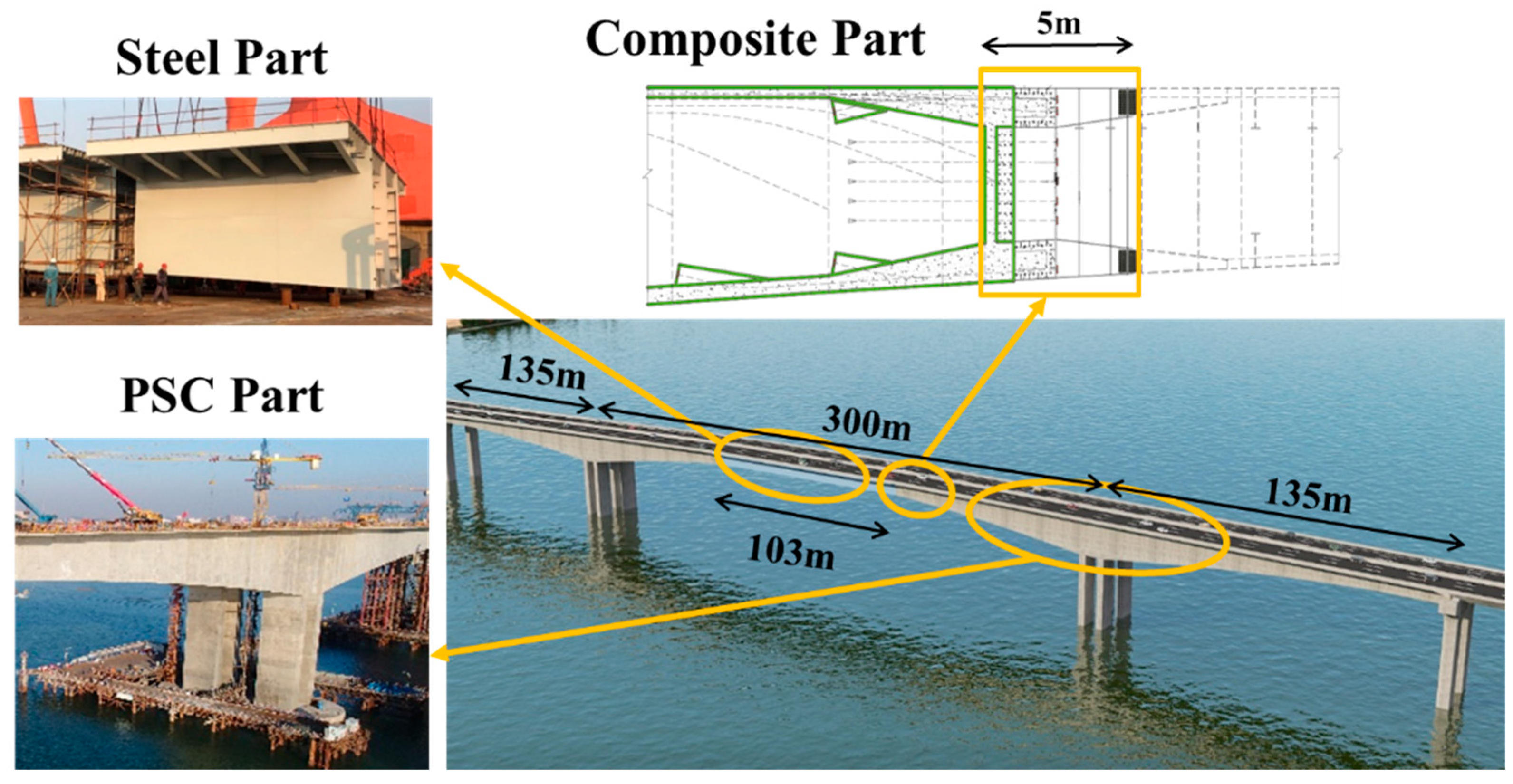
2. Tests Description
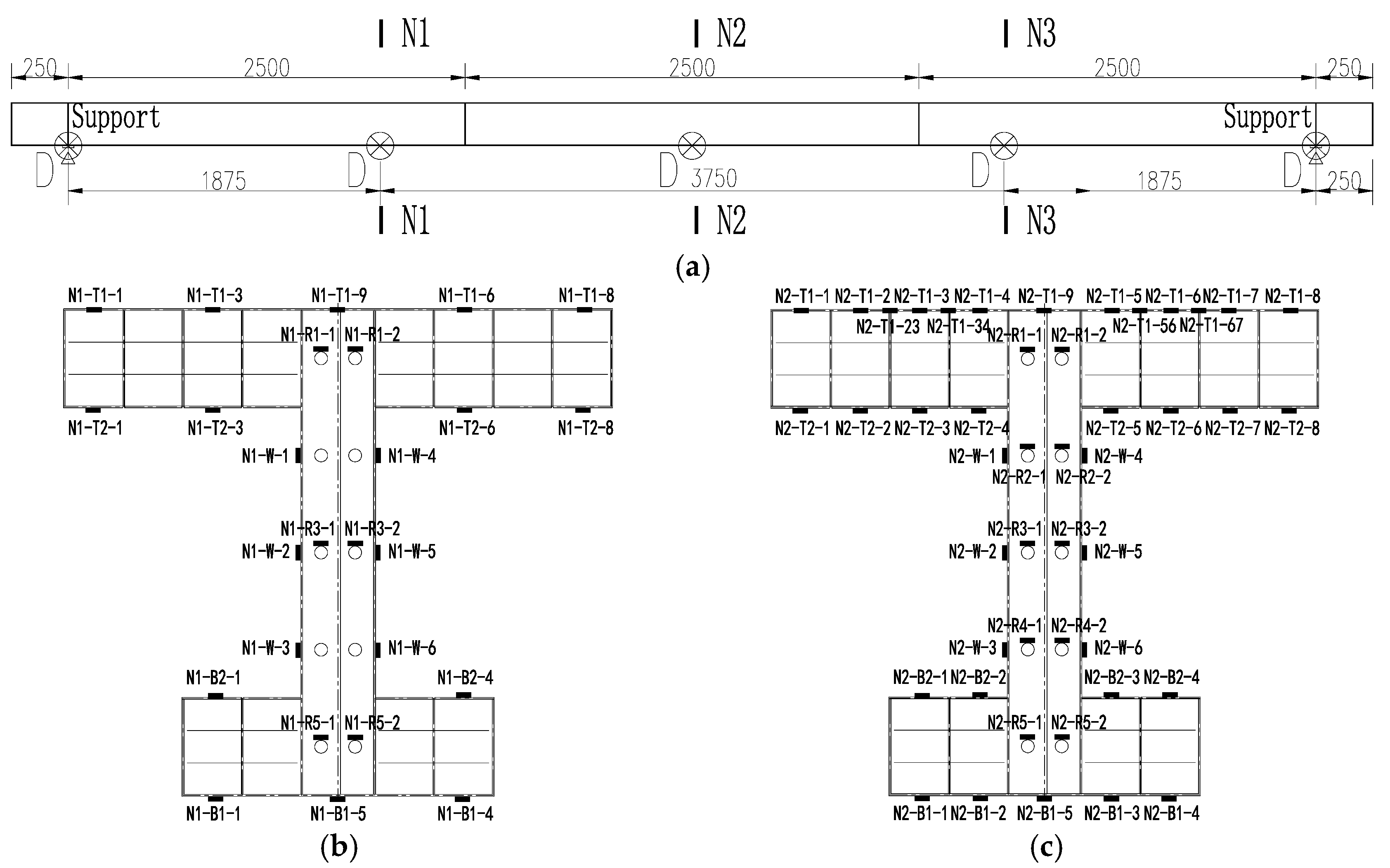
2.1. Specimen Design
2.2. Material Properties
2.3. Loading and Monitoring Setup
3. Experimental Results
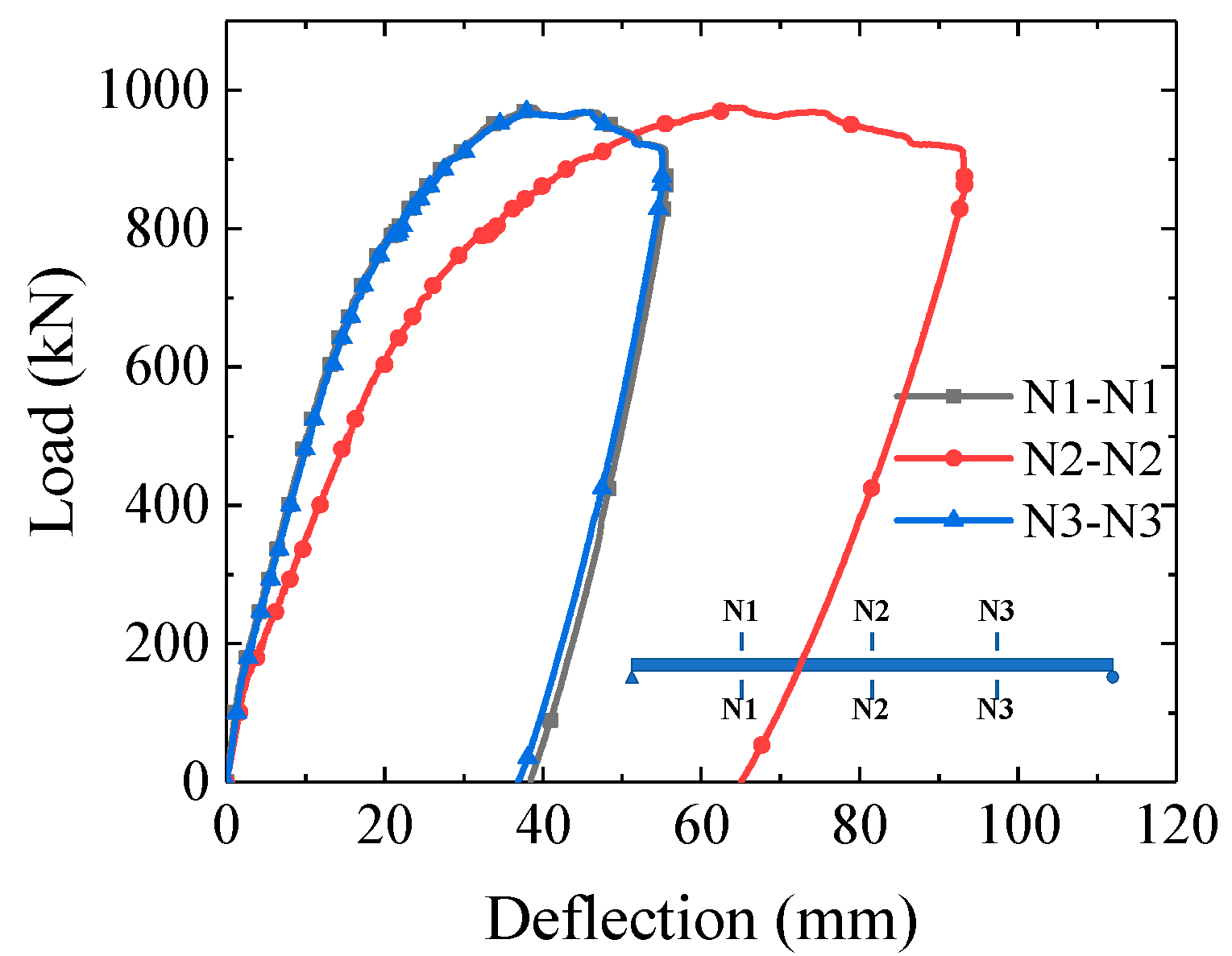
3.1. Load–Deflection Relationship and Failure Mode
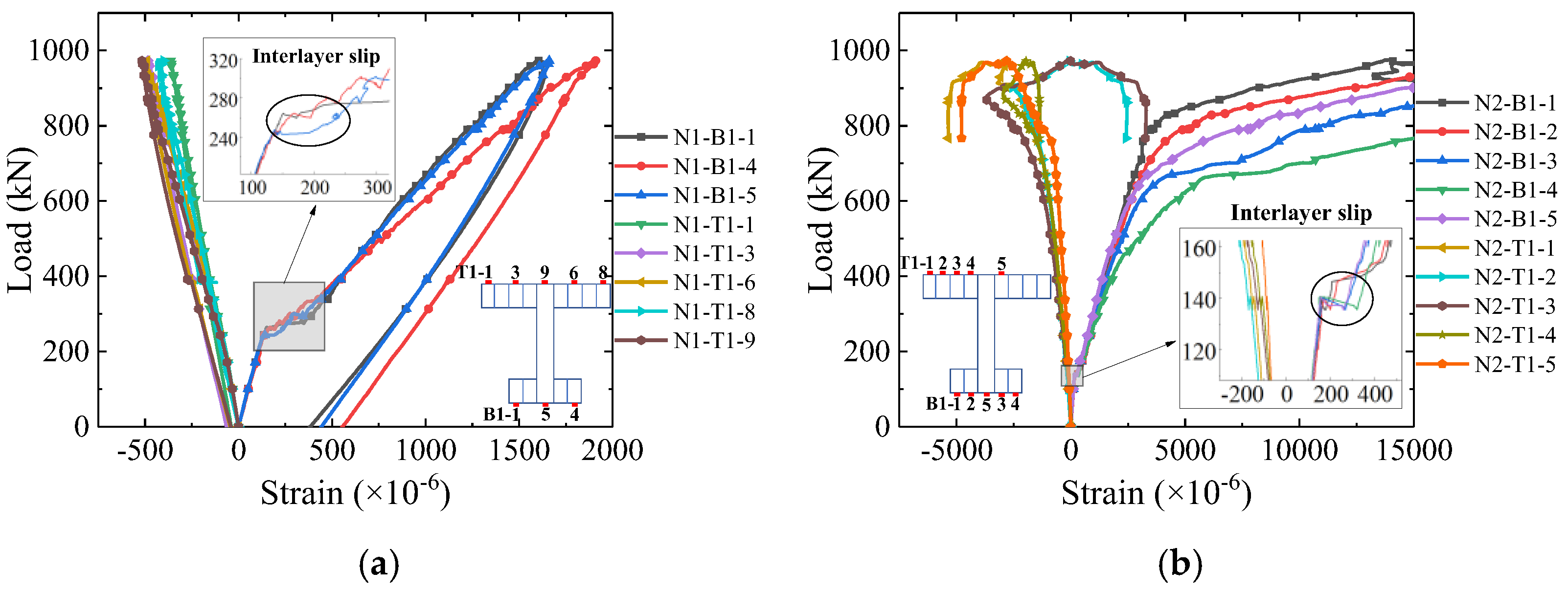
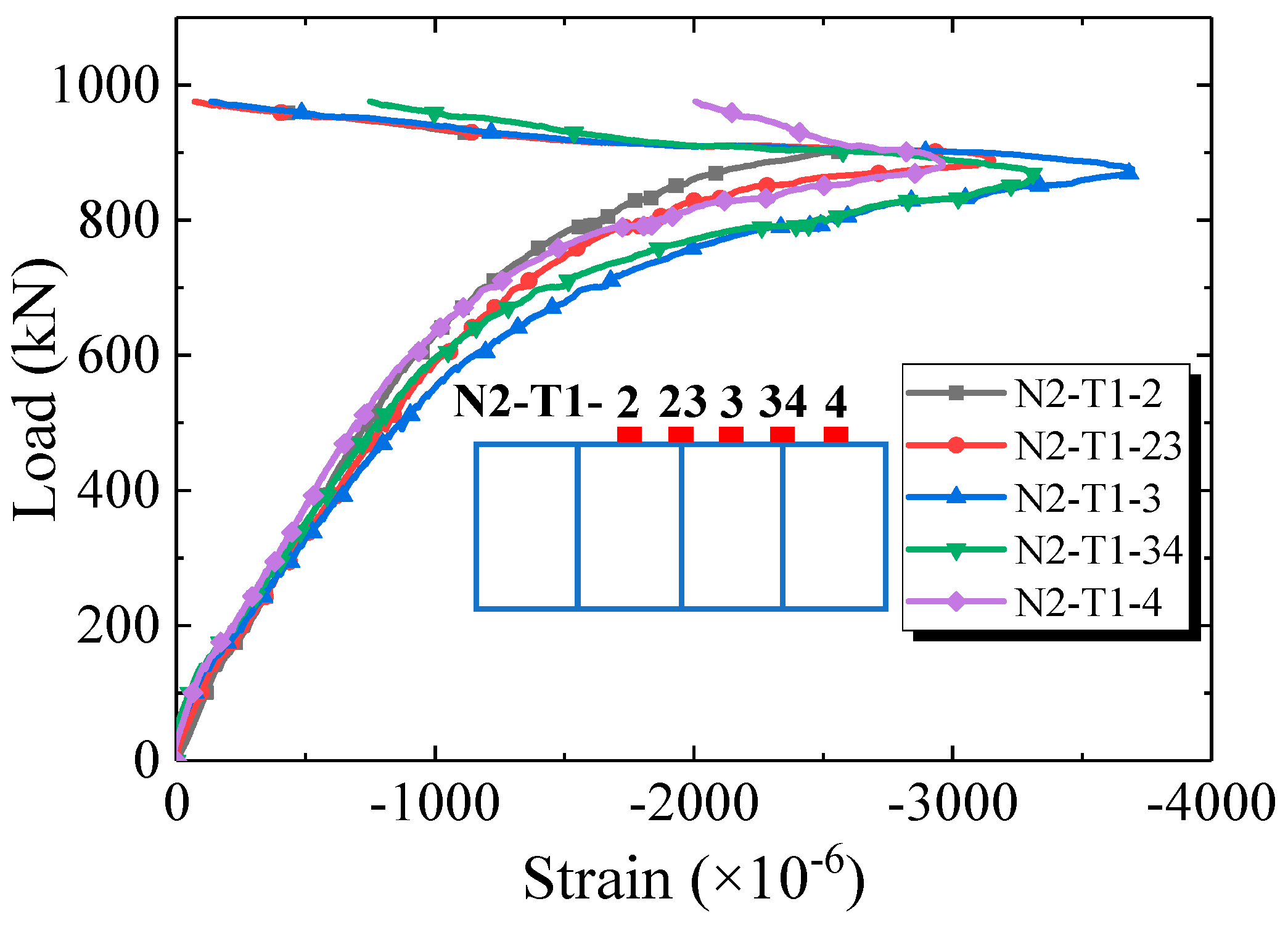
3.2. Strains in Steel Flange and Reinforcing Bars
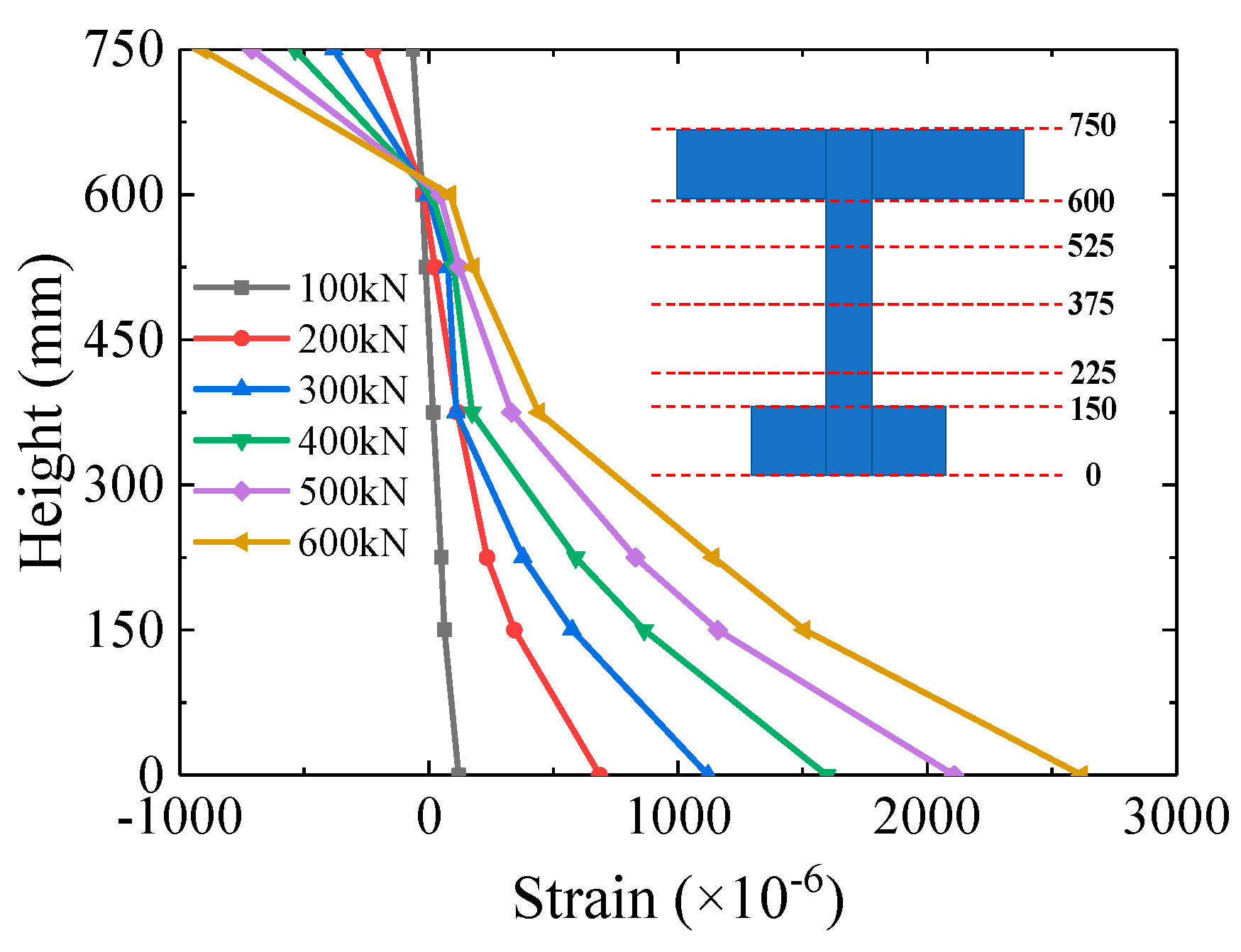
3.3. Sectional Strain Distribution
4. Numerical Analysis
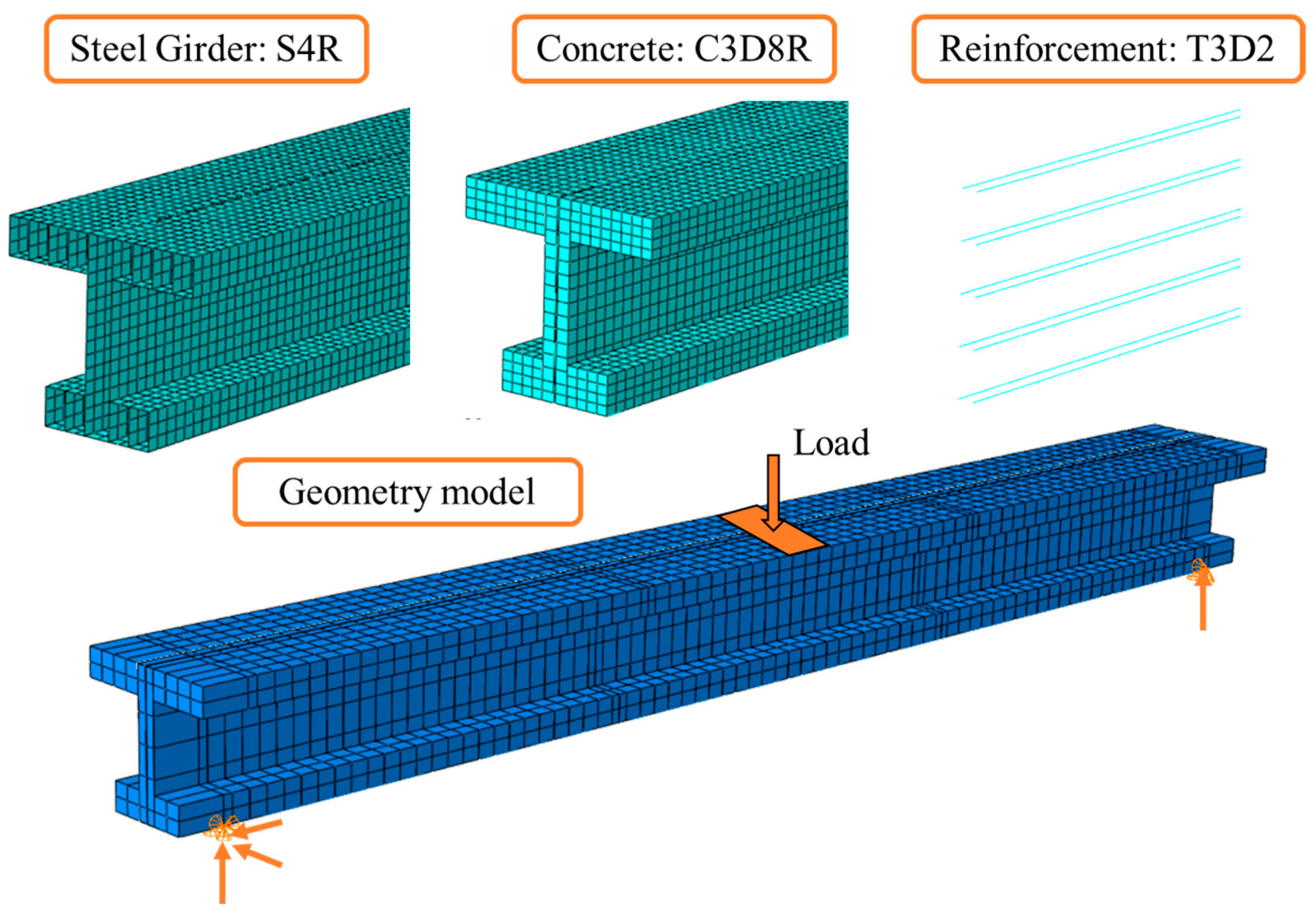
4.1. Numerical Simulation of Composite Girder
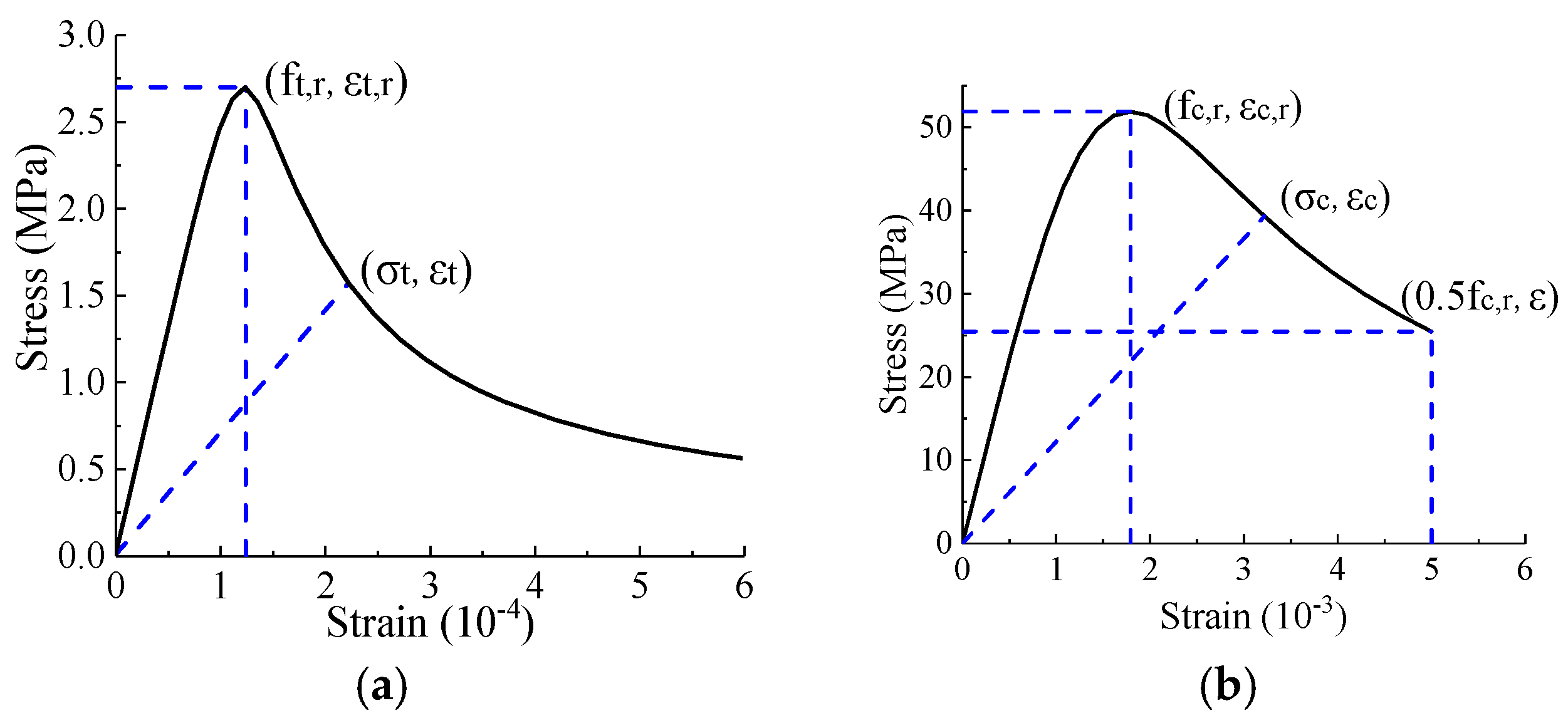
4.2. Material Properties
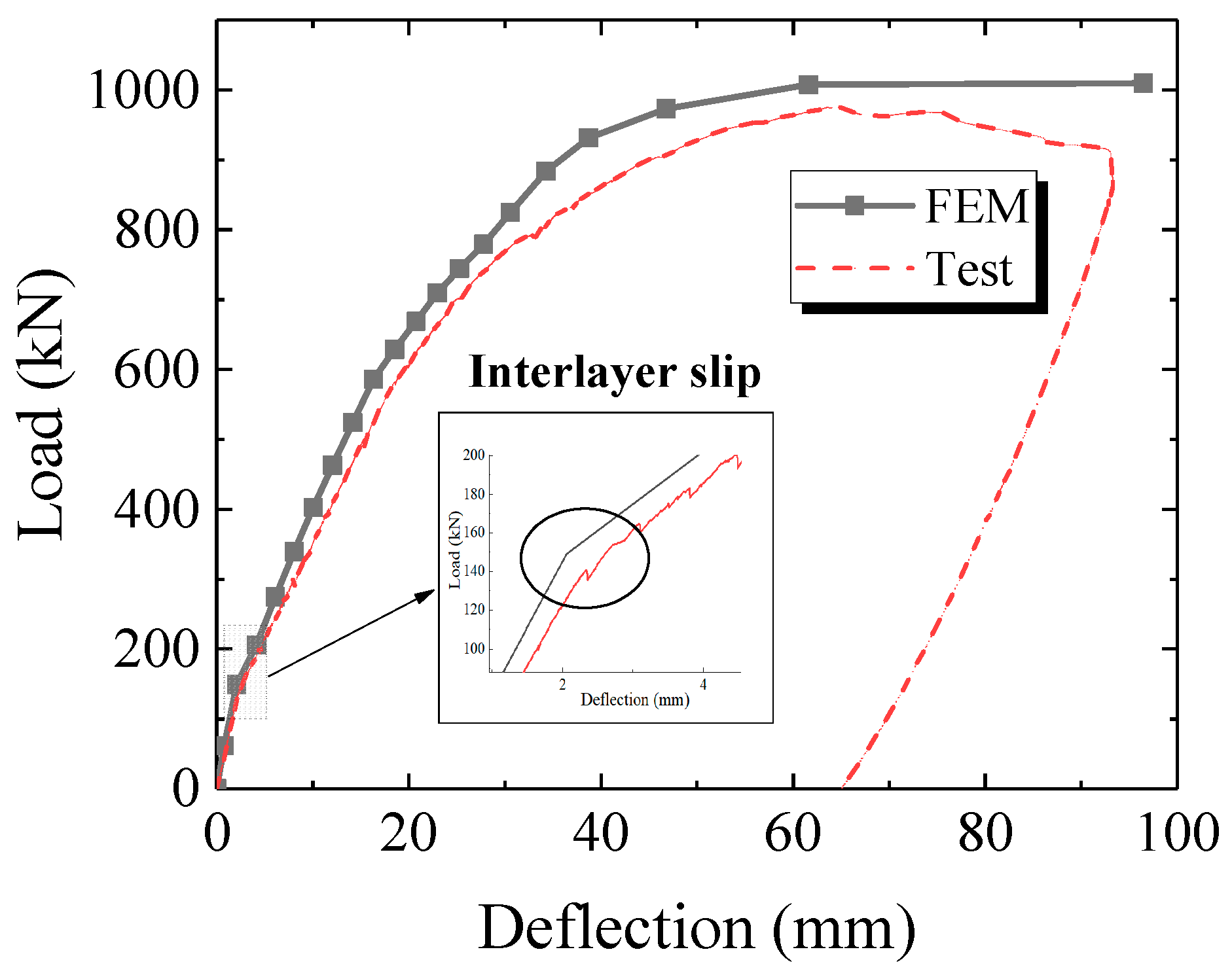
4.3. Validation of FEM Analysis
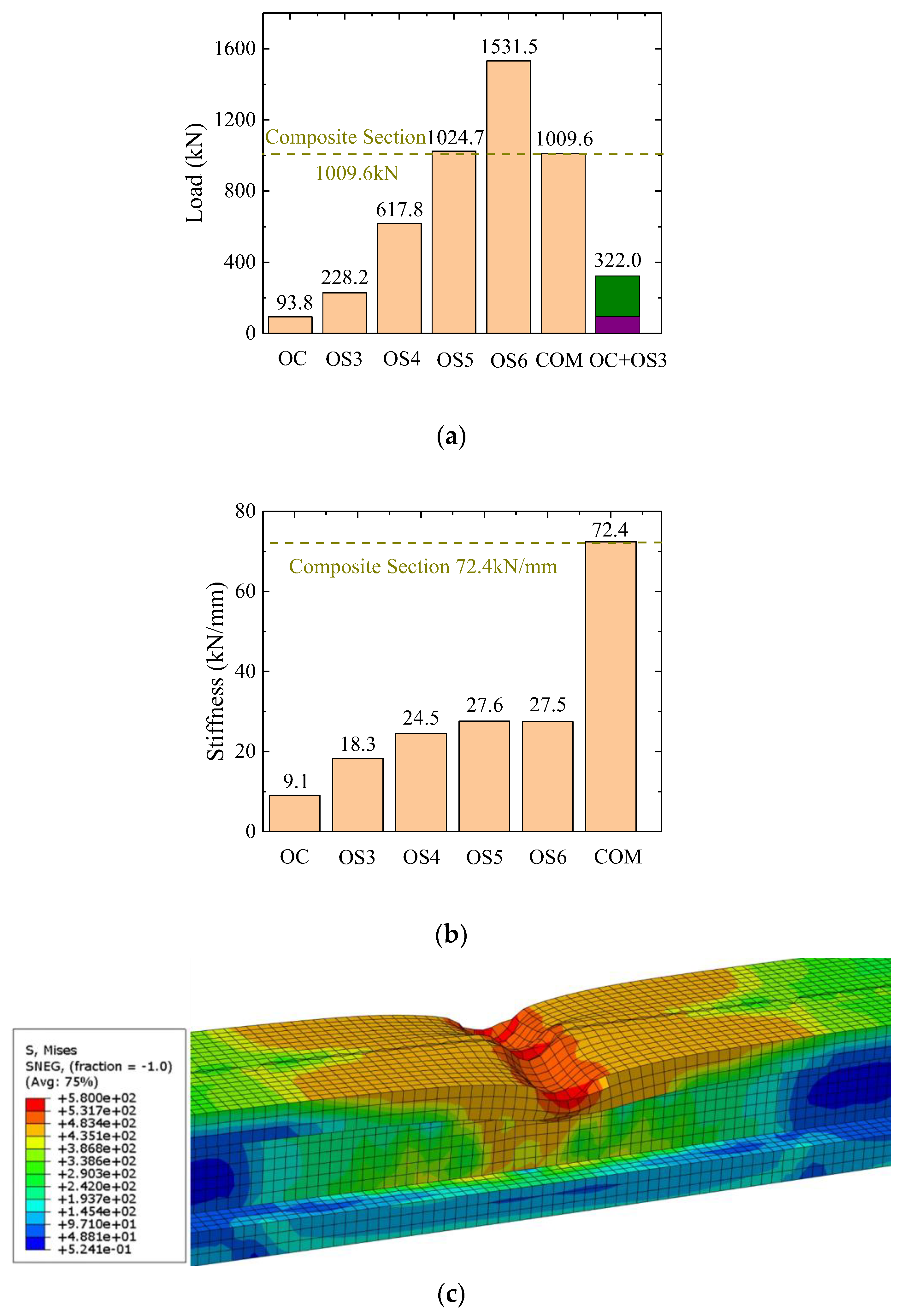
4.4. Influence of Composite Action on Flexural Behaviour
- OC: Specimen with a concrete section only.
- OSN: Specimen with a steel section only and a steel plate thickness equal to N mm.
- COM: Specimen with a composite section and a steel plate thickness equal to 3 mm.
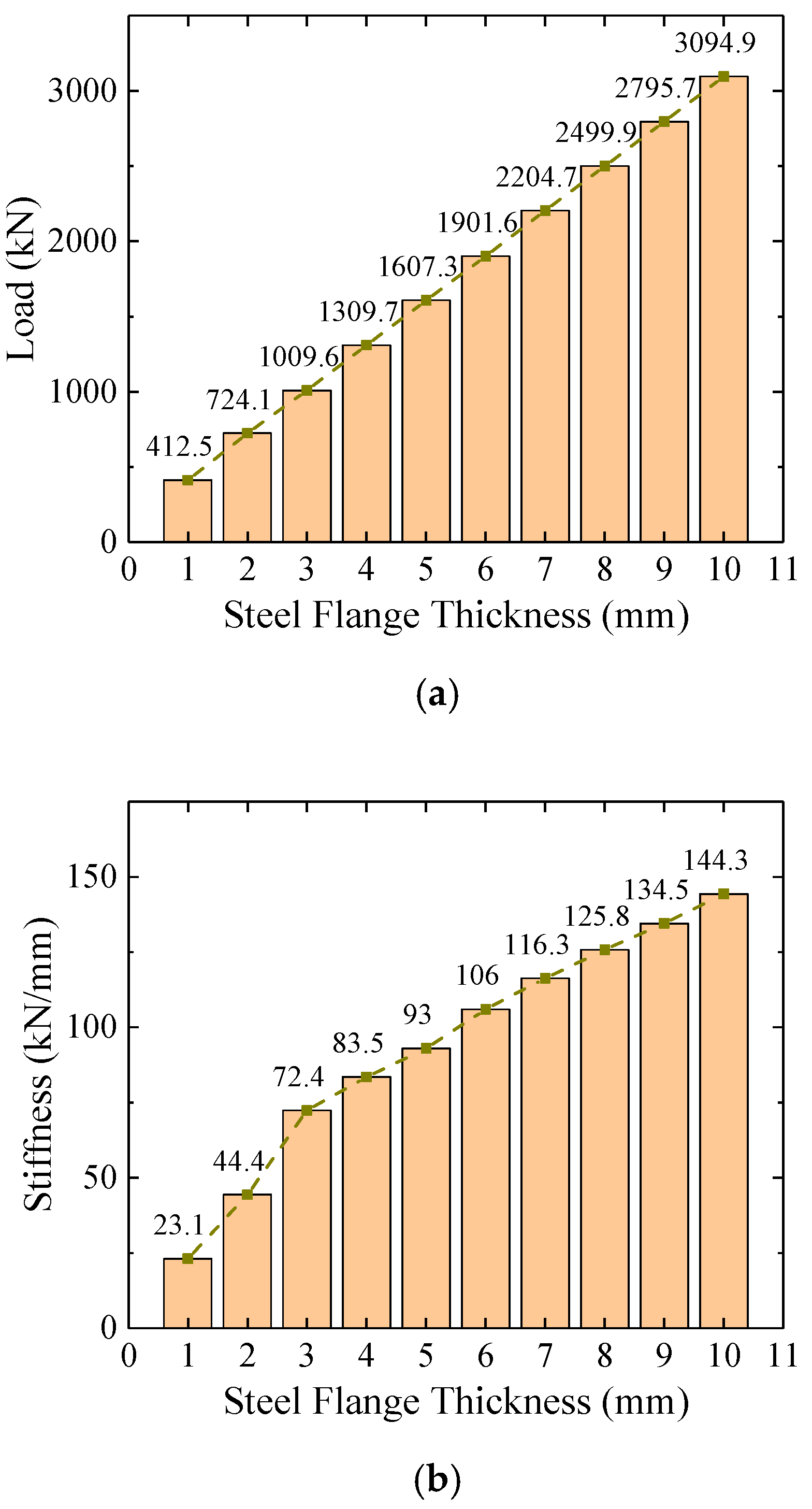
4.5. Parametric Analysis on Steel Flange Thickness
5. Conclusions
- According to the test results, the failure mode of the specimen was fracture of the steel bottom flange along with steel local buckling of the upper flange. The stiffening ribs on the upper flange determined the position of the local buckling but did not have a significant impact on the strain variation during the loading. The concrete girder prevented the steel flange from extensive buckling, which significantly improved the load-carrying capacity of the specimen.
- According to the test, there was an obvious phenomenon of steel–concrete interlayer slip both at mid-span (at 140 kN) and quarter-span (at 240 kN) in the steel bottom flange. The steel bottom flange was observed to be completely detached from the concrete. Thus, strengthening the interaction between the steel and concrete helps to prevent the interlayer slip and simultaneously contributes to a higher flexural stiffness.
- Based on the numerical analysis, the FEM model was proved to be reliable with sufficient accuracy. The deviation from the experimental results could be attributed to the lack of accuracy of the material constitutive laws as well as to the not fully correct simulation of the steel–concrete interlayer interaction.
- Based on the numerical parametric analysis, it is observed how the load-carrying capacity of the specimen with a composite section is much larger than that of specimens with a solo concrete sections and solo steel sections. While the steel girder provided greater load-carrying capacity, the concrete in the composite section prevented local buckling and increased the load-carrying capacity of the joint section. In addition, an increase of steel flange thickness in the specimen with a solo steel section had limited influence on the initial stiffness, while the composite section drastically increases it.
- Based on the parametric analysis, the load-carrying capacity showed a linear relation with the steel flange thickness, indicating that the flexural strength depended mainly on the steel girder. As the main failure mode of the test specimen was steel flange fracture, this conclusion is consistent with the experimental results. Thus, the primary function of the concrete filling was to prevent the steel local buckling, while it had limited influence on the load-carrying capacity of the joint section. In addition, the increase of the steel flange thickness also contributed to an improvement of the initial stiffness.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alghazali, H.H.; Myers, J.J. Time-dependent prestress loss behavior of girders in Missouri bridge A7957 compared with a US data set of high-performance concrete bridge girders. PCI J. 2017, 62, 76–87. [Google Scholar] [CrossRef]
- Xiang, Z.; Chan, T.H.T.; Thambiratnam, D.P.; Nguyen, A. Prestress and excitation force identification in a prestressed concrete box-girder bridge. Comput. Concr. 2017, 20, 617–625. [Google Scholar]
- Yu, X.; Ye, J.; Wu, W. Spatial Stress Analysis of Long Span Prestressed Concrete Box Girder Bridges. In Advances in Civil Engineering II, PTS 1–4; Trans Tech Publications Ltd.: Guilin, China, 2013; pp. 1693–1696. [Google Scholar]
- Yuan, M.; Yan, D.-h. Optimization on Closure Scheme of Multi-Span Prestressed Concrete Box-Girder Bridge. In Advances in Structures, PTS 1–5; Trans Tech Publications Ltd.: Guilin, China, 2011; pp. 2369–2375. [Google Scholar]
- Azizinarnini, A.; Hash, J.B.; Yake, A.J.; Farimani, R. Shear capacity of hybrid plate girders. J. Bridge Eng. 2007, 12, 535–543. [Google Scholar] [CrossRef]
- Dai, G.; Su, M.; Liu, W.; Chen, Y.F. New Songhua River Bridge: A Continuous Girder, Tied Arch, Hybrid Bridge with Four Rail Tracks in Harbin, China. Struct. Eng. Int. 2016, 26, 254–259. [Google Scholar] [CrossRef]
- Hejll, A.; Taljsten, B.; Motavalli, M. Large scale hybrid FRP composite girders for use in bridge structures—Theory, test and field application. Compos. Part B Eng. 2005, 36, 573–585. [Google Scholar] [CrossRef]
- Mo, Y.L.; Fan, Y.-L. Torsional design of hybrid concrete box girders. J. Bridge Eng. 2006, 11, 329–339. [Google Scholar] [CrossRef]
- Wagner, P. Design developments for roadway bridges based on new hybrid structures—Part 2: Cable stayed bridges. Stahlbau 2013, 82, 851–867. [Google Scholar] [CrossRef]
- Zhang, G.Y. Long-Term Monitoring of a Hybrid Cable-Stayed Bridge. In Sensing Issues in Civil Structural Health Monitoring; Springer: Berlin/Heidelberg, Germany, 2005; pp. 485–494. [Google Scholar]
- Zhang, X.-J. Investigation on mechanics performance of cable-stayed-suspension hybrid bridges. Wind. Struct. 2007, 10, 533–542. [Google Scholar] [CrossRef]
- Li, X.; Zhong, J.; Jiang, L.; Yuan, W. Retracted: Analysis of the Seismic Vulnerability of Simply-supported Girder Bridge under Two Level Seismic Hazard. In Proceedings of 2018 3rd International Conference on Smart City and Systems Engineering (ICSCSE), Xiamen, China, 29–30 December 2018; pp. 173–177. [Google Scholar]
- Paultre, P.; Proulx, J.; Begin, T. Dynamic investigation of a hybrid suspension and cable-stayed bridge. Earthq. Eng. Struct. Dyn. 2000, 29, 731–739. [Google Scholar] [CrossRef]
- Kim, S.-H.; Lee, C.-G.; Ahn, J.-H.; Won, J.-H. Experimental study on joint of spliced steel-PSC hybrid girder, Part I: Proposed parallel-perfobond-rib-type joint. Eng. Struct. 2011, 33, 2382–2397. [Google Scholar] [CrossRef]
- Kim, S.-H.; Lee, C.-G.; Kim, S.-J.; Won, J.-H. Experimental study on joint of spliced steel-PSC hybrid girder, part II: Full-scale test of spliced hybrid I-girder. Eng. Struct. 2011, 33, 2668–2682. [Google Scholar] [CrossRef]
- Chen, W.; Liang, B.; Wang, W. Research on Structure of Steel-concrete Joint Section in Hybrid Girder of a Grand Bridge. In Proceedings of the 5th International Conference on Civil Engineering and Transportation 2015, Guangzhou, China, 28–29 November 2015; pp. 370–374. [Google Scholar]
- Xing, W.E.I.; Xiaozhen, L.I.; Jun, L.I.; Shizhong, Q. Using Steel-Concrete Hybrid Structure in Long-Span Continuous Rigid Frame Bridge. China Railw. Sci. 2007, 28, 43–46. [Google Scholar]
- Jiang, X.; Liu, Y.; Sun, X. Model Test and Mechanical Behavior Analysis of Steel-concrete Joint of Hybrid Girder. J. Civ. Archit. Environ. Eng. 2014, 36, 48–53. [Google Scholar]
- Qin, F.J.; Di, J.; Dai, J.; Lu, W.R.; Zhao, M. Study on Rational Position of Joint Section of Steel-Concrete Hybrid Girder Bridge. In Construction and Urban Planning, PTS 1–4; Trans Tech Publications Ltd.: Guizhou, China, 2013; pp. 1007–1011. [Google Scholar]
- Zhang, X.; Zhang, S.; Niu, S. Experimental studies on seismic behavior of precast hybrid steel-concrete beam. Adv. Struct. Eng. 2019, 22, 670–686. [Google Scholar] [CrossRef]
- He, Z.-Q.; Chen, J.; Liu, Z.; Ma, Z.J. An Explicit Approach for Determining the Rational Length of Steel Portion in Steel-Concrete Hybrid Girder Bridges. J. Bridge Eng. 2023, 28, 05022011. [Google Scholar] [CrossRef]
- Su, H.; Su, Q.; Xu, C.; Zhang, X.; Lei, D. Shear performance and dimension rationalization study on the rubber sleeved stud connector in continuous composite girder. Eng. Struct. 2021, 240, 112371. [Google Scholar] [CrossRef]
- Su, H.; Su, Q.; Casas, J.R.; Xu, C.; Tang, J.; Jiang, C. Influence mechanism of Steel-concrete interlayer partial shear connections on mechanical properties of composite girders. Structures 2022, 46, 503–520. [Google Scholar]
- Su, H.; Su, Q.; Xu, C.; Casas, J.R.; Zhou, G. Mechanical performance based rationalization research on steel-concrete double composite action. J. Constr. Steel Res. 2022, 197, 107492. [Google Scholar] [CrossRef]
- Tesser, L.; Scotta, R. Flexural and shear capacity of composite steel truss and concrete beams with inferior precast concrete base. Eng. Struct. 2013, 49, 135–145. [Google Scholar] [CrossRef]
- Colajanni, P.; La Mendola, L.; Monaco, A. Stress transfer and failure mechanisms in steel-concrete trussed beams: Experimental investigation on slab-thick and full-thick beams. Constr. Build. Mater. 2018, 161, 267–281. [Google Scholar] [CrossRef]
- Colajanni, P.; La Mendola, L.; Monaco, A.; Pagnotta, S. Dissipative connections of RC frames with prefabricated steel-trussed-concrete beams. Ing. Sismica 2020, 37, 51–63. [Google Scholar]
- GB/T 50081-2002; Standard for Test Method of Mechanical Properties on Ordinary Concrete. Ministry of Construction People’s Republic of China: Beijing, China, 2002.
- ABAQUS 6.13 User’s Manual; Dassault Systemes Simulia Corp: Providence, RI, USA, 2014.
- Rabbat, B.G.; Russell, H.G. Friction coefficient of steel on concrete or grout. J. Struct. Eng. Asce 1985, 111, 505–515. [Google Scholar] [CrossRef]
- Kaminska, I.; Szwed, A. Modification of Concrete Damaged Plasticity Model. Part II: Formulation and Numerical Tests. In RSP 2017—XXVI R-S-P Seminar 2017 Theoretical Foundation of Civil Engineering; EDP Sciences: Warsaw, Poland, 2017. [Google Scholar]
- Nguyen, G.D.; Korsunsky, A.M. Damage-plasticity modelling of concrete: Calibration of parameters using separation of fracture energy. Int. J. Fract. 2006, 139, 325–332. [Google Scholar] [CrossRef]
- Sarikaya, A.; Erkmen, R.E. A plastic-damage model for concrete under compression. Int. J. Mech. Sci. 2019, 150, 584–593. [Google Scholar] [CrossRef]
- GB50010-2010; Code for Design of Concrete Structures. Ministry of Construction People’s Republic of China: Beijing, China, 2015.
- ENV1992-1-1; Eurocode-2: Design of Concrete Structures, Part1: General Rules and Rules for Buildings. CEN: Brussels, Belgium, 1992.
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. Asce 1988, 114, 1804–1826. [Google Scholar] [CrossRef]








| No. | Dilation Angle (°) | Concrete Layers | Constitutive Model | Mesh Size (mm) | (%) | (%) | |
|---|---|---|---|---|---|---|---|
| Concrete | Steel | ||||||
| 1 | 25 | 4 | fib | 50 | 50 | 4.1% | 2.7% |
| 2 | 37.5 | 4 | fib | 50 | 50 | 1.9% | 1.3% |
| 3 | 50 | 4 | fib | 50 | 50 | 1.5% | 1.4% |
| 4 | 37.5 | 4 | fib | 50 | 50 | 3.3% | 1.6% |
| 5 | 37.5 | 4 | fib | 50 | 50 | 3.9% | 1.9% |
| 6 | 37.5 | 2 | fib | 100 | 100 | 1.6% | 0.8% |
| 7 | 37.5 | 4 | fib | 50 | 100 | 1.5% | 1.0% |
| 8 | 37.5 | 4 | Secant Modulus | 50 | 50 | 3.9% | 1.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shangguan, B.; Su, Q.; Casas, J.R.; Su, H.; Wang, S.; Zhao, R. Modeling and Testing of a Composite Steel–Concrete Joint for Hybrid Girder Bridges. Materials 2023, 16, 3265. https://doi.org/10.3390/ma16083265
Shangguan B, Su Q, Casas JR, Su H, Wang S, Zhao R. Modeling and Testing of a Composite Steel–Concrete Joint for Hybrid Girder Bridges. Materials. 2023; 16(8):3265. https://doi.org/10.3390/ma16083265
Chicago/Turabian StyleShangguan, Bing, Qingtian Su, Joan R. Casas, Hang Su, Shengyun Wang, and Rongxin Zhao. 2023. "Modeling and Testing of a Composite Steel–Concrete Joint for Hybrid Girder Bridges" Materials 16, no. 8: 3265. https://doi.org/10.3390/ma16083265
APA StyleShangguan, B., Su, Q., Casas, J. R., Su, H., Wang, S., & Zhao, R. (2023). Modeling and Testing of a Composite Steel–Concrete Joint for Hybrid Girder Bridges. Materials, 16(8), 3265. https://doi.org/10.3390/ma16083265






