An Analytical Method for Elastic Modulus of the Sandwich BCC Lattice Structure Based on Assumption of Linear Distribution
Abstract
:1. Introduction
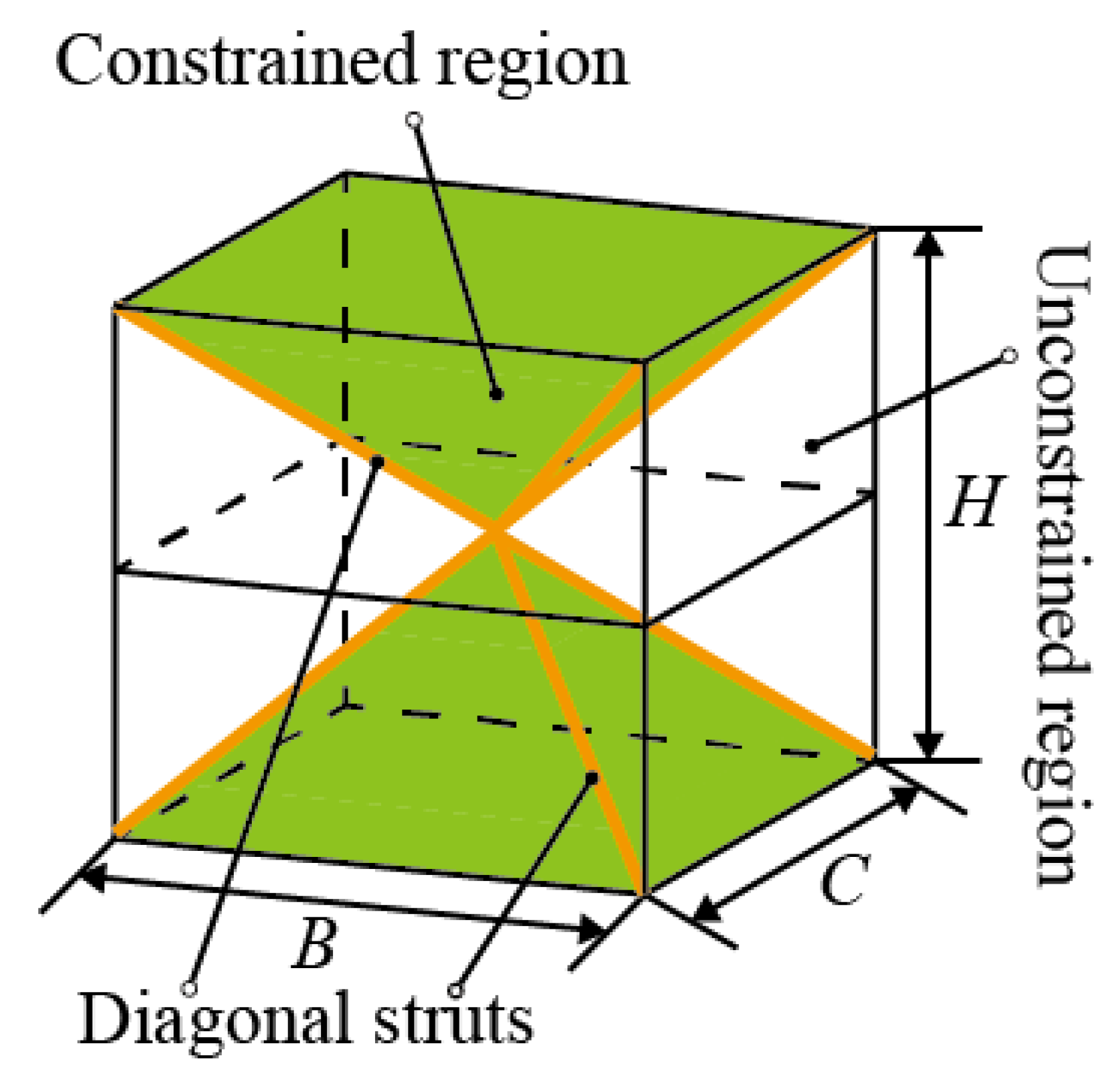
2. Problem Description
3. Elastic Modulus of the Sandwich BCC Lattice Structure
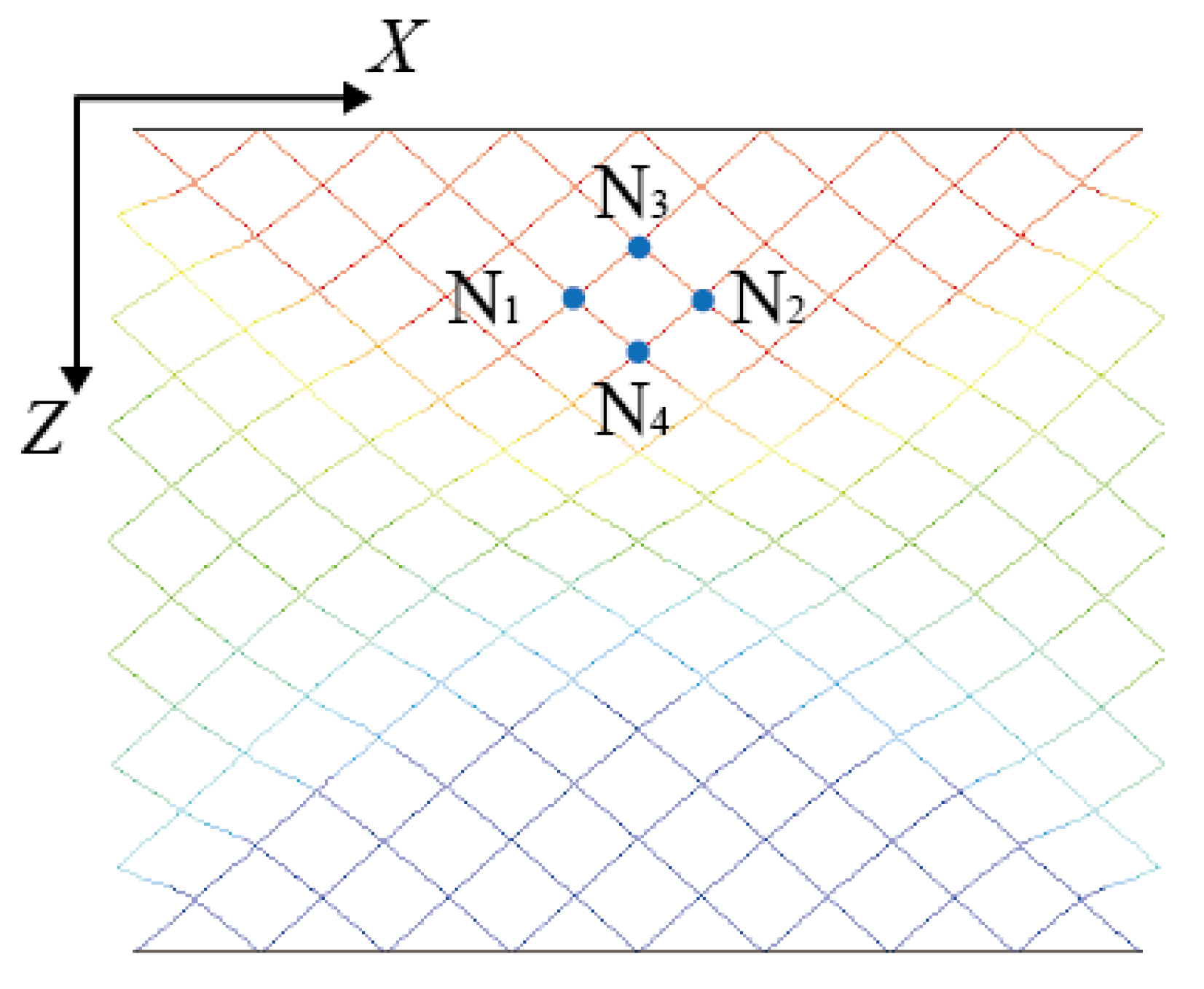
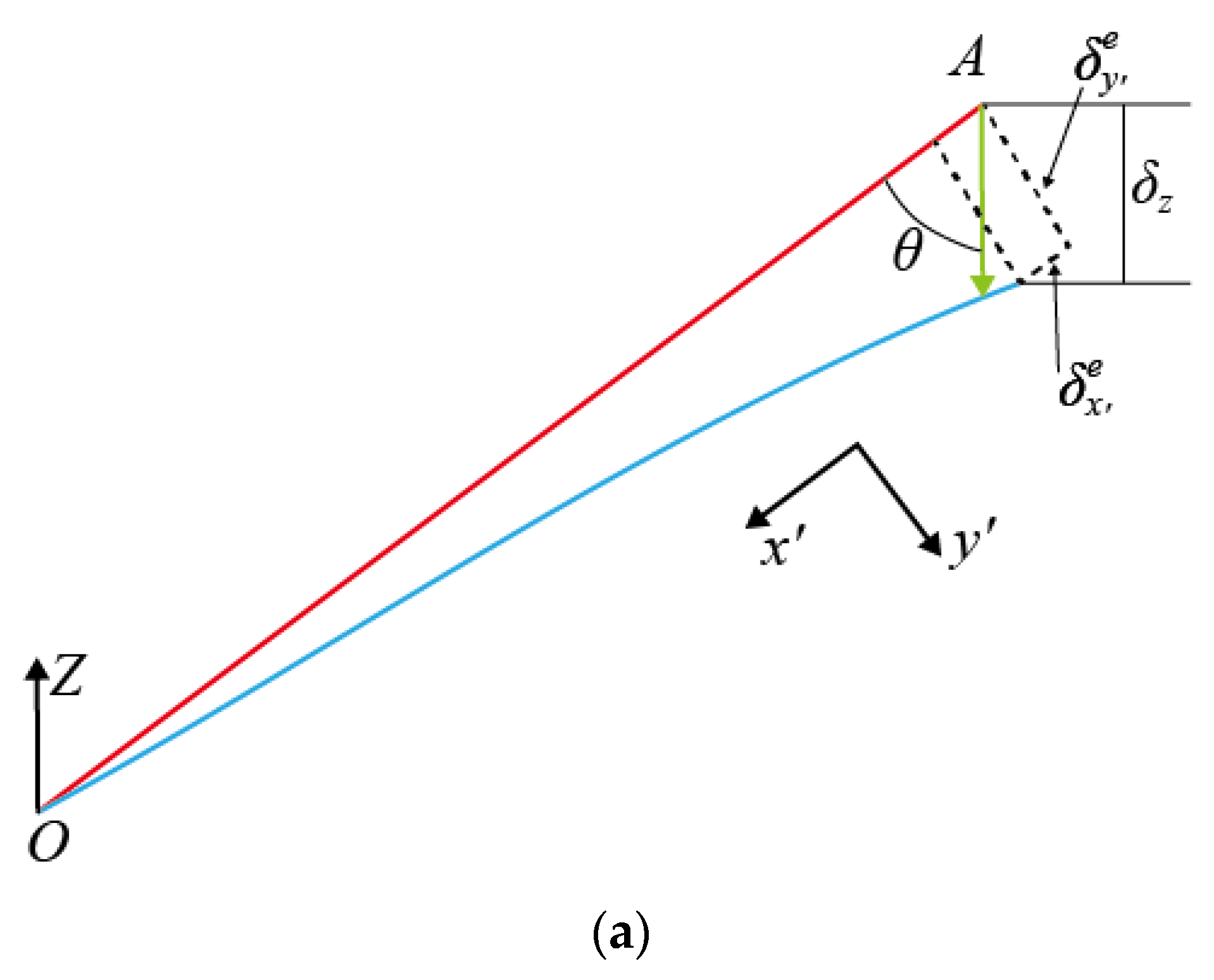
3.1. Displacement Characteristic Analysis
3.2. Elastic Modulus of the Element under Two Kinds of Constraint Conditions
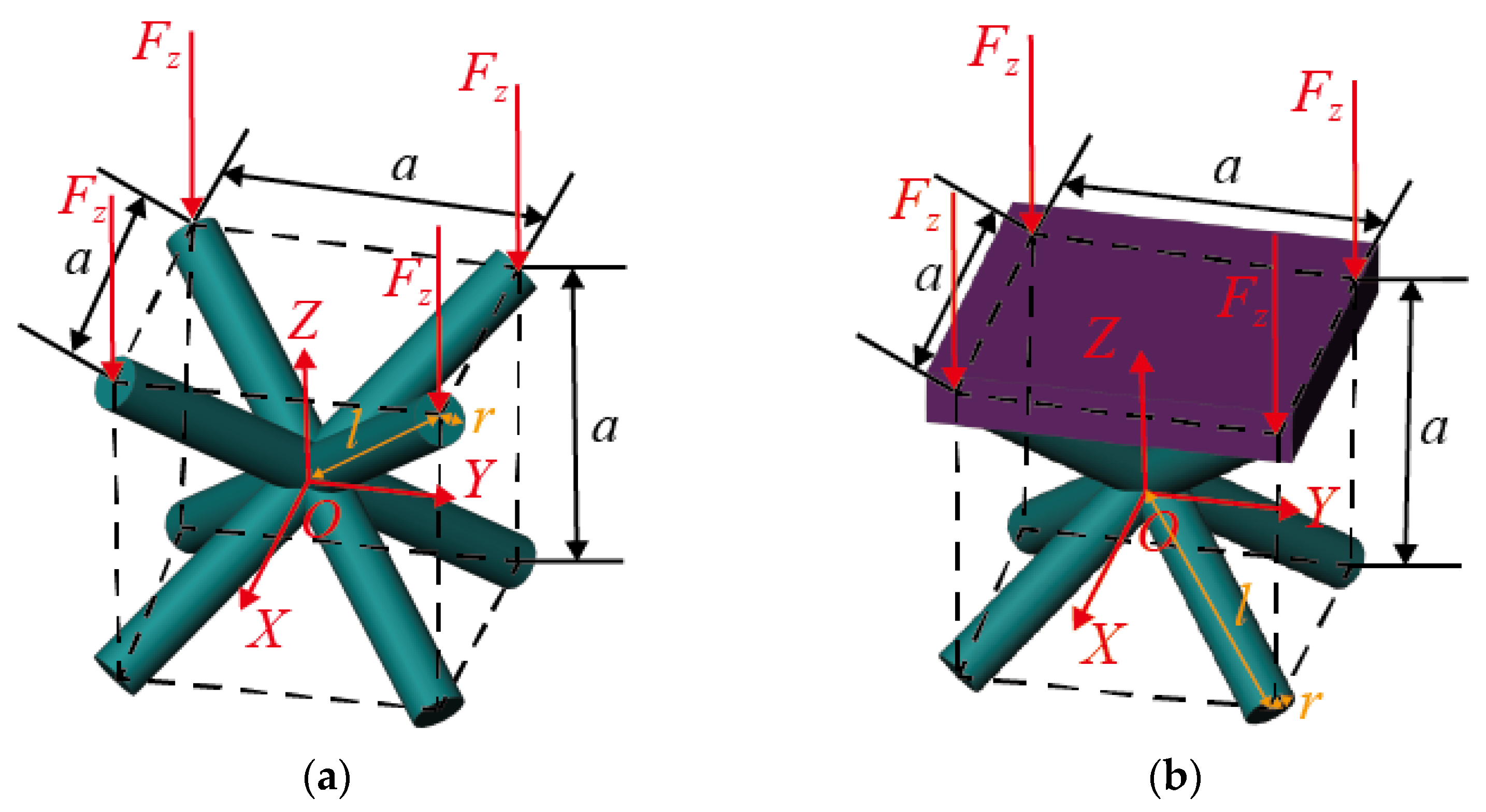
3.2.1. Elastic Modulus of the BCC Element without Plate Constraint
3.2.2. Elastic Modulus of the BCC Element with Plate Constraint
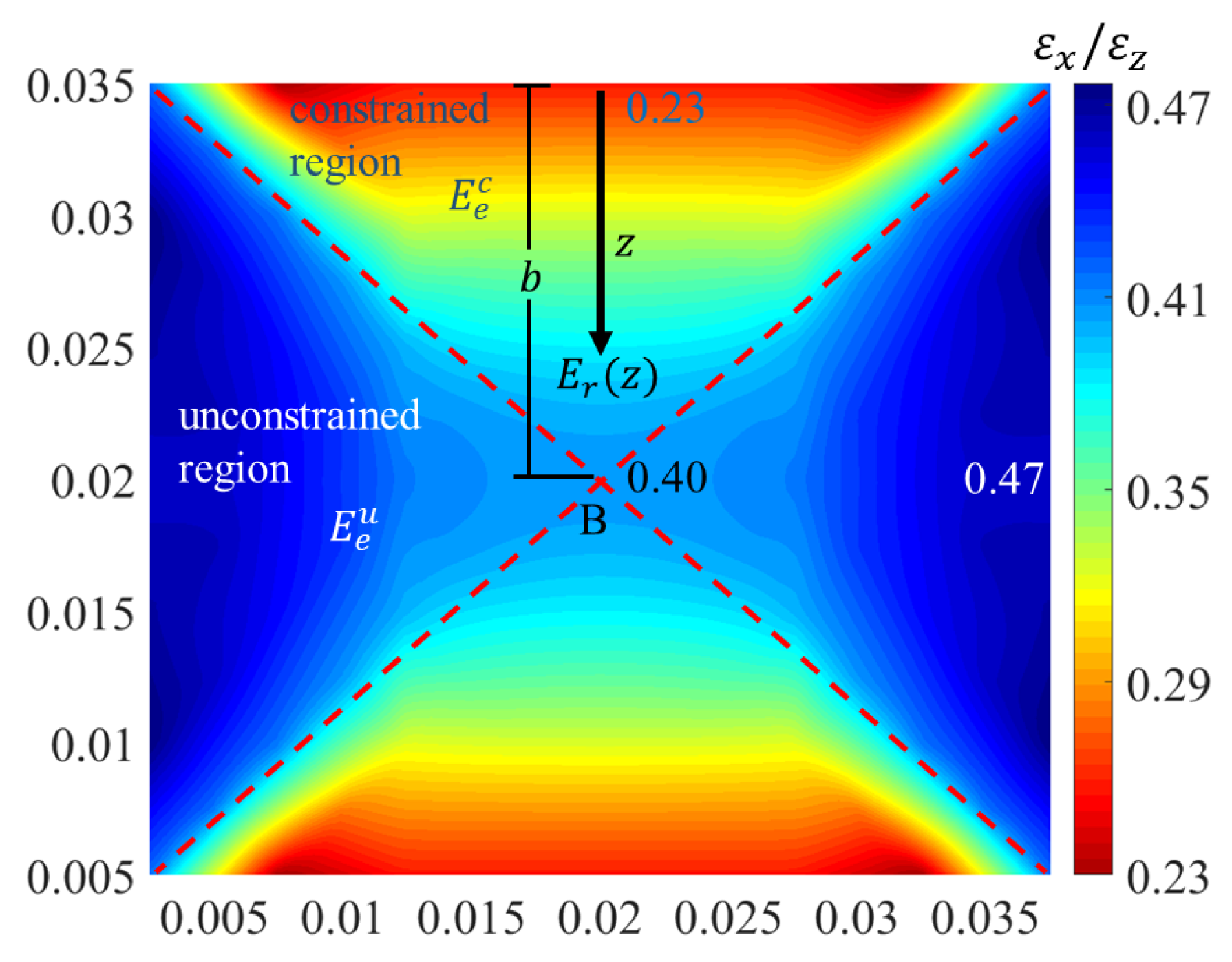
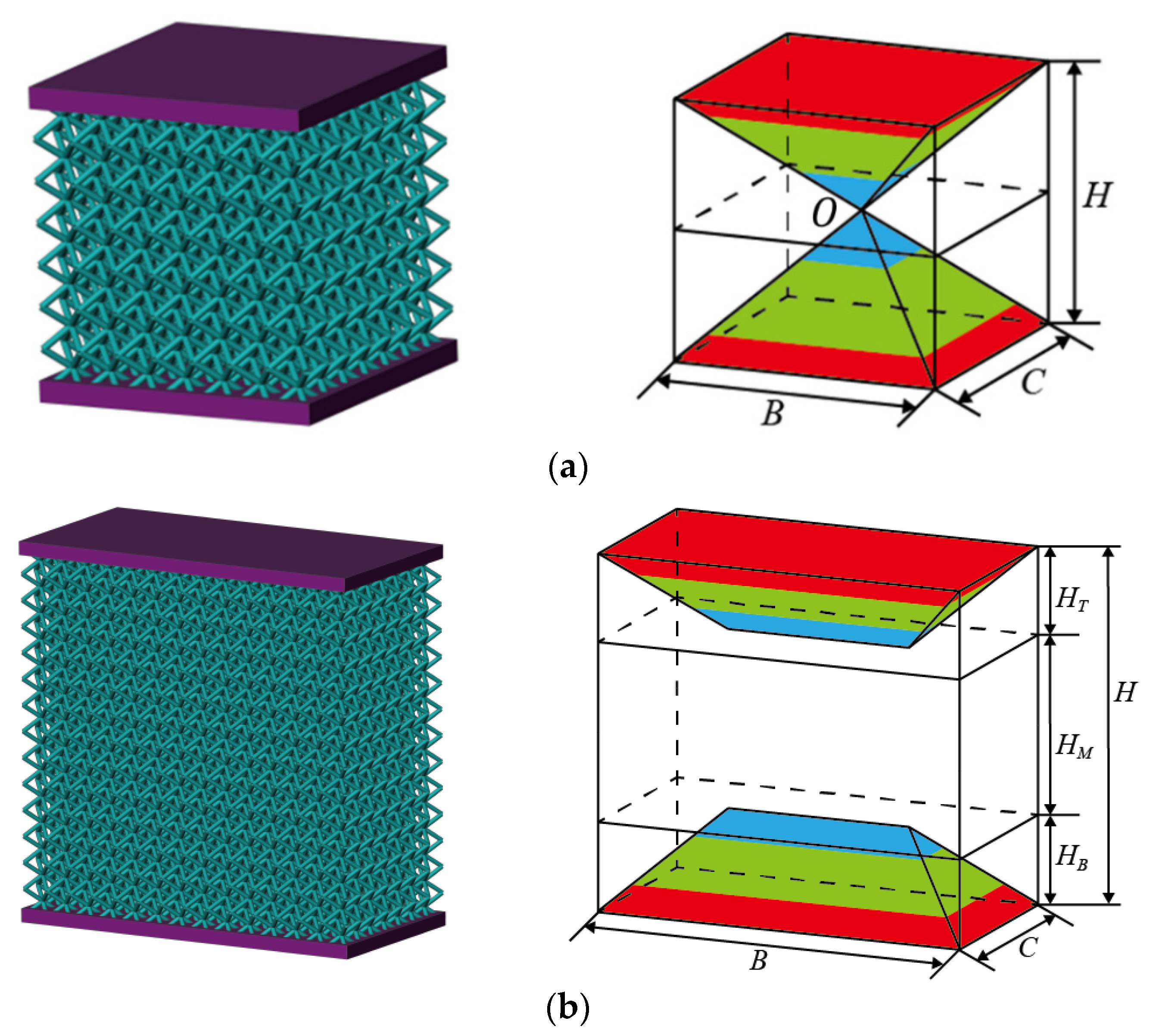
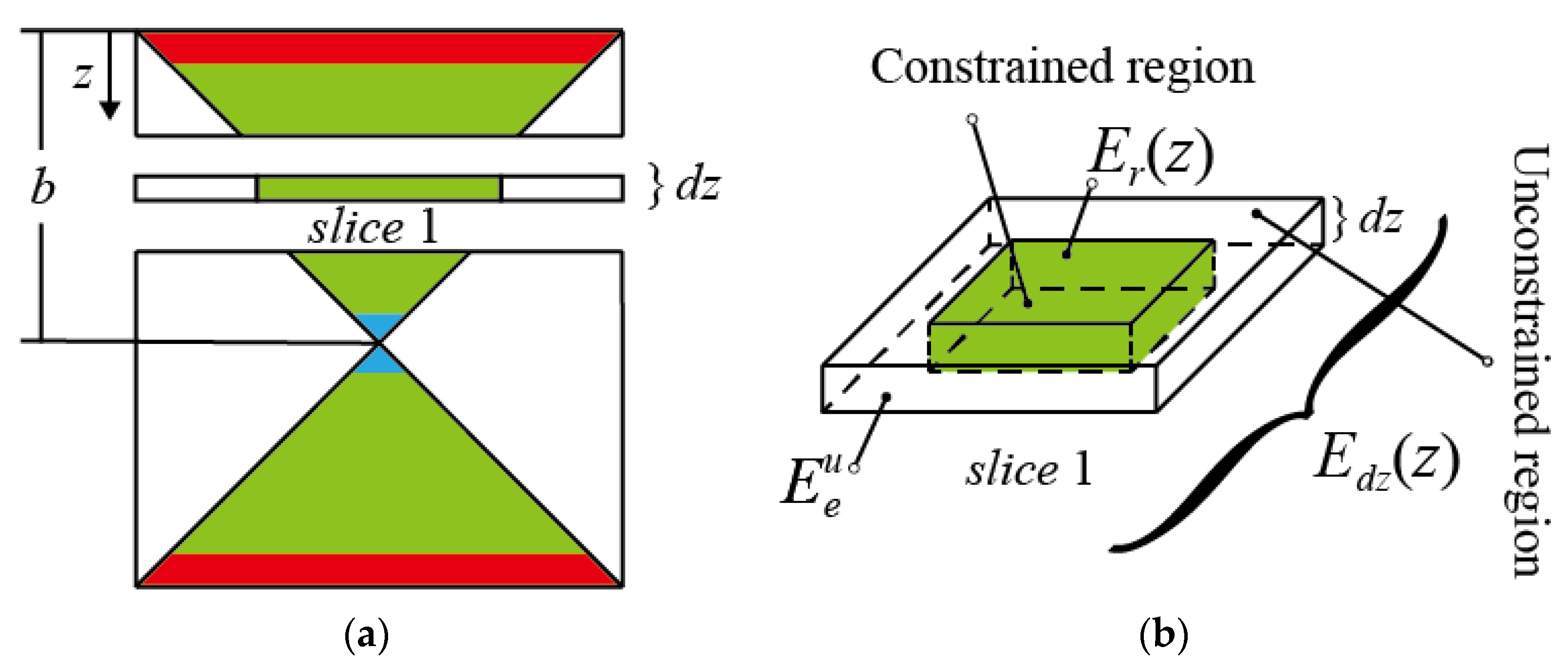
3.3. Elastic Modulus of the Sandwich BCC Lattice Structure
3.3.1. Elastic Modulus of the Sandwich BCC Lattice Structure ()
3.3.2. Elastic Modulus of the Sandwich BCC Lattice Structure ( or )
4. Validation of the Analytical Method
4.1. Experiment
- (1)
- Specimens
- (2)
- Experiment
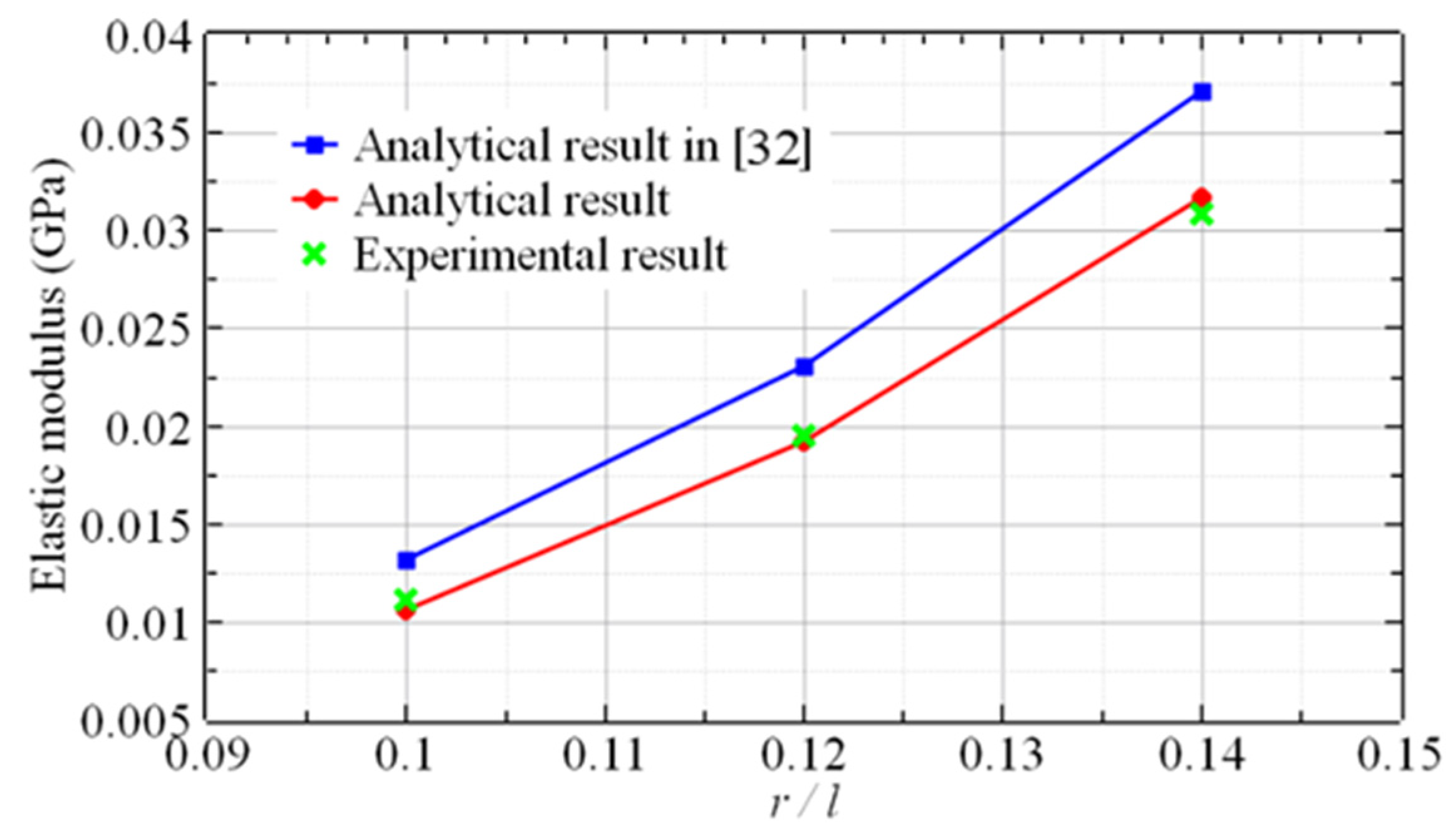
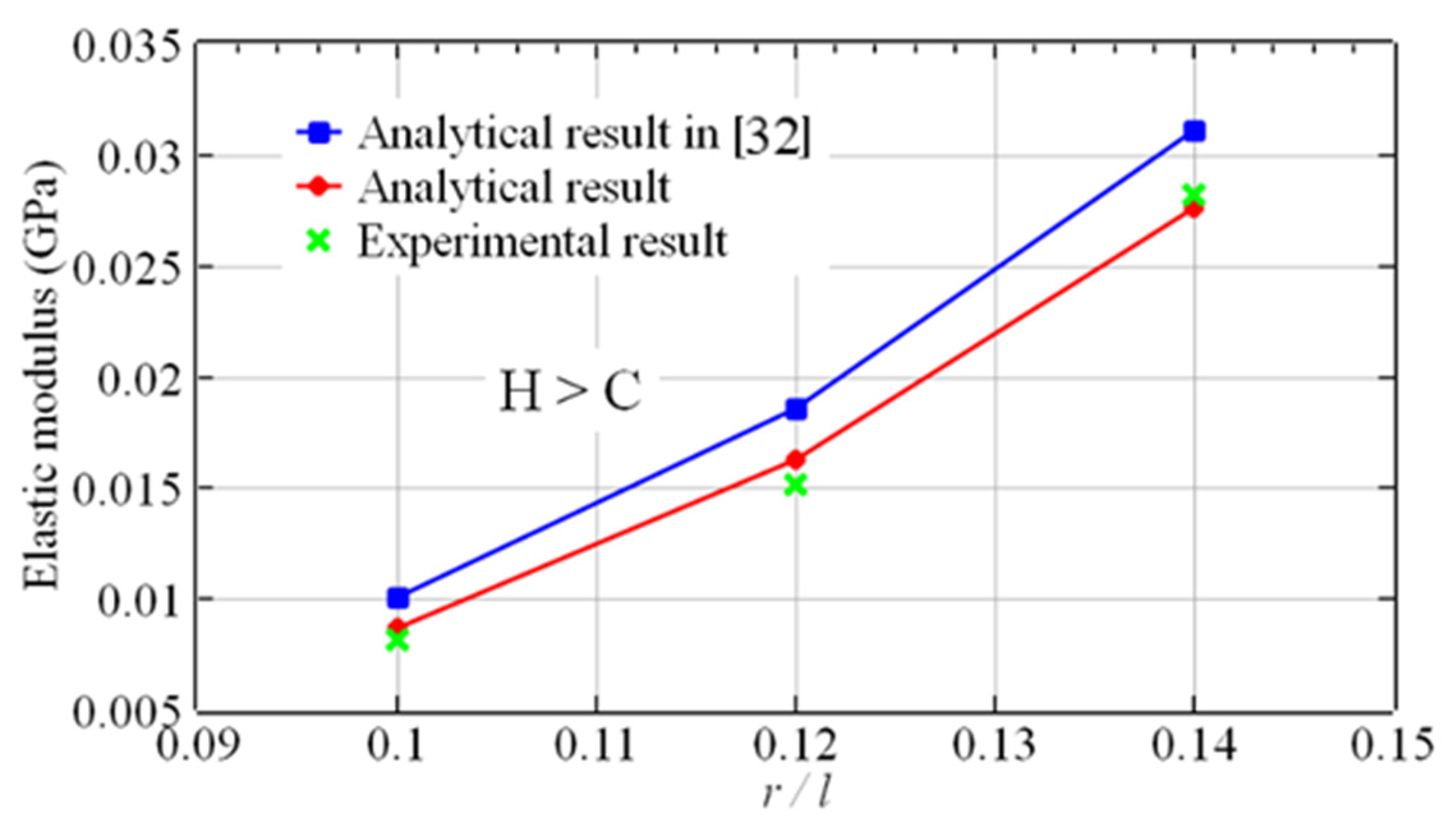
4.2. Result Comparison
5. Conclusions
- (1)
- The assumption of a linearly changing elastic modulus is proposed for predicting the elastic modulus of the sandwich BCC lattice.
- (2)
- The elastic moduli of the elements of a BCC lattice structure with and without plate constraints are analyzed.
- (3)
- The elastic modulus of the sandwich BCC lattice is calculated with single-layer slice and integration methods.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wadley, H.N.G. Multifunctional periodic cellular metals. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 31–68. [Google Scholar] [CrossRef] [PubMed]
- Wadley, H.N.; Fleck, N.A.; Evans, A.G. Fabrication and structural performance of periodic cellular metal sandwich structures. Compos. Sci. Technol. 2003, 63, 2331–2343. [Google Scholar] [CrossRef]
- Hyun, S.; Karlsson, A.; Torquato, S.; Evans, A. Simulated properties of Kagomé and tetragonal truss core panels. Int. J. Solids Struct. 2003, 40, 6989–6998. [Google Scholar] [CrossRef]
- Gautam, R.; Idapalapati, S. Performance of strut-reinforced Kagome truss core structure under compression fabricated by selective laser melting. Mater. Des. 2019, 164, 107541. [Google Scholar] [CrossRef]
- Ma, C.; Lei, H.; Liang, J.; Wu, W.; Wang, T.; Fang, D. Macroscopic mechanical response of chiral-type cylindrical metastructures under axial compression loading. Mater. Des. 2018, 158, 198–212. [Google Scholar] [CrossRef]
- Li, Y.; Gu, H.; Pavier, M.; Coules, H. Compressive behaviours of octet-truss lattices. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 3257–3269. [Google Scholar] [CrossRef]
- Hu, J.W.; Park, T. Continuum Models for the Plastic Deformation of Octet-Truss Lattice Materials Under Multiaxial Loading. J. Eng. Mater. Technol. ASME 2013, 135, 021004. [Google Scholar] [CrossRef]
- Shen, Y.; McKown, S.; Tsopanos, S.; Sutcliffe, C.; Mines, R.; Cantwell, W. The Mechanical Properties of Sandwich Structures Based on Metal Lattice Architectures. J. Sandw. Struct. Mater. 2010, 12, 159–180. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Mohr, D. Elastically-isotropic truss lattice materials of reduced plastic anisotropy. Int. J. Solids Struct. 2018, 138, 24–39. [Google Scholar] [CrossRef]
- Habib, F.N.; Iovenitti, P.; Masood, S.H.; Nikzad, M. Fabrication of polymeric lattice structures for optimum energy absorption using Multi Jet Fusion technology. Mater. Des. 2018, 155, 86–98. [Google Scholar] [CrossRef]
- Xu, S.; Shen, J.; Zhou, S.; Huang, X.; Xie, Y.M. Design of lattice structures with controlled anisotropy. Mater. Des. 2016, 93, 443–447. [Google Scholar] [CrossRef]
- Ushijima, K.; Cantwell, W.; Mines, R.; Tsopanos, S.; Smith, M. An investigation into the compressive properties of stainless steel micro-lattice structures. J. Sandw. Struct. Mater. 2011, 13, 303–329. [Google Scholar] [CrossRef]
- Dong, L. Mechanical responses of Ti-6Al-4V truss lattices having a combined simple-cubic and body-centered-cubic (SC-BCC) topology. Aerosp. Sci. Technol. 2021, 116, 106852. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, Z.; Liang, J.; Ge, J. Determination of the strength of a multilayer BCC lattice structure with face sheets. Int. J. Mech. Sci. 2019, 152, 568–575. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Mohr, D. Stiffness and specific energy absorption of additively-manufactured metallic BCC metamaterials composed of tapered beams. Int. J. Mech. Sci. 2018, 141, 101–116. [Google Scholar] [CrossRef]
- Doyoyo, M.; Hu, J.W. Multi-axial failure of metallic strut-lattice materials composed of short and slender struts. Int. J. Solids Struct. 2006, 43, 6115–6139. [Google Scholar] [CrossRef]
- Dong, L.; Deshpande, V.; Wadley, H. Mechanical response of Ti–6Al–4V octet-truss lattice structures. Int. J. Solids Struct. 2015, 60, 107–124. [Google Scholar] [CrossRef]
- Mohsenizadeh, M.; Gasbarri, F.; Munther, M.; Beheshti, A.; Davami, K. Additively-manufactured lightweight Metamaterials for energy absorption. Mater. Des. 2018, 139, 521–530. [Google Scholar] [CrossRef]
- Song, J.; Wang, Y.; Zhou, W.; Fan, R.; Yu, B.; Lu, Y.; Li, L. Topology optimization-guided lattice composites and their mechanical characterizations. Compos. Part B Eng. 2019, 160, 402–411. [Google Scholar] [CrossRef]
- Ling, C.; Cernicchi, A.; Gilchrist, M.D.; Cardiff, P. Mechanical behaviour of additively-manufactured polymeric octet-truss lattice structures under quasi-static and dynamic compressive loading. Mater. Des. 2019, 162, 106–118. [Google Scholar] [CrossRef]
- Babaei, M.; Kiarasi, F.; Asemi, K.; Hosseini, M. Functionally Graded Saturated Porous Structures: A Review. J. Comput. Appl. Mech. 2022, 53, 297–308. [Google Scholar] [CrossRef]
- Van Hung, N.; Van Dung, N.; Van Minh, P.; Van Ke, T.; Van Thom, D. Vibration Behavior Analysis of the Ammunition Belt of the Gas-Operated Machine Gun. J. Vib. Eng. Technol. 2023, 1–13. [Google Scholar] [CrossRef]
- Marschall, D.; Rippl, H.; Ehrhart, F.; Schagerl, M. Boundary conformal design of laser sintered sandwich cores and simulation of graded lattice cells using a forward homogenization approach. Mater. Des. 2020, 190, 108539. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef]
- Mahbod, M.; Asgari, M.; Mittelstedt, C. Architected functionally graded porous lattice structures for optimized elastic-plastic behavior. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 234, 1099–1116. [Google Scholar] [CrossRef]
- Ptochos, E.; Labeas, G. Elastic modulus and Poisson’s ratio determination of micro-lattice cellular structures by analytical, numerical and homogenisation methods. J. Sandw. Struct. Mater. 2012, 14, 597–626. [Google Scholar] [CrossRef]
- Gümrük, R.; Mines, R.A.W. Compressive behaviour of stainless steel micro-lattice structures. Int. J. Mech. Sci. 2013, 68, 125–139. [Google Scholar] [CrossRef]
- Xiao, L.; Xu, X.; Song, W.; Hu, M. A Multi-Cell Hybrid Approach to Elevate the Energy Absorption of Micro-Lattice Materials. Materials 2020, 13, 4083. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Sekizawa, K.; Suzuki, A.; Takata, N.; Kobashi, M.; Yamada, T. Compressive Properties of Al-Si Alloy Lattice Structures with Three Different Unit Cells Fabricated via Laser Powder Bed Fusion. Materials 2020, 13, 2902. [Google Scholar] [CrossRef]
- Gümrük, R.; Mines, R.A.W.; Karadeniz, S. Static mechanical behaviours of stainless steel micro-lattice structures under different loading conditions. Mater. Sci. Eng. A 2013, 586, 392–406. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, J.; Tan, Y.; Gao, Y.; Wang, J.; Geng, X. Study on the Shear Modulus Based Equivalent Homogenization Methods of Multi-Layer BCC Lattice Sandwich. Materials 2022, 15, 1341. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Shan, M.; Zhao, L.; Qi, D.; Zhang, J. Multiple strut-deformation patterns based analytical elastic modulus of sandwich BCC lattices. Mater. Des. 2019, 181, 107916. [Google Scholar] [CrossRef]

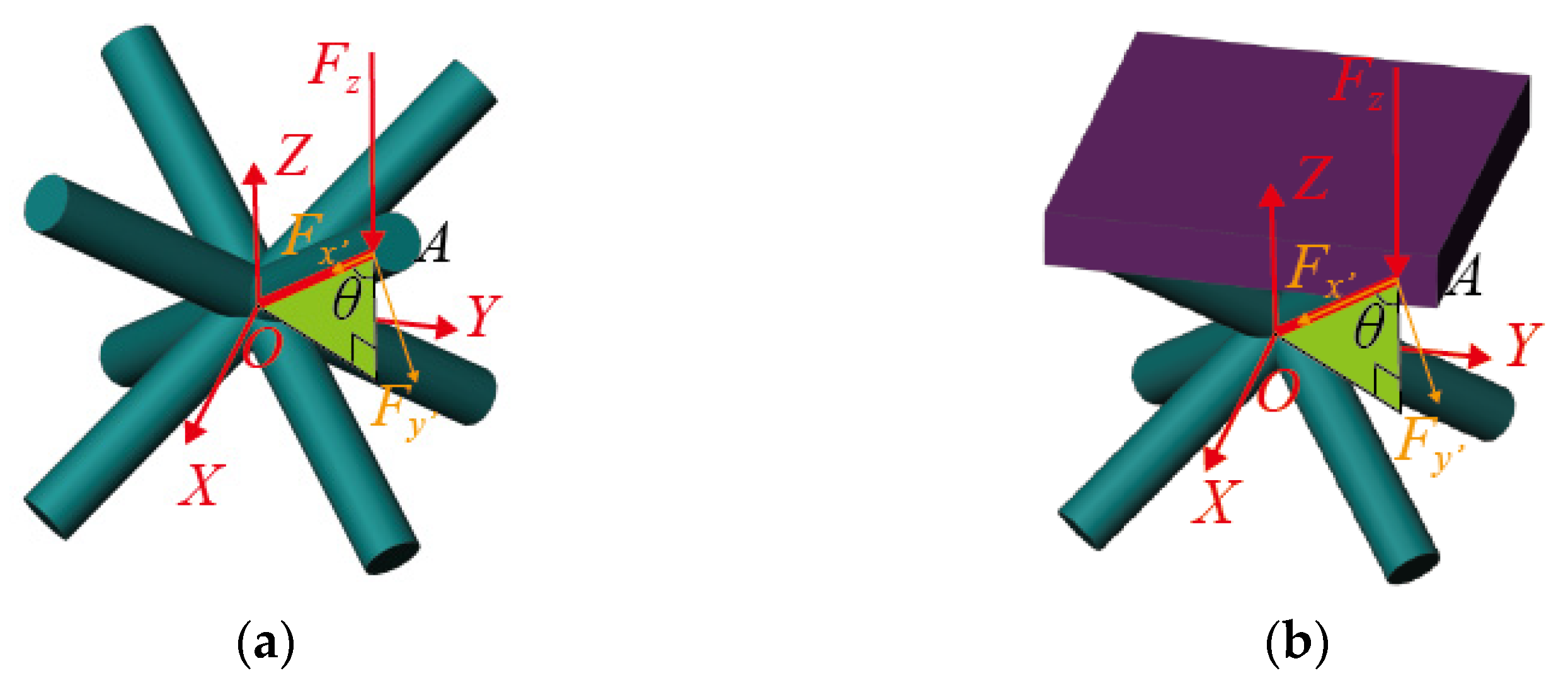



| No. | Element Number | Strut Diameter (mm) | Element Size (mm) | Strut Length (mm) | k | ||
|---|---|---|---|---|---|---|---|
| Min. | Max. | Aver. | |||||
| I | 8 × 8 × 8 | 0.88 | 0.97 | 0.91 | 4.97 | 4.30 | 0.10 |
| II | 8 × 8 × 8 | 1.03 | 1.07 | 1.06 | 4.98 | 4.31 | 0.12 |
| III | 8 × 8 × 8 | 1.20 | 1.24 | 1.23 | 4.97 | 4.30 | 0.14 |
| IV | 12 × 8 × 12 | 0.84 | 0.91 | 0.88 | 4.96 | 4.29 | 0.10 |
| V | 12 × 8 × 12 | 1.02 | 1.05 | 1.04 | 4.98 | 4.31 | 0.12 |
| VI | 12 × 8 × 12 | 1.22 | 1.24 | 1.23 | 4.97 | 4.30 | 0.14 |
| Parameter Name | Parameter Value |
|---|---|
| (ASTM D 638) | 2642 |
| Poisson’s ratio (ASTM D 638) | 0.42 |
| No. | Modulus from Experiments (MPa) | Method in This Research | Method in Ref. [32] | |||
|---|---|---|---|---|---|---|
| Modulus (MPa) | Error (%) | Modulus (MPa) | Error (%) | |||
| I | 0.1 | 11.1 | 10.6 | 5.1 | 13.2 | 18.9 |
| II | 0.12 | 18.9 | 19.2 | 1.6 | 23.1 | 22.2 |
| III | 0.14 | 30.8 | 31.7 | 2.7 | 37.1 | 20.4 |
| IV | 0.1 | 8.1 | 8.7 | 7.4 | 10.1 | 24.7 |
| V | 0.12 | 15.2 | 16.3 | 7.2 | 18.6 | 22.3 |
| VI | 0.14 | 28.2 | 27.6 | 2.1 | 31.1 | 10.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, J.; Wang, K.; Yan, D.; Liu, F.; Wang, L.; Zhao, L. An Analytical Method for Elastic Modulus of the Sandwich BCC Lattice Structure Based on Assumption of Linear Distribution. Materials 2023, 16, 3315. https://doi.org/10.3390/ma16093315
Shang J, Wang K, Yan D, Liu F, Wang L, Zhao L. An Analytical Method for Elastic Modulus of the Sandwich BCC Lattice Structure Based on Assumption of Linear Distribution. Materials. 2023; 16(9):3315. https://doi.org/10.3390/ma16093315
Chicago/Turabian StyleShang, Jinqi, Kangkang Wang, Dongyang Yan, Fengrui Liu, Linjuan Wang, and Libin Zhao. 2023. "An Analytical Method for Elastic Modulus of the Sandwich BCC Lattice Structure Based on Assumption of Linear Distribution" Materials 16, no. 9: 3315. https://doi.org/10.3390/ma16093315





