Influence of In-Situ Stress on Cut Blasting of One-Step Raise Excavation Using Numerical Analysis Based on a Modified Holmquist-Johnson-Cook Model
Abstract
1. Introduction
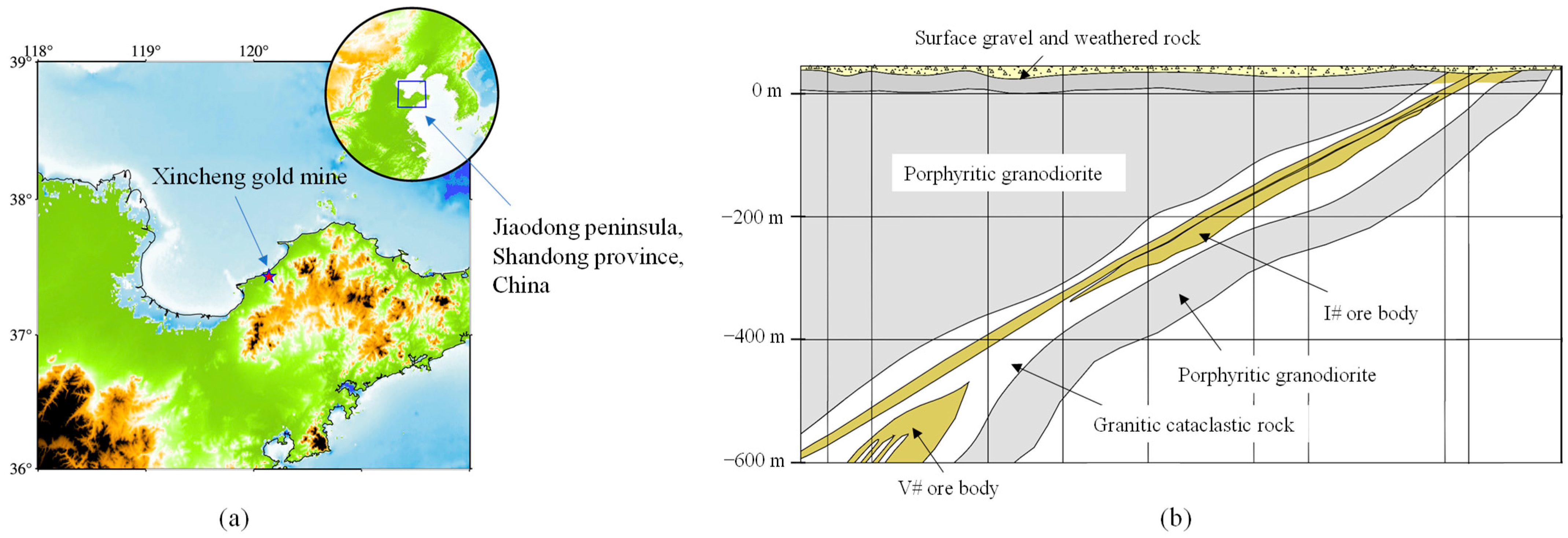
2. Engineering Background
2.1. General
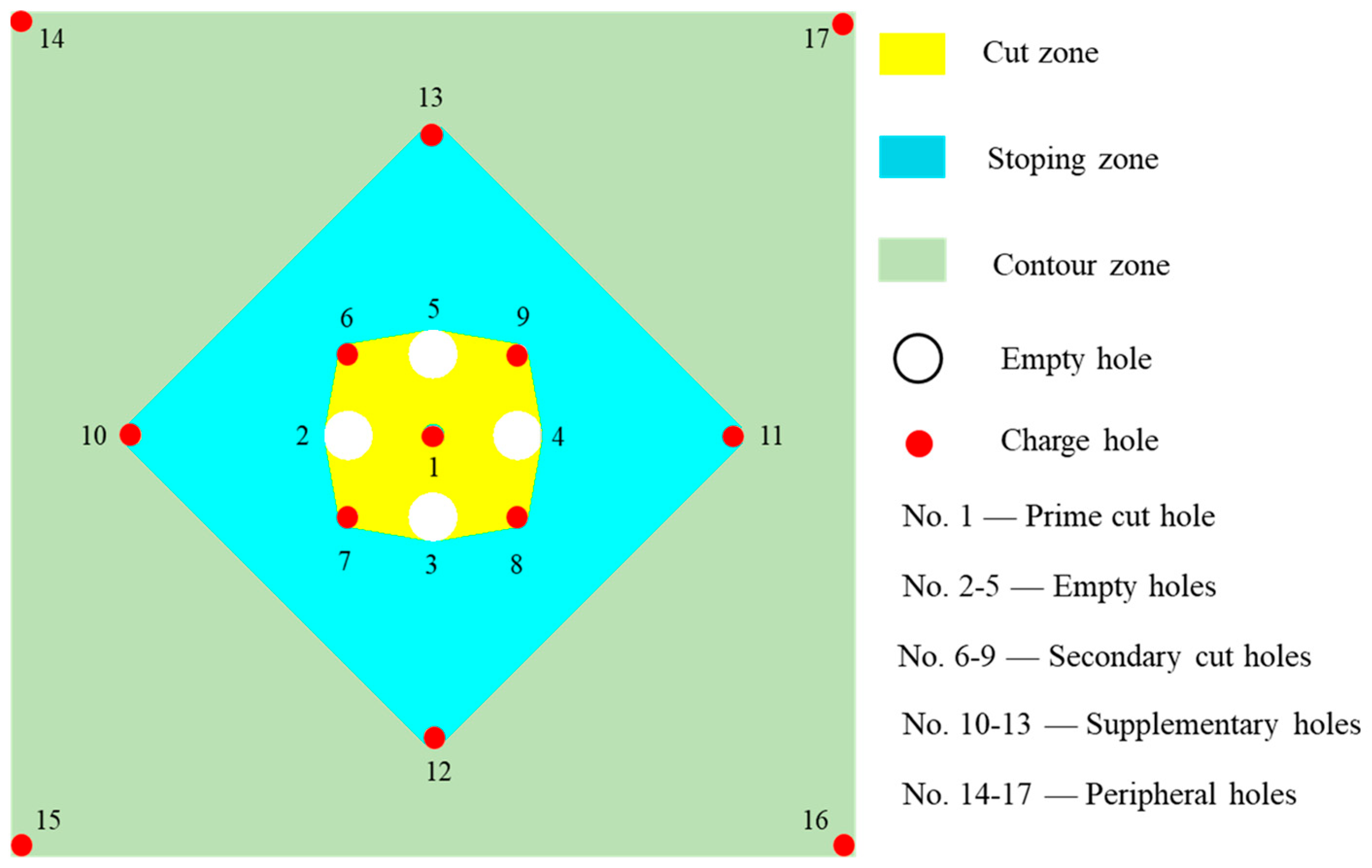
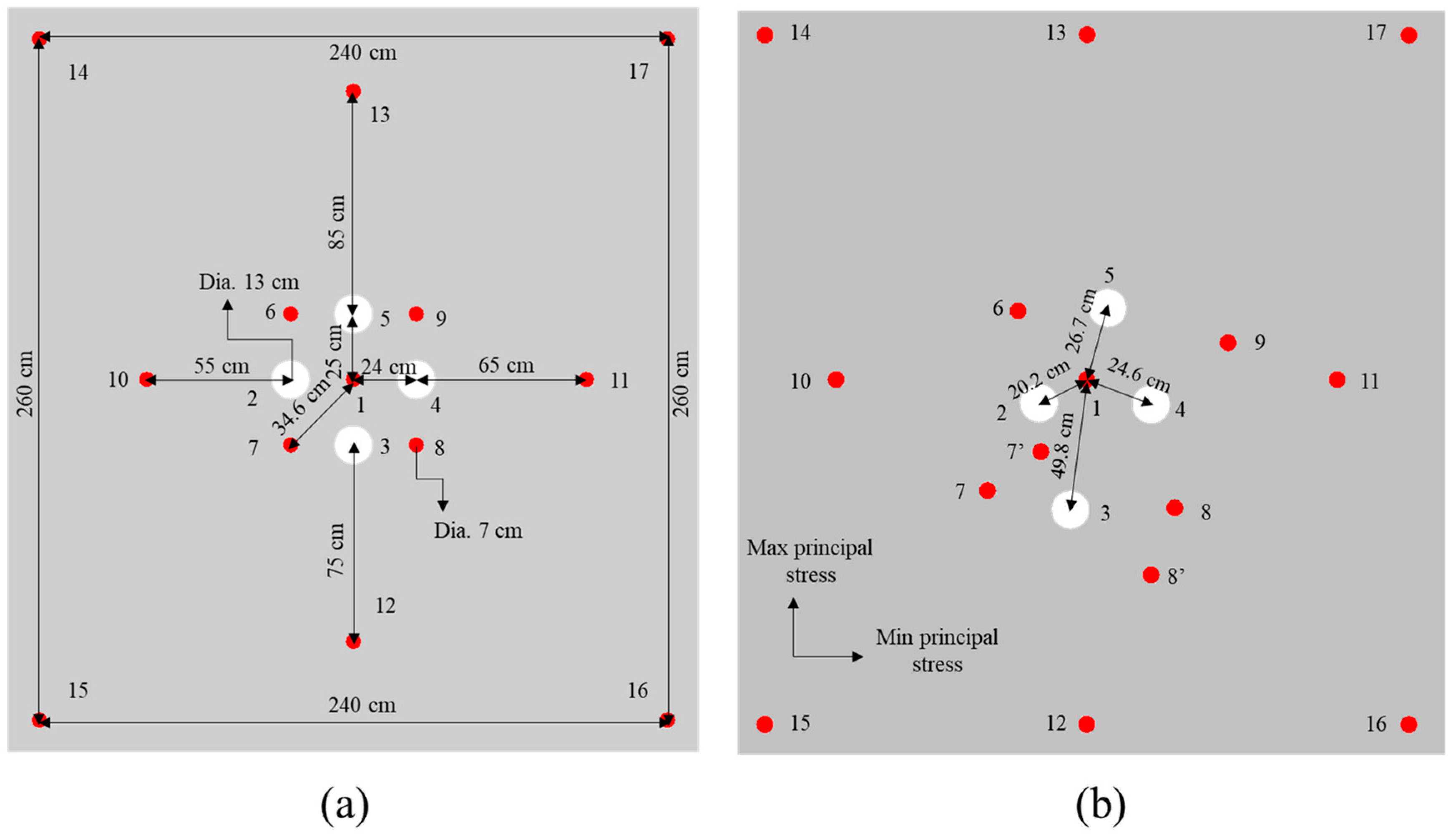
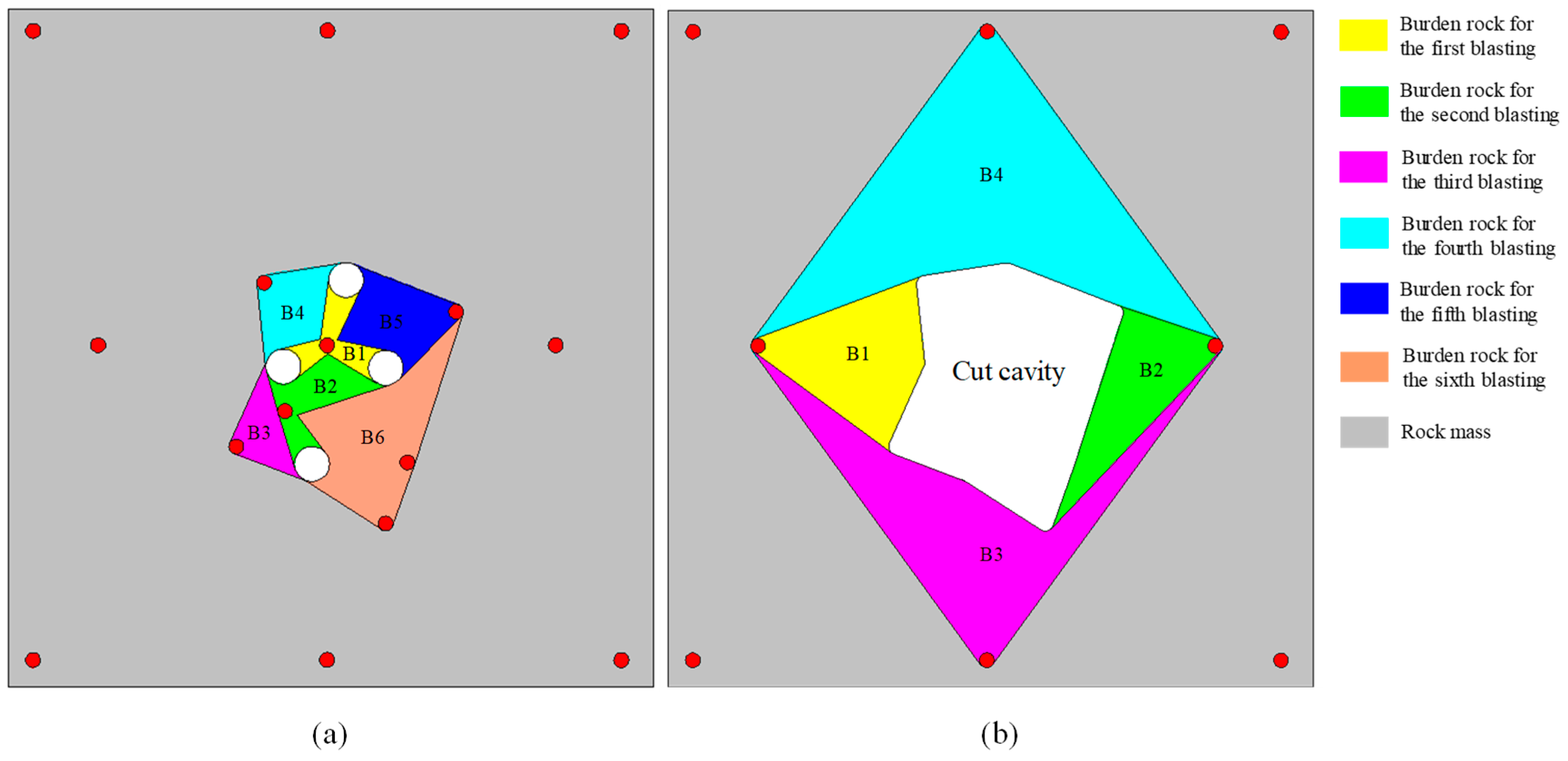
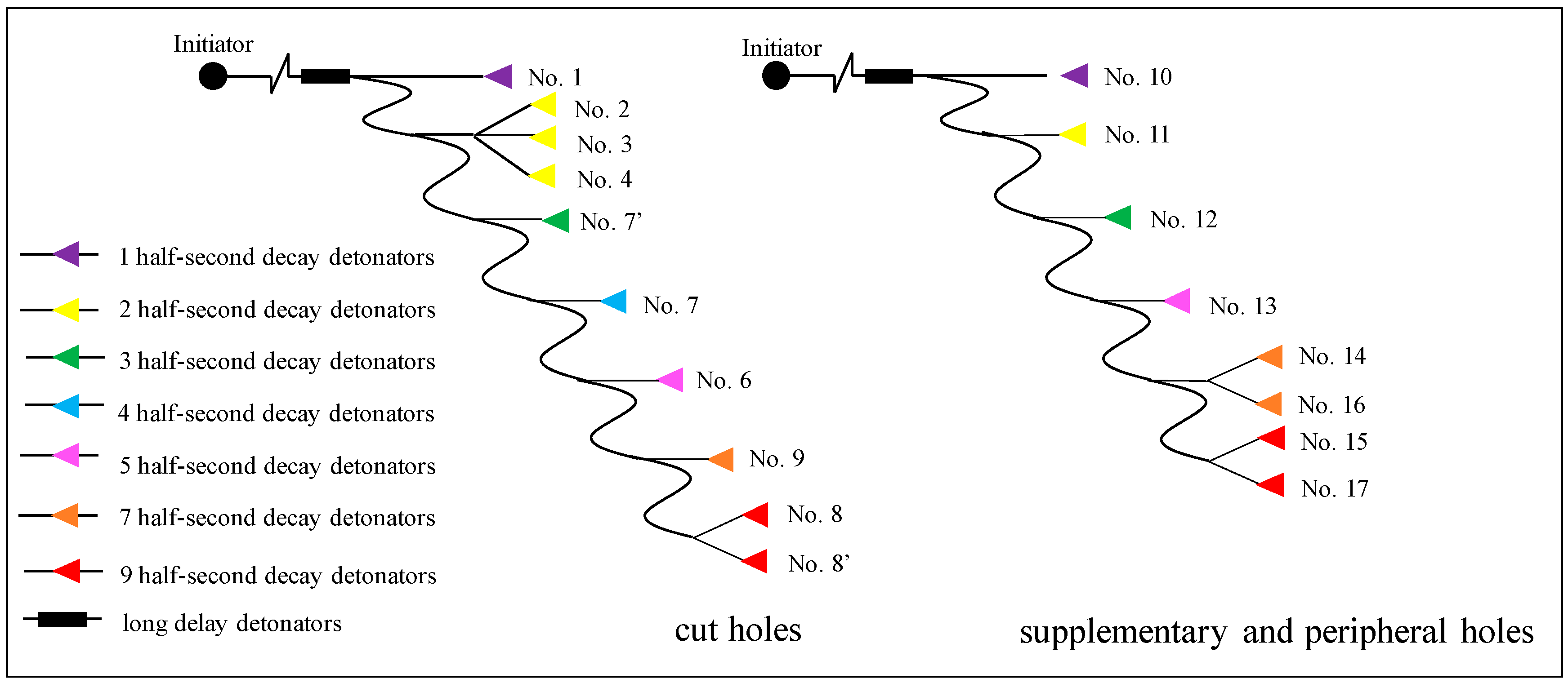
2.2. Design of Cut Blasting for One-Step Raise Excavation
3. Material Model for Numerical
3.1. Blasting Damage Model for Rock Material
3.1.1. Damage Evolution Model
3.1.2. Yield Strength Model
3.1.3. Strain Rate Effect Model
3.2. JWL EOS for Explosive
3.3. Air Material Model
4. Numerical Simulation and Analysis
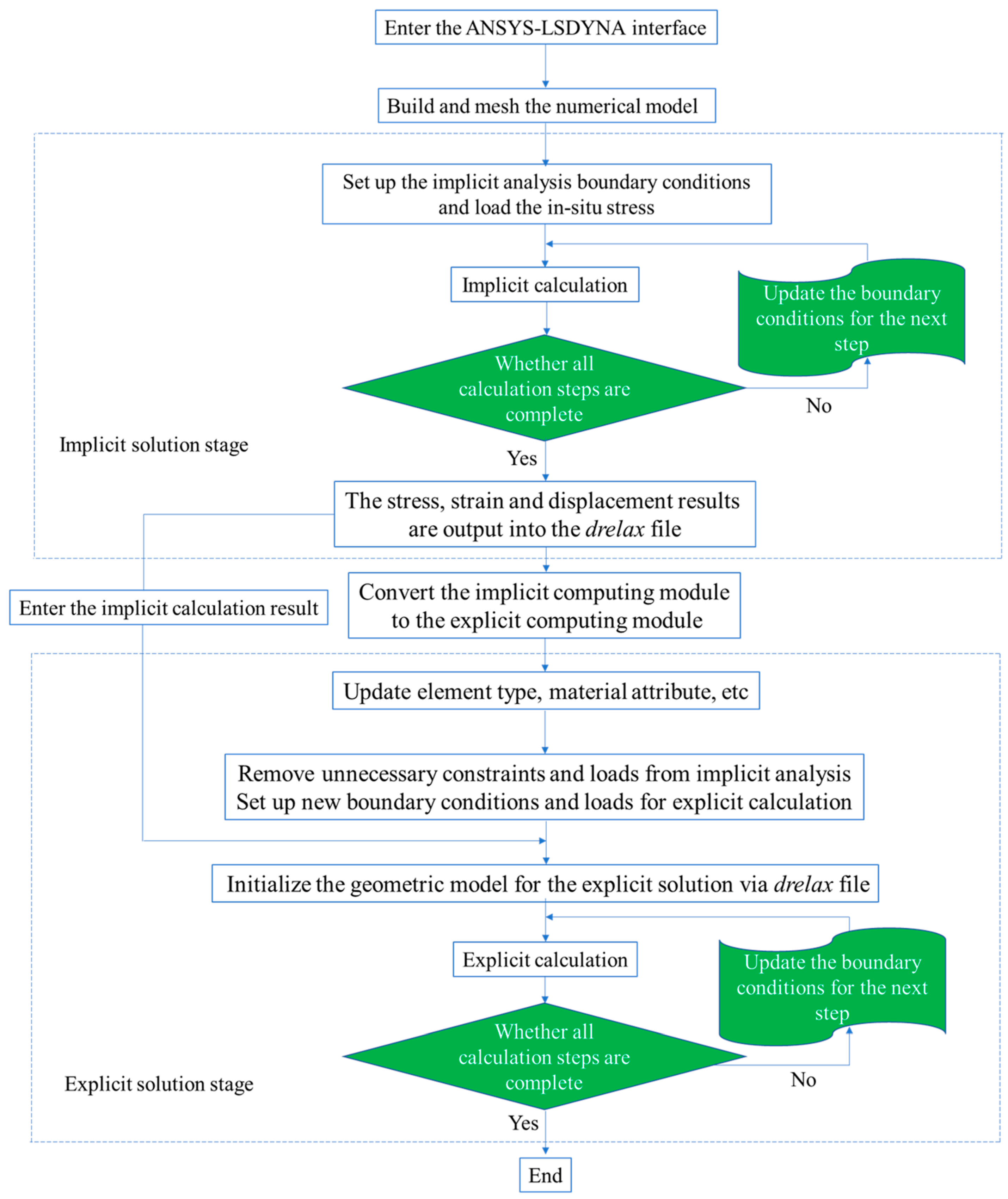
4.1. Research Methodology and Steps
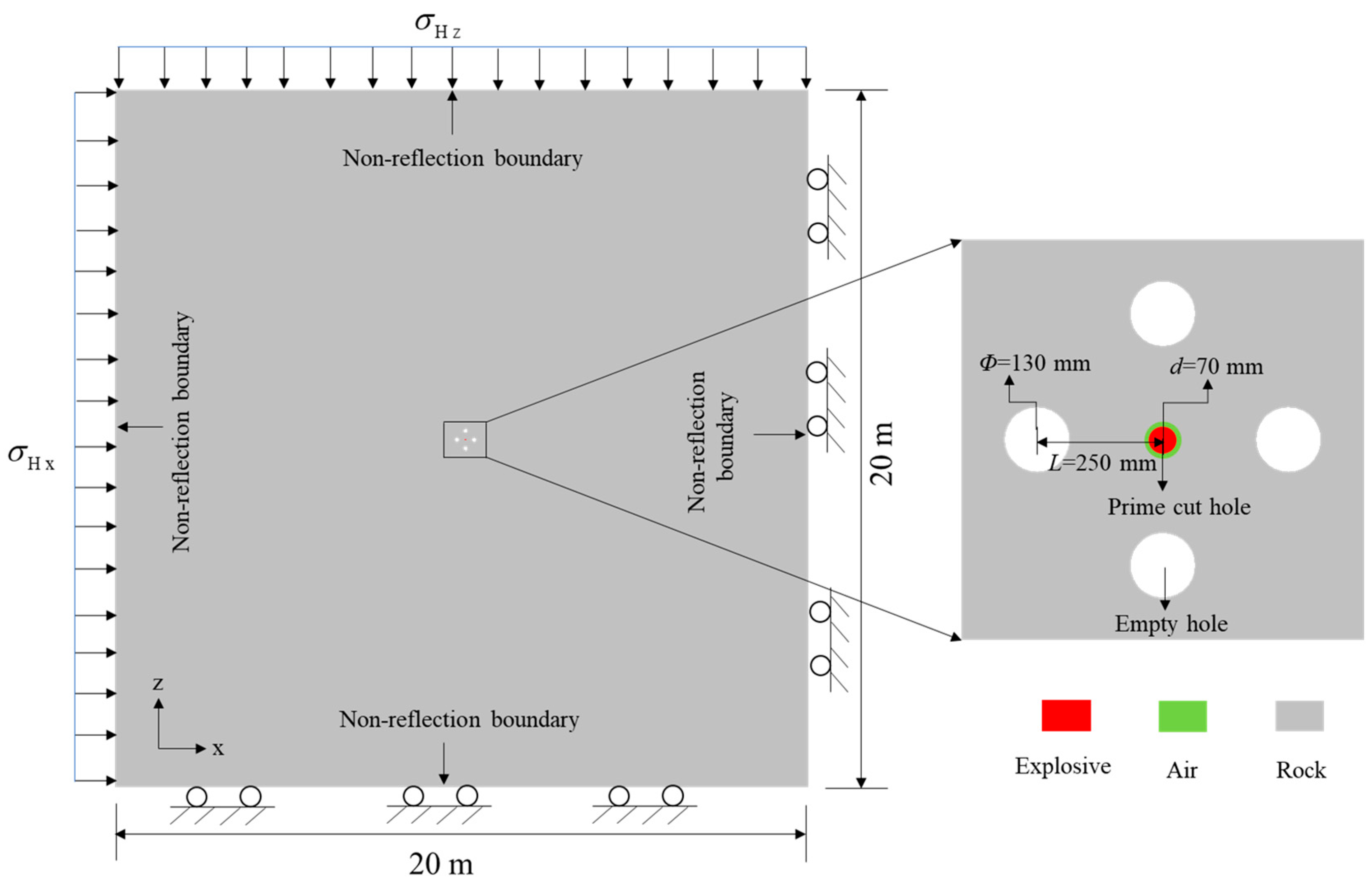
4.2. Numerical Model and Material Paramaters
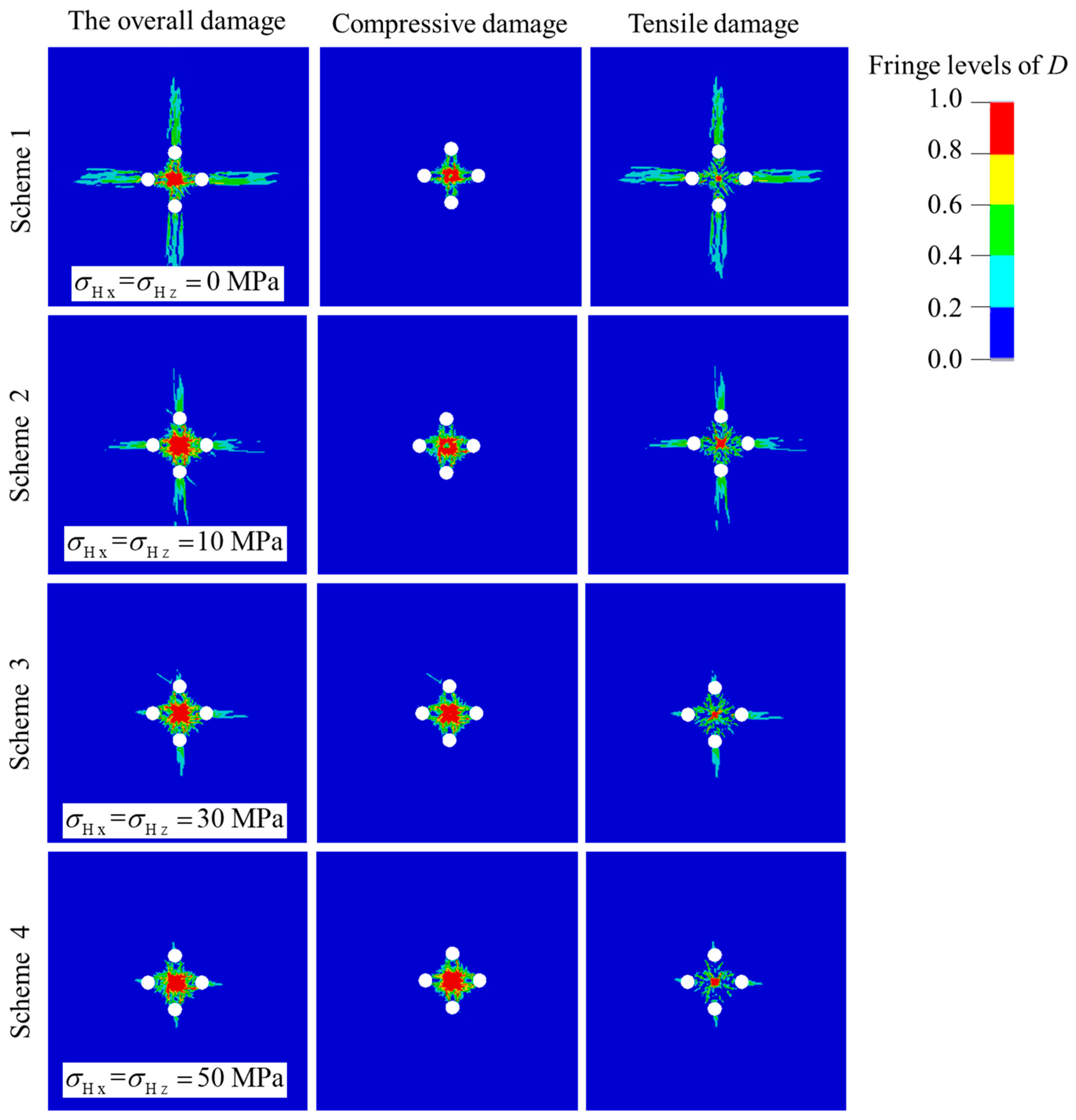
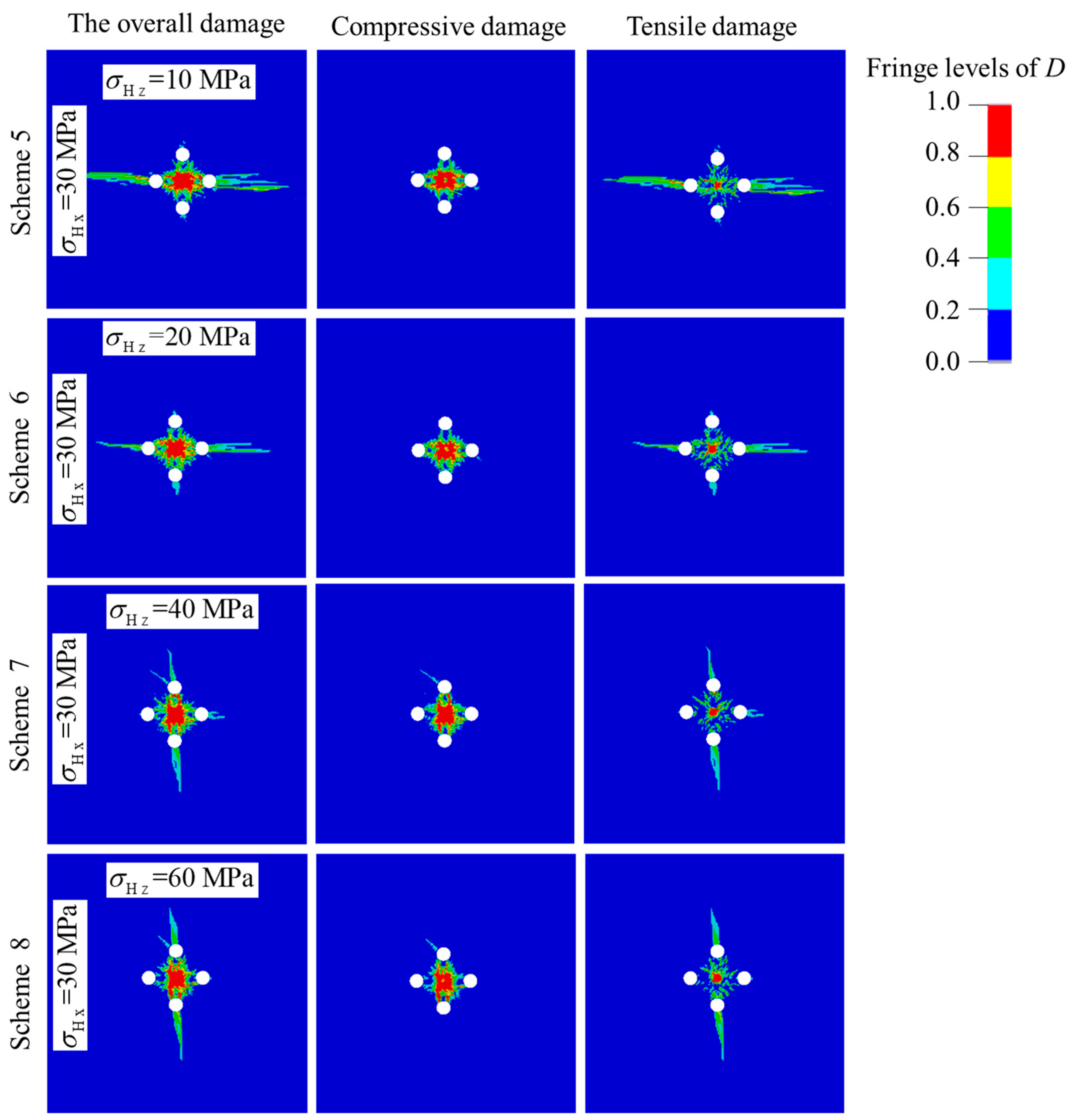
4.3. Damage Evolution under Different In-Situ Stresses
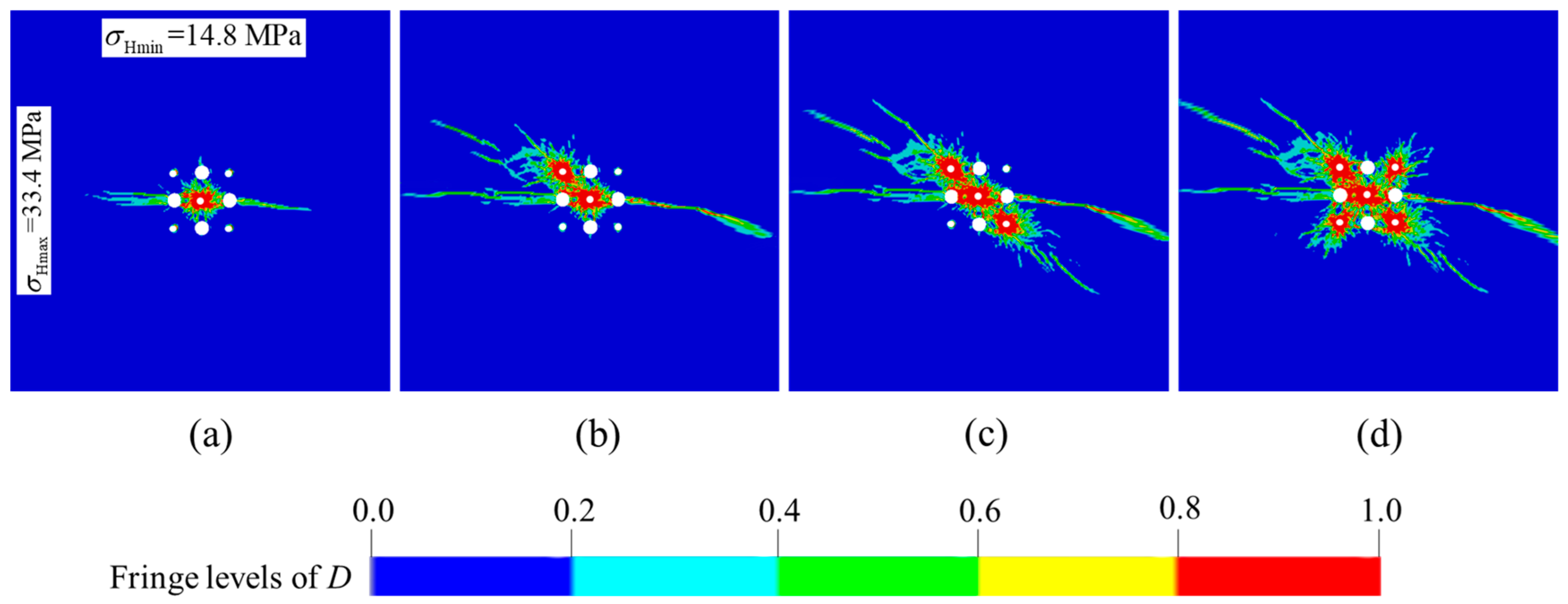
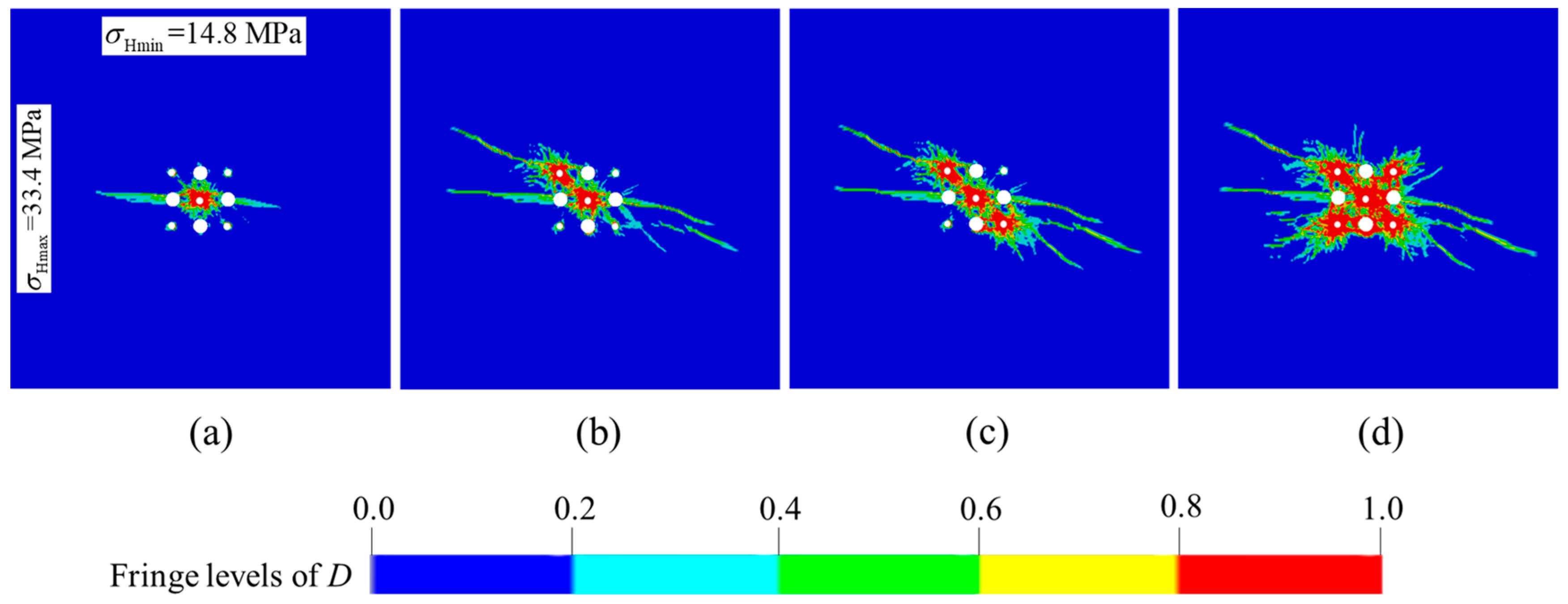
4.4. Case Study of Cut Parameters Optimization for Deep Raise
5. Field Test
6. Discussion
7. Conclusions
- An improved damage blasting model is proposed to describe the tensile and compressive damage separately, and then implemented into LS-DYNA to simulate the rock damage evolution in cut blasting for one-step raise excavation under different in-situ stresses.
- In-situ stress causes resistance on the overall rock damage evolution induced by blasting stress wave. For compressive damage, the damage increases with the increase of in-situ stress, while for tensile damage, it decreases with the increasing in-situ stress. The underlying reason is that in-situ stress can superimpose the peak pressure of the compressive stress component, but weaken that of the tensile stress component.
- The damage zones, including tensile and compressive damage, tend to develop along the direction of the maximum principal stress under the action of anisotropic in-situ stress. The phenomenon becomes distinctive as the difference between the two principal stresses increases, which is the main problem which should be solved in the deep cut blasting.
- For a blind cut raise in −665 m of the Xincheng gold mine, the optimal cut parameters are obtained by numerical simulation results of the improved damage model. The blind cut raise with 8.7 m depth is successfully formed, which demonstrates that the optimization parameters are valid for one-step excavation in deep mines, and the adjustments of design are necessary for the actual situation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, K.W.; Yang, J.C.; Li, X.B.; Hao, H.; Li, Q.Y.; Liu, Z.X.; Wang, C.Y. Study on the long-hole raising technique using one blast based on vertical crater retreat multiple deck shots. Int. J. Rock Mech. Mining Sci. 2018, 109, 52–67. [Google Scholar] [CrossRef]
- Rao, Z.B.; Cai, S.J. The Blasting Test and Blasting Vibration Monitoring of Vertical Crater Retreat Mining Method in the Luohe Iron Mine. Geotech. Geolog. Eng. 2016, 34, 1047–1056. [Google Scholar] [CrossRef]
- Balland, C.; Morel, J.; Armand, G.; Pettitt, W. Ultrasonic velocity survey in Callovo-Oxfordian argillaceous rock during shaft excavation. Int. J. Rock Mech. Min. Sci. 2009, 46, 69–79. [Google Scholar] [CrossRef]
- Liu, K.; Li, Q.Y.; Wu, C.Q.; Li, X.B.; Li, J. A study of cut blasting for one-step raise excavation based on numerical simulation and field blast tests. Int. J. Rock Mech. Min. Sci. 2018, 109, 91–104. [Google Scholar] [CrossRef]
- Li, Q.Y.; Li, X.B.; Fan, Z.P.; Zhang, R.H. One time deep hole raise blasting technology and case study. Chin. J. Rock Mech. Eng. 2013, 32, 664–670. (In Chinese) [Google Scholar]
- Li, Q.Y.; Liu, K.; Li, X.B.; Wang, Z.W.; Weng, L. Cutting parameter optimization for one-step shaft excavation technique based on parallel cutting method. Trans. Nonfer. Metals Soc. China 2018, 28, 1413–1423. [Google Scholar] [CrossRef]
- Xie, L.X.; Lu, W.B.; Zhang, Q.B.; Jiang, Q.H.; Chen, M.; Zhao, J. Analysis of damage mechanisms and optimization of cut basting model under high in-situ stresses. Tunn. Undergr. Space Technol. 2017, 66, 19–33. [Google Scholar] [CrossRef]
- Wang, S.F.; Li, X.B.; Rao, J.R.; Gong, F.Q.; Li, X.; Du, K.; Tao, M.; Huang, L.Q.; Du, S.L. Experimental investigation of rock breakage by a conical pick and its application to non-explosive mechanized mining in deep hard rock. Int. J. Rock Mech. Min. Sci. 2019, 122, 104063. [Google Scholar] [CrossRef]
- Wang, S.F.; Sun, L.C.; Tang, Y.; Jing, Y.; Li, X.B.; Rao, J.R. Field application of non-blasting mechanized mining using high-frequency impact hammer in deep hard rock mine. Trans. Nonfer. Metals Soc. China 2022, 32, 3051–3064. [Google Scholar] [CrossRef]
- Hong, Z.X.; Tao, M.; Cui, X.J.; Wu, C.Q.; Zhao, M.S. Experimental and numerical studies of the blast-induced overbreak and underbreak in underground roadways. Undergr. Space 2023, 8, 61–79. [Google Scholar] [CrossRef]
- Taylor, L. Microcrack-induced damage accumulation in brittle rock under dynamic loading. Comp. Meth. Applied Mech. Eng. 1985, 55, 301–320. [Google Scholar] [CrossRef]
- Liu, L.Q.; Katsabanis, P.D. Development of a continuum damage model for blasting analysis. Int. J. Rock Mech. Mining Sci. 1997, 34, 217–231. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Hao, H.; Lu, Y. Anisotropic dynamic damage and fragmentation of rock materials under explosive loading. Int. J. Eng. Sci. 2003, 41, 917–929. [Google Scholar] [CrossRef]
- Yang, J.H.; Lu, W.B.; Hu, Y.G.; Chen, M.; Yan, P. Numerical simulation of rock mass damage evolution during deep-buried tunnel excavation by drill and blast. Rock Mech. Rock Eng. 2015, 48, 2045–2059. [Google Scholar] [CrossRef]
- Xie, L.X.; Lu, W.B.; Zhang, Q.B.; Jiang, Q.H.; Wang, G.H.; Zhao, J. Damage evolution mechanisms of rock in deep tunnels induced by cut blasting. Tunn. Undergr. Space Technol. 2016, 58, 257–270. [Google Scholar] [CrossRef]
- Tao, M.; Li, X.B.; Wu, C.Q. Characteristics of the unloading process of rocks under high initial stress. Comp. Geotech. 2012, 45, 83–92. [Google Scholar] [CrossRef]
- Brannon, R.M.; Leelavanichkul, S. Survey of Four Damage Models for Concrete; Sandia Report, Sand 2009-5544; Sandia National Laboratories: Albuquerque, NM, USA; Livermore, CA, USA, 2009; pp. 1–82. [Google Scholar]
- Riedel, W.; Thoma, K.; Hiermaier, S.; Schmolinske, E. Penetration of reinforced concrete by BETA-B-500 numerical analysis using a new macroscopic concrete model for hydrocedes. In Proceedings of the 9th International Symposium on the Effects of Munitions with Structures, Berlin, Germany, 3–7 May 1999. [Google Scholar]
- Kong, X.Z.; Qin, F.; Hao, W.; Peng, Y. Numerical predictions of cratering and scabbing in concrete slabs subjected to projectile impact using a modified version of HJC material model. Int. J. Impact Eng. 2016, 95, 61–71. [Google Scholar] [CrossRef]
- Hao, H.; Wu, C.Q.; Seah, C.C. Numerical Analysis of Blast-Induced Stress Waves in a Rock Mass with Anisotropic Continuum Damage Models Part 2: Stochastic Approach. Rock Mech. Rock Eng. 2002, 35, 95–108. [Google Scholar] [CrossRef]
- Li, H.Y.; Shi, G.Y. A dynamic material model for rock materials under conditions of high confining pressures and high strain rates. Int. J. Impact Eng. 2014, 89, 38–48. [Google Scholar] [CrossRef]
- Yi, C.P.; Sjöberg, J.; Johansson, D. Numerical modelling for blast-induced fragmentation in sublevel caving mines. Tunn. Undergr. Space Technol. 2017, 68, 167–173. [Google Scholar] [CrossRef]
- Wang, S.F.; Liu, K.H.; Wang, S.Y.; Liang, Y.T.; Tian, F.C. Three-dimensional stochastic distribution characteristics of void fraction in longwall mining-disturbed overburden. Bull. Eng. Geol. Environ. 2022, 81, 414. [Google Scholar] [CrossRef]
- Zhang, Z.X. Rock blasting in open cut and tunneling. In Rock Fracture and Blasting; Elsevier: Amsterdam, The Netherlands, 2016; pp. 334–352. [Google Scholar]
- Hao, H.; Wu, C.Q.; Zhou, Y. Numerical Analysis of Blast-Induced Stress Waves in a Rock Mass with Anisotropic Continuum Damage Models Part 1: Equivalent Material Property Approach. Rock Mech. Rock Eng. 2002, 35, 79–94. [Google Scholar] [CrossRef]
- Ma, G.W.; An, X.M. Numerical simulation of blasting-induced rock fractures. Int. J. Rock Mech. Min. Sci. 2008, 45, 966–975. [Google Scholar] [CrossRef]
- Yilmaz, O.; Unlu, T. Three dimensional numerical rock damage analysis under blasting load. Tunn. Undergr. Space Technol. 2013, 38, 266–278. [Google Scholar] [CrossRef]
- Hartmann, T.; Pietzsch, A.; Gebbeken, N. A Hydrocode Material Model for Concrete. Int. J. Protective Struc. 2010, 1, 443. [Google Scholar] [CrossRef]
- Weerheijm, J.; Van Doormaal, J.C.A.M. Tensile failure of concrete at high loading rates: New test data on strength and fracture energy from instrumented spalling tests. Int. J. Impact Eng. 2007, 34, 609–626. [Google Scholar] [CrossRef]
- Polanco-Loria, M.; Hopperstad, O.S.; Børvik, T.; Berstad, T. Numerical predictions of ballistic limits for concrete slabs using a modified version of the HJC concrete model. Int. J. Impact Eng. 2008, 35, 290–303. [Google Scholar] [CrossRef]
- Zhang, Q.B.; Zhao, J. A Review of Dynamic Experimental Techniques and Mechanical Behaviour of Rock Materials. Rock Mech. Rock Eng. 2014, 47, 1411–1478. [Google Scholar] [CrossRef]
- Gebbeken, N.; Greulich, S. A new material model for SFRC under high dynamic loadings. In Proceedings of the 1th international Symposium on Interaction of the Effects of Munitions with Structures (ISIEMS), Mannheim, Germany, 5–9 May 2003. [Google Scholar]
- Tedesco, J.W.; Powell, J.C.; Ross, C.A.; Hughes, M.L. A strain-rate-dependent concrete material model for ADINA. Comp. Struct. 1997, 64, 1053–1067. [Google Scholar] [CrossRef]
- Liu, K.; Wu, C.Q.; Li, X.B.; Li, Q.Y.; Fang, J.G.; Liu, J. A modified HJC model for improved dynamic response of brittle materials under blasting loads. Comp. Geotech. 2020, 123, 103584. [Google Scholar] [CrossRef]
- Hu, Y.G.; Lu, W.B.; Chen, M.; Yan, P.; Yang, J.H. Comparison of blast-induced damage between presplit and smooth blasting of high rock slope. Rock Mech. Rock Eng. 2014, 47, 1307–1320. [Google Scholar] [CrossRef]
- Hallquist, J.O. Ls-Dyna Theory Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2006. [Google Scholar]
- Liu, K.; Qiu, J.D. Investigation of Burn Cut Parameters and Model for One-Step Raise Excavation Based on Damage Evolution Mechanisms. Geofluids 2020, 2020, 8879477. [Google Scholar] [CrossRef]
- Kononenko, M.; Khomenko, O. New theory for the rock mass destruction by blasting. Min. Miner. Depos. 2021, 15, 111–123. [Google Scholar] [CrossRef]
- Li, X.B.; Weng, L. Numerical investigation on fracturing behaviors of deep-buried opening under dynamic disturbance. Tunn. Undergr. Space Technol. 2016, 54, 61–72. [Google Scholar] [CrossRef]
- Weng, L.; Huang, L.Q.; Taheri, A.; Li, X.B. Rockburst characteristics and numerical simulation based on a strain energy density index: A case study of a roadway in Linglong gold mine, China. Tunn. Undergr. Space Technol. 2017, 69, 223–232. [Google Scholar] [CrossRef]
- Cai, M.F.; Qiao, L.; Li, C.H. Measuring results and regularity of in situ stress in Xincheng gold mine. Nonfer. Metals. 2000, 52, 1–6. (In Chinese) [Google Scholar]
- Xie, H.P.; Gao, F.; Ju, Y. Research and development of rock mechanics in deep ground engineering. Chin. J. Rock Mech. Eng. 2015, 34, 2161–2178. (In Chinese) [Google Scholar]
- Zare, S.; Bruland, A. Comparison of tunnel blast design models. Tunn. Undergr. Space Technol. 2006, 21, 533–541. [Google Scholar] [CrossRef]
- Holmquist, T.J.; Johnson, G.R.; Cook, W.H. A computational constitutive model for concrete subjected to large strains, high strain rates, and high pressures. In Proceedings of the 14th International Symposium on Ballistics, Quebec, QC, Canada, 26–29 September 1993; pp. 591–600. [Google Scholar]
- Shahzamanian, M.M. Implementation of a rate dependent tensile failure model for brittle materials in ABAQUS. Int. J. Impact Eng. 2016, 97, 127–147. [Google Scholar] [CrossRef]
- Zhu, Z.M.; Xie, H.P.; Mohanty, B.H. Numerical investigation of blasting-induced damage in cylindrical rocks. Int. J. Rock Mech. Min. Sci. 2008, 45, 111–121. [Google Scholar]


| ρ/(kg/m3) | G/GPa | K/GPa | B | N | fc/MPa | ft/MPa | D1 | D2 |
|---|---|---|---|---|---|---|---|---|
| 2810 | 17.2 | 33.2 | 2.57 | 0.62 | 133.5 | 6.76 | 0.04 | 1.0 |
| pc/MPa | µc | p1/GPa | µ1 | K1/GPa | K2/GPa | K3/GPa | EFmin | |
| 44.5 | 0.0013 | 1.89 | 0.110 | 18.8 | 15.3 | 94.1 | 0.03 |
| VoD (m/s) | PCJ (GPa) | AJ (GPa) | BJ (GPa) | R1 | R2 | E0 (GPa) | ||
|---|---|---|---|---|---|---|---|---|
| 1210 | 5660 | 9.7 | 214.4 | 0.182 | 4.2 | 0.9 | 0.15 | 4.192 |
| Loading Schemes | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Horizontal stress in the x direction (MPa) | 0 | 10 | 30 | 50 | 30 | 30 | 30 | 30 |
| Horizontal stress in the z direction (MPa) | 0 | 10 | 30 | 50 | 10 | 20 | 40 | 60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Li, Q.; Wu, C.; Li, X.; Zhu, W. Influence of In-Situ Stress on Cut Blasting of One-Step Raise Excavation Using Numerical Analysis Based on a Modified Holmquist-Johnson-Cook Model. Materials 2023, 16, 3415. https://doi.org/10.3390/ma16093415
Liu K, Li Q, Wu C, Li X, Zhu W. Influence of In-Situ Stress on Cut Blasting of One-Step Raise Excavation Using Numerical Analysis Based on a Modified Holmquist-Johnson-Cook Model. Materials. 2023; 16(9):3415. https://doi.org/10.3390/ma16093415
Chicago/Turabian StyleLiu, Kai, Qiyue Li, Chengqing Wu, Xibing Li, and Wei Zhu. 2023. "Influence of In-Situ Stress on Cut Blasting of One-Step Raise Excavation Using Numerical Analysis Based on a Modified Holmquist-Johnson-Cook Model" Materials 16, no. 9: 3415. https://doi.org/10.3390/ma16093415
APA StyleLiu, K., Li, Q., Wu, C., Li, X., & Zhu, W. (2023). Influence of In-Situ Stress on Cut Blasting of One-Step Raise Excavation Using Numerical Analysis Based on a Modified Holmquist-Johnson-Cook Model. Materials, 16(9), 3415. https://doi.org/10.3390/ma16093415







