CFD–PBM Simulation for Continuous Hydrothermal Flow Synthesis of Zirconia Nanoparticles in a Confined Impinging Jet Reactor
Abstract
1. Introduction
2. Experimental and Modeling
2.1. CHFS–CJM System Conditions
2.2. Characterization Methods
2.3. CFD–PBM Model Development
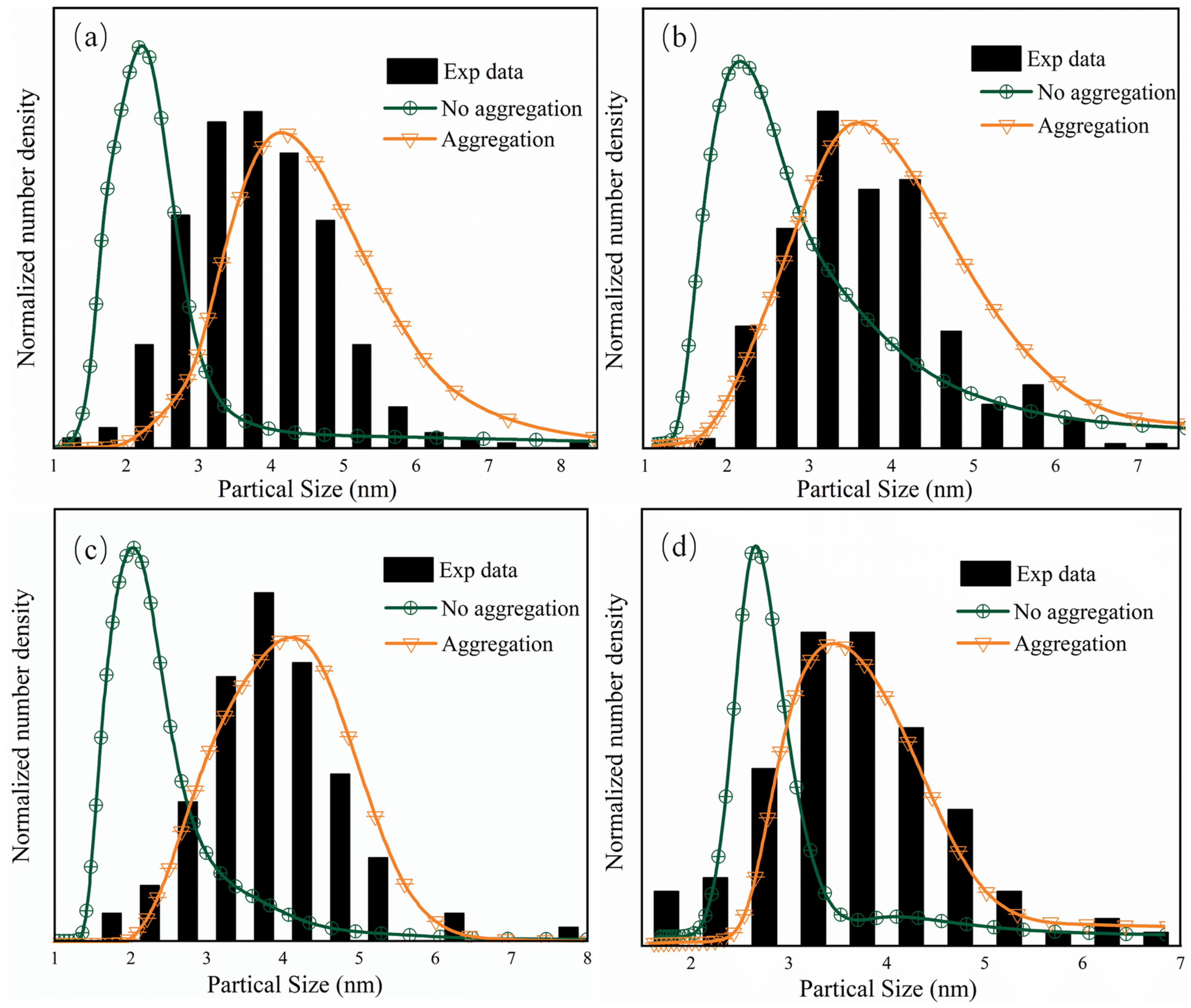
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Q.; Danlos, Y.; Song, B.; Zhang, B.; Yin, S.; Liao, H. Effect of high-temperature preheating on the selective laser melting of yttria-stabilized zirconia ceramic. J. Mater. Process. Technol. 2015, 222, 61–74. [Google Scholar] [CrossRef]
- Naik, A.J.T.; Gruar, R.; Tighe, C.J.; Parkin, I.P.; Darr, J.A.; Binions, R. Environmental sensing semiconducting nanoceramics made using a continuous hydrothermal synthesis pilot plant. Sens. Actuators B Chem. 2015, 217, 136–145. [Google Scholar] [CrossRef]
- Liu, J.; He, Y.; Yan, L.; Li, K.; Zhang, C.; Xiang, H.; Wen, X.; Li, Y. Nano-sized ZrO2 derived from metal–organic frameworks and their catalytic performance for aromatic synthesis from syngas. Catal. Sci. Technol. 2019, 9, 2982–2992. [Google Scholar] [CrossRef]
- Akune, T.; Morita, Y.; Shirakawa, S.; Katagiri, K.; Inumaru, K. ZrO2 Nanocrystals As Catalyst for Synthesis of Dimethylcarbonate from Methanol and Carbon Dioxide: Catalytic Activity and Elucidation of Active Sites. Langmuir 2018, 34, 23–29. [Google Scholar] [CrossRef]
- Kim, J.-Y.; Kim, C.-S.; Chang, H.-K.; Kim, T.-O. Effects of ZrO2 addition on phase stability and photocatalytic activity of ZrO2/TiO2 nanoparticles. Adv. Powder Technol. 2010, 21, 141–144. [Google Scholar] [CrossRef]
- Kim, J.-R.; Myeong, W.-J.; Ihm, S.-K. Characteristics in oxygen storage capacity of ceria–zirconia mixed oxides prepared by continuous hydrothermal synthesis in supercritical water. Appl. Catal. B Environ. 2007, 71, 57–63. [Google Scholar] [CrossRef]
- de Carvalho, J.M.; Rodrigues, L.C.V.; Felinto, M.C.F.C.; Nunes, L.A.O.; Hölsä, J.; Brito, H.F. Structure–property relationship of luminescent zirconia nanomaterials obtained by sol–gel method. J. Mater. Sci. 2015, 50, 873–881. [Google Scholar] [CrossRef]
- Dell’agli, G.; Esposito, S.; Mascolo, G.; Mascolo, M.C.; Pagliuca, C. Films by slurry coating of nanometric YSZ (8mol% Y2O3) powders synthesized by low-temperature hydrothermal treatment. J. Eur. Ceram. Soc. 2005, 25, 2017–2021. [Google Scholar] [CrossRef]
- Li, G.; Wang, Q.; Zhao, B.; Zhou, R. Modification of Ce0.67Zr0.33O2 mixed oxides by coprecipitated/impregnated Co: Effect on the surface and catalytic behavior of Pd only three-way catalyst. J. Mol. Catal. A Chem. 2010, 326, 69–74. [Google Scholar] [CrossRef]
- Eggersdorfer, M.L.; Gröhn, A.J.; Sorensen, C.M.; McMurry, P.H.; Pratsinis, S.E. Mass-mobility characterization of flame-made ZrO2 aerosols: Primary particle diameter and extent of aggregation. J. Colloid Interface Sci. 2012, 387, 12–23. [Google Scholar] [CrossRef]
- Mishra, M.K.; Tyagi, B.; Jasra, R.V. Synthesis and characterization of nano-crystalline sulfated zirconia by sol–gel method. J. Mol. Catal. A Chem. 2004, 223, 61–65. [Google Scholar] [CrossRef]
- Nakonieczny, D.; Paszenda, Z.; Drewniak, S.; Radko, T.; Lis, M. sZrO2-CeO2 ceramic powders obtained from a sol-gel process using acetylacetone as a chelating agent for potential application in prosthetic dentistry. Acta Bioeng. Biomech. 2016, 18, 53–60. [Google Scholar] [PubMed]
- Zielke, P.; Xu, Y.; Simonsen, S.B.; Norby, P.; Kiebach, R. Simulation, design and proof-of-concept of a two-stage continuous hydrothermal flow synthesis reactor for synthesis of functionalized nano-sized inorganic composite materials. J. Supercrit. Fluids 2016, 117, 1–12. [Google Scholar] [CrossRef]
- Darr, J.A.; Zhang, J.; Makwana, N.M.; Weng, X. Continuous Hydrothermal Synthesis of Inorganic Nanoparticles: Applications and Future Directions. Chem. Rev. 2017, 117, 11125–11238. [Google Scholar] [CrossRef] [PubMed]
- Aimable, A.; Xin, B.; Millot, N.; Aymes, D. Continuous hydrothermal synthesis of nanometric BaZrO3 in supercritical water. J. Solid State Chem. 2008, 181, 183–189. [Google Scholar] [CrossRef]
- Tighe, C.J.; Gruar, R.I.; Ma, C.Y.; Mahmud, T.; Wang, X.Z.; Darr, J.A. Investigation of counter-current mixing in a continuous hydrothermal flow reactor. J. Supercrit. Fluids 2012, 62, 165–172. [Google Scholar] [CrossRef]
- Loppinet-Serani, A.; Aymonier, C.; Cansell, F. Current and Foreseeable Applications of Supercritical Water for Energy and the Environment. Chemsuschem 2008, 1, 486–503. [Google Scholar] [CrossRef]
- Gavi, E.; Marchisio, D.L.; Barresi, A.A. CFD modelling and scale-up of Confined Impinging Jet Reactors. Chem. Eng. Sci. 2007, 62, 2228–2241. [Google Scholar] [CrossRef]
- Leybros, A.; Piolet, R.; Ariane, M.; Muhr, H.; Bernard, F.; Demoisson, F. CFD simulation of ZnO nanoparticle precipitation in a supercritical water synthesis reactor. J. Supercrit. Fluids 2012, 70, 17–26. [Google Scholar] [CrossRef]
- Nadimpalli, N.K.V.; Bandyopadhyaya, R.; Runkana, V. A coupled CFD-PBM and thermodynamic analysis of continuous supercritical hydrothermal synthesis of nanoparticles. J. Supercrit. Fluids 2018, 136, 164–179. [Google Scholar] [CrossRef]
- Demoisson, F.; Ariane, M.; Leybros, A.; Muhr, H.; Bernard, F. Design of a reactor operating in supercritical water conditions using CFD simulations. Examples of synthesized nanomaterials. J. Supercrit. Fluids 2011, 58, 371–377. [Google Scholar] [CrossRef]
- Ma, C.Y.; Chen, M.; Wang, X.Z. Modelling and simulation of counter-current and confined jet reactors for hydrothermal synthesis of nano-materials. Chem. Eng. Sci. 2014, 109, 26–37. [Google Scholar] [CrossRef]
- Ma, C.Y.; Liu, J.J.; Zhang, Y.; Wang, X.Z. Simulation for scale-up of a confined jet mixer for continuous hydrothermal flow synthesis of nanomaterials. J. Supercrit. Fluids 2015, 98, 211–221. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, S.; Xu, D.; Guo, Y. Impact of Mixing for the Production of CuO Nanoparticles in Supercritical Hydrothermal Synthesis. Ind. Eng. Chem. Res. 2013, 53, 481–493. [Google Scholar] [CrossRef]
- Huddle, T.; Al-Atta, A.; Moran, S.; Lester, E. Pseudo fluid modelling used in the design of continuous flow supercritical water oxidation reactors with improved corrosion resistance. J. Supercrit. Fluids 2017, 120, 355–365. [Google Scholar] [CrossRef]
- Metzger, L.; Kind, M. On the transient flow characteristics in Confined Impinging Jet Mixers-CFD simulation and experimental validation. Chem. Eng. Sci. 2015, 133, 91–105. [Google Scholar] [CrossRef]
- Sierra-Pallares, J.; Huddle, T.; Alonso, E.; Mato, F.A.; García-Serna, J.; Cocero, M.J.; Lester, E. Prediction of residence time distributions in supercritical hydrothermal reactors working at low Reynolds numbers. Chem. Eng. J. 2016, 299, 373–385. [Google Scholar] [CrossRef]
- Ma, C.Y.; Mahmud, T.; Wang, X.Z.; Tighe, C.J.; I Gruar, R.; Darr, J.A. Numerical Simulation of Fluid Flow and Heat Transfer in a Counter-Current Reactor System for Nanomaterial Production. Chem. Prod. Process. Model. 2011, 6. [Google Scholar] [CrossRef]
- Ma, C.Y.; Tighe, C.J.; Gruar, R.I.; Mahmud, T.; Darr, J.A.; Wang, X.Z. Numerical modelling of hydrothermal fluid flow and heat transfer in a tubular heat exchanger under near critical conditions. J. Supercrit. Fluids 2011, 57, 236–246. [Google Scholar] [CrossRef]
- Hulburt, H.; Katz, S. Some problems in particle technology: A statistical mechanical formulation. Chem. Eng. Sci. 1964, 19, 555–574. [Google Scholar] [CrossRef]
- Chen, M.; Ma, C.Y.; Mahmud, T.; Darr, J.A.; Wang, X.Z. Modelling and simulation of continuous hydrothermal flow synthesis process for nano-materials manufacture. J. Supercrit. Fluids 2011, 59, 131–139. [Google Scholar] [CrossRef]
- Winterer, M.; Nitsche, R.; Redfern, S.A.T.; Schmahl, W.W.; Hahn, H. Phase stability in nanostructured and coarse grained zirconia at high pressures. Nanostruct. Mater. 1995, 5, 679–688. [Google Scholar] [CrossRef]
- Becker, J.; Hald, P.; Bremholm, M.; Pedersen, J.S.; Bo, B.I.J.A.N. Critical Size of Crystalline ZrO2 Nanoparticles Synthesized in Near- and Supercritical Water and Supercritical Isopropyl Alcohol. ACS Nano 2008, 2, 1058–1068. [Google Scholar] [CrossRef] [PubMed]
- Masoodiyeh, F.; Mozdianfard, M.R.; Karimi-Sabet, J. Modeling zirconia nanoparticles prepared by supercritical water hydrothermal synthesis using population balance equation. Powder Technol. 2017, 317, 264–274. [Google Scholar] [CrossRef]
- Liu, L.; Wang, S.; Zhang, B.; Jiang, G.; Yang, J.; Li, Y.; Liu, W.; Wang, J.; Kong, W. From modification to mechanism: Supercritical hydrothermal synthesis of nano-zirconia. Ceram. Int. 2022, 48, 4401–4423. [Google Scholar] [CrossRef]
- Li, Q.Y.; Wang, X.Z. Population Balance and CFD Simulation of Particle Aggregation and Growth in a Continuous Confined Jet Mixer for Hydrothermal Synthesis of Nanocrystals. Crystals 2021, 11, 144. [Google Scholar] [CrossRef]
- Adschiri, T.; Kanazawa, K.; Arai, K. Rapid and Continuous Hydrothermal Crystallization of Metal Oxide Particles in Supercritical Water. J. Am. Ceram. Soc. 1992, 75, 1019–1022. [Google Scholar] [CrossRef]
- Alonso, E.; Montequi, I.; Lucas, S.; Cocero, M.J. Synthesis of titanium oxide particles in supercritical CO2: Effect of operational variables in the characteristics of the final product. J. Supercrit. Fluids 2007, 39, 453–461. [Google Scholar] [CrossRef]
- Wagner, W.; Pruß, A. The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use. J. Phys. Chem. Ref. Data 2002, 31, 387–535. [Google Scholar] [CrossRef]
- Zhang, D.; Deen, N.G.; Kuipers, J.A.M. Euler−Euler Modeling of Flow, Mass Transfer, and Chemical Reaction in a Bubble Column. Ind. Eng. Chem. Res. 2008, 48, 47–57. [Google Scholar] [CrossRef]
- Pan, H.; Liang, X.-F.; Luo, Z.-H. CFD modeling of the gas–solid two-fluid flow in polyethylene FBRs: From traditional operation to super-condensed mode. Adv. Powder Technol. 2016, 27, 1494–1505. [Google Scholar] [CrossRef]
- Launder, B.; Reece, G.; Rodi, W. Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 1975, 68, 537–566. [Google Scholar] [CrossRef]
- Tompson, R.V.; Loyalka, S.K. Chapman–Enskog solution for diffusion: Pidduck’s equation for arbitrary mass ratio. Phys. Fluids 1987, 30, 2073–2075. [Google Scholar] [CrossRef]
- Stolzenburg, P.; Garnweitner, G. Experimental and numerical insights into the formation of zirconia nanoparticles: A population balance model for the nonaqueous synthesis. React. Chem. Eng. 2017, 2, 337–348. [Google Scholar] [CrossRef]
- Testino, A.; Buscaglia, V.; Buscaglia, M.T.; Viviani, M.; Nanni, P. Kinetic Modeling of Aqueous and Hydrothermal Synthesis of Barium Titanate (BaTiO3). Chem. Mater. 2005, 17, 5346–5356. [Google Scholar] [CrossRef]
- Wu, M.K.; Friedlander, S.K. Enhanced power law agglomerate growth in the free molecule regime. J. Aerosol Sci. 1993, 24, 273–282. [Google Scholar] [CrossRef]
- Peukert, W.; Schwarzer, H.-C.; Stenger, F. Control of aggregation in production and handling of nanoparticles. Chem. Eng. Process. Process. Intensif. 2005, 44, 245–252. [Google Scholar] [CrossRef]
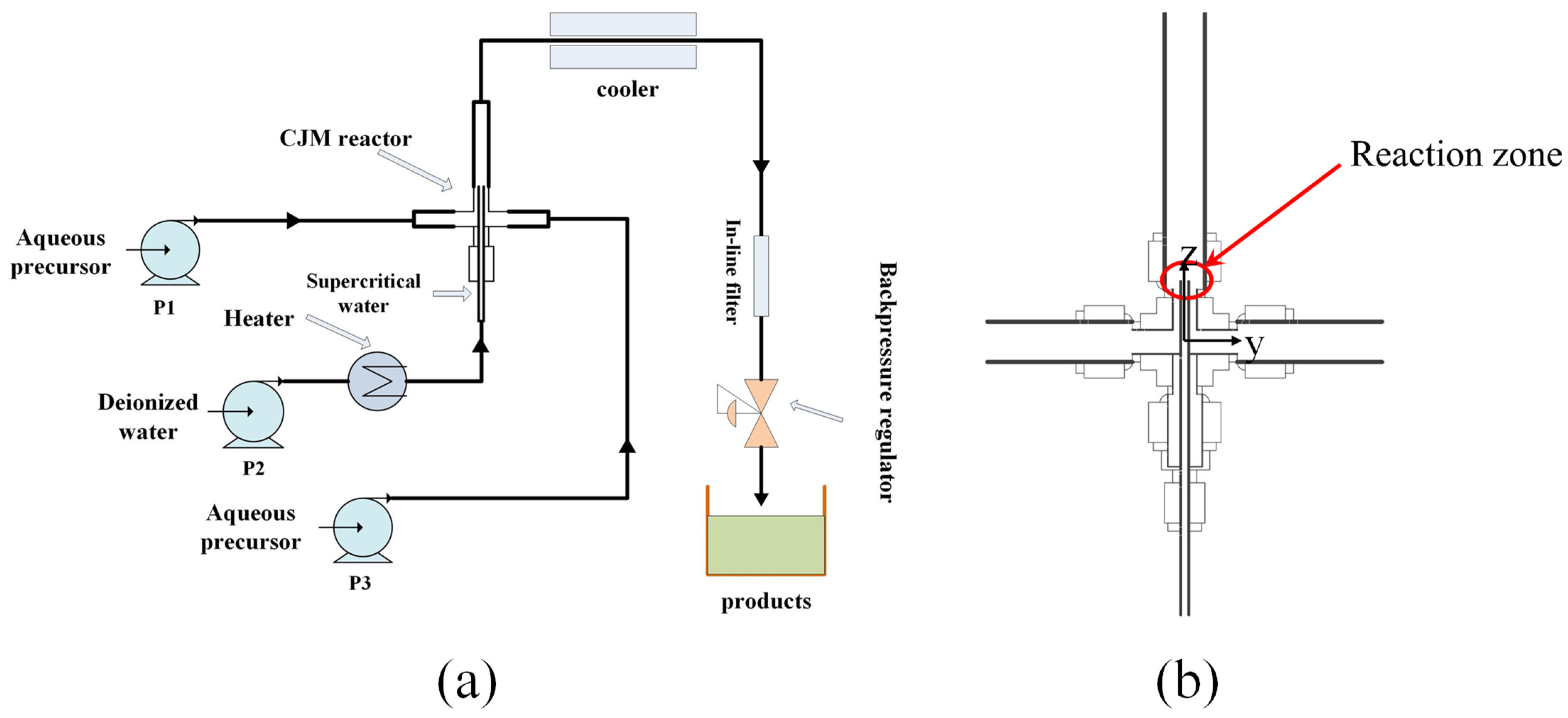


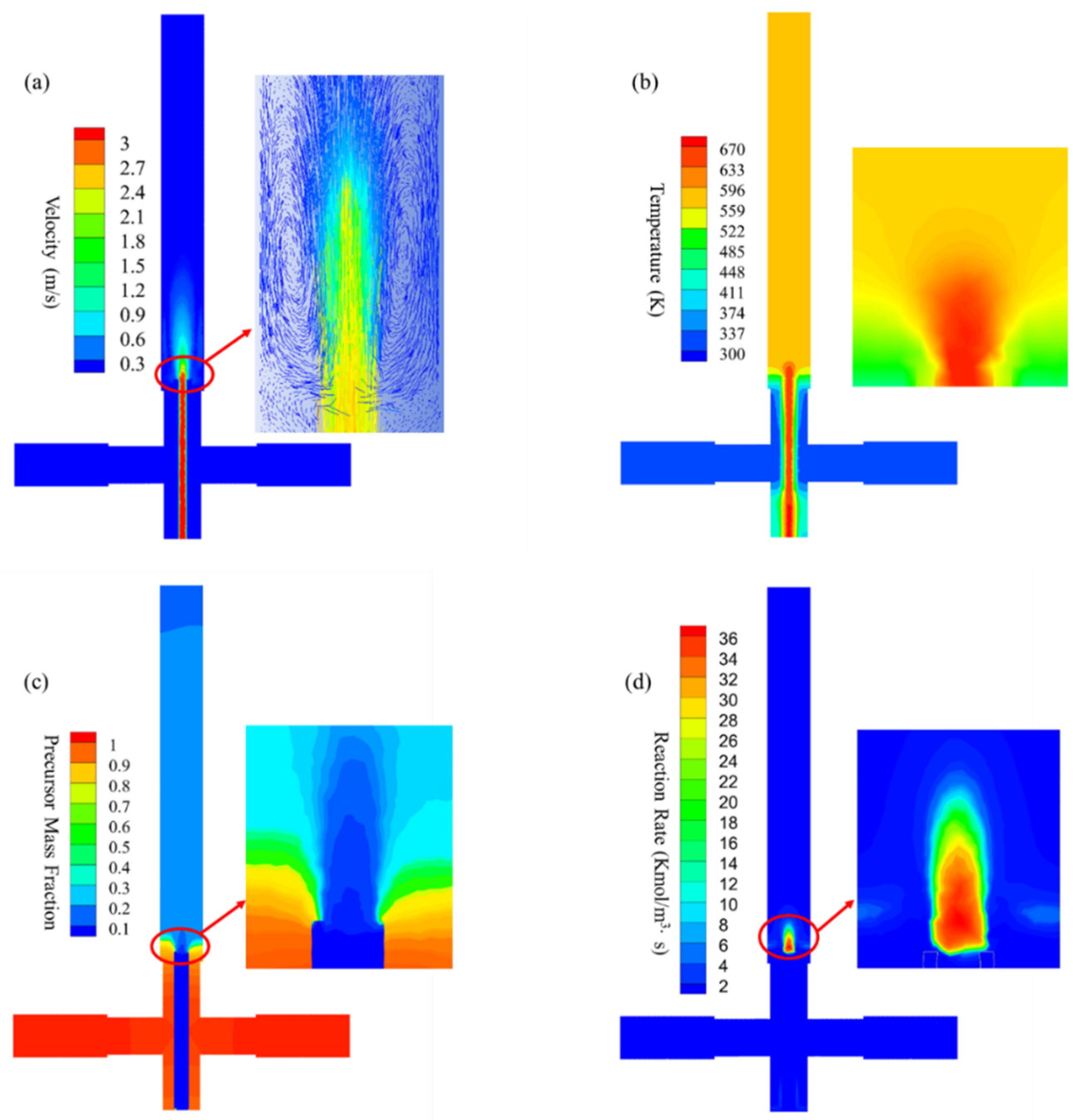

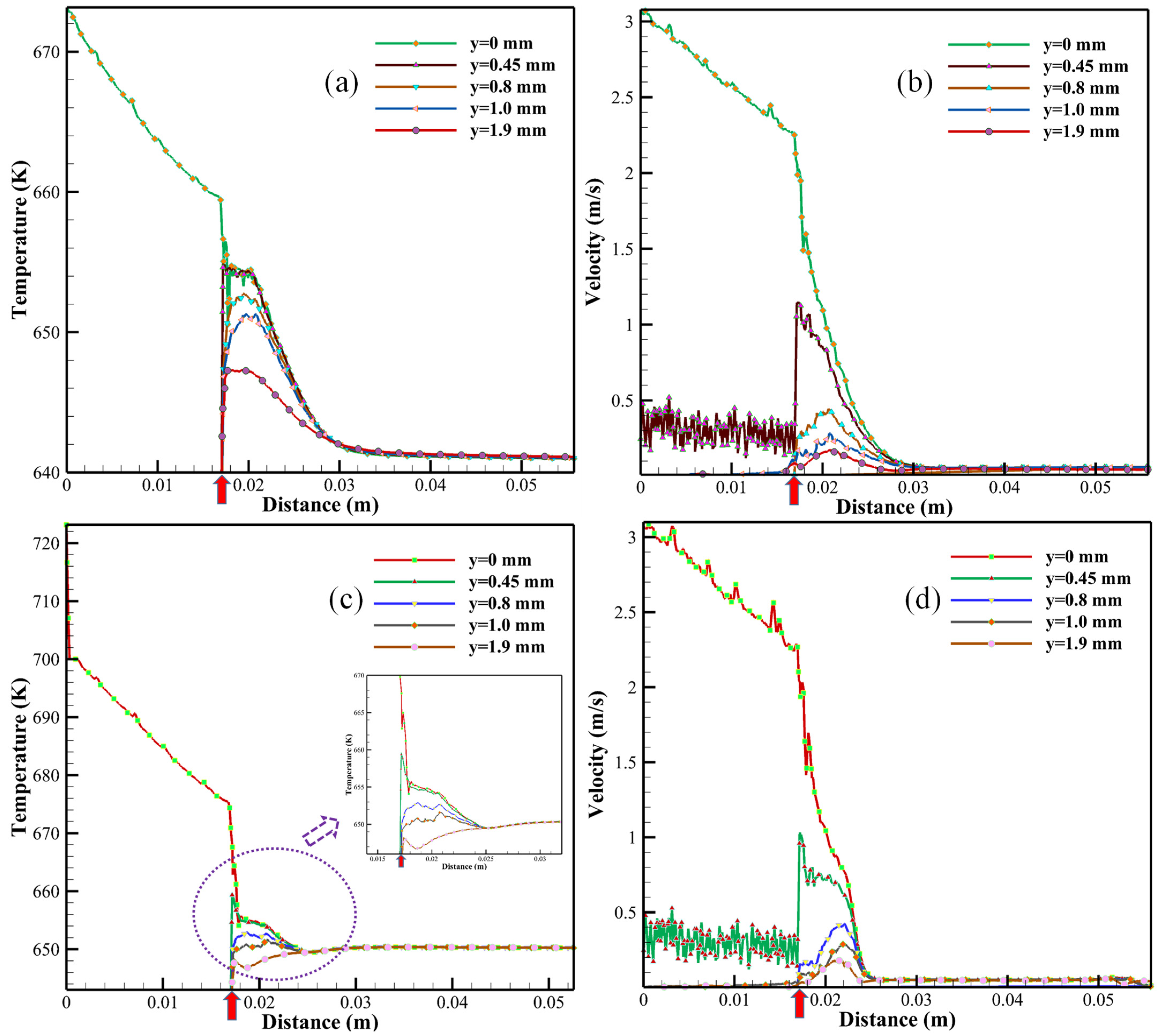
| Samples | Precursors | Flow Rate (mL/min) | SCW Temperature (K) |
|---|---|---|---|
| Case 1 | ZrOCl2 | 5 | 673 |
| Case 2 | ZrOCl2 | 5 | 723 |
| Case 3 | ZrO(NO3)2 | 5 | 673 |
| Case 4 | ZrO(NO3)2 | 5 | 723 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Wang, Z.; Wang, X. CFD–PBM Simulation for Continuous Hydrothermal Flow Synthesis of Zirconia Nanoparticles in a Confined Impinging Jet Reactor. Materials 2023, 16, 3421. https://doi.org/10.3390/ma16093421
Li Q, Wang Z, Wang X. CFD–PBM Simulation for Continuous Hydrothermal Flow Synthesis of Zirconia Nanoparticles in a Confined Impinging Jet Reactor. Materials. 2023; 16(9):3421. https://doi.org/10.3390/ma16093421
Chicago/Turabian StyleLi, Qingyun, Zihua Wang, and Xuezhong Wang. 2023. "CFD–PBM Simulation for Continuous Hydrothermal Flow Synthesis of Zirconia Nanoparticles in a Confined Impinging Jet Reactor" Materials 16, no. 9: 3421. https://doi.org/10.3390/ma16093421
APA StyleLi, Q., Wang, Z., & Wang, X. (2023). CFD–PBM Simulation for Continuous Hydrothermal Flow Synthesis of Zirconia Nanoparticles in a Confined Impinging Jet Reactor. Materials, 16(9), 3421. https://doi.org/10.3390/ma16093421





