Modeling and Model Verification of the Stress-Strain State of Reinforced Polymer Concrete
Abstract
1. Introduction
- to carry out an analysis of force-resistance studies of polymer concrete and reinforced concrete beams;
- to evaluate the physical conditions of polymer concrete structures based on rubber additives;
- to conduct experimental studies of the stress-strain state and strength and deflections of ACRP beams;
- to reveal the peculiarities of failure of ACRP beams by their cross-sections;
- to reveal the peculiarities of the formation of the failure of ACRP beams;
- to reveal the peculiarities of the development of deflections of ACRP beams.
2. Methods and Materials
2.1. Rationale for the Material Choice
2.2. Calculation of Polymer Concrete Structures
- normal stresses, corresponding in shape to the diagram of mechanical tests for axial compression and tension of polymer concrete;
- the hypothesis of planar sections [16].
- Three equations were made by the authors to obtain calculation formulas:
- moments of forces equilibrium;
- projections of forces on the neutral plane equilibrium;
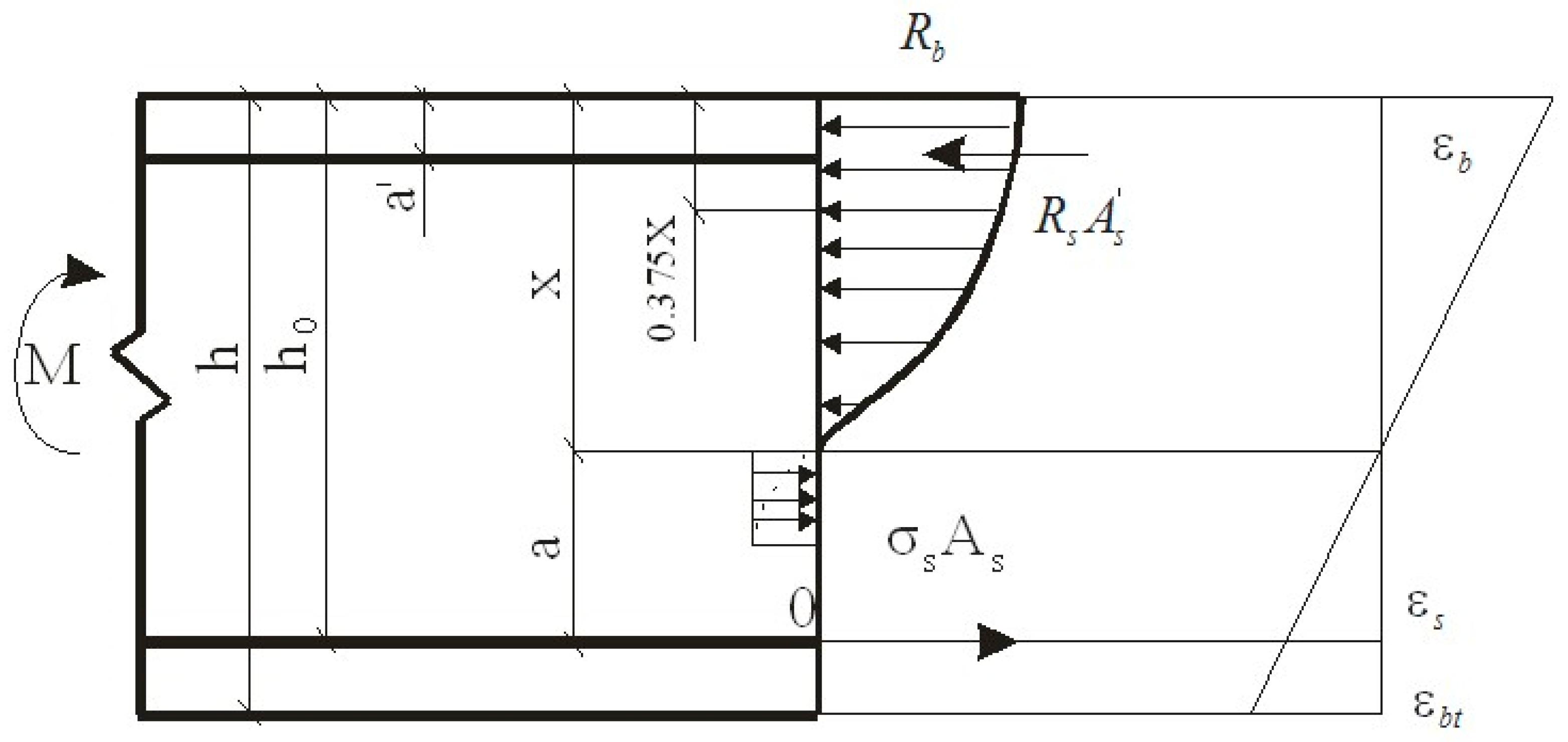
- equations of a ratio of boundary deformations or heights of compressed and stretched zones of the element cross-section. The scheme of forces and the stress diagram in the cross-section normal to the longitudinal axis of the bendable polymer concrete element, when calculating its strength, is shown in Figure 1.
2.3. Experimental Design and Research Program
- the percentage of the longitudinal gain that has the greatest effect on the resistance of the normal part bending element;
- the height of the dispersion reinforcement zone (measured from the bottom edge) with the same percentage of fiber reinforcement over the volume of the reinforced part (µv = 1%, according to composition optimization [22]).
2.4. Materials
- Cis-polybutadiene low molecular weight CBLMW-R rubber (ISO 6743/4). CBLMW-R rubber has a density of 910 kg/m3 and a dynamic viscosity of up to 12 Pa × s;
- fine-dispersed filler being ash of a specific surface of 2500...2700 cm2/g, having the following composition by mass in %: Al O23—16.5–22.5; CaO was 5.5–5.5; Fe O23 was 13.5–15.5; SiO2 was 47–55; MgO was 2–3; K2 O was 1–2; Na2 O was 1; S O23 was 0.4–0.3; others were 6–15;
- vulcanization activator was zinc oxide ZnO (ISO 10262-2016) white powder having a density of 5600–5700 kg/m3;
- vulcanization gas pedal was tetramethyl thiuram disulfide (Tiuram-D) (ISO 4097 2013) being powder of gray-white color and density of 1300–1400 kg/m3;
- calcium oxide CaO was a white powder having a density of 2500–2900 kg/m3;
- Portland cement. It consists of the following ingredients: clinker (calcium silicates); gypsum; plasticizing, hydrophobic, acid-resistant additives; domain fee. The chemical composition of cement: 21.55% silicon oxide and 65.91% calcium oxide. Portland cement is the most durable and high quality, therefore it is widely distributed on the market. It is a cement that is capable of showing an average compressive strength of about 500 kg/m3 after 28 days of preparation. The mixture can be without additives or with various substances introduced into the composition in a certain proportion. The compressive load is 2500 kg/cm. Frost resistance is more than 100 cycles. The bulk density is 1100–1600 kg/m. True density kg/m3 3100. The setting speed is from 45 min to 10 h. The average weight of Portland cement is 3 tons/m3;
- sulfur technical (ISO 3704-76) is a bright yellow powder with a concentration of 2070 kg/m3, having a melting point of 114 °C;
- metal fibers made from scraps of metal cord by sawing. The fibers obtained in this way are wave-shaped fibers at a ratio of a length to a wire diameter of 1/100;
- reinforcing steel bars having a diameter of 8, 10, 12, 14, 16, and 18 mm and a steel wire of a diameter of 5 mm.
2.5. Mechanical Tests
2.6. Sample Production Technology
- washing the fine and coarse aggregate;
- preparation of curing group components and fibers;
- dosage of ingredients;
- drying of the components;
- mixing of the components.
2.7. Test Methods, Basic Instruments and Equipment
3. Discussion
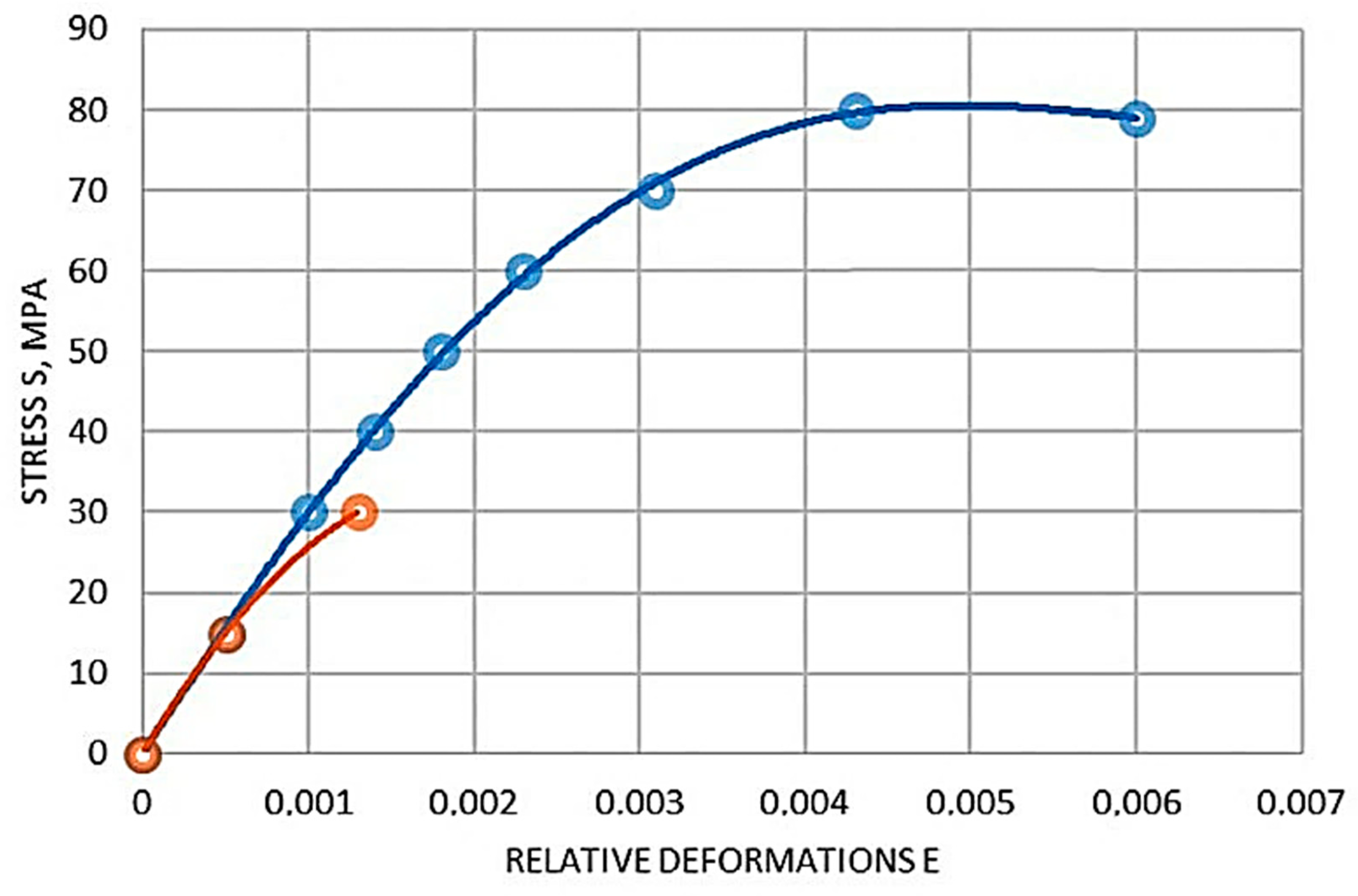
3.1. Results of Experimental Studies of Intensity (Construction of a Material Deformation Diagram “σ-ε”)
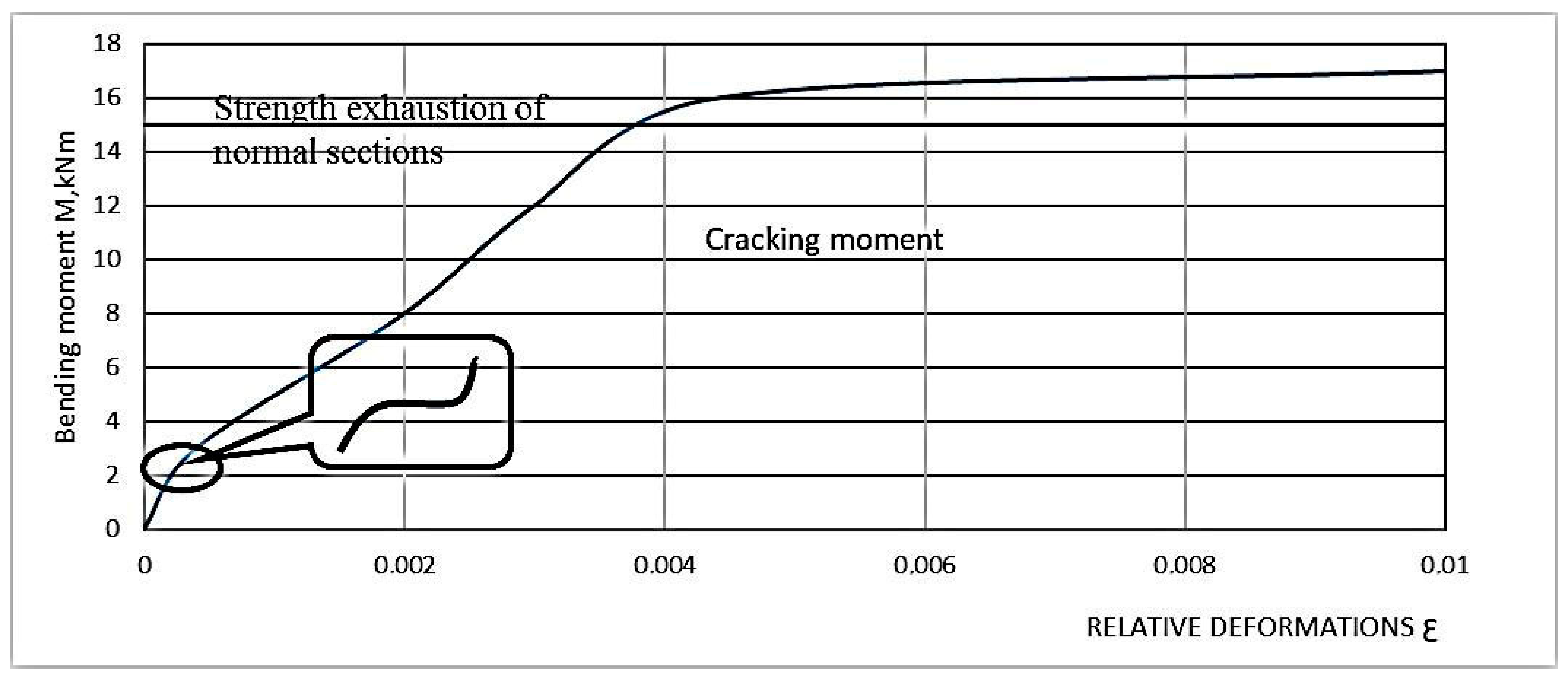
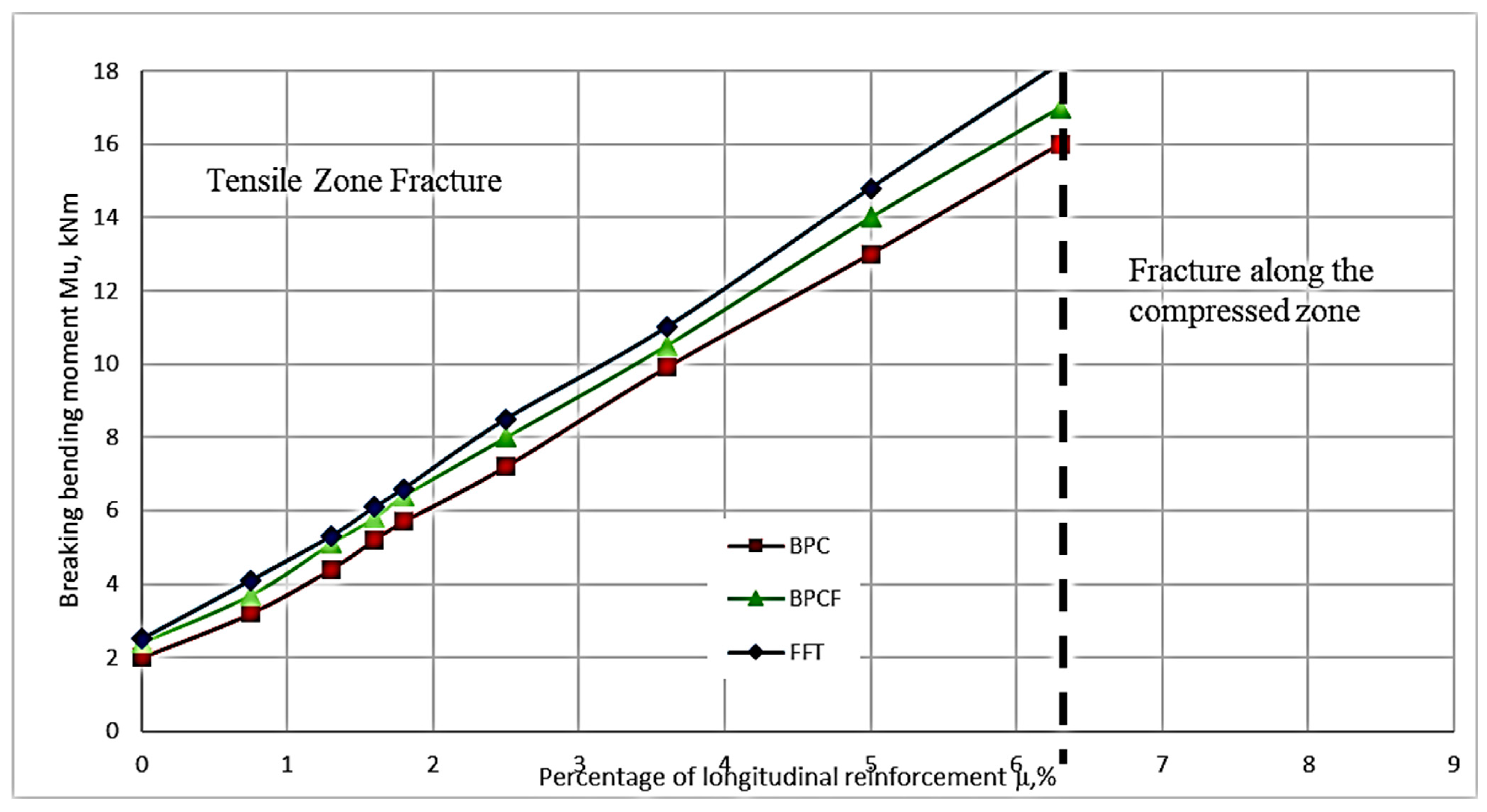
3.2. Strength of Normal Sections
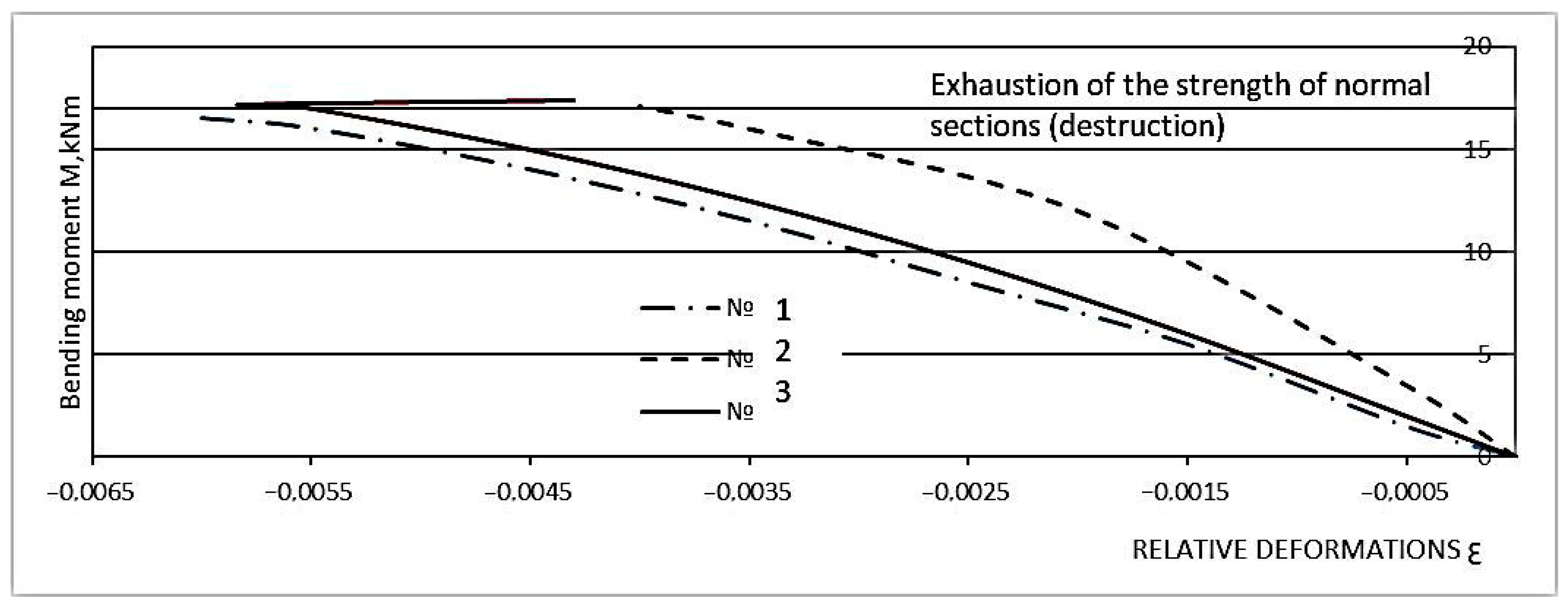
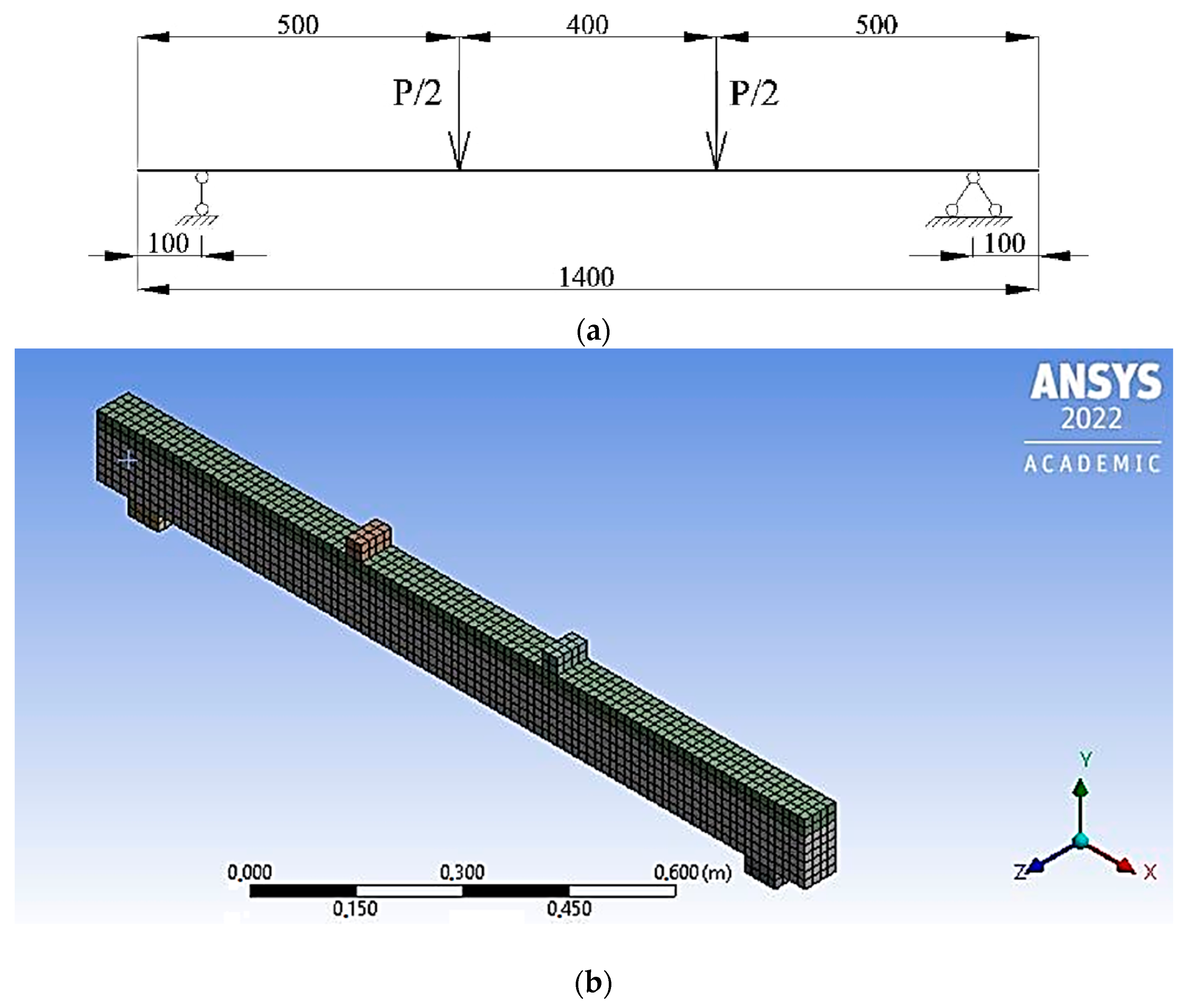
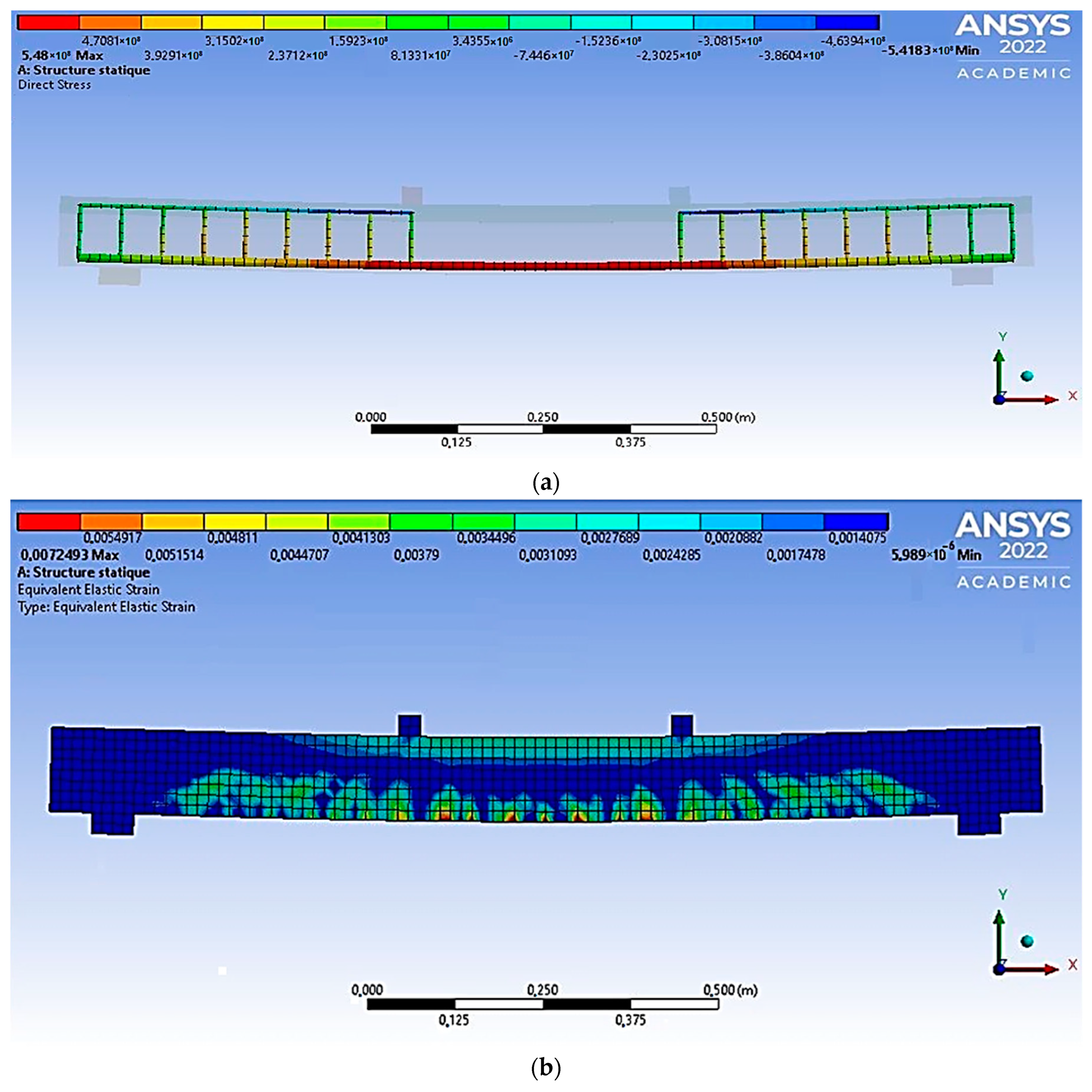
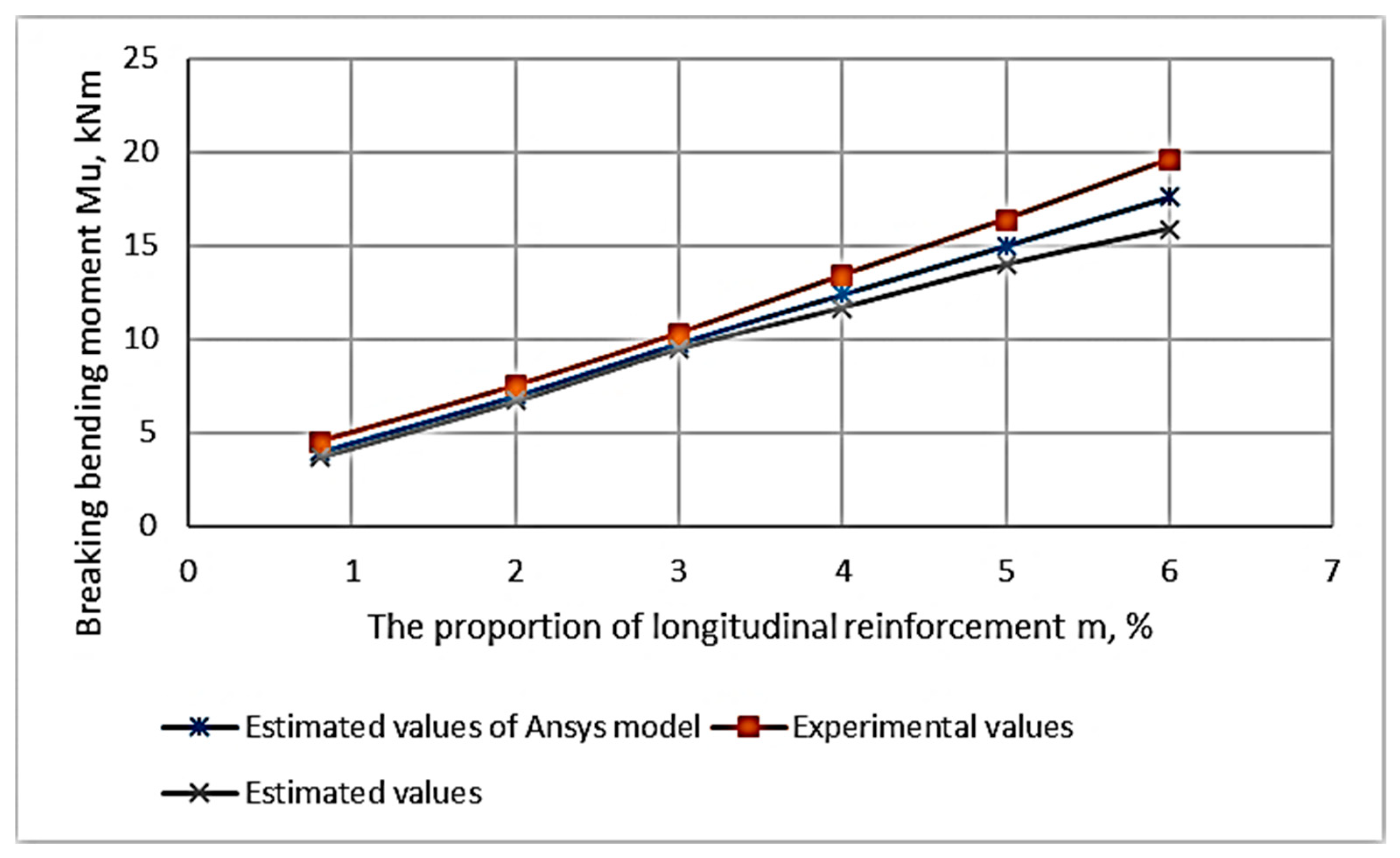
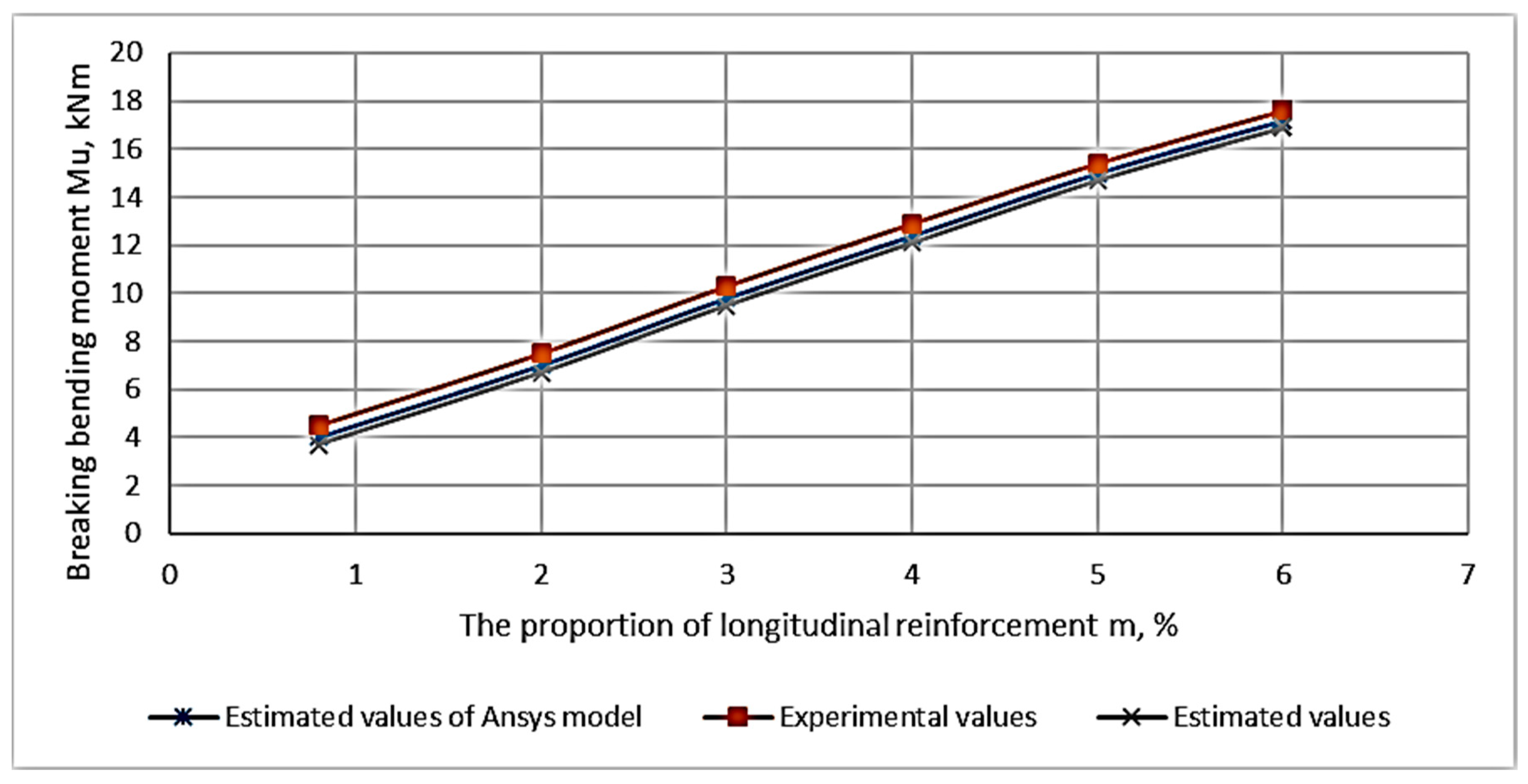
3.3. Finite Element Model of Beams Made of Polymer Concrete on a Rubber Binder Implemented in the Ansys Environment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Results of Experimental Investigations for Breaking Bending Moments of Beam Samples
Appendix A.1. Results of Experimental Investigations for Breaking Bending Moments of Beam Samples
| Girder Type | Percentage of Longitudinal of Reinforcement µ, % | Fibre Layer Height Reinforcement hf, mm | Destruction Zone | Destructive Bending Mu Moment, kNm |
|---|---|---|---|---|
| FPC 001 | 0.00 | 125 | Stretched | 2.4 |
| FPC 002 | 0.80 | 125 | Stretched | 3.67 |
| FPC 003 | 1.25 | 125 | Stretched | 5.21 |
| FPC 004 | 1.60 | 125 | Stretched | 6.28 |
| FPC 005 | 1.80 | 125 | Stretched | 6.68 |
| FPC 006 | 2.5 | 125 | Stretched | 8.75 |
| FPC 007 | 3.55 | 125 | Stretched | 11.31 |
| FPC 008 | 4.95 | 125 | Stretched | 15.09 |
| FPC 009 | 6.3 | 125 | Stretched | 17.48 |
| FPC 010 | 8.4 | 125 | Compressed | 16.69 |
| FPC 011 | 0.00 | 95 | Stretched | 2.28 |
| FPC 012 | 0.80 | 95 | Stretched | 3.71 |
| FPC 013 | 1.80 | 95 | Stretched | 6.29 |
| FPC 014 | 3.55 | 95 | Stretched | 10.92 |
| FPC 015 | 4.95 | 95 | Stretched | 14.78 |
| FPC 016 | 6.4 | 95 | Compressed | 16.39 |
| PC 001 | 0.00 | 0 | Stretched | 1.88 |
| PC 002 | 0.80 | 0 | Stretched | 3.02 |
| PC 003 | 1.25 | 0 | Stretched | 4.31 |
| PC 004 | 1.80 | 0 | Stretched | 5.92 |
| PC 005 | 2.5 | 0 | Stretched | 7.91 |
| PC 006 | 3.55 | 0 | Stretched | 10.29 |
| PC 007 | 4.95 | 0 | Stretched | 14.11 |
| PC 008 | 6.3 | 0 | Stretched | 15.41 |
| PC 009 | 8.4 | 0 | Compressed | 15.91 |
Appendix A.2. Experimental Results for Breaking Bending Moments of Beam Samples
| Girder Code | µ, % | Mut, KnM | Mue, KnM | Mum, KnM | ∆Mum, % | ∆Mut, % |
|---|---|---|---|---|---|---|
| PC 001 | 0.8 | 2.51 | 2.96 | 2.6 | −14.0 | −18.0 |
| PC 002 | 1.25 | 4.02 | 4.28 | 4.2 | −1.9 | −6.5 |
| PC 003 | 1.8 | 5.82 | 5.8 | 6.0 | 3.3 | 0.3 |
| PC 004 | 2.5 | 7.92 | 7.82 | 8.0 | 2.3 | 1.3 |
| PC 005 | 3.6 | 10.86 | 10.3 | 11.2 | 8.0 | 5.2 |
| PC 006 | 4.95 | 14.47 | 14.0 | 15.2 | 7.9 | 3.2 |
| PC 007 | 6.3 | 14.96 | 15.32 | 16.8 | 8.8 | −2.4 |
| FPC 001 | 0.8 | 4.00 | 3.78 | 3.52 | −7.4 | 5.5 |
| FPC 002 | 1.25 | 5.52 | 5.10 | 5.16 | 1.2 | 7.6 |
| FPC 003 | 1.8 | 7.39 | 6.77 | 6.8 | 0.4 | 8.4 |
| FPC 004 | 2.5 | 9.85 | 8.77 | 8.8 | 0.3 | 10.9 |
| FPC 005 | 3.6 | 12.63 | 11.28 | 12.0 | 6.0 | 10.7 |
| FPC 006 | 4.95 | 16.64 | 15.10 | 15.4 | 1.9 | 9.3 |
| FPC 007 | 6.3 | 17.49 | 17.52 | 17.72 | 1.1 | −0.2 |
References
- Jun, Z.; Xiang-Ming, W.; Jian-Min, C.; Kai, Z. Optimization of processing variables in wood-rubber composite panel manufacturing technology. Bioresour. Technol. 2008, 99, 2384–2391. [Google Scholar] [CrossRef] [PubMed]
- Jafari, K.; Toufigh, V. Experimental and analytical evaluation of rubberized polymer concrete. Constr. Build. Mater. 2017, 155, 495–510. [Google Scholar] [CrossRef]
- Siddique, R.; Naik, T.R. Properties of concrete containing scrap-tire rubber-an overview. Waste Manag. 2004, 24, 563–569. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, B.; De, D.; Maiti, S. Reclamation and recycling of waste rubber. Prog. Polym. Sci. 2000, 25, 909–948. [Google Scholar] [CrossRef]
- Fang, Y.; Zhan, M.; Wang, Y. The status of recycling of waste rubber. Mater. Des. 2001, 22, 123–127. [Google Scholar] [CrossRef]
- Issa, C.A.; Salem, G. Utilization of recycled crumb rubber as fine aggregates in concrete mix design. Constr. Build. Mater. 2013, 42, 48–52. [Google Scholar] [CrossRef]
- Hassani, A.; Ganjidoust, H.; Maghanaki, A.A. Use of plastic waste (poly-ethylene terephthalate) in asphalt concrete mixture as aggregate replacement. Waste Manag. Res. 2005, 23, 322–327. [Google Scholar] [CrossRef]
- Isametova, M.E.; Nussipali, R.; Martyushev, N.V.; Malozyomov, B.V.; Efremenkov, E.A.; Isametov, A. Mathe-matical Modeling of the Reliability of Polymer Composite Materials. Mathematics 2022, 10, 3978. [Google Scholar] [CrossRef]
- Busuyi, A.T. Cost evaluation of producing different aggregate sizes in selected quarries in ondo state nigeria. Int. J. Eng. Adv. Technol. Stud. 2016, 4, 6–19. [Google Scholar]
- Tepordei, V.V. Natural Aggregates-Foundation of America’s Future (No. 144-97); US Geological Survey: Reston, VA, USA, 1997.
- Borja, R.; Sanchez, E.; Martin, A.; Jimenez, A.M. Kinetic behavior of waste tyre rubber as microorganism support in an anaerobic digester treating cane molasses distillery slops. Bioprocess. Eng. 1996, 16, 17–23. [Google Scholar] [CrossRef]
- Toutanji, H.A. The use of rubber tire particles in concrete to replace mineral aggregates. Cem. Concr. Compos. 1996, 18, 135–139. [Google Scholar] [CrossRef]
- Collins, K.; Jensen, A.; Mallinson, J.; Roenelle, V.; Smith, I. Environmental impact assessment of scrap tyre artificial reef. ICES J. Mar. Sci. 2002, 59, 243–249. [Google Scholar] [CrossRef]
- Eldin, N.N.; Senouci, A.B. Rubber-tire particles as concrete aggregate. J. Mater. Civil Eng. 1993, 5, 478–496. [Google Scholar] [CrossRef]
- Khatib, Z.K.; Bayomy, F.M. Rubberized portland cement concrete. J. Mater. Civil Eng. 1999, 11, 206–213. [Google Scholar] [CrossRef]
- Gong, Y.; Yang, J.; He, X.; Lyu, X.; Liu, H. Structural Design Calculation of Basalt Fiber Polymer-Modified RPC Beams Subjected to Four-Point Bending. Polymers 2021, 13, 3261. [Google Scholar] [CrossRef]
- Topcu, I.B. The properties of rubberized concretes. Cem. Concr. Res 1995, 25, 304–310. [Google Scholar] [CrossRef]
- Topcu, I.B.; Avcular, N. Collision behaviors of rubberized concrete. Cem. Concr. Res. 1997, 27, 1893–1898. [Google Scholar] [CrossRef]
- Zheng, L.; Huo, X.; Yuan, Y. Experimental investigation on dynamic properties of rubberized concrete. Constr. Mater. 2008, 22, 939–947. [Google Scholar] [CrossRef]
- Khaloo, A.R.; Dehestani, M.; Rahmatabadi, P. Mechanical properties of concrete containing a high volume of tire-rubber particles. Waste Manag. 2008, 28, 2472–2482. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, B.S.; Azmi, N.J. Strength reduction factors for structural rubbercrete. Front. Struct. Civil Eng. 2014, 8, 270–281. [Google Scholar]
- Bravo, M.; de Brito, J. Concrete made with used tyre aggregate: Durability- related performance. J. Clean. Prod. 2012, 25, 42–50. [Google Scholar] [CrossRef]
- Al-Tayeb, M.M.; Bakar, B.A.; Ismail, H.; Akil, H.M. Effect of partial replacement of sand by recycled fine crumb rubber on the performance of hybrid rubberized- normal concrete under impact load: Experiment and simulation. J. Clean. Prod. 2013, 59, 284–289. [Google Scholar] [CrossRef]
- Bedi, R.; Chandra, R. Reviewing some properties of polymer concrete. Indian Concr. J. 2014, 88, 47–68. [Google Scholar]
- Barbuta, M.; Diaconu, D.; Serbanoiu, A.A.; Burlacu, A.; Timu, A.; Gradinaru, C.M. Effects of tire wastes on the mechanical properties of concrete. Proc. Eng. 2017, 181, 346–350. [Google Scholar] [CrossRef]
- Bedi, R.; Chandra, R.; Singh, S.P. Mechanical properties of polymer concrete. J. Compos. 2013, 2013, 948745. [Google Scholar] [CrossRef]
- El-Hawary, M.M.; Abdul-Jaleel, A. Durability assessment of epoxy modified concrete. Constr. Build. Mater. 2010, 24, 1523–1528. [Google Scholar]
- Bai, W.; Zhang, J.; Yan, P.; Wang, X. Study on vibration alleviating properties of glass fiber reinforced polymer concrete through orthogonal tests. Mater. Des. 2009, 30, 1417–1421. [Google Scholar] [CrossRef]
- Reis, J.M.L.; Ferreira, A.J.M. The effects of atmospheric exposure on the fracture properties of polymer concrete. Build. Environ. 2006, 41, 262–267. [Google Scholar] [CrossRef]
- Bruni, C.; Forcellese, A.; Gabrielli, F.; Simoncini, M. Hard turning of an alloy steel on a machine tool with a polymer concrete bed. J. Mater. Proc. Technol. 2008, 202, 493–499. [Google Scholar] [CrossRef]
- Orak, S. Investigation of vibration damping on polymer concrete with polyester resin. Cem. Concr. Res. 2000, 30, 171–174. [Google Scholar] [CrossRef]
- Gupta, K.; Mani, P.; Krishnamoorthy, S. Interfacial adhesion in polyester resin concrete. Int. J. Adhes. Adhes. 1983, 3, 149–154. [Google Scholar] [CrossRef]
- Rebeiz, K.S. Precast use of polymer concrete using unsaturated polyester resin based on recycled PET waste. Const. Build. Mater. 1996, 10, 215–220. [Google Scholar] [CrossRef]
- Bulut, H.A.; Sahin, R. A Study on mechanical properties of polymer concrete containing electronic plastic waste. Compos. Struct. 2017, 178, 50–62. [Google Scholar] [CrossRef]
- Kim, H.S.; Park, K.Y.; Lee, D.G. A study on the epoxy resin concrete for the ultraprecision machine tool bed. J. Mater. Proc. Technol. 1995, 48, 649–655. [Google Scholar] [CrossRef]
- Martyushev, N.V.; Malozyomov, B.V.; Khalikov, I.H.; Kukartsev, V.A.; Kukartsev, V.V.; Tynchenko, V.S.; Tynchenko, Y.A.; Qi, M. Review of Methods for Improving the Energy Efficiency of Electrified Ground Transport by Optimizing Battery Consumption. Energies 2023, 16, 729. [Google Scholar] [CrossRef]
- Chen, D.H.; Lin, H.H.; Sun, R. Field performance evaluations of partial-depth repairs. Constr. Build. Mater. 2011, 25, 1369–1378. [Google Scholar] [CrossRef]
- Chen, D.H.; Zhou, W.; Kun, L. Fiber reinforced polymer patching binder for concrete pavement rehabilitation and repair. Constr. Build. Mater. 2013, 48, 325–332. [Google Scholar] [CrossRef]
- Cortes, F.; Castillo, G. Comparison between the dynamical properties of polymer concrete and grey cast iron for machine tool applications. Mater. Des. 2007, 28, 1461–1466. [Google Scholar] [CrossRef]
- San-Jose, J.T.; Vegas, I.; Ferreira, A. Reinforced polymer concrete: Physical properties of the matrix and static/dynamic bond behavior. Cem. Concr. Compos. 2005, 27, 934–944. [Google Scholar] [CrossRef]
- Fowler, D.W. Future trends in polymer concrete. Spec. Publ. 1989, 116, 129–144. [Google Scholar]
- Rebeiz, K.S.; Serhal, S.P.; Fowler, D.W. Structural behavior of polymer concrete beams using recycled plastic. J. Mater. Civil Eng. 1994, 6, 150–165. [Google Scholar] [CrossRef]
- Kumar, R. A review on epoxy and polyester based polymer concrete and exploration of Polyfurfuryl Alcohol as polymer concrete. J. Polym. 2016, 13, 1–13. [Google Scholar] [CrossRef]
- Toufigh, V.; Shirkhorshidi, S.M.; Hosseinali, M. Experimental investigation and constitutive modeling of polymer concrete and sand interface. Int. J. Geomech. 2016, 17, 04016043. [Google Scholar] [CrossRef]
- Martyushev, N.V.; Malozyomov, B.V.; Sorokova, S.N.; Efremenkov, E.A.; Qi, M. Mathematical Modeling of the State of the Battery of Cargo Electric Vehicles. Mathematics 2023, 11, 536. [Google Scholar] [CrossRef]






| Properties | Indicators for Rubber Concrete Based on Rubber Grades | |
|---|---|---|
| Nitrile Butadiene Rubber (NBR) | Cis-Butadiene Low Molecular Weight Rubber (CBLMW-R) | |
| Compressive strength, MPa | 60–110 | 76.9–100.3 |
| Tensile strength, MPa | 8–20.0 | 13–18 |
| Modulus of elasticity, MPa | (2.0–3.5) ×104 | (1.5–1.8) × 104 |
| Compression duration factor | 0.77–0.78 | 0.72–0.76 |
| Poisson’s ratio | 0.18–0.35 | 0.2–0.3 |
| Heat resistance, °C | 90–100 | 100–110 |
| Freeze resistance, many cycles of a thawing and freezing process | 500 | 500 |
| Abrasibility, g/cm2 | 0.15–0.30 | 0.25–0.79 |
| Water suction, wt. % | 0.05 | 0.05 |
| Reduction, mm/m | 0.17–0.21 | - |
| Filler | Size of Fractions, mm | Bulk Density, g/cm3 | Raft Density, g/cm3 | Specific Surface Area, cm/g2 | Hollowness, % |
|---|---|---|---|---|---|
| Granite rubble | 5.00–10.00 | 1.50 | 2.67 | 5.4 | 41.4 |
| Quartz sand | 1.25–2.50 | 1.61 | 2.65 | 33.0 | 39.1 |
| 0.63–1.25 | |||||
| 0.32–0.63 |
| Name | Component Content, wt. % |
|---|---|
| Quartz sand | 24.2 |
| CBLMW-R low molecular weight rubber | 8.2 |
| Ashes | 7.8 |
| Sulfur technical | 4.0 |
| Zinc oxide | 1.2 |
| Tiuram-D | 0.4 |
| Metal cord fibers (fiber) | 2.5 |
| Calcium oxide | 0.4 |
| Granite rubble | The rest (51.3) |
| Girder Sample Code | Percentage of Longitudinal Reinforcement µ, % | Destruction Zone | Breaking Bending Moment Mu, kNm |
|---|---|---|---|
| PC 001 | 0.80 | Stretched | 2.23 |
| PC 002 | 1.25 | Stretched | 3.55 |
| PC 003 | 1.80 | Stretched | 4.99 |
| PC 004 | 3.55 | Compressed | 5.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yelemessov, K.; Sabirova, L.B.; Martyushev, N.V.; Malozyomov, B.V.; Bakhmagambetova, G.B.; Atanova, O.V. Modeling and Model Verification of the Stress-Strain State of Reinforced Polymer Concrete. Materials 2023, 16, 3494. https://doi.org/10.3390/ma16093494
Yelemessov K, Sabirova LB, Martyushev NV, Malozyomov BV, Bakhmagambetova GB, Atanova OV. Modeling and Model Verification of the Stress-Strain State of Reinforced Polymer Concrete. Materials. 2023; 16(9):3494. https://doi.org/10.3390/ma16093494
Chicago/Turabian StyleYelemessov, Kassym, Layla B. Sabirova, Nikita V. Martyushev, Boris V. Malozyomov, Gulnara B. Bakhmagambetova, and Olga V. Atanova. 2023. "Modeling and Model Verification of the Stress-Strain State of Reinforced Polymer Concrete" Materials 16, no. 9: 3494. https://doi.org/10.3390/ma16093494
APA StyleYelemessov, K., Sabirova, L. B., Martyushev, N. V., Malozyomov, B. V., Bakhmagambetova, G. B., & Atanova, O. V. (2023). Modeling and Model Verification of the Stress-Strain State of Reinforced Polymer Concrete. Materials, 16(9), 3494. https://doi.org/10.3390/ma16093494








