Optical Pump–Terahertz Probe Diagnostics of the Carrier Dynamics in Diamonds
Abstract
:1. Introduction
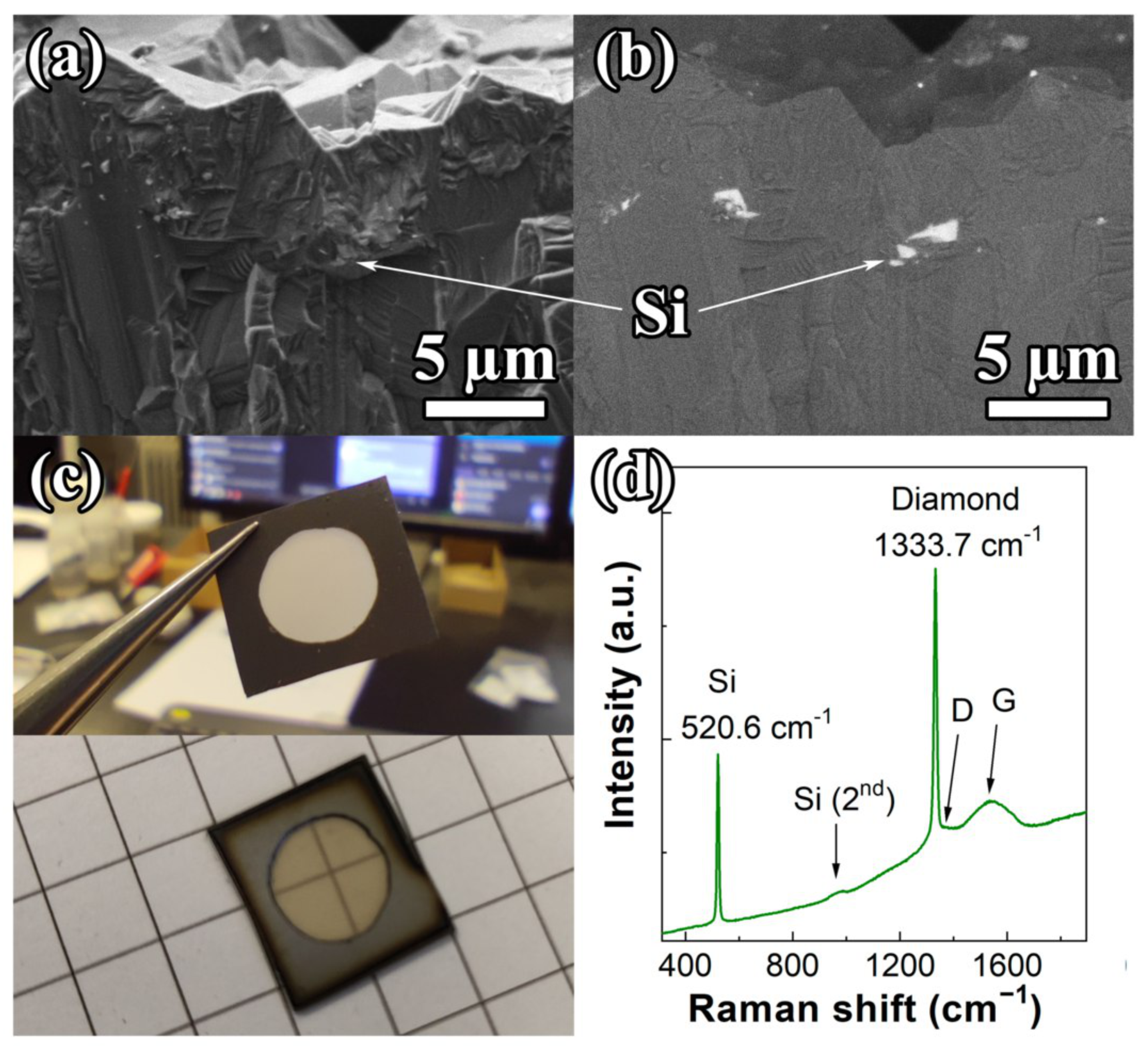
2. Materials and Methods
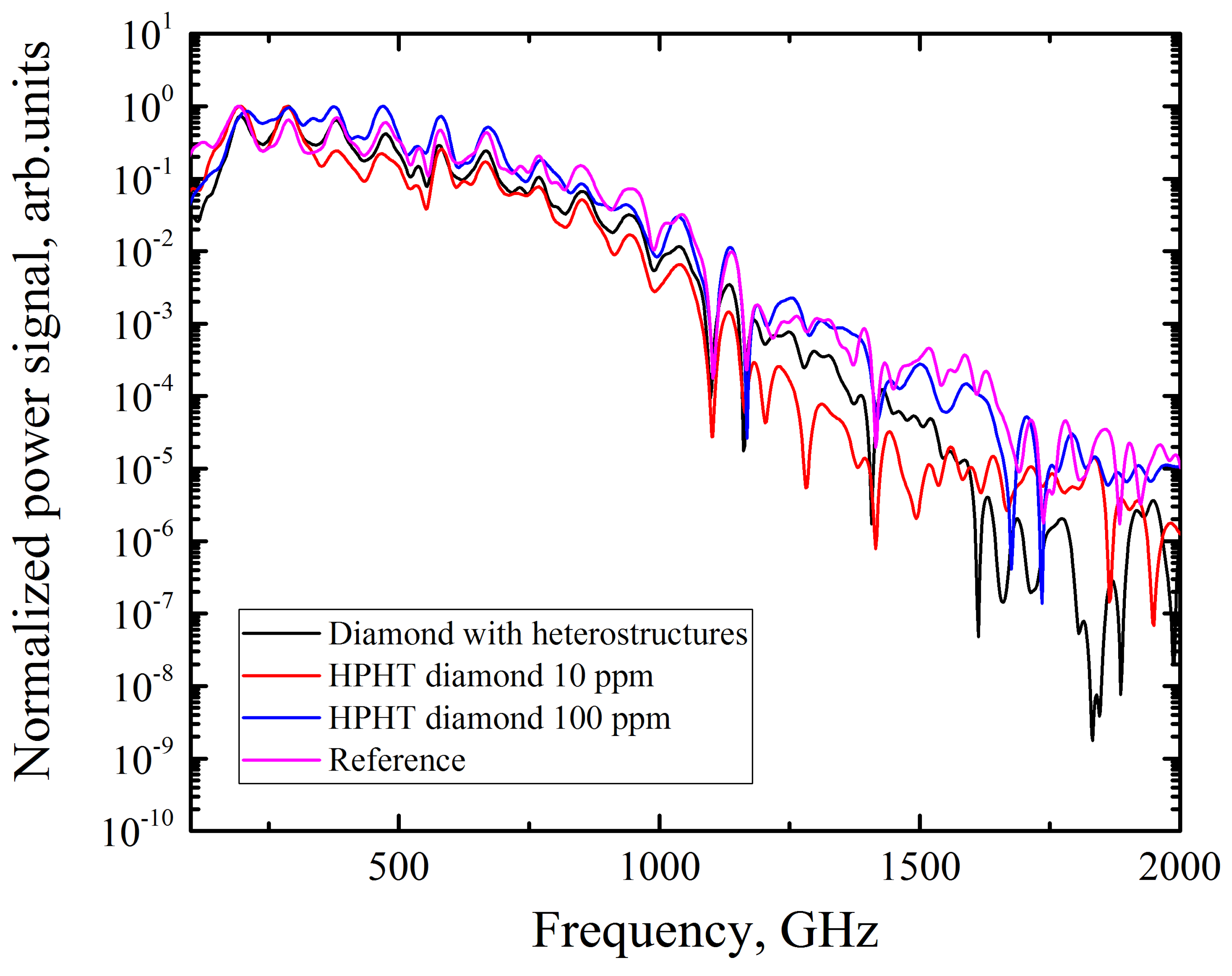
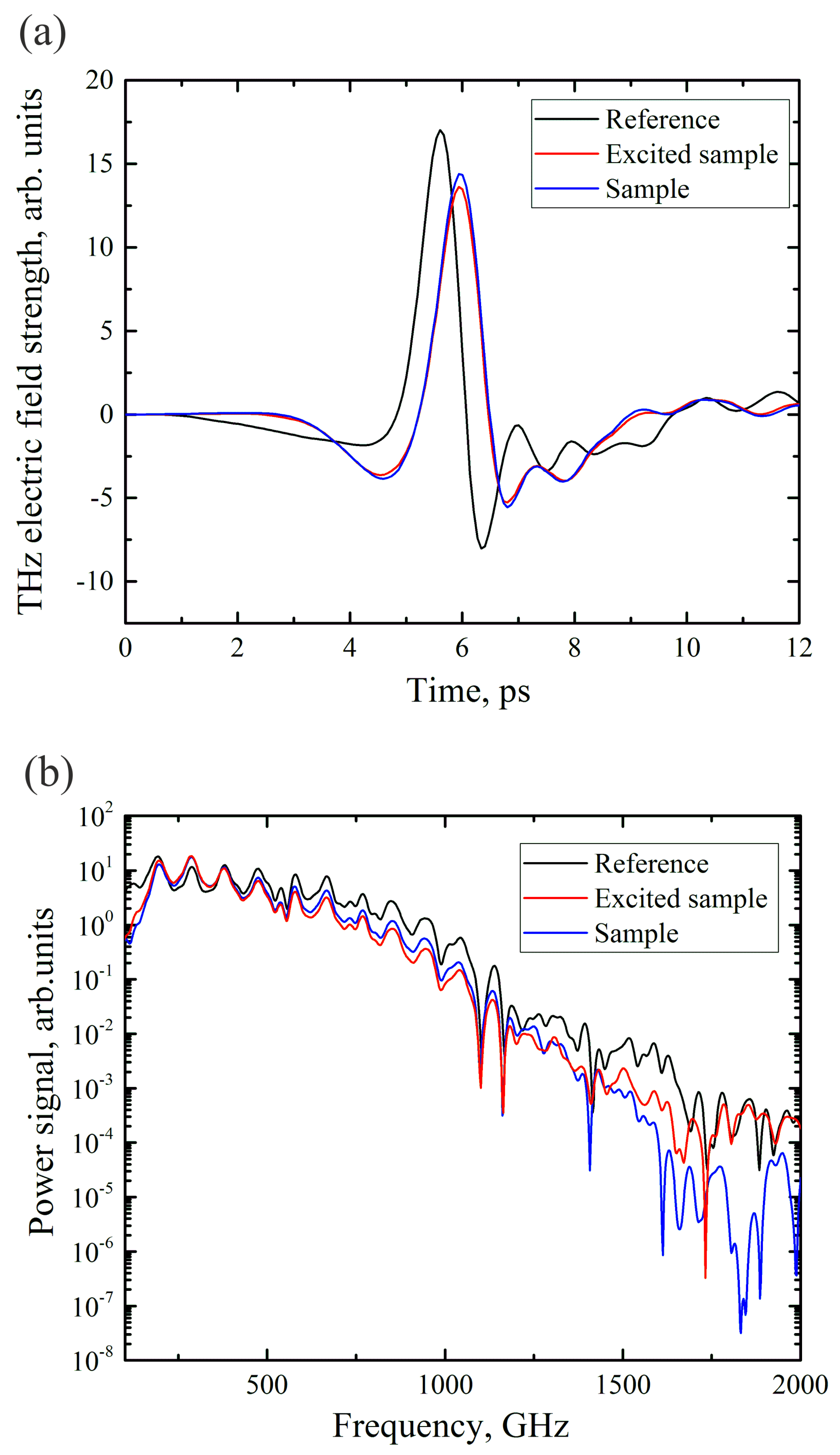
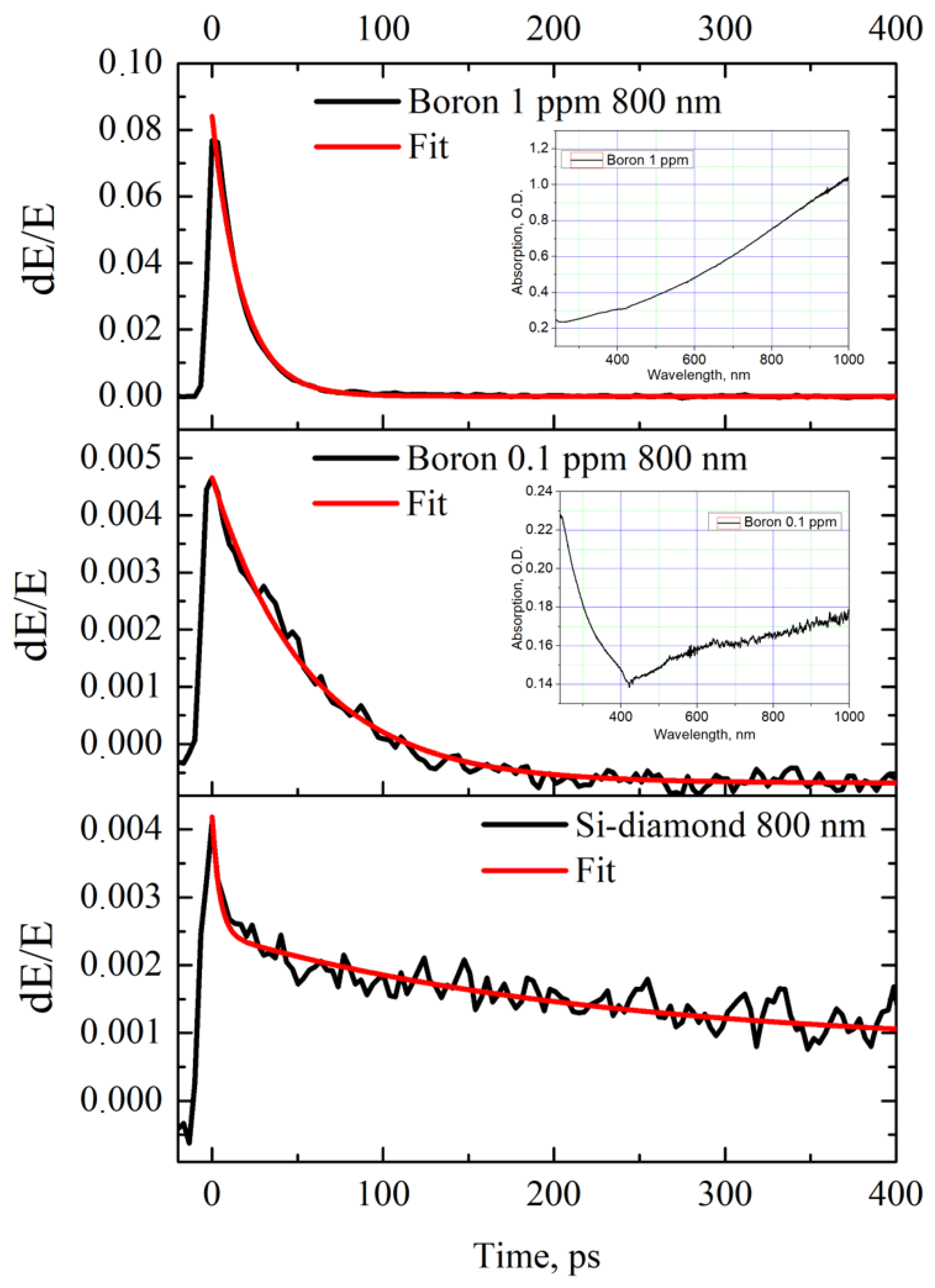
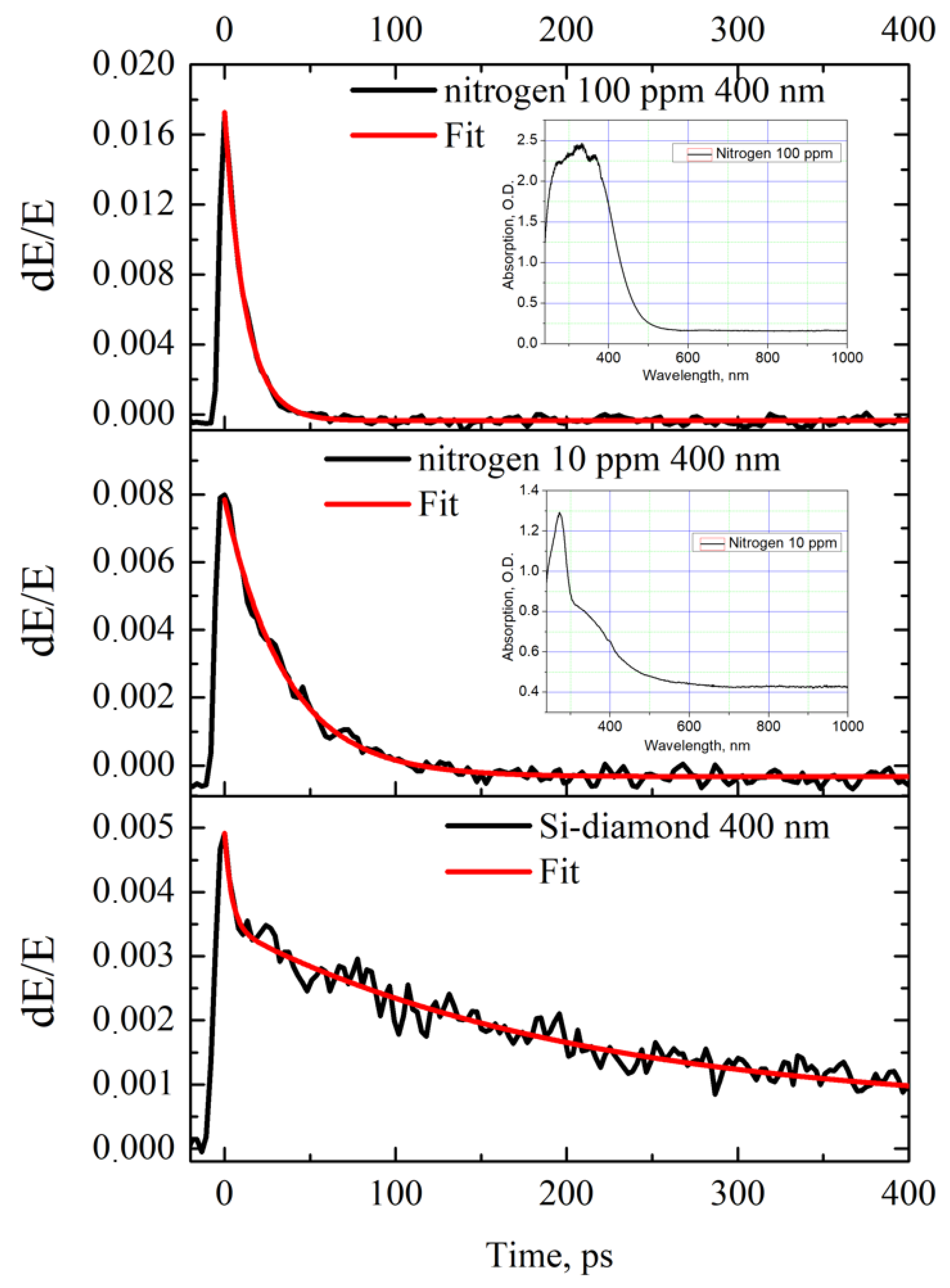
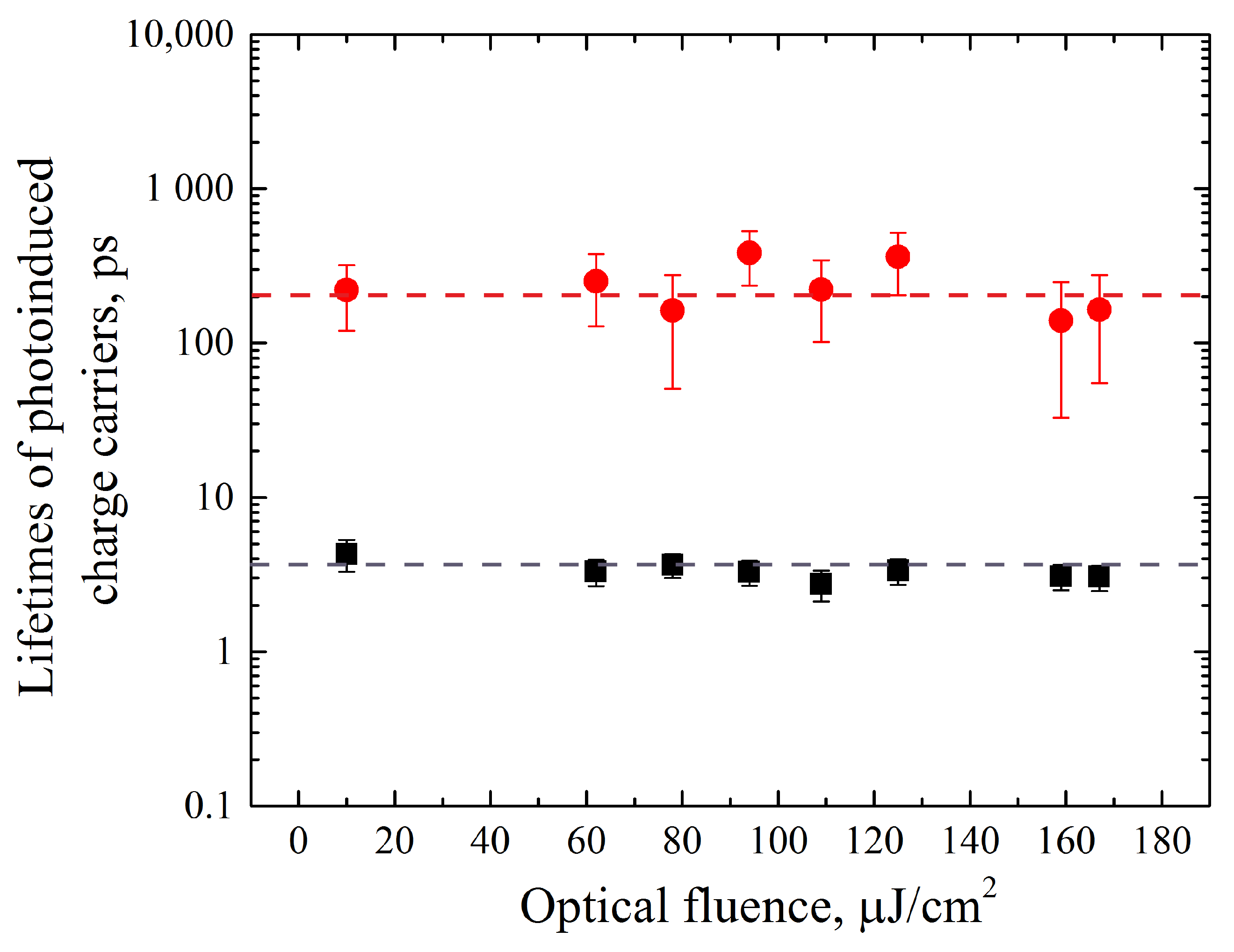
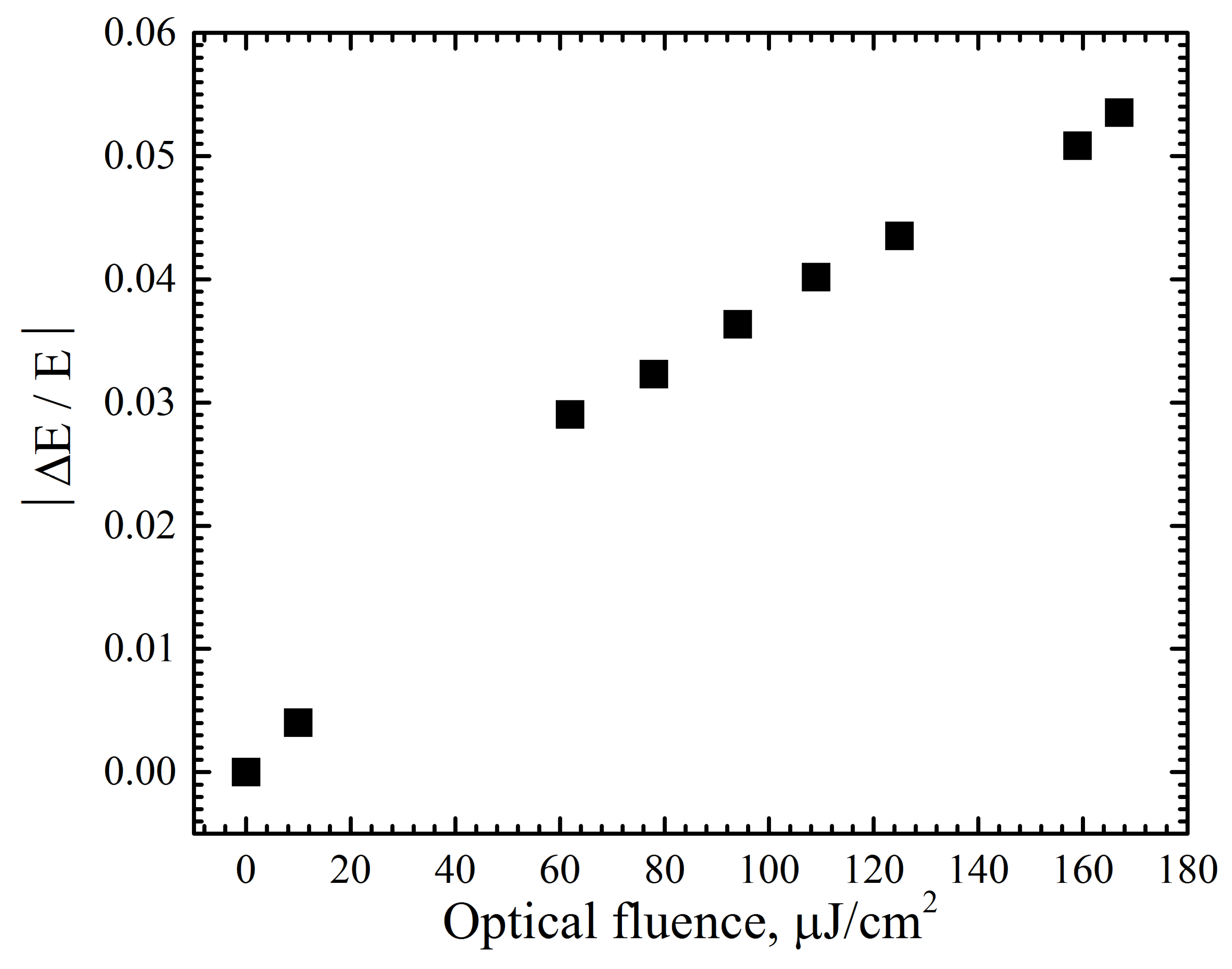
3. Results
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| THz | Terahertz |
| PCA | Photoconductive antenna |
| LAPCA | Large-aperture photoconductive antenna |
| OPTP | Optical pump–Terahertz probe |
| CVD | Chemical vapor deposition |
| MEMS | Micro-electro-mechanical system |
| MPCVD | Microwave plasma chemical vapor deposition |
| GHz | Gigahertz |
| DMSO | Dimethylsulfoxide |
| Si | Silicon |
| PCD | Polycrystalline diamond |
| SEM | Scanning electron microscope |
| SE | Secondary emission |
| BSE | Backscattered electron |
| LiNbO | Lithium niobate |
| ZnTe | Zinc telluride |
| BBO | Beta-barium borate |
| HPHT | High pressure–high temperature |
References
- Stantchev, R.I.; Yu, X.; Blu, T.; Pickwell-MacPherson, E. Real-time terahertz imaging with a single-pixel detector. Nat. Commun. 2020, 11, 2535. [Google Scholar] [CrossRef] [PubMed]
- McDonnell, C.; Deng, J.; Sideris, S.; Ellenbogen, T.; Li, G. Functional THz emitters based on Pancharatnam-Berry phase nonlinear metasurfaces. Nat. Commun. 2021, 12, 30. [Google Scholar] [CrossRef] [PubMed]
- Khalatpour, A.; Paulsen, A.K.; Deimert, C.; Wasilewski, Z.R.; Hu, Q. High-power portable terahertz laser systems. Nat. Photonics 2021, 15, 16–20. [Google Scholar] [CrossRef]
- Bai, P.; Zhang, Y.; Wang, T.; Fu, Z.; Shao, D.; Li, Z.; Wan, W.; Li, H.; Cao, J.; Guo, X.; et al. Broadband THz to NIR up-converter for photon-type THz imaging. Nat. Commun. 2019, 10, 3513. [Google Scholar] [CrossRef] [PubMed]
- Valušis, G.; Lisauskas, A.; Yuan, H.; Knap, W.; Roskos, H.G. Roadmap of terahertz imaging 2021. Sensors 2021, 21, 4092. [Google Scholar] [CrossRef] [PubMed]
- Irizawa, A.; Lupi, S.; Marcelli, A. Terahertz as a frontier area for science and technology. Condens. Matter 2021, 6, 23. [Google Scholar] [CrossRef]
- O’Hara, J.F.; Ekin, S.; Choi, W.; Song, I. A perspective on terahertz next-generation wireless communications. Technologies 2019, 7, 43. [Google Scholar] [CrossRef]
- Ropagnol, X.; Khorasaninejad, M.; Raeiszadeh, M.; Safavi-Naeini, S.; Bouvier, M.; Côté, C.; Laramée, A.; Reid, M.; Gauthier, M.; Ozaki, T. Intense THz pulses with large ponderomotive potential generated from large aperture photoconductive antennas. Opt. Express 2016, 24, 11299–11311. [Google Scholar] [CrossRef]
- Isgandarov, E.; Ropagnol, X.; Singh, M.; Ozaki, T. Intense terahertz generation from photoconductive antennas. Front. Optoelectron. 2021, 14, 64–93. [Google Scholar] [CrossRef]
- He, Y.; Chen, Y.; Zhang, L.; Wong, S.W.; Chen, Z.N. An overview of terahertz antennas. China Commun. 2020, 17, 124–165. [Google Scholar] [CrossRef]
- Hafez, H.; Chai, X.; Ibrahim, A.; Mondal, S.; Férachou, D.; Ropagnol, X.; Ozaki, T. Intense terahertz radiation and their applications. J. Opt. 2016, 18, 093004. [Google Scholar] [CrossRef]
- Chai, X.; Ropagnol, X.; Ovchinnikov, A.; Chefonov, O.; Ushakov, A.; Garcia-Rosas, C.; Isgandarov, E.; Agranat, M.; Ozaki, T.; Savel’ev, A. Observation of crossover from intraband to interband nonlinear terahertz optics. Opt. Lett. 2018, 43, 5463–5466. [Google Scholar] [CrossRef] [PubMed]
- Jones, R.; You, D.; Bucksbaum, P. Ionization of Rydberg atoms by subpicosecond half-cycle electromagnetic pulses. Phys. Rev. Lett. 1993, 70, 1236. [Google Scholar] [CrossRef] [PubMed]
- Chai, X.; Ropagnol, X.; Raeis-Zadeh, S.M.; Reid, M.; Safavi-Naeini, S.; Ozaki, T. Subcycle terahertz nonlinear optics. Phys. Rev. Lett. 2018, 121, 143901. [Google Scholar] [CrossRef] [PubMed]
- Yoneda, H.; Tokuyama, K.; Ueda, K.I.; Yamamoto, H.; Baba, K. Highpower terahertz radiation emitter with a diamond photoconductive switch array. Appl. Opt. 2001, 40, 6733–6736. [Google Scholar] [CrossRef] [PubMed]
- Chizhov, P.A.; Komlenok, M.S.; Kononenko, V.V.; Bukin, V.V.; Ushakov, A.A.; Bulgakova, V.V.; Khomich, A.A.; Bolshakov, A.P.; Konov, V.I.; Garnov, S.V. Photoconductive terahertz generation in nitrogen-doped single-crystal diamond. Opt. Lett. 2022, 47, 86–89. [Google Scholar] [CrossRef]
- Kononenko, V.V.; Zavedeev, E.V.; Dezhkina, M.A.; Bulgakova, V.V.; Komlenok, M.S.; Kononenko, T.V.; Bukin, V.V.; Konov, V.I.; Garnov, S.V.; Khomich, A.A. Generation of Terahertz Radiation in Boron-Doped Diamond. Bull. Lebedev Phys. Inst. 2023, 50, 606–612. [Google Scholar] [CrossRef]
- Mag-usara, V.K.; Funkner, S.; Niehues, G.; Prieto, E.A.; Balgos, M.H.; Somintac, A.; Estacio, E.; Salvador, A.; Yamamoto, K.; Hase, M.; et al. Low temperature-grown GaAs carrier lifetime evaluation by double optical pump terahertz time-domain emission spectroscopy. Opt. Express 2016, 24, 26175–26185. [Google Scholar] [CrossRef]
- Kannegulla, A.; Shams, M.I.B.; Liu, L.; Cheng, L.J. Photo-induced spatial modulation of THz waves: Opportunities and limitations. Opt. Express 2015, 23, 32098–32112. [Google Scholar] [CrossRef]
- Xiao, B.; Chen, H.; Liu, J.; Yu, J.; Xiao, L. Multifunctional and tunable terahertz coding metasurfaces based on vanadium dioxide. Opt. Commun. 2023, 549, 129928. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, F.; Ma, Y.; Zhang, A.; Zhang, K. Tunable and switchable terahertz absorber based on photoconductive silicon and vanadium dioxide. Opt. Laser Technol. 2023, 163, 109329. [Google Scholar] [CrossRef]
- Sussmann, R.S. CVD Diamond for Electronic Devices and Sensors; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Salvatori, S.; Pettinato, S.; Piccardi, A.; Sedov, V.; Voronin, A.; Ralchenko, V. Thin diamond film on silicon substrates for pressure sensor fabrication. Materials 2020, 13, 3697. [Google Scholar] [CrossRef] [PubMed]
- Pettinato, S.; Barettin, D.; Sedov, V.; Ralchenko, V.; Salvatori, S. Fabry-Perot Pressure Sensors Based on Polycrystalline Diamond Membranes. Materials 2021, 14, 1780. [Google Scholar] [CrossRef] [PubMed]
- Windischmann, H.; Epps, G.F. Properties of diamond membranes for x-ray lithography. J. Appl. Phys. 1990, 68, 5665–5673. [Google Scholar] [CrossRef]
- Komlenok, M.S.; Dezhkina, M.A.; Sedov, V.S.; Klimenko, O.A.; Dyakov, S.A.; Gippius, N.A. Laser Ablated Nanocrystalline Diamond Membrane for Infrared Applications. Sensors 2022, 22, 829. [Google Scholar] [CrossRef] [PubMed]
- Sedov, V.; Kuznetsov, S.; Martyanov, A.; Ralchenko, V. Luminescent diamond composites. Funct. Diam. 2022, 2, 53–63. [Google Scholar] [CrossRef]
- Kuznetsov, S.; Sedov, V.; Martyanov, A.; Batygov, S.C.; Vakalov, D.; Boldyrev, K.; Tiazhelov, I.; Popovich, A.; Pasternak, D.; Bland, H.; et al. Cerium-doped gadolinium-scandium-aluminum garnet powders: Synthesis and use in X-ray luminescent diamond composites. Ceram. Int. 2022, 48, 12962–12970. [Google Scholar] [CrossRef]
- Němec, H.; Kadlec, F.; Kužel, P. Methodology of an optical pump-terahertz probe experiment: An analytical frequency-domain approach. J. Chem. Phys. 2002, 117, 8454–8466. [Google Scholar] [CrossRef]
- Joyce, H.J.; Boland, J.L.; Davies, C.L.; Baig, S.A.; Johnston, M.B. A review of the electrical properties of semiconductor nanowires: Insights gained from terahertz conductivity spectroscopy. Semicond. Sci. Technol. 2016, 31, 103003. [Google Scholar] [CrossRef]
- Nashima, S.; Morikawa, O.; Takata, K.; Hangyo, M. Measurement of optical properties of highly doped silicon by terahertz time domain reflection spectroscopy. Appl. Phys. Lett. 2001, 79, 3923–3925. [Google Scholar] [CrossRef]
- Jeon, T.I.; Grischkowsky, D. Characterization of optically dense, doped semiconductors by reflection THz time domain spectroscopy. Appl. Phys. Lett. 1998, 72, 3032–3034. [Google Scholar] [CrossRef]
- Prabhu, S.; Ralph, S.; Melloch, M.; Harmon, E. Carrier dynamics of low-temperature-grown GaAs observed via THz spectroscopy. Appl. Phys. Lett. 1997, 70, 2419–2421. [Google Scholar] [CrossRef]
- Parkinson, P.; Joyce, H.J.; Gao, Q.; Tan, H.H.; Zhang, X.; Zou, J.; Jagadish, C.; Herz, L.M.; Johnston, M.B. Carrier lifetime and mobility enhancement in nearly defect-free core- shell nanowires measured using time-resolved terahertz spectroscopy. Nano Lett. 2009, 9, 3349–3353. [Google Scholar] [CrossRef] [PubMed]
- Martin, P.; Guizard, S.; Daguzan, P.; Petite, G.; D’Oliveira, P.; Meynadier, P.; Perdrix, M. Subpicosecond study of carrier trapping dynamics in wide-band-gap crystals. Phys. Rev. B 1997, 55, 5799–5810. [Google Scholar] [CrossRef]
- Kononenko, V.V.; Zavedeev, E.V.; Latushko, M.I.; Konov, V.I. Observation of fs laser-induced heat dissipation in diamond bulk. Laser Phys. Lett. 2013, 10, 036003. [Google Scholar] [CrossRef]
- Martyanov, A.; Tiazhelov, I.; Savin, S.; Voronov, V.; Konov, V.; Sedov, V. Synthesis of Polycrystalline Diamond Films in Microwave Plasma at Ultrahigh Concentrations of Methane. Coatings 2023, 13, 751. [Google Scholar] [CrossRef]
- Mandal, S. Nucleation of diamond films on heterogeneous substrates: A review. RSC Adv. 2021, 11, 10159–10182. [Google Scholar] [CrossRef]
- Hebling, J.; Almási, G.; Kozma, I.Z.; Kuhl, J. Velocity matching by pulse front tilting for large-area THz-pulse generation. Opt. Express 2002, 10, 1161–1166. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulgakova, V.; Chizhov, P.; Ushakov, A.; Ratnikov, P.; Goncharov, Y.; Martyanov, A.; Kononenko, V.; Savin, S.; Golovnin, I.; Konov, V.; et al. Optical Pump–Terahertz Probe Diagnostics of the Carrier Dynamics in Diamonds. Materials 2024, 17, 119. https://doi.org/10.3390/ma17010119
Bulgakova V, Chizhov P, Ushakov A, Ratnikov P, Goncharov Y, Martyanov A, Kononenko V, Savin S, Golovnin I, Konov V, et al. Optical Pump–Terahertz Probe Diagnostics of the Carrier Dynamics in Diamonds. Materials. 2024; 17(1):119. https://doi.org/10.3390/ma17010119
Chicago/Turabian StyleBulgakova, Vladislava, Pavel Chizhov, Alexander Ushakov, Pavel Ratnikov, Yuri Goncharov, Artem Martyanov, Vitali Kononenko, Sergey Savin, Ilya Golovnin, Vitaly Konov, and et al. 2024. "Optical Pump–Terahertz Probe Diagnostics of the Carrier Dynamics in Diamonds" Materials 17, no. 1: 119. https://doi.org/10.3390/ma17010119
APA StyleBulgakova, V., Chizhov, P., Ushakov, A., Ratnikov, P., Goncharov, Y., Martyanov, A., Kononenko, V., Savin, S., Golovnin, I., Konov, V., & Garnov, S. (2024). Optical Pump–Terahertz Probe Diagnostics of the Carrier Dynamics in Diamonds. Materials, 17(1), 119. https://doi.org/10.3390/ma17010119






