Analysis of Critical Current Dependence on Specimen Length and Crack Size Distribution in Cracked Superconductor
Abstract
:1. Introduction
2. Materials and Methods
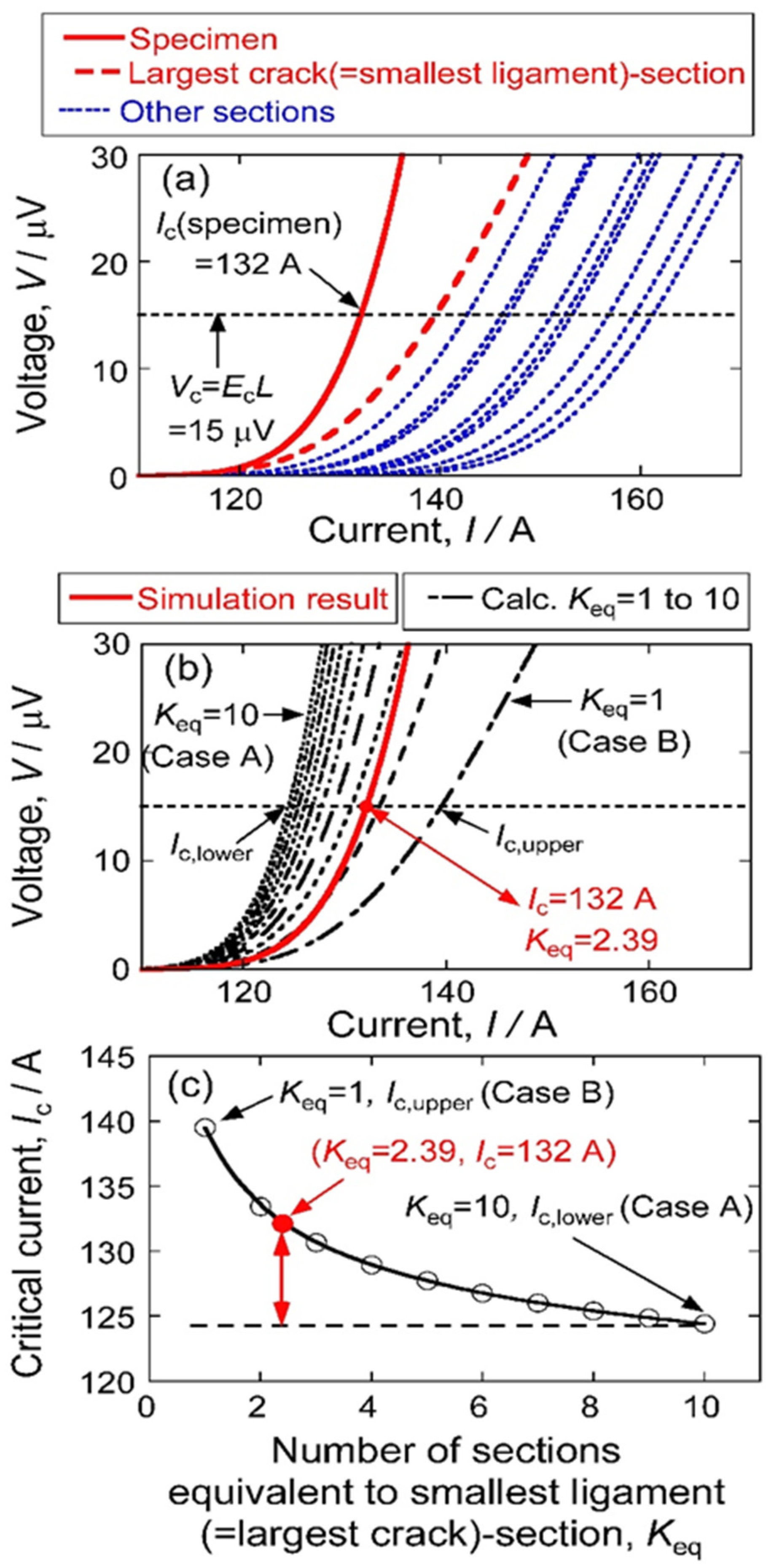
2.1. Simulation to Obtain Critical Current Values under Various Specimen Lengths and Various Distribution Widths of Crack Size
2.2. Model Analysis of the Specimen Length (L)-Dependence of Critical Current (Ic) under Various Distribution-Widths of Crack Size (ΔLp)
3. Results
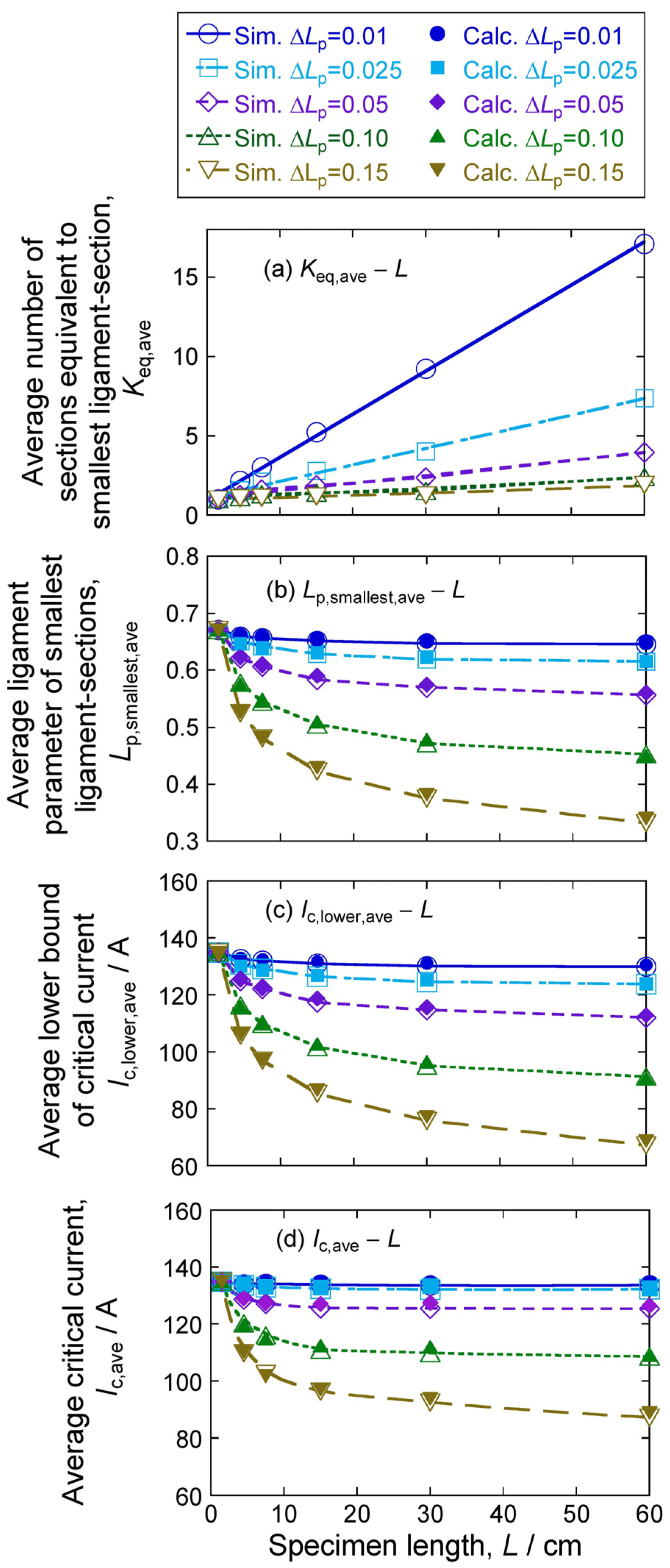
- The average smallest ligament parameter Lp,smallest,ave decreases with an increase in L. Namely, the average size of the largest crack increases with an increase in L. The extent of the increment of the size of the largest crack with L is enhanced with an increase in ΔLp;
- Average critical current Ic,ave decreases with an increase in specimen length L. The extent of the decrease in Ic,ave with L increases with the increase in the standard deviation of the ligament size (=standard deviation of crack size) ΔLp;
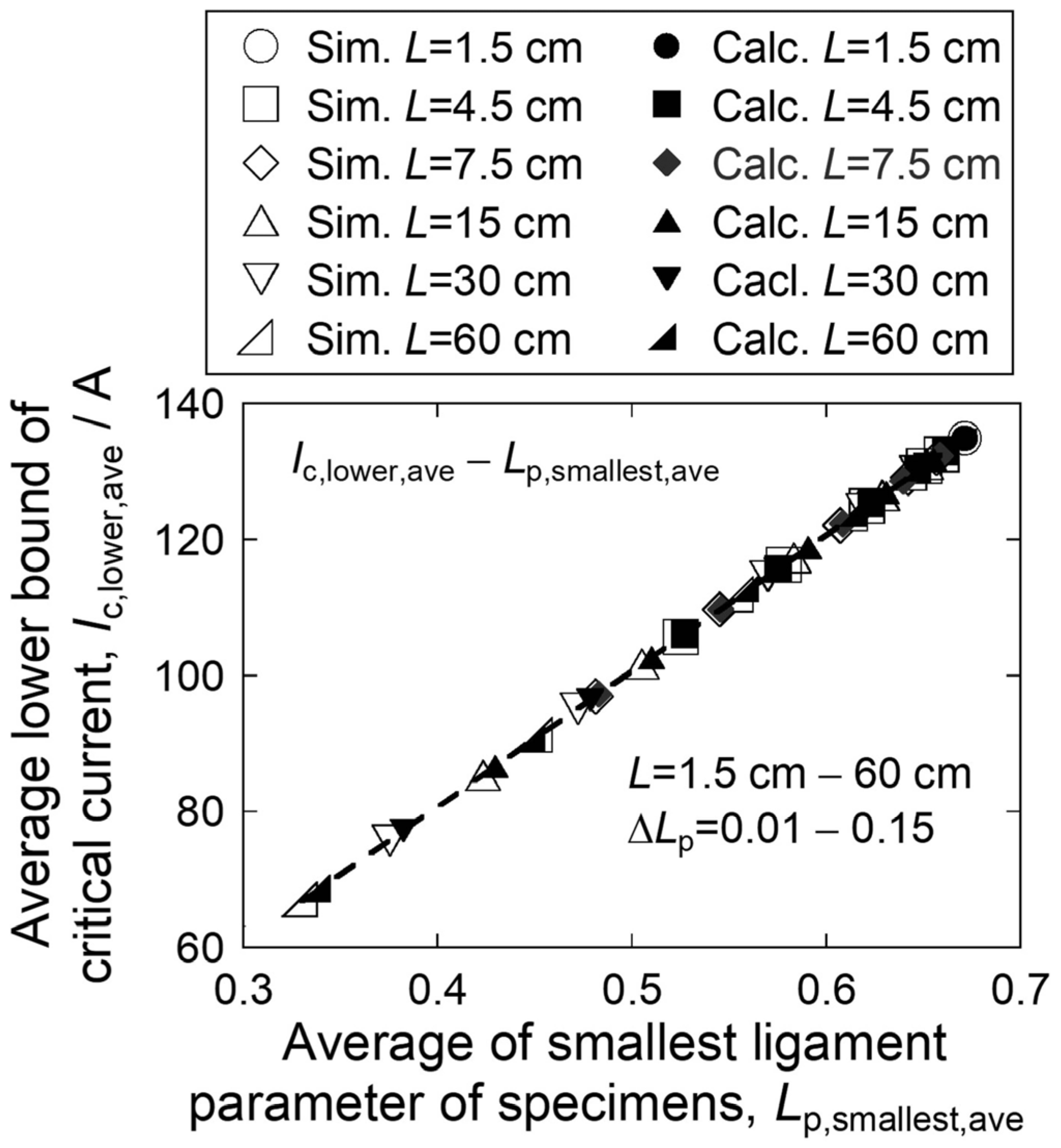
- The change in the average of critical current Ic,ave and the average of the lower bound of critical) current Ic,lower,ave with an increase in specimen length L is similar to the change in Lp,smallest,ave. This result suggests that the decrease in Lp,smallest,ave, namely the increase in the size of the largest crack, has a significant influence on the determination of critical current.
4. Discussion
4.1. Calculation of Average Values of the Smallest Ligament Parameter, Lower Bound of Critical Current, Critical Current, and the Correlation between the Smallest Ligament Parameter and Lower Bound of Critical Current
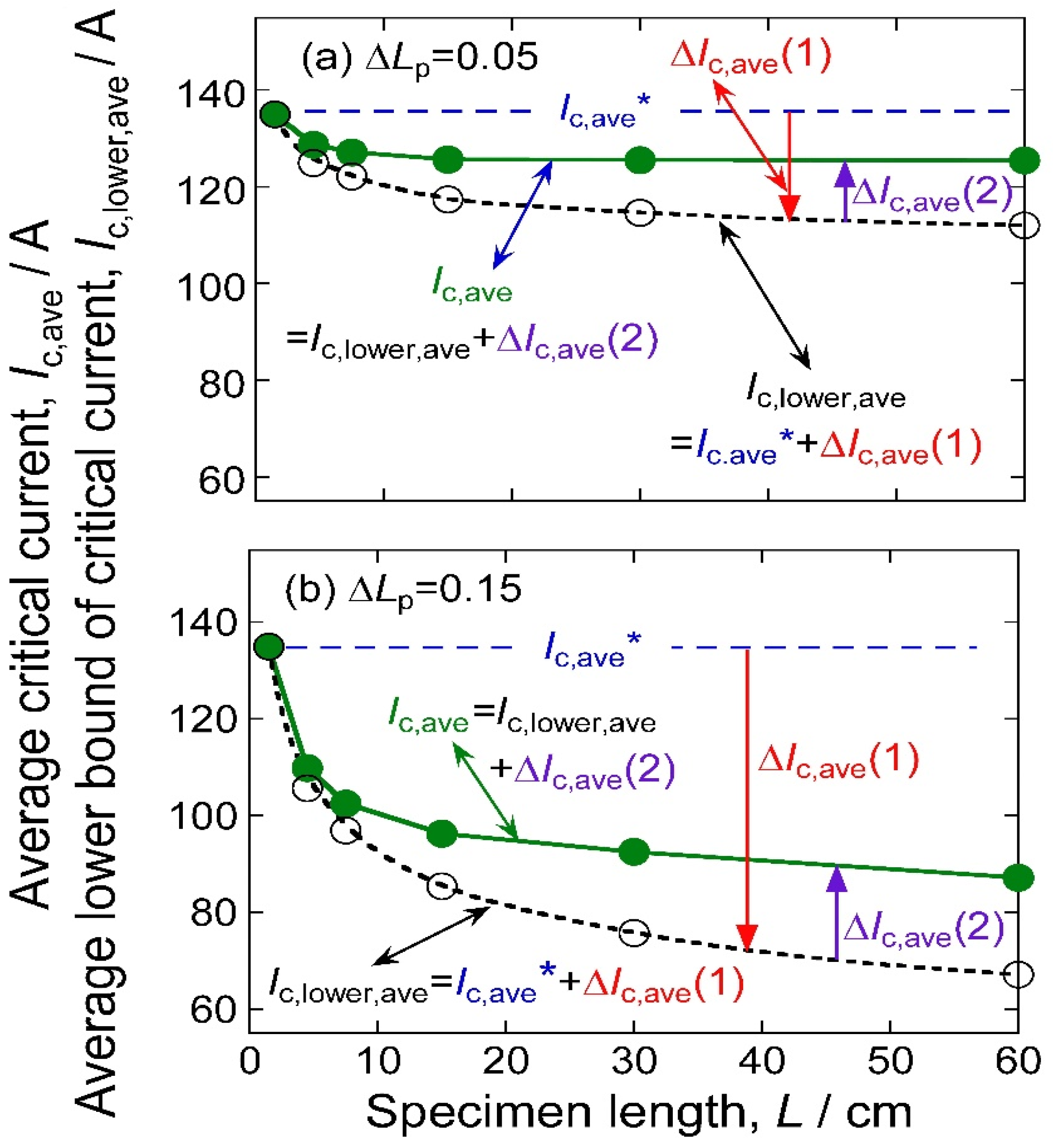
4.2. Separate Assessment of Effects of Factor 1 and Factor 2 on Specimen Length-Dependence of Critical Current
- (1)
- ΔIc,ave (1), arising from the increase in the size of the largest crack (Factor 1), increases in minus direction with increasing specimen length L and standard deviation of crack-size distribution ΔLp;
- (2)
- ΔIc,ave (2), arising from the difference in crack size (Factor 2), increases in the plus direction with increasing L and ΔLp;
- (3)
- (4)
- The change in the minus (ΔIc,ave (1))—and plus (ΔIc,ave (2))—effects with specimen length becomes moderate in long specimens.
5. Conclusions
- (1)
- The calculation- and simulation-results showed the following features of the specimen length-dependence of the critical current. (a) Large Factor 1 plays a role in reducing critical current. (b) Large Factor 2 plays a role in raising critical current under a given size of the largest crack. (c) The effect of Factor 1 is larger than that of Factor 2, and hence, the critical current decreases with increasing specimen length. This feature is enhanced with increasing standard deviation of crack size;
- (2)
- For a quantitative description of the results mentioned in (1), the effect of Factor 1 on the critical current of the specimen was formulated by combining the smallest ligament parameter, corresponding to the largest crack section, with a shunting of the current model at the crack. The effect of Factor 2 on critical current was formulated using the number of sections equivalent to the largest crack section at the critical voltage of the specimen’s critical current. With the application of the present approach to the calculation and simulation results, the following results were obtained: (a) The critical current-reducing effect caused by an increase in Factor 1 and the critical current-raising effect caused by the increase in Factor 2 were assessed separately, and the critical current of the specimen was described as a function of specimen length. (b) The features mentioned in (1) were quantitatively described.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cheggour, N.; Ekin, J.W.; Thieme, C.H.L.; Xie, Y.-Y.; Selvamanickam, V.; Feenstra, R. Reversible Axial-strain Effect in Y–Ba–Cu–O Coated Conductors. Supercond. Sci. Technol. 2005, 18, S319–S324. [Google Scholar] [CrossRef]
- Van der Laan, D.C.; Ekin, J.W.; Douglas, F.F.; Clickner, C.C.; Stauffer, T.C.; Goodrich, L.F. Effect of Strain, Magnetic Field and Field Angle on the Critical Current Density of YBa2Cu3O7−δ Coated Conductors. Supercond. Sci. Technol. 2010, 23, 072001. [Google Scholar] [CrossRef]
- Ochiai, S.; Arai, T.; Toda, A.; Okuda, H.; Sugano, M.; Osamura, K.; Prusseit, W. Influences of Cracking of Coated Superconducting Layer on Voltage-Current Curve, Critical Current and n-value in DyBCO-Coated Conductor Pulled in Tension. J. Appl. Phys. 2010, 108, 063905. [Google Scholar] [CrossRef]
- Shin, H.S.; Marlon, J.; Dedicatoria, H.; Kim, H.S.; Lee, N.J.; Ha, H.S.; Oh, S.S. Electro-Mechanical Property Investigation of Striated REBCO Coated Conductor Tapes in Pure Torsion Mode. IEEE Trans. Appl. Supercond. 2011, 21, 2997–3000. [Google Scholar] [CrossRef]
- Oguro, H.; Suwa, T.; Suzuki, T.; Awaji, S.; Watanabe, K.; Sugano, M.; Machiya, S.; Sato, T.; Koganezawa, T.; Machi, T.; et al. Relation between the Crystal Axis and the Strain Dependence of Critical Curren under Tensile Strain for GdBCO Coated Conductors. IEEE Trans. Appl. Supercond. 2013, 23, 8400304. [Google Scholar] [CrossRef]
- Zhao, Y.; Ji, P. Crack-Inclusion Problem in a Superconducting Cylinder with Exponential Distribution of Critical Current Density. J. Supercond. Nov. Magn. 2020, 33, 2907–2912. [Google Scholar] [CrossRef]
- Gannon, J.J.; Malozemoff, A.P.; Diehl, R.C.; Antaya, P.; Mori, A. Effect of Length Scale on Critical Current Measurement in High Temperature Superconductor Wires. IEEE Trans. Appl. Supercond. 2013, 23, 8002005. [Google Scholar] [CrossRef]
- Ma, J.; Gao, Y. Numerical Analysis of the Mechanical and Electrical Properties of (RE)BCO Tapes with Multiple Edge Cracks. Supercond. Sci. Technol. 2023, 36, 095013. [Google Scholar] [CrossRef]
- Jiang, Z.; Huang, Y.; Jiang, D.; Chen, W.; Kuang, G. Influence of Edge Crack Propagation on Critical Current Degradation of REBCO Tape Studied by Phase-Field Fracture Method and Current Shunting Model. IEEE Trans. Appl. Supercond. 2023, 33, 8400111. [Google Scholar] [CrossRef]
- Yong, D.; Yang, Y.; Zhou, Y.H. Dynamic Fracture Behavior of a Crack in the Bulk Superconductor under Electromagnetic Force. Eng. Frac. Mech. 2016, 158, 167–178. [Google Scholar] [CrossRef]
- Feng, W.J.; Zhang, R.; Ding, H.M. Crack Problem for an Inhomogeneous Orthotropic Superconducting Slab under an Electromagnetic Force. Phys. C Supercond. 2012, 477, 32–36. [Google Scholar] [CrossRef]
- Gao, P.; Mao, J.; Chen, J.; Wang, X.; Zhou, Y. Electromechanical Degradation of REBCO Coated Conductor Tapes under Combined Tension and Torsion Loading. Int. J. Mech. Sci. 2020, 223, 107314. [Google Scholar] [CrossRef]
- Ochiai, S.; Okuda, O.; Fujii, N. Features of Crack Size Distribution- and Voltage Probe Spacing-Depend ences of Critical Current and n-Value in Cracked Superconducting Tape, Depicted by Simulation. Mater. Trans. 2018, 59, 1628–1636. [Google Scholar] [CrossRef]
- Ochiai, S.; Okuda, H. Effects of Size of the Largest Crack and Size Difference among Cracks on Critical Current of Superconducting Tape with Multiple Cracks in Superconducting Layer. Mater. Trans. 2020, 61, 766–775. [Google Scholar] [CrossRef]
- Akdemir, E.; Pakdil, M.; Bilge, H.; Kahraman, M.F.; Yildirim, G.; Bekiroglu, E.; Zalaoglu, Y.; Doruk, E.; Oz, M. Degeneration of Mechanical Characteristics and Performances with Zr Nanoparticles Inserted in Bi-2223 Superconducting Matrix and Increment in Dislocation Movement and Cracks Propagation. J. Mater. Sci. Mater Electron. 2016, 27, 2276–2287. [Google Scholar] [CrossRef]
- Shigue, C.Y.; Baldan, C.A.; Oliveira, U.R.; Carvalho, F.J.H.; Filho, E.R. Critical Current Degradation of Bi-2223 Composite Tapes Induced by Cyclic Deformation and Fatigue-Related Effects. IEEE Trans. Appl. Supercond. 2006, 16, 1027–1030. [Google Scholar] [CrossRef]
- Fang, Y.; Danyluk, S.; Lanagan, M.T. Effects of Cracks on Critical Current Density in Ag-sheathed Superconductor Tape. Cryogenics 1996, 36, 957–962. [Google Scholar] [CrossRef]
- Van Eck, H.J.M.; Vargas, L.; ten Haken, B.; ten Kate, H.H.J. Bending and Axial Strain Dependence of the Critical Current in Superconducting BSCCO Tapes. Supercond. Sci. Technol. 2002, 15, 1213. [Google Scholar] [CrossRef]
- Gao, P.; Wang, X. Theory Analysis of Critical Current Degeneration in Bended Superconducting Tapes of Multifiment Composite Bi2223/Ag. Phys. C 2015, 517, 31–36. [Google Scholar] [CrossRef]
- Ochiai, S.; Okuda, H.; Sugano, M.; Hojo, M.; Osamura, K. Prediction of Variation in Critical Current with Applied Tensile/Bending Strain of Bi2223 Composite Tape from Tensile Stress-Strain Curve. J. Appl. Phys. 2010, 107, 083904. [Google Scholar] [CrossRef]
- Kitaguchi, H.; Matsumoto, A.; Hatakeyama, H.; Kumakura, H. V–I Characteristics of MgB2 PIT CopositeTapes: N-Values under Strain, in High Fields, or at High Temperatures. Phys. C Supercond. 2004, 401, 246–250. [Google Scholar] [CrossRef]
- Murakami, A.; Iwamoto, A.; Noudem, J.G. Mechanical Properties of Bulk MgB2 Superconductors Processed by Spark Plasma Sintering at Various Temperatures. IEEE Trans. Appl. Supercond. 2018, 28, 8400204. [Google Scholar] [CrossRef]
- Nishijima, G.; Ye, S.J.; Matsumoto, A.; Togano, K.; Kumakura, H.; Kitaguchi, H.; Oguro, H. Mechanical Properties of MgB2 Superconducting Wires Fabricated by Internal Mg Diffusion Process. Supercond. Sci. Technol. 2012, 25, 054012. [Google Scholar] [CrossRef]
- Krinitsina, T.P.; Kuznetsova, E.I.; Degtyarev, M.V.; Blinova, Y.V. MgB2-Based Superconductors: Structure and Properties. Phys. Metals Metallogr. 2021, 122, 1183–1206. [Google Scholar] [CrossRef]
- Alknes, P.; Hagner, M.; Bjoerstad, R.; Scheuerlein, C.; Bordini, B.; Sugano, M.; Hudspeth, J.; Ballarino, A. Mechanical Properties and Strain Induced Filament Degradation of Ex-Situ and In-Situ MgB2 wires. IEEE Trans. Appl. Supercond. 2016, 26, 8401205. [Google Scholar] [CrossRef]
- Miyoshi, Y.; Van Lanen, E.P.A.; Dhallé, M.M.; Nijhuits, N. Distinct Voltage–Current Characteristics of Nb3Sn Strands with Dispersed and Collective Crack Distributions. Supercond. Sci. Technol. 2009, 22, 1085009. [Google Scholar] [CrossRef]
- Feng, Y.; Yong, H.; Zhou, Y. Efficient Multiscale Investigation of Mechanical Behavior in Nb3Sn Superconducting Accelerator Magnet Based on Self-consistent Clustering Analysis. Comp. Struct. 2023, 324, 117541. [Google Scholar] [CrossRef]
- Lenoir, G.; Manil, P.; Nunio, F.; Aubin, V. Mechanical Behavior Laws for Multiscale Numerical Model of Nb3Sn Conductors. IEEE Trans. Appl. Supercond. 2019, 29, 8401706. [Google Scholar] [CrossRef]
- Sheth, M.K.; Lee, P.; McRae, D.M.; Walsh, R.; Starch, W.L.; Jewell, M.C.; Devred, A.; Larbalestier, D.C. Procedures for Evaluating Filament Cracking during Fatigue Testing of Nb3Sn Strand. AIP Conf. Proc. 2012, 1435, 201–208. [Google Scholar] [CrossRef]
- Ta, W.; Li, Y.; Gao, Y. A 3D Model on the Electromechanical Behavior of a Multifilament Twisted Nb3Sn Super conducting Strand. J. Supercond. Nov. Magn. 2015, 28, 2683–2695. [Google Scholar] [CrossRef]
- Zhang, Z.; Sh, L. Elastic–Plastic Mechanical Behavior Analysis of a Nb3Sn Superconducting Strand with Initial Thermal Damage. Appl. Sci. 2022, 12, 8313. [Google Scholar] [CrossRef]
- Nakamura, T.; Takamura, Y.; Amemiya, N.; Nakao, K.; Izumi, T. Longitudinal Inhomogeneity of DC Current Transport Properties in Gd-system HTS Tapes—Statistical Approach for System Design. Cryogenics 2014, 63, 17–24. [Google Scholar] [CrossRef]
- Gumbel, E.J. Statistics of Extremes; Columbia University Press: New York, NY, USA, 1958. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ochiai, S.; Okuda, H. Analysis of Critical Current Dependence on Specimen Length and Crack Size Distribution in Cracked Superconductor. Materials 2024, 17, 176. https://doi.org/10.3390/ma17010176
Ochiai S, Okuda H. Analysis of Critical Current Dependence on Specimen Length and Crack Size Distribution in Cracked Superconductor. Materials. 2024; 17(1):176. https://doi.org/10.3390/ma17010176
Chicago/Turabian StyleOchiai, Shojiro, and Hiroshi Okuda. 2024. "Analysis of Critical Current Dependence on Specimen Length and Crack Size Distribution in Cracked Superconductor" Materials 17, no. 1: 176. https://doi.org/10.3390/ma17010176
APA StyleOchiai, S., & Okuda, H. (2024). Analysis of Critical Current Dependence on Specimen Length and Crack Size Distribution in Cracked Superconductor. Materials, 17(1), 176. https://doi.org/10.3390/ma17010176





