A Study on Chloride Corrosion Resistance of Reactive Powder Concrete (RPC) with Copper Slag Replacing Quartz Sand under Freeze–Thaw Conditions
Abstract
:1. Introduction
2. Materials and Method
2.1. Copper Slag (CS)
2.1.1. Physical Properties of CS
2.1.2. Chemical Components
2.2. Other Raw Materials
2.2.1. Portland Cement
2.2.2. Silica Fume (SF)
2.2.3. Steel Fiber
2.2.4. Polycarboxylate Superplasticizer (PS)
2.3. Experimental Scheme
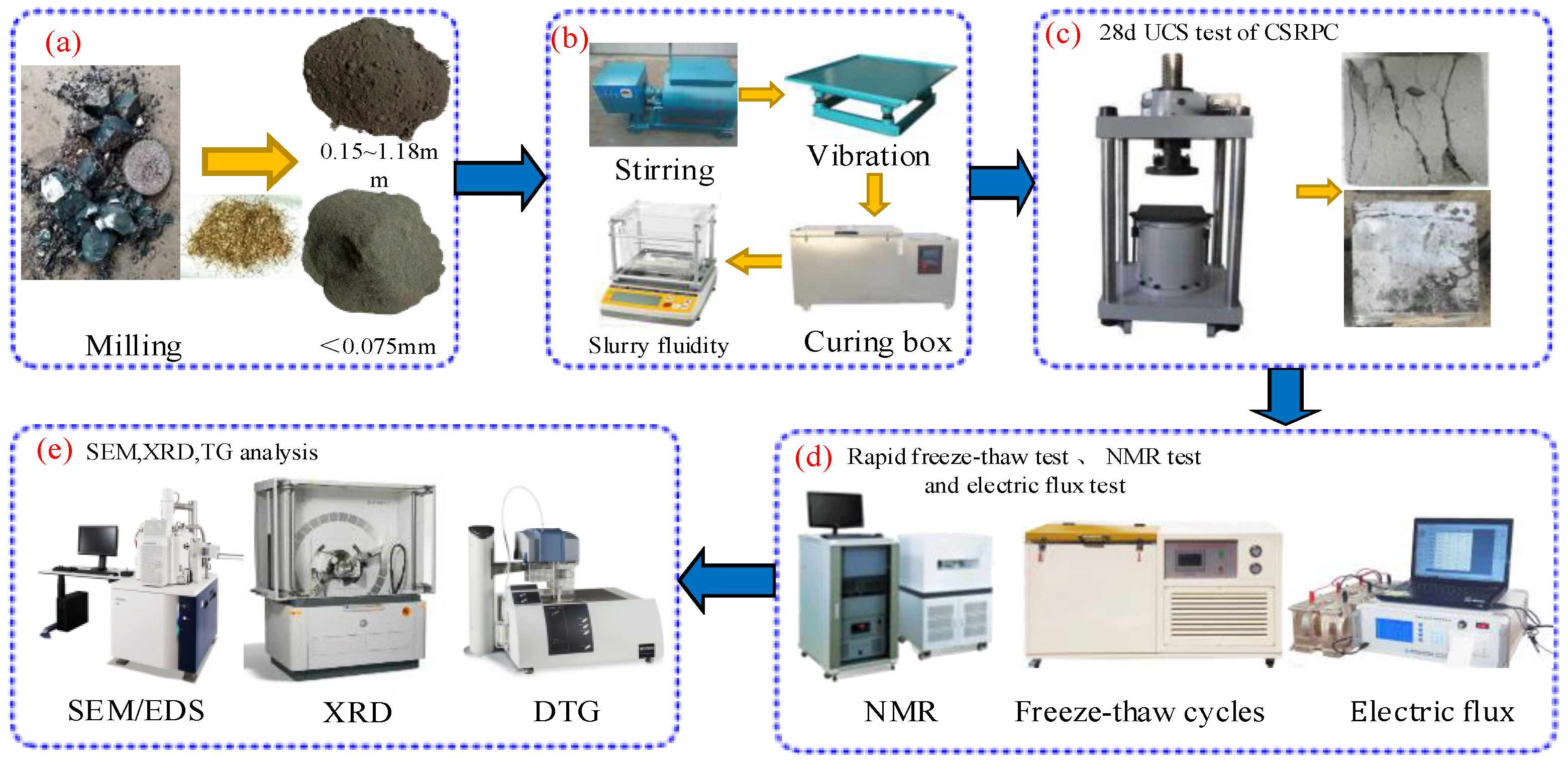
2.3.1. Specimen Preparation
2.3.2. The 28d UCS Test
2.3.3. Rapid Freeze–Thaw Test and NMR Test
2.3.4. Electric Flux Test
2.3.5. SEM, XRD, and TG Analysis
3. Results and Discussion
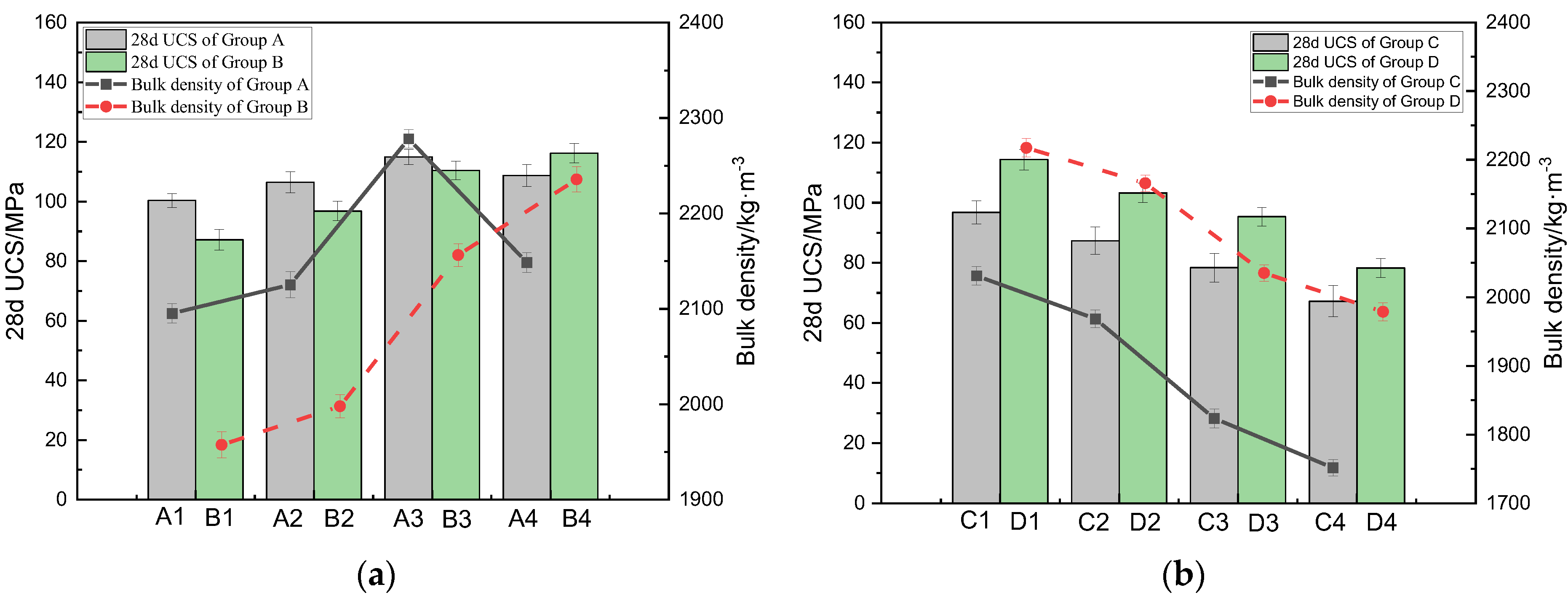
3.1. Effect of the CS Substitution Rate on the Mechanical Properties of CSRPC
3.2. Pore Structure Characteristics of CSRPC
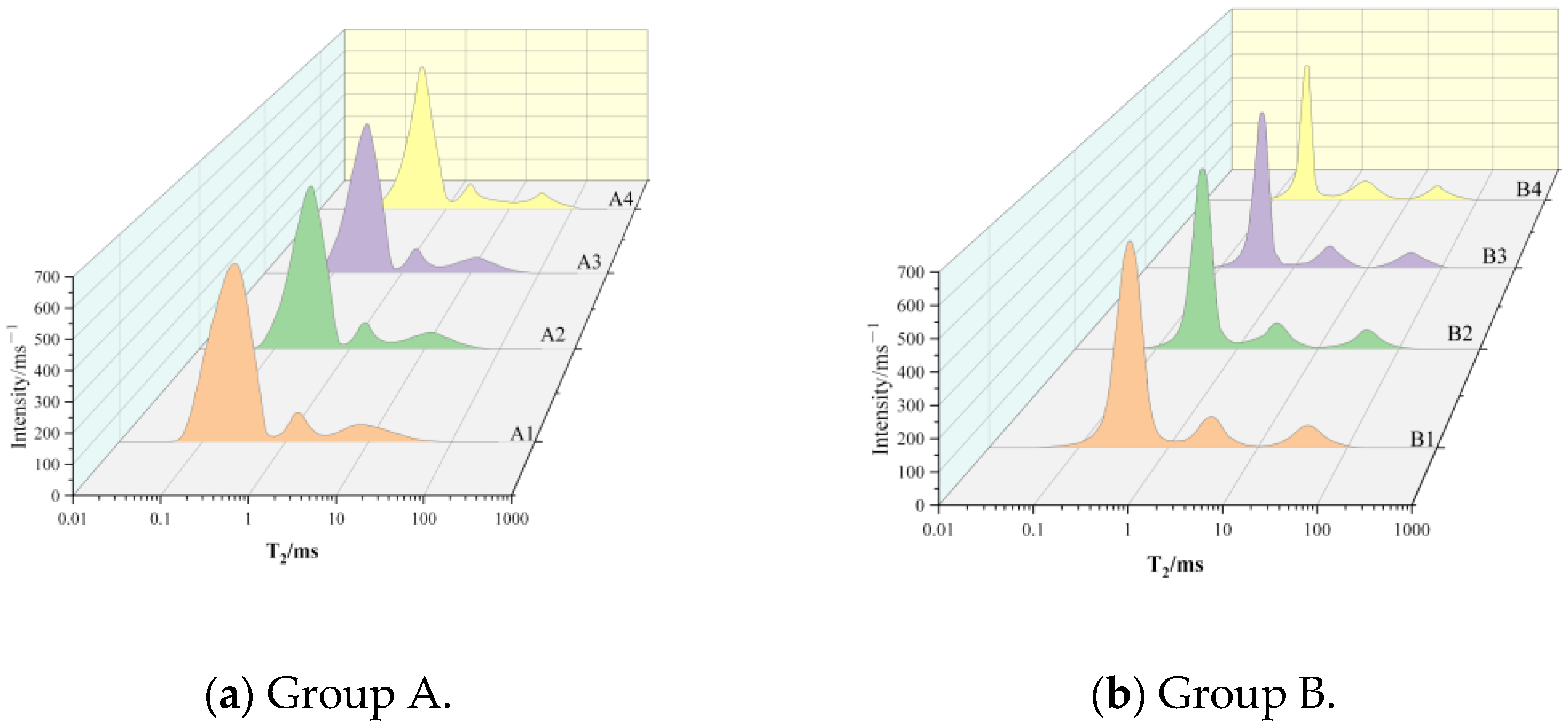
3.2.1. CSRPC Relaxation Properties
3.2.2. CSRPC Pore Structure Characteristics
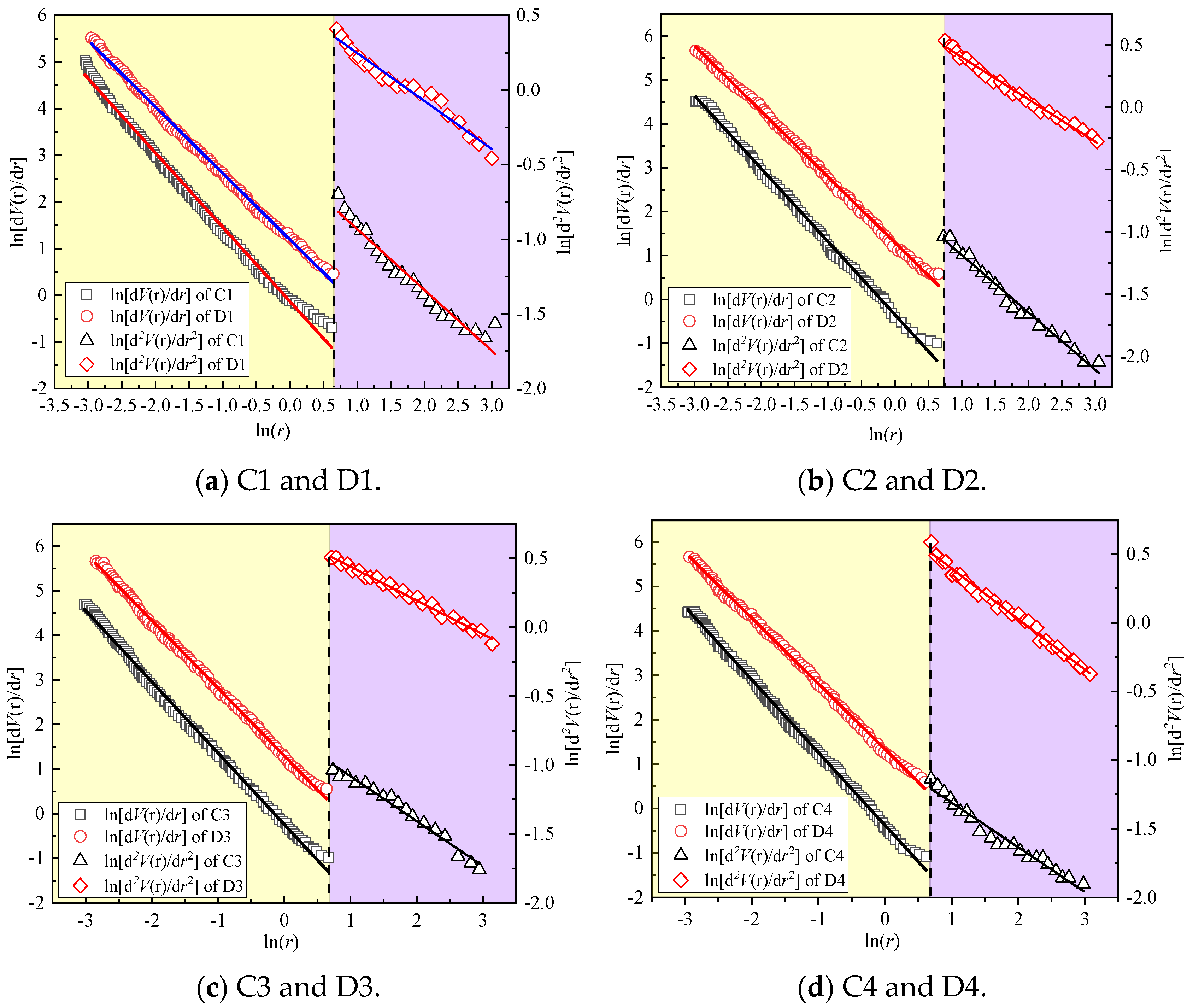
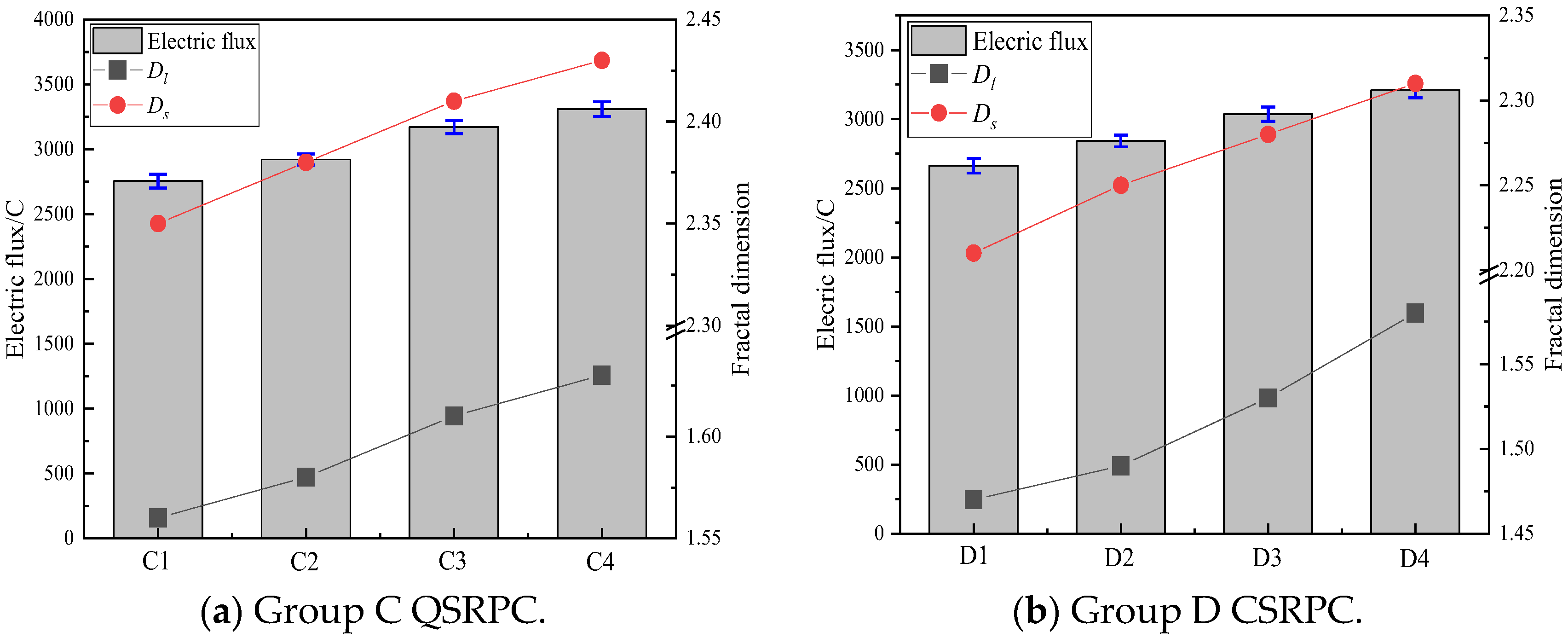
3.2.3. Fractal Dimension of the Pore of CSRPC
3.3. Effect of Freeze–Thaw Cycles on Electric Flux
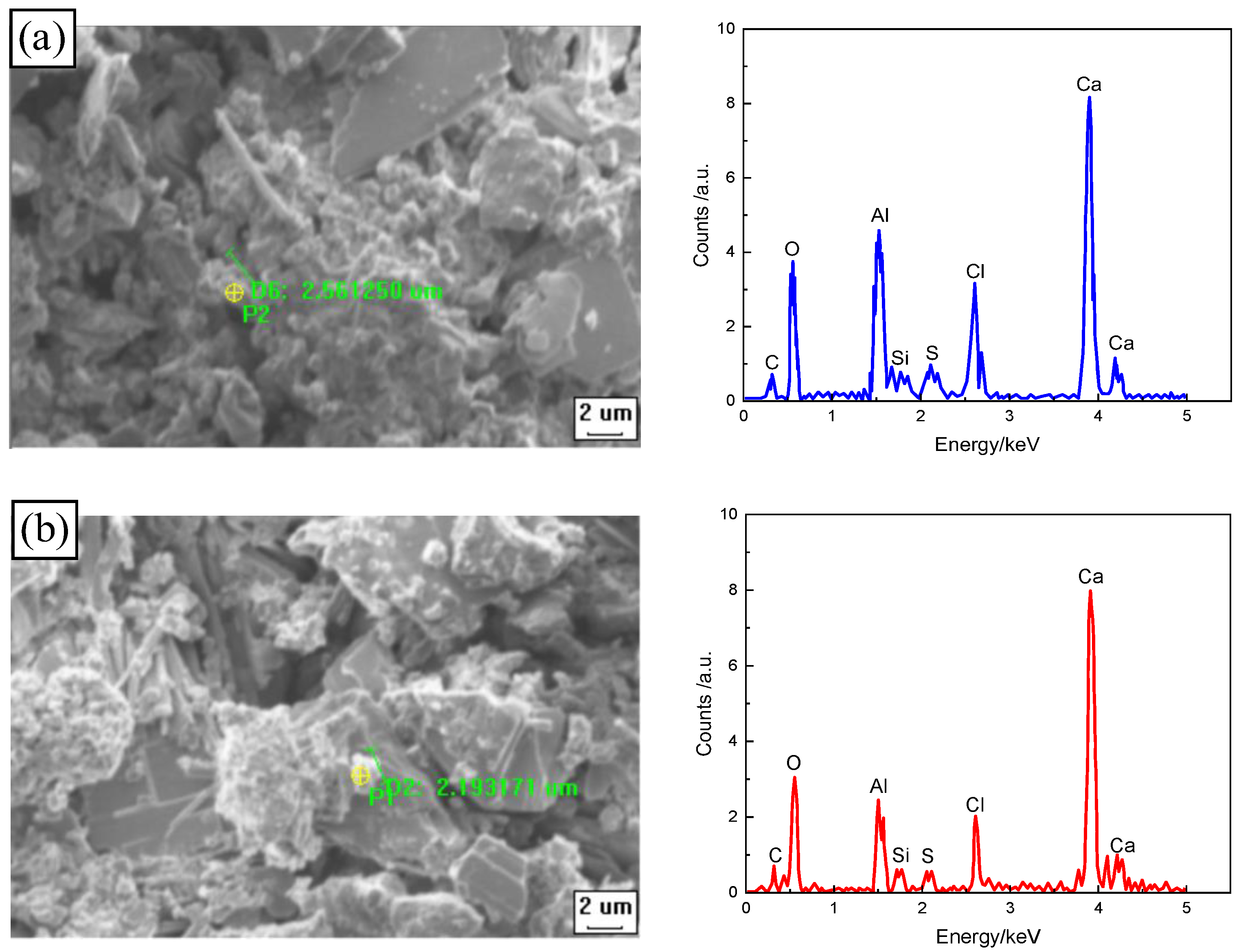
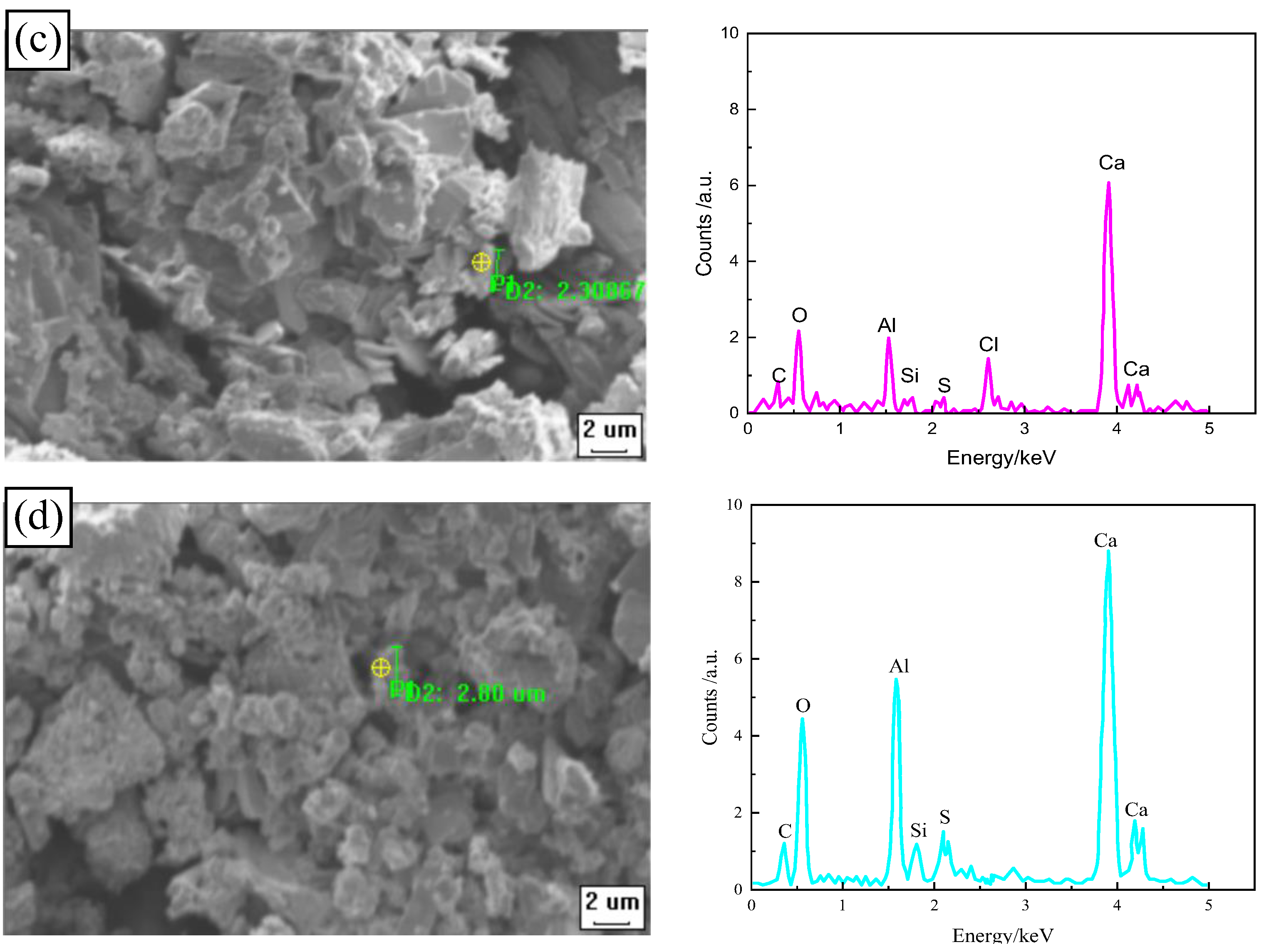
3.4. Analysis of Micro-Structure and Chemical Composition
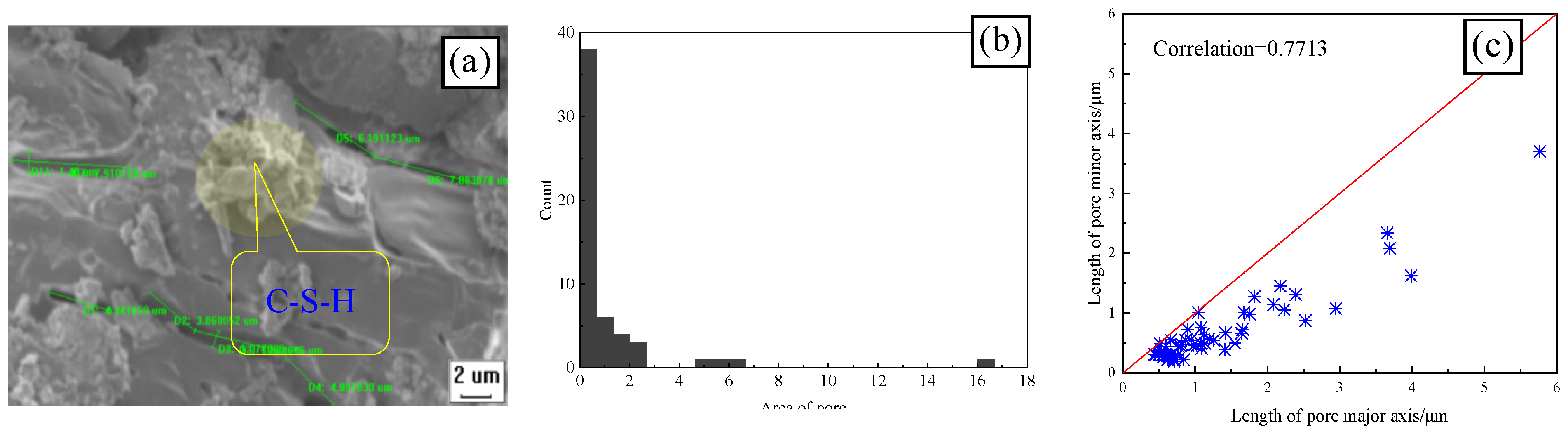
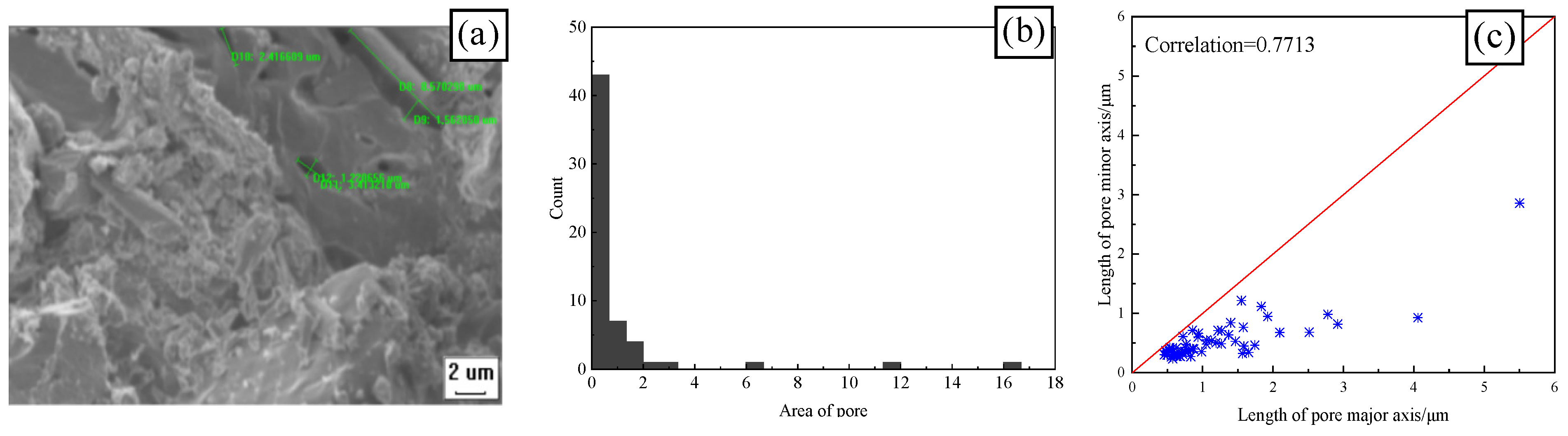
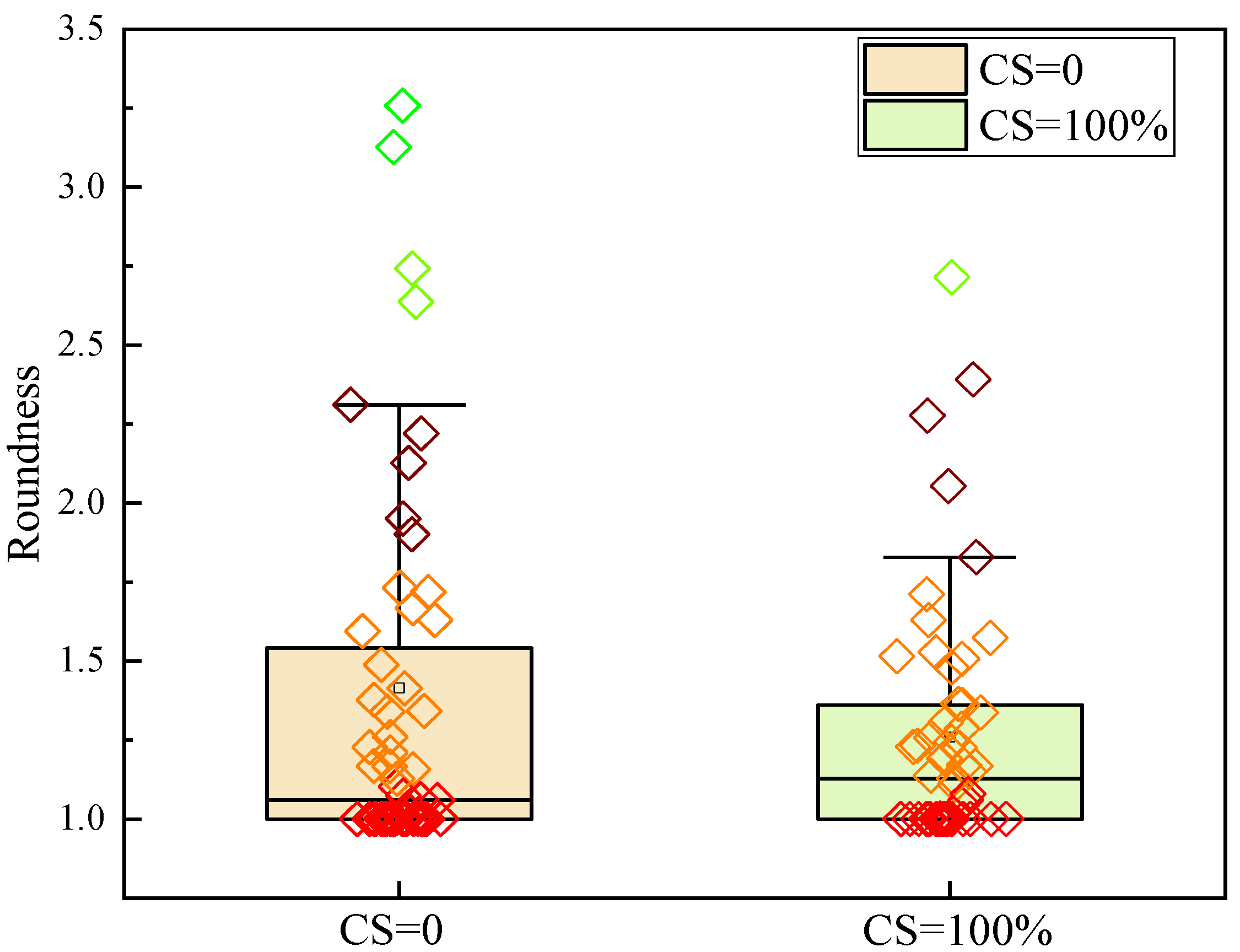
3.4.1. Effect of Freeze–Thaw on the Geometric Characteristics of CSRPC Pores
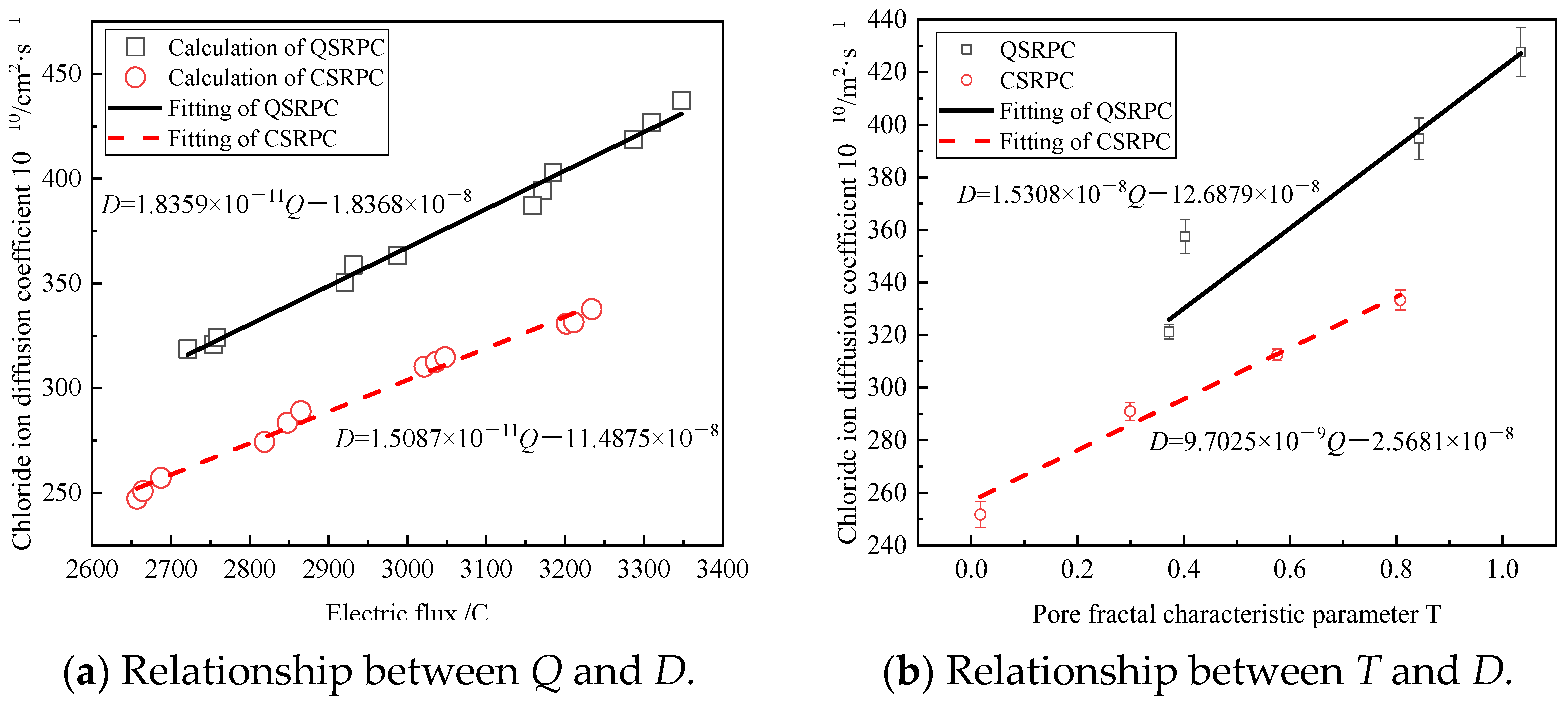
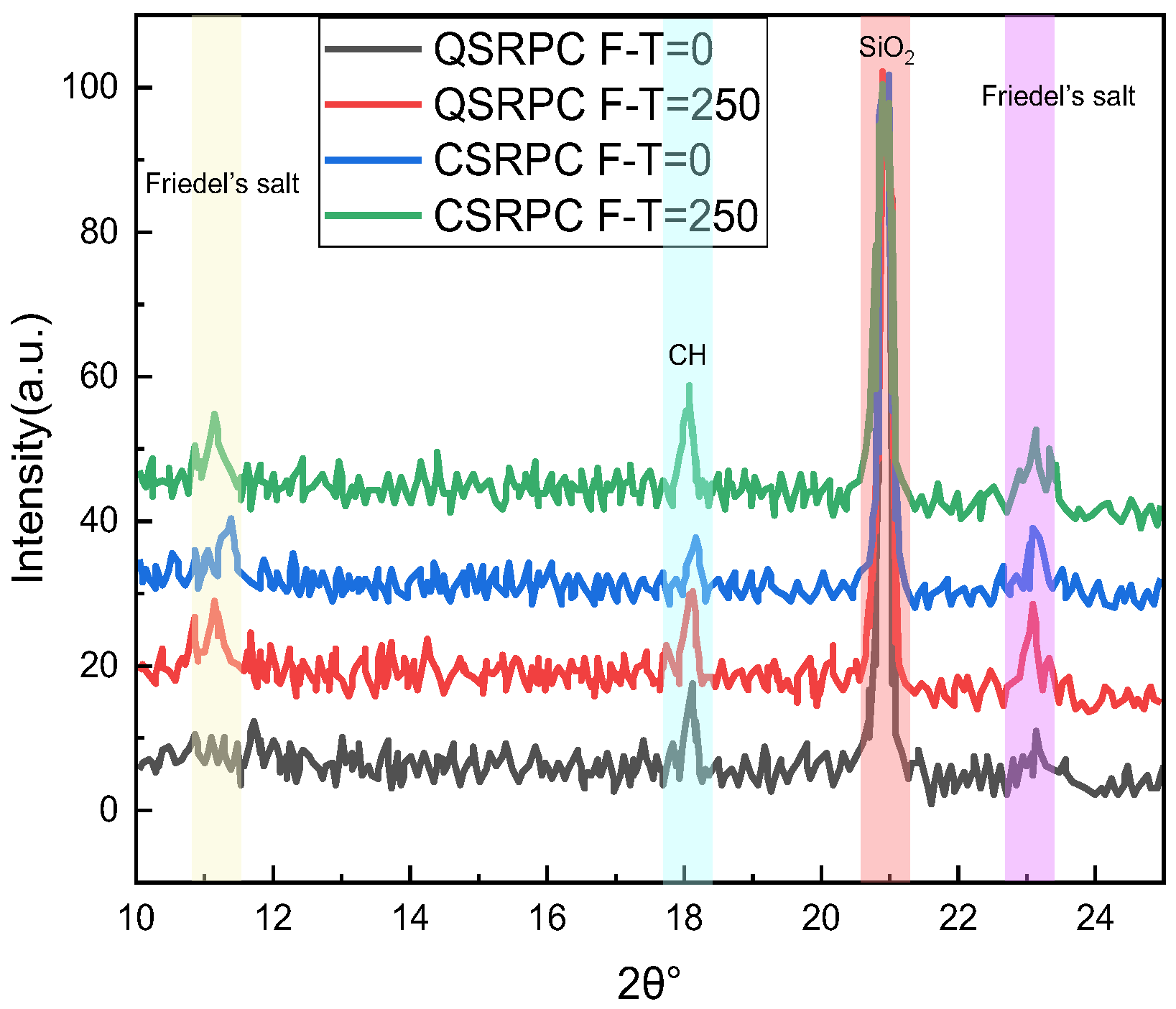
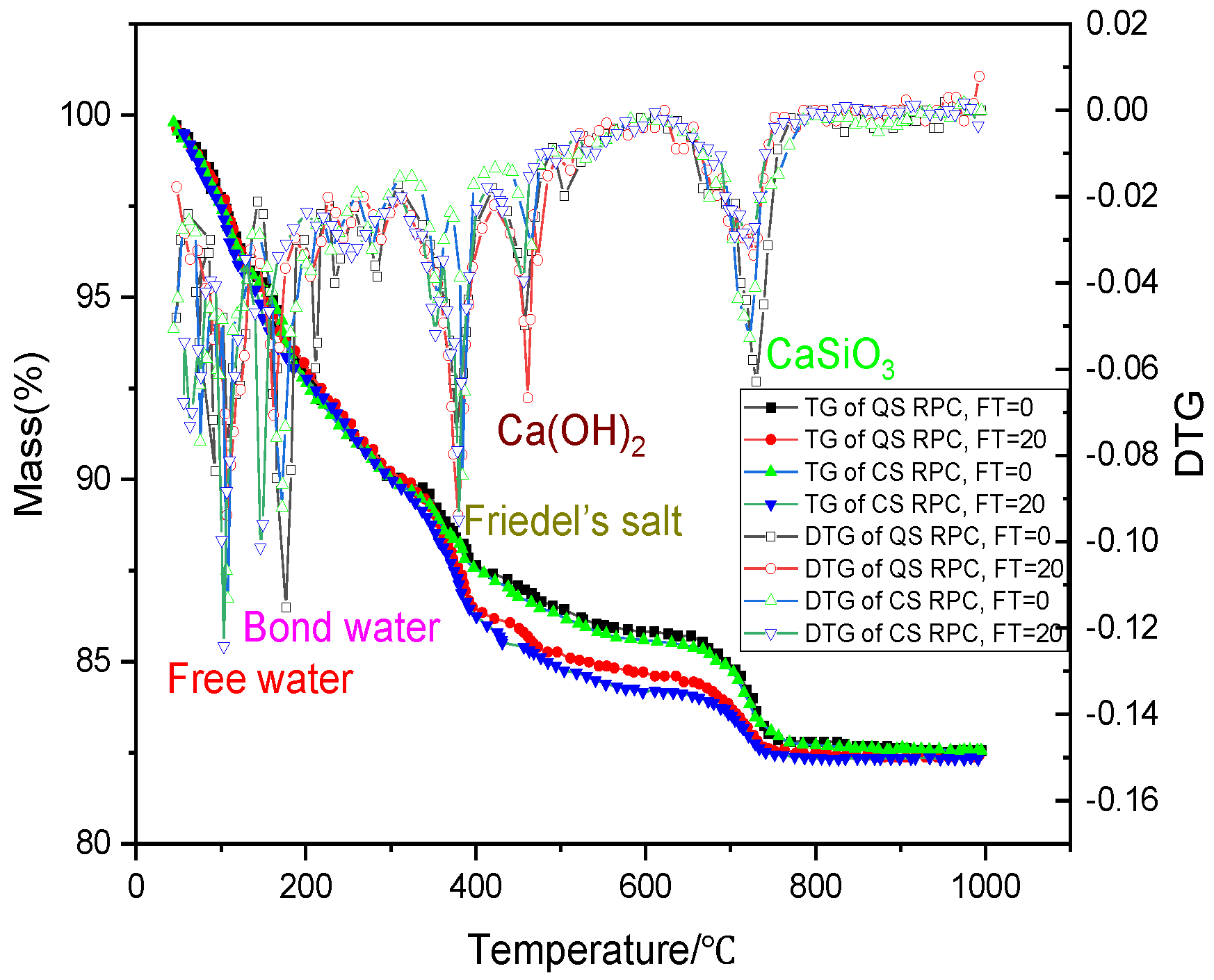
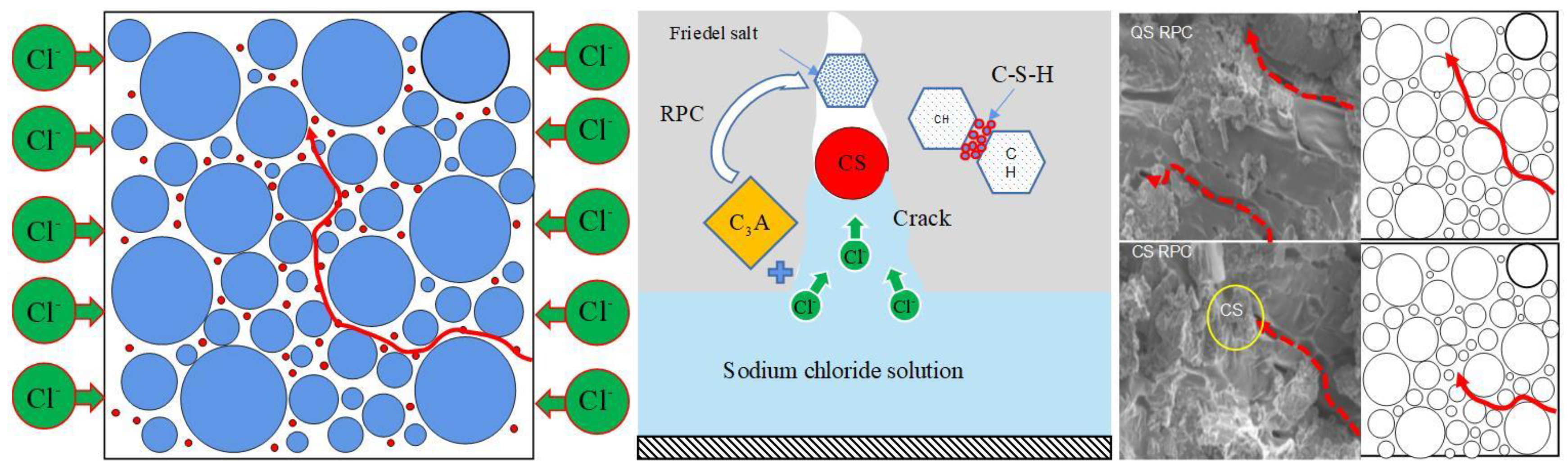
3.4.2. Effect of Freeze–Thaw Cycles on Chloride Diffusion Resistance of CSRPC
3.4.3. Effect of Freeze–Thaw Cycles on Chloride Diffusion of CSRPC
4. Conclusions
- (1)
- When the substitution rate of CS reaches 70%, the 28d UCS of CSRPC reaches the maximum; when it is lower than this substitution rate, CS shows pozzolanic activity, generating a small amount of C-S-H gel to cement the aggregate; and when it is greater than this substitution rate, the C-S-H gel reacts with water to cause the volume to expand, causing RPC to crack. At the same freeze–thaw cycles, the 28d UCS of CSRPC with a 100% CS substitution rate is higher than QSRPC, indicating that CSRPC has better freeze–thaw damage resistance than QSRPC.
- (2)
- With the increase in freeze–thaw cycles, the proportion of micro-pores gradually decreases, while the proportion of meso-pores and macro-pores gradually increases. The substitution of CS for QS in RPC can effectively reduce the proportion of meso-pores and macro-pores and alleviate the degree of freeze–thaw damage of RPC. The active SiO2 in CS has pozzolanic activity, and the reaction with CH will lead to an increase in the curvature of the pore throat, a reduction in the connectivity of the pore, and an increase in chloride ion diffusion resistance.
- (3)
- The fractal dimensions of different sizes of pores are determined, and the pore fractal characteristic parameter T is used to characterize the pore complexity and resistance to the chloride ion penetration of CSRPC. Under freeze–thaw cycles, the chloride ion diffusion coefficient of CSRPC with different CS substitution rates has a linear relationship with the pore fractal dimension.
- (4)
- When chloride ion diffuses into RPC, one part is absorbed and solidified by C-S-H gel, and the other part reacts with aluminum hydrate to generate Friedel’s salt, whose volume will expand when encountering water, filling small pores, refining large pores, and increasing the compactness of RPC after freeze–thaw damage. The active silica in CS reacts with the cement hydration product CH to form C-S-H gel, enhancing the chloride ion diffusion resistance of CSRPC after freeze–thaw cycles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bao, H.; Zhang, X.; Wang, H. Research progress on the separation of iron and silicon from copper slag. Nonferrous Met. Sci. Eng. 2021, 12, 30–38. [Google Scholar]
- Hao, J.; Dou, Z.H.; Zhang, T.A.; Jiang, B.C.; Wang, K.; Wan, X.Y. Manufacture of wear-resistant cast iron and copper-bearing antibacterial stainless steel from molten copper slag via vortex smelting reduction. J. Clean. Prod. 2022, 375, 134202. [Google Scholar] [CrossRef]
- He, Z.W.; Hu, X.J.; Chou, K.C. Synergetic modification of industrial basic oxygen furnace slag and copper slag for efficient iron recovery. Process Saf. Environ. Prot. 2022, 165, 487–495. [Google Scholar] [CrossRef]
- Wang, K.; Liu, Y.; Jiang, B. Recovery of Au, Ag and Cu from Copper Slag by Vortex Dilution Method. Rare Met. Mater. Eng. 2021, 50, 3417–3421. [Google Scholar]
- Zuo, Z.L.; Feng, Y.; Dong, X.J.; Luo, S.Y.; Ren, D.D. Advances in recovery of valuable metals and waste heat from copper slag. Fuel Process. Technol. 2022, 235, 107361. [Google Scholar] [CrossRef]
- Holland, K.; Eriç, R.; Taskinen, P.; Jokilaakso, A. Upgrading copper slag cleaning tailings for re-use. Miner. Eng. 2019, 133, 35–42. [Google Scholar] [CrossRef]
- Luo, Y.; Zhou, X.; Luo, Z.; Ma, H.; Wei, Y.; Liu, Q. A novel iron phosphate cement derived from copper smelting slag and its early age hydration mechanism. Cem. Concr. Compos. 2022, 133, 104653. [Google Scholar] [CrossRef]
- Chen, S.; Gao, M.; Lin, W.; Liang, J.; Li, D. Effects of incorporating large quantities of copper tailings with various particle sizes on the strength and pore structure of cement-based materials. Constr. Build. Mater. 2022, 329, 127150. [Google Scholar] [CrossRef]
- Ghazi, A.B.; Jamshidi-Zanjani, A.; Nejati, H. Clinkerisation of copper tailings to replace Portland cement in concrete construction. J. Build. Eng. 2022, 51, 104275. [Google Scholar] [CrossRef]
- Alp, İ.; Deveci, H.; Süngün, H. Utilization of flotation wastes of copper slag as raw material in cement production. J. Hazard. Mater. 2008, 159, 390–395. [Google Scholar] [CrossRef]
- Ali, M.M.; Agarwal, S.K.; Pahuja, A. Potentials of copper slag utilisation in the manufacture of ordinary Portland cement. Adv. Cem. Res. 2013, 25, 208–216. [Google Scholar] [CrossRef]
- Pavez, O.; Nazer, A.; Rivera, O. Copper slag from different dumps in the Atacama Region used in mortars as partial replacement of cement. Materia 2019, 24. [Google Scholar] [CrossRef]
- Li, Z. The Replacement of Granulated Copper Slag for Sand Concrete. J. Qingdao Inst. Archit. Eng. 2003, 24, 20–22. [Google Scholar]
- Juan, Z.Y. Application of shrend copper ash as substitute of sand in architectural work. Guangxi Water Resour. Hydropower Eng. 2004, 4, 22–24. [Google Scholar]
- Ambily, P.S.; Umarani, C.; Ravisankar, K.; Prem, P.R.; Bharatkumar, B.H.; Iyer, N.R. Studies on ultra high performance concrete incorporating copper slag as fine aggregate. Constr. Build. Mater. 2015, 77, 233–240. [Google Scholar] [CrossRef]
- Richard, P.; Cheyrezy, M. Composition of reactive powder concretes. Cem. Concr. Res. 1995, 25, 1501–1511. [Google Scholar] [CrossRef]
- Khitab, A.; Kırgız, M.S.; Nehdi, M.L.; Mirza, J.; Galdino, A.G.S.; Pour, A.K. Mechanical thermal durability and microstructural behavior of hybrid waste-modified green reactive powder concrete. Constr. Build. Mater. 2022, 344, 128184. [Google Scholar] [CrossRef]
- Sreekumaran, S.; Mohan, K.S.R. Low-Velocity impact resistance of reactive powder concrete modified using ground granulated blast furnace slag and rice husk ash. Constr. Build. Mater. 2022, 341, 127891. [Google Scholar] [CrossRef]
- Vigneshwari, M.; Arunachalam, K.; Angayarkanni, A. Replacement of silica fume with thermally treated rice husk ash in Reactive Powder Concrete. J. Clean. Prod. 2018, 188, 264–277. [Google Scholar] [CrossRef]
- Yazıcı, H.; Yiğiter, H.; Karabulut, A.Ş.; Baradan, B. Utilization of fly ash and ground granulated blast furnace slag as an alternative silica source in reactive powder concrete. Fuel 2008, 87, 2401–2407. [Google Scholar] [CrossRef]
- Tian, W.; Liu, Y.; Wang, M.; Wang, W. Performance and economic analyses of low-energy ohmic heating cured sustainable reactive powder concrete with dolomite powder as fine aggregates. J. Clean. Prod. 2021, 329, 129692. [Google Scholar] [CrossRef]
- Ying, L.X.; Jun, L.; Yuan, L.Z.; Li, H.; Kun, C.J. Preparation and properties of reactive powder concrete by using titanium slag aggregates. Constr. Build. Mater. 2020, 234, 117342. [Google Scholar]
- Xue, G.; Fu, Q.; Xu, S.; Li, J.J. Macroscopic mechanical properties and microstructure characteristics of steel slag fine aggregate concrete. J. Build. Eng. 2022, 56, 104742. [Google Scholar] [CrossRef]
- Sun, R.J.; Lu, W.; Ma, C.Y.; Tawfek, A.M.; Guan, Y.H.; Hu, X.L.; Zhang, H.Z.; Ling, Y.F.; Šavija, B. Effect of crack width and wet-dry cycles on the chloride penetration resistance of engineered cementitious composite (ECC). Constr. Build. Mater. 2022, 352, 129030. [Google Scholar] [CrossRef]
- Zhu, C.; Liu, X.G.; Liu, C.; Yu, W.H.; Bai, G.L. Study on the chloride ion transport mechanism of recycled mixed aggregate concrete based on evolution characteristics of pore structure. Constr. Build. Mater. 2022, 353, 129101. [Google Scholar] [CrossRef]
- Guo, Y.C.; Wu, S.L.; Yu, Z.H.; Shen, A.Q.; Yin, L.; Xue, C.Z. Pore structure characteristics and performance of construction waste composite powder-modified concrete. Constr. Build. Mater. 2021, 269, 121262. [Google Scholar] [CrossRef]
- Jin, S.S.; Zheng, G.P.; Yu, J. A micro freeze-thaw damage model of concrete with fractal dimension. Constr. Build. Mater. 2020, 257, 119434. [Google Scholar] [CrossRef]
- GB/T 31387-2015; Reactive Powder Concrete. Standards Press of China: Beijing, China, 2015.
- GB/T 50082-2009; Standard for Test Method of Long-Term Performance and Durability of Ordinary Concrete. Standards Press of China: Beijing, China, 2009.
- Kun, W.; Yu, Z.H.; Jie, L. Application of NMR technology in characterization of petrophysics and pore structure. Chin. J. Sci. Instrum. 2020, 41, 101–114. [Google Scholar]
- Lee, S.H.; Kim, H.J.; Sakai, E.; Daimon, M. Effect of particle size distribution of fly ash–cement system on the fluidity of cement pastes. Cem. Concr. Res. 2003, 33, 763–768. [Google Scholar] [CrossRef]
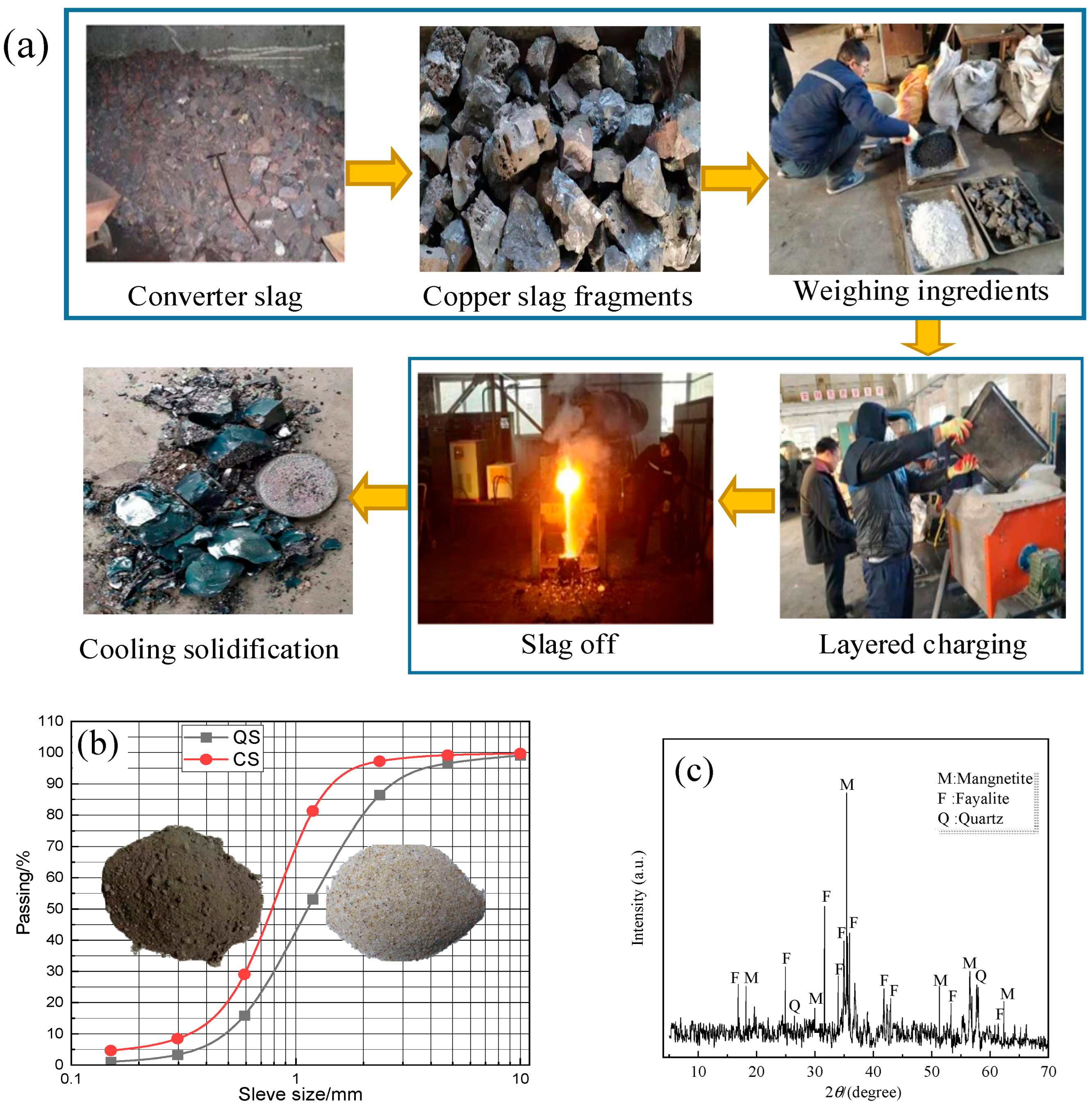


| Physical Parameters | Loose Unit Weight/g | Density/g·cm−3 | Mohs Hardness Degrees | Large Fragment Diameter/mm |
|---|---|---|---|---|
| Results | 2.0~2.4 | 3.5~4.3 | 7~9 | 4.25~20 |
| Chemical Composition | Fe2O3 | CuO | CaO | SiO2 | Al2O3 | Mn2O3 | Na2O | Others |
|---|---|---|---|---|---|---|---|---|
| Content/% | 18.29 | 1.2 | 32.5 | 29.11 | 11.20 | 0.42 | 0.58 | 6.7 |
| Chemical Composition/% | Cement Burning Loss/% | Fineness/% | |||||
|---|---|---|---|---|---|---|---|
| CaO | SiO2 | Al2O3 | Fe2O3 | MgO | SO3 | ||
| 64.37 | 23.27 | 3.85 | 4.57 | 2.37 | 2.5 | 3.5 | 6 |
| Particle Size Distribution | Median Diameter/μm | Specific Surface Area/m2·g−1 | |||
|---|---|---|---|---|---|
| 2.6 | 1.6 | 1.3 | |||
| Proportion/% | 31 | 57 | 12 | 1.6 | 14.3 |
| Chemical Composition | SiO2 | C | CaO | Fe2O3 | MgO | Na2O | K2O | Silica Fume Burning Loss |
|---|---|---|---|---|---|---|---|---|
| Content/% | 92.95 | 2.06 | 0.95 | 0.49 | 0.37 | 0.16 | 0.87 | 2.2 |
| NO. | CS Substitution Rate | Freeze–Thaw Cycles | Freeze–Thaw Condition |
|---|---|---|---|
| A1 | 0 | 0 | - |
| A2 | 50 | 0 | |
| A3 | 70 | 0 | |
| A4 | 100 | 0 | |
| B1 | 0 | 50 | Freezing temperature = −20 °C, Thawing temperature = 20 °C |
| B2 | 50 | 50 | |
| B3 | 70 | 50 | |
| B4 | 100 | 50 | |
| C1 | 0 | 100 | |
| C2 | 0 | 150 | |
| C3 | 0 | 200 | |
| C4 | 0 | 250 | |
| D1 | 100 | 100 | |
| D2 | 100 | 150 | |
| D3 | 100 | 200 | |
| D4 | 100 | 250 |
| NO. | Spectral Area | Total Spectral Area | Spectral Area Growth Rate/% | Proportion | ||||
|---|---|---|---|---|---|---|---|---|
| Micro-Pore | Meso-Pore | Macro-Pore | Micro-Pore | Meso-Pore | Macro-Pore | |||
| A1 | 1864.25 | 672.15 | 7.21 | 2622.61 | - | 71.08 | 25.63 | 3.29 |
| A2 | 1635.21 | 623.58 | 6.86 | 2334.65 | −10.98 | 70.04 | 26.71 | 3.25 |
| A3 | 1513.58 | 601.87 | 6.14 | 2178.59 | −16.93 | 69.48 | 27.63 | 2.90 |
| A4 | 1378.39 | 587.35 | 5.87 | 2018.61 | −23.03 | 68.28 | 29.10 | 2.62 |
| B1 | 1935.49 | 688.27 | 8.69 | 2715.45 | - | 71.28 | 25.35 | 3.38 |
| B2 | 1727.15 | 665.89 | 7.25 | 2480.29 | −8.66 | 69.64 | 26.85 | 3.52 |
| B3 | 1686.75 | 633.48 | 6.28 | 2396.51 | −11.75 | 70.38 | 26.43 | 3.18 |
| B4 | 1536.78 | 592.15 | 6.12 | 2195.05 | −19.16 | 70.01 | 26.98 | 3.01 |
| C1 | 2257.64 | 757.21 | 10.35 | 3125.2 | - | 72.24 | 24.23 | 3.53 |
| C2 | 2536.25 | 925.43 | 23.87 | 3585.55 | 14.73 | 70.74 | 25.81 | 3.45 |
| C3 | 2775.38 | 1238.79 | 56.21 | 4170.38 | 33.44 | 66.55 | 29.70 | 3.75 |
| C4 | 3162.41 | 1765.21 | 77.15 | 5104.77 | 47.47 | 61.95 | 34.58 | 3.47 |
| D1 | 1931.47 | 535.42 | 4.15 | 2541.04 | - | 76.01 | 23.07 | 2.92 |
| D2 | 2127.36 | 713.45 | 15.47 | 2936.28 | 15.55 | 72.45 | 24.30 | 3.25 |
| D3 | 2298.75 | 1075.27 | 22.36 | 3496.38 | 37.60 | 65.75 | 30.75 | 3.50 |
| D4 | 2871.43 | 1445.86 | 59.32 | 4476.61 | 76.17 | 64.14 | 32.30 | 3.56 |
| NO. | /% | X × 10−3/μm | n | ||||
|---|---|---|---|---|---|---|---|
| C1 | 1.56 | 2.35 | 3.25 | 2.63 | 1.69 | 1509.27 | 0.3724 |
| C2 | 1.58 | 2.38 | 3.87 | 3.53 | 2.28 | 1621.37 | 0.4025 |
| C3 | 1.61 | 2.41 | 4.36 | 4.27 | 2.50 | 1725.35 | 0.8425 |
| C4 | 1.63 | 2.43 | 4.78 | 4.85 | 2.52 | 1921.28 | 1.0341 |
| D1 | 1.47 | 2.21 | 2.71 | 3.04 | 2.37 | 1623.84 | 0.0174 |
| D2 | 1.49 | 2.25 | 2.97 | 5.35 | 2.95 | 1735.96 | 0.2990 |
| D3 | 1.53 | 2.28 | 3.12 | 8.29 | 3.04 | 1921.08 | 0.5758 |
| D4 | 1.58 | 2.31 | 3.47 | 15.09 | 3.94 | 1978.85 | 0.8075 |
| RPC | Freeze–Thaw Cycles | Free Water (%) | Bond Water (%) | Friedel’s Salt (%) | Ca(OH)2 (%) | CaSiO3 (%) |
|---|---|---|---|---|---|---|
| QSRPC | 0 | 10.35 | 22.36 | 4.87 | 12.43 | 19.26 |
| QSRPC | 250 | 12.17 | 25.48 | 8.35 | 15.46 | 18.51 |
| CSRPC | 0 | 11.57 | 18.24 | 3.27 | 8.37 | 14.35 |
| CSRPC | 250 | 8.75 | 16.78 | 6.68 | 10.25 | 8.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Liu, X.; Chen, M.; Tian, L.; Liu, J. A Study on Chloride Corrosion Resistance of Reactive Powder Concrete (RPC) with Copper Slag Replacing Quartz Sand under Freeze–Thaw Conditions. Materials 2024, 17, 212. https://doi.org/10.3390/ma17010212
Li J, Liu X, Chen M, Tian L, Liu J. A Study on Chloride Corrosion Resistance of Reactive Powder Concrete (RPC) with Copper Slag Replacing Quartz Sand under Freeze–Thaw Conditions. Materials. 2024; 17(1):212. https://doi.org/10.3390/ma17010212
Chicago/Turabian StyleLi, Jun, Xianzhang Liu, Minghao Chen, Lijun Tian, and Jiao Liu. 2024. "A Study on Chloride Corrosion Resistance of Reactive Powder Concrete (RPC) with Copper Slag Replacing Quartz Sand under Freeze–Thaw Conditions" Materials 17, no. 1: 212. https://doi.org/10.3390/ma17010212






