Quantum-Size Effects in Ultra-Thin Gold Films on Pt(111) Surface
Abstract
:1. Introduction
2. Calculation Method
3. Calculation Results and Discussion
3.1. Crystal Structure
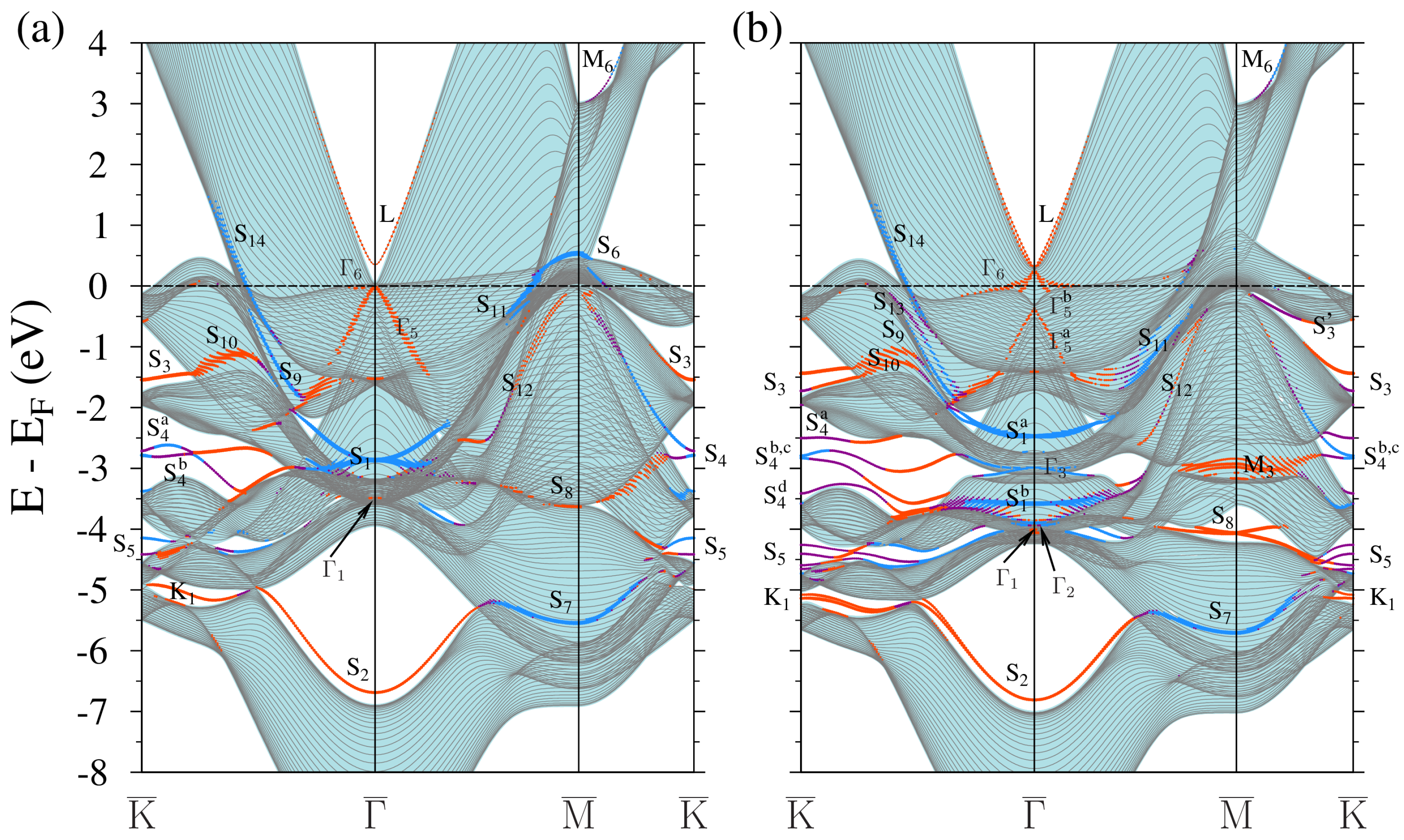
3.2. Electronic Structure
3.2.1. Clean Pt(111) and Au(111) Surfaces
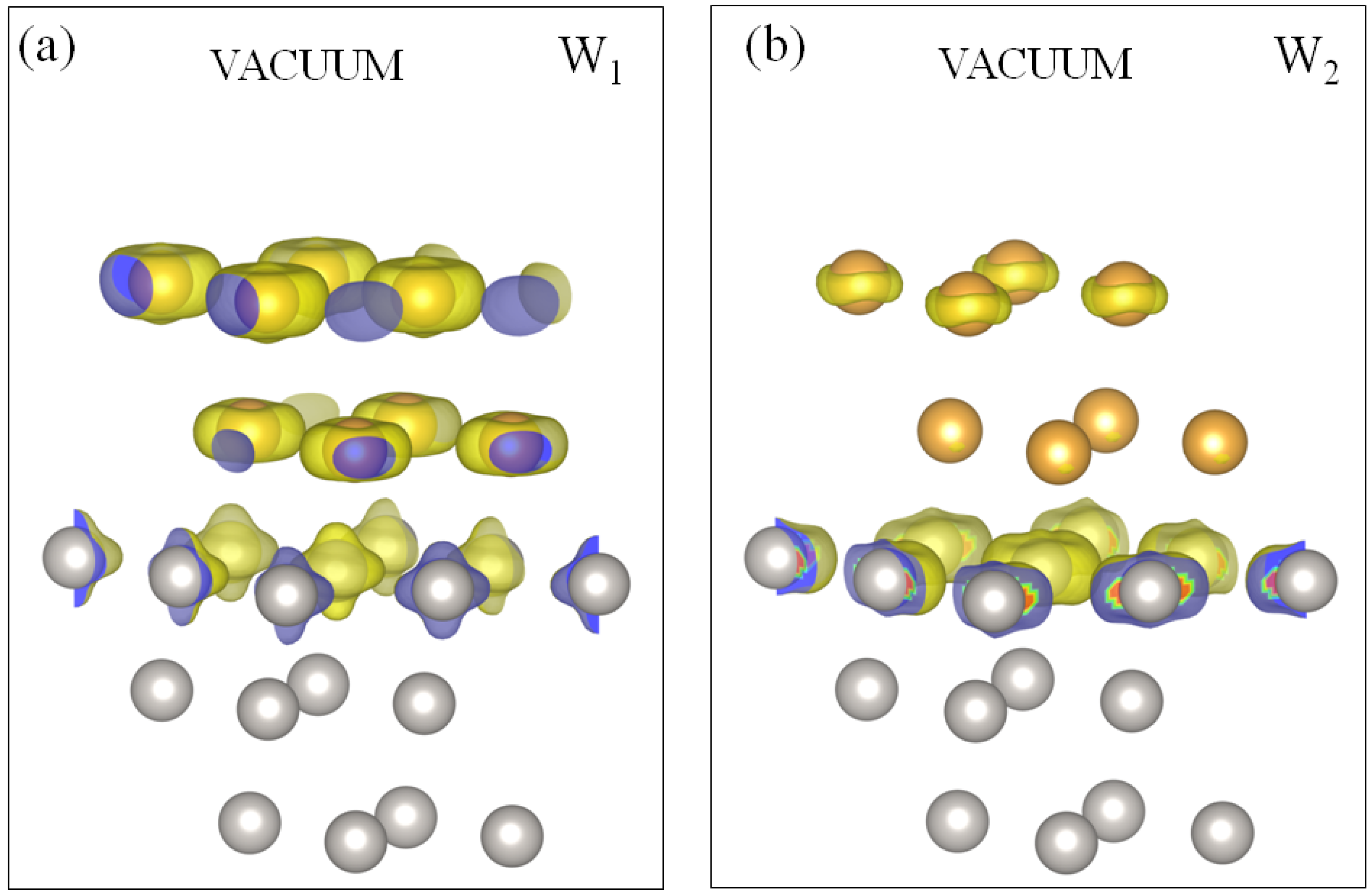
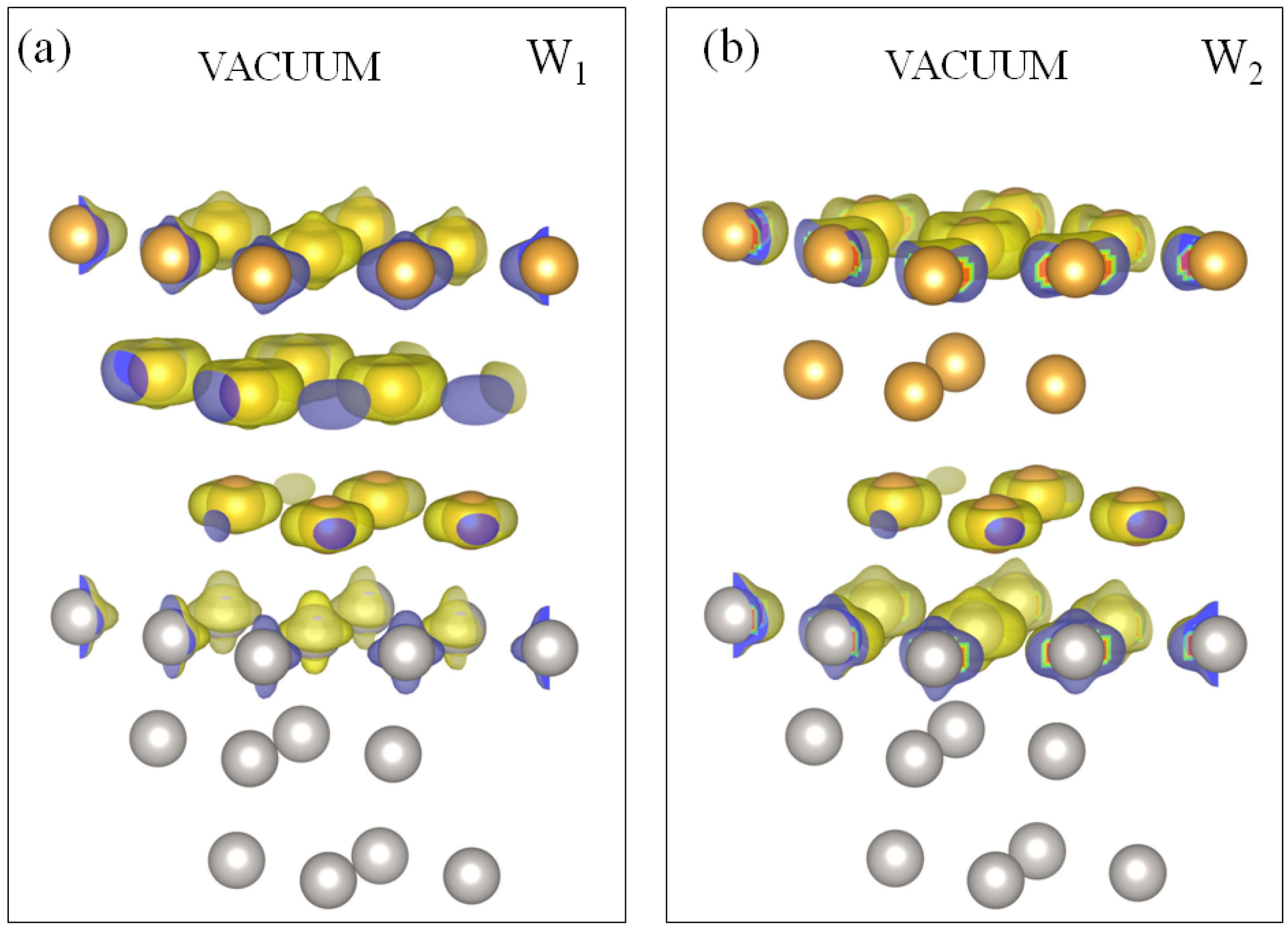
3.2.2. nML-Au/Pt(111) Systems
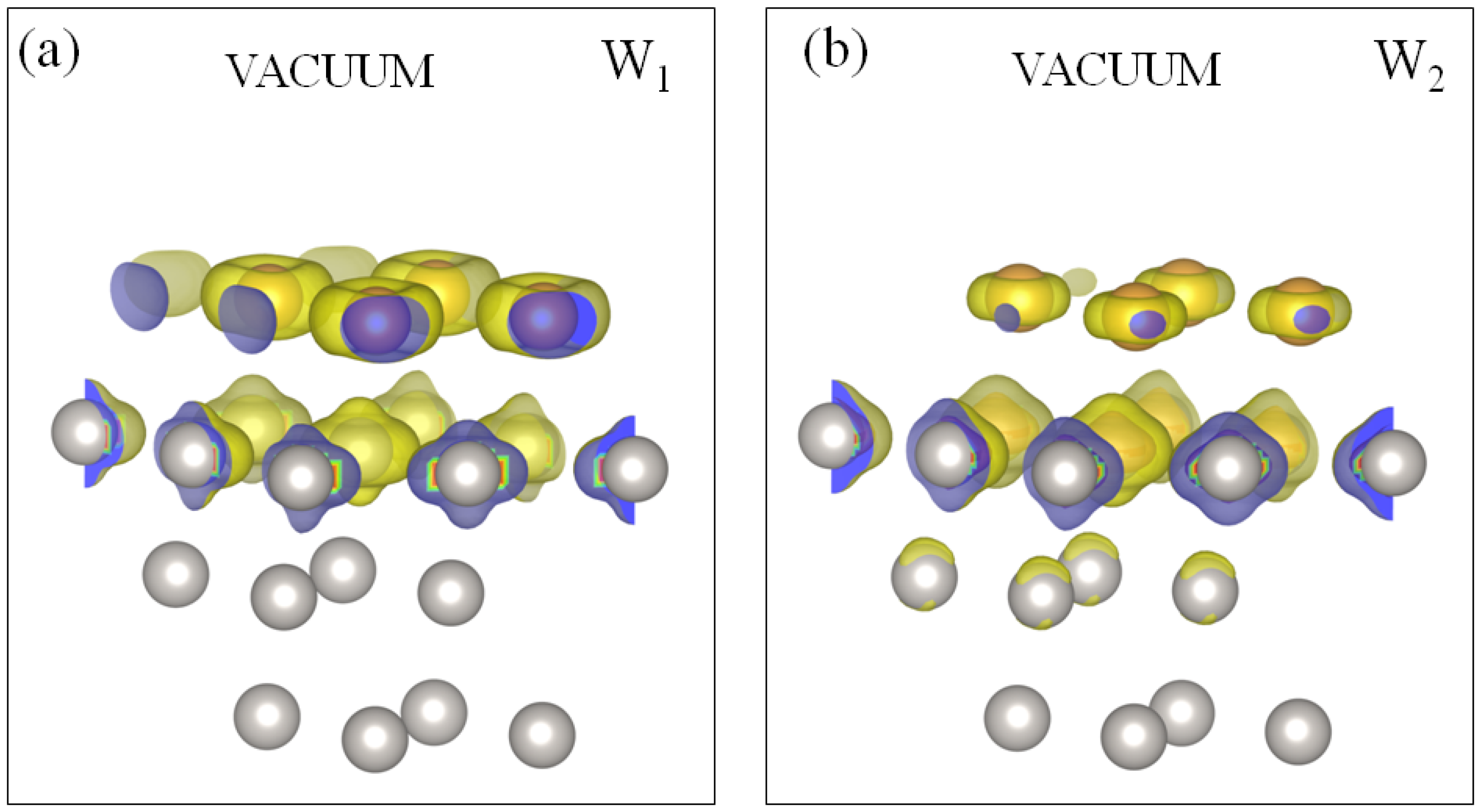
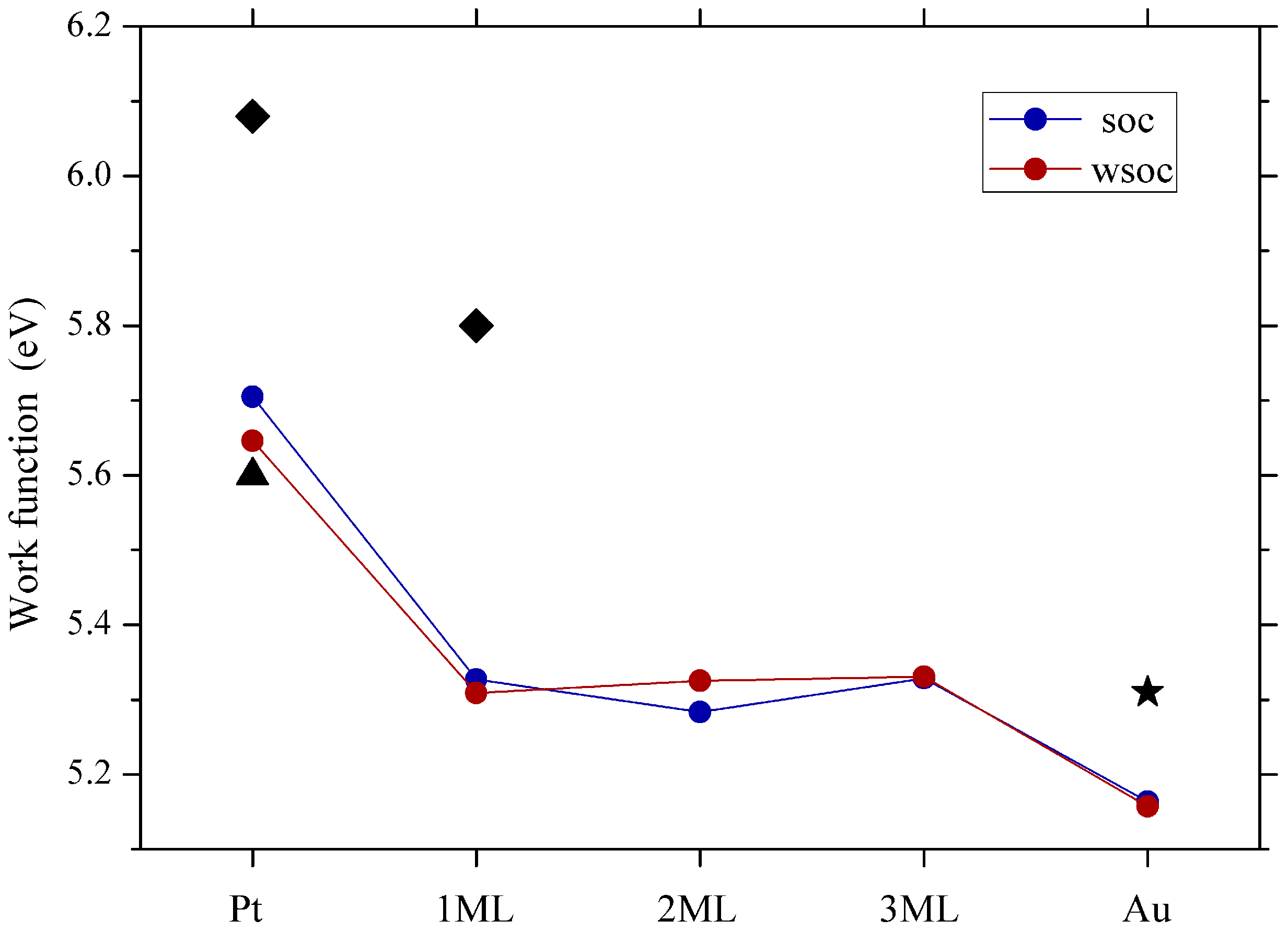
3.3. Work Function
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Thomas, R.E. Interference Effects in the Reflection of Low-Energy Electrons from Thin Films of Au on Ir. J. Appl. Phys. 1970, 41, 5330–5334. [Google Scholar] [CrossRef]
- Jaklevic, R.C.; Lambe, J.; Mikkor, M.; Vassell, W.C. Observation of Electron Standing Waves in a Crystalline Box. Phys. Rev. Lett. 1971, 26, 88–92. [Google Scholar] [CrossRef]
- Chiang, T.C. Photoemission studies of quantum well states in thin films. Surf. Sci. Rep. 2000, 39, 181–235. [Google Scholar] [CrossRef]
- Lindgren, S.A.; Walldén, L. Discrete Valence-Electron States in Thin Metal Overlayers on a Metal. Phys. Rev. Lett. 1987, 59, 3003–3006. [Google Scholar] [CrossRef]
- Miller, T.; Samsavar, A.; Franklin, G.E.; Chiang, T.C. Quantum-Well States in a Metallic System: Ag on Au(111). Phys. Rev. Lett. 1988, 61, 1404–1407. [Google Scholar] [CrossRef]
- Clemens, W.; Kachel, T.; Rader, O.; Vescovo, E.; Blügel, S.; Carbone, C.; Eberhardt, W. Quantum size effects and the enhancement of the exchange splitting in ultrathin Co overlayers on Cu (100). Solid State Commun. 1992, 81, 739–744. [Google Scholar] [CrossRef]
- Ortega, J.E.; Himpsel, F.J. Quantum well states as mediators of magnetic coupling in superlattices. Phys. Rev. Lett. 1992, 69, 844–847. [Google Scholar] [CrossRef]
- Garrison, K.; Chang, Y.; Johnson, P.D. Spin polarization of quantum well states in copper thin films deposited on a Co(001) substrate. Phys. Rev. Lett. 1993, 71, 2801–2804. [Google Scholar] [CrossRef]
- Carbone, C.; Vescovo, E.; Rader, O.; Gudat, W.; Eberhardt, W. Exchange split quantum well states of a noble metal film on a magnetic substrate. Phys. Rev. Lett. 1993, 71, 2805–2808. [Google Scholar] [CrossRef]
- Mankey, G.J.; Willis, R.F.; Ortega, J.E.; Himpsel, F.J. Quantum size effects in ultrathin Cu(100) films. J. Vac. Sci. Technol. A 1994, 12, 2183–2186. [Google Scholar] [CrossRef]
- Johnson, P.D.; Garrison, K.; Dong, Q.; Smith, N.V.; Li, D.; Mattson, J.; Pearson, J.; Bader, S.D. Hybridization and the effective mass of quantum-well states in magnetic multilayers. Phys. Rev. B 1994, 50, 8954–8956. [Google Scholar] [CrossRef]
- Shikin, A.M.; Adamchuk, V.K. Quantum confinement effects in thin metal layers on the surface of single crystals and their analysis. Phys. Solid State 2008, 50, 1170–1185. [Google Scholar] [CrossRef]
- Altfeder, I.B.; Matveev, K.A.; Chen, D.M. Electron Fringes on a Quantum Wedge. Phys. Rev. Lett. 1997, 78, 2815–2818. [Google Scholar] [CrossRef]
- Su, W.B.; Chang, S.H.; Jian, W.B.; Chang, C.S.; Chen, L.J.; Tsong, T.T. Correlation between Quantized Electronic States and Oscillatory Thickness Relaxations of 2D Pb Islands on Si(111)-(7 × 7) Surfaces. Phys. Rev. Lett. 2001, 86, 5116–5119. [Google Scholar] [CrossRef]
- Starfelt, S.; Johansson, L.S.O.; Zhang, H.M. STM/STS and photoemission study of Ag thin films on Ga/Si(111) (3 × 3) R30°. Surf. Sci. 2019, 682, 25–32. [Google Scholar] [CrossRef]
- Valla, T.; Kralj, M.; Siber, A.; Milun, M.; Pervan, P.; Johnson, P.D.; Woodruff, D.P. Oscillatory electron-phonon coupling in ultra-thin silver films on V(100). J. Phys. Condens. Matter 2000, 12, L477–L482. [Google Scholar] [CrossRef]
- Corriol, C.; Silkin, V.M.; Sánchez-Portal, D.; Arnau, A.; Chulkov, E.V.; Echenique, P.M.; von Hofe, T.; Kliewer, J.; Kröger, J.; Berndt, R. Role of Elastic Scattering in Electron Dynamics at Ordered Alkali Overlayers on Cu(111). Phys. Rev. Lett. 2005, 95, 176802. [Google Scholar] [CrossRef]
- Özer, M.M.; Thompson, J.R.; Weitering, H.H. Hard superconductivity of a soft metal in the quantum regime. Nat. Phys. 2006, 2, 173–176. [Google Scholar] [CrossRef]
- Sklyadneva, I.Y.; Heid, R.; Bohnen, K.P.; Echenique, P.M.; Chulkov, E.V. Mass enhancement parameter in free-standing ultrathin Pb(111) films: The effect of spin-orbit coupling. Phys. Rev. B 2013, 87, 085440. [Google Scholar] [CrossRef]
- Otero, R.; Vázquez de Parga, A.L.; Miranda, R. Observation of preferred heights in Pb nanoislands: A quantum size effect. Phys. Rev. B 2002, 66, 115401. [Google Scholar] [CrossRef]
- Aballe, L.; Rogero, C.; Kratzer, P.; Gokhale, S.; Horn, K. Probing Interface Electronic Structure with Overlayer Quantum-Well Resonances: Al/Si(111). Phys. Rev. Lett. 2001, 87, 156801. [Google Scholar] [CrossRef] [PubMed]
- Kirchmann, P.S.; Wolf, M.; Dil, J.H.; Horn, K.; Bovensiepen, U. Quantum size effects in Pb-Si(111) investigated by laser-induced photoemission. Phys. Rev. B 2007, 76, 075406. [Google Scholar] [CrossRef]
- Hong, I.P.; Brun, C.; Patthey, F.; Sklyadneva, I.Y.; Zubizarreta, X.; Heid, R.; Silkin, V.M.; Echenique, P.M.; Bohnen, K.P.; Chulkov, E.V.; et al. Decay mechanisms of excited electrons in quantum-well states of ultrathin Pb islands grown on Si(111): Scanning tunneling spectroscopy and theory. Phys. Rev. B 2009, 80, 081409. [Google Scholar] [CrossRef]
- Kirchmann, P.S.; Rettig, L.; Zubizarreta, X.; Silkin, V.M.; Chulkov, E.V.; Bovensiepen, U. Quasiparticle lifetimes in metallic quantum-well nanostructures. Nat. Phys. 2010, 6, 782–785. [Google Scholar] [CrossRef]
- Muiño, R.D.; Sánchez-Portal, D.; Silkin, V.M.; Chulkov, E.V.; Echenique, P.M. Time-dependent electron phenomena at surfaces. Proc. Natl. Acad. Sci. USA 2011, 108, 971. [Google Scholar] [CrossRef] [PubMed]
- Paggel, J.J.; Wei, C.M.; Chou, M.Y.; Luh, D.A.; Miller, T.; Chiang, T.C. Atomic-layer-resolved quantum oscillations in the work function: Theory and experiment for Ag/Fe(100). Phys. Rev. B 2002, 66, 233403. [Google Scholar] [CrossRef]
- Ma, X.; Jiang, P.; Qi, Y.; Jia, J.; Yang, Y.; Duan, W.; Li, W.X.; Bao, X.; Zhang, S.B.; Xue, Q.K. Experimental observation of quantum oscillation of surface chemical reactivities. Proc. Natl. Acad. Sci. USA 2007, 104, 9204. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Qin, S.; Yao, W.; Niu, Q.; Chou, M.Y.; Shih, C.K. Quantum size effects on the work function of metallic thin film nanostructures. Proc. Natl. Acad. Sci. USA 2010, 107, 12761. [Google Scholar] [CrossRef]
- Kim, J.; Zhang, C.; Kim, J.; Gao, H.; Chou, M.Y.; Shih, C.K. Anomalous phase relations of quantum size effects in ultrathin Pb films on Si(111). Phys. Rev. B 2013, 87, 245432. [Google Scholar] [CrossRef]
- Liu, R.Y.; Huang, A.; Huang, C.C.; Lee, C.Y.; Lin, C.H.; Cheng, C.M.; Tsuei, K.D.; Jeng, H.T.; Matsuda, I.; Tang, S.J. Deeper insight into phase relations in ultrathin Pb films. Phys. Rev. B 2015, 92, 115415. [Google Scholar] [CrossRef]
- Zhang, Z.; Niu, Q.; Shih, C.K. “Electronic Growth” of Metallic Overlayers on Semiconductor Substrates. Phys. Rev. Lett. 1998, 80, 5381–5384. [Google Scholar] [CrossRef]
- Liu, X.; Wang, C.Z.; Hupalo, M.; Lin, H.Q.; Ho, K.M.; Tringides, M.C. Quantum confinement induced oscillatory electric field on a stepped Pb(111) film and its influence on surface reactivity. Phys. Rev. B 2014, 89, 041401. [Google Scholar] [CrossRef]
- Jia, Y.; Wu, B.; Weitering, H.H.; Zhang, Z. Quantum size effects in Pb films from first principles: The role of the substrate. Phys. Rev. B 2006, 74, 035433. [Google Scholar] [CrossRef]
- Nagao, T.; Han, G.; Hoang, C.; Wi, J.S.; Pucci, A.; Weber, D.; Neubrech, F.; Silkin, V.M.; Enders, D.; Saito, O.; et al. Plasmons in nanoscale and atomic-scale systems. Sci. Technol. Adv. Mater. 2010, 11, 054506. [Google Scholar] [CrossRef] [PubMed]
- Politano, A.; Chiarello, G. The influence of electron confinement, quantum size effects, and film morphology on the dispersion and the damping of plasmonic modes in Ag and Au thin films. Prog. Surf. Sci. 2015, 90, 144–193. [Google Scholar] [CrossRef]
- Li, X.D.; Chen, T.P.; Liu, Y.; Leong, K.C. Evolution of the localized surface plasmon resonance and electron confinement effect with the film thickness in ultrathin Au films. J. Nanopart. Res. 2015, 17, 67. [Google Scholar] [CrossRef]
- Pfnür, H.; Brand, C.; Jäger, M.; Rönspies, J.; Tegenkamp, C. Between one and two dimensions: Pb/Si(557) close to monolayer coverage. Surf. Sci. 2016, 643, 79–86. [Google Scholar] [CrossRef]
- Zubizarreta, X.; Chulkov, E.V.; Chernov, I.P.; Vasenko, A.S.; Aldazabal, I.; Silkin, V.M. Quantum-size effects in the loss function of Pb(111) thin films: An ab initio study. Phys. Rev. B 2017, 95, 235405. [Google Scholar] [CrossRef]
- Aballe, L.; Barinov, A.; Locatelli, A.; Heun, S.; Kiskinova, M. Tuning Surface Reactivity via Electron Quantum Confinement. Phys. Rev. Lett. 2004, 93, 196103. [Google Scholar] [CrossRef]
- Tringides, M.C.; Jałochowski, M.; Bauer, E. Quantum size effects in metallic nanostructures. Phys. Today 2007, 60, 50–54. [Google Scholar] [CrossRef]
- Wei, C.M.; Chou, M.Y. Theory of quantum size effects in thin Pb(111) films. Phys. Rev. B 2002, 66, 233408. [Google Scholar] [CrossRef]
- Speer, N.J.; Brinkley, M.K.; Liu, Y.; Wei, C.M.; Miller, T.; Chiang, T.C. Surface vs. bulk electronic structure of silver determined by photoemission. Europhys. Lett. 2009, 88, 67004. [Google Scholar] [CrossRef]
- Zangwill, A. Physics at Surfaces; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Davison, S.G.; Stȩślicka, M. Basic Theory of Surface States; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Lüth, H. Surface and Interfaces of Solids; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Silkin, I.V.; Koroteev, Y.M.; Echenique, P.M.; Chulkov, E.V. Formation of Surface and Quantum-Well States in Ultra Thin Pt Films on the Au(111) Surface. Materials 2017, 10, 1409. [Google Scholar] [CrossRef] [PubMed]
- Haruta, M. Size- and support-dependency in the catalysis of gold. Catal. Today 1997, 36, 153–166. [Google Scholar] [CrossRef]
- Meyer, R.; Lemire, C.; Shaikhutdinov, S.K.; Freund, H.J. Surface chemistry of catalysis by gold. Gold Bull. 2004, 37, 72–124. [Google Scholar] [CrossRef]
- Salmerón, M.; Ferrer, S.; Jazzar, M.; Somorjai, G.A. Photoelectron-spectroscopy study of the electronic structure of Au and Ag overlayers on Pt(100), Pt(111), and Pt(997) surfaces. Phys. Rev. B 1983, 28, 6758–6765. [Google Scholar] [CrossRef]
- Vogt, B.; Schmiedeskamp, B.; Heinzmann, U. Spin-resolved photoemission from epitaxial Au layers on Pt(111): Coverage dependence of the bandstructure and evidence of surface resonances. Z. Phys. B Condens. Matter 1990, 80, 359–364. [Google Scholar] [CrossRef]
- Kobiela, T.; Moors, M.; Linhart, W.; Cebula, I.; Krupski, A.; Becker, C.; Wandelt, K. Characterization of bimetallic Au-Pt(111) surfaces. Thin Solid Films 2010, 518, 3650–3657. [Google Scholar] [CrossRef]
- Krupski, K.; Moors, M.; Jóźwik, P.; Kobiela, T.; Krupski, A. Structure Determination of Au on Pt(111) Surface: LEED, STM and DFT Study. Materials 2015, 8, 2935–2952. [Google Scholar] [CrossRef]
- Feeley, G.M.; Hemmingson, S.L.; Campbell, C.T. Energetics of Au Adsorption and Film Growth on Pt(111) by Single-Crystal Adsorption Calorimetry. J. Phys. Chem. C 2019, 123, 5557–5561. [Google Scholar] [CrossRef]
- Sachtler, J.W.A.; Van Hove, M.A.; Bibérian, J.P.; Somorjai, G.A. Enhanced Reactivity of Ordered Monolayers of Gold on Pt(100) and Platinum on Au(100) Single-Crystal Surfaces. Phys. Rev. Lett. 1980, 45, 1601–1603. [Google Scholar] [CrossRef]
- Sachtler, J.W.A.; Somorjai, G.A. Influence of ensemble size on CO chemisorption and catalytic n-hexane conversion by Au-Pt(111) bimetallic single-crystal surfaces. J. Catal. 1983, 81, 77–94. [Google Scholar] [CrossRef]
- Yeates, R.C.; Somorjai, G.A. Surface structure sensitivity of alloy catalysis: Catalytic conversion of n-hexane over Au-Pt(111) and Au-Pt(100) alloy crystal surfaces. J. Catal. 1987, 103, 208–212. [Google Scholar] [CrossRef]
- Eyrich, M.; Diemant, T.; Hartmann, H.; Bansmann, J.; Behm, R.J. Interaction of CO with Structurally Well-Defined Monolayer PtAu/Pt(111) Surface Alloys. J. Phys. Chem. C 2012, 116, 11154–11165. [Google Scholar] [CrossRef]
- Stoppmanns, P.; Heidemann, B.; Irmer, N.; Müller, N.; Vogt, B.; Schmiedeskamp, B.; Heinzmann, U.; Tamura, E.; Feder, R. Au-induced surface state on Pt(111) revealed by spin-resolved photoemission with linearly polarized light. Phys. Rev. Lett. 1991, 66, 2645–2648. [Google Scholar] [CrossRef] [PubMed]
- Silkin, I.V.; Koroteev, Y.M.; Silkin, V.M.; Chulkov, E.V. Modification of a Shockley-Type Surface State on Pt(111) upon Deposition of Gold Thin Layers. Materials 2018, 11, 2569. [Google Scholar] [CrossRef] [PubMed]
- Wimmer, E.; Krakauer, H.; Weinert, M.; Freeman, A.J. Full-potential self-consistent linearized-augmented-plane-wave method for calculating the electronic structure of molecules and surfaces: O2 molecule. Phys. Rev. B 1981, 24, 864–875. [Google Scholar] [CrossRef]
- Available online: http://www.flapw.de (accessed on 2 December 2022).
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Waseda, Y.; Hirata, K.; Ohtani, M. High-temperature thermal expansion of platinum, tantalum, molybdenum, and tungsten measured by x-ray diffraction. High Temp.-High Press. 1975, 7, 221–226. [Google Scholar]
- Wolfschmidt, H.; Baier, C.; Gsell, S.; Fischer, M.; Schreck, M.; Stimming, U. STM, SECPM, AFM and Electrochemistry on Single Crystalline Surfaces. Materials 2010, 3, 4196–4213. [Google Scholar] [CrossRef] [PubMed]
- Kesmodel, L.L.; Somorjai, G.A. Structure determination of the platinum (111) crystal face by low-energy-electron diffraction. Phys. Rev. B 1975, 11, 630–637. [Google Scholar] [CrossRef]
- Adams, D.L.; Nielsen, H.B.; Van Hove, M.A. Quantitative analysis of low-energy-electron diffraction: Application to Pt(111). Phys. Rev. B 1979, 20, 4789–4806. [Google Scholar] [CrossRef]
- Feder, R.; Pleyer, H.; Bauer, P.; Müller, N. Spin polarization in low-energy electron diffraction: Surface analysis of Pt(111). Surf. Sci. 1981, 109, 419–434. [Google Scholar] [CrossRef]
- Hayek, K.; Glassl, H.; Gutmann, A.; Leonhard, H.; Prutton, M.; Tear, S.P.; Welton-Cook, M.R. A LEED analysis of the structure of Pt(111)(3 × 3) R30°-S. Surf. Sci. 1985, 152–153, 419–425. [Google Scholar] [CrossRef]
- Ogletree, D.F.; Van Hove, M.A.; Somorjai, G.A. LEED intensity analysis of the structures of clean Pt(111) and of CO adsorbed on Pt(111) in the c(4 × 2) arrangement. Surf. Sci. 1986, 173, 351–365. [Google Scholar] [CrossRef]
- Materer, N.; Starke, U.; Barbieri, A.; Döll, R.; Heinz, K.; Van Hove, M.A.; Somorjai, G.A. Reliability of detailed LEED structural analyses: Pt(111) and Pt(111)-p(2 × 2)-O. Surf. Sci. 1995, 325, 207–222. [Google Scholar] [CrossRef]
- Felici, R.; Pedio, M.; Borgatti, F.; Iannotta, S.; Capozi, M.; Ciullo, G.; Stierle, A. X-ray-diffraction characterization of Pt(111) surface nanopatterning induced by C60 adsorption. Nat. Mater. 2005, 4, 688–692. [Google Scholar] [CrossRef]
- Singh-Miller, N.E.; Marzari, N. Surface energies, work functions, and surface relaxations of low-index metallic surfaces from first principles. Phys. Rev. B 2009, 80, 235407. [Google Scholar] [CrossRef]
- Zólyomi, V.; Vitos, L.; Kwon, S.K.; Kollár, J. Surface relaxation and stress for 5d transition metals. J. Phys. Condens. Matter 2009, 21, 095007. [Google Scholar] [CrossRef]
- Dal Corso, A. Clean Ir(111) and Pt(111) electronic surface states: A first-principle fully relativistic investigation. Surf. Sci. 2015, 637–638, 106–115. [Google Scholar] [CrossRef]
- Baud, S.; Ramseyer, C.; Bihlmayer, G.; Blügel, S.; Barreteau, C.; Desjonquères, M.C.; Spanjaard, D.; Bernstein, N. Comparative study of ab initio and tight-binding electronic structure calculations applied to platinum surfaces. Phys. Rev. B 2004, 70, 235423. [Google Scholar] [CrossRef]
- Da Silva, J.L.; Stampfl, C.; Scheffler, M. Converged properties of clean metal surfaces by all-electron first-principles calculations. Surf. Sci. 2006, 600, 703–715. [Google Scholar] [CrossRef]
- Moré, S.; Berndt, W.; Bradshaw, A.M.; Stumpf, R. Ordered phases of potassium on Pt111: Experiment and theory. Phys. Rev. B 1998, 57, 9246–9254. [Google Scholar] [CrossRef]
- Kesmodel, L.; Stair, P.; Somorjai, G. On the relaxation of the Pt(111) surface: Results of dynamical LEED calculations. Surf. Sci. 1977, 64, 342–344. [Google Scholar] [CrossRef]
- Feibelman, P.J. First-principles calculations of stress induced by gas adsorption on Pt(111). Phys. Rev. B 1997, 56, 2175–2182. [Google Scholar] [CrossRef]
- Nichols, R.J.; Nouar, T.; Lucas, C.A.; Haiss, W.; Hofer, W.A. Surface relaxation and surface stress of Au(111). Surf. Sci. 2002, 513, 263–271. [Google Scholar] [CrossRef]
- Mazzarello, R.; Corso, A.D.; Tosatti, E. Spin-orbit modifications and splittings of deep surface states on clean Au(111). Surf. Sci. 2008, 602, 893–905. [Google Scholar] [CrossRef]
- Drube, R.; Dose, V.; Goldmann, A. Empty electronic states at the (1 × 1) and (5 × 20) surfaces of Pt(100): An inverse photoemission study. Surf. Sci. 1988, 197, 317–326. [Google Scholar] [CrossRef]
- Link, S.; Dürr, H.A.; Bihlmayer, G.; Blügel, S.; Eberhardt, W.; Chulkov, E.V.; Silkin, V.M.; Echenique, P.M. Femtosecond electron dynamics of image-potential states on clean and oxygen-covered Pt(111). Phys. Rev. B 2001, 63, 115420. [Google Scholar] [CrossRef]
- Sheverdyaeva, P.M.; Requist, R.; Moras, P.; Mahatha, S.K.; Papagno, M.; Ferrari, L.; Tosatti, E.; Carbone, C. Energy-momentum mapping of d-derived Au(111) states in a thin film. Phys. Rev. B 2016, 93, 035113. [Google Scholar] [CrossRef]
- Edelstein, V. Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems. Solid State Commun. 1990, 73, 233–235. [Google Scholar] [CrossRef]
- Tokatly, I.V.; Krasovskii, E.E.; Vignale, G. Current-induced spin polarization at the surface of metallic films: A theorem and an ab initio calculation. Phys. Rev. B 2015, 91, 035403. [Google Scholar] [CrossRef]
- Feng, Y.P.; Shen, L.; Yang, M.; Wang, A.; Zeng, M.; Wu, Q.; Chintalapati, S.; Chang, C.R. Prospects of spintronics based on 2D materials. WIREs Comp. Mol. Sci. 2017, 7, e1313. [Google Scholar] [CrossRef]
- Bergman, D.J.; Stockman, M.I. Surface Plasmon Amplification by Stimulated Emission of Radiation: Quantum Generation of Coherent Surface Plasmons in Nanosystems. Phys. Rev. Lett. 2003, 90, 027402. [Google Scholar] [CrossRef]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef]
- Silkin, V.M.; García-Lekue, A.; Pitarke, J.M.; Chulkov, E.V.; Zaremba, E.; Echenique, P.M. Novel low-energy collective excitation at metal surfaces. Europhys. Lett. 2004, 66, 260–264. [Google Scholar] [CrossRef]
- Diaconescu, B.; Pohl, K.; Vattuone, L.; Savio, L.; Hofmann, P.; Silkin, V.M.; Pitarke, J.M.; Chulkov, E.V.; Echenique, P.M.; Farías, D.; et al. Low-energy acoustic plasmons at metal surfaces. Nature 2007, 448, 57–59. [Google Scholar] [CrossRef]
- Ritchie, R.H. Plasma Losses by Fast Electrons in Thin Films. Phys. Rev. 1957, 106, 874–881. [Google Scholar] [CrossRef]
- Maier, S.A.; Atwater, H.A. Plasmonics: Localization and guiding of electromagnetic energy in metal/dielectric structures. J. Appl. Phys. 2005, 98, 011101. [Google Scholar] [CrossRef]
- Pitarke, J.M.; Silkin, V.M.; Chulkov, E.V.; Echenique, P.M. Theory of surface plasmons and surface-plasmon polaritons. Rep. Prog. Phys. 2007, 70, 1–87. [Google Scholar] [CrossRef]
- Park, S.J.; Palmer, R.E. Acoustic Plasmon on the Au(111) Surface. Phys. Rev. Lett. 2010, 105, 016801. [Google Scholar] [CrossRef] [PubMed]
- Vattuone, L.; Smerieri, M.; Langer, T.; Tegenkamp, C.; Pfnür, H.; Silkin, V.M.; Chulkov, E.V.; Echenique, P.M.; Rocca, M. Correlated Motion of Electrons on the Au(111) Surface: Anomalous Acoustic Surface-Plasmon Dispersion and Single-Particle Excitations. Phys. Rev. Lett. 2013, 110, 127405. [Google Scholar] [CrossRef] [PubMed]
- Pischel, J.; Welsch, E.; Skibbe, O.; Pucci, A. Acoustic Surface Plasmon on Cu(111) as an Excitation in the Mid-Infrared Range. J. Phys. Chem. C 2013, 117, 26964–26968. [Google Scholar] [CrossRef]
- Despoja, V.; Novko, D.; Lončarić, I.; Golenić, N.; Marušić, L.; Silkin, V.M. Strong acoustic plasmons in chemically doped graphene induced by a nearby metal surface. Phys. Rev. B 2019, 100, 195401. [Google Scholar] [CrossRef]
- Jakovac, J.; Marušić, L.; Andrade-Guevara, D.; Chacón-Torres, J.C.; Despoja, V. Infra-Red Active Dirac Plasmon Serie in Potassium Doped-Graphene (KC8) Nanoribbons Array on Al2O3 Substrate. Materials 2021, 14, 4256. [Google Scholar] [CrossRef] [PubMed]
- Marušić, L.; Kalinić, A.; Radović, I.; Jakovac, J.; Mišković, Z.L.; Despoja, V. Resolving the Mechanism of Acoustic Plasmon Instability in Graphene Doped by Alkali Metals. Int. J. Mol. Sci. 2022, 23, 4770. [Google Scholar] [CrossRef] [PubMed]
- Schulte, F. A theory of thin metal films: Electron density, potentials and work function. Surf. Sci. 1976, 55, 427–444. [Google Scholar] [CrossRef]
- Collins, D.M.; Spicer, W.E. The adsorption of CO, O2, and H2 on Pt: II. Ultraviolet photoelectron spectroscopy studies. Surf. Sci. 1977, 69, 114–132. [Google Scholar] [CrossRef]
- Michaelson, H.B. The work function of the elements and its periodicity. J. Appl. Phys. 1977, 48, 4729–4733. [Google Scholar] [CrossRef]
- Nieuwenhuys, B.; Sachtler, W. Crystal face specificity of nitrogen adsorption on a platium field emission tip. Surf. Sci. 1973, 34, 317–336. [Google Scholar] [CrossRef]
- Nieuwenhuys, B.E.; Meijer, D.T.; Sachtler, W.H.M. Adsorption of Xenon on platinum studied by field emission microscopy. Phys. Status Solidi (A) 1974, 24, 115–122. [Google Scholar] [CrossRef]
- Hulse, J.; Küppers, J.; Wandelt, K.; Ertl, G. UV-photoelectron spectroscopy from xenon adsorbed on heterogeneous metal surfaces. Appl. Surf. Sci. 1980, 6, 453–463. [Google Scholar] [CrossRef]
- Fisher, G.B. The electronic structure of two forms of molecular ammonia adsorbed on Pt(111). Chem. Phys. Lett. 1981, 79, 452–458. [Google Scholar] [CrossRef]
- Derry, G.N.; Ji-Zhong, Z. Work function of Pt(111). Phys. Rev. B 1989, 39, 1940–1941. [Google Scholar] [CrossRef] [PubMed]
- Reuß, C.; Wallauer, W.; Fauster, T. Image states of Ag on Au(111). Surf. Rev. Lett. 1996, 03, 1547–1554. [Google Scholar] [CrossRef]
- Andreev, T.; Barke, I.; Hövel, H. Adsorbed rare-gas layers on Au(111): Shift of the Shockley surface state studied with ultraviolet photoelectron spectroscopy and scanning tunneling spectroscopy. Phys. Rev. B 2004, 70, 205426. [Google Scholar] [CrossRef]
- Otálvaro, D.; Veening, T.; Brocks, G. Self-Assembled Monolayer Induced Au(111) and Ag(111) Reconstructions: Work Functions and Interface Dipole Formation. J. Phys. Chem. C 2012, 116, 7826–7837. [Google Scholar] [CrossRef]
- Gossenberger, F.; Roman, T.; Forster-Tonigold, K.; Groß, A. Change of the work function of platinum electrodes induced by halide adsorption. Beilstein J. Nanotechnol. 2014, 5, 152–161. [Google Scholar] [CrossRef]
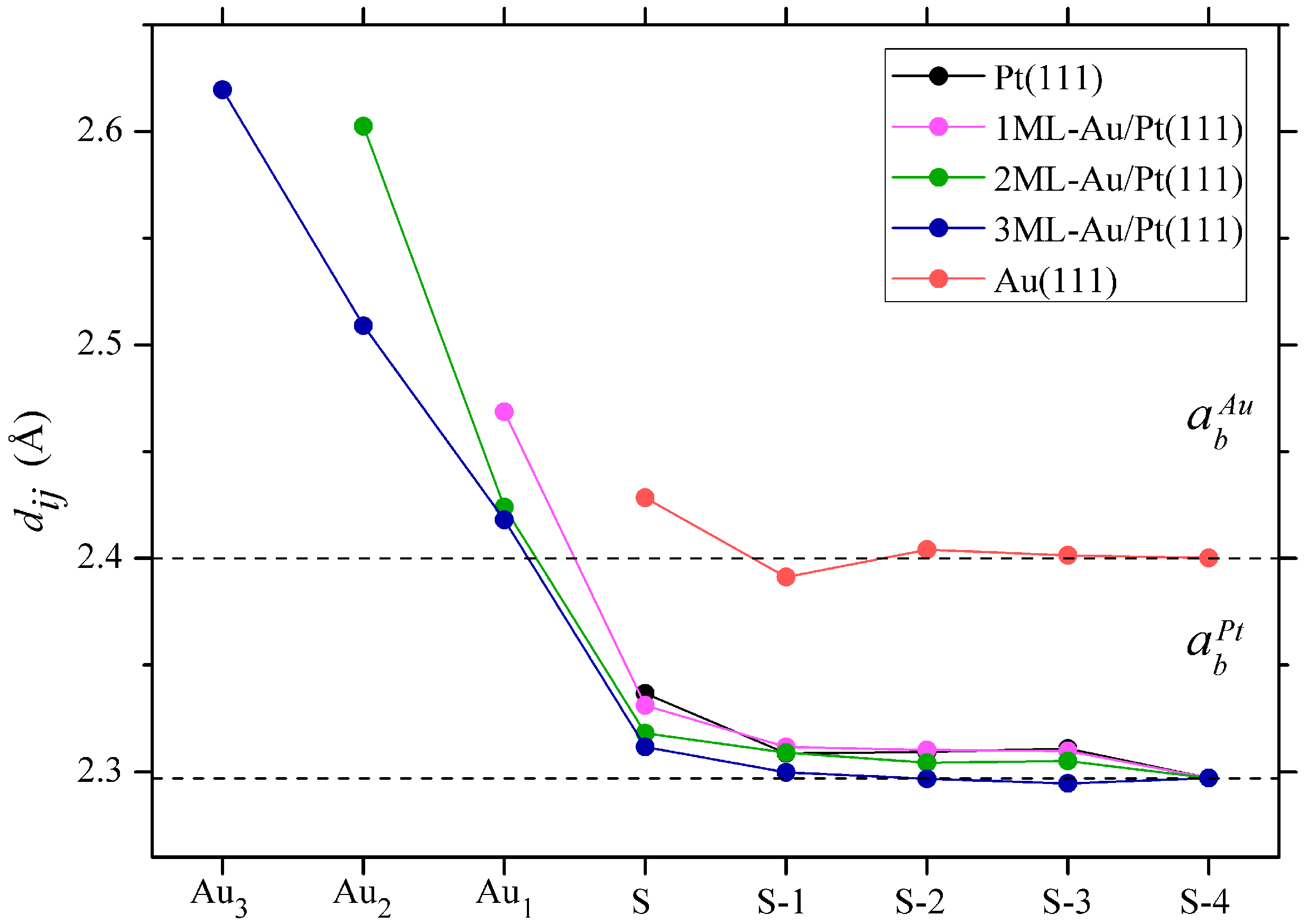


| - | Pt(111) | 1ML-Au/Pt(111) | 2ML-Au/Pt(111) | 3ML-Au/Pt(111) | ||||
|---|---|---|---|---|---|---|---|---|
| (Å) | (%) | (Å) | (%) | (Å) | (%) | (Å) | (%) | |
| Au-Au | − | − | − | − | − | − | 2.620 | 9.15 |
| Au-Au | − | − | − | − | 2.602 | 8.40 | 2.509 | 4.53 |
| Au-Pt | − | − | 2.469 | 5.12 | 2.424 | 3.21 | 2.418 | 2.95 |
| Pt-Pt | 2.337 | 1.72 | 2.331 | 1.47 | 2.318 | 0.91 | 2.312 | 0.63 |
| Pt-Pt | 2.309 | 0.50 | 2.312 | 0.63 | 2.309 | 0.52 | 2.300 | 0.11 |
| Pt-Pt | 2.309 | 0.53 | 2.310 | 0.57 | 2.304 | 0.31 | 2.297 | −0.02 |
| Pt-Pt | 2.311 | 0.60 | 2.310 | 0.55 | 2.305 | 0.35 | 2.295 | −0.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koroteev, Y.M.; Silkin, I.V.; Silkin, V.M.; Chulkov, E.V. Quantum-Size Effects in Ultra-Thin Gold Films on Pt(111) Surface. Materials 2024, 17, 63. https://doi.org/10.3390/ma17010063
Koroteev YM, Silkin IV, Silkin VM, Chulkov EV. Quantum-Size Effects in Ultra-Thin Gold Films on Pt(111) Surface. Materials. 2024; 17(1):63. https://doi.org/10.3390/ma17010063
Chicago/Turabian StyleKoroteev, Yury M., Igor V. Silkin, Vyacheslav M. Silkin, and Evgueni V. Chulkov. 2024. "Quantum-Size Effects in Ultra-Thin Gold Films on Pt(111) Surface" Materials 17, no. 1: 63. https://doi.org/10.3390/ma17010063
APA StyleKoroteev, Y. M., Silkin, I. V., Silkin, V. M., & Chulkov, E. V. (2024). Quantum-Size Effects in Ultra-Thin Gold Films on Pt(111) Surface. Materials, 17(1), 63. https://doi.org/10.3390/ma17010063






